Stability and Regularity for Double Wall Carbon Nanotubes Modeled as Timoshenko Beams with Thermoelastic Effects and Intermediate Damping

The discovery of structures called carbon nanotubes (CNTs) occurred in 1987 and later officially disclosed to the scientific community in 1991 [11] as the multi wall carbon nanotubes (MWCNTs); they were discovered experimentally in the search for a molecular structure called Fullerene. Fullerene is a closed carbon structure with a spherical format (geodesic dome) formed by 12 pentagons and 20 hexagons, whose formula is $C_{60}$. Carbon nanotubes are cylindrical macromolecules composed of carbon atoms in a periodic hexagonal array with $sp^{2}$ hybridization, similar to graphite [9]. They are made like rolled sheets of graphene and can be as thick as a single carbon atom. They receive this name due to their tubular morphology in nanometric dimensions ($1nm=10^{-9}m.$). According to Shen and Brozena [24], CNTs are classified in three ways: single wall carbon nanotubes (SWCNTs), double wall carbon nanotubes (DWCNTs) and (MWCNTs), where the concentric cylinders interact with each other through the Van der Walls force, the authors also point out that DWCNTs are an emerging class of carbon nanostructures and represent the simplest way to study the physical effects of coupling between the walls of carbon nanotubes.

The discovery of this new structure at the molecular level contributed in the last decade to the advancement of nanotechnology. In [31] an analysis of the main properties of CNTs was presented, the study confirmed that CNTs have excellent properties; mechanical, electronic and chemical; they are about ten times stronger and six times lighter than steel. They transmit electricity like a superconductor and are excellent transmitters of temperature. Due to their superior electronic and mechanical properties to currently used materials, carbon nanotubes are candidates to be used in products and equipment that require nanoscale structures.

In the future, CNTs should become the base material for nanoelectronics, nanodevices, and nanocomposites. The main problems that have to be overcome for this to happen are the difficult controlled experiments at the nanoscale: the high cost of molecular dynamics simulations and the high time consumption of these simulations. Knowing better the models of continuous mechanics, which are governed by the modeling through the Euler elastic beam model and the Timoshenko beam model used to study the mechanics of linear and nonlinear deformations, should help to make this possible.

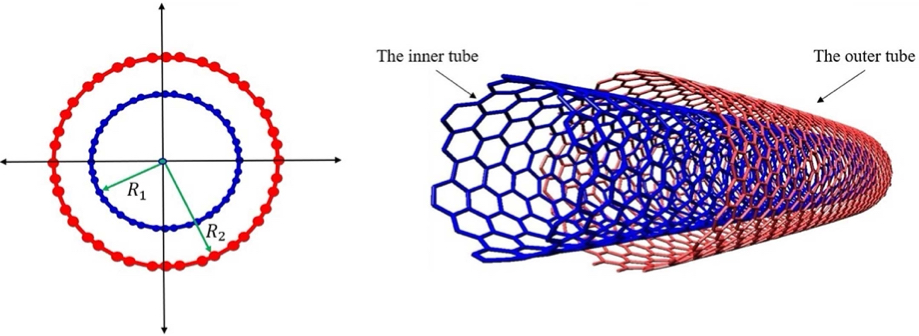
The Euler-Bernoulli beam model disregards the effects of shear and rotation, and according to [30, 31] the vibrations in carbon nanotubes are animated by high frequencies, above $1Thz$. According to Yoon and others [34], the effects of rotational inertia and shear are significant in the study of terahertz frequencies ($10^{12}$), hence Yoon [34] considers questionable the Euler-Bernoulli model applied to (CNTs). Therefore, the Timoshenko Model is the most suitable. For double-walled nanotubes (DWCNTs) or concentric multi-walled nanotubes (MWCNTs), the most used continuous models in the literature assume that all nested tubes of MWCNTs remain coaxial during deformation and thus can be described by a single deflection model. However, this model cannot be used to describe the relative vibration between adjacent tubes of MWCNTs. In 2003, it was proposed by [31] that the fittings of concentric tubes are considered as individual beams, and that the deflections of all nested tubes are coupled through the van der Waals interaction force between two adjacent tubes [3, 4]. So, each of the inner and outer tubes is modeled as a beam.

In the pioneering work on the carbon nanotube model by Yoon et al. [33], the authors proposed a coupled system of partial differential equations inspired by the Timoshenko beam model to model DWCNTs. The model consists of the following equations

	$\displaystyle\rho A_{1}\dfrac{\partial^{2}Y_{1}}{\partial t^{2}}-\kappa GA_{1}\bigg{(}\dfrac{\partial^{2}Y_{1}}{\partial x^{2}}-\dfrac{\partial\varphi_{1}}{\partial x}\bigg{)}-P$	$\displaystyle=$	$\displaystyle 0,$
	$\displaystyle\rho I_{1}\dfrac{\partial^{2}\varphi_{1}}{\partial t^{2}}-EI_{1}\dfrac{\partial^{2}\varphi_{1}}{\partial x^{2}}-\kappa GA_{1}\bigg{(}\dfrac{\partial Y_{1}}{\partial x}-\varphi_{1}\bigg{)}$	$\displaystyle=$	$\displaystyle 0,$
	$\displaystyle\rho A_{2}\dfrac{\partial^{2}Y_{2}}{\partial t^{2}}-\kappa GA_{2}\bigg{(}\dfrac{\partial^{2}Y_{2}}{\partial x^{2}}-\dfrac{\partial\varphi_{2}}{\partial x}\bigg{)}+P$	$\displaystyle=$	$\displaystyle 0,$
	$\displaystyle\rho I_{2}\dfrac{\partial^{2}\varphi_{2}}{\partial t^{2}}-EI_{2}\dfrac{\partial^{2}\varphi_{2}}{\partial x^{2}}-\kappa GA_{2}\bigg{(}\dfrac{\partial Y_{2}}{\partial x}-\varphi_{2}\bigg{)}$	$\displaystyle=$	$\displaystyle 0.$

Where $Y_{i}$ and $\varphi_{i}$ ($i=1,2$) represent respectively the total deflection and the inclination due to the bending of the nanotube $i$ and the constants $I_{i}$, $A_{i}$ denote the moment of inertia and the cross-sectional area of the tube $i$, respectively, and $P$ is the Van der Waals force acting on the interaction between the two tubes per unit of axial length. Also according to [33], it can be seen that the deflections of the two tubes are coupled through the Van der Waals interaction $P$ (see [29]) between the two tubes, and as the tubes inside and outside of a DWCNTs are originally concentric, the Van der Waals interaction is determined by the spacing between the layers. Therefore, for a small-amplitude linear vibration, the interaction pressure at any point between the two tubes linearly depends on the difference in their deflection curves at that point, that is, it depends on the term

$$P=\jmath(Y_{2}-Y_{1}).$$

(1)

In particular, the Van der Waals interaction coefficient $\jmath$ for the interaction pressure per unit axial length can be estimated based on an effective interaction width of the tubes as found in [32, 21]. Thus, this model treats each of the nested and concentric nanotubes as individual Timoshenko beams interacting in the presence of Van der Waals forces (see Figure: (3)).

Currently in the literature there are few investigations related to the study of asymptotic behavior and/or regularity for DWCNTs models, or for DWCNTs systems coupled with the heat equation governed by Fourier’s law (DWCNTs-Fourier). The DWCNTs model was studied in 2015 in the thesis [17], where the author studied the asymptotic behavior of the model:

	$\displaystyle\rho_{1}\varphi_{tt}-\kappa_{1}(\varphi_{x}-\psi)_{x}-\jmath(y-\varphi)+\alpha_{0}\varphi_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(2)
	$\displaystyle\rho_{2}\psi_{tt}-b_{1}\psi_{xx}-\kappa_{1}(\varphi_{x}-\psi)+\alpha_{1}\psi_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(3)
	$\displaystyle\rho_{3}y_{tt}-\kappa_{2}(y_{x}-z)_{x}+\jmath(y-\varphi)+\alpha_{2}y_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(4)
	$\displaystyle\rho_{4}z_{tt}-b_{2}z_{xx}-\kappa_{2}(y_{x}-z)+\alpha_{3}z_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(5)

with the initial conditions

	$\displaystyle\varphi(x,0)=\varphi_{0}(x),\quad\varphi_{t}(x,0)=\varphi_{1}(x),\quad\psi(x,0)=\psi_{0}(x),\quad\psi_{t}(x,0)=\phi_{1}(x)$	$\displaystyle{\rm in}\quad x\in(0,l),$			(6)
	$\displaystyle y(x,0)=y_{0}(x),\quad y_{t}(x,0)=y_{1}(x),\quad z(x,0)=z_{0}(x),\quad z_{t}(x,0)=z_{1}(x)$	$\displaystyle{\rm in}\quad x\in(0,l),$			(7)

and subject to boundary conditions

	$\displaystyle\varphi(0,t)=\varphi(l,t)=\psi(0,t)=\psi(l,t)=0\quad{\rm for\quad all}\quad t>0,$		(8)
	$\displaystyle y(0,t)=y(l,t)=z(0,t)=z(l,t)=0\quad{\rm for\quad all}\quad t>0.$		(9)

For the case that $\alpha_{0}=0$ and $\alpha_{i}>0$, for $i=1,2,3$, in [17] the author demonstrated the lack of exponential decay of the semigroup $(S(t))_{t\geq 0}$ associated with the system (2)–(9), when $\frac{\rho_{1}}{\kappa_{1}}\not=\frac{\rho_{2}}{b_{1}}$ and $\jmath\big{(}\frac{\rho_{2}}{b_{1}}-\frac{\rho_{1}}{\kappa_{1}}\big{)}\not=\frac{\kappa_{1}}{b_{1}}$, and also proved that if $\chi=\frac{\kappa_{1}\rho_{2}-b_{1}\rho_{1}}{\kappa_{1}^{2}-\jmath\rho_{2}\kappa_{1}+\jmath b_{1}\rho_{1}}=0$, then $(S(t))_{t\geq 0}$ is exponentially stable, and if $\chi\not=0$, $(S(t))_{t\geq 0}$ is exponentially stable. Beyond, is proved that if $\chi\not=0$, then $(S(t))_{t\geq 0}$ is polynomially stable with optimal rate $o(t^{-\frac{1}{2}})$. In addition, in Chapter 4 of [17], the author validates through numerical analysis, using the finite difference method, the results previously demonstrated, and in addition to presenting graphs of other cases, such as considering $\alpha_{i}=0$ and $\alpha_{i}>0$ for $i=1,2,3,4$.

Recently, in 2023, two new investigations emerged: One of them is the DWCNTs-Fourier system with friction dampers, see [20]; in this work the authors consider the problem of heat conduction in carbon nanotubes modeled as Timoshenko beams, inspired by the work of Yoon et al. [Comp. Part B: Ing. 35 (2004) 87–93]. The system is given by

	$\displaystyle\rho_{1}\varphi_{tt}-\kappa_{1}(\varphi_{x}-\psi)_{x}-\jmath(y-\varphi)+\gamma_{1}\varphi_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(10)
	$\displaystyle\rho_{2}\psi_{tt}-b_{1}\psi_{xx}-\kappa_{1}(\varphi_{x}-\psi)+\delta\theta_{xx}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(11)
	$\displaystyle\rho_{3}y_{tt}-\kappa_{2}(y_{x}-z)_{x}+\jmath(y-\varphi)+\gamma_{2}y_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(12)
	$\displaystyle\rho_{4}z_{tt}-b_{2}z_{xx}-\kappa_{2}(y_{x}-z)+\gamma_{3}z_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(13)
	$\displaystyle\rho_{5}\theta_{t}-K\theta_{xx}+\beta\psi_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(14)

subject to boundary conditions (8), (9) and

$$\theta(0,t)=\theta(l,t)=0\qquad\text{ for all}\quad t>0.$$

(15)

Note that the system (8)–(15) presents three friction dissipators (weak damping): $\gamma_{1}\varphi_{t},\gamma_{2}y_{t}$ and $\gamma_{3}z_{t}$. The authors apply semigroup theory of linear operators to demonstrate the exponential stabilization of the semigroup $S(t)$ associated with the system (8)–(15), and their results are independent of the relationship between the coefficients. Furthermore, they analyze the totally discrete problem using a finite difference scheme, introduced by a space-time discretization that combines explicit and implicit integration methods. The authors also show the construction of numerical energy and simulations that validate the theoretical results of exponential decay and convergence rates.

By the year of 2023, [22] investigated the one-dimensional equations for the double wall carbon nanotubes modeled by coupled Timoshenko elastic beam system with nonlinear arbitrary localized damping:

	$\displaystyle\rho_{1}\varphi_{tt}-\kappa_{1}(\varphi_{x}-\psi)_{x}-\jmath(y-\varphi)+\alpha_{1}(x)g_{1}(\varphi_{t})=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(16)
	$\displaystyle\rho_{2}\psi_{tt}-b_{1}\psi_{xx}-\kappa_{1}(\varphi_{x}-\psi)+\alpha_{2}(x)g_{2}(\psi_{t})=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(17)
	$\displaystyle\rho_{3}y_{tt}-\kappa_{2}(y_{x}-z)_{x}+\jmath(y-\varphi)+\alpha_{3}(x)g_{3}(y_{t})=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(18)
	$\displaystyle\rho_{4}z_{tt}-b_{2}z_{xx}-\kappa_{2}(y_{x}-z)+\alpha_{4}(x)g_{4}(z_{t})=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(19)

where the localizing functions $\alpha_{i}(x)$ are supposed to be smooth and nonnegative, while the nonli-near functions $g_{i}(x),i=1,\cdots,4$, are continuous and monotonic increasing. The system (16)–(19) is subject to Dirichlet boundary conditions; in (8) and (9), see [22], the authors showed that damping placed on an arbitrary small support, not quantized at the origin, leads to uniform (time asymptotic) decay rates for the energy function of the system.

In the same direction of this last paper, we would like to mention the work of Shubov and Rojas-Arenaza [27] where they considered the system (16)-(19) with $\alpha_{i}(x)=1,g_{i}(s)=s,i=1,\cdots,4$, initial conditions (6)-(7). Subject to boundary conditions of type:

$$\left\{\begin{array}[]{cc}\kappa_{1}(\varphi_{x}-\psi)(l,t)=-\rho_{2}\gamma_{1}\varphi_{t}(l,t)&t\geq 0,\\ b_{1}\psi_{x}(l,t)=-\rho_{2}\gamma_{2}\psi_{t}(l,t),&t\geq 0,\\ \kappa_{2}(y_{x}-z)(l,t)=\rho_{4}\gamma_{3}y_{t}(l,t),&t\geq 0,\\ b_{2}z_{x}(l,t)=-\rho_{4}\gamma_{4}z_{t}(l,t),&t\geq 0.\end{array}\right.$$

(20)

They first proved that the energy associated to the system, with boundary conditions (20), is decreasing if $\jmath=0$. After they proved that the semigroup generator is an unbounded non self-adjoint operator with a compact resolvent.

The two systems that we study in this research are for models of carbon nanotubes coupled with the heat equation given by Fourier’s Law. The difference between these two systems is in the coupling of the DWCNTs model and the heat equation. The first system is a generalization of the model presented in [20]: we consider the 3 fractional damping; $\gamma_{1}(-\partial_{xx})^{\tau_{1}}\varphi_{t}$, $\gamma_{2}(-\partial_{xx})^{\tau_{2}}y_{t}$ and $\gamma_{3}(-\partial_{xx})^{\tau_{3}}z_{t}$, for the parameters $\tau_{i},i=1,2,3$, varying in the interval $[0,1]$. We note that when $(\tau_{1},\tau_{2},\tau_{3})=(0,0,0)$ the system is the one studied in [20]. The second system studied in this work is given by:

	$\displaystyle\rho_{1}\varphi_{tt}-\kappa_{1}(\varphi_{x}-\psi)_{x}-\jmath(y-\varphi)+\gamma_{1}(-\partial_{xx})^{\beta_{1}}\varphi_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(21)
	$\displaystyle\rho_{2}\psi_{tt}-b_{1}\psi_{xx}-\kappa_{1}(\varphi_{x}-\psi)+\delta\theta_{xx}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(22)
	$\displaystyle\rho_{3}y_{tt}-\kappa_{2}(y_{x}-z)_{x}+\jmath(y-\varphi)+\gamma_{2}(-\partial_{xx})^{\beta_{2}}y_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(23)
	$\displaystyle\rho_{4}z_{tt}-b_{2}z_{xx}-\kappa_{2}(y_{x}-z)+\gamma_{3}(-\partial_{xx})^{\beta_{3}}z_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(24)
	$\displaystyle\rho_{5}\theta_{t}-K\theta_{xx}-\delta\psi_{xxt}=0\quad{\rm in}\quad(0,l)\times(0,\infty).$		(25)

We study the system (21)–(25) subject to boundary conditions

	$\displaystyle\varphi(0,t)=\varphi(l,t)=\psi(0,t)=\psi(l,t)=0\quad{\rm for\quad all}\quad t>0,$		(26)
	$\displaystyle y(0,t)=y(l,t)=z(0,t)=z(l,t)=0\quad{\rm for\quad all}\quad t>0,$		(27)
	$\displaystyle\theta(0,t)=\theta(l,t)=0\quad{\rm for\quad all}\quad t>0.$		(28)

And the initial conditions are given by

	$\displaystyle\varphi(x,0)=\varphi_{0}(x),\;\varphi_{t}(x,0)=\varphi_{1}(x),\;\psi(x,0)=\psi_{0}(x),\quad{\rm for}\;x\in(0,l),$		(29)
	$\displaystyle\psi_{t}(x,0)=\psi_{1}(x),\;y(x,0)=y_{0}(x),\;y_{t}(x,0)=y_{1}(x),\quad{\rm for}\;x\in(0,l),$		(30)
	$\displaystyle z(x,0)=z_{0}(x),\;z_{t}(x,0)=z_{1}(x),\;\theta(x,0)=\theta_{0}(x),\quad{\rm for}\;x\in(0,l).$		(31)

Note that the difference between these systems is in the coupling term in the heat equation. For the first system, the coupling is $\beta\psi_{t}$, which presents a derivative of zero order with respect to the spatial variable. In the second system, the coupling term is given by $\delta\psi_{txx}$, which presents a second order derivative with respect to spatial variable $x$. The coupling considered by the second system is the most common, this type of coupling is known as strong coupling. In our research it helps to show the existence of Gevrey classes and also to demonstrate the analyticity of the associated $S_{2}(t)$ semigroup to the second system. During the development of this investigation, we were able to observe that the zero order of the derivative in relation to the space of the coupling term for the first system was decisive for not obtaining the estimates: $|\lambda|^{\phi}\|v\|^{2}\leq C\|F\|_{\mathbb{H}_{1}}\|U\|_{\mathbb{H}_{1}}$ and $|\lambda|^{\phi}\|A^{\frac{1}{2}}\psi\|^{2}\leq C\|F\|_{\mathbb{H}_{1}}\|U\|_{\mathbb{H}_{1}}$ for $0<\phi\leq 1$, which made it impossible to obtain regularity results of the first system.

During the last decades, various investigations focused on the study of the asymptotic behavior and regularity of the Tymoshenko beam system, thermoviscoelastic Timoshenko system with diffusion effect and also of Timoshenko beam systems coupled with heat equations from Fourier’s law, Cateneo’s and thermoelasticity of type III. Results of exponential decay and regularity for these systems are mostly provided with dissipative terms, at least in the equations that do not refer to heat or do not have heat coupling terms. We will cite some of these works below.

In 2005, Raposo et al.[19] studies the Timoshenko system, provided for two frictional dissipations $\varphi_{t}$ and $\psi_{t}$, and proves that the semigroup associated with the system decays exponentially. For the same Timoshenko system, when the stress-strain constitutive law is of Kelvin-Voigt type, given by

$$S=\kappa(\varphi_{x}+\psi)+\gamma_{1}(\varphi_{x}+\psi)_{t}\qquad\text{and}\qquad M=b\psi_{x}+\psi_{xt},$$

Malacarne A. and Rivera J. in [14] shows that $S(t)$ is analytical if and only if the viscoelastic damping is present in both the shear stress and the bending moment. Otherwise, the corresponding semigroup is not exponentially stable no matter the choice of the coefficients. They also showed that the solution decays polynomially to zero as $t^{-1/2}$, no matter where the viscoelastic mechanism is effective and that the rate is optimal whenever the initial data are taken on the domain of the infinitesimal operator. In 2023, Suárez [26] studied the regularity of the model given in [19], substituting the two damping weaks $\varphi_{t}$ and $\psi_{t}$, for fractional dampings $(-\partial_{xx})^{\tau}\varphi_{t}$ and $(-\partial_{xx})^{\sigma}\psi_{t}$ where the parameters $(\tau,\sigma)\in[0,1]$, and proved the existence of Gevrey classes $s>\frac{r+1}{2r}$, for $r=\min\{\tau,\sigma\},\quad\forall(\tau,\sigma)\in(0,1)^{2}$, of the semigroup $S(t)$ associated to the system, and analyticity of $S(t)$ when the two parameters $\tau$ and $\sigma$ vary in the interval $[1/2,1]$.

In 2021, M. Elhindi and T. EL Arwadi [7] studied the Timoshenko beam model with thermal, mass diffusion and viscoelastic effects:

$$\left\{\begin{array}[]{l}\rho_{1}\varphi_{tt}-\kappa(\varphi_{x}-\psi)_{x}-\gamma_{1}(\varphi_{x}+\psi)_{xt}=0,\\ \rho_{2}\psi_{tt}-\alpha\psi_{xx}-\gamma_{2}\psi_{xxt}+\kappa(\varphi_{x}+\psi)+\gamma_{1}(\varphi_{x}+\psi)_{t}-\xi_{1}\theta_{x}-\xi_{2}P_{x}=0,\\ c\theta_{t}+dP_{t}-\kappa\theta_{xx}-\xi_{1}\psi_{tx}=0,\\ d\theta_{t}+rP_{t}-hP_{xx}-\xi_{2}\psi_{tx}=0.\end{array}\right.$$

(32)

Using semigroup theory, they proved that the considered problem is well posed with the Dirichlet boundary conditions. An exponential decay is obtained by constructing the Lyapunov functional. Finally, a numerical study based on the $P_{1}-$finite element approximation for spatial discretization and implicit Euler scheme for temporal discretization is carried out, where the stability of the scheme is studied, as well as error analysis and some numerical simulations are obtained. By the year of 2023, Mendes et al. in [15], present the study of the regularity of two thermoelastic beam systems defined by the Timoshenko beam model coupled with the heat conduction of Green-Naghdiy theory of type III; both mathematical models are differentiated by their coupling terms that arise as a consequence of the constitutive laws initially considered. The systems presented in this work have 3 fractional dampings: $(-\partial_{xx})^{\tau}\phi_{t},(-\partial_{xx})^{\sigma}\psi_{t}$ and $(-\partial_{xx})^{\xi}\theta_{t}$, where $\phi,\psi$ and $\theta$ are: transverse displacement, rotation angle and empirical temperature of the beam respectively and the parameters $(\tau,\sigma,\xi)\in[0,1]^{3}$.

The main contribution of this article is to show that the corresponding semigroup $S_{i}(t)=e^{\mathcal{B}_{i}t}$, with $i=1,2$, is of Gevrey class $s>(r+1)/(2r)$ for $r=\min\{\tau,\sigma,\xi\}\;\forall(\tau,\sigma,\xi)\in(0,1)^{3}$. It is also showed that $S_{1}(t)=e^{\mathcal{B}_{1}t}$ is analytic in the region $RA_{1}:=\{(\tau,\sigma,\xi)\in[1/2,1]^{3}\}$ and $S_{2}(t)=e^{\mathcal{B}_{2}t}$ is analytic in the region $RA_{2}:=\{(\tau,\sigma,\xi)\in[1/2,1]^{3}/\tau=\xi\}$. Some articles published in the last decade that study the asymptotic behavior and regularity of coupled systems and/or fractional dissipations can be consulted at [1, 5, 10, 16, 23].

The paper is organized as follows. In section 2, we study the well-posedness and exponential decay of the system (33)-(43) through semigroup theory. In section 3, we study the well-posedness, exponential decay, existence of Gevrey classes and analyticity of the system (80)–(84) with initial conditions (29)–(31), for all the results we use again the semigroup theory, the good properties of fractional operator $A^{r}:=(-\partial_{xx})^{r}$ for $r\in\mathbb{R}$, a proper decomposition of the functions $u,s,w$ and the Interpolation Theorem 16.

In this section we present the study of the well-posedness and the exponential decay of the first system, for both results the semigroup theory is used, the first system is given by:

	$\displaystyle\rho_{1}\varphi_{tt}-\kappa_{1}(\varphi_{x}-\psi)_{x}-\jmath(y-\varphi)+\gamma_{1}(-\partial_{xx})^{\tau_{1}}\varphi_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(33)
	$\displaystyle\rho_{2}\psi_{tt}-b_{1}\psi_{xx}-\kappa_{1}(\varphi_{x}-\psi)+\delta\theta_{xx}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(34)
	$\displaystyle\rho_{3}y_{tt}-\kappa_{2}(y_{x}-z)_{x}+\jmath(y-\varphi)+\gamma_{2}(-\partial_{xx})^{\tau_{2}}y_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(35)
	$\displaystyle\rho_{4}z_{tt}-b_{2}z_{xx}-\kappa_{2}(y_{x}-z)+\gamma_{3}(-\partial_{xx})^{\tau_{3}}z_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(36)
	$\displaystyle\rho_{5}\theta_{t}-K\theta_{xx}+\beta\psi_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(37)

subject to boundary conditions

	$\displaystyle\varphi(0,t)=\varphi(l,t)=\psi(0,t)=\psi(l,t)=0\quad{\rm for\quad all}\quad t>0,$		(38)
	$\displaystyle y(0,t)=y(l,t)=z(0,t)=z(l,t)=0\quad{\rm for\quad all}\quad t>0,$		(39)
	$\displaystyle\theta(0,t)=\theta(l,t)=0\quad{\rm for\quad all}\quad t>0.$		(40)

And the initial conditions are given by

	$\displaystyle\varphi(x,0)=\varphi_{0}(x),\;\varphi_{t}(x,0)=\varphi_{1}(x),\;\psi(x,0)=\psi_{0}(x),\quad{\rm for}\;x\in(0,l),$		(41)
	$\displaystyle\psi_{t}(x,0)=\psi_{1}(x),\;y(x,0)=y_{0}(x),\;y_{t}(x,0)=y_{1}(x),\quad{\rm for}\;x\in(0,l),$		(42)
	$\displaystyle z(x,0)=z_{0}(x),\;z_{t}(x,0)=z_{1}(x),\;\theta(x,0)=\theta_{0}(x),\quad{\rm for}\;x\in(0,l).$		(43)

Let’s define the operator $A\colon\mathfrak{D}(A)=H^{2}(0,l)\cap H_{0}^{1}(0,l)\to L^{2}(0,l)$, such that $A:=-\partial_{xx}$. Using this operator $A$ the system (33)-(43) can be written in the following setting

	$\displaystyle\rho_{1}\varphi_{tt}+\kappa_{1}A\varphi+\kappa_{1}\psi_{x}-\jmath(y-\varphi)+\gamma_{1}A^{\tau_{1}}\varphi_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(44)
	$\displaystyle\rho_{2}\psi_{tt}+b_{1}A\psi-\kappa_{1}(\varphi_{x}-\psi)-\delta A\theta=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(45)
	$\displaystyle\rho_{3}y_{tt}+\kappa_{2}Ay+\kappa_{2}z_{x}+\jmath(y-\varphi)+\gamma_{2}A^{\tau_{2}}y_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(46)
	$\displaystyle\rho_{4}z_{tt}+b_{2}Az-\kappa_{2}(y_{x}-z)+\gamma_{3}A^{\tau_{3}}z_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(47)
	$\displaystyle\rho_{5}\theta_{t}+KA\theta+\beta\psi_{t}=0\quad{\rm in}\quad(0,l)\times(0,\infty),$		(48)

with the initial conditions (41)–(43).