Spiral-wave dynamics in excitable media: Insights from dynamic mode decomposition
Abstract
Spiral waves are ubiquitous spatiotemporal patterns that occur in various excitable systems. In cardiac tissue, the formation of these spiral waves is associated with life-threatening arrhythmias, and, therefore, it is important to study the dynamics of these waves. Tracking the trajectory of a spiral-wave tip can reveal important dynamical features of a spiral wave, such as its periodicity, and its vulnerability to instabilities. We show how to employ the data-driven spectral-decomposition method, called dynamic mode decomposition (DMD), to detect a spiral tip trajectory (TT) in three settings: (1) a homogeneous medium; (2) a heterogeneous medium; and (3) with external noise. We demonstrate that the performance of DMD-based TT (DMDTT) is either comparable to or better than the conventional tip-tracking method, called the isopotential-intersection method (IIM), in the cases (1)-(3): (1) Both IIM and DMDTT capture TT patterns at small values of the image-sampling interval ; however, IIM is more sensitive than DMDTT to the changes in . (2) In a heterogeneous medium, IIM yields TT patterns, but with a background of scattered noisy points, which are suppressed in DMDTT. (3) DMDTT is more robust to external noise than IIM. We show, finally, that DMD can be used to reconstruct, and hence predict, the spatiotemporal evolution of spiral waves in the models we study.
I Introduction
The spatiotemporal organization of nonlinear waves into spirals occurs in various excitable media [1, 2, 3, 4, 5, 6, 7]. In cardiac tissue, the formation of such spiral waves of electrical activation is associated with life-threatening cardiac arrhythmias [8, 9, 10, 11, 12]. A stable rotating spiral wave is linked to ventricular tachycardia (VT), i.e., rapid heart beats; a spiral wave, with a meandering core, can cause polymorphic VT (with aperiodic heart beats); and a multiple-spiral state is linked to ventricular fibrillation (VF) and chaotic heart beats. These arrhythmias are a leading cause of death. It is, therefore, crucial to understand the dynamics of a spiral wave in cardiac tissue. By tracking the trajectory of the phase singularity at the tip of a spiral wave, we can reveal some of its dynamical features. For example, the tip of a stably rotating spiral wave, with one fundamental frequency, typically traces a circular trajectory; a spiral wave that rotates with two or more incommensurate fundamental frequencies can exhibit complicated tip-trajectory (TT) patterns [13, 14, 15], which can lead to irregular heart rates. Such complicated TTs are prone to instabilities [14] that cause the spiral wave to break up into multiple daughter spiral waves, which lead in turn to a spiral-turbulent state. Therefore, tracking the TT of a spiral wave yields valuable insights into its dynamics; and the detection of phase singularities of spiral waves, in ex-vivo and in-vivo experiments and in in silico studies of mathematical models, is of great importance [16, 17, 18, 12]. In particular, the location of such phase singularities, with high specificity and selectivity, can be employed for accurate ablation, which can help in the termination of life-threatening arrhythmias.
We show that the data-driven spectral-decomposition method known as dynamic mode decomposition (DMD), which has been used to analyze complex spatiotemporal evolution in a variety of spatially extended systems [19, 20, 21, 22, 23, 24, 25], can be used fruitfully in excitable medial (a) to identify spiral-wave TTs and (b) to study the spatiotemporal evolution of spiral waves. Although the DMD method has been used to uncover coherent structures in fluid flows, to the best of our knowledge it has not been used to study nonlinear waves in mathematical models for cardiac tissue. Two studies have applied DMD to spiral waves: one that deals with the extraction of an approximate governing equation for the spiral waves [26]; and the other study that extracts observables that are possible candidates for Koopman operators [22]. Our application of DMD to spiral waves in mathematical models for excitable media and cardiac tissue leads to new insights into spiral-tip trajectories and the prediction of the dynamics of these waves.
We use DMD to investigate the spatiotemporal evolution of spiral waves in two mathematical models for cardiac tissue; and we show that DMD can be used effectively (a) to identify TT patterns and (b) to reconstruct and predict the spatiotemporal evolution of spiral waves by using the DMD eigenmodes. There are conventional methods of tracking TT in in-silico studies, among which the most common is the isopotential-intersection method (IIM) [13]. We compare the versatility of the DMDTT method relative to the IIM technique in three different settings: (1) a homogeneous medium; (2) a heterogeneous medium; and (3) with external noise. We compare the performance of DMD-based TT (DMDTT) with the conventional isopotential intersection method (IIM) [13] and show that the former is either comparable to or better and more versatile than the latter: In case (1), both IIM and DMDTT capture TT patterns at small values of the image-sampling interval ; however, IIM is more sensitive than DMDTT to changes in . In case (2), we find that IIM yields TT patterns, but with a background of scattered noisy points; by contrast, DMDTT does not lead to such noise. In case (3), we show that DMDTT is more robust to external noise than IIM. We show, finally, that DMD can be used to reconstruct, and hence predict, the spatiotemporal evolution of spiral waves in the models we study.


The remainder of our paper is organized as follows. In Section II, on Models and Methods, we describe the mathematical models, numerical schemes, DMD, and the tip tracking IIM that we use in our study. We present the findings of our study in Section III. Finally, in Section IV, we summarize our conclusions and provide a discussion of our results in the light of earlier studies.
II Models and Methods
We begin with a description of the mathematical models we use in Subsection II.1. In Subsection II.2 we present a brief overview of the conventional IIM. We give a short introduction to the DMD methods we use in Subsection II.3.
II.1 Reaction-diffusion models for electrical-excitation waves in cardiac tissue
We use two mathematical models for cardiac tissue to illustrate the application of DMD to the study of spiral waves in excitable media. The first is the set of two-variable coupled partial differential equations (PDEs) called the Barkley model [27]; and the second is the biophysically realistic O’Hara-Rudy (ORd) model [28]. The Barkley-model PDEs are:
| (1) | |||||
| (2) |
and are the fast-excitation and slow-recovery variables, respectively, at the point and time ; the time-scale separation between and is controlled by the value of ; the parameter sets the duration of excitation, and sets the threshold of excitation. is the diffusion constant of the medium (we use ). We solve Eqs. (1) and ( 2) by using the forward-Euler method for time marching and a five-point stencil for the Laplacian. The temporal and spatial resolutions are set to be (arbitrary units ) and .
For our study with inexcitable obstacles in the medium, we use the O’Hara-Rudy (ORd) model [28] for cardiac myocytes. In a homogeneous medium, the ORd model uses the following PDE for the transmembrane potemtial :
| (3) | |||||
here, is the membrane capacitance, the diffusion coefficient (for simplicity, chosen to be a scalar), and the total ionic current is a sum of the following ion-channel currents: the fast inward Na+ current ; the transient outward K+ current ; the L-type Ca2+ current ; the Na+ current through the L-type Ca2+ channel ; the current through the L-type Ca2+ channel ; the rapid delayed rectifier current ; the slow delayed rectifier current ; the inward rectifier current ; the NaCa2+ exchange current ; the NaK+ ATPase current ; the Na+ background current ; the Ca2+ background current ; the K+ background current ; the sarcolemmal Ca2+ pump current ; for a full list of these currents and the equations that govern their evolution we refer the reader to Refs. [28, 29, 30], which also describe the finite-difference numerical methods that we use. In both the models we study, we restrict ourselves to two spatial dimensions and we employ no-flux boundary conditions.
Excitation waves in the Barkley model [Eqs. (1) and ( 2)] have small wavelengths, so they are vulnerable to wavebreaks, especially in the presence of heterogeneities in the medium. In contrast, the ORd model [Eq. (3)] yields waves with large wavelengths; these waves are more stable in heterogeneous media than their Barkley-model counterparts. As our objective is to investigate the detection of the phase singularity of a stable spiral wave, we use the ORd model for our study with a heterogeneous medium; the coupling between cells in the presence of inexcitable obstacles is modelled as in Refs. [31, 30].
II.2 Isopotential intersection method (IIM)
The tracking of the tip of a spiral wave, as described in Ref. [13], is based on the idea that the normal velocity of the spiral wave at its tip is zero. We illustrate this for the Barkley model Eqs. 1-2, in which at the spiral tip. We choose isopotential lines with value ; we then track the intersection point of with at different times, i.e., we record the position , at a given time, where.
| (4) |
The locus of these intersection points gives the spiral TT.
II.3 Dynamic Mode Decomposition (DMD)
The data-driven DMD method employs a linear operator to model the spatiotemporal evolution of fields in a complex, typically nonlinear, system. If represents the vector form of some spatial data (typically an image) at the time instant, then the best estimate of the linear operator that translates to its value , at the next time step, follows from the minimization problem
| (5) |
where represents the -norm, and is the total number of images (spatial data), each one of which is separated from its predecessor and successor by the sampling-time interval . The eigenvalues and eigenvectors of contain useful information about the evolution of the system and can be calculated efficiently by using singular value decomposition [32, 23]. In our analysis we choose such that it is greater than all the macroscopic time-scales (spiral-rotational periods) that are present in our system. We construct a matrix , with column vectors of images at discrete times labelled , and a similar matrix , with column vectors of images at discrete times labelled as follows:
| (6) |
The operator that best fits Eq. (5) is
| (7) |
where is the Moore-Penrose pseudoinverse [33, 34]. By using the DMD algorithm [23], we get the following spectral decomposition:
| (8) |
here, and denote the eigenvalue and eigenmode of , respectively. Depending on whether , , or , the corresponding eigenmode grows, remains constant, or decays, respectively, in time. In Section I of the Supplemental Material [35] we give the SVD-based method that we use to get a low-rank version of and thence the dominant eigenmodes. We refer the reader to [23] for a detailed discussion of DMD.
III Results
We begin with our results for TT via DMD in Subsection III.1. In Subsection III.2 we present our DMDTT results in a heterogeneous-cardiac-tissue model and also in the presence of external noise. We then give a short introduction to how DMD can be used to reconstruct spiral-wave dynamics in Subsection III.3.

III.1 Spiral TT in a homogeneous medium
We characterize spiral-wave dynamics here by spiral-TT patterns and the wave-rotation frequencies. We illustrate this for the Barkley model [Eqs. (1) and ( 2)]. To obtain the frequencies of a spiral wave, we record the time series of , Fig. 1 (B), from a representative point, which is marked by a yellow star in the simulation domain [Fig. 1 (A)]. From the power spectrum of this time series we obtain the most important frequencies, like the frequency of the highest peak in this spectrum. We then use the IIM and DMD methods to obtain the TTs. In the illustrative plots of Fig. 2 we show four different types of TTs, in each one of the panels (A)-(D); the sub-figures in the left columns show the TTs obtained from the IIM; those in the middle columns show, via pseudocolor plots of the modulus of a DMD eigenmode , with eigen value , that contains an imprint of the TT; the right columns show the power spectra . The circular TT in Fig. 2 (A) arises from periodic motion, with a fundamental frequency , which appears clearly in the power spectrum along with its harmonics. The TTs in Figs. 2 (B), (C), and (D) exhibit meandering patterns with petals on a circular trajectory, rosettes, and a rectangular trajectory with petals, respectively; these patterns arise from aperiodic motions with more than one fundamental frequency; e.g., the peaks in the in Fig. 2 (B) can be labelled as , with and integers (positive or negative), and , and the ratio an irrational number. We show other TT patterns, for different parameter sets, in Fig. S2 in the Supplementary Material [35]. From Fig. 2 we conclude that both IIM and DMD methods can detect complicated TT patterns equally well in a homogeneous medium.
| 0.002 | 10 |
|---|---|
| 0.008 | 50 |
| 0.011 | 70 |
| 0.015 | 90 |
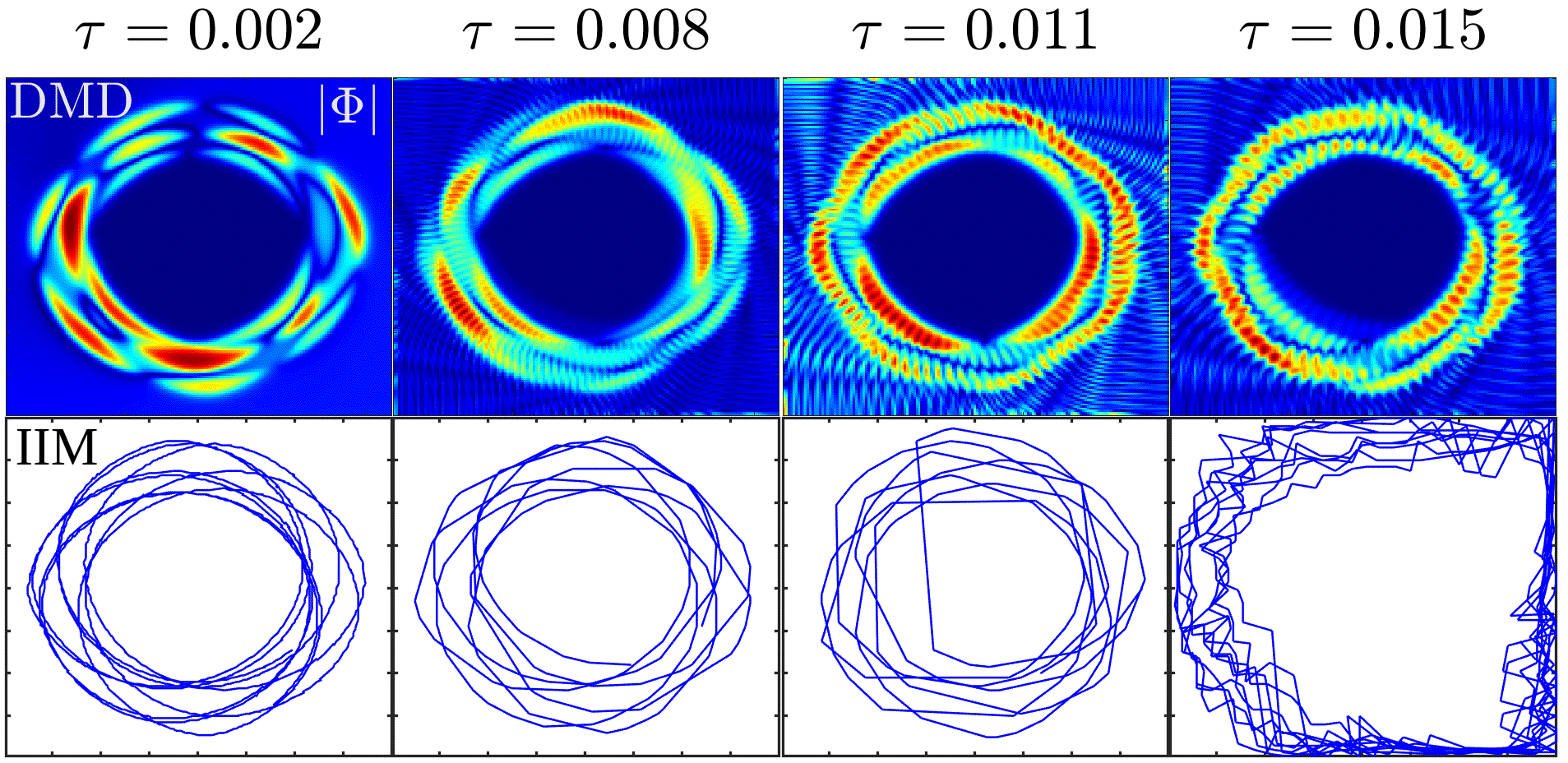
We show, in Fig. 3, how the TT patterns vary with the non-dimensionalised sampling interval (Table 1) in both the IIM and DMD methods. For specificity, we use the rosette pattern in Fig. 3 (C). The TT pattern is roughly conserved as we increase ; however, the IIM yields noisy TTs for , whereas the DMD method yields a TT pattern that is less noisy than its IIM counterpart.
We now demonstrate that DMD can be used to determine the positions of phase singularities even when there are multiple spiral waves in the medium. For the Barkley model [Eqs. (1) and ( 2)], we illustrate this in Fig. 4 (A), which shows a pseudocolor plot of in a multiple-spiral state; and Fig. 4 (B) depicts the modulus of a DMD eigenmode that exhibits clearly the locations of the phase singularities that are present in this pseudocolor plot. In Fig. 4 (B) we also see the boundaries between the domains with spiral waves.


III.2 Spiral TT in the presence of heterogeneities in the medium or noise
We use the O’Hara-Rudy model [28] of cardiac excitation waves for our study of TTs in a heterogeneous medium. Figure 5 shows how DMD and IIMs track TT in the medium with two different percentages of obstacles. We find that, although both methods can locate the region where the TT is confined, the TT plot from the IIM is associated with randomly scattered points in the background, which are suppressed in the TT pattern extracted by the DMD eigenmode. Moreover, we check how these two methods perform in the presence of noise in the signal. Such noise can arise in the data-collection processes in real experiments. Figure 6 shows TTs for three different values of signal-to-noise (SNR). It shows that IIM is more sensitive to noise and it fails to track the TT for SNR , whereas DMD can still capture the TT pattern. DMD can produce the TT pattern upto SNR. In summary, our results demonstrate that, with external noise, DMDTT is a more robust and versatile method for tracking TTs than IIM.

III.3 DMD prediction of spiral-wave dynamics
The DMD technique can also be used to reconstruct (approximately), and hence predict, the spatiotemporal evolution of the spiral waves in the models we consider. For this reconstruction we require the eigenmodes , their eigenvalues , and the amplitudes associated with every mode (see, e.g., Ref. [25]). We illustrate this for the Barkley model [Eqs. (1) and (2)], where we predict the spiral-wave dynamics as follows; at any instant of time , the predicted solution is
| (9) |
where the coefficient , the denotes Hermitian adjoint, is the number of columns in , and is the first column in (Eq.( 6)). We show in Figs. 7(A), (B), and (C) pseudocolor plots of [from Eqs. (1) and (2)], the DMD prediction [from Eq. (9)], and the error , respectively. From the plots in Figs. 7(A), (B), and (C) we conclude that the DMD-based spiral-wave reconstruction works well here because the error . We suggest that such a DMD-based prediction can be used mutatis mutandis with potentiometric voltage data for spiral waves from ex-vivo and in-vitro experiments.
IV Conclusions
The DMD method has been used to extract coherent structures in various fluid-dynamical experiments [21, 19] and simulations [23]. It has been applied in the study of spatially extended systems to analyze spatiotemporal patterns emerging from the evolution of nonlinear PDEs [23]. The working principles of DMD have been linked to the Koopman operator theory of dynamical systems [36, 22, 37]. Furthermore, DMD provides a data-driven approach for reduced-order modeling of high-rank dynamical systems [19, 20, 21, 22, 23, 24, 25].
We have demonstrated that DMD provides a powerful method for (a) the detection of spiral-wave TT patterns and (b) spiral-wave reconstruction in excitable media such as cardiac tissue, for which we employ the two-variable Barkley model [Eqs. (1) and (2)] and the biophysically realistic ORd model [Eq. (3)]. Such a detailed application of the DMD method to the study of spiral-wave evolution in excitable media has not been attempted hitherto. [Two studies have applied DMD to spiral waves: one discusses the extraction of an approximate governing equation for the spiral waves [26]; and the other extracts observables that are possible candidates for Koopman operators [22].] Our application of DMD to spiral waves in mathematical models for excitable media and cardiac tissue shows leads to new insights into spiral-tip trajectories and the prediction of the dynamics of these waves. Furthermore, our methods can be used, in both experimental and numerical investigations, of such waves in all excitable and oscillatory media.
We have carried out a comparison of the conventional IIM and our DMD-based TT for mathemtatical models of cardiac tissue in (a) a homogeneous medium, (2) with heterogeneities in the medium, and (c) in the presence of external noise in the signal. We find that both DMDTT and IIM can track various patterns, including the circular and complicated ones shown in Figs. 2 and 3, if the sampling interval is small. However, for a large value of , the IIM fails to track the TT, whereas DMD can still capture the TT pattern. We show, furthermore (Fig. 4), that DMD can be used to locate (a) phase singularities, even when there are multiple spiral waves, and (b) the domain boundaries between different spiral waves. In a medium with heterogeneities, both DMD and IIM can track TTs; however, TT plots from the IIM can show randomly scattered points in the background, which are suppressed in the TT patterns we obtain via DMD. Finally, in the presence of external noise in the signal, which can be present in experimental data, we show that IIM fails to track TT for the signal-to-noise ratio SNR ; by contrast, our DMD method can capture TT patterns up until SNR , so DMD provides a more robust method to track TTs, in the presence of noise, as compared to IIM.
We have noted already that the accurate tracking of the tip of a spiral wave and the mapping of phase singularities can give valuable information about its evolution of the spiral waves [16, 17, 18, 12]. Complicated meandering TT patterns are vulnerable to spiral-wave instabilities [14, 38]; TTs can provide insights into the underlying mechanisms of transitions from single- to multiple-spiral states, which are of great interest in the study of cardiac arryhthmias [38]. Therefore, it is important to develop versatile methods for tracking TTs; these methods should be applicable in varied experimental settings. We have shown, by using three settings, that DMDTT can be more versatile than the commonly used IIM for tracking TTs.
We expect that the DMD methods, which we have elucidated above, can be used to study electrical-activation patterns in mammalian hearts, at least in ex-vivo optical-mapping experiments with Lagendroff-perfused hearts. These methods can be applied on a set of optical images, collected successively at certain intervals of time, for the detection of phase singularities. The precise location of such phase singularities can be used for accurate ablation, which can help in terminating life-threatening cardiac arrhythmias. Furthermore, our DMD methods can be used fruitfully for such singularity detection in conjunction with conventional phase-singularity-mapping methods [18, 39].
We have demonstrated how to carry out spiral-wave reconstruction in excitable media, such as cardiac tissue, by using the DMD eigenmodes [see Eq.( 9) and Fig. 7]. Such a DMD-based prediction can be used mutatis mutandis with experimental data for spiral waves of electrical activation from ex-vivo and in-vitro experiments. We hope our work will lead to such experimental investigations, which have the potential to play an important role in the field of life-threatening cardiac arrhythmias.
We end our paper by discussing some limitations of our study. Here, we have focused only on the detection of the phase singularity of a spiral wave and its TT; however, other forms of activation patterns have been implicated in the occurrence of arrhythmias, such as focal or multiple-wave activation patterns [40, 29, 41]. In future work we will conduct a detailed analysis of how DMD can be used to characterize such activation patterns and how DMD can discriminate such patterns from spiral waves. Moreover, our study is restricted to two-dimensions. We will extended this to three-dimensional and anatomically realistic domains, which display rich forms of spatiotemporal organizations like scroll waves of excitation (see, e.g., Refs. [42, 43, 44, 45]).
Acknowledgements.
We thank SERC (IISc) for computational resources and CSIR, SERB, and the National Supercomputing Mission (NSM) for the support.References
- Winfree [1972] A. T. Winfree, Spiral waves of chemical activity, Science 175, 634 (1972).
- Lechleiter et al. [1991] J. Lechleiter, S. Girard, E. Peralta, and D. Clapham, Spiral calcium wave propagation and annihilation in xenopus laevis oocytes, Science 252, 123 (1991).
- Tyson and Murray [1989] J. J. Tyson and J. Murray, Cyclic amp waves during aggregation of dictyostelium amoebae, Development 106, 421 (1989).
- Falcke et al. [1992] M. Falcke, M. Bär, H. Engel, and M. Eiswirth, Traveling waves in the co oxidation on pt (110): Theory, The Journal of chemical physics 97, 4555 (1992).
- Seiden and Curland [2015] G. Seiden and S. Curland, The tongue as an excitable medium, New Journal of Physics 17, 033049 (2015).
- McGuire et al. [2021] M. K. McGuire, C. A. Fuller, J. F. Lindner, and N. Manz, Geographic tongue as a reaction–diffusion system, Chaos: An Interdisciplinary Journal of Nonlinear Science 31, 033118 (2021).
- Marino and Giacomelli [2019] F. Marino and G. Giacomelli, Excitable wave patterns in temporal systems with two long delays and their observation in a semiconductor laser experiment, Physical Review Letters 122, 174102 (2019).
- Allessie et al. [1977] M. A. Allessie, F. Bonke, and F. Schopman, Circus movement in rabbit atrial muscle as a mechanism of tachycardia. iii. the” leading circle” concept: a new model of circus movement in cardiac tissue without the involvement of an anatomical obstacle., Circulation research 41, 9 (1977).
- Davidenko et al. [1990] J. M. Davidenko, P. F. Kent, D. R. Chialvo, D. C. Michaels, and J. Jalife, Sustained vortex-like waves in normal isolated ventricular muscle., Proceedings of the National Academy of Sciences 87, 8785 (1990).
- Pertsov et al. [1993] A. M. Pertsov, J. M. Davidenko, R. Salomonsz, W. T. Baxter, and J. Jalife, Spiral waves of excitation underlie reentrant activity in isolated cardiac muscle., Circulation research 72, 631 (1993).
- Gray et al. [1995] R. A. Gray, J. Jalife, A. V. Panfilov, W. T. Baxter, C. Cabo, J. M. Davidenko, A. M. Pertsov, P. Hogeweg, and A. T. Winfree, Mechanisms of cardiac fibrillation, Science 270, 1222 (1995).
- Gray et al. [1998] R. A. Gray, A. M. Pertsov, and J. Jalife, Spatial and temporal organization during cardiac fibrillation, Nature 392, 75 (1998).
- Fenton and Karma [1998] F. Fenton and A. Karma, Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: Filament instability and fibrillation, Chaos: An Interdisciplinary Journal of Nonlinear Science 8, 20 (1998).
- Qu et al. [2000] Z. Qu, F. Xie, A. Garfinkel, and J. N. Weiss, Origins of spiral wave meander and breakup in a two-dimensional cardiac tissue model, Annals of biomedical engineering 28, 755 (2000).
- Gray et al. [2009] R. A. Gray, J. P. Wikswo, and N. F. Otani, Origin choice and petal loss in the flower garden of spiral wave tip trajectories, Chaos: An Interdisciplinary Journal of Nonlinear Science 19, 033118 (2009).
- Aronis et al. [2017] K. N. Aronis, R. D. Berger, and H. Ashikaga, Rotors: how do we know when they are real? (2017).
- Umapathy et al. [2010] K. Umapathy, K. Nair, S. Masse, S. Krishnan, J. Rogers, M. P. Nash, and K. Nanthakumar, Phase mapping of cardiac fibrillation, Circulation: Arrhythmia and Electrophysiology 3, 105 (2010).
- BRAY et al. [2001] M.-A. BRAY, S.-F. LIN, R. R. Aliev, B. J. Roth, and J. P. Wikswo Jr, Experimental and theoretical analysis of phase singularity dynamics in cardiac tissue, Journal of cardiovascular electrophysiology 12, 716 (2001).
- Schmid [2010] P. J. Schmid, Dynamic mode decomposition of numerical and experimental data, Journal of fluid mechanics 656, 5 (2010).
- Schmid et al. [2011] P. J. Schmid, L. Li, M. P. Juniper, and O. Pust, Applications of the dynamic mode decomposition, Theoretical and Computational Fluid Dynamics 25, 249 (2011).
- Schmid [2011] P. J. Schmid, Application of the dynamic mode decomposition to experimental data, Experiments in fluids 50, 1123 (2011).
- Nathan Kutz et al. [2018] J. Nathan Kutz, J. L. Proctor, and S. L. Brunton, Applied koopman theory for partial differential equations and data-driven modeling of spatio-temporal systems, Complexity 2018 (2018).
- Kutz et al. [2016] J. N. Kutz, S. L. Brunton, B. W. Brunton, and J. L. Proctor, Dynamic mode decomposition: data-driven modeling of complex systems (SIAM, 2016).
- Krake et al. [2021] T. Krake, S. Reinhardt, M. Hlawatsch, B. Eberhardt, and D. Weiskopf, Visualization and selection of dynamic mode decomposition components for unsteady flow, Visual Informatics 5, 15 (2021).
- Tu [2013] J. H. Tu, Dynamic mode decomposition: Theory and applications, Ph.D. thesis, Princeton University (2013).
- Champion et al. [2019] K. Champion, B. Lusch, J. N. Kutz, and S. L. Brunton, Data-driven discovery of coordinates and governing equations, Proceedings of the National Academy of Sciences 116, 22445 (2019).
- Barkley [1991] D. Barkley, Physica D: Nonlinear Phenomena 49, 61 (1991).
- O’Hara et al. [2011] T. O’Hara, L. Virág, A. Varró, and Y. Rudy, Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation, PLoS computational biology 7, e1002061 (2011).
- Zimik et al. [2015] S. Zimik, A. R. Nayak, and R. Pandit, A computational study of the factors influencing the pvc-triggering ability of a cluster of early afterdepolarization-capable myocytes, PloS one 10, e0144979 (2015).
- Zimik and Pandit [2017] S. Zimik and R. Pandit, Reentry via high-frequency pacing in a mathematical model for human-ventricular cardiac tissue with a localized fibrotic region, Scientific reports 7, 1 (2017).
- Ten Tusscher and Panfilov [2007] K. H. Ten Tusscher and A. V. Panfilov, Influence of diffuse fibrosis on wave propagation in human ventricular tissue, Europace 9, vi38 (2007).
- Darling and Widrow [2019] K. Darling and L. M. Widrow, Eigenfunctions of galactic phase space spirals from dynamic mode decomposition, Monthly Notices of the Royal Astronomical Society 490, 114 (2019).
- Barata and Hussein [2012] J. C. A. Barata and M. S. Hussein, The moore–penrose pseudoinverse: A tutorial review of the theory, Brazilian Journal of Physics 42, 146 (2012).
- Penrose [1955] R. Penrose, A generalized inverse for matrices, in Mathematical proceedings of the Cambridge philosophical society, Vol. 51 (Cambridge University Press, 1955) pp. 406–413.
- [35] Supplemental material, Supplemental Material .
- Rowley et al. [2009] C. W. Rowley, I. Mezić, S. Bagheri, P. Schlatter, and D. S. Henningson, Spectral analysis of nonlinear flows, Journal of fluid mechanics 641, 115 (2009).
- Brunton et al. [2021] S. L. Brunton, M. Budišić, E. Kaiser, and J. N. Kutz, Modern koopman theory for dynamical systems, arXiv preprint arXiv:2102.12086 (2021).
- Fenton et al. [2002] F. H. Fenton, E. M. Cherry, H. M. Hastings, and S. J. Evans, Multiple mechanisms of spiral wave breakup in a model of cardiac electrical activity, Chaos: An Interdisciplinary Journal of Nonlinear Science 12, 852 (2002).
- Laughner et al. [2012] J. I. Laughner, F. S. Ng, M. S. Sulkin, R. M. Arthur, and I. R. Efimov, Processing and analysis of cardiac optical mapping data obtained with potentiometric dyes, American Journal of Physiology-Heart and Circulatory Physiology 303, H753 (2012).
- Miragoli et al. [2007] M. Miragoli, N. Salvarani, and S. Rohr, Myofibroblasts induce ectopic activity in cardiac tissue, Circulation research 101, 755 (2007).
- Alonso et al. [2016] S. Alonso, R. W. Dos Santos, and M. Bär, Reentry and ectopic pacemakers emerge in a three-dimensional model for a slab of cardiac tissue with diffuse microfibrosis near the percolation threshold, PloS one 11, e0166972 (2016).
- Maucher and Sutcliffe [2017] F. Maucher and P. Sutcliffe, Length of excitable knots, Physical Review E 96, 012218 (2017).
- Maucher and Sutcliffe [2019] F. Maucher and P. Sutcliffe, Dynamics of linked filaments in excitable media, Nonlinearity 32, 942 (2019).
- Weingard [2017] D. Weingard, Scroll Waves and How They Interact with Non-Reactive Spheres, Tori, and Knots, Ph.D. thesis, The Florida State University (2017).
- Rajany et al. [2021] K. V. Rajany, R. Majumder, A. R. Nayak, and R. Pandit, The effects of inhomogeneities on scroll-wave dynamics in an anatomically realistic mathematical model for canine ventricular tissue, Physics Open 9, 100090 (2021).