Spin-orbital-angular-momentum-coupled quantum gases
Abstract
We briefly review the recent progress of theories and experiments on spin-orbital-angular-momentum (SOAM)-coupled quantum gases. The coupling between the intrinsic degree of freedom of particles and their external orbital motions widely exists in the universe, and leads to a broad variety of fundamental phenomena in both classical physics and quantum mechanics. The recent realization of synthetic SOAM coupling in cold atoms has attracted a great deal of attention, and stimulated a large amount of considerations on exotic quantum phases in both Bose and Fermi gases. In this review, we present a basic idea of engineering SOAM coupling in neutral atoms, starting from a semiclassical description of atom-light interaction. Unique features of single-particle physics in the presence of SOAM coupling are discussed. The intriguing ground-state quantum phases of weakly interacting Bose gases are introduced, with emphasis on a so-called angular stripe phase, which has not yet been observed at present. It is demonstrated how to generate a stable giant vortex in a SOAM-coupled Fermi superfluid. We also discuss the topological characters of a Fermi superfluid in the presence of SOAM coupling. We then introduce the experimental achievement of SOAM coupling in 87Rb Bose gases and its first observation of phase transitions. The most recent development of SOAM-coupled Bose gases in experiments is also summarized. Regarding the controllability of ultracold quantum gases, it opens a new era, from the quantum simulation point of view, to study the fundamental physics resulting from SOAM coupling as well as newly emergent quantum phases.
I Introduction
The spin-orbital-angular-momentum (SOAM) coupling, the coupling between the spin degree of freedom and the external orbital motion, is one of the most common phenomena in our nature. A prominent example in classical physics is the astronomical fact that the Moon always shows the same side to the Earth, known as the tidal locking or the spin-orbit locking Barnes2010F . In atomic physics, SOAM coupling is a relativistic effect, which gives rise to the fine structure of energy levels of hydrogen atoms Landau2007Q . A similar effect occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model (Talmi1963N, ). In condensed-matter physics, an analogous coupling between the electron spin and its velocity, namely the spin-linear-momentum (SLM) coupling or spin-orbit (SO) coupling, results in a variety of intriguing and fundamental phenomena, such as the spin-Hall effect or topological insulators (Qi2010T, ), which have potential applications in quantum devices. Although numerous fascinating behaviors of many-body quantum systems are closely related to SOAM or SO coupling, they are mostly intractable or manifest themselves under extreme conditions. Therefore, it is of important significance to find a system, which could mimic the unique features of SOAM- or SO-coupled quantum systems in a controllable way.
Owing to the advances in the experimental technique, ultracold atomic gases acquire a high degree of controllability and tunability in interatomic interaction, geometry, purity, atomic species, and lattice constant (of optical lattices) Bloch2008M ; Giorgini2008T ; Kohler2006P ; Chin2010F ; Gross2017Q . To date, ultracold quantum gases have emerged as a versatile platform for exploring a broad variety of many-body phenomena and can realize physical effects with analogs throughout physics Qi2010T ; Dalibard2011A ; Abanin2019C . However, unlike charged particles, neutral atoms cannot experience the influence of external electromagnetic fields. Fortunately, thanks to the controlling of atom-light interaction, the internal hyperfine states of neutral atoms, playing a role of (pseudo-)spin, are coupled to their linear momentum of center-of-mass motion, which equivalently introduces a class of SO couplings experienced by atoms. For example, the theoretical scheme of realizing a one-dimensional (1D) SO coupling with equal Rashba and Dresselhaus strengths was proposed in cold atoms according to a Raman process with a simple -type configuration liu2009E . Then the basic idea was broadly applied in experiments with both bosonic and fermionic atoms Lin2011S ; Williams2013S ; Wang2012S ; Cheuk2012S ; Zhang2012C ; Olson2014T ; Fu2014P ; Ji2014E ; Ji2015S ; Hamner2015S ; Jimenez-Garcia2015T ; Burdick2016L ; Song2016S ; Li2016S ; Livi2016S . Soon, an impressive amount of theoretical and experimental efforts have been devoted to the realization of high-dimensional SO coupling Osterloh2005C ; Ruseckas2005N ; Juzeliunas2010G ; Campbell2011R ; Sau2011C ; Anderson2013M ; Xu2013A ; Liu2014R ; Anderson2013S ; Lu2020I ; Wang2018D ; Huang2016E ; Wu2016R ; Wang2021R . The high-dimensional SO coupling corresponds to a non-Abelian gauge field and has nontrivial geometric or topological effects, which are absent in systems with 1D SO coupling. Regarding the controllability of ultracold quantum gases, it opens a new era, from the quantum simulation point of view, to study the fundamental physics resulting from SO-coupling as well as newly emergent quantum phases Zhai2012S ; Zhai2015D ; Zhang2018S .
Though the SO coupling has intensively been studied in the field of condensed matter as well as in ultracold atoms, it is different from the original meaning of SO coupling in atomic physics, in which it indicates the coupling between the spin and the orbital angular momentum. Recently, such type of SO coupling, i.e., the SOAM coupling, is theoretically proposed in cold atoms and enriches our understanding of quantum many-body physics (Liu2006G, ; DeMarco2015A, ; Sun2015S, ; Qu2015Q, ; Hu2015H, ; Chen2016S, ; Vasic2016E, ; Hou2017A, ). It is experimentally achieved in 87Rb Bose gases according to a Raman process by using a pair of copropagating laser beams operated in Laguerre-Gaussian (LG) modes Chen2018S ; Chen2018R ; Zhang2019G . The ground-state phase diagram of the systems is confirmed. The hysteresis loop is observed across the phase boundary, which is a hallmark of the first-order phase transitions. This is due to the unique property of the quantized angular momentum, unlike that of the linear momentum in SLM-coupled systems Li2012Q ; Martone2012A ; Chen2017Q ; Chen2018Q . Later on, a considerable amount of attention has been paid to a supersolid-like phase Chen2020A ; Chen2020Ground ; Duan2020S ; Chiu2020V ; Bidasyuk2022F , namely the angular stripe phase, which breaks the U(1) gauge symmetry to behave like a superfluid and also breaks the angular translational symmetry (or the rotational symmetry) to manifest spatial order in the angular density Boninsegni2012C . Nevertheless, this kind of angular stripe phases has not yet been observed because of the narrow window of parameters that is hardly reached in experiments at present (Chiu2020V, ).
Soon, the idea of SOAM coupling is theoretically generalized to fermionic systems Chen2020G ; Wang2021E , where the pairing mechanics plays a crucial role in the Fermi superfluid. While it is shown that the SOAM coupling leads to the spin-dependent vortex formation in Bose-Einstein condensates, SOAM coupling alone does not induce vortices in a Fermi superfluid, since fermions in a Cooper pair would acquire opposite orbital angular momenta that cancel each other, yielding a superfluid devoid of vortices. However, by introducing a moderate detuning away from the two-photon resonance in the Raman process, which breaks the time-reversal symmetry of systems, a giant vortex superfluid phase could remain stable in SOAM-coupled Fermi gases. The Cooper pairs can possess quantized angular momenta, featured as an angular analog of the Fulde-Ferrell pairing state in SO-coupled Fermi gases, where Cooper pairs inevitably carry finite center-of-mass momentum due to the asymmetry of SO-dressed Fermi surface under Zeeman field Dong2013F ; Shenoy2013F ; Wu2013U ; Qu2013T ; Zhang2013T ; Chen2013I ; Liu2013T . These SOAM-coupling induced vortices have fascinating and unique features. For example, their size could be as strikingly large as the length scale comparable to the waist of Raman beams. This is markedly different from previously studied vortices in atomic Fermi superfluids, where changes in the vortex-core structure predominantly take place within a short-length scale set by the interatomic separation Sensarma2006V ; Chien2006G . Besides, the vortex core exhibits a large spin imbalance, which originates from spin-polarized vortex-bound states, or the so-called Caroli–de Gennes–Matricon (CdGM) states Caroli1964B , and would serve as an ideal experimental signal. Subsequently, the topological characters of a ring-shape SOAM-coupled Fermi superfluid are explored, in which the ac-stark potential of Raman beams provides a strong radial confinement (Chen-22, ). The genic features of topological superfluid are encoded in the quantized angular degree of freedom. Nevertheless, a fundamental hurdle to the experimental observation of the SOAM-coupling-induced pairing states is the inevitable heating during the Raman process, which makes it difficult to cool the system below the superfluid transition temperature. Instead, it is reasonable to expect that molecule states in the SOAM-coupled Fermi gases could survive even above the critical temperature, as what occurs in SO-coupled systems Williams2013R ; Fu2014P . Accordingly, a scenario, using the radio-frequency spectroscopy based on two-body physics, provides an accessible detection of the pairing mechanics under current experimental conditions Han2022M .
The rest of the review is arranged as follows. In the next section, we present the theoretical scheme of how the SOAM-coupling effect could be achieved in cold atoms according to a Raman transition. Starting from a semiclassical description of atom-light interaction, the effective Hamiltonian of a single atom is derived. The possible symmetries of the system are then discussed, which play an important role in understanding the fundamental properties of the system. In Sec. III, single-particle physics is introduced, including the energy spectrum and the intriguing spin texture of the ground state. The emergent synthetic gauge field experienced by cold atoms in the presence of atom-light interaction is also demonstrated. In Sec. IV, the ground-state properties of weakly interacting SOAM-coupled Bose gases are discussed, based on the solution of the Gross-Pitaevskii equation. The quantum phases of Bose condensates are then identified as well. The emphasis on the properties of the angular stripe phases is presented. We also propose possible scenarios to enlarge the window of parameters that might be accessible in experiments to observe them. It follows the discussion on the ground state of interacting SOAM-coupled Fermi gases in Sec. V. The pairing mechanism of fermions in the presence of SOAM-coupling is introduced. Two exotic pairing states, i.e., SOAM-coupling-induced giant vortex and topological superfluid states, are shown to be stabilized under SOAM coupling. Subsequently, the most recent progress of experiments related to SOAM-coupled quantum gases is summarized in Sec. VI. Sec. VII is devoted to the conclusions and outlooks for future advances.
II Spin-orbital-angular-momentum coupling
The key idea of generating SOAM coupling in neutral atoms has been proposed by several earlier works DeMarco2015A ; Sun2015S ; Qu2015Q , in which two hyperfine states of atoms are coupled by a pair of copropagating LG beams according to a Raman process as shown in Fig. 1. The two LG beams carry different orbital angular momenta along the direction of beam propagation, that leads to an orbital angular momentum change of atoms when transitioning between the two ground hyperfine states. In the following, we are going to derive the effective Hamiltonian of an alkali metal atom in the presence of a pair of Raman LG beams based on the semiclassical description of atom-light interaction Scully2008Q ; Liu2006G ; Marzlin1997V .

II.1 Semiclassical theory of atom-light interactions
In the semiclassical theory, the atom-light interaction during the Raman process is described by the following Hamiltonian
| (1) |
in the bare hyperfine basis , where () is the bare energy of atoms in different hyperfine states, and characterizes the dipole interactions between the valence electron and light fields. Here, is the electric moment of the valence electron and
| (2) |
are the electric fields experienced by atoms, where denote the unit vectors of the polarization direction of light, are the angular frequencies of Raman beams, and are the spatial complex amplitudes. The wave function of atoms can also be written in the bare hyperfine basis as
| (3) |
and are arbitrary factors that are chosen for later convenience. Inserting Eqs. (1) and (3) into the Schrödinger equation and by choosing
| (4) | |||||
| (5) | |||||
| (6) |
we easily obtain
| (7) | |||||
| (8) | |||||
| (9) |
under the rotating-wave approximation (RWA) Scully2008Q , where and are the matrix elements of the electric dipole moments, and and are respectively the two-photon and single-photon detunings. When the excited state is far from the resonance, we may adiabatically eliminate it by setting , and then Eq. (9) yields
| (10) |
After inserting Eq. (10) into Eqs. (7) and (8), we arrive at
| (11) |
where
| (12) | |||||
| (13) |
are respectively the diagonal and off-diagonal ac-stark shifts. We find that the diagonal ac-stark shift provides an effective trapping potential for atoms that could be removed by properly choosing a tune-out wavelength of LG beams in the experiment (Zhang2019G, ; Holmgren2012M, ; Herold2012P, ). The off-diagonal ac-stark shift leads to a space-dependent coupling between two hyperfine states and , and then results in a SOAM coupling of atoms as we will see below.
II.2 SOAM-coupled Hamiltonian and symmetries
Without loss of generality, we consider a two-dimensional (2D) configuration for simplicity in that atoms are confined in the plane, and the pair of Raman LG beams copropagate along the direction with the spatial complex amplitude
| (14) |
where and are respectively the intensity and waist of the beams, and are their winding numbers. Here, we have adopted a polar coordinate . Consequently, the single-atom Hamiltonian in the presence of Raman LG beams takes an effective form of
| (15) |
with
| (16) |
where is the external harmonic potential, is the angular momentum transferred to atoms, and , with the coupling strength , is the radial Rabi frequency. Here, we have assumed for simplicity, which is only dependent on . Besides, we also discard the internal phase difference between the matrix elements of electric dipole moments and that is irrelevant to the problem.
Let us then analyse the possible symmetries of the single-atom Hamiltonian (15). It is obvious that the rotational symmetry with respect to the axis is broken by the dependence of Raman coupling on the azimuthal angle . The orbital angular momentum of the atom is thus no longer conserved, since it follows a change of orbital angular momentum accompanied by the spin flip in the Raman process DeMarco2015A ; Chen2020A ; Duan2020S . By introducing a unitary transformation , the single-atom Hamiltonian becomes , i.e.,
| (17) |
where , and are Pauli matrices. We find that the angular momentum commutes with the single-atom Hamiltonian under the unitary transformation , and thus is conserved. Therefore, the original single-atom Hamiltonian demonstrates the symmetry under the redefined rotational transformation . Then may be regarded as the operator of quasi-angular momentum (QAM), and each eigenstate of the system possesses definite values of QAM characterized by the corresponding quantum number . It is related to the angular momentum of each spin component in the laboratory frame by . Here, we find that the term of appears, which characterizes the crucial SOAM-coupling effect that is well familiar to us in atomic physics.
At the resonance of Raman coupling with , the system demonstrates an additional symmetry, namely the time-reversal symmetry. The single-atom Hamiltonian commutes with the time-reversal operator , and thus is invariant under the time-reversal transformation, where denotes the operator of complex conjugation DeMarco2015A ; Duan2020S . This symmetry may be translated into a QAM frame as , and then we have . The time-reversal symmetry guarantees that the spectrum of a single atom is symmetric about the QAM .
III Single-particle physics
III.1 Single-particle spectrum
Regarding the rotational symmetry of the single-atom Hamiltonian (17), each eigenstate of a single atom should possess a definite QAM , whose wave function may be written as
| (18) |
Then the Schrödinger equation reduces to two coupled one-dimensional radial equations of , which are easily solved by using the finite-difference method DeMarco2015A . The single-particle dispersion relations between the energy and QAM are shown in Fig. 2 for three typical coupling strengths. Here, the winding numbers of two Raman beams are respectively chosen to be and , and we consider the situation at the two-photon resonance with . The symmetry of the single-particle dispersion about is guaranteed by the time-reversal symmetry discussed above. This means that the Schrödinger equation is invariant under the exchange of the spin indices, which sends as well.
In the absence of SOAM coupling, i.e., , the energy band structure is simply that of the spinor harmonic oscillator with the excitation interval . The ground state is characterized by the QAM , which is doubly degenerate. The angular momentum for each spin component in the laboratory frame is and corresponding to the QAM and , respectively. As the SOAM-coupling strength gradually increases, the spin is no longer a good quantum number, and small amounts of atoms are transferred into the previously vacant spin component, while the ground state still has the two-fold degeneracy with definite QAM. By further increasing the coupling strength, the system finally jumps into the QAM ground state, which gives rise to a first-order phase transition to a spin-balanced population (Zhang2019G, ). This is due to the unique property of the quantized angular momentum in SOAM-coupled systems. In SLM-coupled systems, such phase transition is a continuous type, where the doubly degenerate ground states finally merge into each other as the Raman-coupling strength increases Li2012Q ; Martone2012A ; Chen2017Q ; Chen2018Q .

Let us look closely at the evolution of the lowest-energy band as presented in Fig. 3 at different coupling strengths. Its symmetry about is preserved by the time-reversal symmetry at the two-photon resonance as shown in Fig. 3(b). We demonstrate how the ground state evolves from the doubly degenerate states () into a single one () as the coupling strength increases. However, away from the two-photon resonance with , we find that the degeneracy of the ground states at weak coupling strength is lifted, since the time-reversal symmetry is broken by the two-photon detuning (as shown in Fig. 3(a) and (c)). The ground state is located either at or determined by the sign of the two-photon detuning. This gives rise to an additional first-order phase transition by continuously varying the two-photon detuning Zhang2019G . At strong coupling strength, the system again jumps into the QAM ground state as we discussed above.

III.2 Spin textures
The SO coupling gives rise to intriguing spin textures. For example, it has been found in studies of 2D Rashba SO-coupled BECs Hu2012S ; Ramachandhran2012H and BECs exposed to LG beams (Leslie2009C, ) that the spin texture contains a topological knot known as a 2D skyrmion. It is one kind of topological defects protected by their topological nontriviality. Regarding the spin texture of SOAM-coupled systems, it is useful to define a spin vector DeMarco2015A ; Hu2012S ; Ramachandhran2012H
| (19) |
with the spin operator . The skyrmion number defined as
| (20) |
is a measure of the winding of the spin texture, which distinguishes a skyrmion texture from that of the vacuum. If it equals or , a topological knot exists in the spin texture Binz2008C ; Muhlbauer2009S . The ground-state spin texture at four typical coupling strengths is presented in Fig. 4. At weak coupling strength, the two-fold degenerate ground state gives rise to a spin texture corresponding to a half skyrmion. As the coupling strength increases, the ground state finally jumps to the QAM state. The system reaches a spin-balanced state, which does not support a skyrmion texture. The local spin becomes planar and lies in the plane, and thus the skyrmion number vanishes.

III.3 Artificial gauge field
In the following, we are going to demonstrate how the artificial (synthetic) gauge field may emerge for neutral atoms in the presence of atom-light interactions. It is one of the essential ingredients for the simulation of charged particles moving in the electromagnetic field by using cold atoms Dum1996G ; Visser1998G ; Lin2009S ; Lin2009B ; Dalibard2011A , which gives rise to a series of intriguing phenomena, such as the spin Hall effect Zhu2006S ; Liu2007O ; Beeler2013T . To this end, we may simply rewrite the atom-light Hamiltonian (16) in an explicit form of
| (21) |
with the effective Zeeman field
| (22) |
We find easily that the Raman-induced atom-light interaction effectively provides a spin-magnetic interaction equivalent to that for a spin-half charged particle in a space-dependent Zeeman field . The diagonalization of simply gives the dressed spin states Dalibard2011A , i.e.,
| (23) |
with eigenvalues , respectively, and and , which determine the orientation of the effective Zeeman field. It is obvious that denotes the states that the pseudo-spin of the atom aligns along or inversely to the direction of the local Zeeman field. In the following, let us consider the atom moves slowly in the space-dependent Zeeman field , and its pseudo-spin follows adiabatically one of the eigenstates of , namely for example . Then the full wave function of the atom can be written as , the evolution of which is governed by the Schrödinger equation under the Hamiltonian (15). Here, is the spatial wave function characterizing the center-of-mass motion of the atom in the internal dressed state . By projecting the Schrödinger equation onto the internal dressed state , we obtain easily
| (24) |
Two geometric potentials and emerge in addition to the external trapping potential and Zeeman energy , which are respectively the vector potential Dalibard2011A
| (25) |
and the scalar potential
| (26) |
It is obvious that Eq. (24) takes the same form as that for a spin-half particle with a unit charge () (Landau2007Q, ). The effective magnetic field associated with is
| (27) |
Here, we should pay special attention to the difference between the Zeeman field and the effective magnetic field : the Zeeman field only lifts the degeneracy of the bare spin states and does not affect the center-of-mass motion of the atom, while is the magnetic field experienced by the center-of-mass motion of the atom when it moves in the presence of the atom-light interaction and keeps staying in the internal dressed state . In the presence of Raman LG beams, the effective magnetic field takes the explicit form of
| (28) |
which is perpendicular to the plane and along the axis.
IV SOAM-coupled Bose gases
The interatomic interaction plays a crucial role in interacting many-body quantum systems. In this section, we are going to introduce the ground-state quantum phases of weakly-interacting Bose-Einstein condensates (BECs) in the presence of SOAM coupling, within the framework of the mean-field theory based on the Gross-Pitaevskii (GP) equation. The interaction gives rise to the appearance of a variety of intriguing angular stripe phases, which have not yet been observed in current experiments. The possible theoretical scheme is proposed for observing angular stripe phases in the 41K atomic gas with tunable interatomic interactions.
The mean-field Hamiltonian of a weakly interacting Bose gas in the presence of SOAM coupling takes the form of
| (29) |
where is the single-particle Hamiltonian (17), is the spinor wave function for the condensate, and is the effective 2D intra- () and inter-species () interaction strength.
IV.1 Gross-Pitaevskii theory and a variational approach
When the interaction is taken into account, the nonlinearity may spontaneously break the rotational symmetry of the system. We can no longer assume that the condensate possesses the definite QAM . The ground-state solution of the GP equation is first attempted by using a split-step imaginary time evolution DeMarco2015A . Three kinds of quantum phases are identified: two of them still preserve the rotational symmetry as the many-body analogs of the single-particle ground state, while the third one is a newly emergent angular stripe phase, which does not possess a definite QAM and breaks the rotational symmetry.

Therefore, apart from the angular stripe phase, one may take the states with a definite QAM for the condensates as a good starting point when taking into account interactions. If the system or the condensate wave function preserves the axial symmetry, one may consider the QAM as a good quantum number and adopt the Ansatz for the condensate Chen2020A
| (30) |
with the radial wave function , and substitute it into the GP equation,
| (31) |
where is the chemical potential, and the diagonal element takes the form of (spin index ). Thus, one can then determine the ground-state wave function of the rotationally symmetric phases at zero temperature by solving self-consistently this GP equation.
Nonetheless, to capture the exotic angular stripe phase that does not possess a definite QAM, a variational Ansatz with various angular momenta is adopted for the condensate wave function in determining the ground state with an energy-minimizing method Chen2020A .
In the realistic configuration of recent experiments Chen2018S ; Zhang2019G , the orbital angular momentum transferred by the LG lasers is , giving rise to minima with the QAM located at , or in the single-particle dispersion. Thus, the adopted variational Ansatz could be taken as
| (32) |
with real weighting coefficients and the associated phases , , and . In general, is the state with a definite QAM , which can either be the single-particle state or the one obtained by self-consistently solving the GP equation (31) when the interaction is taken into account. Nonetheless, the latter is adopted here which contributes a lower mean-field energy than the one from the single-particle states particularly at low Rabi frequencies or at relatively strong interactions Chen2020A . Therefore, the ground-state wave function is then determined from the minimization of the mean-field energy in Eq. (29) with respect to the variational parameters. It’s worth mentioning that, three definite-QAM states are merely sufficient here, regarding the recent experimental configuration with the transferred orbital angular momentum Zhang2019G . One may need more definite-QAM states in the variational Ansatz for larger .

IV.2 Typical ground-state phases
| Vortex-antivortex pair phase | Half-skyrmion phase | Angular stripe phases | Reference | |
|---|---|---|---|---|
| Spin polarizations | , | , | , | Zhang2019G ; Chen2020A ; Duan2020S |
| Magnetization | non-magnetic | magnetic | non-magnetic | Zhang2019G ; Chen2020A ; Duan2020S |
| Coefficients in Eq. (32) | or | or | Chen2020A | |
| in Eq. (30) | 0 | or | indefinite | Chen2020Ground ; Chiu2020V ; Duan2020S |
| in | or | indefinite | Chen2020Ground ; Chiu2020V ; Duan2020S | |
| Symmetry111, and denote the time-reversal symmetry, continuous and two-fold rotational symmetries, respectively. | Duan2020S | |||
| Symmetry in | or | Chen2020A | ||
| Single-particle dispersion | single minimum | double degeneracy | double degeneracy | Chen2018S ; Zhang2019G ; Chen2020A ; Chen2020Ground |
| Excitation spectrum | symmetric, single phonon | asymmetric, roton structure | symmetric, two phonons | Chen2020A ; Chen2020Ground |
After solving self-consistently the GP equation in Eq. (31) and minimizing the total energy in Eq. (29) with a constructed variational Ansatz, the ground-state wave function can then be calculated and the phase diagram at zero temperature is conveniently depicted for a weakly-interacting SOAM-coupled Bose gas Chen2020A . In general, four distinct phases can be identified in the parameter space of and at a vanishing two-photon detuning . The first is the vortex-antivortex pair phase which behaves as a vortex, as shown by the first column in Fig. 5. It locates at zero QAM (i.e., ) with zero magnetization and . The second one is the half-skyrmion phase with two spin-component densities being a Thomas-Fermi-like distribution and a vortex (see the second column in Fig. 5). This phase is magnetic, i.e., and , with a definite QAM at or (i.e., or ). The third and fourth ones are called angular stripe phases shown by the peanut-like and halo-like density profiles in the last two columns of Fig. 5. Both of them have no definite with or and they have no magnetization and . In addition, one can further investigate the elementary excitation spectrum to distinguish these phases and then characterize the phase transitions. The spectrum of a SOAM-coupled Bose gas is discrete due to the quantized angular momentum. In detail, the vortex-antivortex pair phase possesses a symmetric spectrum with a single phonon mode, see Fig. 7(a). However, the half-skyrmion phase breaks spontaneously the double degeneracy in the single-particle dispersion and thus has an excitation spectrum with a discrete roton-maxon structure Chen2020A , as shown in Fig. 7(b). Most interestingly, owing to the spontaneous breaking of both the U gauge symmetry and the continuous rotational symmetry, the excitation spectrum in the angular stripe phase exhibits two gapless Goldstone modes Chen2020Ground , see Fig. 7(c). A summary of the properties of these typical phases can be found in Table 1. It should be noted that these phases described above are based on recent experimental configurations with small transferred angular momentum , and we use them for a brief illustration. It is possible to find more nontrivial phases such as other angular stripe phases with superposition of large-angular-momentum states under the condition of larger Chen2020Ground ; Chiu2020V or complex vortex molecule states Duan2020S . Among these typical ground-state phases, the most intriguing one is the angular stripe phase, which attracts intensive research attention and will be discussed in detail in the following.

IV.3 Exotic angular stripe phases
In the past decade, an exotic phase of matter has attracted tremendous attention in ultracold quantum gases, i.e., namely the stripe phase, which breaks spontaneously U gauge symmetry and spatial translational symmetry wang2010spin ; Wu2011U ; ho2011bose ; Li2012Q . As a consequence, quantum gases will exhibit a superfluid behaviour and meanwhile show a periodic modulation in the density distribution. These counterintuitive features associate closely this nontrivial phase to the long-sought supersolid phase in solid Helium since the 1960s Boninsegni2012C , i.e., a rigid, spatially ordered solid that flows like a fluid without friction. Whether such a superfluid state can exist remains unclear for more than 50 years until the seminal breakthroughs using ultracold atoms. In 2017, two groups from ETH Zurich and MIT created successfully an ultracold quantum gas featuring supersolid properties using Bose-Einstein condensates with optical cavities or spin-orbit coupling leonard2017supersolid ; li2017stripe . Later in 2019, three independent groups from Stuttgart, Florence, and Innsbruck observed supersolidity using dipolar quantum gases of lanthanide atoms (i.e., 162Dy, 164Dy, and 166Er) without any external optical lattice tanzi2019observation ; bottcher2019transient ; chomaz2019long , and very recently one of them extended successfully into two dimensions norcia2021two .
In the presence of SOAM coupling, several kinds of angular stripe phases are theoretically predicted as introduced above, which take the analogous behavior as that of supersolid. Here, we have discussed two kinds of angular stripe phases: phase (III), a superposition state of two orbital-angular-momentum states (), and phase (IV), a superposition state of three orbital-angular-momentum states (). Although experimentalists have achieved successfully most of the ground-state quantum phases of a SOAM-coupled Bose gas, the nontrivial angular stripe phase remains elusive in the laboratory. There are two main obstacles. Firstly, the typical energy scale of the SOAM coupling is about with the atomic cloud size . To enhance the SOAM-coupling effect to reach the regime of the angular stripe phase, one needs to reduce the atomic size which decreases the perimeter of the cloud and instead presents fewer periods of density order in the angular direction. Secondly, recent experimental attempts are made in a 87Rb BEC. The critical Rabi frequency of the angular stripe phase is thus small due to the tiny difference between the intra- and inter-species interactions. As a consequence, the period of stripes becomes so small that the stripes show too low contrast and visibility, which makes them hard to be detected.
The interatomic interaction is one of the crucial factors to affect the parameter space of angular stripe phases as well as the visibility. This is quite similar to the situation when concerning the stripe phase in a SO-coupled Bose gas Li2012Q . The stripe phase prefers the region where the inter-species interaction is pretty smaller than the intra-species interaction. To this end, 41K atomic gases provide a promising candidate for exploring angular stripe phases with tunable interactions according to the Feshbach resonance centered at the magnetic field G Chen2020A . Near the Feshbach resonance, the intraspecies scattering lengths are approximately constant, and the interspecies one can be tuned in a wide range Lysebo2010F ; Tanzi2018F . By setting typical realistic parameters, the phase diagram is determined and the angular stripe phases can occupy a relatively large parameter space, as shown in Fig. 6. An angular density-density correlation function can be introduced to estimate the visibility in density profile, with the angular density , and the label for each spin component and null for the total density. In contrast to other phases, the novel angular stripe phases break the rotational symmetry and exhibit spatial density modulation in the angular direction. Two angular stripe phases feature considerable spatial modulation and contrast in the angular density-density correlation for both spin components as well as the total one, as shown in Figs. 5(c) and 5(d). This hallmark feature might be useful in directly probing the existence of the angular stripes in future experiments with ultracold atoms.
There are also other theoretical attempts and developments emphasizing the angular stripe phases in SOAM-coupled Bose gases. For example, by utilizing LG beams with higher-order orbital angular momenta, it is shown that angular stripe phases can be achieved in a wide window of experimentally accessible parameters with high visibility contrast Chen2020G ; Chiu2020V . Besides, A number of distinct quantum phases are identified according to the symmetry analysis, and a complex vortex molecule state is discovered, which plays an important role in the continuous phase transitions Duan2020S . For a ring-shaped BEC in the presence of SOAM coupling, the fine structures of angular stripe phases are explored Bidasyuk2022F .
V SOAM-coupled Fermi gases
The pairing mechanism plays a crucial role in the Fermi superfluid. While it is shown that the SOAM coupling leads to the spin-dependent vortex formation in Bose-Einstein condensates, SOAM coupling alone does not induce vortices in a Fermi superfluid, since fermions in a Cooper pair would acquire opposite orbital angular momenta that cancel each other, yielding a superfluid devoid of vortices. In this section, we are going to discuss the unique features of SOAM-coupled Fermi superfluid at zero temperature, with emphasis on two exotic pairing states, i.e., SOAM-coupling-induced vortex and topological superfluid states.
V.1 Pairing physics under SOAM coupling
It is well known that a two-component spin-balance Fermi gas becomes unstable in the presence of an arbitrary small attractive interaction. The resulting instability gives rise to a Bardeen-Cooper-Schrieffer (BCS) ground state with zero center-of-mass momentum. It is also well accepted that in a Fermi superfluid with spin-imbalance or Zeeman fields, exotic pairing states emerge, for instance, Fulde-Ferrell and Larkin-Ovchinnikov states FF ; LO , where the former pairing state carries finite center-of-mass momentum and the latter oscillates both in coordinate and momentum spaces. Whereas, these novel states are only stable in a very small parameter region, which is one of the reasons for the exclusiveness of their experimental observations. However, the experimental achievement of SO coupling in cold atoms offers a new platform to pursue these long sought-after states. For instance, the interplay of SO coupling, Zeeman fields and interactions provides an alternative mechanism to induce Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) states Dong2013F ; Shenoy2013F ; Wu2013U ; Qu2013T ; Zhang2013T ; Chen2013I ; Liu2013T . Besides SO-coupling-induced FFLO states, topological band structures become accessible under SO coupling Huang2016E ; Wu2016R ; Zhang-16 ; xjliu1D ; xjliu2D , which lays the fertile ground for topological superfluid–for instance, aided by the Zeeman fields and interactions, a topological superfluid emerges in a 2D Fermi gas under the Rashba-type SO coupling Kane-08 ; tsfsolid1 ; tsfsolid2 ; tsfsolid3 ; tsfsolid4 ; soc1 ; Yi-11 .
Intuitively, SOAM coupling as an angular analog of the conventional SO coupling, two novel pairing states can be expected. One is the SOAM-coupling-induced pairing state with finite quantized angular momenta, which is nothing but a vortex state. The other is the SOAM-coupling-induced angular topological superfluid state, the analog of the topological superfluid state in a one-dimensional lattice gas under a one-dimensional SO coupling, where quantized angular momenta in the former play the role of discretized linear momenta of the latter. In this review, whether the above two expectational pairing states, i.e., SOAM-coupling-induced vortex and topological superfluid states, could be stabilized is clarified. In the following, the former issue will be addressed in Sec. V.2 and the latter in Sec. V.3.

V.2 SOAM-coupling-induced vortex states
As illustrated in Fig. 8, a two-component Fermi gas is confined in the plane, where the two ground states are labeled by and , respectively. The two-photon Raman process is driven by two copropagating Raman beams carrying different orbital angular momenta and [see Figs. 8(a), 8(b)], and is characterized by the inhomogeneous Raman coupling , two-photon detuning and a phase winding . Here, the polar coordinate is taken. After a unitary transformation, the effective single-particle Hamiltonian again reduces to Eq. (17). As we can see that the Raman coupling and two-photon detuning serve as effective transverse and longitudinal Zeeman fields, respectively, which play crucial roles in stabilizing vortices. Different from the LG Raman beams used in previous experiments Chen2018S ; Zhang2019G , Chen et al. propose Raman coupling as Chen2020G , with the peak intensity and the beam waist, which can be experimentally realized Rumala-17 . Such a choice of the Raman beams is mainly on the basis that the LG Raman beams used in current experiments are suppressed over a considerable region near , giving rise to an almost vanishing spin mixing effect in the vicinity, which is unfavorable for vortex formation essentially. Here, Raman lasers are assumed to operate at the tune-out wavelength Holmgren2012M ; Herold2012P ; Zhang2019G , leading to a vanishing diagonal ac-stark potential that is consistent with the experiment Zhang2019G . The external potential is chosen as an isotropic hard-wall box trap with a radius , which offers a natural boundary.
It is helpful for understanding the mechanism of vortex formation by analysis of the single-particle properties before moving to the many-body calculation. Figs. 8(c) and (d) illustrate the impact of the two-photon detuning on the single-particle spectrum. At the resonance with , the time-reversal symmetry gives rise to . Whereas away from the resonance at finite , the breaking of the time-reversal symmetry results in a deformation of the Fermi surface. In the many-body setting when the attractive interaction is taken into account, pairing predominantly occurs between unlike spins with the same radial quantum number to maximize the overlap of radial wave functions. Thus, for the symmetric eigenspectrum under , it is more favorable for two fermions with opposite angular quantum numbers ( and ), forming a Cooper pair with a zero total angular momenta. In contrast, under a finite with asymmetric eigenspectrum, the two fermions in a Cooper pair may possess different values of , leading to a pairing state with a nonzero quantized angular momentum, which is the so-called vortex state. Such a mechanism for the vortex formation is analogous to that of the SO-coupling-induced Fulde-Ferrell states, where the interplay between SO coupling and Zeeman fields gives rise to the deformation of Fermi surfaces with broken time-reversal symmetry in the momentum space Wu2013U ; Qu2013T ; Zhang2013T ; Chen2013I ; Liu2013T .

Chen et al. confirm the above analysis by solving the many-body problem under the Bogoliubov–de Gennes (BdG) formalism Chen2020G . Specifically, the order parameter is written in the form of , where the vorticity () indicates the superfluid (vortex) state. With different , the BdG equation and are solved self-consistently with a fixed particle number. The ground state is then determined by comparing the free energies of vortex states with different , the usual superfluid state (), and the normal state ().
As shown in Fig. 9(a), Chen et al. give a typical phase diagram of the system with SOAM coupling in the – plane. For (), vortex states with () emerge, with the phase boundaries unchanged to the sign of . At small and , the ground state is a usual superfluid (SF) with a zero vorticity . Under sufficiently large and/or , the free-energy difference between the SF and normal () states becomes vanishingly small, and hence the system enters the normal state. Remarkably, two vortex states emerge between SF and states. For example, with a fixed [see Fig. 9(a)], the ground state is in the SF state under small detunings , and becomes a fully-gapped vortex state () beyond a critical value of . Further increase of gives rise to a gapless vortex state (), whose bulk excitation gap closes. In Figs. 9(b), 9(c), free energies of different states are compared, as the phase diagram is traversed. Especially, for the case with , the ground state remains vortexless for finite , despite the deformation of the Fermi surface under SOAM coupling and effective Zeeman fields. This originates from the quantized nature of the angular momentum, and is on the sharp contrary to the SO-coupling-induced Fulde-Ferrell state which carries a nonzero, continuously varying center-of-mass momentum in the presence of SO coupling and Zeeman fields Dong2013F ; Shenoy2013F ; Wu2013U ; Qu2013T ; Zhang2013T ; Chen2013I ; Liu2013T .

Remarkably, as illustrated in Fig. 10, the SOAM-induced vortex state features a giant and tunable vortex-core size, similar to that in a BEC interacting with a microwave field Qin2016S . The vortex-core size, characterized by variations of the order parameter, is comparable to the waist of LG beams. Compared to the conventional vortex states in atomic Fermi superfluids, where changes in the vortex-core structure predominantly take place within a short length scale set by the interatomic separation Sensarma2006V ; Chien2006G , these SOAM-coupling-induced vortex states, with tunable size and core structure, provide unprecedented experimental access to topological defects in Fermi superfluids.
Different from Chen et al.’s configuration, Wang et al. investigate a similar vortex-forming scheme under SOAM coupling Wang2021E . Most strikingly, they predict that an unprecedented vortex state, which is an angular analog of SO-coupling-induced Larkin-Ovchinnikov state, to occur.
Nevertheless, for the inevitable heating introduced by the Raman process, it is difficult to cool a realistic Fermi gas with SOAM coupling below the superfluid temperature heating , which leads to the exclusiveness of SOAM-coupling-induced novel states. Instead, concerning the persistence of dressed molecules above the critical temperature in Fermi gases with SO coupling Williams2013R ; Fu2014P , it is reasonable to expect that molecular states in a SOAM-coupled Fermi gas should be readily accessible under typical experimental conditions. Based on the above consideration, Han et al. studied the two-body bound states in a SOAM-coupled quantum gas of fermions very recently Han2022M . They identify the condition for the emergence of molecular states with finite total angular momenta and propose to detect the molecules according to the radio-frequency spectroscopy. As the molecular states can form above the superfluid transition temperature, Han et al. offer an experimentally more accessible route toward the study of the underlying pairing mechanism under SOAM coupling.
V.3 SOAM-coupling-induced topological states
As discussed in Sec. V.1, it is expected that SOAM coupling can induce a topological superfluid with the help of Zeeman fields and interactions. While, implemention of SOAM coupling relies on the spatial dependence of the LG beams, which gives rise to the dimensionality of atomic gases must higher than one; whereas, it is also realized that the Fermi superfluid becomes gapless and losses its topological features when its spatial dimensionality higher than that of SO coupling Wu2013U ; yisoc . Such that the one-dimensional nature of the SOAM coupling (coupling only occurs along the azimuthal direction) imposes a stringent constraint on the stability of an angular topological superfluid. Whether such a topological superfluid can also be stabilized under SOAM coupling should be verified. It is shown that the stability of a fully gapped angular topological superfluid survives the constraint above, provided that the radial motion of atoms is sufficiently suppressed and then the topological gap is not closed Chen-22 .

The survives of the angular topological superfluid can be understood through the following analysis. As shown in Eq. (17), the Raman coupling and the diagonal ac-stark potential can be written as and , consistent with configurations of current experiments on SOAM coupling Chen2018S ; Zhang2019G . Here, is the effective SOAM-coupling strength, is the trapping strength of the diagonal ac-stark potential, and is the spatial intensity profile of LG lasers, with the beam waist. Different from the SOAM-induced vortex state in Sec. V.2, here, provides an extra confinement potential, which plays an important role in stabilizing the topological superfluid. For a confinement that is sufficiently tight along the radial direction, the radial degrees of freedom of the atoms are frozen, and the remaining quantized angular motion is then well-captured by an effective one-dimensional model with discretized modes. Intuitively, such a scenario occurs when the trap depth is so large that the radial excitation energy () becomes much larger than any other relevant energy scales of the system. The atoms are then localized near in the radial direction and the system reduces to an effective one-dimensional model along the angular direction.
The above analysis is confirmed through the BdG approach Chen-22 . As illustrated in Fig. 11, Chen et al. show the Bogoliubov quasiparticle spectrum in a sufficiently deep ac-stark potential with in the unit of energy . For the case with , the ground state always emerges at . Here, consistent with Sec. V.2, the vorticity () denotes the superfluid (vortex) state. By increasing the coupling strength , the Bogoliubov spectrum undergoes a gap-closing and re-opening process, reminiscent of that of a topological phase transition. Specifically, the Bogoliubov quasiparticle excitation is fully gapped under small [Fig. 11(a)], and then becomes gapless at a critical [Fig. 11(b)], and finally is again fully gapped for further increasing [Fig. 11(c)]. The process of gap closing and re-opening is further demonstrated as a topological phase transition by calculating the Zak phase of the one-dimensional effective Hamiltonian Chen-22 . Besides, it is also demonstrated that the angular topological superfluid is stabilized when the ac-stark potential becomes sufficiently large.

Building upon the topological superfluid state above, an exotic topological vortex state can be induced by taking the two-photon detuning into account, which deforms the Fermi surface. As shown in Figs. 12(a)–12(c), the free energy is generically asymmetric with respect to at a finite . The asymmetry becomes more apparent with increasing , until the ground-state order parameter eventually acquires a finite phase with . Intriguingly, such a transition into the vortex state is topological. As demonstrated in Chen-22 , while the Fermi-surface deformation is manifested as the asymmetric spectral shape with respect to , the closing and re-opening of the energy gap persist. Indeed, after the gap is reopened, the angular momentum of the ground state jumps from to . The ground state simultaneously becomes topological, which is confirmed by the Zak-phase calculation. Conceptually, such an exotic topological vortex state is the angular version of the topological Fulde-Ferrell state under the conventional SO coupling Qu2013T ; Zhang2013T ; Chen2013I ; Liu2013T .
In addition, the topological vortex leaves a direct signature in the angular-momentum-space density profile, as illustrated in Figs. 12(d)–(f). The density profile of the minority spin species exhibits a dip close to only in the topological vortex state [Fig. 12(f)], since the spin polarization in the vortex state is a direct result of the two-photon detuning, which plays the role of an effective Zeeman field. Similar signatures have been identified in the topological Fulde-Ferrell state under SO coupling.
The origin of angular topological superfluid comes from the interplay of interactions, Zeeman fields and SOAM couplings. As topological superfluids are believed to host Majorana zero modes at boundaries, once a boundary is created, for instance, by shining a strong laser beam to break the ring geometry of the ac stark potential, Majorana zero modes should be observed.
VI Experiment achievements
The SOAM coupling has been achieved in 87Rb Bose gases independently by two experiment groups Chen2018S ; Chen2018R ; Zhang2019G , following the earlier theoretical proposals DeMarco2015A ; Sun2015S ; Qu2015Q . The Zeeman sublevels of the ground hyperfine manifold |F = 1⟩ are coupled by a pair of copropagating LG beams according to a Raman transition. It leads to an orbital angular momentum change of atoms during the transition between the ground Zeeman states, which play the role of spin. The realization of SOAM coupling in cold atoms has recently been reported in a spin- 87Rb BEC Chen2018S , in which the atoms are loaded into the middle-energy state of three Raman-dressed states. The correlations between spin and orbital angular momentum in this Raman-dressed state are confirmed. Then the ground-state quantum phase transitions are observed in the same bosonic system Chen2018R , known as the Hess-Fairbank effect Hess1967M ; Ishiguro2004V . Meanwhile, the SOAM coupling was also demonstrated in an effective spin-half atomic gas Zhang2019G , following a similar Raman scheme. The ground-state phase diagram is comprehensively studied, and the first-order phase transitions are identified. In the follows, we are going to introduce the main achievements in these experiments.
In the experiment of Lin’s group Chen2018S , the three hyperfine states of the ground-state manifold of 87Rb atoms are coupled by a pair of Raman beams as illustrated in Fig. 13, one of which is an LG beam carrying orbital angular momentum . The center-of-mass angular momentum of atoms changes during the transition between different hyperfine states. This effectively produces a light-induced effect of a spin particle moving in a magnetic Zeeman field , which results in a SOAM coupling after a local spin rotation. In the experiment, the BEC is initially prepared in the bare hyperfine state , and then is transferred to . After slowly switching on the Raman fields, the atoms are adiabatically loaded into the Raman-dressed polar state with , the middle-energy eigenstate of with the form of Ho1998S
| (33) |
in the bare hyperfine basis , where is the polar angle of the light-induced magnetic Zeeman field . Here, is the Raman-coupling strength and is the Raman detuning. After the adiabatic loading, one easily finds a correlation between the atom spin (hyperfine state) and its orbital angular momentum: the atoms acquire an orbital angular momentum () when transitioning from to (). Therefore, the vortex structures are anticipated in the bare hyperfine states . The Raman-dressed state is conveniently characterized by the QAM in the rotating frame, and the angular momenta of bare hyperfine states in the laboratory frame are, respectively, and .

The vortex structures in the bare hyperfine states could be probed according to a Stern-Gerlach scheme after a time-of-flight (TOF) expansion by simultaneously turning off the Raman beams and external trap. The density profile of bare hyperfine components after ms TOF with holding time ms are presented in Fig. 14(a) for different Raman detunings, as well as the corresponding total density profile (or optical density) presented in Fig. 14(b). It is easily found that the component carries zero angular momentum, while the components carry the same magnitude of angular momentum indicated from their same hole sizes. The interference pattern between components shown in Fig. 14(c) implies that they carry the opposite rotation directions of vortices with angular momentum .

While the SOAM coupling is demonstrated according to adiabatically loading atoms into the middle-energy Raman-dressed state , the effective light-induced gauge potential in this dressed state is zero, i.e., Chen2018S , which leads to a vanishing magnetic field experienced by atoms, i.e., . Subsequently, Lin’s group further reports the realization of non-zero gauge potential with SOAM coupling by adiabatically loading atoms into the Raman-dressed state , the lowest-energy eigenstate of (Ho1998S, ; Chen2018R, ),
| (34) |
where is the phase introduced by a gauge transformation. Then an azimuthal gauge potential is induced by SOAM coupling, taking the form of under the choice of , which gives rise to an effective magnetic field experienced by atoms. The magnetic flux through the atomic cloud can be tuned via the Raman detuning . This leads to a phase transition of the SOAM-coupled ground state from one to another QAM. In the experiment (Chen2018R, ), it is demonstrated that the QAM of the ground state changes from to as the Raman detuning continuously decreases. The phase transition occurs at the critical Raman detuning Hz as shown in Fig. 15(a). At a detuning below the critical value, i.e., Hz, the system stays at the ground state with QAM . The corresponding mechanical angular momenta of bare hyperfine states are for in the laboratory frame. The same hole sizes in the and are observed in the experiment as shown in Fig. 15(a). At a detuning above the critical value, i.e., Hz, the SOAM-coupled ground state transits to the state with QAM , which corresponds to the mechanical angular momenta of bare hyperfine states for in the laboratory frame. Then the vortex with larger hole size in , compared to that in , is anticipated and is experimentally confirmed.

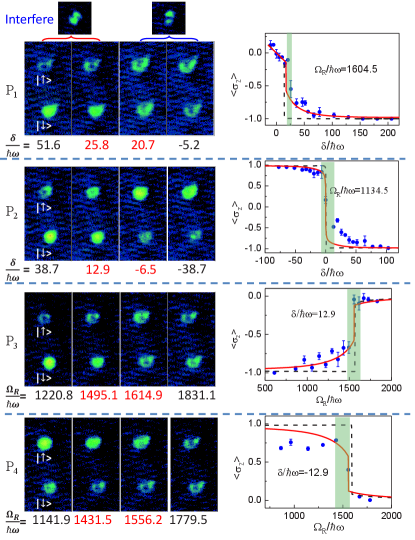
Soon, the ground-state quantum phase diagram of this SOAM-coupled system is comprehensively studied in an effective spin-half 87Rb atomic gas Zhang2019G . Due to a larger quadratic Zeeman shift kHz compared to that of Chen2018S ; Chen2018R , the third Zeeman hyperfine state is far-off-resonant, and is then dropped out from the problem. In addition, one of the two Raman beams is operated in a higher LG mode with a winding number . It gives rise to a rich ground-state phase diagram as presented in Fig. 16. The whole system is therefore governed by the Hamiltonian (15) in the presence of LG Raman beams, which introduces an effective SOAM coupling as seen in Eq. (17) after a unitary transformation. Here, a tune-out wavelength of LG beams is chosen Schmidt2016W . It ensures that any observed circular structure of atomic clouds is resulted from the vortex formation due to the SOAM coupling, excluding the trapping effect of the diagonal ac-stark potential of LG beams.
In order to explore the ground-state quantum phases of the system, the Raman beams need to be introduced adiabatically. After preparing the BEC in the hyperfine state by setting a large detuning kHz, the Raman beams are turned on. Then the detuning is ramped to the desired value adiabatically. This process keeps the system remaining in the ground state all the time. Subsequently, the transitions between different ground-state quantum phases could be studied following different paths as shown in Fig. 16(c). For example, along the path , the Raman coupling strength is fixed at in the unit of harmonic energy, while the detuning adiabatically decreases across the phase boundary. The SOAM-coupled system transits from the half-skyrmion phase with QAM to the vortex-antivortex phase with QAM . The phase transition can experimentally be identified according to the change of density profiles of bare hyperfine states: the vortex structure exists only in the spin- atomic cloud in the half-skyrmion phase, while both spin states exhibit vortex formations in the vortex-antivortex phase. The analogous procedures are performed along the paths .

The spin-resolved density profiles are presented in Fig. 17 across different phase boundaries. To confirm the formation of vortices that the circular structures of atom clouds carry angular momenta, a resonant radio-frequency (rf) pulse is applied, that transfers the atoms between internal Zeeman hyperfine states and Matthews1999V ; Andersen2006Q ; Wright2009S . The appearance of the interference pattern in each spin component during TOF, as shown in Fig. 17, implies that the circular structures are indeed vortices before the rf transition. The spin polarization is an additional indicator of the phase transitions, which jumps among across different phase boundaries. Here, is the atom number for the spin-component. The spin polarization is presented as a function of the two-photon detuning in Fig. 17. The evident jump behavior during phase transitions is observed in the experiment even at finite temperatures. Regarding these characteristic behaviors across the phase transitions, it allows us to identify the boundaries of different ground-state quantum phases. Then the ground-state phase diagram is conveniently mapped out in the parameter space spanned by the detuning and the coupling strength , as illustrated in Fig. 18.

VII Conclusions and outlooks
In conclusion, the most recent advances in both the theories and experiments of spin-orbital-angular-momentum (SOAM) coupled quantum gases are briefly summarized in this review. The basic idea of engineering SOAM coupling in ultracold atoms is presented, and exotic quantum phases of Bose gases are introduced as well as those of Fermi gases in the presence of SOAM coupling. In spite of remarkable progress in this field, it is far from the end of the story. There could be further developments in SOAM-coupled quantum gases, since several issues still require more theoretical and experimental efforts.
Few-body physics—As a building block of interacting many-body systems, the few-body problem is of important significance in ultracold atoms. For instance, the two-body physics determines the essential interaction parameter in the many-body Hamiltonian, and even dominates crucial quantum correlations in many-body systems, such as Tan’s relations (Tan2008E, ; Tan2008L, ; Tan2008G, ). Besides, the few-body problem itself displays intriguing features such as the Feshbach resonance and Efimov effect. The few-body problem has intensively been studied in spin-linear-momentum-coupled quantum gases Cui2012M ; Zhang2012M ; Cui2014U ; Shi2014U ; Peng2018C ; Zhang2020U ; Zhang2021U , while the theory for SOAM-coupled systems is still elusive to date. Rich physics in this new few-body system is remained to be discovered in near future, which could provide deep insight into many-body properties of SOAM-coupled quantum gases.
Finite-temperature phase diagrams—The current theory of SOAM-coupled quantum systems is constructed in the framework of the zero-temperature mean-field theory. For example, the ground-state quantum phases of Bose gases are based on the solution of the Gross-Pitaevskii equation, while the giant vortex Fermi superfluid is predicted by the zero-temperature Bogoliubov-de Gennes formalism. The natural question arises whether these exotic quantum phases are stable enough against the thermal fluctuation at finite temperature as well as against the quantum fluctuation at zero temperature beyond the mean-field theory Chen2017Q . A more comprehensive theoretical analysis is required to address these issues, and is necessary for the comparison with experimental observations as well.
Experimental perspectives—The angular stripe phases of SOAM-coupled Bose gases have not yet been observed in experiments. It is energetically favored for an intraspecies interaction strength larger than the interspecies one (i.e., ). However, there is no convenient Feshbach resonance of 87Rb atoms to adjust interactions. The angular stripe phase lies in a narrow parameter window due to the small difference between (or ) and for 87Rb atomic gases. For this reason, the 41K atomic gas becomes one of the promising candidates for future experiments Chen2020A , in which the interspecies scattering length can be tuned in a wide range near the Feshbach resonance centered at the magnetic field G, while the intraspecies scattering lengths are approximately constant. By choosing appropriately the interatomic scattering lengths, the window of angular stripe phases in the parameter space is enlarged, which can be operated easily in experiments Chen2020A .
Moreover, the SOAM coupling is not realized in Fermi gases at present, which would provide a new platform to investigate exotic vortex and topological superfluid states. Other interesting directions, such as the non-equilibrium or the dynamics, BCS-BEC crossover, and quantum fluctuations of Fermi gases with SOAM coupling are yet to be explored. All these fascinating and remarkable phenomena are devoted to future studies.
VIII acknowledgments
We are grateful for inspiring discussions with Tian-You Gao, Wei Yi and Fan Wu. SGP and KJ are supported by the National Natural Science Foundation of China under Grant Nos. 11974384 and 12121004, the National Key R&D Program under Grant No. 2022YFA1404102, Chinese Academy of Sciences under Grant No. YJKYYQ20170025, K. C. Wong Education Foundation under Grant No. GJTD-2019-15, and the Natural Science Foundation of Hubei Province under Grant No. 2021CFA027. XLC is supported by the Natural Science Foundation of China under Grant No. 12204413 and the Science Foundation of Zhejiang Sci-Tech University under Grant No. 21062339-Y. KJC is supported by the Natural Science Foundation of China under Grant No. 12104406 and the Science Foundation of Zhejiang Sci-Tech University under Grant No. 21062338-Y. PZ is supported by the National Natural Science Foundation of China under Grant No. 11804177. LYH is supported by the National Key R&D Program under Grant No. 2018YFA0306503.
References
- (1) R. Barnes, Formation and Evolution of Exoplanets (Wiley-VCH 2010).
- (2) L. D. Landau and E. M. Lifshitz, Quantum mechanics (Non-relativistic theory) (Butterworth-Heinemann, Oxford 2007).
- (3) I. Talmi, Nuclear shell theory, (Academic Press 1963).
- (4) X.-L. Qi and S.-C. Zhang, The quantum spin hall effect and topological insulators, Physics Today 63, 33 (2010).
- (5) I. Bloch, J. Dalibard, and W. Zwerger, Many-body physics with ultracold gases, Rev. Mod. Phys. 80, 885 (2008).
- (6) S. Giorgini, L. P. Pitaevskii, and S. Stringari, Theory of ultracold atomic Fermi gases, Rev. Mod. Phys. 80, 1215 (2008).
- (7) T. Kohler, K. Goral, and P. S. Julienne, Production of cold molecules via magnetically tunable Feshbach resonances, Rev. Mod. Phys. 78, 1311 (2006).
- (8) C. Chin, R. Grimm, P. Julienne, and E. Tiesinga, Feshbach resonances in ultracold gases, Rev. Mod. Phys. 82, 1225 (2010).
- (9) C. Gross and I. Bloch, Quantum simulations with ultracold atoms in optical lattices, Science 357, 995 (2017).
- (10) J. Dalibard, F. Gerbier, G. Juzeliunas, and P. Ohberg, Colloquium: Artificial gauge potentials for neutral atoms, Rev. Mod. Phys. 83, 1523 (2011).
- (11) D. A. Abanin, E. Altman, I. Bloch, and M. Serbyn, Colloquium: Many-body localization, thermalization, and entanglement, Rev. Mod. Phys. 91, 021001 (2019).
- (12) X.-J. Liu, M. F. Borunda, X. Liu, and J. Sinova, Effect of Induced Spin-Orbit Coupling for Atoms via Laser Fields, Phys. Rev. Lett. 102, 046402 (2009).
- (13) Y.-J. Lin, K. Jimenez-Garcia, and I. B. Spielman, Spin-orbit-coupled Bose-Einstein condensates, Nature 471, 83 (2011).
- (14) R. A. Williams, L. J. LeBlanc, K. Jimenez-Garcia, M. C. Beeler, A. R. Perry, W. D. Phillips, and I. B. Spielman, Synthetic Partial Waves in Ultracold Atomic Collisions, Science 335, 314 (2012).
- (15) P.-J. Wang, Z- Q. Yu, Z.-K. Fu, J. Miao, L.-H. Huang, S.-J. Chai, H. Zhai, and J. Zhang, Spin-orbit coupled degenerate Fermi gases, Phys. Rev. Lett. 109, 095301 (2012).
- (16) L. W. Cheuk, A. T. Sommer, Z. Hadzibabic, T. Yefsah, W. S. Bakr, and M. W. Zwierlein, Spin-injection spectroscopy of a spin-orbit coupled Fermi gas, Phys. Rev. Lett. 109, 095302 (2012).
- (17) J.-Y. Zhang, S.-C. Ji, Z. Chen, L. Zhang, Z.-D. Du, B. Yan, G.-S. Pan, B. Zhao, Y.-J. Deng, H. Zhai, S. Chen, and J.-W. Pan, Collective Dipole Oscillations of a Spin-Orbit Coupled Bose-Einstein Condensate, Phys. Rev. Lett. 109, 115301 (2012).
- (18) A. J. Olson, S.-J. Wang, R. J. Niffenegger, C.-H. Li, C. H. Greene, and Y.-P. Chen, Tunable Landau-Zener transitions in a spin-orbit-coupled Bose-Einstein condensate, Phys. Rev. A 90, 013616 (2014).
- (19) Z.-K. Fu, L.-H. Huang, Z.-M. Meng, P.-J. Wang, L. Zhang, S.-Z. Zhang, H. Zhai, P. Zhang, and J. Zhang, Production of Feshbach molecules induced by spin-orbit coupling in Fermi gases, Nat. Phys. 10, 110 (2014).
- (20) S.-C. Ji, J.-Y. Zhang, L. Zhang, Z.-D. Du, W. Zheng, Y.-J. Deng, H. Zhai, S. Chen, and J.-W. Pan, Experimental determination of the finite-temperature phase diagram of a spin-orbit coupled Bose gas, Nat. Phys. 10, 314 (2014).
- (21) S.-C. Ji, L. Zhang, X.-T. Xu, Z. Wu, Y.-J. Deng, S. Chen, and J.-W. Pan, Softening of Roton and Phonon Modes in a Bose-Einstein Condensate with Spin-Orbit Coupling, Phys. Rev. Lett. 114, 105301 (2015).
- (22) C. Hamner, Y.-P. Zhang, M. A. Khamehchi, M. J. Davis, and P. Engels, Spin-Orbit-Coupled Bose-Einstein Condensates in a One-Dimensional Optical Lattice, Phys. Rev. Lett. 114, 070401 (2015).
- (23) K. Jimenez-Garcia, L. J. LeBlanc, R. A. Williams, M. C. Beeler, C. Qu, M. Gong, C. Zhang, and I. B. Spielman, Tunable Spin-Orbit Coupling via Strong Driving in Ultracold-Atom Systems, Phys. Rev. Lett. 114, 125301 (2015).
- (24) N. Q. Burdick, Y.-J. Tang, and B. L. Lev, Long-Lived Spin-Orbit-Coupled Degenerate Dipolar Fermi Gas, Phys. Rev. X 6, 031022 (2016).
- (25) B. Song, C.-D. He, S.-C. Zhang, E. Hajiyev, W. Huang, X.-J. Liu, and G. B. Jo, Spin-orbit-coupled two-electron Fermi gases of ytterbium atoms, Phys. Rev. A 94, 061604 (2016).
- (26) J.-R. Li, W.-J. Huang, B. Shteynas, S. Burchesky, F. C. Top, E. Su, J. Lee, A. O. Jamison, and W. Ketterle, Spin-Orbit Coupling and Spin Textures in Optical Superlattices, Phys. Rev. Lett. 117, 185301 (2016).
- (27) L. F. Livi, G. Cappellini, M. Diem, L. Franchi, C. Clivati, M. Frittelli, F. Levi, D. Calonico, J. Catani, M. Inguscio, and L. Fallani, Synthetic Dimensions and Spin-Orbit Coupling with an Optical Clock Transition, Phys. Rev. Lett. 117, 220401 (2016).
- (28) K. Osterloh, M. Baig, L. Santos, P. Zoller, and M. Lewenstein, Cold atoms in non-Abelian gauge potentials: From the Hofstadter "Moth" to lattice gauge theory, Phys. Rev. Lett. 95, 010403 (2005).
- (29) J. Ruseckas, G. Juzeliunas, P. Ohberg, and M. Fleischhauer, Non-Abelian gauge potentials for ultracold atoms with degenerate dark states, Phys. Rev. Lett. 95, 010404 (2005).
- (30) G. Juzeliunas, J. Ruseckas, and J. Dalibard, Generalized Rashba-Dresselhaus spin-orbit coupling for cold atoms, Phys. Rev. A 81, 053403 (2010).
- (31) D. L. Campbell, G. Juzeliunas, and I. B. Spielman, Realistic Rashba and Dresselhaus spin-orbit coupling for neutral atoms, Phys. Rev. A 84, 025602 (2011).
- (32) J. D. Sau, R. Sensarma, S. Powell, I. B. Spielman, and S. Das Sarma, Chiral Rashba spin textures in ultracold Fermi gases, Phys. Rev. B 83, 140510 (2011).
- (33) B. M. Anderson, I. B. Spielman, and G. Juzeliunas, Magnetically Generated Spin-Orbit Coupling for Ultracold Atoms, Phys. Rev. Lett. 111, 125301 (2013).
- (34) Z.-F. Xu, L. You, and M. Ueda, Atomic spin-orbit coupling synthesized with magnetic-field-gradient pulses, Phys. Rev. A 87, 063634 (2013).
- (35) X.-J. Liu, K. T. Law, and T. K. Ng, Realization of 2D Spin-Orbit Interaction and Exotic Topological Orders in Cold Atoms, Phys. Rev. Lett. 112, 086401 (2014).
- (36) B. M. Anderson, G. Juzeliunas, V. M. Galitski, and I. B. Spielman, Synthetic 3D Spin-Orbit Coupling, Phys. Rev. Lett. 108, 235301 (2012).
- (37) Y. H. Lu, B. Z. Wang, and X. J. Liu, Ideal Weyl semimetal with 3D spin-orbit coupled ultracold quantum gas, Science Bulletin 65, 2080 (2020).
- (38) B.-Z. Wang, Y.-H. Lu, W. Sun, S. Chen, Y.-J. Deng, and X.-J. Liu, Dirac-, Rashba-, and Weyl-type spin-orbit couplings: Toward experimental realization in ultracold atoms, Phys. Rev. A 97, 011605 (2018).
- (39) L.-H. Huang, Z.-M. Meng, P.-J. Wang, P. Peng, S.-L. Zhang, L.-C. Chen, D.-H. Li, Q. Zhou, and J. Zhang, Experimental realization of two-dimensional synthetic spin-orbit coupling in ultracold Fermi gases, Nat. Phys. 12, 540 (2016).
- (40) Z. Wu et al., Realization of two-dimensional spin-orbit coupling for Bose-Einstein condensates, Science 354, 83 (2016).
- (41) Z.-Y. Wang, X.-C. Cheng, B.-Z. Wang, J.-Y. Zhang, Y.-H. Lu, C.-R. Yi, S. Niu, Y.-J. Deng, X.-J. Liu, S. Chen, and J.-W. Pan, Realization of an ideal Weyl semimetal band in a quantum gas with 3D spin-orbit coupling, Science 372, 271 (2021).
- (42) H. Zhai, Spin-orbit coupled quantum gases, Int. J. Mod. Phys. B 26, 1230001 (2012).
- (43) H. Zhai, Degenerate quantum gases with spin-orbit coupling: A review, Rep. Prog. Phys. 78, 026001 (2015).
- (44) L. Zhang, and X.-J. Liu, Spin-orbit coupling and topological phases for ultracold atoms, arXiv:1806.05628 (2018) (published book, Synthetic Spin-Orbit Coupling in Cold Atoms, pp. 1-87 (2018) Chapter 1: Spin-orbit Coupling and Topological Phases for Ultracold Atoms).
- (45) X.-J. Liu, H. Jing, X. Liu, and M.-L. Ge, Generation of two-flavor vortex atom laser from a five-state medium, Eur. Phys. J. D 37, 261 (2006).
- (46) M. DeMarco and H. Pu, Angular spin-orbit coupling in cold atoms, Phys. Rev. A 91, 033630 (2015).
- (47) K. Sun, C.-L. Qu, and C.-W. Zhang, Spin-orbital-angular-momentum coupling in Bose-Einstein condensates, Phys. Rev. A 91, 063627 (2015).
- (48) C.-L. Qu, K. Sun, and C. W. Zhang, Quantum phases of Bose-Einstein condensates with synthetic spin-orbital-angular-momentum coupling, Phys. Rev. A 91, 053630 (2015).
- (49) Y.-X. Hu, C. Miniatura, and B. Gremaud, Half-skyrmion and vortex-antivortex pairs in spinor condensates, Phys. Rev. A 92, 033615 (2015).
- (50) L. Chen, H. Pu, and Y.-B. Zhang, Spin-orbit angular momentum coupling in a spin-1 Bose-Einstein condensate, Phys. Rev. A 93, 13629 (2016).
- (51) I. Vasic and A. Balaz, Excitation spectra of a Bose-Einstein condensate with an angular spin-orbit coupling, Phys. Rev. A 94, 033627 (2016).
- (52) J.-P. Hou, X.-W. Luo, K. Sun, and C.-W. Zhang, Adiabatically tuning quantized supercurrents in an annular Bose-Einstein condensate, Phys. Rev. A 96, 011603 (2017).
- (53) H. R. Chen et al., Spin-orbital-angular-momentum coupled Bose-Einstein condensates, Phys. Rev. Lett. 121, 113204 (2018).
- (54) P. K. Chen, L. R. Liu, M. J. Tsai, N. C. Chiu, Y. Kawaguchi, S. K. Yip, M. S. Chang, and Y. J. Lin, Rotating atomic quantum gases with light-induced azimuthal gauge potentials and the observation of the Hess-Fairbank effect, Phys. Rev. Lett. 121, 250401 (2018).
- (55) D. Zhang et al., Ground-state phase diagram of a spin-orbital-angular-momentum coupled Bose-Einstein condensate, Phys. Rev. Lett. 122, 110402 (2019).
- (56) Y. Li, L. P. Pitaevskii, and S. Stringari, Quantum tricriticality and phase transitions in spin-orbit coupled Bose-Einstein condensates, Phys. Rev. Lett. 108, 225301 (2012).
- (57) G. I. Martone, Y. Li, L. P. Pitaevskii, and S. Stringari, Anisotropic dynamics of a spin-orbit-coupled Bose-Einstein condensate, Phys. Rev. A 86, 063621 (2012).
- (58) X.-L. Chen, X.-J. Liu, and H. Hu, Quantum and thermal fluctuations in a Raman spin-orbit-coupled Bose gas, Phys. Rev. A 96, 013625 (2017).
- (59) X.-L. Chen, J. Wang, Y. Li, X.-J. Liu, and H. Hu, Quantum depletion and superfluid density of a supersolid in Raman spin-orbit-coupled Bose gases, Phys. Rev. A 98, 013614 (2018).
- (60) X.-L. Chen, S.-G. Peng, P. Zou, X.-J. Liu, and H. Hu, Angular stripe phase in spin-orbital-angular-momentum coupled Bose condensates, Phys. Rev. Research 2, 033152 (2020).
- (61) K.-J. Chen, F. Wu, J.-S. Hu, and L.-Y. He, Ground-state phase diagram and excitation spectrum of a Bose-Einstein condensate with spin-orbital-angular-momentum coupling, Phys. Rev. A 102, 013316 (2020).
- (62) Y. Duan, Y. M. Bidasyuk, and A. Surzhykov, Symmetry breaking and phase transitions in bose-einstein condensates with spin-orbital-angular-momentum coupling, Phys. Rev. A 102, 063328 (2020).
- (63) N. C. Chiu, Y. Kawaguchi, S. K. Yip, and Y. J. Lin, Visible stripe phases in spin-orbital-angular-momentum coupled Bose-Einstein condensates, New J. Phys. 22, 093017 (2020).
- (64) Y. M. Bidasyuk, K. S. Kovtunenko, and O. O. Prikhodko, Fine structure of the stripe phase in ring-shaped Bose-Einstein condensates with spin-orbital-angular-momentum coupling, Phys. Rev. A 105, 023320 (2022).
- (65) M. Boninsegni and N. V. Prokof’ev, Colloquium: Supersolids: What and where are they?, Rev. Mod. Phys. 84, 759 (2012).
- (66) K.-J. Chen, F. Wu, S.-G. Peng, W. Yi, and L. He, Generating giant vortex in a Fermi superfluid via spin-orbital-angular-momentum coupling, Phys. Rev. Lett. 125, 260407 (2020).
- (67) L.-L. Wang, A.-C. Ji, Q. Sun, and J. Li, Exotic vortex states with discrete rotational symmetry in atomic Fermi gases with spin-orbital-angular-momentum coupling, Phys. Rev. Lett. 126, 193401 (2021).
- (68) L. Dong, L. Jiang, H. Hu, and H. Pu, Finite-momentum dimer bound state in a spin-orbit-coupled Fermi gas, Phys. Rev. A 87, 043616 (2013).
- (69) V. B. Shenoy, Flow-enhanced pairing and other unusual effects in Fermi gases in synthetic gauge fields, Phys. Rev. A 88, 033609 (2013).
- (70) F. Wu, G.-C. Guo, W. Zhang, and W. Yi, Unconventional superfluid in a two-dimensional Fermi gas with anisotropic spin-orbit coupling and Zeeman fields, Phys. Rev. Lett. 110, 110401 (2013).
- (71) C.-L. Qu, Z. Zheng, M. Gong, Y. Xu, L. Mao, X.-B. Zou, G.-C. Guo, and C.-W. Zhang, Topological superfluids with finite-momentum pairing and Majorana fermions, Nat. Comm. 4, 2710 (2013).
- (72) W. Zhang and W. Yi, Topological Fulde-Ferrell-Larkin-Ovchinnikov states in spin-orbit-coupled Fermi gases, Nat. Comm. 4, 2711 (2013).
- (73) C. Chen, Inhomogeneous topological superfluidity in one-dimensional spin-orbit-coupled Fermi gases, Phys. Rev. Lett. 111, 235302 (2013).
- (74) X.-J. Liu and H. Hu, Topological Fulde-Ferrell superfluid in spin-orbit-coupled atomic Fermi gases, Phys. Rev. A 88, 023622 (2013).
- (75) R. Sensarma, M. Randeria, and T. L. Ho, Vortices in superfluid Fermi gases through the BEC to BCS crossover, Phys. Rev. Lett. 96, 090403 (2006).
- (76) C.-C. Chien, Y. He, Q.-J. Chen, and K. Levin, Ground-state description of a single vortex in an atomic Fermi gas: From BCS to Bose-Einstein condensation, Phys. Rev. A 73, 041603 (2006).
- (77) C. Caroli, P. G. Degennes, and J. Matricon, Bound fermion states on a vortex line in a type-II superconductor, Phys. Lett. 9, 307 (1964).
- (78) K.-J. Chen, F. Wu, L. He, and W. Yi, Angular topological superfluid and topological vortex in an ultracold Fermi gas, Phys. Rev. Research 4, 033023 (2022).
- (79) R. A. Williams, M. C. Beeler, L. J. LeBlanc, K. Jimenez-Garcia, and I. B. Spielman, Raman-induced interactions in a single-component Fermi gas near an s-wave Feshbach resonance, Phys. Rev. Lett. 111, 095301 (2013).
- (80) Y. Han, S.-G. Peng, K.-J. Chen, and W. Yi, Molecular state in a spin-orbital-angular-momentum coupled Fermi gas, Phys. Rev. A 106, 043302 (2022).
- (81) M. O. Scully and M. S. Zubairy, Quantum optics (Cambridge University Press, 2008).
- (82) K. P. Marzlin, W.-P. Zhang, and E. M. Wright, Vortex coupler for atomic Bose-Einstein condensates, Phys. Rev. Lett. 79, 4728 (1997).
- (83) W. F. Holmgren, R. Trubko, I. Hromada, and A. D. Cronin, Measurement of a wavelength of light for which the energy shift for an atom vanishes, Phys. Rev. Lett. 109, 243004 (2012).
- (84) C. D. Herold, V. D. Vaidya, X. Li, S. L. Rolston, J. V. Porto, and M. S. Safronova, Precision measurement of transition matrix elements via light shift cancellation, Phys. Rev. Lett. 109, 243003 (2012).
- (85) H. Hu, B. Ramachandhran, H. Pu, and X.-J. Liu, Spin-orbit coupled weakly interacting Bose-Einstein condensates in harmonic traps, Phys. Rev. Lett. 108, 010402 (2012).
- (86) B. Ramachandhran, B. Opanchuk, X.-J. Liu, H. Pu, P. D. Drummond, and H. Hu, Half-quantum vortex state in a spin-orbit-coupled Bose-Einstein condensate, Phys. Rev. A 85, 023606 (2012).
- (87) L. S. Leslie, A. Hansen, K. C. Wright, B. M. Deutsch, and N. P. Bigelow, Creation and detection of skyrmions in a Bose-Einstein condensate, Phys. Rev. Lett. 103, 250401 (2009).
- (88) B. Binz and A. Vishwanath, Chirality induced anomalous-hall effect in helical spin crystals, Physica B Condens. Matter 403, 1336 (2008).
- (89) S. Muhlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, and P. Boni, Skyrmion lattice in a chiral magnet, Science 323, 915 (2009).
- (90) Y.-J. Lin, R. L. Compton, K. Jimenez-Garcia, J. V. Porto, and I. B. Spielman, Synthetic magnetic fields for ultracold atoms, Nature 462, 627 (2009).
- (91) Y.-J. Lin, R. L. Compton, A. R. Perry, W. D. Phillips, J. V. Porto, I. B. Spielman, and B. Collaboration, Bose-Einstein condensate in a uniform light-induced vector potential, Phys. Rev. Lett. 102, 130401 (2009).
- (92) R. Dum and M. Olshanii, Gauge structures in atom-laser interaction: Bloch oscillations in a dark lattice, Phys. Rev. Lett. 76, 1788 (1996).
- (93) P. M. Visser and G. Nienhuis, Geometric potentials for subrecoil dynamics, Phys. Rev. A 57, 4581 (1998).
- (94) S.-L. Zhu, H. Fu, C.-J. Wu, S.-C. Zhang, and L.-M. Duan, Spin Hall effects for cold atoms in a light-induced gauge potential, Phys. Rev. Lett. 97, 240401 (2006).
- (95) X.-J. Liu, X. Liu, L. C. Kwek, and C. H. Oh, Optically induced spin-Hall effect in atoms, Phys. Rev. Lett. 98, 026602 (2007).
- (96) M. C. Beeler, R. A. Williams, K. Jimenez-Garcia, L. J. LeBlanc, A. R. Perry, and I. B. Spielman, The spin Hall effect in a quantum gas, Nature 498, 201 (2013).
- (97) C. Wang, C. Gao, C.-M. Jian, and H. Zhai, Spin-Orbit Coupled Spinor Bose-Einstein Condensates, Phys. Rev. Lett. 105, 160403 (2010).
- (98) C.-J. Wu, I. Mondragon-Shem, and X.-F. Zhou, Unconventional Bose-Einstein Condensations from Spin-Orbit Coupling, Chin. Phys. Lett. 28, 097102 (2011).
- (99) T.-L. Ho and S. Zhang, Bose-Einstein Condensates with Spin-Orbit Interaction, Phys. Rev. Lett. 107, 150403 (2011).
- (100) J. Léonard, A. Morales, P. Zupancic, T. Esslinger, and T. Donner, Supersolid formation in a quantum gas breaking a continuous translational symmetry, Nature 543, 87 (2017).
- (101) J.-R. Li, J. Lee, W. Huang, S. Burchesky, B. Shteynas, F. C. Top, A. O. Jamison, and W. Ketterle, A stripe phase with supersolid properties in spin–orbit-coupled Bose–Einstein condensates, Nature 543, 91 (2017).
- (102) L. Tanzi, E. Lucioni, F. Famá, J. Catani, A. Fioretti, C. Gabbanini, R. N. Bisset, L. Santos, and G. Modugno, Observation of a Dipolar Quantum Gas with Metastable Supersolid Properties, Phys. Rev. Lett. 122, 130405 (2019).
- (103) F. Böttcher, J.-N. Schmidt, M. Wenzel, J. Hertkorn, M. Guo, T. Langen, and T. Pfau, Transient Supersolid Properties in an Array of Dipolar Quantum Droplets, Phys. Rev. X 9, 011051 (2019).
- (104) L. Chomaz, D. Petter, P. Ilzhöfer, G. Natale, A. Trautmann, C. Politi, G. Durastante, R. M. W. van Bijnen, A. Patscheider, M. Sohmen, M. J. Mark, and F. Ferlaino, Long-Lived and Transient Supersolid Behaviors in Dipolar Quantum Gases, Phys. Rev. X 9, 021012 (2019).
- (105) M. A. Norcia, C. Politi, L. Klaus, E. Poli, M. Sohmen, M. J. Mark, R. N. Bisset, L. Santos, and F. Ferlaino, Two-dimensional supersolidity in a dipolar quantum gas, Nature 596, 357 (2021).
- (106) M. Lysebo and L. Veseth, Feshbach resonances and transition rates for cold homonuclear collisions between 39K and 41K atoms, Phys. Rev. A 81, 032702 (2010).
- (107) L. Tanzi, C. R. Cabrera, J. Sanz, P. Cheiney, M. Tomza, and L. Tarruell, Feshbach resonances in potassium Bose-Bose mixtures, Phys. Rev. A 98, 062712 (2018).
- (108) P. Fulde and R. A. Ferrell, Superconductivity in a Strong Spin-Exchange Field, Phys. Rev. 135, A550 (1964).
- (109) A. I. Larkin and Y. N. Ovchinnikov, Nonuniform State of Superconductors, Sov. Phys. JETP 20, 762 (1965).
- (110) X.-J. Liu, Z.-X. Liu, and M. Cheng, Manipulating Topological Edge Spins in a One-Dimensional Optical Lattice, Phys. Rev. Lett. 110, 076401 (2013).
- (111) X.-J. Liu, K.T. Law, and T.K. Ng, Realization of 2D Spin-Orbit Interaction and Exotic Topological Orders in Cold Atoms, Phys. Rev. Lett. 112, 086401 (2014).
- (112) Z. Meng, L. Huang, P. Peng, D. Li, L. Chen, Y. Xu, C. Zhang, P. Wang, and J. Zhang, Experimental Observation of a Topological Band Gap Opening in Ultracold Fermi Gases with Two-Dimensional Spin-Orbit Coupling, Phys. Rev. Lett. 117, 235304 (2016).
- (113) L. Fu and C. L. Kane, Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator, Phys. Rev. Lett. 100, 096407 (2008).
- (114) J. D. Sau, R. M. Lutchyn, S. Tewari, and S. Das Sarma, Generic New Platform for Topological Quantum Computation Using Semiconductor Heterostructures, Phys. Rev. Lett. 104, 040502 (2010).
- (115) J. Alicea, Majorana fermions in a tunable semiconductor device, Phys. Rev. B 81. 125318 (2010).
- (116) Y. Oreg, G. Refael, and F. von Oppen, Helical Liquids and Majorana Bound States in Quantum Wires, Phys. Rev. Lett. 105, 177002 (2010).
- (117) L. Mao, J. Shi, Q. Niu, and C. Zhang, Superconducting Phase with a Chiral f-Wave Pairing Symmetry and Majorana Fermions Induced in a hole-doped Semiconductor, Phys. Rev. Lett. 106, 157003 (2011).
- (118) S. Tewari, T. D. Stanescu, J. D. Sau, and S. Das Sarma, Topologically non-trivial superconductivity in spin-orbit-coupled systems: bulk phases and quantum phase transitions, New J. Phys. 13, 065004 (2011).
- (119) J. Zhou, W. Zhang, and W. Yi, Topological superfluid in a trapped two-dimensional polarized Fermi gas with spin-orbit coupling, Phys. Rev. A 84, 063603 (2011).
- (120) Y. S. Rumala and A. E. Leanhardt, Optical vortex with a small core and Gaussian intensity envelope for light-matter interaction, J. Opt. Soc. Am. B 34, 909 (2017).
- (121) J.-L. Qin, G.-J. Dong, and B. A. Malomed, Stable giant vortex annuli in microwave-coupled atomic condensates, Phys. Rev. A 94, 053611 (2016).
- (122) X. Cui, B. Lian, T.-L. Ho, B. L. Lev, and H. Zhai, Synthetic gauge field with highly magnetic lanthanide atoms, Phys. Rev. A 88, 011601(R) (2013).
- (123) W. Yi and G.-C. Guo, Phase separation in a polarized Fermi gas with spin-orbit coupling, Phys. Rev. A 84, 031608(R) (2011).
- (124) G. B. Hess and W. M. Fairbank, Measurements of Angular Momentum in Superfluid Helium, Phys. Rev. Lett. 19, 216 (1967).
- (125) R. Ishiguro, O. Ishikawa, M. Yamashita, Y. Sasaki, K. Fukuda, M. Kubota, H. Ishimoto, R. E. Packard, T. Takagi, T. Ohmi, and T. Mizusaki, Vortex Formation and Annihilation in Three Textures of Rotating Superfluid -, Phys. Rev. Lett. 93, 125301 (2004).
- (126) T.-L. Ho, Spinor Bose Condensates in Optical Traps, Phys. Rev. Lett. 81, 742 (1998).
- (127) F. Schmidt, D. Mayer, M. Hohmann, T. Lausch, F. Kindermann, and A. Widera, Precision measurement of the 87Rb tune-out wavelength in the hyperfine ground state at nm, Phys. Rev. A 93, 022507 (2016).
- (128) M. R. Matthews, B. P. Anderson, P. C. Haljan, D. S. Hall, C. E. Wieman, and E. A. Cornell, Vortices in a Bose-Einstein condensate, Phys. Rev. Lett. 83, 2498 (1999).
- (129) M. F. Andersen, C. Ryu, P. Clade, V. Natarajan, A. Vaziri, K. Helmerson, and W. D. Phillips, Quantized rotation of atoms from photons with orbital angular momentum, Phys. Rev. Lett. 97, 170406 (2006).
- (130) K. C. Wright, L. S. Leslie, A. Hansen, and N. P. Bigelow, Sculpting the Vortex State of a Spinor BEC, Phys. Rev. Lett. 102, 030405 (2009).
- (131) S. Tan, Energetics of a strongly correlated Fermi gas, Ann. Phys. 323, 2952 (2008).
- (132) S. Tan, Large momentum part of a strongly correlated Fermi gas, Ann. Phys. 323, 2971 (2008).
- (133) S. Tan, Generalized virial theorem and pressure relation for a strongly correlated Fermi gas, Ann. Phys. 323, 2987 (2008).
- (134) X.-L. Cui, Mixed-partial-wave scattering with spin-orbit coupling and validity of pseudopotentials, Phys. Rev. A 85, 022705 (2012).
- (135) P. Zhang, L. Zhang, and Y. J. Deng, Modified Bethe-Peierls boundary condition for ultracold atoms with spin-orbit coupling, Phys. Rev. A 86, 053608 (2012).
- (136) X.-L. Cui and W. Yi, Universal Borromean Binding in Spin-Orbit-Coupled Ultracold Fermi Gases, Phys. Rev. X 4, 031026 (2014).
- (137) Z.-Y. Shi, X.-L. Cui, and H. Zhai, Universal Trimers Induced by Spin-Orbit Coupling in Ultracold Fermi Gases, Phys. Rev. Lett. 112, 013201 (2014).
- (138) S.-G. Peng, C.-X. Zhang, S. Tan, and K. Jiang, Contact Theory for Spin-Orbit-Coupled Fermi Gases, Phys. Rev. Lett. 120, 060408 (2018).
- (139) C.-X. Zhang, S.-G. Peng, and K.-J. Jiang, Universal relations for spin-orbit-coupled Fermi gases in two and three dimensions, Phys. Rev. A 101, 043616 (2020).
- (140) C.-X. Zhang and S.-G. Peng, Universal scattering phase shift in the presence of spin-orbit coupling, Phys. Rev. Research 3, 013054 (2021).