Spin-orbit torque switching of Néel order in two-dimensional \chCrI3

Introduction.— Spin-orbit torque is a mechanism for electrically switching thin-film magnets, and has the potential to enable scalable magnetic random access memory and devices for next-generation computing  [1]. The effect occurs in magnetically ordered systems that lack inversion symmetry - such as heavy metal-ferromagnet bilayers [2, 3] - when a DC current or electric field is applied. Spin-orbit torque can be decomposed into a component that is even under time-reversal, which is also known as the “dampinglike” torque, and a component that is odd under time-reversal, known as the “fieldlike” torque [4]. Knowledge of the dominant component of spin-orbit torque can help to identify the microscopic source of the torque and can assist in optimizing the effect [5].

In addition to switching ferromagnets, spin-orbit torque has been shown to switch antiferromagnets [6, 7, 8, 9, 10, 11]. Antiferromagnets are of particular interest due to their insensitivity to stray magnetic fields and the fast time scales of their excitations [8, 10, 1]. It was shown [6] that spin-orbit torque is present in bulk antiferromagnets in which inversion symmetry is locally broken on individual magnetic sublattices, while the crystal lattice retains global inversion symmetry. More precisely, in antiferromagnets that are invariant under the combined operations of inversion and time-reversal, the spin-orbit torques acting on the magnetic sublattices cooperatively switch the antiferromagnetic Néel vector ${\bf L}$ [6, 7]. In these types of materials studied so far, such as CuMnAs and \chMn2Au, the magnetic exchange energy is much larger than other energy scales, and the mechanism for switching is a uniform fieldlike torque present on both magnetic sublattices [6, 7].

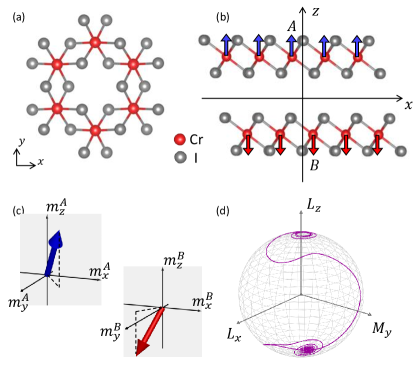
In this work we consider the spin-orbit torque in the recently discovered class of two-dimensional Van der Waals magnetic materials [12, 13, 14], exemplified by antiferromagnetic bilayer \chCrI3. In this semiconducting material, the two magnetic \chCrI3 layers are antiferromagnetically coupled and the ground state Néel vector is oriented perpendicular to the plane [12] (see Fig. 1). There is intense recent interest in this material due to its unique and potentially useful properties, including the tunability and control of its magnetic state through gating and doping [15, 16, 17] and its spin-filtering effects [18, 19, 20]. From the structure shown in Fig. 1(b), it’s clear that bilayer \chCrI3 shares some characteristics with previously mentioned antiferromagnets, such as CuMnAs: Inversion symmetry is locally broken on the magnetic sublattices (denoted A and B), while in the purely antiferromagnetic state, the bilayer is invariant under the combined operations of inversion plus time-reversal.

There is a key difference between this and previously studied materials, namely that the magnetic exchange constant is similar in magnitude to the magnetic anisotropy energy [21, 22]. This allows for significant current-induced canting of the sublattice magnetization and the development of a net magnetization, which breaks the combination of inversion plus time-reversal symmetry. For this material, we show that the important symmetry is instead a 2-fold rotational symmetry about the $y$-axis; this symmetry constrains the magnetic dynamics to a subspace of spin configurations and enables spin-orbit torque switching of the Néel vector. We also show that the dominant mechanism for spin-orbit torque switching of the Néel vector is the dampinglike torque, which is staggered on the two sublattices of the antiferromagnet. These conclusions are based on first-principles calculations of the spin-orbit torque as a function of the magnetic configuration, and an analysis of the ensuing spin dynamics.

Spin dynamics in CrI3 — We first consider the spin dynamics in \chCrI3 and show that the crystal symmetry confines the spins a subspace of magnetic configurations. In the general case, the time evolution of the spin orientations $\hat{\mathbf{m}}^{\rm A,B}$ are described by the coupled set of Landau-Lifshitz-Gilbert (LLG) equations [23, 24, 25]:

$\displaystyle\frac{d{\hat{\mathbf{m}}}^{\rm A,B}}{dt}$

$\displaystyle=$

$\displaystyle\hat{\mathbf{m}}^{\rm A,B}\times\left(\frac{\gamma}{m}\frac{\delta E}{\delta\hat{\mathbf{m}}^{\rm A,B}}+\alpha~{}\frac{d{\hat{\mathbf{m}}}^{\rm A,B}}{dt}\right)+\boldsymbol{\mathcal{T}}^{\rm A,B},$

where $m$ is the magnitude of the magnetic moment (assumed equal on both sublattices), $\gamma$ is the absolute value of the gyromagnetic ratio, and $\alpha$ is the Gilbert damping parameter. The energy $E$ is comprised of an easy-axis anisotropy (along $\hat{\bf z}$) and Heisenberg exchange coupling: $E(\hat{\mathbf{m}}^{\rm A},\hat{\mathbf{m}}^{\rm B})=-\frac{1}{2}mH_{A}[\left(\hat{\mathbf{m}}^{\rm A}\cdot\hat{\bf z}\right)^{2}+\left(\hat{\mathbf{m}}^{\rm B}\cdot\hat{\bf z}\right)^{2}]+mH_{E}\left(\hat{\mathbf{m}}^{\rm A}\cdot\hat{\mathbf{m}}^{\rm B}\right)$, where $H_{A}$ and $H_{E}$ are the effective magnetic fields from anisotropy and exchange, respectively. $\boldsymbol{\mathcal{T}}^{\rm A,B}$ is the spin-orbit torque on the A,B sublattice, which we discuss in more detail in the next section.

The dynamics of the coupled spin system can be quite complex in the general case and analytical treatments are often not possible. A commonly studied limit is $H_{E}\gg H_{A}$, which is applicable to many metallic antiferromagnets. In this case the system can be simplified to a single vector equation of motion for the Néel vector ${\bf L}=({\bf m}^{\rm A}-{\bf m}^{\rm B})/2$, while the net magnetization ${\bf M}=({\bf m}^{\rm A}+{\bf m}^{\rm B})/2$ is no longer an independent variable [24, 25]. For \chCrI3, $H_{E}\approx H_{A}$ [21] and this simplification is no longer valid. We next discuss an alternative simplification that follows the system crystal symmetry.

We consider an applied electric field along the $y$-axis and spin configurations that are staggered in $(x,z)$ and uniform in $y$: $m^{\rm A}_{x/z}=-m^{\rm B}_{x/z}$ and $m^{\rm A}_{y}=m^{\rm B}_{y}$. In this case, the system retains 2-fold rotation symmetry about the $y$-axis (see Fig. 1). Any torque on the spins is therefore symmetry-constrained to satisfy $\mathcal{T}^{\rm A}_{x/z}=-\mathcal{T}^{\rm B}_{x/z}$ and $\mathcal{T}^{\rm A}_{y}=\mathcal{T}^{\rm B}_{y}$. The $x$ and $z$ components of the spins then remain staggered and the $y$ components remain uniform. The trajectory of the spins is thus symmetry-confined to the subspace $(L_{x},M_{y},L_{z})$. This motivates the definition of a “mixed” order parameter ${\bf N}\equiv\left(L_{x},M_{y},L_{z}\right)$ [26]. Eq. Spin-orbit torque switching of Néel order in two-dimensional \chCrI3 leads to the following equation of motion for $\hat{{\bf N}}$:

	$\displaystyle\frac{d{\hat{\mathbf{N}}}}{dt}$	$\displaystyle=$	$\displaystyle{\hat{\mathbf{N}}}\times\left(\frac{\gamma}{m}\frac{\delta E}{\delta{\hat{\mathbf{N}}}}+\alpha\frac{d{\hat{\mathbf{N}}}}{dt}\right)+\mathcal{T}^{\rm odd}\left({\hat{\mathbf{N}}}\times\hat{\bf p}\right)$		(2)
			$\displaystyle~{}~{}~{}~{}+\mathcal{T}^{\rm even}({\hat{\mathbf{N}}}\times(\hat{\bf p}\times{\hat{\mathbf{N}}})),$

where the energy is comprised of the easy-axis anisotropy along $\hat{\bf z}$ and an effective hard-axis anisotropy along $\hat{\bf y}$, which encodes the magnetic exchange:

$\displaystyle E(\hat{\mathbf{N}})$

$\displaystyle=$

$\displaystyle-\frac{1}{2}mH_{A}\left(\hat{\mathbf{N}}\cdot\hat{\mathbf{z}}\right)^{2}+mH_{E}\left(\hat{\mathbf{N}}\cdot\hat{\mathbf{y}}\right)^{2}.$

(3)

The last two terms on the right-hand-sided of Eq. 2 are the spin-orbit torques, consisting of terms that are odd and even under time reversal, as indicated (note the prefactors $\mathcal{T}^{\rm odd,even}$ are assumed to be constants, independent of $\hat{{\bf N}}$). $\hat{\bf p}$ is a direction related to the system symmetry, and the spin-orbit torque vanishes when $\hat{{\bf N}}$ is aligned to $\hat{\bf p}$. We discuss the spin-orbit torque terms in detail in the next section; for now they can be taken as a general representation of a torque which is spanned by the two vectors perpendicular to ${\bf N}$. We have verified that fluctuations away from the ${\bf N}$ subspace do not alter the steady state dynamics [27]. One important feature of this system which enables this simplification is that the easy-axis anisotropy is perpendicular to the axis of 2-fold rotation symmetry. If this were not the case, then the anisotropy torque would immediately drive the spin configuration out of the subspace.

The simple form of the time evolution of $\hat{{\bf N}}$ allows for an analytical treatment of fixed points and an intuitive description of the dynamics. For $\hat{\bf p}$ along $\hat{\bf z}$, the dampinglike torque $\mathcal{T}^{\rm even}$ competes with $\gamma\alpha(H_{E}+H_{A})$ while the fieldlike torque $\mathcal{T}^{\rm odd}$ competes with $\gamma H_{A}$. For \chCrI3, $H_{A}\approx 1.77~{}\rm T$, $H_{E}\approx 0.76~{}\rm T$, and $\alpha\approx 0.04$ [21], so that the dampinglike torque is the dominant mechanism for switching. In the next section we show that $\hat{\bf p}$ has the standard $x$ component, and due to additional mirror plane symmetry breaking in \chCrI3, also has a $z$ component. For $\hat{\bf p}=\left(p_{x},0,p_{z}\right)$, the fixed points to lowest order in spin-orbit torque are $\hat{{\bf N}}=(-\frac{\mathcal{T}^{\rm odd}p_{x}}{\gamma H_{A}},\pm\frac{\mathcal{T}^{\rm even}p_{x}}{\gamma(2H_{E}+H_{A})},\pm 1)$. The instability threshold to switch between fixed points is:

$$|\mathcal{T}^{\rm even}p_{z}|>\gamma\alpha(H_{E}+H_{A}).$$

(4)

A typical switching trajectory is shown in Fig. 1(d): the spin-orbit torque drives $\hat{{\bf N}}$ from north pole to the fixed point close to south pole. For previously studied antiferromagnets, $H_{E}$ is sufficiently large so that switching with $\mathcal{T}^{\rm even}$ is not feasible, and the switching relies instead on $\mathcal{T}^{\rm odd}$ exceeding $H_{A}$. The utilization of $\mathcal{T}^{\rm even}$ for switching the Néel vector of \chCrI3 is one of the material’s distinguishing features.

Microsopic calculations of spin-orbit torques — Having established the relevant degrees of freedom for the spin configuration in \chCrI3 as ${\bf N}$, we next present microscopic calculations of the spin-orbit torque per applied electric field - a quantity known as the “torkance” - as a function of $\hat{{\bf N}}$. The procedure for this calculation is well-established [28, 29], and we briefly provide a description here and refer the reader to the Supplementary Information for more technical details. We first obtain the Hamiltonian in a localized atomic orbital basis using a combination of Quantum Espresso [30] and Wannier90 [31]. We then utilize linear response theory to compute the torkance on each magnetic sublattice. The torkance is classified as even or odd according to its behavior under time-reversal. We denote the $j^{\rm th}$ component of the torkance on atom $\rm A,B$ in response to an electric field along the $i$-direction with $\tau_{ij}^{\rm A,B}$. The even and odd components of the torkance are given by:

$$\left(\tau^{\rm A,B}_{ij}\right)^{\rm even}=2e~{}\text{Im}\sum_{\begin{subarray}{c}n,m\neq n\end{subarray}}f_{n}\frac{\left(\frac{\partial H}{\partial k_{i}}\right)_{n,m}\left(\mathcal{T}^{\rm A,B}_{j}\right)_{m,n}}{(E_{m}-E_{n})^{2}+\eta^{2}},$$

(5)

$$\left(\tau^{A}_{ij}\right)^{\rm odd}=-e\sum_{\begin{subarray}{c}n\end{subarray}}\frac{1}{2\eta}\frac{\partial f_{n}}{\partial E_{n}}\left(\frac{\partial H}{\partial k_{i}}\right)_{n,n}\left(\mathcal{T}^{\rm A,B}_{j}\right)_{n,n}$$

(6)

The sum in Eqs. 5-6 is over eigenstates $|\psi_{n}\rangle$ of the ${\bf k}$-dependent Hamiltonian $H_{\bf k}$, where ${\bf k}$ is the Bloch wave vector and the eigenstate label $n$ includes ${\bf k}$ and band index. $\left(O\right)_{n,m}=\langle\psi_{n}|O|\psi_{m}\rangle$ is the matrix element of the operator $O$, and $f_{n}=(e^{(E_{n}-\mu)/k_{\rm B}T}+1)^{-1}$ is the equilibrium Fermi-Dirac distribution function. $\mu$ is the Fermi level, $\eta$ is the broadening parameter, and $e$ is the electron charge. The atom-resolved torque operator is $\boldsymbol{\mathcal{T}}^{\rm A,B}=\frac{\rm i}{2\hbar}\left\{[\mathbf{S},\Delta],P^{\rm A,B}\right\}$, where $\mathbf{S}$ is the spin operator, $\Delta$ is the spin-dependent exchange-correlation potential, and $P^{\rm A(B)}$ is the projection operator onto the orbitals centered on atomic site A (B). To compute the torque as a function of $\hat{{\bf N}}$, we manually rotate the spins on A and B sublattices.

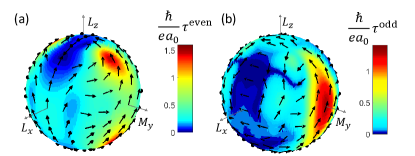
Figure 2 shows the $\hat{{\bf N}}$-dependence of the torkance with (a) and (b) showing the dampinglike (time-reversal even) and fieldlike (time-reversal odd) torkance, respectively. The fixed points of both dampinglike and fieldlike torkance lie in the $L_{x}-L_{z}$ plane, away from the $L_{z}=0$ equator. This is an important feature and is a consequence of the lack of mirror symmetry with respect to the $yz$ plane. This position of the fixed point ensures that the spin-orbit torque drives $\hat{{\bf N}}$ to a point in the northern or southern hemisphere; after the spin-orbit torque is removed, $\hat{{\bf N}}$ then relaxes to the nearest easy-axis along $+\hat{\bf z}$ or $-\hat{\bf z}$. Previous studies on systems with similar in-plane mirror symmetry breaking, such as \chWTe2-Py heterostructures [32, 33, 34, 29], have verified that this symmetry breaking results in a spin-orbit torque that drives the magnetic order parameter to a point away from the equator. Exploiting this property has emerged as an approach for deterministically switching perpendicularly magnetized thin films with spin-orbit torque, and we show here that this also enables switching of the perpendicular Néel vector.

We note that the $\hat{{\bf N}}$-dependence of the torkance is quite complex, deviating substantially from the simple, lowest order form used in the analysis of the previous section. In the Supplementary Information, we provide the full symmetry-allowed expansion of the torkance and quantify the substantial contribution from higher order terms. We additionally find that the fixed points for even and odd torkance are different. These features of the microscopically computed torkance have important consequences for the details of the dynamics of $\hat{{\bf N}}$ under spin-orbit torque, which we show in the next section.

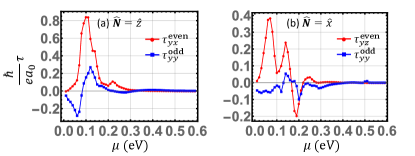
We next consider the torkance versus Fermi level for $\hat{{\bf N}}$ along $\hat{\bf z}$ and $\hat{{\bf x}}$ directions, shown in Figs. 3 (a) and (b), respectively. Both even and odd components are peaked for Fermi energies near the conduction band minimum. For $\hat{{\bf N}}=\hat{\bf z}$, the even torkance is approximately $1~{}ea_{0}/\hbar$ ($a_{0}\approx 0.0529~{}{\rm nm}$ is the Bohr radius) at $0.1~{}\rm{eV}$ above the conduction band minimum, which is larger than the even torkance in the ferromagnetic Pt/Co bilayer ($\approx 0.6~{}ea_{0}/\hbar$) [28]. This large magnitude is due to band crossings in the conduction band from $p$-orbitals of the heavy Iodine atoms. For $\hat{{\bf N}}=\hat{\bf x}$, the even torkance magnitude is around $0.4~{}ea_{0}/\hbar$. The even torkance for this $\hat{{\bf N}}$ configuration is solely a consequence of the in-plane mirror symmetry breaking. This value is notably larger than the corresponding torkance derived from in-plane mirror symmetry breaking in the ferromagnetic 1T’-\chWTe2/Co bilayer ($\approx 0.1~{}ea_{0}/\hbar$) [29].

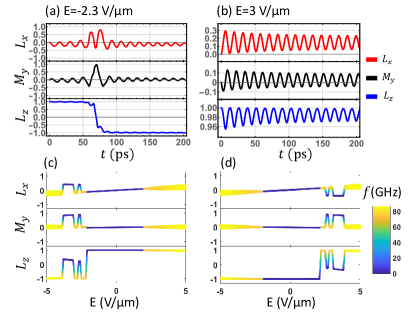
Magnetization dynamics — Given the significant deviation of the $\hat{{\bf N}}$-dependence of the microscopically computed spin-orbit torque from the simple form given in the earlier analysis, it’s worthwhile to compute the spin dynamics with the ab initio spin-orbit torque (Fig. 2) as input into the coupled LLG equations (Eq. Spin-orbit torque switching of Néel order in two-dimensional \chCrI3). $\hat{\bf N}$ is parameterized by spherical coordinates $(\theta,\phi)$, and we use a bilinear interpolation of a dense $80\times 80$ mesh of spin-orbit torque obtained from first-principles to obtain the full $\hat{\bf N}$-dependence.

Figure 4 shows the spin-orbit torque driven dynamics. We find that the spin-orbit torque can either induce switching or induce steady state oscillations of $\hat{{\bf N}}$. Figure 4(a) shows that for an applied electric field $E={\rm-2.3~{}V/\mu m}$, the spin-orbit torque switches the Néel order $L_{z}$ from the north pole to the southern hemisphere within 100 ps and generates a finite in-plane magnetization $M_{y}$. By separately turning off the fieldlike (odd) or dampinglike (even) contributions to the spin-orbit torque, we find that the switching of $L_{z}$ originates from the dampinglike torque, while the fieldlike torque helps to accelerate the switching dynamics and reduce the E-field threshold. Figure 4(b) shows an oscillating steady state for $E={\rm 3~{}V/\mu m}$, with a frequency of approximately 80 GHz. We find that both dampinglike and fieldlike torque are required to induce steady state oscillation.

We summarize the final steady states as a function of the applied field $E$ for two initial magnetization configurations $L_{z}=+1$ and $L_{z}=-1$ in Fig. 4 (c) and (d), respectively. The switching of the Néel vector occurs at approximately $|E|=2~{}{\rm V/\mu m}$. This threshold compares well with the estimate provided by Eq. 4. Reaching the larger scale oscillations at large applied $E$ will rely on the material to sustain large power dissipation, which depends in turn on factors such as the carrier mobility. The flatness of the conduction bands implies a low mobility, as seen experimentally [35], which should enable larger applied electric fields. Fig. 4 (c) and (d) demonstrate hysteretic switching of the Néel vector, and are related by mirror symmetry about the $xz$ plane.

Discussion— The experimental detection of the Néel vector reversal is challenging. For bilayer \chCrI3, out-of-plane magnetic-optical Kerr effect (MOKE) imaging has previously been used to discriminate between $L_{z}=+1$ and $L_{z}=-1$ [16], and transport effects such as nonlinear anisotropic magnetoresistance can also detect ${\bf N}$ [11]. We also note that the moderate exchange energy leads to the development of a substantial steady state in-plane magnetization of the driven system, which may be detected experimentally with in-plane MOKE. Aside from the particulars of \chCrI3, we show generally that antiferromagnets in the weak to moderate exchange coupling regime exhibit different behaviors from their more commonly studied large $H_{E}$ counterparts. The switching criteria for these antiferromagnets is reduced by a factor of magnetic damping, offering potentially easier routes to electrical manipulation. Continued progress in the field of Van der Waals antiferromagnets should provide further opportunities for unique modes of electrical control of these materials.

F.X. acknowledges support under the Cooperative Research Agreement between the University of Maryland and the National Institute of Standards and Technology Physical Measurement Laboratory, Award 70NANB14H209, through the University of Maryland.