Spin liquid behavior of a three-dimensional magnetic system Ba3NiIr2O9 with = 1
Abstract
The quantum spin liquid (QSL) is an exotic phase of magnetic materials where the spins continue to fluctuate without any symmetry breaking down to zero temperature. Among the handful reports of QSL with spin 1, examples with magnetic ions on a three-dimensional magnetic lattice are extremely rare since both larger spin and higher dimension tend to suppress quantum fluctuations. In this work, we offer a new strategy to achieve 3-D QSL with high spin by utilizing two types of transition metal ions, both are magnetically active but located at crystallographically inequivalent positions. We design a 3-D magnetic system Ba3NiIr2O9 consisting of interconnected corner shared NiO6 octahedra and face shared Ir2O9 dimer, both having triangular arrangements in a-b plane. X-ray absorption spectroscopy measurements confirm the presence of Ni2+ (=1). Our detailed thermodynamic and magnetic measurements reveal that this compound is a realization of gapless QSL state down to at least 100 mK. Ab-initio calculations find a strong magnetic exchange between Ir and Ni sublattices and in-plane antiferromagnetic coupling between the dimers, resulting in dynamically fluctuating magnetic moments on both the Ir and Ni sublattice.
Experimental realization and theoretical description of the highly entangled quantum spin liquid phase remain challenging topics of quantum many-body physics Anderson (1973). Over the last fifteen years, several spin-1/2 systems with two-dimensional frustrated lattice have been reported as probable candidates with QSL behavior Balents (2010); Savary and Balents (2016); Zhou, Kanoda, and Ng (2017); Knolle and Moessner (2019); Broholm et al. (2020). Since experimental reports of QSL with either spin 1 Cheng et al. (2011); Chamorro et al. (2018) or three dimensional arrangement of spins Okamoto et al. (2007a); Koteswararao et al. (2014); Balz et al. (2016); Gao et al. (2019); Chillal et al. (2020) are very few, it can be easily anticipated that chances of having a QSL with both higher spin and 3-D geometry is extremely low Plumb et al. (2019). Many of the attempts to obtain spin-1 QSL have been focused on stabilizing Ni within various structural network Nakatsuji et al. (2005); Cheng et al. (2011); Lu et al. (2018); Chamorro et al. (2018); Plumb et al. (2019); Medrano et al. (2018). However, the magnetic behavior of these = 1 systems at low temperature differs widely from each other, even in the compounds with similar structural geometry. For example, unlike to the well known 120∘ spin structure Starykh (2015), as observed in NiNb2O9 Lu et al. (2018), Ba3NiSb2O9 shows characteristic spin liquid behavior Cheng et al. (2011); Fåk et al. (2017); Quilliam et al. (2016), whereas NiGa2S4 hosts a spin nematic phase Bhattacharjee, Shenoy, and Senthil (2006). The interaction of such Ni-based = 1 triangular lattice with another magnetically active sublattice might result in an exotic magnetic phase in three-dimensional materials. However, only very few 3-D compounds with such feasibility exist Treiber, Kemmler-Sack, and Ehmann (1982); Lightfoot and Battle (1990); Ferreira et al. (2018).
Six-layered hexagonal (6) perovskite O9 (Fig. 1(a)) with magnetic and ions constitutes a 3-D spin system. Both, O6 octahedral units and face-shared O9 dimers form a triangular lattice in - plane (Fig. 1(b)-(c)) and would become geometrically frustrated in the presence of antiferromagnetic interaction. Moreover, the -O- connectivity constitutes a buckled honeycomb lattice (Fig. 1(d)), which could host a Kitaev spin liquid phase in case of spin-1/2 ions with strong spin-orbit coupling (SOC) Kitaev (2006); Takagi et al. (2019). In search of SOC driven elusive nonmagnetic = 0 state and excitonic magnetism in system, several BaIr2O9 compounds with nonmagnetic have been investigated recently Khaliullin (2013); Nag et al. (2016, 2018a); Khan et al. (2019). However, the comparable strength of SOC, non-cubic crystal field, Hund’s coupling, and superexchange interaction gives rise to a small but finite moment on the Ir sublattice. Moreover, interdimer hopping results in a spin-orbital liquid phase in Ba3ZnIr2O9 Nag et al. (2016). Replacing the nonmagnetic Zn2+ by an isovalent magnetic ion such as Ni2+ should provide a unique opportunity to investigate the magnetic response of a triangular lattice with = 1 in presence of the interconnected Ir sublattice with fluctuating magnetic moments. If both Ni and Ir moments of Ba3NiIr2O9 fluctuate dynamically, then it would offer a new route to realize 3-D QSL by involving two different magnetic ions. Also, it would be a 3-D QSL with a new type of structural network as compared to all existing examples with pyrochlore Gao et al. (2019); Plumb et al. (2019), hyperkagome Okamoto et al. (2007a), and hyper hyperkagome structure Koteswararao et al. (2014); Chillal et al. (2020).

In this paper, we report on the electronic and magnetic behavior of Ba3NiIr2O9 (BNIO). The phase purity and absence of any cationic site disorder have been demonstrated by powder X-ray diffraction (XRD) measurement. X-ray absorption spectroscopy (XAS) experiments have confirmed the desired +2 oxidation state of Ni. Persisting spin fluctuations down to 100 mK have been revealed by magnetization, specific heat and muon spin-rotation (SR) measurements. We have also investigated BNIO by density functional theory calculations including Hubbard and SOC within the framework of LSDA+ (local spin density approximation + ) approach. We have found not only appreciable magnetic exchange between Ni and Ir-sublattice but also antiferromagnetic coupling in the triangular sublattice of Ir. This geometrical frustration prohibits any long-range magnetic ordering and makes BNIO a rare example of three-dimensional QSL involving = 1.
Results
Polycrystalline BNIO was synthesized by solid state synthesis route. Members of the O9 series can have site disorder between face shared, and corner shared octahedra Middey et al. (2011). It is also well known that structural disorder often jeopardizes QSL behavior, resulting in magnetic order or spin glass freezing Zhong et al. (2019). All peaks of the powder XRD pattern of BNIO (Fig. 1(e)) can be indexed and refined with 6 structure having space group . The refinement also confirms that all corner-shared (face-shared) octahderal units are occupied by Ni (Ir) without any Ni-Ir site disorder. The structural parameters obtained from the refinement have been listed in SM sup . The temperature dependent XRD measurements down to 15 K also rules out any structural transition. Having confirmed that both Ni and Ir ions form triangular lattices in a-b plane without any disorder, we want to verify whether Ni has indeed = 1 state. For this purpose, XAS measurements were carried out Freeland, Van Veenendaal, and Chakhalian (2016). The comparison of Ni XAS line shape and energy position of BNIO, Ni2+O, and NdNi3+O3 (Fig. 1(e)) testifies the desired +2 oxidation of Ni in present case. The octahedral crystal field of Ni2+ (: , ) ensures = 1 on Ni sublattice.
Electrical measurement demonstrates insulating nature of the sample (inset of Fig.2 (a)), which can be fitted using Mott’s variable range hopping (VRH) Hill (1976) model in three-dimensions () as shown in Fig.2 (a). We also note that the insulating behavior of Ba3ZnIr2O9 is well described by VRH in two-dimensions. This difference between two compounds is a manifestation of electron hopping paths along the Ni-O-Ir bonds. Our electronic structure calculations (see SM sup ) further demonstrate that the insulating state can be obtained only by considering both electron correlation and SOC, implying that BNIO is a SOC driven Mott insulator Kim et al. (2008).

The temperature dependent field cooled and zero-field cooled magnetic susceptibility does not differ from each other and also do not show any anomaly (Fig. 2(b)). This strongly implies absence of any long range magnetic ordering and spin glass behavior. We have fitted the data by a modified Cuire-Weiss law ( = + ) where , and represents temperature independent susceptibility contribution, Curie constant and Curie temperature, respectively. The fitting, shown as plot of 1/(-) vs. in right axis of Fig. 2(b), results a -15 K. Negative values of Curie-Weiss temperature signify net antiferromagnetic interaction among the spins of BNIO. The relatively smaller value of is related to the presence of multiple exchange pathways, which will be discussed in later part of this paper. The effective magnetic moment (= ) is found to be 3.65 from the fitting. Interestingly, the effective magnetic moment of a similar compound Ba3NiSb2O9, with nonmagnetic Sb5+ was reported to be around 3.54 Cheng et al. (2011). This gives an estimate of -factor 2.5, similar to other Ni2+ based systems carlin_paramagnetism_1986 . If we assume similar value for the present compound, the effective Ir moment turns out to be 0.9 per dimer (= ) i.e. 0.64 /Ir. This is very similar to the Ir moment (0.5 - 0.6 ) reported for Ba3MgIr2O9 Nag et al. (2018a), though a nonmagnetic = 0 state is expected for Ir5+ from a pure ionic picture. Thus, our analysis highlights both Ni2+ and Ir5+ participate in magnetism of BNIO compound. The estimated magnetic moments from our LSDA+U+SOC calculations (shown in SM sup ) are also in good agreement with our experimental results. Fig. 2 (c) shows - done at 2 K between 9 T. The absence of any hysteresis again confirms absence of ferromagnetism and spin glass freezing at 2 K. The presence of antiferromagnetic interaction without any long range magnetic ordering or spin glass transition strongly indicates that BNIO is a favorable candidate of QSL.
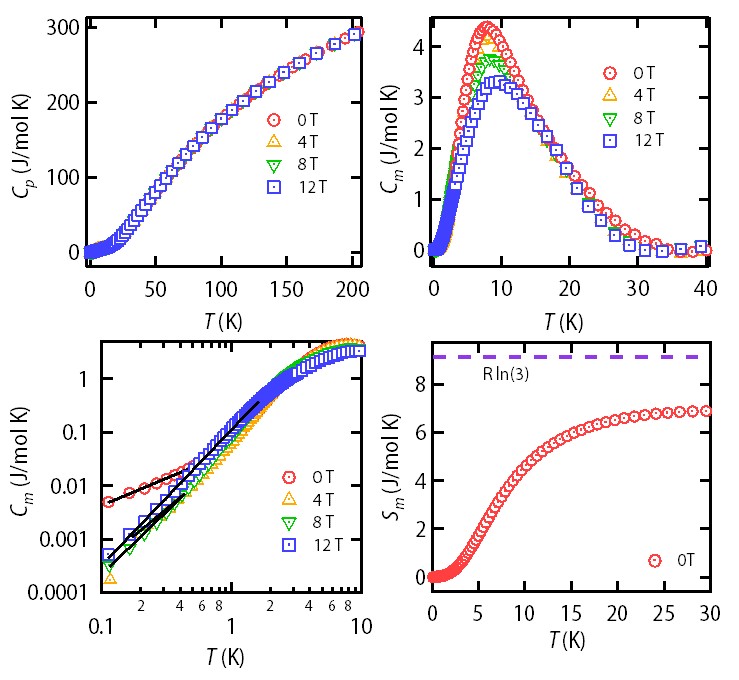
In order to further investigate the magnetic nature of the sample, we have measured specific heat () from 100 mK to 200 K. not only probes the presence/absence of any long-range magnetic ordering but also provides very crucial information about the nature of low energy excitation. The absence of any -anomaly (Fig. 3(a)) again confirms absence of long-range order and/or any structural transition down to 100 mK, consistent with the magnetic measurement and XRD results, respectively. For an insulating compound with magnetic spins, consists of lattice specific heat () and magnetic specific heat (). In absence of any analogous non-magnetic compound, the contribution of has been evaluated by fitting in 30 K - 200 K range by a Debye-Einstein equation with one Debye term and two Einstein terms (details are in SM sup ) and extrapolating the fitted curve down to 100 mK. A broad peak is observed around 7 K in vs. plot (Fig. 3(a)). We can not capture this feature by Schottky anomaly, arising due to energy level splitting (see SM sup ). On the other hand, such feature is commonly observed in spin liquid materials and thus, could be considered as a signature of crossover from thermally disordered paramagnet to quantum disordered spin liquid state Okamoto et al. (2007b); Balents (2010); Li et al. (2015); Dey et al. (2017). The position of this broad peak shows negligible shifts with the application of magnetic field (shifts 1 K for applied field of 12 T).
At low temperature, follows power-law behavior = (Fig. 3(c)). For zero field, the magnitude of coefficient is 45 mJ/mol K2 and the exponent is 1.00.05 within 0.1 K - 0.6 K range. The value of is very similar to other gapless spin liquid candidates: like Ba3CuSb2O9 (43.4 mJ/mol K2) Zhou et al. (2011), Ba2YIrO6 (44 mJ/mol K2) Nag et al. (2018b), Ba3ZnIr2O9 (25.9 mJ/mol K2) Nag et al. (2016), Sr2Cu(Te0.5W0.5)O6 (54.2 mJ/mol K2) Mustonen et al. (2018). Also, the linear behavior with nonzero in an insulator comes due to gapless spinon excitations with a Fermi surface and has been reported in several organic and inorganic spin liquid candidates Yamashita et al. (2008, 2011); Zhou et al. (2011); Cheng et al. (2011); Mustonen et al. (2018); Clark et al. (2014); Uematsu and Kawamura (2019). Otherwise, any gapped excitation would result in an exponential dependence of on . becomes 2.60.05 within 0.8 K - 2.1 K. Interestingly, the application of an external field destroys the linear behavior of . For = 4 T, becomes 2 for 0.15 K 0.50 K and 2.9 for 0.5 K 2.4 K. We note that is found to be between 2 to 3 for several spin nematic phase Nakatsuji et al. (2005, 2007); Povarov et al. (2019); Kohama et al. (2019). Further studies are necessary to investigate the possibility of transition from spin liquid to spin nematic phase by the application of a magnetic field. The amount of released magnetic entropy () is evaluated by integrating w.r.t. and is shown in Fig. 3(d). For BNIO, the entropy saturates at 6.9 J/mol K for zero field measurement, which is only 75% of the total entropy expected for even a system [ln(2+1), where is universal gas constant]. The retention of a large amount of entropy at low temperature is another signature of the spin-liquid nature of BNIO, which has been reported as well for many other QSL Zhou et al. (2011); Cheng et al. (2011); Mustonen et al. (2018); Yamashita et al. (2008).
To have a further understanding of the magnetic behavior at low temperature, we have performed SR measurements, which is a very sensitive local probe to detect a weak magnetic field, even of the order of 0.1 Oe Blundell (1999). Fig. 4(a) shows asymmetry vs time curves for zero-field (ZF) measurements at selected temperatures. Neither any oscillation nor the characteristic 1/3rd recovery of the asymmetry is observed down to 60 mK, strongly implying the absence of long-range magnetic ordering or spin freezing. For a system with two interacting spin networks, the local magnetic field, felt by a muon at a stopping site is contributed by both magnetic sublattices. In such cases, the muon relaxation function is generally described by a product of two response functions, representing local fields from two spin networks Uemura et al. (1985). However, our such attempts considering different possible combinations of relaxation functions, including a spin glass like relaxation Morenzoni et al. (2008); Uemura et al. (1985), did not provide a satisfactory fitting of the experimental observed data (see SM sup ). This further supports the absence of spin glass freezing in present case.

Interestingly, similar to the other hexagonal BaIr2O9 Nag et al. (2016, 2018a), these asymmetry curves consist of one fast relaxing, one moderately relaxing, and one hardly relaxing components. We have fitted these curves using a combination of two dynamical relaxation functions with a common fluctuation rate and a Kubo-Toyabe function (KT) Hayano et al. (1979),
| (1) |
where , , are amplitudes. The static KT function, corresponding to the hardly relaxing component, accounts for the muons stopping at the silver sample holder as we find that the relaxation curve from the bare sample holder can also be described by a KT function with similar . The dynamical relaxation, arising due to the presence of a field distribution () with a fluctuation rate () is represented by the Keren function Keren (1994). The presence of two dynamical relaxations implies two inequivalent muon stopping sites, which are likely to be related with the two types of crystallographically inequivalent oxygen in hexagonal BaIr2O9 Nag et al. (2016, 2018a). The asymmetry data over a large temperature range (60 mK - 150 K) have been fitted by allowing to vary with and, the extracted values of has been shown as a function of in Fig. 4(b). The background contribution is different between measurements in dilution refrigerator and helium cryostat and, has been kept fixed for our analysis within the corresponding temperature range. The inequality ( = muon gyromagnetic ratio = 2135.5 Mrad s-1 T-1) holds for both relaxing components as 0.425 MHz and 0.09 MHz for the lowest temperature of our measurement (60 mK). This justifies the use of dynamical relaxation functions and establishes spin liquid nature of BNIO. We note that the value of ( 4 MHz) at low temperature for BNIO is one order of magnitude smaller than Ba3ZnIr2O9 Nag et al. (2016) and is likely to be related with the involvement of large spins on the Ni sublattice.
-SR spectra, recorded at 100 mK in presence of an applied longitudinal field (LF) have further corroborated QSL nature of BNIO. In case of relaxation arising from a static internal field distribution with width , an applied LF 5-10 would completely suppress the relaxation. From the analysis of ZF SR data, we found 5 Gauss and 1 Gauss. No such decoupling is observed in the present case in measurement up to 200 Gauss (see inset of Fig. 4(b) and SM sup ), establishing the dynamic nature of spins in BNIO down to atleast 100 mK.
Discussion
To understand the underlying mechanism of the observed QSL state, we estimated the inter-atomic magnetic exchange interactions from the converged LSDA++SOC calculations using the formalism of Ref. Kvashnin et al., 2015a (see Method section and SM sup for details). As shown in Table-I, the strongest interaction is antiferromagnetic, which is between the Ir ions of the structural dimer. The strong Ir-Ni interaction further testifies three-dimensional nature of BNIO. Most importantly, Ir-Ir exchange in the a-b plane () is found to be antiferromagnetic, resulting in-plane magnetic frustration and explains the origin of the QSL behavior of the present system. However, the presence of strong Ir-Ni and Ni-Ni ferromagnetic exchange reduces the net antiferromagnetic exchange of this system, resulting a relatively lower value of negative . We further note that the ferromagnetic Ni-Ni exchange has been observed also in antiferromagnetic phase of analogous compound Ba3NiRu2O9 Lightfoot and Battle (1990).
| Exchange | Interacting | Number | Magnitude | Type | z/ |
|---|---|---|---|---|---|
| () | pair | of neighbor () | (meV) | ||
| Ir-Ir | 1 | -8.91 | AFM | 1 | |
| Ir-Ni | 3 | 0.96 | FM | 0.32 | |
| Ir-Ir | 3 | 0.10 | FM | 0.03 | |
| Ir-Ir | 6 | -0.17 | AFM | 0.11 | |
| Ni-Ni | 6 | 0.09 | FM | 0.06 |
To summarize, our detailed measurements reveal that 6 BNIO containing =1 hosts a gapless spin liquid phase below 2 K. The involvement of Ir5+ and Ni2+ in the magnetic properties of BNIO is revealed by dc magnetic measurements, SR experiments, and electronic structure calculation. The antiferromagnetic interaction between Ir2O9 dimers in a-b plane facilitates geometrical frustration driven QSL phase of BNIO. Since many Ba3O9 compounds can be stabilized in 6 structure, we believe this work will lead to the realization of many 3-D QSLs with large spin by judicial choice of and .
Method
Stoichiometric amount of BaCO3, NiO and Ir metal power were used as starting materials for the solid state synthesis of BNIO. The mixture was heated multiple times at 1175∘ C with intermediate grindings till the desired phase is formed. Powder XRD was carried out using a lab based Rigaku Smartlab diffractometer and also in the Indian beamline (BL-18B) at the Photon Factory, KEK, Japan. The diffraction pattern of the final phase was refined by Reitveild method using FULLPROF Rodríguez-Carvajal (1993).
XAS spectra of Ni -edges were recorded in bulk sensitive total fluorescence yield mode in 4-ID-C beam line of Advanced Photon Source, USA. DC magnetic measurements were carried using a Quantum Design (QD) SQUID magnetometer. Heat capacity measurements () were done in a dilution refrigerator insert coupled with a 16T QD-PPMS system using relaxation calorimetry. SR experiments down to 60 mK were performed using pulsed muon beam at MuSR spectrometer of ISIS Neutron and Muon Source, UK. A dilution fridge was used to record SR data from 60 mK to 4 K and a cryostat was used for temperatures above 1.5 K.
The density functional theory (DFT) calculations have been performed in the local spin-density approximation + Hubbard (LSDA+U) approach with and without including spin-orbit coupling (SOC) by means of a full potential linearized muffin-tin orbital method (FP-LMTO) Andersen (1975); Wills and Cooper (1987) as implemented in the RSPt code Wills et al. (2000). The Brillouin-zone (BZ) integration is carried out by using the thermal smearing method with 10 10 4 k-mesh. For the charge density and potential angular decomposition inside the muffin-tin (MT) spheres, the value of maximum angular momentum was taken equal to . To describe the electron-electron correlation within LSDA+U approach, we have taken = 6 eV, =0.8 eV for Ni- states and = 2 eV, =0.6 eV for the Ir- states. The set of the correlated orbitals located on Ni and Ir sites were obtained by projecting the electron density onto the corresponding MT sphere with a certain angular character (so-called “MT-heads” projectionGrechnev et al. (2007)).
After obtaining the self-consistent fully converged LSDA++SOC calculations, the magnetic force theorem Liechtenstein et al. (1987); Katsnelson and Lichtenstein (2000) was used to extract the effective inter-site magnetic-interaction parameters (). In this approach the magnetic system is mapped onto the Heisenberg Hamiltonian:
| (2) |
Further, are extracted in a linear-response manner via Green’s function technique. A detailed discussion of the implementation of the magnetic force theorem in RSPt is provided in Ref. Kvashnin et al., 2015b. This method is considered to be one of the most accurate techniques for the estimation of exchange interactions and also been successfully employed for many transition metal compounds Panda et al. (2016).
Acknowledgement
S.M. acknowledges financial support from ISRO-IISc Space Technology Cell and Infosys Foundation, Bangalore. S.M. and S.K. acknowledge insightful discussions with Dr. Subhro Bhattacharjee, Dr. Yogesh Singh, Dr. Pabitra Biswas. Authors thank the Department of Science and Technology, India for the financial support, Saha Institute of Nuclear Physics and Jawaharlal Nehru Centre for Advanced Scientific Research, India for facilitating the experiments at the Indian Beamline, Photon Factory, KEK, Japan. The authors also acknowledge the experimental support from UGC-DAE CSR, Indore, staffs of LT & Cryogenics especially Er. P. Saravanan for their technical support. This research used resources of the Advanced Photon Source, a U.S. Department of Energy Office of Science User Facility operated by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. Experiments at the ISIS Neutron and Muon Source were supported by a beamtime allocation RB1920396 from the Science and Technology Facilities Council.
References
- Anderson (1973) P. W. Anderson, Materials Research Bulletin 8, 153 (1973).
- Balents (2010) L. Balents, Nature 464, 199 (2010).
- Savary and Balents (2016) L. Savary and L. Balents, Reports on Progress in Physics 80, 016502 (2016).
- Zhou, Kanoda, and Ng (2017) Y. Zhou, K. Kanoda, and T.-K. Ng, Reviews of Modern Physics 89, 025003 (2017).
- Knolle and Moessner (2019) J. Knolle and R. Moessner, Annual Review of Condensed Matter Physics 10, 451 (2019).
- Broholm et al. (2020) C. Broholm, R. Cava, S. Kivelson, D. Nocera, M. Norman, and T. Senthil, Science 367 (2020).
- Cheng et al. (2011) J. G. Cheng, G. Li, L. Balicas, J. S. Zhou, J. B. Goodenough, C. Xu, and H. D. Zhou, Phys. Rev. Lett. 107 (2011), 10.1103/PhysRevLett.107.197204, arXiv:1108.2897 .
- Chamorro et al. (2018) J. R. Chamorro, L. Ge, J. Flynn, M. A. Subramanian, M. Mourigal, and T. M. McQueen, Phys. Rev. Materials 2, 034404 (2018).
- Okamoto et al. (2007a) Y. Okamoto, M. Nohara, H. Aruga-Katori, and H. Takagi, Physical Review Letters 99, 137207 (2007a).
- Koteswararao et al. (2014) B. Koteswararao, R. Kumar, P. Khuntia, S. Bhowal, S. K. Panda, M. R. Rahman, A. V. Mahajan, I. Dasgupta, M. Baenitz, K. H. Kim, and F. C. Chou, Phys. Rev. B 90, 035141 (2014).
- Balz et al. (2016) C. Balz, B. Lake, J. Reuther, H. Luetkens, R. Schönemann, T. Herrmannsdörfer, Y. Singh, A. N. Islam, E. M. Wheeler, J. A. Rodriguez-Rivera, et al., Nature Physics 12, 942 (2016).
- Gao et al. (2019) B. Gao, T. Chen, D. W. Tam, C.-L. Huang, K. Sasmal, D. T. Adroja, F. Ye, H. Cao, G. Sala, M. B. Stone, et al., Nature Physics 15, 1052 (2019).
- Chillal et al. (2020) S. Chillal, Y. Iqbal, H. O. Jeschke, J. A. Rodriguez-Rivera, R. Bewley, P. Manuel, D. Khalyavin, P. Steffens, R. Thomale, A. N. Islam, et al., Nature communications 11, 1 (2020).
- Plumb et al. (2019) K. Plumb, H. J. Changlani, A. Scheie, S. Zhang, J. Krizan, J. Rodriguez-Rivera, Y. Qiu, B. Winn, R. J. Cava, and C. L. Broholm, Nature Physics 15, 54 (2019).
- Nakatsuji et al. (2005) S. Nakatsuji, Y. Nambu, H. Tonomura, O. Sakai, S. Jonas, C. Broholm, H. Tsunetsugu, Y. Qiu, and Y. Maeno, science 309, 1697 (2005).
- Lu et al. (2018) Z. Lu, L. Ge, G. Wang, M. Russina, G. Günther, C. dela Cruz, R. Sinclair, H. Zhou, and J. Ma, Physical Review B 98, 094412 (2018).
- Medrano et al. (2018) C. Medrano, D. Freitas, E. Passamani, J. Resende, M. Alzamora, E. Granado, C. Galdino, E. Baggio-Saitovitch, M. Continentino, and D. Sanchez, Physical Review B 98, 054435 (2018).
- Starykh (2015) O. A. Starykh, Reports on Progress in Physics 78, 052502 (2015).
- Fåk et al. (2017) B. Fåk, S. Bieri, E. Canévet, L. Messio, C. Payen, M. Viaud, C. Guillot-Deudon, C. Darie, J. Ollivier, and P. Mendels, Phys. Rev. B 95, 1 (2017).
- Quilliam et al. (2016) J. A. Quilliam, F. Bert, A. Manseau, C. Darie, C. Guillot-Deudon, C. Payen, C. Baines, A. Amato, and P. Mendels, Phys. Rev. B 93, 214432 (2016).
- Bhattacharjee, Shenoy, and Senthil (2006) S. Bhattacharjee, V. B. Shenoy, and T. Senthil, Phys. Rev. B 74, 092406 (2006).
- Treiber, Kemmler-Sack, and Ehmann (1982) U. Treiber, S. Kemmler-Sack, and A. Ehmann, Zeitschrift für anorganische und allgemeine Chemie 487, 189 (1982).
- Lightfoot and Battle (1990) P. Lightfoot and P. Battle, Journal of Solid State Chemistry 89, 174 (1990).
- Ferreira et al. (2018) T. Ferreira, S. M. Heald, M. D. Smith, and H.-C. zur Loye, Inorganic chemistry 57, 2973 (2018).
- Kitaev (2006) A. Kitaev, Annals of Physics 321, 2 (2006).
- Takagi et al. (2019) H. Takagi, T. Takayama, G. Jackeli, G. Khaliullin, and S. E. Nagler, Nature Reviews Physics 1, 264 (2019).
- Khaliullin (2013) G. Khaliullin, Phys. Rev. Lett. 111, 1 (2013).
- Nag et al. (2016) A. Nag, S. Middey, S. Bhowal, S. K. Panda, R. Mathieu, J. C. Orain, F. Bert, P. Mendels, P. G. Freeman, M. Mansson, H. M. Ronnow, M. Telling, P. K. Biswas, D. Sheptyakov, S. D. Kaushik, V. Siruguri, C. Meneghini, D. D. Sarma, I. Dasgupta, and S. Ray, Phys. Rev. Lett. 116, 1 (2016).
- Nag et al. (2018a) A. Nag, S. Bhowal, F. Bert, A. D. Hillier, M. Itoh, I. Carlomagno, C. Meneghini, T. Sarkar, R. Mathieu, I. Dasgupta, and S. Ray, Phys. Rev. B 97, 1 (2018a).
- Khan et al. (2019) M. S. Khan, A. Bandyopadhyay, A. Nag, V. Kumar, A. V. Mahajan, and S. Ray, Phys. Rev. B 100, 064423 (2019).
- Freeland, Van Veenendaal, and Chakhalian (2016) J. W. Freeland, M. Van Veenendaal, and J. Chakhalian, Journal of Electron Spectroscopy and Related Phenomena 208, 56 (2016).
- Middey et al. (2011) S. Middey, S. Ray, K. Mukherjee, P. L. Paulose, E. V. Sampathkumaran, C. Meneghini, S. D. Kaushik, V. Siruguri, K. Kovnir, and D. D. Sarma, Phys. Rev. B 83, 144419 (2011).
- Zhong et al. (2019) R. Zhong, S. Guo, G. Xu, Z. Xu, and R. J. Cava, Proceedings of the National Academy of Sciences 116, 14505 (2019).
- (34) See Supplemental Material.
- Hill (1976) R. M. Hill, Phys. status solidi 34, 601 (1976).
- Kim et al. (2008) B. J. Kim, H. Jin, S. J. Moon, J.-Y. Kim, B.-G. Park, C. S. Leem, J. Yu, T. W. Noh, C. Kim, S.-J. Oh, J.-H. Park, V. Durairaj, G. Cao, and E. Rotenberg, Phys. Rev. Lett. 101, 076402 (2008).
- (37) R. L. Carlin, in Magnetochemistry, edited by R. L. Carlin (Springer, Berlin, Heidelberg, 1986) Chap. 4.
- Okamoto et al. (2007b) Y. Okamoto, M. Nohara, H. Aruga-Katori, and H. Takagi, Phys. Rev. Lett. 99, 137207 (2007b).
- Li et al. (2015) Y. Li, H. Liao, Z. Zhang, S. Li, F. Jin, L. Ling, L. Zhang, Y. Zou, L. Pi, Z. Yang, et al., Scientific reports 5, 1 (2015).
- Dey et al. (2017) T. Dey, M. Majumder, J. C. Orain, A. Senyshyn, M. Prinz-Zwick, S. Bachus, Y. Tokiwa, F. Bert, P. Khuntia, N. Büttgen, A. A. Tsirlin, and P. Gegenwart, Phys. Rev. B 96, 174411 (2017), arXiv:1702.08305 .
- Zhou et al. (2011) H. D. Zhou, E. S. Choi, G. Li, L. Balicas, C. R. Wiebe, Y. Qiu, J. R. D. Copley, and J. S. Gardner, (2011), 10.1103/PhysRevLett.106.147204.
- Nag et al. (2018b) A. Nag, S. Bhowal, A. Chakraborty, M. M. Sala, A. Efimenko, F. Bert, P. K. Biswas, A. D. Hillier, M. Itoh, S. D. Kaushik, V. Siruguri, C. Meneghini, I. Dasgupta, and S. Ray, Phys. Rev. B 98, 014431 (2018b).
- Mustonen et al. (2018) O. Mustonen, S. Vasala, E. Sadrollahi, K. P. Schmidt, C. Baines, H. C. Walker, I. Terasaki, F. J. Litterst, E. Baggio-Saitovitch, and M. Karppinen, Nat. Commun. 9, 1085 (2018).
- Yamashita et al. (2008) S. Yamashita, Y. Nakazawa, M. Oguni, Y. Oshima, H. Nojiri, Y. Shimizu, K. Miyagawa, and K. Kanoda, Nat. Phys. 4, 459 (2008).
- Yamashita et al. (2011) S. Yamashita, T. Yamamoto, Y. Nakazawa, M. Tamura, and R. Kato, Nat. Commun. 2, 1 (2011).
- Clark et al. (2014) L. Clark, G. J. Nilsen, E. Kermarrec, G. Ehlers, K. S. Knight, A. Harrison, J. P. Attfield, and B. D. Gaulin, Phys. Rev. Lett. 113, 117201 (2014).
- Uematsu and Kawamura (2019) K. Uematsu and H. Kawamura, Phys. Rev. Lett. 123, 087201 (2019).
- Nakatsuji et al. (2007) S. Nakatsuji, H. Tonomura, K. Onuma, Y. Nambu, O. Sakai, Y. Maeno, R. T. Macaluso, and J. Y. Chan, Phys. Rev. Lett. 99, 157203 (2007).
- Povarov et al. (2019) K. Y. Povarov, V. K. Bhartiya, Z. Yan, and A. Zheludev, Phys. Rev. B 99, 24413 (2019), arXiv:1807.09549 .
- Kohama et al. (2019) Y. Kohama, H. Ishikawa, A. Matsuo, K. Kindo, N. Shannon, and Z. Hiroi, Proc. Natl. Acad. Sci. U. S. A. 166, 10686 (2019).
- Blundell (1999) S. J. Blundell, Contemporary Physics 40, 175 (1999), https://doi.org/10.1080/001075199181521 .
- Uemura et al. (1985) Y. J. Uemura, T. Yamazaki, D. R. Harshman, M. Senba, and E. J. Ansaldo, Phys. Rev. B 31, 546 (1985).
- Morenzoni et al. (2008) E. Morenzoni, H. Luetkens, T. Prokscha, A. Suter, S. Vongtragool, F. Galli, M. B. S. Hesselberth, N. Garifianov, and R. Khasanov, Phys. Rev. Lett. 100, 147205 (2008).
- Hayano et al. (1979) R. S. Hayano, Y. J. Uemura, J. Imazato, N. Nishida, T. Yamazaki, and R. Kubo, Physical Review B 20, 850 (1979).
- Keren (1994) A. Keren, Phys. Rev. B 50, 10039 (1994).
- Kvashnin et al. (2015a) Y. O. Kvashnin, O. Grånäs, I. Di Marco, M. I. Katsnelson, A. I. Lichtenstein, and O. Eriksson, Phys. Rev. B 91, 125133 (2015a).
- Rodríguez-Carvajal (1993) J. Rodríguez-Carvajal, Phys. B Phys. Condens. Matter 192, 55 (1993).
- Andersen (1975) O. K. Andersen, Phys. Rev. B 12, 3060 (1975).
- Wills and Cooper (1987) J. M. Wills and B. R. Cooper, Phys. Rev. B 36, 3809 (1987).
- Wills et al. (2000) J. M. Wills, O. Eriksson, M. Alouni, and D. L. Price, Electronic Structure and Physical Properties of Solids: The Uses of the LMTO Method (Springer-Verlag, Berlin, 2000).
- Grechnev et al. (2007) A. Grechnev, I. Di Marco, M. I. Katsnelson, A. I. Lichtenstein, J. Wills, and O. Eriksson, Phys. Rev. B 76, 035107 (2007).
- Liechtenstein et al. (1987) A. Liechtenstein, M. Katsnelson, V. Antropov, and V. Gubanov, Journal of Magnetism and Magnetic Materials 67, 65 (1987).
- Katsnelson and Lichtenstein (2000) M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B 61, 8906 (2000).
- Kvashnin et al. (2015b) Y. O. Kvashnin, O. Grånäs, I. Di Marco, M. I. Katsnelson, A. I. Lichtenstein, and O. Eriksson, Phys. Rev. B 91, 125133 (2015b).
- Panda et al. (2016) S. K. Panda, Y. O. Kvashnin, B. Sanyal, I. Dasgupta, and O. Eriksson, Phys. Rev. B 94, 064427 (2016).