Spin-dependent electron transport along hairpin-like DNA molecules

We first consider the dephasing effect on the spin transport along DNA hairpins. Figures 2(a) and 2(b) show the spin-up conductance $G_{\uparrow}$ (black lines), spin-down conductance $G_{\downarrow}$ (cyan lines), and spin polarization $P_{s}$ (red lines) for model I and model II, respectively, as a function of the electron energy $E$ in the presence of dephasing. It clearly appears that the transmission spectra of DNA hairpins are completely different from the dsDNA molecules gam1 , although the model parameters of these two systems are identical. For both models of DNA hairpins, the conductances are nonzero over the entire energy spectrum which can be definitely classified into two categories, the oscillation regions at $[-0.35,-0.11]\cup[0.43,0.61]$ and the smooth ones in the remaining areas. We stress that these two oscillation regions coincide exactly with the electronic bands of the dsDNA molecules gam1 . One can see that both $G_{\uparrow}$ and $G_{\downarrow}$ oscillate with $E$ in the oscillation regions, owing to the quantum interference effect. The oscillation frequency, i.e., the density of the transmission peaks, becomes higher when $E$ is close to the central smooth region, which is related to the SOC effect. Meanwhile, the conductances tend to decrease as the electron energy in the right (left) oscillation region is shifted towards higher (lower) energies, because of the increment of the scattering from the nucleobases.

The transmission profiles are, however, different in the smooth regions which are divided into three parts by the oscillation ones and absent in the dsDNA molecules gam1 . In the smooth regions where $E$ locates beyond the electronic bands, the oscillating behavior of $G_{\uparrow/\downarrow}$ vs $E$ vanishes as the quantum interference effect is negligible in these areas. In the central smooth region where $E$ is close to the potential energies of all the nucleobases, $G_{\uparrow/\downarrow}$ is very large and roughly independent of $E$. While in the other smooth regions where $E$ is far away from the potential energies, the electrons suffer strong scattering and $G_{\uparrow/\downarrow}$ becomes small. By further separating $E$ from the center of the energy spectrum, $G_{\uparrow/\downarrow}$ is declined monotonically as the scattering is gradually enhanced.

Apart from the unique features mentioned above, one can see other important phenomena. In the oscillation regions, $G_{\uparrow}$ is obviously distinct from $G_{\downarrow}$ for both models, indicating the spin-filtering effect of DNA hairpins. The spin polarization is nonzero over the whole oscillation regions and can achieve 15.9% (16.3%) for model I (II). In particular, $P_{s}$ oscillates with $E$ as well [see the bumps of the red lines in Figs. 2(a) and 2(b)], which cannot be observed in the dsDNA molecules gam1 ; gam3 . In the right (left) oscillation region, $P_{s}$ is positive (negative), which may correspond to the holes (electrons). In fact, a critical value $E_{0}\simeq 0.19$ is found in the curve $P_{s}$-$E$ that $P_{s}>0$ for $E>E_{0}$ and $P_{s}<0$ for $E<E_{0}$. When the holes migrate along the direction from, e.g., the source to the drain, it could be regarded as the situation of electron transmission along the opposite direction, leading to the sign reversal of $P_{s}$ in the two oscillation regions. Whereas in the smooth regions, no observable difference can be detected between $G_{\uparrow}$ and $G_{\downarrow}$, and $P_{s}$ is very small with the order of magnitude being $10^{-4}$. Except for these similarities, one can see that the oscillating amplitude of $G_{\uparrow/\downarrow}/P_{s}$ is smaller in model I as compared with model II, because of the extra lead—lead 3—in the former model. This is a universal phenomenon which holds for other model parameters, as demonstrated in the following numerical results, indicating that lead 3 in multi-terminal DNA devices can induce dephasing as well, just like the Büttiker's virtual leads. Therefore, the electrons will lose their phase memory more quickly in model I.

To provide insight into the spin-filtering effect of DNA hairpins, Figs. 2(c) and 2(d) show $G_{\uparrow}$ and $P_{s}$ for model I and model II, respectively, as a function of $E$ by disconnecting to any Büttiker's virtual lead, $\Gamma_{d}=0$. It is obvious that the transmission spectra of DNA hairpins can also be classified into the oscillation regions and the smooth ones. However, one can identify several distinct features in the absence of Büttiker's virtual leads. The oscillating amplitude of $G_{\uparrow}$ is significantly enhanced [see the black line in Fig. 2(c)], because the electrons do not experience any inelastic scattering from the nucleobases except for the last base pair and the quantum interference effect is strengthened. Interestingly, $P_{s}$ is also nonzero in the oscillation regions and can reach greater value of 25.8% [see the bumps of the red line in Fig. 2(c)], which is comparable to the dsDNA molecules gam1 . This is attributed to the fact that the device is switched into a multi-terminal one in the presence of lead 3 which plays a similar role as Büttiker's virtual leads, giving rise to the spin-filtering effect of DNA hairpins. Contrarily, $P_{s}$ is declined to zero exactly in the smooth regions. While for model II, the oscillating amplitude of $G_{\uparrow}$ is even larger, as the electron transport process is completely coherent, due to the absence of lead 3 and Büttiker's virtual ones. In this case, no spin polarization appears [see the red line in Fig. 2(d)], regardless of the model parameters and consistent with previous works gam1 ; mas1 ; ay1 . This arises from the time-reversal symmetry and the phase-locking effect in two-terminal devices gam3 ; sqf1 .

In order to further understand the physical nature of the spin-filtering effect, the local spin currents of DNA hairpins with finite $P_{s}$ are calculated and compared with the situation of $P_{s}=0$. To this end, we consider both models in the absence of Büttiker's virtual leads. Figures 3(a)-3(c) plot the spatial distributions of the local spin-up current $I_{m\rightarrow n}^{\uparrow}$ (black arrows) and the local spin-down one $I_{m\rightarrow n}^{\downarrow}$ (cyan arrows) for model I at typical electron energies which are marked by the square, circle, and down triangle in Fig. 2(c), where $P_{s}\simeq-10.7\%$, 0, and 25.1%, respectively. As a comparison, Figs. 3(d)-3(f) dsiplay the local spin current distributions for model II at the same electron energies with $P_{s}=0$. Here, the size of the arrows is proportional to the magnitude of the local spin currents. We find that the local current flowing from site $\{1,n\}$ to $\{1,n+1\}$ is always identical to that from $\{2,n+1\}$ to $\{2,n\}$, i.e.,

for $n\in[1,N-1]$, because of the current conservation. Besides, $G_{\uparrow/\downarrow}$ and $P_{s}$ obtained from Fig. 3 are the same as Fig. 2, demonstrating the validity of our numerical results.

It is clear that in the oscillation regions, the electrons can propagate along the longitudinal direction of DNA hairpins [Figs. 3(a), 3(c), 3(d), and 3(f)], although the source and drain are connected to their left side [Figs. 1(b) and 1(c)], because $E$ locates within the electronic bands of the hairpin stem. The local spin-up and spin-down currents flow almost in opposite directions except for only a few nucleobases neighboring to the source/drain [see the first and second base pairs in Figs. 3(a), 3(c), 3(d), and 3(f)]. Interestingly, the local spin currents can flow circularly in space, giving rise to vortex-like patterns, which have been reported in other molecular systems ns1 ; zyy1 ; sgc1 . Let us consider $I_{m\rightarrow n}^{\uparrow}$ in Fig. 3(a) as an example and similar phenomena can be observed for $I_{m\rightarrow n}^{\downarrow}$. The local spin-up current can flow along the circular pathway

and form a clockwise vortex [see the black arrows in the leftmost part of Fig. 3(a)]. Inside such a large vortex, there exist three small vortices, such as

and

all of which have the same chirality as the large vortex. Subsequently, a vortex cluster appears where a big vortex contains several small vortices. The vortex clusters in either oscillation region possess identical chirality and inside a single cluster different vortices will interfere with each other, leading to the instructive quantum interference effect. As a result, $G_{\uparrow}$ oscillates with $E$ in the electronic bands [see the black lines in Figs. 2(c) and 2(d)], and the local spin currents inside a vortex cluster can be much greater than the corresponding spin component of the source-drain current [Figs. 3(a), 3(c), and 3(f)]. Besides, two neighboring vortex clusters are usually separated by a single vortex with opposite chirality. For instance, the aforementioned vortex cluster is separated from its neighboring one by a counterclockwise vortex

By inspecting Figs. 3(a)-3(c), it is important to notice that the local spin currents flowing from $\{1,29\}$ ($\{2,29\}$) to $\{1,30\}$ ($\{2,30\}$) are unequal to the corresponding spin current flowing within the last base pair, which holds for all $E$'s. In other words, a spin-flip-like process takes place at the last base pair when it is connected to lead 3, which is caused by the spin phase memory loss of the electrons when transmitting through this extra lead. In contrast, such process cannot occur at the last base pair in the absence of lead 3 [Figs. 3(d)-3(f)]. When $E$ is adjusted from the left oscillation region to the right one, the chirality of the vortex clusters is reversed [Figs. 3(a) and 3(c)], which may correspond to the case that the type of charge carriers is switched from the electrons to the holes, thus inducing the sign reversal of $P_{s}$. It is interesting that in the left oscillation region where $G_{\uparrow}$ is smaller than $G_{\downarrow}$ with $P_{s}<0$, conversely $I_{m\rightarrow n}^{\uparrow}$ is larger than the corresponding $I_{m\rightarrow n}^{\downarrow}$ [Fig. 3(a)]; while in the right oscillation region where $G_{\uparrow}$ is larger than $G_{\downarrow}$, $I_{m\rightarrow n}^{\uparrow}$ is smaller than $I_{m\rightarrow n}^{\downarrow}$ [Fig. 3(c)].

Regarding the smooth regions, however, the local spin current distributions are totally different. The local spin currents decay exponentially and eventually become zero within the numerical accuracy when flowing along the longitudinal direction of DNA hairpins, as illustrated in Fig. 3(e) and the left part of Fig. 3(b), because $E$ locates outside the electronic bands and all the nucleobases function as strong potential barriers. Subsequently, the electrons passing through DNA hairpins are mainly contributed by the first base pair [Figs. 3(b) and 3(e)], and the quantum interference effect is negligible. As a result, the oscillating behavior of $G_{\uparrow}$ vs $E$ cannot be observed in the smooth regions [Figs. 2(c) and 2(d)]. Besides, one notices that the local spin-up and spin-down currents possess identical direction and will not exhibit vortex-like patterns. In contrast, for model I the local spin currents reappear in the right part of DNA hairpins and are gradually enhanced when the nucleobases are farther away from the source/drain [see the right part of Fig. 3(b)], due to the finite voltage of lead 3. The local spin currents flow in opposite directions accompanied by a series of vortices. However, the spin polarization is exactly zero in the smooth regions as the source-drain current is hardly affected by lead 3.

As the transmission spectra of DNA hairpins are similar between the left energy range $E<E_{0}$ and the right one $E>E_{0}$, we focus on the right energy range for clarity. Figures 4(a)-4(b) and 4(c)-4(d) plot $G_{\uparrow}$ vs $E$ and $P_{s}$ vs $E$, respectively, for both models with typical values of $\Gamma_{d}$. It clearly appears that the curves $G_{\uparrow}$-$E$ and $P_{s}$-$E$ oscillate around a certain one for different $\Gamma_{d}$'s. The oscillating amplitude of $G_{\uparrow}/P_{s}$ is large in the weak dephasing regime (see the black lines in Fig. 4) and decreases with increasing $\Gamma_{d}$ for both models as expected, because the electrons suffer stronger inelastic scattering from the nucleobases in the regime of larger $\Gamma_{d}$ and the quantum interference effect becomes weaker. Although the oscillating amplitude of $G_{\uparrow}/P_{s}$ is smaller in model I than that in model II, their difference becomes smaller with increasing $\Gamma_{d}$, as the electrons lose their phase memory more quickly in the regime of larger $\Gamma_{d}$ and then the phase memory loss induced by lead 3 will be reduced. In other words, the hairpin loop has little effect on the spin transport along DNA hairpins in the strong dephasing regime.

The transmission ability of DNA hairpins, however, is very robust against the dephasing. $G_{\uparrow}$ is slightly declined in the smooth regions and can be enhanced around the valley regions even if $\Gamma_{d}$ is increased by two orders of magnitude, in sharp contrast to the dsDNA molecules whose conductance decreases with $\Gamma_{d}$ gam1 . Further studies indicate that the averaged conductance $\langle G_{\uparrow}\rangle$, obtained from the right oscillation region, increases with $\Gamma_{d}$ for $\Gamma_{d}<\Gamma_{d}^{g}$ and decreases with $\Gamma_{d}$ for $\Gamma_{d}>\Gamma_{d}^{g}$ [Figs. 9(a) and 9(b)]. Here, $\Gamma_{d}^{g}\simeq 0.002$ for model I, which is smaller than the critical value $\Gamma_{d}^{g}\simeq 0.004$ of model II, another signature that lead 3 indeed generates additional dephasing in the former model. This dephasing-assisted electron transport in the weak dephasing regime originates from the fact that with increasing $\Gamma_{d}$, the electrons will preferentially pass through DNA hairpins via the base pairs neighboring to the source/drain and not suffer inelastic scattering from distant nucleobases, leading to the enhancement of the conductance.

More importantly, the spin-filtering effect of DNA hairpins is pronounced for different values of $\Gamma_{d}$. $P_{s}$ is nonzero within the entire oscillation regions and can also be enhanced around the valley regions. When $\Gamma_{d}=0.0001$, $P_{s}$ can be 25.5% (22.6%) for model I (II). When $\Gamma_{d}=0.01$, $P_{s}$ can still be 14.4% for both models. We then calculate the averaged spin polarization, $\langle P_{s}\rangle$, which is defined as:

Our results indicate that the dependence of $\langle P_{s}\rangle$ on $\Gamma_{d}$ is nonmonotonic as well, where $\langle P_{s}\rangle$ increases with $\Gamma_{d}$ for $\Gamma_{d}<\Gamma_{d}^{p}$ and decreases with $\Gamma_{d}$ for $\Gamma_{d}>\Gamma_{d}^{p}$ [Figs. 9(c) and 9(d)]. Here, $\Gamma_{d}^{p}\simeq 0.0035$ (0.0055) for model I (II), which is slightly larger than $\Gamma_{d}^{g}$ of model I (II). This nonmonotonic behavior arises from the competing effects of the openness and the phase memory loss induced by the connection to Büttiker's virtual leads, where the former effect can generate the spin selectivity and conversely the latter one diminishes the spin polarization gam1 ; gam2 . In the weak dephasing regime, the system becomes more open for larger $\Gamma_{d}$ and leads to higher $\langle P_{s}\rangle$. While in the strong dephasing regime, the electrons have already lost their phase memory considerably and the spin polarization will be declined by further increasing $\Gamma_{d}$.

As $P_{s}=0$ always holds for model II in the absence of dephasing, we will consider three cases in the following:

($S_{1}$) Model I with $\Gamma_{d}=0.005$,

($S_{2}$) Model II with $\Gamma_{d}=0.005$, and

($S_{3}$) Model I with $\Gamma_{d}=0$.

We then study the effect of the molecular length $N$ on the spin transport along DNA hairpins. Figures 5(a)-5(c) and 5(d)-5(f) show $G_{\uparrow}$ vs $E$ and $P_{s}$ vs $E$, respectively, for $S_{i}$ ($i=1,2,3$) with several values of $N$. One can see that in the presence of Büttiker's virtual leads, the curves $G_{\uparrow}$-$E$ and $P_{s}$-$E$ of both models also oscillate around a certain one for all investigated values of $N$ [Figs. 5(a), 5(b), 5(d), and 5(e)]. The oscillating amplitude of $G_{\uparrow}/P_{s}$ is large for short DNA hairpins and declined by increasing $N$, because the electrons will suffer inelastic scattering from more and more nucleobases when transmitting through longer DNA hairpins in the case of $\Gamma_{d}\neq 0$ and consequently the quantum interference effect is weakened. While in the absence of Büttiker's virtual leads, $G_{\uparrow}/P_{s}$ oscillates between two certain envelopes and the corresponding oscillating amplitude remains unchanged for different $N$'s [Figs. 5(c) and 5(f)], because the inelastic scattering that the electrons suffer only comes from lead 3 which is independent of $N$. Since the number of the electronic states is proportional to $N$, the oscillation frequency of $G_{\uparrow}/P_{s}$ increases with $N$.

Contrary to the physical intuition that the transmission ability should be poorer for longer molecular wires, just as in the dsDNA molecules gam1 , it is interesting that the averaged conductance, $\langle G_{\uparrow}\rangle$, could be enhanced by increasing $N$ for both models, as illustrated in Fig. 6(a). This arises from the increasing probability of electron transmission through DNA hairpins mediated by the base pairs close to the source/drain, similar to the aforementioned dephasing-assisted electron transport which can be further confirmed by the following phenomena. For model I, $\langle G_{\uparrow}\rangle$ is larger in the case of $\Gamma_{d}=0.005$ than the case of $\Gamma_{d}=0$ when the molecular length satisfies $N>6$ [see the black-solid and red-dashed lines in Fig. 6(a)]. Although additional dephasing is introduced by lead 3 in model I, its $\langle G_{\uparrow}\rangle$ is greater than that of model II for relatively short DNA hairpins with $N=3\sim 20$ [see the black-solid and blue-dotted lines in Fig. 6(a)]. This implies that the transmission ability of short DNA hairpins is sensitive to their hairpin loops, in agreement with previous experiments lfd3 ; rn2 . While in the smooth regions, $G_{\uparrow}$ is almost independent of $N$ for all $S_{i}$'s as expected [Figs. 5(a)-5(c)], because the electron transmission in these areas is dominated by the first base pair and will not be affected by distant nucleobases.

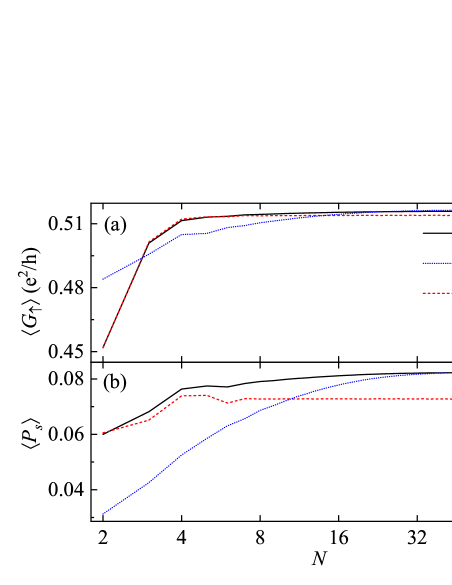
By inspecting Fig. 6(b), one may notice that the averaged spin polarization depends on the dephasing strength and the hairpin loop. This phenomenon is related to the openness induced by the connection to extra real/virtual leads. On the one hand, since the number of Büttiker's virtual leads is proportional to $N$, the system becomes more open for longer DNA hairpins when $\Gamma_{d}\neq 0$. As a result, model I with $\Gamma_{d}=0.005$ exhibits higher $\langle P_{s}\rangle$ as compared with the case of $\Gamma_{d}=0$, and their difference increases with $N$ [see the black-solid and red-dashed lines in Fig. 6(b)]. On the other hand, since lead 3 promotes the openness of model I, its $\langle P_{s}\rangle$ can be greater than that of model II for short DNA hairpins with $N<11$ [Fig. 6(b)], indicating that lead 3 plays an important role in the spin transport along short DNA hairpins. Nevertheless, the difference of $\langle P_{s}\rangle$ between both models is decreased by increasing $N$ [see the black-solid and blue-dotted lines in Fig. 6(b)], because the system cannot feel additional openness coming from lead 3 when it is sufficient open for long DNA hairpins. This implies that the spin transport properties are almost independent of the hairpin loop when the molecular length is sufficiently long.

Furthermore, one can see that $\langle P_{s}\rangle$ increases with $N$ for short DNA hairpins and then saturates at a critical molecular length $N_{c}$ for all $S_{i}$'s. The critical molecular length depends strongly on the dephasing strength and the hairpin loop, where $N_{c}=21$, $31$, and $5$ for $S_{1}$, $S_{2}$, and $S_{3}$, respectively. This behavior arises from the competition between the openness and the phase memory loss, which compensate for each other in the regime of large $N$ and thus $\langle P_{s}\rangle$ saturates for long DNA hairpins. Despite their strong dependence upon the dephasing and the loop, DNA hairpins exhibit pronounced spin-filtering effect for different molecular lengths. When $N=10$, $P_{s}$ can be 19.8% (22.8%) and $\langle P_{s}\rangle\simeq 8.0\%$ (7.2%) for model I (II); when $N=100$, $P_{s}$ can still be 15.6% and $\langle P_{s}\rangle\simeq 8.2\%$ for both models.

We now turn to study the influence of the interchain coupling $\lambda$ on the spin transport along DNA hairpins. Figures 7(a)-7(c) and 7(d)-7(f) show $G_{\uparrow}$ vs $E$ and $P_{s}$ vs $E$, respectively, with $\lambda$ changing from $0$ to $-0.5$. When the interchain coupling is switched off, the two helical chains decouple with each other. Then, the electrons cannot transmit within the base pairs and the transport properties are mainly determined by the hairpin loop. For model I where the hairpin loop is conductive, the electrons can transport from the source to the drain mediated by the conducting loop and a transmission band, associated with the electronic structures of both helical chains, emerges around the band center [see the cyan lines in Figs. 7(a) and 7(c)]. In this case, however, the spin-filtering effect disappears for whatever the values of model parameters [see the cyan lines in Figs. 7(d) and 7(f)], because the system is simplified as a single-helical chain with only one transport pathway, consistent with previous works gb1 ; gam1 ; gam2 . While for model II where the hairpin loop is insulating, there does not exist any transport pathway. Then, both $G_{\uparrow}$ and $G_{\downarrow}$ are exactly zero [see the cyan line in Fig. 7(b)], and $P_{s}$ is uncertain.

When the interchain coupling is switched on, the original transmission band at $\lambda=0$ evolves into two oscillation regions which are separated by a smooth one, exhibiting distinct features in comparison to the case of $\lambda=0$. With increasing $\lambda$, one can see several general phenomena for both models. (i) $G_{\uparrow}$ is considerably increased over the entire energy spectrum, because the electron transmission is enhanced along the transverse direction and suppressed along the longitudinal one. In other words, the probability of electron transmission from the source to the drain, mediated by the neighboring base pairs and not suffering any scattering from the distant nucleobases, is strongly increased, which is analogous to the electron transport mechanism found in the smooth regions. Subsequently, the quantum interference effect becomes weaker and the oscillating amplitude of $G_{\uparrow}/P_{s}$ decreases in general, accompanied by the decrement of $P_{s}$ [Figs. 7(d) and 7(e)]. (ii) The two oscillation regions are further separated from each other and become narrower, owing to the repulsion effect between the two helical chains driven by the interchain coupling, so do the energy regions with finite $P_{s}$ [Figs. 7(d)-7(f)]. In sharp contrast, the width of the smooth regions is dramatically increased, as can be seen from, e.g., the central smooth regions in Figs. 7(a)-7(c). As a result, the energy spectrum of finite $G_{\uparrow}$ becomes wider with increasing $\lambda$. (iii) More importantly, although $P_{s}$ is reduced by increasing $\lambda$ in the presence of Büttiker's virtual leads, the spin-filtering effect remains significant for various $\lambda$'s, especially in the case of $\Gamma_{d}=0$ [Fig. 7(f)]. For example, when $\lambda=-0.5$, $P_{s}$ can be 13.2% for model II with $\Gamma_{d}=0.005$ and 25.3% for model I with $\Gamma_{d}=0$.

Finally, we investigate the contact effect on the spin transport along DNA hairpins. The contact between the molecule and the leads in various experiments can generally be divided into two categories, i.e., the physisorbed contact and the chemisorbed one. In the former case, the end sites of the molecule are directly attracted to the leads by electrostatic trapping and the contact is usually poor. In the latter case, the contact is realized by chemical bonding between the end sites and the leads via thiol groups, allowing reproducible transport measurements. The contact effect can then be simulated by considering different coupling strengths between the hairpin stem and the source/drain. Figures 8(a)-8(c) and 8(d)-8(f) show $G_{\uparrow}$ vs $E$ and $P_{s}$ vs $E$, respectively, for typical values of $\Gamma$. When $\Gamma$ is small, the contact functions as a strong tunnelling barrier and majority of the electrons will be reflected at the interface between the source and the hairpin stem. As a result, $G_{\uparrow}$ is small in the oscillation regions and becomes smaller in the smooth ones due to the stronger suppression of the electron transmission along the first base pair [see the black lines in Figs. 8(a)-8(c)]. By increasing $\Gamma$, the electron transmission across the interface is enhanced and the conductance is increased within most of the smooth regions (data not shown). Nevertheless, the conductance profiles in the oscillation regions are distinct and present nonmonotonic behavior, which can be further demonstrated in Figs. 9(a) and 9(b) where the two-dimensional (2D) plots of $\langle G_{\uparrow}\rangle$ for both models are displayed as functions of $\Gamma_{d}$ and $\Gamma$.

One can see from Figs. 9(a) and 9(b) that by fixing $\Gamma_{d}$, a turning point can always be observed in the curves $\langle G_{\uparrow}\rangle$-$\Gamma$, where $\langle G_{\uparrow}\rangle$ increases with $\Gamma$ for $\Gamma<\Gamma^{g}$ and decreases with $\Gamma$ for $\Gamma>\Gamma^{g}$, regardless of $\Gamma_{d}$. This turning point increases almost linearly with $\Gamma_{d}$, from $\Gamma^{g}\simeq 0.4$ at $\Gamma_{d}=0$ to $\Gamma^{g}\simeq 0.49$ at $\Gamma_{d}=0.1$ for both models, as illustrated by the horizontal white-dashed lines in Figs. 9(a) and 9(b). This optimal contact configuration for efficient electron transport through DNA hairpins is different from other one-dimensional molecular wires zy1 ; gam4 and can be controlled by the dephasing. While fixing $\Gamma$, there also exists a turning point in the curves $\langle G_{\uparrow}\rangle$-$\Gamma_{d}$ that $\langle G_{\uparrow}\rangle$ increases with $\Gamma_{d}$ for $\Gamma_{d}<\Gamma_{d}^{g}$ and decreases with $\Gamma_{d}$ for $\Gamma_{d}>\Gamma_{d}^{g}$, as can be seen from the vertical white-dashed lines in Figs. 9(a) and 9(b). This indicates that the dephasing-assisted electron transport is a general phenomenon for DNA hairpins in the weak dephasing regime. One may notice that $\Gamma_{d}^{g}$ of model I is always smaller than that of model II as lead 3 introduces additional dephasing in the former model I, and both $\Gamma_{d}^{g}$'s increase slowly with $\Gamma$. Besides, although the electrons are strongly reflected at the interface in the regime of weak $\Gamma$, DNA hairpins exhibit strong transmission ability in a very wide range of $\Gamma_{d}$ and $\Gamma$ with $\langle G_{\uparrow}\rangle>0.1e^{2}/h$, as illustrated by the colorful areas except the blue ones in Figs. 9(a) and 9(b).

By inspecting Figs. 8(d)-8(f), it clearly appears that the spin polarization increases with $\Gamma$ at first and is then suppressed by further increasing $\Gamma$, accompanied by the increment of the oscillating amplitude of $P_{s}$. This nonmonotonic behavior can also be detected in Figs. 9(c) and 9(d), where the 2D plots of $\langle P_{s}\rangle$ vs $\Gamma_{d}$ and $\Gamma$ are shown for both models. When $\Gamma_{d}$ is fixed, $\langle P_{s}\rangle$ increases with $\Gamma$ for $\Gamma<\Gamma^{p}$ and decreases with $\Gamma$ for $\Gamma>\Gamma^{p}$, for whatever the values of $\Gamma_{d}$, as illustrated by the oblique white-dashed lines in Figs. 9(c) and 9(d). Interestingly, this optimized contact condition of the spin-selectivity effect is distinct from that of efficient electron transport mentioned above, $\Gamma^{p}\neq\Gamma^{g}$. Here, $\Gamma^{p}$ is decreased from $\Gamma^{p}\simeq 0.36$ (0.38) at $\Gamma_{d}=0.0005$ to $\Gamma^{p}\simeq 0.35$ at $\Gamma_{d}=0.001$ (0.003) and then increased almost linearly to $\Gamma^{p}\simeq 0.69$ at $\Gamma_{d}=0.1$ for model I (II). When $\Gamma$ is fixed, the dependence of $\langle P_{s}\rangle$ on $\Gamma_{d}$ is also nonmonotonic that $\langle P_{s}\rangle$ increases with $\Gamma_{d}$ for $\Gamma<\Gamma_{d}^{p}$ and decreases with $\Gamma_{d}$ for $\Gamma>\Gamma_{d}^{p}$, regardless of $\Gamma$. This turning point depends weakly on $\Gamma$ and will be slightly increased from $\Gamma_{d}^{p}\simeq 0.002$ (0.0035) at $\Gamma=0.01$ to $\Gamma_{d}^{p}\simeq 0.0035$ (0.0055) at $\Gamma=1$ for model I (II) [see the vertical white-dashed lines in Figs. 9(c) and 9(d)]. Note that $\Gamma_{d}^{p}>\Gamma_{d}^{g}$ always for either model of DNA hairpins.

Besides, we find that $\langle P_{s}\rangle$ of model I is greater than that of model II in the weak dephasing regime [see the leftmost part of Figs. 9(c) and 9(d)], as lead 3 promotes the openness of the former model and plays a dominant role in this regime. While in the strong dephasing regime, there is no observable difference of $\langle P_{s}\rangle$ between both models, further demonstrating that the hairpin loop will hardly influence the spin transport properties of DNA hairpins. Despite the complicated dependence of the spin polarization on the dephasing strength and the molecule-lead coupling, the spin-filtering effect of DNA hairpins is pronounced in a wide range of $\Gamma_{d}$ and $\Gamma$. For example, when $\Gamma_{d}=0.002$ and $\Gamma=0.2$, $P_{s}$ can reach 22.8% (26.7%) and $\langle P_{s}\rangle\simeq 8.8\%$ (8.1%) for model I (II); when $\Gamma_{d}=0.05$ and $\Gamma=0.8$, $P_{s}$ can still be 9.6% and $\langle P_{s}\rangle\simeq 6.7\%$ for both models.