Spherically symmetric formation of localized vortex tangle around a heat source in superfluid ⁴He

The motion of a quantized vortex follows the local superfluid flow, as described by Helmholtz’s theorems. Taking into account the temperature-dependent mutual frictions, $\alpha$ and $\alpha^{\prime}$, the equation of motion of a vortex segment at $\bm{s}(\xi)$ is Schwarz (1985)

$$\begin{split}\frac{\textrm{d}\bm{s}(\xi,t)}{\textrm{d}t}=\bm{v}_{\textrm{s}}&+\alpha\bm{s}^{\prime}(\xi)\times\bm{v}_{\textrm{ns}}\\ &-\alpha^{\prime}\bm{s}^{\prime}(\xi)\times\left[\bm{s}^{\prime}(\xi)\times\bm{v}_{\textrm{ns}}\right],\\ \end{split}$$

(3)

with

$$\bm{v}_{s}=\bm{v}_{s,\textrm{ind}}+\bm{v}_{s,\textrm{BS}}\quad\textrm{and}\quad\bm{v}_{n}=\bm{v}_{n,\textrm{ind}}.$$

(4)

Here, $\xi$ is the arc-length parameterization of the vortex filaments, and $\bm{s}^{\prime}(\xi)$ is the unit normal vector along the vortex filament at $\xi$, and $\bm{v}_{s,\textrm{ind}}$ and $\bm{v}_{n,\textrm{ind}}$ refer to the velocity fields thermally excited by the heater. The superfluid velocity $\bm{v}_{s,\textrm{BS}}$ includes velocity contribution from all the vortices, and is written in the form of Biot-Savart integral;

$$\begin{split}\bm{v}_{s,\textrm{BS}}=&\frac{\kappa}{4\pi}\int_{\mathcal{L}}\frac{\bm{s}^{\prime}(\xi)\times(\bm{s}(\xi_{0})-\bm{s}(\xi))}{|\bm{s}(\xi_{0})-\bm{s}(\xi)|^{3}}\textrm{d}\xi\\ =&\bm{v}_{s,\textrm{loc}}+\bm{v}_{s,\textrm{non-loc}}.\\ \end{split}$$

(5)

The divergence of the integral in the right-hand-side of Eq. (5) as $\xi\rightarrow\xi_{0}$ can be avoided by separating it into two terms, a localized induction velocity $\bm{v}_{s,\textrm{loc}}\approx\beta\bm{s}^{\prime}\times\bm{s}^{\prime\prime}$ and a nonlocal contribution $\bm{v}_{s,\textrm{non-loc}}$, where $\beta=(\kappa/4\pi)\ln(R/a)$ and $\bm{s}^{\prime\prime}$ is the second derivative of $\bm{s}(\xi)$ with respect to $\xi$. The interaction between the normal fluid and the vortices takes place through $\bm{v}_{ns}=\bm{v}_{n}-\bm{v}_{s}$ in the mutual friction terms in Eq. (3). By discretizing the vortices in line segments of a suitable resolution $\Delta\xi$, we solve the integro-differential equation. Also, the time-integration is calculated with a suitable time resolution $\Delta t$, adopting the fourth-order Runge-Kutta scheme.

To simulate a realistic spherical heater onto which vortices can be trapped, calculation of vortex dynamics is subjected to a spherical solid boundary condition. The condition can be satisfied by finding a boundary induced velocity field $\bm{v}_{s,b}$ such that

$$\left(\bm{v}_{s,BS}+\bm{v}_{s,b}\right)\cdot\bm{\hat{n}}=0$$

(6)

holds at the surface of the sphere of radius $r_{0}$. Here, $\bm{\hat{n}}$ is the unit normal vector on the surface. Since the velocity $\bm{v}_{s,b}$ satisfies the system of equations

$$\begin{split}\nabla\times\bm{v}_{s,b}&=0\\ \nabla\cdot\bm{v}_{s,b}&=0,\\ \end{split}$$

(7)

we can solve Eq.(7) in terms of the associated Legendre polynomials Schwarz (1985).

For the sake of clarity in the later discussion, we shall consider a single vortex ring traveling toward and away from a point heater immersed into a superfluid ⁴He bath at $T=1.6$ K as shown in Fig.1(a). The heater is a sphere of radius $a=100$ $\mu$m, around which we prescribe the spherical thermal counterflow such that the relative velocity between normal fluid and superfluid at some distance $r$ from the center of the heater is $\bm{v}_{\textrm{ns}}(\bm{r})=\frac{1}{\rho_{\textrm{s}}\sigma T}\frac{W}{4\pi r^{2}}\hat{\bm{r}}$. This can be obtained by replacing the area $A$ in Eq.(2) with $4\pi r^{2}$. We consider Eq.(3) for this case. By ignoring the nonlocal term in Eq.(5), the superfluid velocity $\bm{v}_{\textrm{s}}$ in Eq.(4) becomes

$$\bm{v}_{\textrm{s}}\approx\beta\bm{s}^{\prime}\times\bm{s}^{\prime\prime}-\displaystyle\frac{\rho_{\textrm{n}}}{\rho_{\textrm{s}}}\frac{v_{0}}{L^{2}+R^{2}}\hat{\bm{r}},$$

(8)

where $v_{0}\equiv W/4\pi\rho\sigma T$, and $L$ is the distance between the centers of the heater and the vortex ring. Substituting Eq.(8) into Eq.(3), one obtains a system of differential equations for the distance $L$ and the vortex radius $R$

	$\displaystyle\dot{L}\approx(-1)^{p}\frac{\beta}{R}-\frac{\rho_{\textrm{n}}}{\rho}\frac{v_{0}}{L^{2}+R^{2}}\textrm{cos}\theta-(-1)^{p}\frac{\alpha v_{0}}{L^{2}+R^{2}}\textrm{sin}\theta$		(9a)
	$\displaystyle\dot{R}\approx-\frac{\rho_{\textrm{n}}}{\rho}\frac{v_{0}}{L^{2}+R^{2}}\textrm{sin}\theta-\alpha\left[\frac{\beta}{R}-(-1)^{p}\frac{v_{0}}{L^{2}+R^{2}}\textrm{cos}\theta\right],$		(9b)

where $\theta=\tan^{-1}(R/L)$ and the terms with $\alpha^{\prime}$ are neglected. In Eq.(9), $p$ is a parameter indicating the direction of the ring propagation; $p=0$ if the orientation of the vortex, $\it{i.e.}$ $\bm{s}^{\prime}\times\bm{s}^{\prime\prime}$, is radially outward, and $p=1$ if that is radially inward. Figures 1(b) and (c) show Eq.(9) as vector fields $(\dot{L}(L,R),\dot{R}(L,R))$ with $p=0$ and $p=1$, respectively, at $T=1.6$ K. The trajectory of a vortex can be obtained by drawing a smooth stream line parallel to the vector at each point from an arbitrary initial point $(L_{0},R_{0})$ in the coordinate. In the case with $p=1$, a vortex of any radius $R$ shrinks itself to vanish at some distance $L$ away or “collides with” the heater at $L=100$ $\mu$m with time. On the other hand, when $p=0$, a vortex could grow in size depending on its initial values, $R_{0}$ and $L_{0}$.

Though in a highly developed vortex tangle, this simple single-loop analysis may not hold without modification, we can learn from this analysis that the orientation of each vortex ring that constitutes the tangle tends to orient itself in the outward direction. In preceding studies with a simple channel flow geometry, the homogeneity or/and isotropy of the vortex orientations are often assumed, which allows us to derive the Vinen’s equation which predicts the time-evolution of a vortex line density Vinen (1957c). However, in the present study there is no guarantee that the same equation holds because the vortex orientations are polarized.

A sphere of a radius $r_{0}=0.1$ mm is immersed in a bulk superfluid ⁴He. The length of each vortex segment $\Delta\xi$ is set to be within the range $1\sim 2\times 10^{-2}$ mm. Now, the sphere is assumed to be heated homogeneously and sets up a steady thermal counterflow profile of the form

$$\bm{v}_{ns}=v_{ns,0}\frac{r_{0}^{2}}{r^{2}}\bm{\hat{r}},$$

(10)

where $v_{ns,0}$ is the magnitude of the relative counterflow velocity at the surface $r=r_{0}$. In reality there should exist a “thermal boundary layer” with finite thickness where the two fluids are accelerated and the profile in Eq.(10) is not valid in the vicinity of the heater, as it is reported in Refs. Švančara et al. (2018); Hrubcová et al. (2018). However, we ignore such effect in this study, assuming the width of the layer is much less than the particle radius $r_{0}$.

Figure 2 shows the time evolution of six seed vortices symmetrically placed near a heater.

In the simulation, we set the temperature of the system to be $T=1.3$ K and the counterflow velocity to be $v_{ns,0}=100$ cm/s. Out of the six vortices, four are initially reconnected onto the spherical surface. An end of the vortex line reconnected to the heater surface is bent in order to meet the boundary condition of Eq.(6), $\it{i.e.}$, the vortex segment at the surface needs to be perpendicular to the surface so that the vertical velocity component vanishes where they meet on the surface. As we discussed in Sec.II.2, under a radial counterflow, the orientation of vortices are selected in a way that they tend to induce velocity away from the heater, which seems to explain a spiral-shape structure formed near the vortex-surface intersection (see Fig.3). The rapid growth of the tangle due to the spiral-shaped structure is also understood as the manifestation of the Donnelly-Glaberson (DG) instability Schwarz (1990); Glaberson and Donnelly (1966); Donnelly (1991). In the vicinity of the heater surface, the magnitude of the counterflow is strong, which makes the vortex lines unstable and excites Kelvin waves along them. Again, the Kelvin waves with outward orientation are likely to be amplified; while the others tend to vanish because of the converging counterflow. This growth mechanism driven by DG instability would not hold for vortices that traveled far enough from the heater because the counterflow magnitude drops as $1/r^{2}$. We discuss the vortex tangle growth mechanism out of the DG instability regime in Sec. IV.

The vortex line density of the tangle as a function of the radius is plotted in Fig.4. A single curve in the plot shows the radial vortex line density (RVLD) at time $t$ in the entire tangle, and the change in color (blue $\rightarrow$ red) indicates the lapse of time (early $\rightarrow$ late). Although the maximum RVLD has an upper bound due to the numerical limitation ($L_{\textrm{max}}\sim\Delta\xi^{-2}$), the tangle seems to grow unboundedly, as long as some vortices are kept reconnected onto the heater surface at $r=r_{0}(=0.1$ mm).

With time, a bottleneck appears in RVLD near the heater, which may be understood as follows: The vortices in the tangle are constantly pulled toward the center of the heater by its induced superfluid velocity $\bm{v}_{s,\textrm{ind}}$. At the same time, a free vortex ring travels approximately with a localized induction velocity $\bm{v}_{s,\textrm{loc}}$ in Eq.(5), which is inversely proportional to the local curvature radius. Therefore, a smaller radius of a vortex ring results in a stronger resistance to the counter flow that pulls it toward the heater. In the vicinity of the surface, only a few vortices can survive in the strong counterflow, while others are ‘sucked’ into the heater. On the other hand, the counterflow becomes weaker as $1/r^{2}$, and more and more vortices can overcome the pull as they go farther away from the heater.

Supposing a heater placed at the origin is point-like, we ignore the boundary condition of Eq.(6), but the radius of the heater is set to be $r_{0}=0.1$ mm to obtain the counterflow velocity profile according to Eq.(10). The vortex resolution is $\Delta\xi\sim 0.5\times 10^{-2}$ mm for this simulation. By placing several seed vortices we investigated their development into a vortex tangle, and its dependence on the counterflow magnitude $v_{ns}$ and the temperature $T$.

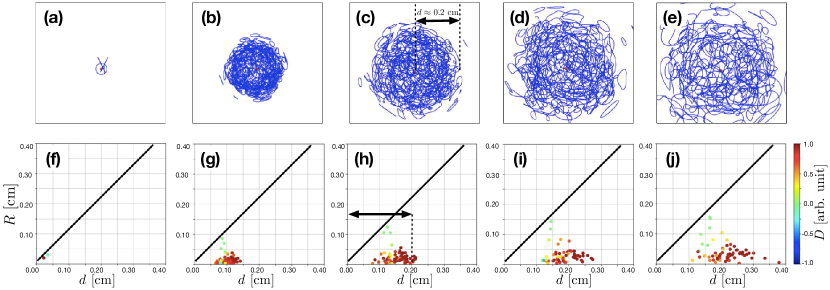
A typical time-evolution process is summarized in Fig.5. The panels (a)–(e) in Fig.5 show the snapshots of the simulation. A single dot in the panels (f)–(j) of Fig.5 shows a vortex loop in the tangle corresponding to the moments when the snapshots (a)–(e) are taken. The horizontal and vertical axes in the panels (f)–(j) represent the radial distance $d$ of a vortex loop, defined as the average distance between the origin and each vortex segment within a single loop, and the size $R$ of the loop is defined as the average distance between each vortex segment and the center of the loop. In terms of the lengths defined in Fig.1(a), the radius distance $d$ is expressed as $\sqrt{L^{2}+R^{2}}$. The color of the dot in the panels indicates the loop polarization $D$, which is defined as

$$D=\hat{\bm{r}}\cdot\oint_{\textrm{a loop}}\bm{s}^{\prime}(\xi)\times\bm{s}^{\prime\prime}(\xi)\textrm{d}\xi/\mathcal{N},$$

(11)

where $\hat{\bm{r}}$ is the unit radial vector at the center of the loop, and $\mathcal{N}$ is a properly chosen numerical factor that normalizes the integral. The vortex loops with $D\approx 1$ travel radially outward and are colored in red; while, the ones with $D\approx-1$ travel radially inward and are colored in blue. It turns out that the small number of initial vortex loops grows swiftly. The loops quickly form a spherical tangle surrounding the point heater. The tangle front propagates radially outward, as it leaves a hollow region inside the tangle. Solid slopes of roughly $d=R$ are drawn for reference in Fig.5(f)–(j). Apparently, the maximum loop size $R_{\textrm{max}}$ appears in the vicinity of the slopes at each panel, which indicates that the value of $R_{\textrm{max}}$ can be used as a good measure of the radius of the tangle.

The existence of the large vortex loops of size comparable to the tangle size with polarization $D\approx 0$ seems to play the key role for the tangle front propagation. Such large loops frequently collide with each other and emit small vortices with random orientations. The orientations, however, are polarized because of the radial thermal counterflow. As we have seen in Sec. II, small vortices with inward orientation shrink, while ones with outward orientation can survive for longer time. Therefore, if the radii of outward vortices are small enough to overcome the counterflow that tries to suck them into the heater, then the radius of the vortex tangle can grow, which would explain the monotonous growth in radius of the tangle with a hollow inside. This tangle front propagation process driven by small outward vortices can be observed at the outmost region of the tangle in Fig.5(h), (i) and (j). Also, see movies in supplementary materials.

The tangle front propagates radially outward against the superfluid velocity $\bm{v}_{s,\textrm{ind}}$ induced by the point heater. The relative counterflow profile $\bm{v}_{ns}$ at the tangle front $R_{\textrm{f}}$ is given by Eq.(10), equating $r=R_{\textrm{f}}$. Assuming that the conservation of mass is valid locally, the velocity $\bm{v}_{s,\textrm{ind}}$ can be obtained from the following relation:

$$\rho_{s}\bm{v}_{s,\textrm{ind}}(R_{\textrm{f}})+\rho_{n}\bm{v}_{n,\textrm{ind}}(R_{\textrm{f}})=0,$$

(12)

where $\bm{v}_{n,\textrm{ind}}-\bm{v}_{s,\textrm{ind}}=\bm{v}_{ns}$. Since a vortex ring of radius $R$ travels with velocity $v_{s}\sim\beta/R$, the only vortex loops with radius $R_{c}<\beta/v_{s,\textrm{ind}}(R_{\textrm{f}})$ can travel against the counterflow and gradually expand the “edge” of the tangle, while the other vortices are presumably well-confined within the region of radius $R_{\textrm{f}}$.

When it comes to the study of the homogeneous vortex tangles, the vortex line density (VLD) $\mathcal{L}$ is the quantity that is uniquely determined experimentally and computationally and is frequently used to analyze the nature of the tangles. However, in the case of the localized inhomogeneous vortex tangles, there remains some arbitrariness in the value of $\mathcal{L}$ depending on the scheme to estimate the volume $V$ occupied by the vortex lines in the tangle. The maximum value of spatially-independent VLD $\mathcal{L}$ may be achieved if the volume $V$ is estimated by the box-counting method, $\it{i.e.}$, dicing up the computational space into cubes with suitable lengths, we count the number of the cubes that contain the (segments of ) vortices and calculate the total volume $V_{\textrm{BC}}$. If we take the lengths of the cubes to be the average vortex loop size, then $\mathcal{L}=l/V_{\textrm{BC}}$, where $l$ is the total vortex line length (TVLL), gives the VLD averaged over the volume. On the other hand, since most of the vortices in the tangle are localized in a sphere of volume $V_{\textrm{loc}}=4\pi R_{\textrm{f}}^{3}/3$, the minimum value of $\mathcal{L}$ is achieved when we let the volume $V$ be a constant such that $V>V_{\textrm{loc}}$ for all time. Then the TVLL $l$ in this case is essentially the same as the VLD $\mathcal{L}$, which is the quantity we shall mainly discuss in this section.

Figure 6(a) shows the profile of the TVLL $l$ as a function of time. Initially, $l(t)$ grows rapidly within the region of radius $R_{\textrm{f}}$. As we have discussed in Sec. IV.1, in the initial growing stage, there are number of large vortex loops of the order of the tangle size. Since a large vortex loop cannot travel against the thermal counterflow, those with large radii or small local curvatures are essentially enclosed in the spherical region, inside of which vortices grow in length via mutual friction and in number because of the repeated reconnections. However, the growth rate decreases, and the total length $l(t)$ finds its maximum value $l_{\textrm{max}}$. In the case of $T=1.8$ K and $v_{ns,0}=30$ cm/s, the tangle grows up to $l_{\textrm{max}}\approx 15$ cm at time $t\approx 4$ s, after having some fluctuation around the maximum value for about a few seconds. Then, it finally starts to decay gradually. The dependence of $l_{\textrm{max}}$ on $T$ and $v_{ns,0}$, is summarized in Fig.6(b). The radii of the circles are proportional to the values of $l_{\textrm{max}}$ at $(T,v_{ns,0})$, and the thickness of the circle color indicates the time it takes to reach $l_{\textrm{max}}$. Below $T\approx 2.0$ K, the TVLL profile $l(t)$ has a plateau for several seconds after a swift growth, during which the maximum value $l_{\textrm{max}}$ is attained. Above $T\gtrsim 2.1$ K, on the other hand, the tangle behaves differently since the value of the mutual friction coefficient $\alpha^{\prime}$ becomes negative. If $T\gtrsim 2.1$ K, there is a critical velocity $v_{c}$, between $v_{ns,0}=20$ cm/s and $30$ cm/s, that determines whether a tangle can develop or not. Above the critical velocity $v_{c}$, the tangle may not be formed; while, below $v_{c}$, the tangle tends to grow unboundedly.

Aside from the “gradual decay” while the heater is on, we have also investigated the “free decay” turning off the heater suddenly during the tangle development process. Figure 7(a) plots $1/l$ as a function of time $t$. The broken curve represents the“gradual decay” where the heater is kept on. At time $t_{\textrm{free}}$ indicated by the solid circles on the $1/l$ plot, the point heater is turned off, and the time evolutions of the tangle for time $t>t_{\textrm{free}}$ are simulated. The solid branches departing from the broken curve represent the results of the “free decay” simulations.

After turning off the heater, the TVLL $l$ tends to decay inversely proportional to time for several seconds as it is indicated by the straight lines in Fig. 7(a). What this indicates is that the form of the decay term coincides with that of Vinen’s equation (VE) Vinen (1957c)

$$\left(\frac{\textrm{d}\mathcal{L}}{\textrm{d}t}\right)_{\textrm{decay}}=-\chi_{2}\frac{\kappa}{2\pi}\mathcal{L}^{2}$$

(13)

that describes the time evolution of a homogeneous VLD $\mathcal{L}$, where $\chi_{2}$ is a phenomenological parameter of order unity. Substituting $\mathcal{L}=l/V_{\textrm{BC}}$ into Eq.(13), we obtain

$$\frac{\textrm{d}l}{\textrm{d}t}-\frac{l}{V_{\textrm{BC}}}\frac{\textrm{d}V_{\textrm{BC}}}{\textrm{d}t}=-\frac{\chi_{2}}{V_{\textrm{BC}}}\frac{\kappa}{2\pi}l^{2}.$$

(14)

Since the computational result shows that the second term in the left hand side of Eq.(14) is smaller than the first term by over an order of magnitude, we ignore the second term. Then, Eq.(14) has a simple solution of the form

$$\frac{1}{l}=\frac{1}{l_{0}}+\frac{\chi_{2}}{V_{\textrm{BC}}}\frac{\kappa}{2\pi}t,$$

(15)

where $l_{0}$ is the initial TVLL at $t=t_{\textrm{free}}$. Since $\mathcal{L}=l/V_{\textrm{BC}}$, the value of $\chi_{2}$ can be found as a slope by rescaling the vertical axis $1/l$ to be $(2\pi/\kappa)(1/\mathcal{L})$. Rescaling all the “gradual decay” and “free decay” profiles in Fig. 7(a), it turns out that all curves tends to collapse onto a single line of the slope $\chi_{2}\approx 3.79$, as we can see in Fig. 7(b). Considering the fact that the experimental value of $\chi_{2}$ in a homogeneous vortex tangle is of order unity, the value we obtained here with the localized vortex tangle may not be unreasonable, although the value of $\chi_{2}$ seems to be sensitive to the volume $V$ occupied by the vortex loops. Here, we have applied the box-counting method to estimate the volume $V_{\textrm{BC}}$. However, the way of estimating the occupied volume is not unique, and there remains some uncertainty in the determination of the value of $\chi_{2}$ in the localized vortex tangles. Also, the approximation which allows us to obtain Eq.(15) only holds for sufficiently short time after turning off the heater, since the average distance among the vortices becomes larger than the average vortex loop size, which leads to the underestimation of the volume occupied by the vortices. The consequence of this effect can be observed in Fig. 7(b), $\it{i.e.}$, the VLD $\mathcal{L}$ is overestimated, and the solid curves tend to drop below the broken curve whose slope is roughly $\chi_{2}\approx 3.79$ after following it for at least a few second.