SPH Simulations for Shape Deformation of Rubble-Pile Asteroids Through Spinup: The Challenge for Making Top-Shaped Asteroids Ryugu and Bennu
Abstract
Asteroid 162173 Ryugu and asteroid 101955 Bennu, which were recently visited by spacecraft Hayabusa2 and OSIRIS-REx, respectively, are spinning top-shaped rubble piles. Other axisymmetric top-shaped near-Earth asteroids have been observed with ground-based radar, most of which rotate near breakup rotation periods of hours. This suggests that rotation-induced deformation of asteroids through rotational spinup produces top shapes. Although some previous simulations using the Discrete Element Method showed that spinup of rubble piles may produce oblate top shapes, it is still unclear what kinds of conditions such as friction angles of constituent materials and spinup timescales are required for top-shape formation. Here we show, through Smoothed Particle Hydrodynamics simulations of granular bodies spinning-up at different rates, that the rotation-induced deformation of spherical rubble piles before breakup can be classified into three modes according to the friction angle : quasi-static and internal deformation for , dynamical and internal deformation for , and a set of surface landslides for . Note that these apparent large values of friction angle can be acceptable if we consider the effect of cohesion among blocks of a rubble pile under weak gravity. Bodies with evolve into oblate spheroids through internal deformation, but never form pronounced equators defining a top shape. In contrast, bodies with deform into axisymmetric top shapes through an axisymmetric set of surface landslides if spinup timescales are a few days. In addition, through slow spinups with timescales month, bodies with deform into non-axisymmetric shapes via localized sets of landslides. We suggest that rapid spinup mechanisms are preferable for the formation of axisymmetric top shapes.
keywords:
Asteroids, rotation; Asteroids, surfaces; Rotational dynamics; Regoliths1 Introduction
The Japan Aerospace Exploration Agency (JAXA) spacecraft Hayabusa2 arrived at asteroid 162173 Ryugu in June 2018 and investigated its detailed physical and geometrical properties via remote-sensing instruments. The proximity observation revealed that Ryugu is a rubble-pile asteroid with a so-called “spinning-top” shape having a prominent equatorial ridge (Watanabe et al., 2019). Radar observations already found some top-shaped near-Earth asteroids such as 1999 KW4, 2001 SN263, and 65803 Didymos (Ostro et al., 2006; Becker et al., 2015; Benner et al., 2010), and the recent proximity observation with the NASA spacecraft OSIRIS-REx confirmed that 101955 Bennu also has a top shape (Lauretta et al., 2019; Barnouin et al., 2019). Top-shaped asteroids have several common geometrical characteristics: polar-to-equatorial axis ratios of , pronounced equatorial ridges, nearly conical surfaces extending from the equators to the mid-latitudes, and almost axisymmetric shapes.
The fast rotation of a rubble-pile asteroid results in its deformation or breakup because the centrifugal force exceeds self-gravity at the equatorial radius, and the critical rotation period at which the centrifugal force equals self-gravity at the equator is using a typical bulk density of C-type asteroids (Carry, 2012), where is the gravitational constant. The spin periods of the top-shaped asteroids 1999 KW4, 2001 SN263, Didymos, and Bennu are , , , and , respectively (Ostro et al., 2006; Becker et al., 2015; Richardson et al., 2016; Lauretta et al., 2019). Although the current rotation period of Ryugu is (Watanabe et al., 2019), surface slope distribution and failure analysis of Ryugu suggest that Ryugu once had a rotation period of (Watanabe et al., 2019; Hirabayashi et al., 2019). This strongly suggests that Ryugu was reshaped by centrifugally induced deformation during the period of rapid rotation (Watanabe et al., 2019). Thus, other top-shaped asteroids may have also formed through deformation due to rapid rotation.
All the top-shaped asteroids found so far are near-Earth asteroids and have diameters several kilometers (Ostro et al., 2006; Benner et al., 2010; Brozović et al., 2011; Busch et al., 2011; Rozitis et al., 2014; Becker et al., 2015; Lauretta et al., 2019; Watanabe et al., 2019). Their top shapes were identified through radar or proximity observations, which are mainly possible only for near-Earth asteroids. About half of the top-shaped asteroids have satellites (2001 NE263:Becker et al., 2015, 1999 KW4:Ostro et al., 2006, 1994 CC:Brozović et al., 2011, Didymos:Benner et al., 2010). The orbits and sizes of the satellites and the fraction of the top-shaped asteroids with satellites may further constrain the formation process of top shapes.
Torque induced by the absorption of sunlight and its thermal re-emission changes the rotation of asteroids. The spinup or spindown mechanism is called the Yarkovsky-O’Keefe-Radzievskii-Paddack (YORP) effect (e.g., Rubincam, 2000; Walsh, 2018), and the YORP spinup of several asteroids has already been confirmed (Taylor et al., 2007; Kaasalainen et al., 2007; Hergenrother et al., 2019). On the other hand, impacts with other small asteroids also change rotation states. Merging collisions and accretion of fragments after catastrophic collisions tend to increase spin rates due to angular momentum supply (e.g., Sugiura et al., 2018, 2020; Michel et al., 2020). The spinup of asteroids caused by such mechanisms eventually leads to global deformation, and sometimes probably results in top shapes (Walsh et al., 2008). The spinup also induces breakup of bodies to form satellites, which is consistent with the omnipresence of satellites around top-shaped asteroids.
How rapidly rotating rubble piles deform has been investigated in various studies through analytical approaches (Holsapple, 2001, 2004; Sharma et al., 2009; Holsapple, 2010; Sharma, 2013, 2018; Hirabayashi, 2015) and numerical simulations (Walsh et al., 2008, 2012; Hirabayashi et al., 2015; Sánchez & Scheeres, 2016; Zhang et al., 2017, 2018; Sánchez & Scheeres, 2018; Leisner et al., 2020). Most of the previous simulations about spinup of bodies have been conducted using the Discrete Element Methods (DEMs), in which usually spherical particles subject to gravity and contact forces represent the rubble-pile constituents. The simulations of spinup show that a body with a closely packed particle configuration experiences surface landslides and deforms into a top shape, while a body with a loosely packed particle configuration experiences internal deformation (Walsh et al., 2008; Zhang et al., 2017). This suggests that the interlocking of particles may affect deformation modes. DEM simulations correctly represent bulk friction of rubble piles if the sizes of DEM particles are comparable to those of blocks or regolith particles of asteroids. Practical sizes of DEM particles for asteroid simulations, however, are much larger than those of regolith particles due to computational limitations. The difference of the particle sizes possibly affects details of deformation modes of spinning-up bodies. Using a plastic finite element model (FEM) technique, some researches analyzed detailed relationship between cohesive strength and failure modes of rapidly rotating asteroids (e.g., Hirabayashi, 2015; Hirabayashi & Scheeres, 2015, 2019), while they could not investigate resultant shapes produced through the failure due to the limitation of FEM. Although the axisymmetric top-shaped figures are shown to be in equilibrium as a granular body (Harris et al., 2009), the formation process for such bodies is still unclear. Thus, the quantitative conditions of friction angle and acceleration rate required to form top shapes are still unclear.
The Smoothed Particle Hydrodynamics (SPH) method was recently applied to numerical simulations of shape deformation of asteroids (Jutzi, 2015). In the SPH simulations, a rubble-pile body is considered as a continuum of granular material and we explicitly set a specific value of friction angle of the material. Thus, we expect that the SPH method has the advantage of precise control of bulk friction of rubble piles. So far the SPH method has mainly been used to investigate shapes of impact outcomes (e.g., Jutzi & Asphaug, 2015; Jutzi & Benz, 2017; Leleu et al., 2018; Sugiura et al., 2018, 2019, 2020), and this is the first work applying the SPH method to the rotational deformation of small bodies.
In this paper, we present the results of SPH simulations about spinups of spherical rubble-pile bodies with various values of friction angles of constituent material. We then examine the friction angles required for the formation of top shapes. To clarify the spinup rate dependence, we also present the results of simulations with a slower spinup rate. Although the adopted rate is even much faster than the typical YORP spinup rate owing to the limitation of computational time, the comparison of these simulations with different spinup rates will help us to consider what kinds of acceleration mechanisms are appropriate for the top-shape formation.
2 Method, simulation setup, and analysis of results
2.1 Method
The numerical code utilized in this study is based on a version of the SPH code described in Sugiura et al., (2018, 2019). The code solves hydrodynamic equations (e.g., the equations of continuity and motion) with self-gravity and yield processes with the aid of a friction model that determines shear strength of granular material (Jutzi, 2015). For the surface of a granular body, the time evolution of the density distribution of the body is calculated by solving the equation of continuity. The code is parallelized for distributed memory computers by using the Framework for Developing Particle Simulator (Iwasawa et al., 2015, 2016). Sugiura, (2020) verified the validity of our SPH approach for granular materials through the comparison with laboratory experiments of cliff collapse (Lajeunesse et al., 2005).
We investigated the rotational deformation of a kilometer-sized granular body, where compressional stresses derived from self-gravity are too small for granular material to experience plastic compression. This enables us to use the following elastic equation of state:
| (1) |
where is the pressure, is the bulk density, is the bulk sound speed, and is the bulk density at uncompressed states. We set , which is the common value of the measured bulk densities of Ryugu and Bennu (Watanabe et al., 2019; Lauretta et al., 2019). We used a typical sound speed of granular material for (Teramoto & Yano, 2005). Simulation results only weakly depend on the adopted sound speed or the equations of state (see Appendix A). Note that we ignored the direct effect of cohesion, i.e., tensile forces, and thus we set if becomes negative.
2.2 Simulation setup and analysis method
We mainly investigated the rotational deformation of a uniform and spherical body with a radius of , which is similar to Ryugu’s equatorial radius (Watanabe et al., 2019). Note that the deformation process and resultant shape are almost independent of the size of the body in our simulations (see Appendix A). We briefly mention the dependence of initial shapes on the deformation process by simulating bodies slightly different from the sphere in Section 3.3. The total number of SPH particles comprising the body is about 25,000 (or SPH particles in the radial direction), which has a sufficient resolution to capture shape-related features of a resultant body. The SPH particles were initially not placed on a regular lattice, but distributed randomly around the lattice points with a uniform density based on a procedure described by Sugiura et al., (2018).
In general, the shear strength of cohesive granular material as a function of the confining pressure can be represented as , where and are the “real” friction angle and the cohesive strength, respectively. For simplicity, we adopted the relation in a form with the “effective” friction angle by interpreting that the relation would be valid for cohesive granular materials. The effective friction angle used in our simulations can be expected to mimic an aspect of cohesion. The cohesion of a subsurface layer of asteroid Ryugu is estimated to be up to from an artificial impact experiment done in the Hayabusa2 mission (Arakawa et al., 2020), whereas the central pressure of a spherical body with a radius of and mean density of is only , so that the effective friction angle is up to . To mimic large effective friction angles due to cohesion, we varied from to . This treatment allows us to understand the detailed dependence of deformation modes on one parameter . The validity of using such large effective friction angles instead of introducing the cohesion is discussed in Section 4.1.
We adopted an inertial coordinate system with origin at the center of mass of the body and the -axis directed along the initial rotation axis of the body. The initial spherical shape of the body is stable for slow rotations, and the minimum rotation period required for keeping the initial configuration gets shorter for larger (Holsapple, 2001). We set the initial rotation period of the body in each simulation with an effective friction angle to be longer than for the corresponding . To represent the spinup process of a body, we accelerated the rotation of the body around the -axis as follows. We added an increment of velocity in the rotational direction to the -th SPH particle comprising the body at each numerical step as
| (2) |
where is the predetermined angular acceleration of rotation, is the time step, is the unit vector parallel to the -axis, and is the position vector of the -th SPH particle. The incremental velocity would increase the rotation rate by if its shape did not change. However, deformation actually changes the moment of inertia of the body, which results in a further change of the rotation rate. We set , where is the angular acceleration in the nominal case defining the dimensionless parameter . Here, we define the spinup timescale of a body as the elapsed time of spinup from the rotation period of to . In the nominal case (), the spinup timescale is , which corresponds to 8.0 rotations. The nominal rotational acceleration of is much faster than that due to the actual YORP effect for a kilometer-sized asteroid, which corresponds to (Kaasalainen et al., 2007; Hergenrother et al., 2019). We present the results of rotational deformation through spinups with in Section 3.1 and with much smaller in Section 3.2.
The spinup of the body eventually results in structural deformation and the ejection of surface masses. We accelerated only the SPH particles that comprise the main body, i.e., the largest clump of SPH particles, each of which has a distance from the nearest member of less than 1.5 times the smoothing length of a SPH particle. We identified clumps using a friends-of-friends algorithm (e.g., Huchra & Geller, 1982).
Major deformation of the initial spherical body is followed by or accompanied by major mass ejection. In this study, we focused on the analysis of the shape of the main body formed through the major deformation event. To check the stability of the final shape of a deformed body, we stopped acceleration after 1% of the total mass was ejected and continued the simulations for more than , which is longer than a typical deformation timescale of the body.
The ejected mass at some stage of a simulation is defined as the total mass of SPH particles that do not belong to the main body at that time. We measured the ratio of the minor to major axis of the main body using the top-down method (e.g., Capaccioni et al., 1984), where the two axis lengths or were measured as the distances between two parallel plates that bound the main body. The rotation period of the main body is calculated as , where and are, respectively, the moment of inertia and the angular momentum of the main body around the -axis. Note that the angle between the angular momentum vector and the -axis is Although we do not do any corrections for the rotation axis of the body, the rotation axis is almost aligned with the -axis. Thus, calculated from and is a reliable measure for the rotation period.
3 Results
3.1 Spinup with
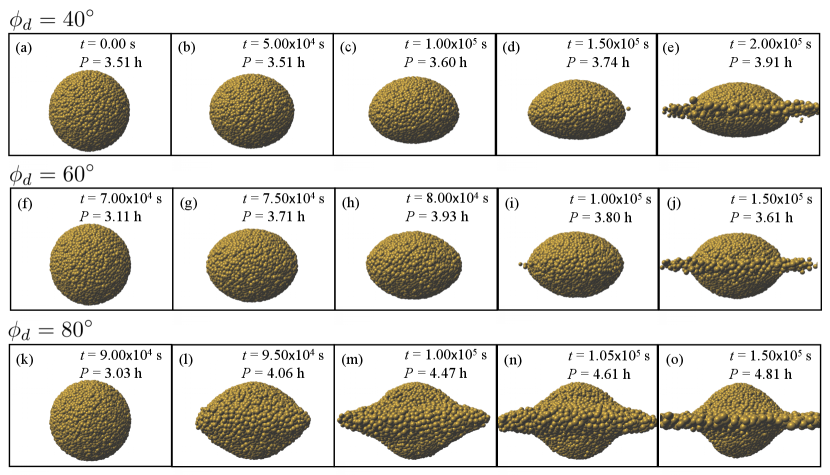
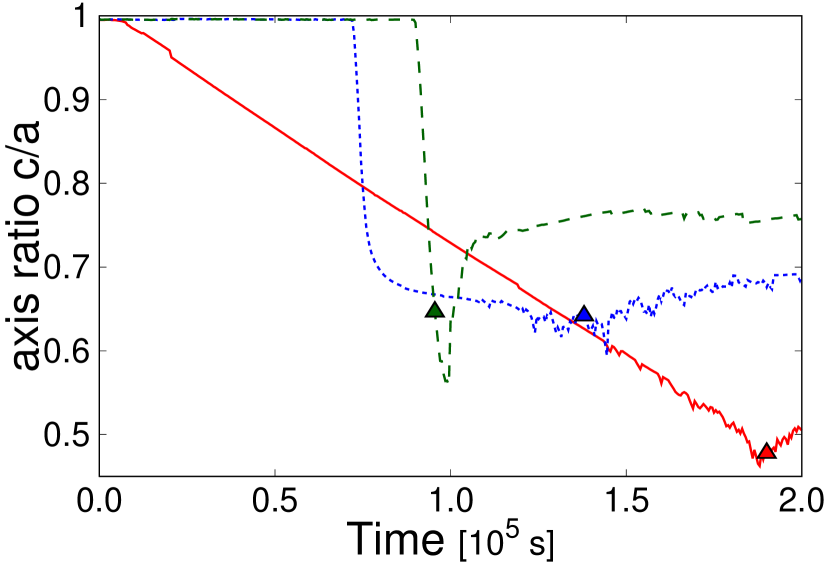
In simulations with the nominal spinup rate , we set the initial rotation periods for to be and those for to be in order to save the computational time because in the latter cases deformation of the body never occurs during the periods when . Figure 1 shows side-view snapshots of the spinup of the granular spherical bodies with the effective friction angles , , and . Figure 2 shows a time evolution of the axis ratio of the main body obtained from the same simulations. Because of the difference of the initial rotation periods, time when deformation occurs for is later than those for and . For better comparison, elapsed time from after the start of the simulation is shown for in Figs. 1a-e and 2.
All the deformed bodies in Fig. 1 have kept almost axisymmetric shapes, indicating that the spinup of a spherical body with results in axisymmetric deformation. This behavior is quite different from a self-gravitating fluid body, for which rapid rotation induces a non-axisymmetric instability to form a series of Jacobi triaxial ellipsoids (Chandrasekhar, 1969)111The stability of granular asteroids has been investigated by Sharma, (2013) in detail. Although the work is relevant to our simulations, direct comparison between the work and our simulations is difficult because setups are different. Especially, our present study simulates bodies in which global plastic deformation hardly occurs, so that analysis of Sharma, (2013) on plastic modulus is not expected to affect our present study. In future work, we are planning to perform simulations that use the same setup as the work and discuss application for the stability of granular asteroids.. The non-axisymmetric deformation into triaxial ellipsoids with small intermediate-to-major axis ratio occurs only for . This suggests that relatively small values of () of granular bodies will prevent the deformation into triaxial ellipsoids. Note that non-axisymmetric sets of landslides occurring in slower spinup of bodies with (see Section 3.2) belong to a different deformation mode from the internal deformation forming non-axisymmetric triaxial ellipsoids for .
For , the axis ratio decreases from unity (Fig. 1a) to (Fig. 1d) during (Fig. 2). Timescale of the deformation is comparable to the spinup timescale , and the deformation of the body almost halts once we stop the spinup. We define this spinup-driven deformation mode as a quasi-static deformation. Further acceleration of the rotation during leads to mass ejection from the body’s surface in the equatorial plane (Figs. 1e and 2). Note that the body spins down because of the increase in the moment of inertia due to the deformation of the body, although the angular momentum increases owing to the imposed spinup condition. In addition, the vertically asymmetric shape is formed (see Figs. 1c-e), which is probably caused by initial asymmetry of SPH particle distribution along -direction.
For , the initial spherical shape remains unchanged until when a rapid deformation occurs (Fig. 2). The deformation timescale of is much shorter than the spinup timescale . Once the significant deformation occurs, the deformation is promoted even without the spin acceleration. We define this deformation mode as a dynamical deformation. After , the decrease rate of the axis ratio slows until . Significant mass ejection occurs at (Fig. 2). The mass ejection under the slow-deformation phase seems similar to the case with .
For , the axis ratio suddenly decreases at , which is a similar dynamical deformation to the case with (Fig. 2). However, the mass ejection from the surface in the equatorial plane is accompanied by the deformation of the main body (Figs. 1n and 2). Significant deformation begins at the time when (Fig. 1k). At the equator, the centrifugal forces are almost equal to the gravitational attraction of the body. Thus, the deformation pushes the material near the equator out of the surface of the body, which rapidly leads to mass ejection (Fig. 1n). The amount of the ejected mass is of the main body. The angular momentum loss due to the mass ejection increases the rotation period, which stalls further deformation. The main body finally has axis ratio (Fig. 2) and rotation period (Fig. 1o). The final shape seems similar to a top shape (Fig. 1o, see also the supplementary movie), but the axis ratio is smaller than that of Ryugu and Bennu (Watanabe et al., 2019; Lauretta et al., 2019).
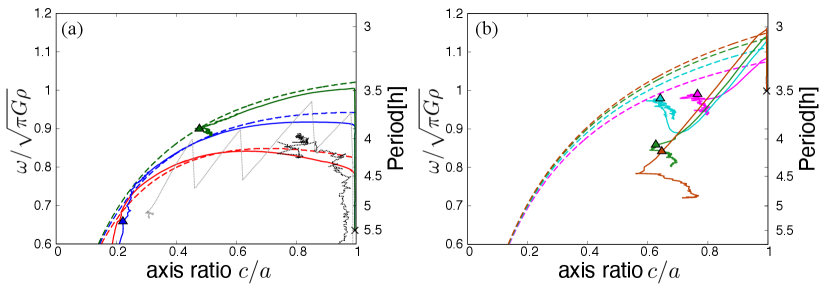
Figure 3 shows the instantaneous spin rate of the main body as a function of axis ratio obtained from our numerical simulations with various effective friction angles in comparison with the maximum equilibrium spin of oblate spheroids given by an analytic formula found by Holsapple, (2001) and Sharma et al., (2009). For the cases with low effective friction angles , , and , initially increases while the bodies maintain their spherical shapes () until approaches the maximum equilibrium angular speed. Then and vary mostly according to the maximum equilibrium spin state. The mass ejection begins after significant deformation with .
Figure 3a also shows the normalized spin rates and axis ratios of spinning-up bodies simulated using the DEMs for cohesionless granular materials: the Hard-Sphere DEM (HSDEM) simulation in Walsh et al., (2012) (red solid curve in Fig. 9 of the paper) and the Soft-Sphere DEM (SSDEM) simulation in Sánchez & Scheeres, (2012) (red solid curve in Fig. 26 of the paper). We only plot the data of the DEM simulations until major mass ejection events. The precise evaluation of the bulk friction is difficult for the DEM simulations, but the DEM results roughly correspond to the maximum equilibrium spin curves with . Although not only the methods but also the particle numbers, spinup rates, and spinup procedures are different from those of our simulations, the evolution paths of the DEM simulations are consistent with those of our simulations with . On the other hand, the axis ratio of the HSDEM simulation at the epoch of mass ejection is largely different from those of the SSDEM and our simulations: , , and for the HSDEM, the SSDEM, and our simulation with , respectively. This suggests that SSDEM and SPH simulations provide more similar results than HSDEM simulations.
For , , , and , exceeds the maximum equilibrium angular speed without deformation followed by sudden dynamical deformation in which both and decrease (Fig. 3b). These are quite different from the quasi-equilibrium evolution path for lower (Fig. 3a). The dynamical deformation timescale is much shorter than the spinup timescale (see Fig. 2). The sudden deformation allows the spin rate to be smaller than the maximum spin rate in equilibrium. Mass ejection occurs after the dynamical deformation for and , while during the dynamical deformation for and .
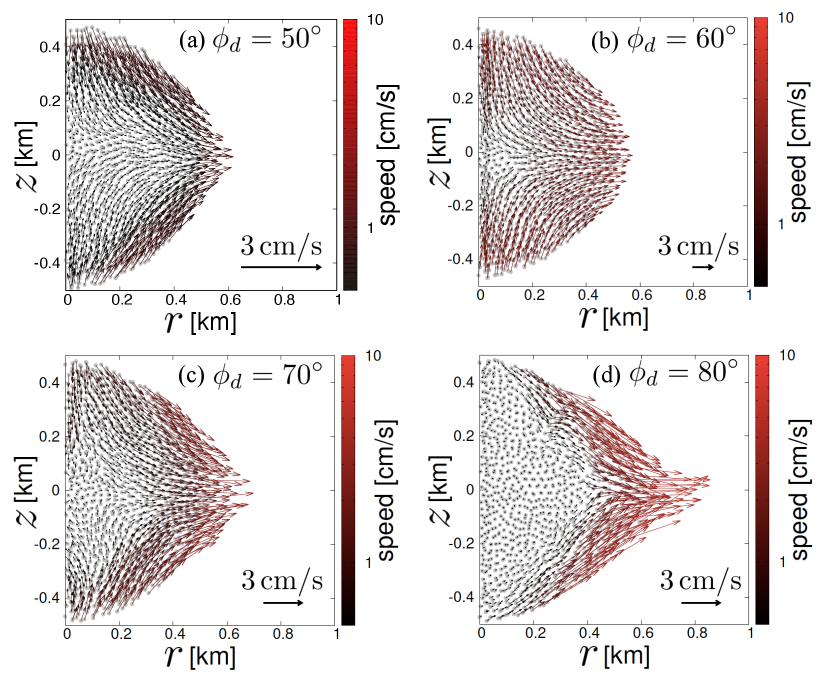
Figure 4 shows the cross-sectional snapshots of the main bodies with different during the dynamical deformation. The simulations with and (Fig. 4a and b) show that the deformation speeds at the polar regions and the equatorial regions are almost the same, and not only the surface but also the deep interior of the bodies deform. A typical flow pattern can be seen in the case with (Fig. 4b), where streamlines are similar to rectangular hyperbolae that tend to flatten the body. We define this deformation mode as internal deformation.
For and (Fig. 4c and d), deformation speeds in the surface layers from equator to mid-latitudes are faster than those in polar and internal regions, and deformation vectors in the surface layers point toward the equators. The typical flow pattern can be seen for (Fig. 4d), where deformation is negligible in the internal region and the deformation speeds are significant only at the surface layers. We define this deformation mode as surface landslides. The deformation occurs at the time when for and for . These rotation periods are very close to the rotational breakup period for a spherical body without tensile strength. Thus, the deformation directly causes significant mass ejection (see also Fig. 1k-m), and the sudden mass ejection from the equatorial surface triggers a set of surface landslides. The mass ejection simultaneously occurs at various longitudes, which induces an axisymmetric occurrence of multiple landslides at almost the same time. We refer to the axisymmetric and simultaneous occurrence of multiple landslides as an axisymmetric set of landslides.
In summary, three deformation modes according to the effective friction angle are identified through our simulations with : quasi-static and internal deformation for (Fig. 1a-e and Fig 3a); dynamical and internal deformation for (Fig. 4a and b); and an axisymmetric set of surface landslides for (Fig. 4c and d).
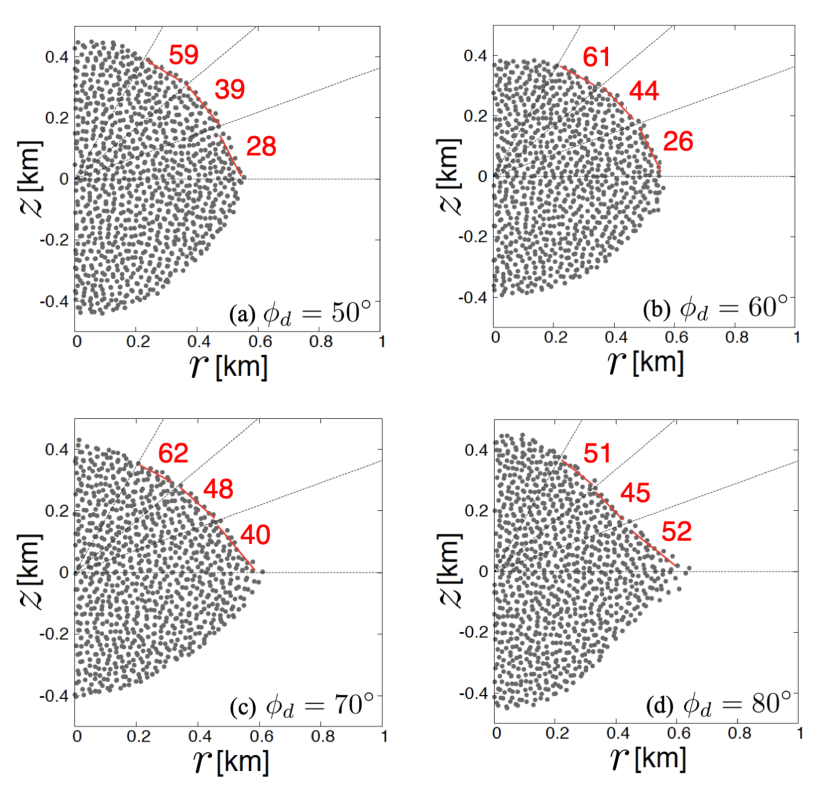
Figure 5 shows the cross-sections of the main bodies at the end of the simulations. For and , oblate spheroidal shapes without equatorial ridges are formed (Fig. 5a and b). The surface tilt angles relative to the -direction are at low latitudes (latitudes of ) and at mid latitudes (latitudes of ). The large tilt angle differences of between the low- and mid-latitudes show that the main body has a near-spheroidal surface.
For and , the final shapes of the main bodies seem to have conical surfaces rather than spheroidal surfaces (Fig. 5c and d). The difference of the surface tilt angles between the low- and mid-latitudes is for and for . Ryugu has differences of the surface tilt angles between low- and mid-latitudes at almost all longitudes (Watanabe et al., 2019). Thus the final shapes resulting from our simulations with have conical surfaces similar to that of Ryugu. Such conical surfaces are most likely produced by landslides. Moreover, a top shape has a characteristic that the topographic distance from the center of the body has a minimum at a mid-latitude, and that characteristic is reproduced for the bodies formed through the simulations with . Therefore, top shapes can be produced through an axisymmetric set of landslides caused by spinup with and (Figs.1o and 4d).
One cannot distinguish top shapes from spheroids by their axis ratios. Here, we adopt a quantitative method to distinguish top shapes from spherical shapes. We define the relative volume difference as
| (3) |
where and are the volume of a body and an ellipsoid with the same triaxial dimensions as the body, respectively. We measured the axis length of the body by the top-down method (e.g., Capaccioni et al., 1984). Bodies with ellipsoidal or rounded shapes have , while bodies with angular shapes such as top shapes have large . Ryugu has (Watanabe et al., 2019).
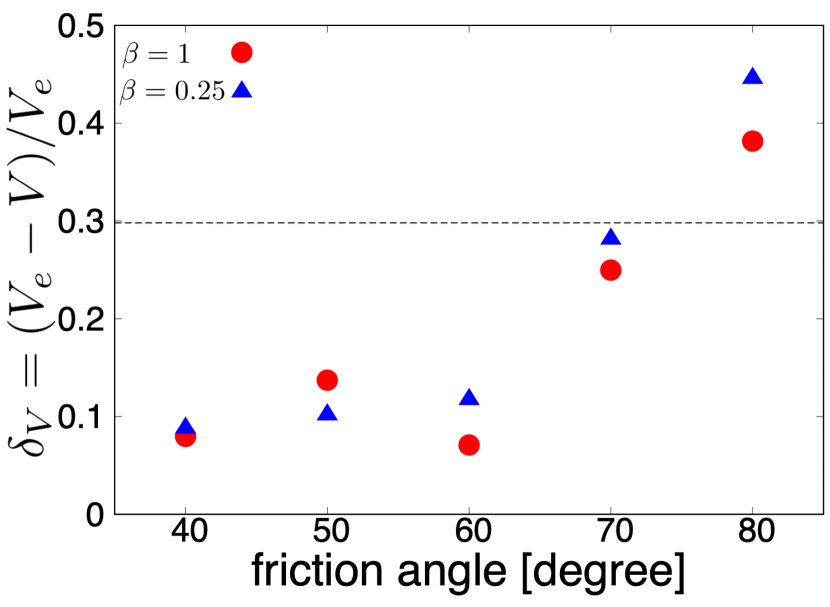
Figure 6 shows of the main body resulting from the spinup of the spherical body with and . For both values, is for , , and and increases with increasing for . For and , is close to or larger than that of Ryugu. This tendency is consistent with the results of our simulations: the body has spheroidal shapes for but angular shapes for (Fig. 5). Thus, we quantitatively confirmed that our simulations produce top shapes for .
It should be noted that the top shape produced in the simulation with has , while almost all of the top shapes found so far have (e.g., Ostro et al., 2006; Busch et al., 2011; Watanabe et al., 2019; Lauretta et al., 2019). Landslides mainly induce material transfer from high latitudes to equatorial regions (see Fig. 4d), and thus it is basically difficult for bodies to keep of about unity through landslides. The discrepancy regarding between the observed top shapes and that produced through our simulations should be considered in future work.
3.2 Spinup with
The deformation processes of the body with under spinup with are similar to those with , i.e., the quasi-static, axisymmetrical, and internal deformation occurs for , and the dynamical, axisymmetrical, and internal deformation occurs for . The resultant shapes are axisymmetric. Thus, the spinup rate does not seem to affect the deformation modes of the body with a low effective friction angle .

In contrast, simulations of the body with under spinup with result in a different deformation mode from those under . Figure 7 shows the snapshots of the simulation with and . The initial rotation period of the main body is set to be . At , the rotation period becomes and the mass ejection mainly starts from an equatorial region (Fig. 7b and e). At , a significant amount of mass ( of the total mass) is ejected, but it does not come from an equatorial region around the -direction (Fig. 7c and f). Therefore, non-axisymmetric mass ejection occurs. The rotation period becomes due to angular momentum loss through the mass ejection.
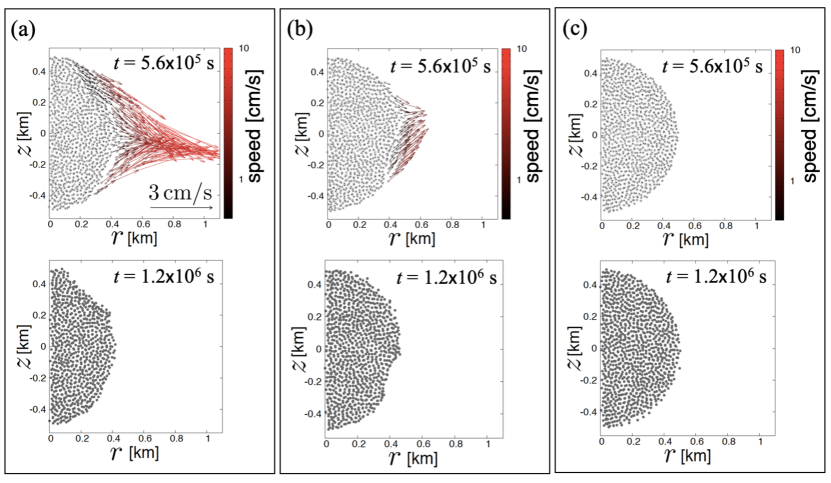
Figure 8 shows the cross-sections of the main body at different longitudes. The landslides occur at a longitude of E (Fig. 8a), where the straight surface in the meridional cross-section appears in the northern hemisphere. However, only a small portion of mass is ejected from longitudes around E (Fig. 8b), and no mass ejection occurs at longitudes around E (Fig. 8c). The body’s surface profiles in the cross-sections at longitudes around E and E maintain almost circular profiles.
Although the main body initially has an almost uniform density, small fluctuations in the SPH particle distribution cause slight locational variations in surface roughness and local slopes, which cause different stability levels against local landslides at different surface positions. In the case of the spinup with , major landslides occur when (Fig. 1k). Under such a fast rotation, landslides are induced everywhere by strong centrifugal forces regardless of local surface slopes. However, in the case of slower spinup with , major landslides occur at an earlier time when (Fig. 7). Owing to the weaker centrifugal forces at that time, landslides seem to selectively occur on surfaces with locally steeper slopes, allowing surfaces with locally shallower slopes to remain mostly intact. This may result in localized landslides or a non-axisymmetric set of landslides, forming a non-axisymmetric shape. The angular momentum of the main body is lost due to the landslides in regions with locally steeper slopes, which leads to a decrease of the rotation rate. Thus, further landslides in the regions with locally shallower slopes do not occur.
3.3 Spinup of a body with an equatorial ridge
As shown in Section 3.2, even small fluctuations of SPH particle distribution cause non-axisymmetric distribution of landslides. Thus, we expect that a visible surface topographic high affects occurrence of landslides. We examined the spinup of a body with an equatorial ridge as an example of spinup of a body with surface topographic high. For simplicity, we put a half torus with a height of on a spherical body to represent an equatorial ridge (see Fig. 9a). We set the effective friction angle to and the initial rotation period to .
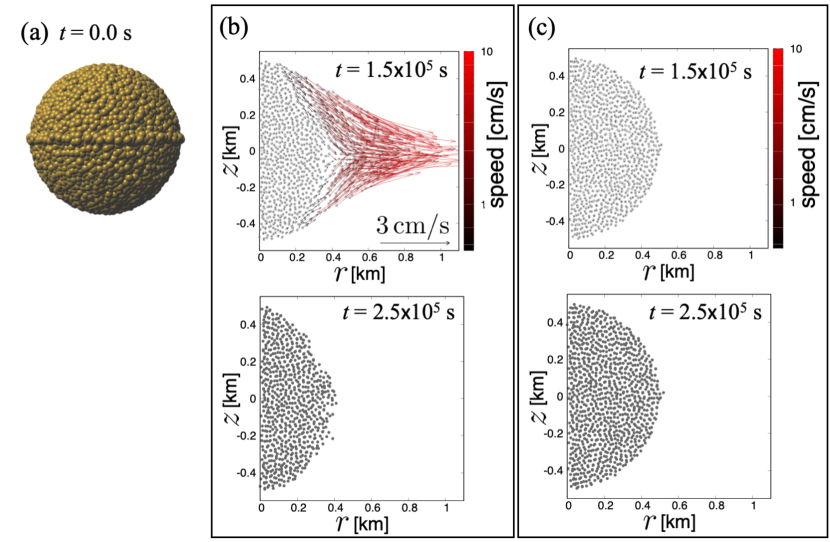
We found that the simulation of spinup with and results in a non-axisymmetric set of landslides. Figure 9b and c show cross-sections of the body at two different longitudes. At a longitude of E (Fig. 9b), landslides occur and a straight surface in this meridional cross section that resembles those seen in cross-sections of top shapes is produced. However, at the longitude of E (Fig. 9c), no landslides occur and the resultant cross-section remains spherical. Thus, the spinup of a body with the surface topographic highs results in a non-axisymmetric set of landslides.
In contrast, the simulation with and faster spinup rate results in an axisymmetric set of landslides, producing a top shape. In Sections 3.1 and 3.2, we see that the simulation with and results in an axisymmetric set of landslides, but that with and results in a non-axisymmetric set of landslides. These results suggest that critical spinup rates that are required for an axisymmetric set of landslides become slower for bodies with less surface roughness.
4 Discussion
Here, we discuss implications for the formation of real top-shaped asteroids in light of the results of our simulations using the SPH method.
4.1 Cohesion and large effective friction angle
Our simulations demonstrated that the effective friction angle of the constituent material mainly determines the deformation modes of the rotating bodies. We found that spinup of a spherical body with effective friction angles induces quasi-static and internal deformation, whereas that with results in dynamical deformation. In the dynamical regime, internal deformation occurs in the cases with , whereas surface landslides occur in . These transitions of the deformation modes seem to be irrespective of the spinup rate according to our simulations with . However, for , axisymmetricity of the resultant shape depends on ; landslides occur almost axisymmetrically through fast spinup (), while local landslides with a non-axisymmetric distribution occur through slow spinup ().
A body with deforms into an oblate spheroid through internal deformation, but never into a top shape that has conical surfaces extending from the equator to the northern and southern mid-latitudes. In contrast, a body with can deform into an axisymmetric top shape through an axisymmetric set of landslides. Thus, we suggest that the formation of top shapes requires large effective friction angles of . As we discussed in Section 2.2, we interpreted used in our simulations as the effective friction angle that mimics an aspect of cohesion. Here, we show the validity of using large effective friction angles instead of introducing the cohesion.
Recall, the shear strength of granular material is expressed as
| (4) |
where is the friction angle, is the confining pressure, and is the cohesion. Thus, the effective friction angle , i.e., the arctangent value of the ratio of the shear strength to the confining pressure, is expressed as
| (5) |

We conducted numerical simulations with the same setup shown in Section 3.1 but with the shear strength of Eq. (4). We set and , and , which, respectively, correspond to the effective friction angles of , and for the central pressure of an asteroid with radius and density . Note that the central pressure is the maximum pressure in an asteroid and gives the minimum estimated value of effective friction angles. We found that the resultant shapes obtained from the simulations with , and are an oblate spheroid (Fig. 10a), a slightly flattened top shape (Fig. 10b), and a top shape (Fig. 10c), respectively. The resultant shapes and axis ratios with , and are similar to those with effective friction angles of (Fig. 1j and Fig. 4b), (Fig. 4c), and (Fig. 1o and Fig. 4d), respectively. For example, of the body in Fig. 1o and Fig. 10c is 0.76 and 0.75, respectively. Thus, the simulations with the shear strength of Eq. (4) agree well with those with the shear strength of and corresponding effective friction angles .
While we find the agreement, obviously Eq. (4) is not completely the same as even with corresponding effective friction angles . For example, the confining pressures vary in post-yield flow of grain material, which may be minor effect for the spinup deformation of kilometer sized asteroids, and the shear strength with Eq. (4) somewhat deviates from that with . The surface profile of the body shown in Fig. 10a is more bumpy than that with the effective friction angle (Fig. 5), of which difference is quantitatively represented by the difference of ; for the former is 0.16 while that for the latter is 0.071. This may be caused by the difference of the constitutive laws. Moreover, we ignored the direct effect of cohesion, that is, tensile forces of cohesive materials, which may affect the results of our simulations. Investigation of the detailed effect of cohesion is planned for future work.
The cohesion of a subsurface layer of Ryugu (Arakawa et al., 2020) results in the effective friction angle with a typical confining pressure for a kilometer sized body and a friction angle . Thus, large effective friction angles of are plausible for -sized asteroids. In contrast, a larger object has larger confining pressure and smaller effective friction angle. The central pressure of a -sized asteroid is , which leads to an effective friction angle even with . Thus, our simulations imply that it would be difficult to form a top-shaped body with a diameter larger than through spinup, which is consistent with the fact that all top-shaped asteroids found so far are smaller than .
4.2 Formation of a top shape through fast spinup
Our results show that top shapes are formed by the fast spinup () of spherical bodies with effective friction angles (Fig. 1k-o). However, the slow spinup () of spherical bodies with induces a non-axisymmetric set of landslides and results in non-axisymmetric shapes (Fig. 7). Moreover, surface roughness or topography suppresses top-shape formation. The fast spinup () of a body with a high equatorial ridge results in a non-axisymmetric shape (Fig. 9).
We discuss the formation of axisymmetric top shapes through YORP spinup (Section 4.2.1). We also discuss fast spinup through the reaccumulation of fragments after catastrophic collisions (Section 4.2.2), although applying our spinup simulations to spinup through the accretion requires the assumption that mass increase and shape changes are negligible through the accretion, which is discussed in Section 4.2.2. In addition, we discuss possibilities of other spinup mechanisms (Section 4.2.3). Here, instead of spinup rate , we use spinup timescale , which is defined as the elapsed time to spin up the body from rotation period to : .
4.2.1 YORP effect
The YORP effect for a kilometer-sized asteroid causes spinup with a timescale (e.g., Kaasalainen et al., 2007; Hergenrother et al., 2019). We showed that a non-axisymmetric set of landslides tends to occur under slower spinups even in the case with or . This suggests that a non-axisymmetric set of landslides and the formation of a non-axisymmetric shape are likely results from the YORP spinup of an asteroid.
We showed that a body with less surface roughness experiences an axisymmetric set of landslides even for slower spinup. The kilometer-sized spherical bodies with 25,000 SPH particles initially set in our simulations are estimated to have a surface roughness of due to discretization of the bodies using SPH particles. The numerical roughness is larger than typical surface roughness of asteroids (e.g., Sugita et al., 2019), and thus the spinup timescale of asteroids required for an axisymmetric set of landslides may be longer than what we obtained in the simulations. We extrapolated the results obtained in Sections 3.2 and 3.3 through a power-law fitting and found that an axisymmetric set of landslides for bodies with surface roughness requires ; the required spinup timescale is still much shorter than the timescale of the YORP effect.
However, we do not rule out the possibility that the YORP spinup will produce a top-shaped asteroid. The YORP effect may spin up an asteroid even after a major landslide event if deformation and topographical changes caused by the major landslides insignificantly alter the direction of the net YORP torque exerted on the body, which eventually causes further landslides. The place where a local landslide has occurred has a locally conical surface and has been stabilized against further landslides. Thus, the subsequent landslides due to further YORP spinup may occur at the longitudes where significant local landslides have not occurred yet, and eventually multiple occurrences of local landslides at different longitudes would produce an almost axisymmetric top shape. Since we only investigated a shape formed until a single major landslide event, we do not rule out the possibility of the formation of top shapes through multiple cycles of the YORP spinup and local landslides.
4.2.2 Reaccumulation of fragments
The reaccumulation phase after catastrophic disruption of the parent body of a rubble-pile asteroid by a collision is yet another practical situation for fast spinup of the asteroid through accretion (Sugiura et al., 2020; Michel et al., 2020). Note that Michel et al., (2020) focus on the possibility of top-shape formation through deformation due to the accretion process, but we focus on top-shape formation through spinup due to accretion. The catastrophic collision produces a sheet-like structure composed of fragments, and dense parts of the sheet gravitationally collapse into small cores of remnants. Then, the remaining fragments accumulate on the remnants to supply angular momentum. Note that the supplied angular momentum originates from the small part of the sheet with not random but specific velocity field around it, so that the accretion of the fragments typically causes continuous spinup of the remnant. Moreover, the timescale of the reaccumulation is , which is shorter than the spinup timescale required for the formation of an axisymmetric top shape . The fast spinup caused through the reaccumulation may form a top shape.
Accretion of fragments supplies not only angular momentum but also mass onto the core. Moreover, accretion may induce surface mass flow, which may affect how subsequent landslides occur. These effects were not represented in our simulations; we just accelerated the spin of the initial body. However, the mass of fragments required for spinup may be negligible compared to the core mass. We estimated angular momentum increase due to the accretion as , where is the total mass of fragments accreting on the core, is the radius of the core, and is the escape speed from the core. Note that roughly explains angular momentum increase through accretion in the simulations of the catastrophic collisions (Sugiura et al., 2020). The amount of fragments required to accelerate the core’s rotation period from to is estimated to be only 4% of the core mass. Thus, our simulations of the spinup possibly mimic the spinup due to the reaccumulation of fragments. The possibility remains to be studied in future works.
4.2.3 Other mechanisms with short spinup timescales
Acceleration rates until the rotation periods of bodies reach the critical rotation period are not related to how landslides occur. Thus, the following formation procedure of axisymmetric top shapes is possible: the YORP effect accelerates the rotation periods of bodies up to and then other mechanisms with short spinup timescales further accelerate the bodies and cause an axisymmetric set of landslides. In this case, small amounts of angular momentum supply due to the fast spinup mechanisms are sufficient to cause an axisymmetric set of landslides.
A non-destructive impact of a small asteroid supplies angular momentum and may cause fast spinup. A prograde impact (i.e., angular momentum vector provided by an impactor is parallel to that of a rotating body) tends to cause tentative spinup while the impactor contacts with the rotating body. Since the impact may erode the body and take away angular momentum to some extent, the process is not straightforward and thus this phenomena should be investigated via simulations in future works.
An asteroid passing around the Roche radius of a planet acquires angular momentum via tidal torque (Hyodo et al., 2016), while an encounter much closer than the Roche radius results in elongation and disruption of the asteroid (e.g., Walsh & Richardson, 2006). A moderate encounter may result in the spinup of an asteroid with keeping its shape. All the top-shaped asteroids found so far are near-Earth asteroids, so that a close encounter with the Earth is one possible spinup mechanism for the formation of top-shaped asteroids.
4.3 Subsequent evolution of ejected materials via landslides
Our simulations showed that an axisymmetric set of landslides that produces a top-shaped asteroid ejects fragments with mass (Section 3.1), where is the mass of the central body. The ejected fragments produce satellites with of the total fragments (Hyodo et al., 2015). The mass of the satellites of host asteroids is consistent with those of satellites around observed top-shaped asteroids (Ostro et al., 2006; Brozović et al., 2011; Becker et al., 2015). However, about half of observed top-shaped asteroids do not have satellites (e.g., Ryugu or Bennu). This suggests that there is a mechanism to remove satellites from the top-shaped asteroids within their lifetimes.
An orbit of a satellite is mainly altered by tidal interaction with a host asteroid (e.g., Goldreich & Sari, 2009), the binary YORP (BYORP) effect (e.g., Ćuk & Burns, 2005; McMahon & Scheeres, 2010a, b), and a close encounter with a planet (e.g., Walsh & Richardson, 2008). The YORP effect is probably the dominant satellite-evolution mechanism for a binary near-Earth asteroids with binary separation the Roche radius of a host asteroid, although the orbital evolution through each mechanism highly depends on various physical parameters. The BYORP effect is an analog of the YORP effect for a binary system with a satellite spinning synchronously with its orbital motion, and torque induced by the absorption of sunlight by and the thermal re-emission from the irregularly shaped satellite changes the orbit of the satellite. The timescale of the secular evolution of the semimajor axis due to the BYORP effect is estimated as (McMahon & Scheeres, 2010a; Walsh & Jacobson, 2015)
| (6) |
where is the bulk density of the binary asteroids, is the critical spin frequency, is the radius of the host asteroid, is the mass ratio of the satellite and the host asteroid, the heliocentric orbit factor is at (Scheeres, 2007), and the dimensionless parameter that depends on the satellite’s shape is estimated to be (McMahon & Scheeres, 2010a; Walsh & Jacobson, 2015). If the BYORP effect causes the outward migration of the satellite, the satellite is ejected from the binary system within , which is much shorter than the dynamical lifetime of near-Earth asteroids (Gladman et al., 2000). Thus the BYORP effect can eject the satellite during its stay in the near-Earth space, which may explain the lack of satellites for several top-shaped asteroids.
5 Summary
Rubble-pile asteroids Ryugu and Bennu visited by the spacecraft Hayabusa2 and OSIRIS-REx, respectively, have a similar spinning-top shape with an axisymmetric equatorial ridge. Many top-shaped asteroids rotate near their break-up periods of hours. The axisymmetricity and present-day high spin rates suggest that these top-shaped asteroids were formed through some spinup processes. However, how a rubble-pile body with a specific friction angle deforms under various spinup rates is still under debate.
Given the radius and bulk density, we numerically simulated the spinup of a spherical rubble-pile body with different effective friction angles using the SPH method for granular material. The high mimics the effect of shear cohesion, and we confirmed that the simulation results with are similar to those with the real cohesive strength law (Eq. (4)) with corresponding values of cohesion. The non-dimensional acceleration rate of the rotation was defined as , where a normalizing acceleration rate corresponds to a decrease in rotation period from to within ( rotations). We also defined the spinup timescale as .
We mainly investigated spinups of a spherical body with an acceleration rate () and effective friction angles . Contrary to the fluid cases (), our simulations show that a moderate effective friction angle () will suppress the deformation into a triaxial ellipsoid. In the cases with , quasi-static and internal deformation occurred, forming oblate spheroids (Fig. 1a-e). The simulations with resulted in dynamical internal deformation and formed oblate spheroids (Fig. 1f-j, Fig. 4a, b, and Fig. 5a, b), indicating that internal deformation will not lead to top-shape formation. In contrast, spinup of spherical bodies with induced an axisymmetric set of surface landslides, producing axisymmetric top shapes (Fig. 1k-o, Fig. 4c, d, and Fig. 5c, d).
We also investigated spinup with a slower acceleration rate () for comparison. We found that the change of probably does not affect the principal deformation modes found in the nominal case (): quasi-static and internal deformation for ; dynamical and internal deformation for ; and a set of surface landslides for . However, the slower affects axisymmetricity of the distribution of landslides for . The simulation with and () showed that a non-axisymmetric shape is formed through a set of local landslides.
We showed that the formation of axisymmetric top shapes through spinup requires an effective friction angle , which is much larger than those of cohesionless granular materials. However, estimated small values of the cohesion for kilometer-sized asteroids () make effective friction angles larger than . Thus, the cohesion of asteroids plays an important role for the formation of axisymmetric top shapes.
In addition, our simulations showed that the formation of axisymmetric top shapes prefers fast spinup with timescales shorter than . The timescale of the YORP spinup () is much longer than the spinup timescales required for the formation of axisymmetric top shapes, suggesting a difficulty to produce axisymmetric top shapes via deformation through YORP spinup itself. On the other hand, catastrophic collisions of parent asteroids produce many small remnants and accretion of fragments onto these remnants may spins them up within the reaccumulation timescale . Thus, catastrophic collisions are one possible origin of axisymmetric top shapes. Besides reaccumulation of fragments after catastrophic collisions, coalescence of fragments that are ejected through the YORP spinup, a non-destructive and prograde impact of an asteroid, and tidal torque caused by a close encounter with a planet may spin up asteroids with short timescales and may lead to the formation of top shapes. Our simulations showed that the formation of top-shaped asteroids is accompanied by surface mass ejection, which leads to the formation of satellites. About half of observed top-shaped asteroids do not have satellite, and this can be explained by the ejection of satellites such as outward migration of satellites’ orbits due to the BYORP effect.
Acknowledgements
K.S. acknowledges the financial support of JSPS KAKENHI Grant (JP20K14536, JP20J01165) and the financial support as JSPS Research Fellow. K.S. and H.G. were supported by MEXT KAKENHI Grant No. JP17H06457. H.K acknowledges the financial support of JSPS KAKENHI Grant (JP17H01103, JP17K05632, JP17H01105, JP18H05438, JP18H05436, JP20H04612). S.W acknowledges KAKENHI support from JSPS (JP17H06459, JP19H01951). R.H. acknowledges the financial support of JSPS Grants-in-Aid (JP17J01269, 18K13600). Numerical simulations in this work were carried out on the Cray XC50 supercomputer at the Center for Computational Astrophysics, National Astronomical Observatory of Japan.
Appendix A. Dependence of resultant shapes on the size, the sound speed, and equations of state
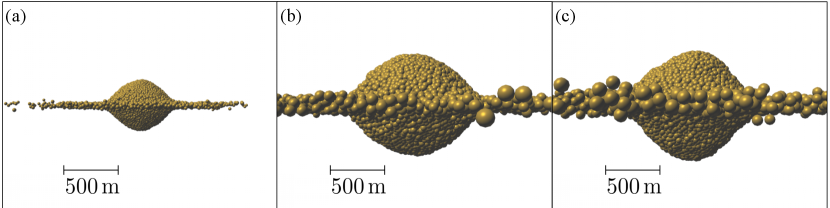
Here, we show that the results of spinup simulations are almost independent of the radius of bodies, the value of the sound speed, and the choice of equations of state. The radius, the sound speed, and the equation of state in nominal simulations are , , and Eq. (1), respectively. We investigated the deformation of the spherical bodies with the effective friction angle through spinup with the acceleration rate . We used the same conditions as those in the simulation of Fig. 1k-o, but we used a different radius of the body (Fig. 11a), a different value of the sound speed (Fig. 11b), and the Tillotson equation of state (Fig. 11c). For the simulation with the Tillotson equation of state (Fig. 11c), we used the same parameter for basaltic material described in Benz & Asphaug, (1999) except for the density and the bulk modulus , which leads to the sound speed .
In these three simulations, we observed similar axisymmetric sets of landslides to those shown in Fig. 1k-o. Although the axis ratios of the bodies resulting from these simulations are slightly different, they have top shapes with cone-like surfaces similar to the body shown in Fig. 1o. Thus, the dependence on the size, the sound speed, and the choice of equations of state are minor for our simulations with the given effective friction angle .
References
- Arakawa et al., (2020) Arakawa, M., et al. 2020. An artificial impact on the asteroid 162173 Ryugu formed a crater in the gravity-dominated regime. Science, 368, 67–71.
- Barnouin et al., (2019) Barnouin, O. S., et al. 2019. Shape of (101955) Bennu indicative of a rubble pile with internal stiffness. Nature Geosci., 12, 247–252.
- Becker et al., (2015) Becker, T. M., et al. 2015. Physical modeling of triple near-Earth Asteroid (153591) 2001 SN263 from radar and optical light curve observations. Icarus, 248, 499–515.
- Benner et al., (2010) Benner, L. A. M., et al. 2010. Radar Imaging and a Physical Model of Binary Asteroid 65803 Didymos. Page 13.17 of: AAS/Division for Planetary Sciences Meeting Abstracts #42. AAS/Division for Planetary Sciences Meeting Abstracts.
- Benz & Asphaug, (1999) Benz, W., & Asphaug, E. 1999. Catastrophic Disruptions Revisited. Icarus, 142, 5–20.
- Brozović et al., (2011) Brozović, M., et al. 2011. Radar and optical observations and physical modeling of triple near-Earth Asteroid (136617) 1994 CC. Icarus, 216, 241–256.
- Busch et al., (2011) Busch, M. W., et al. 2011. Radar observations and the shape of near-Earth ASTEROID 2008 EV5. Icarus, 212, 649–660.
- Capaccioni et al., (1984) Capaccioni, F., et al. 1984. Shapes of asteroids compared with fragments from hypervelocity impact experiments. Nature, 308, 832–834.
- Carry, (2012) Carry, B. 2012. Density of asteroids. Planet. Space Sci., 73, 98–118.
- Chandrasekhar, (1969) Chandrasekhar, S. 1969. Ellipsoidal figures of equilibrium. The Silliman Foundation Lectures, New Haven: Yale University Press.
- Ćuk & Burns, (2005) Ćuk, M., & Burns, J. A. 2005. Effects of thermal radiation on the dynamics of binary NEAs. Icarus, 176, 418–431.
- Gladman et al., (2000) Gladman, B., Michel, P., & Froeschlé, C. 2000. The Near-Earth Object Population. Icarus, 146, 176–189.
- Goldreich & Sari, (2009) Goldreich, P., & Sari, R. 2009. Tidal Evolution of Rubble Piles. Astrophys. J., 691, 54–60.
- Harris et al., (2009) Harris, A. W., Fahnestock, E. G., & Pravec, P. 2009. On the shapes and spins of “rubble pile” asteroids. Icarus, 199, 310–318.
- Hergenrother et al., (2019) Hergenrother, C. W., et al. 2019. The operational environment and rotational acceleration of asteroid (101955) Bennu from OSIRIS-REx observations. Nature comm., 10, 1291.
- Hirabayashi, (2015) Hirabayashi, M. 2015. Failure modes and conditions of a cohesive, spherical body due to YORP spin-up. Mon. Not. R. Astron. Soc., 454, 2249–2257.
- Hirabayashi & Scheeres, (2015) Hirabayashi, M., & Scheeres, D. J. 2015. Stress and Failure Analysis of Rapidly Rotating Asteroid (29075) 1950 DA. Astrophys. J., 798, L8.
- Hirabayashi & Scheeres, (2019) Hirabayashi, M., & Scheeres, D. J. 2019. Rotationally induced failure of irregularly shaped asteroids. Icarus, 317, 354–364.
- Hirabayashi et al., (2015) Hirabayashi, M., Sánchez, D. P., & Scheeres, D. J. 2015. Internal Structure of Asteroids Having Surface Shedding Due to Rotational Instability. Astrophys. J., 808, 63.
- Hirabayashi et al., (2019) Hirabayashi, M., et al. 2019. The Western Bulge of 162173 Ryugu Formed as a Result of a Rotationally Driven Deformation Process. Astrophys. J., 874, L10.
- Holsapple, (2001) Holsapple, K. A. 2001. Equilibrium Configurations of Solid Cohesionless Bodies. Icarus, 154, 432–448.
- Holsapple, (2004) Holsapple, K. A. 2004. Equilibrium figures of spinning bodies with self-gravity. Icarus, 172, 272–303.
- Holsapple, (2010) Holsapple, K. A. 2010. On YORP-induced spin deformations of asteroids. Icarus, 205, 430–442.
- Huchra & Geller, (1982) Huchra, J. P., & Geller, M. J. 1982. Groups of Galaxies. I. Nearby groups. Astrophys. J., 257, 423–437.
- Hyodo et al., (2015) Hyodo, R., Ohtsuki, K., & Takeda, T. 2015. Formation of Multiple-satellite Systems From Low-mass Circumplanetary Particle Disks. Astrophys. J., 799, 40.
- Hyodo et al., (2016) Hyodo, R., Charnoz, S., Genda, H., & Ohtsuki, K. 2016. Formation of Centaurs’ Rings through Their Partial Tidal Disruption during Planetary Encounters. Astrophys. J., 828, L8.
- Iwasawa et al., (2015) Iwasawa, M., Tanikawa, A., Hosono, N., Nitadori, K., Muranushi, T., & Makino, J. 2015. FDPS: A Novel Framework for Developing High-performance Particle Simulation Codes for Distributed-memory Systems. Pages 1:1–1:10 of: Proceedings of the 5th International Workshop on Domain-Specific Languages and High-Level Frameworks for High Performance Computing. WOLFHPC ’15. New York, NY, USA: ACM.
- Iwasawa et al., (2016) Iwasawa, M., Tanikawa, A., Hosono, N., Nitadori, K., Muranushi, T., & Makino, J. 2016. Implementation and performance of FDPS: a framework for developing parallel particle simulation codes. Publ. Astron. Soc. Japan, 68, 54.
- Jutzi, (2015) Jutzi, M. 2015. SPH calculations of asteroid disruptions: The role of pressure dependent failure models. Planet. Space Sci., 107, 3–9.
- Jutzi & Asphaug, (2015) Jutzi, M., & Asphaug, E. 2015. The shape and structure of cometary nuclei as a result of low-velocity accretion. Science, 348, 1355–1358.
- Jutzi & Benz, (2017) Jutzi, M., & Benz, W. 2017. Formation of bi-lobed shapes by sub-catastrophic collisions. A late origin of comet 67P’s structure. Astron. Astrophys., 597, A62.
- Kaasalainen et al., (2007) Kaasalainen, M., Ďurech, J., Warner, B. D., Krugly, Y. N., & Gaftonyuk, N. M. 2007. Acceleration of the rotation of asteroid 1862 Apollo by radiation torques. Nature, 446, 420–422.
- Lajeunesse et al., (2005) Lajeunesse, E., Monnier, J. B., & Homsy, G. M. 2005. Granular slumping on a horizontal surface. Physics of Fluids, 17, 103302–103302–15.
- Lauretta et al., (2019) Lauretta, D. S., et al. 2019. The unexpected surface of asteroid (101955) Bennu. Nature, 568, 55–60.
- Leisner et al., (2020) Leisner, A. M., Richardson, D. C., Statler, T. S., Nichols, W., & Zhang, Y. 2020. An extended parameter space study of the effect of cohesion in gravitational aggregates through spin-up simulations. Planet. Space Sci., 182, 104845.
- Leleu et al., (2018) Leleu, A., Jutzi, M., & Rubin, M. 2018. The peculiar shapes of Saturn’s small inner moons as evidence of mergers of similar-sized moonlets. Nature Astronomy, 2, 555–561.
- McMahon & Scheeres, (2010a) McMahon, J., & Scheeres, D. 2010a. Detailed prediction for the BYORP effect on binary near-Earth Asteroid (66391) 1999 KW4 and implications for the binary population. Icarus, 209, 494–509.
- McMahon & Scheeres, (2010b) McMahon, J., & Scheeres, D. 2010b. Secular orbit variation due to solar radiation effects: a detailed model for BYORP. Celest. Mech. Dynam. Astron., 106, 261–300.
- Michel et al., (2020) Michel, P., et al. 2020. Collisional formation of top-shaped asteroids and implications for the origins of Ryugu and Bennu. Nature comm., 11, 2655.
- Ostro et al., (2006) Ostro, S. J., et al. 2006. Radar Imaging of Binary Near-Earth Asteroid (66391) 1999 KW4. Science, 314, 1276–1280.
- Richardson et al., (2016) Richardson, D. C., et al. 2016. Dynamical and Physical Properties of 65803 Didymos, the Proposed AIDA Mission Target. Page 123.17 of: AAS/Division for Planetary Sciences Meeting Abstracts #48. AAS/Division for Planetary Sciences Meeting Abstracts.
- Rozitis et al., (2014) Rozitis, B., Maclennan, E., & Emery, J. P. 2014. Cohesive forces prevent the rotational breakup of rubble-pile asteroid (29075) 1950 DA. Nature, 512, 174–176.
- Rubincam, (2000) Rubincam, D. P. 2000. Radiative Spin-up and Spin-down of Small Asteroids. Icarus, 148, 2–11.
- Sánchez & Scheeres, (2012) Sánchez, D. P., & Scheeres, D. J. 2012. DEM simulation of rotation-induced reshaping and disruption of rubble-pile asteroids. Icarus, 218, 876–894.
- Sánchez & Scheeres, (2016) Sánchez, P., & Scheeres, D. J. 2016. Disruption patterns of rotating self-gravitating aggregates: A survey on angle of friction and tensile strength. Icarus, 271, 453–471.
- Sánchez & Scheeres, (2018) Sánchez, P., & Scheeres, D. J. 2018. Rotational evolution of self-gravitating aggregates with cores of variable strength. Planet. Space Sci., 157, 39–47.
- Scheeres, (2007) Scheeres, D. J. 2007. The dynamical evolution of uniformly rotating asteroids subject to YORP. Icarus, 188, 430–450.
- Sharma, (2013) Sharma, I. 2013. Structural stability of rubble-pile asteroids. Icarus, 223, 367–382.
- Sharma, (2018) Sharma, I. 2018. Shapes and Dynamics of Granular Minor Planets. Springer.
- Sharma et al., (2009) Sharma, I., Jenkins, J. T., & Burns, J. A. 2009. Dynamical passage to approximate equilibrium shapes for spinning, gravitating rubble asteroids. Icarus, 200, 304–322.
- Sugita et al., (2019) Sugita, S., et al. 2019. The geomorphology, color, and thermal properties of Ryugu: Implications for parent-body processes. Science, 364, 252–252.
- Sugiura, (2020) Sugiura, K. 2020. Development of a Numerical Simulation Method for Rocky Body Impacts and Theoretical Analysis of Asteroidal Shapes. Springer Singapore.
- Sugiura et al., (2018) Sugiura, K., Kobayashi, H., & Inutsuka, S. 2018. Toward understanding the origin of asteroid geometries. Variety in shapes produced by equal-mass impacts. Astron. Astrophys., 620, A167.
- Sugiura et al., (2019) Sugiura, K., Kobayashi, H., & Inutsuka, S. 2019. Collisional elongation: Possible origin of extremely elongated shape of 1I/’Oumuamua. Icarus, 328, 14–22.
- Sugiura et al., (2020) Sugiura, K., Kobayashi, H., & Inutsuka, S. 2020. High-Resolution Simulations of Catastrophic Disruptions: Resultant Shape Distributions. Planet. Space Sci., 181, 104807.
- Taylor et al., (2007) Taylor, P. A., et al. 2007. Spin Rate of Asteroid (54509) 2000 PH5 Increasing Due to the YORP Effect. Science, 316, 274.
- Teramoto & Yano, (2005) Teramoto, K., & Yano, H. 2005. Measurements of Sound Speed in Granular Materials Simulated Regolith. Page 1856 of: Mackwell, Stephen, & Stansbery, Eileen (eds), 36th Annual Lunar and Planetary Science Conference. Lunar and Planetary Science Conference.
- Walsh, (2018) Walsh, K. J. 2018. Rubble Pile Asteroids. Annu. Rev. Astron. Astrophys., 56, 593–624.
- Walsh & Jacobson, (2015) Walsh, K. J., & Jacobson, S. A. 2015. Formation and Evolution of Binary Asteroids. Pages 375–393.
- Walsh & Richardson, (2006) Walsh, K. J., & Richardson, D. C. 2006. Binary near-Earth asteroid formation: Rubble pile model of tidal disruptions. Icarus, 180, 201–216.
- Walsh & Richardson, (2008) Walsh, K. J., & Richardson, D. C. 2008. A steady-state model of NEA binaries formed by tidal disruption of gravitational aggregates. Icarus, 193, 553–566.
- Walsh et al., (2008) Walsh, K. J., Richardson, D. C., & Michel, P. 2008. Rotational breakup as the origin of small binary asteroids. Nature, 454, 188–191.
- Walsh et al., (2012) Walsh, K. J., Richardson, D. C., & Michel, P. 2012. Spin-up of rubble-pile asteroids: Disruption, satellite formation, and equilibrium shapes. Icarus, 220, 514–529.
- Watanabe et al., (2019) Watanabe, S., et al. 2019. Hayabusa2 arrives at the carbonaceous asteroid 162173 Ryugu—A spinning top shaped rubble pile. Science, 364, 268–272.
- Zhang et al., (2017) Zhang, Y., et al. 2017. Creep stability of the proposed AIDA mission target 65803 Didymos: I. Discrete cohesionless granular physics model. Icarus, 294, 98–123.
- Zhang et al., (2018) Zhang, Y., Richardson, D. C., Barnouin, O. S., Michel, P., Schwartz, S. R., & Ballouz, R.-L. 2018. Rotational Failure of Rubble-pile Bodies: Influences of Shear and Cohesive Strengths. Astrophys. J., 857, 15.