Spectral Regularized Kernel Two-Sample Tests
Abstract
Over the last decade, an approach that has gained a lot of popularity to tackle nonparametric testing problems on general (i.e., non-Euclidean) domains is based on the notion of reproducing kernel Hilbert space (RKHS) embedding of probability distributions. The main goal of our work is to understand the optimality of two-sample tests constructed based on this approach. First, we show the popular MMD (maximum mean discrepancy) two-sample test to be not optimal in terms of the separation boundary measured in Hellinger distance. Second, we propose a modification to the MMD test based on spectral regularization by taking into account the covariance information (which is not captured by the MMD test) and prove the proposed test to be minimax optimal with a smaller separation boundary than that achieved by the MMD test. Third, we propose an adaptive version of the above test which involves a data-driven strategy to choose the regularization parameter and show the adaptive test to be almost minimax optimal up to a logarithmic factor. Moreover, our results hold for the permutation variant of the test where the test threshold is chosen elegantly through the permutation of the samples. Through numerical experiments on synthetic and real data, we demonstrate the superior performance of the proposed test in comparison to the MMD test and other popular tests in the literature.
MSC 2010 subject classification: Primary: 62G10; Secondary: 65J20, 65J22, 46E22, 47A52.
Keywords and phrases: Two-sample test, maximum mean discrepancy, reproducing kernel Hilbert space, covariance operator, U-statistics, Bernstein’s inequality, minimax separation, adaptivity, permutation test, spectral regularization
1 Introduction
Given , and , where and are defined on a measurable space , the problem of two-sample testing is to test against . This is a classical problem in statistics that has attracted a lot of attention both in the parametric (e.g., -test, -test) and nonparametric (e.g., Kolmogorov-Smirnoff test, Wilcoxon signed-rank test) settings (Lehmann and Romano, 2006). However, many of these tests either rely on strong distributional assumptions or cannot handle non-Euclidean data that naturally arise in many modern applications.
Over the last decade, an approach that has gained a lot of popularity to tackle nonparametric testing problems on general domains is based on the notion of reproducing kernel Hilbert space (RKHS) (Aronszajn, 1950) embedding of probability distributions (Smola et al., 2007, Sriperumbudur et al., 2009, Muandet et al., 2017). Formally, the RKHS embedding of a probability measure is defined as
where is the unique reproducing kernel (r.k.) associated with the RKHS with satisfying . If is characteristic (Sriperumbudur et al., 2010, Sriperumbudur et al., 2011), this embedding induces a metric on the space of probability measures, called the maximum mean discrepancy () or the kernel distance (Gretton et al., 2012, Gretton et al., 2006), defined as
| (1.1) |
MMD has the following variational representation (Gretton et al., 2012, Sriperumbudur et al., 2010) given by
| (1.2) |
which clearly reduces to (1.1) by using the reproducing property: for all , . We refer the interested reader to Sriperumbudur et al. (2010), Sriperumbudur (2016), and Simon-Gabriel and Schölkopf (2018) for more details about . Gretton et al. (2012) proposed a test based on the asymptotic null distribution of the -statistic estimator of , defined as
and showed it to be consistent. Since the asymptotic null distribution does not have a simple closed form—the distribution is that of an infinite sum of weighted chi-squared random variables with the weights being the eigenvalues of an integral operator associated with the kernel w.r.t. the distribution —, several approximate versions of this test have been investigated and are shown to be asymptotically consistent (e.g., see Gretton et al., 2012 and Gretton et al., 2009). Recently, Li and Yuan (2019) and Schrab et al. (2021) showed these tests based on to be not optimal in the minimax sense but modified them to achieve a minimax optimal test by using translation-invariant kernels on . However, since the power of these kernel methods lies in handling more general spaces and not just , the main goal of this paper is to construct minimax optimal kernel two-sample tests on general domains.
Before introducing our contributions, first, we will introduce the minimax framework pioneered by Burnashev (1979) and Ingster (1987, 1993) to study the optimality of tests, which is essential to understanding our contributions and their connection to the results of Li and Yuan (2019) and Schrab et al. (2021). Let be any test that rejects when and fails to reject when . Denote the class of all such asymptotic (resp. exact) -level tests to be (resp. ). Let be a set of probability measures on . The Type-II error of a test (resp. ) w.r.t. is defined as where
is the class of -separated alternatives in probability metric , with being referred to as the separation boundary or contiguity radius. Of course, the interest is in letting as (i.e., shrinking alternatives) and analyzing for a given test, , i.e., whether . In the asymptotic setting, the minimax separation or critical radius is the fastest possible order at which such that , i.e., for any such that , there is no test that is consistent over . A test is asymptotically minimax optimal if it is consistent over with . On the other hand, in the non-asymptotic setting, the minimax separation is defined as the minimum possible separation, such that , for . A test is called minimax optimal if for some . In other words, there is no other -level test that can achieve the same power with a better separation boundary.
In the context of the above notation and terminology, Li and Yuan (2019) considered distributions with densities (w.r.t. the Lebesgue measure) belonging to
| (1.3) |
where with being the Fourier transform of , with and being the densities of and , respectively, and showed the minimax separation to be . Furthermore, they chose to be a Gaussian kernel on , i.e., in with at an appropriate rate as (reminiscent of kernel density estimators) in contrast to fixed in Gretton et al. (2012), and showed the resultant test to be asymptotically minimax optimal w.r.t. based on (1.3) and . Schrab et al. (2021) extended this result to translation-invariant kernels (particularly, as the product of one-dimensional translation-invariant kernels) on with a shrinking bandwidth and showed the resulting test to be minimax optimal even in the non-asymptotic setting. While these results are interesting, the analysis holds only for as the kernels are chosen to be translation invariant on , thereby limiting the power of the kernel approach.
In this paper, we employ an operator theoretic perspective to understand the limitation of and propose a regularized statistic that mitigates these issues without requiring . In fact, the construction of the regularized statistic naturally gives rise to a certain which is briefly described below. To this end, define and which is well defined as . It can be shown that where is an integral operator defined by (see Section 3 for details), which is in fact a self-adjoint positive trace-class operator if is bounded. Therefore, where are the eigenvalues and eigenfunctions of . Since is trace-class, we have as , which implies that the Fourier coefficients of , i.e., , for large , are down-weighted by . In other words, is not powerful enough to distinguish between and if they differ in the high-frequency components of , i.e., for large . On the other hand,
does not suffer from any such issue, with being a probability metric that is topologically equivalent to the Hellinger distance (see Lemma A.18 and Le Cam, 1986, p. 47). With this motivation, we consider the following modification to :
where , called the spectral regularizer (Engl et al., 1996) is such that as (a popular example is the Tikhonov regularizer, ), i.e., , the identity operator—refer to (4.1) for the definition of . In fact, in Section 4, we show to be equivalent to , i.e., if and , where denotes the range space of an operator , is the smoothness index (large corresponds to “smooth” ), and is defined by choosing in (4.1). This naturally leads to the class of -separated alternatives,
| (1.4) |
for , where can be interpreted as an interpolation space obtained by the real interpolation of and at scale (Steinwart and Scovel, 2012, Theorem 4.6)—note that the real interpolation of Sobolev spaces and yields Besov spaces (Adams and Fournier, 2003, p. 230). To compare the class in (1.4) to that obtained using (1.3) with , note that the smoothness in (1.4) is determined through instead of the Sobolev smoothness where the latter is tied to translation-invariant kernels on . Since we work with general domains, the smoothness is defined through the interaction between and the probability measures in terms of the behavior of the integral operator, . In addition, as , , while as , where is defined through a translation invariant kernel on with bandwidth . Hence, we argue that (1.4) is a natural class of alternatives to investigate the performance of and . In fact, recently, Balasubramanian et al. (2021) considered an alternative class similar to (1.4) to study goodness-of-fit tests using .
Contributions
The main contributions of the paper are as follows:
(i) First, in Theorem 3.1, we show that the test based on cannot achieve a separation boundary better than w.r.t. in (1.4). However, this separation boundary depends only on the smoothness of , which is determined by but is completely oblivious to the intrinsic dimensionality of the RKHS, , which is controlled by the decay rate of the eigenvalues of . To this end, by taking into account the intrinsic dimensionality of , we show in Corollaries 3.3 and 3.4 (also see Theorem 3.2) that the minimax separation w.r.t. is for if , , i.e., the eigenvalues of decay at a polynomial rate , and is if , i.e., exponential decay. These results clearly establish the non-optimality of the MMD-based test.
(ii) To resolve this issue with MMD, in Section 4.2, we propose a spectral regularized test based on and show it to be minimax optimal w.r.t. (see Theorems 4.2, 4.3 and Corollaries 4.4, 4.5). Before we do that, we first provide an alternate representation for as , which takes into account the information about the covariance operator, along with the mean elements, , and , thereby showing resemblance to Hotelling’s -statistic (Lehmann and Romano, 2006) and its kernelized version (Harchaoui et al., 2007). This alternate representation is particularly helpful to construct a two-sample -statistic (Hoeffding, 1992) as a test statistic (see Section 4.1), which has a worst-case computational complexity of in contrast to of the MMD test (see Theorem 4.1). However, the drawback of the test is that it is not usable in practice since the critical level depends on , which is unknown since is unknown. Therefore, we refer to this test as the Oracle test.
(iii) In order to make the Oracle test usable in practice, in Section 4.3, we propose a permutation test (e.g., see Lehmann and Romano, 2006, Pesarin and Salmaso, 2010, and Kim et al., 2022) leading to a critical level that is easy to compute (see Theorem 4.6), while still being minimax optimal w.r.t. (see Theorem 4.7 and Corollaries 4.8, 4.9).
However, the minimax optimal separation rate is tightly controlled by the choice of the regularization parameter, , which in turn depends on the unknown parameters, and (in the case of the polynomial decay of the eigenvalues of ). This means the performance of the permutation test depends on the choice of . To make the test completely data-driven, in Section 4.4, we present an aggregate version of the permutation test by aggregating over different and show the resulting test to be minimax optimal up to a factor (see Theorems 4.10 and 4.11). In Section 4.5, we discuss the problem of kernel choice and present an adaptive test by jointly aggregating over and kernel , which we show to be minimax optimal up to a factor (see Theorem 4.12).
(iv) Through numerical simulations on benchmark data, we demonstrate the superior performance of the spectral regularized test in comparison to the adaptive MMD test (Schrab et al., 2021), Energy test (Szekely and Rizzo, 2004) and Kolmogorov-Smirnov (KS) test (Puritz et al., 2022; Fasano and Franceschini, 1987), in Section 5.
All these results hinge on Bernstein-type inequalities for the operator norm of a self-adjoint Hilbert-Schmidt operator-valued U-statistics (Sriperumbudur and Sterge, 2022). A closely related work to ours is by Harchaoui et al. (2007) who consider a regularized MMD test with (see Remark 4.2 for a comparison of our regularized statistic to that of Harchaoui et al., 2007). However, our work deals with general , and our test statistic is different from that of Harchaoui et al. (2007). In addition, our tests are non-asymptotic and minimax optimal in contrast to that of Harchaoui et al. (2007), which only shows asymptotic consistency against fixed alternatives and provides some asymptotic results against local alternatives.
2 Definitions & Notation
For a topological space , denotes the Banach space of -power -integrable function, where is a finite non-negative Borel measure on . For , denotes the -norm of . is the -fold product measure. denotes a reproducing kernel Hilbert space with a reproducing kernel . denotes the equivalence class of the function , that is the collection of functions such that . For two measures and , denotes that is dominated by which means, if for some measurable set , then .
Let and be abstract Hilbert spaces. denotes the space of bounded linear operators from to . For , denotes the adjoint of . is called self-adjoint if . For , , , and denote the trace, Hilbert-Schmidt and operator norms of , respectively. For , is an element of the tensor product space of which can also be seen as an operator from as for any .
For constants and , (resp. ) denotes that there exists a positive constant (resp. ) such that (resp. . denotes that there exists positive constants and such that . We denote for .
3 Non-optimality of test
In this section, we establish the non-optimality of the test based on . First, we make the following assumption throughout the paper.
is a
second countable (i.e., completely separable) space endowed with Borel -algebra . is an RKHS of real-valued functions on with a continuous reproducing kernel satisfying
The continuity of ensures that is Bochner-measurable for all , which along with the boundedness of ensures that and are well-defined (Dinculeanu, 2000). Also the separability of along with the continuity of ensures that is separable (Steinwart and Christmann, 2008, Lemma 4.33). Therefore,
| (3.1) |
where and . Define , , which is usually referred in the literature as the inclusion operator (e.g., see Steinwart and Christmann, 2008, Theorem 4.26), where . It can be shown (Sriperumbudur and Sterge, 2022, Proposition C.2) that , . Define . It can be shown (Sriperumbudur and Sterge, 2022, Proposition C.2) that , where , . Since is bounded, it is easy to verify that is a trace class operator, and thus compact. Also, it is self-adjoint and positive, thus spectral theorem (Reed and Simon, 1980, Theorems VI.16, VI.17) yields that
where are the eigenvalues and are the orthonormal system of eigenfunctions (strictly speaking classes of eigenfunctions) of that span with the index set being either countable in which case or finite. In this paper, we assume that the set is countable, i.e., infinitely many eigenvalues. Note that represents an equivalence class in . By defining , it is clear that and . Throughout the paper, refers to this definition. Using these definitions, we can see that
| (3.2) |
Remark 3.1.
From the form of in (3.1), it seems more natural to define , , so that , , leading to —an expression similar to (3.2). However, since , as specified by , it is clear that lies in the span of the eigenfunctions of , while being orthogonal to constant functions in since . Defining the inclusion operator with centering as proposed under (3.1) guarantees that the eigenfunctions of are orthogonal to constant functions since , which implies that constant functions are also orthogonal to the space spanned by the eigenfunctions, without assuming that the kernel is degenerate with respect to , i.e., . The orthogonality of eigenfunctions to constant functions is crucial in establishing the minimax separation boundary, which relies on constructing a specific example of from the span of eigenfunctions that is orthogonal to constant functions (see the proof of Theorem 3.2). On the other hand, the eigenfunctions of with as considered in this remark are not guaranteed to be orthogonal to constant functions in .
Suppose . Then where and follows from Lemma A.18 by noting that . As mentioned in Section 1, might not capture the difference between between and if they differ in the higher Fourier coefficients of , i.e., for large .
The following result shows that the test based on cannot achieve a separation boundary of order better than .
Theorem 3.1 (Separation boundary of MMD test).
Suppose holds. Let , , , for some constant , and
| (3.3) |
Then for any ,
where ,
and , with being the quantile of the permutation function of based on permutations of the samples .
Furthermore, suppose as and one of the following holds: (i) , (ii) , Then for any decay rate of ,
Remark 3.2.
(i) The MMD test with threshold is simply based on Chebyshev’s inequality, while the data-dependent threshold is based on a permutation test. Theorem 3.1 shows that both these tests yield a separation radius of , which in fact also holds if
is replaced by its Monte-Carlo approximation using only random permutations instead of all as long as is large enough. This can be shown using the same approach as in Lemma A.14.
(ii) Theorem 3.1 shows that the power of the test based on does not go to one, even when , which implies that asymptotically the separation boundary of such test is of order . For the threshold , we can also show a non asymptotic result that if for some , then However, for the threshold , since our proof technique depends on the asymptotic distribution of , the result is presented in the asymptotic setting of .
(iii) The condition in (3.3) implies that for all . Note that , i.e., if and for , . When , with the property that: for all , such that and . In other words, can be approximated by some function in an RKHS ball of radius with the approximation error decaying polynomially in (Cucker and Zhou, 2007, Theorem 4.1).
(iv) The uniform boundedness condition does not hold in general, for example, see Minh et al. (2006, Theorem 5), which shows that for , where denotes the -dimensional unit sphere, , for all for any kernel of the form with being continuous. An example of such a kernel is the Gaussian kernel on . On the other hand, when , the Gaussian kernel satisfies the uniform boundedness condition. Also, when , the uniform boundedness condition is satisfied by the Gaussian kernel (Steinwart et al., 2006).
In this paper, we provide results both with and without the assumption of to understand the impact of the assumption on the behavior of the test. We would like to mention that this uniform boundedness condition has been used in the analysis of the impact of regularization in kernel learning (see Mendelson and Neeman, 2010, p. 531).
(v) Theorem 3.1 can be viewed as a generalization and extension of Theorem 1 in Balasubramanian et al. (2021), which shows the separation boundary of the goodness-of-fit test, vs. based on a V-statistic estimator of to be of the order when . In their work, the critical level is chosen from the asymptotic distribution of the test statistic under the null with being known, assuming the uniform boundedness of the eigenfunctions of and . Note that the zero mean condition is not satisfied by many popular kernels including the Gaussian and Matérn kernels. In contrast, Theorem 3.1 deals with a two-sample setting based on a -statistic estimator of , with no requirement of the uniform boundedness assumption and , while allowing arbitrary , and the critical levels being non-asymptotic (permutation and concentration-based).
The following result provides general conditions on the minimax separation rate w.r.t. , which together with Corollaries 3.3 and 3.4 demonstrates the non-optimality of the MMD tests presented in Theorem 3.1.
Theorem 3.2 (Minimax separation boundary).
Suppose , where is a strictly decreasing function on , and . Then, for any there exists such that if
then
where
Furthermore if , then the above condition on can be replaced by
Corollary 3.3 (Minimax separation boundary-Polynomial decay).
Suppose , . Then
provided one of the following holds: (i) , (ii) ,
Corollary 3.4 (Minimax separation boundary-Exponential decay).
Suppose , , . Then for all we have
provided one of the following holds: (i) , (ii) ,
Remark 3.3.
(i) Observe that for any bounded kernel satisfying is a trace class operator. This implies has to satisfy as . Without further assumptions on the decay rate (i.e., if we allow the space to include any decay rate of order ), then we can show that provided that (or in the case of ). However, assuming specific decay rates (i.e., considering a smaller space ), the separation boundary can be improved, as shown in Corollaries 3.3 and 3.4. Note that and for any , implying that the separation boundary of MMD is larger than the minimax separation boundary w.r.t. irrespective of the decay rate of the eigenvalues of .
(ii) The minimax separation boundary depends only on (the degree of smoothness of ), and (the decay rate of the eigenvalues), with controlling the smoothness of the RKHS. While one may think that the minimax rate is independent of , it is actually not the case since depends on . Minh et al. (2006, Section 5.2) provides examples of kernels with explicit decay rates of eigenvalues. For example, when , , (i) The Spline kernel, defined as , where denotes the Legendre polynomial of degree in dimension and is some normalization constant depending on and , has , for (ii) The polynomial kernel with degree , defined as , has , and (iii) The Gaussian kernel with bandwidth satisfies , for
4 Spectral regularized MMD test
To address the limitation of the MMD test, in this section, we propose a spectral regularized version of the MMD test and show it to be minimax optimal w.r.t. . To this end, we define the spectral regularized discrepancy as
where the spectral regularizer, satisfies (more concrete assumptions on will be introduced later). By functional calculus, we define applied to any compact, self-adjoint operator defined on a separable Hilbert space, as
| (4.1) |
where has the spectral representation, with being the eigenvalues and eigenfunctions of . A popular example of is , yielding , which is well known as the Tikhonov regularizer. We will later provide more examples of spectral regularizers that satisfy additional assumptions.
Remark 4.1.
We would like to highlight that the common definition of in the inverse problem literature (see Engl et al., 1996, Section 2.3) does not include the term , which represents the projection onto the space orthogonal to . The reason for adding this term is to ensure that is invertible whenever . Moreover, the condition that is invertible will be essential for the power analysis of our test.
Based on the definition of , it is easy to verify that so that as where holds if . In fact, it can be shown that and are equivalent up to constants if and is large enough compared to (see Lemma A.7). Therefore, the issue with can be resolved by using as a discrepancy measure to construct a test. In the following, we present details about the construction of the test statistic and the test using . To this end, we first provide an alternate representation for which is very useful to construct the test statistic. Define , which is referred to as the covariance operator. It can be shown (Sriperumbudur and Sterge, 2022, Proposition C.2) that is a positive, self-adjoint, trace-class operator, and can be written as
| (4.2) |
where . Note that
| (4.3) |
where follows from Lemma A.8(i) that states . Define .
Remark 4.2.
Suppose . Then . Note that for any , which implies . Therefore, in (4.3) can be written as
| (4.4) |
This means the regularized discrepancy involves test functions that belong to a growing ball in as in contrast to a fixed unit ball as in the case with (see (1.2)). Balasubramanian et al. (2021) considered a similar discrepancy in a goodness-of-fit test problem, vs. where is known, by using in (4.4) but with being replaced by . In the context of two-sample testing, Harchaoui et al. (2007) considered a discrepancy based on kernel Fisher discriminant analysis whose regularized version is given by
where the constraint set in the above variational form is larger than the one in (4.4) since .
4.1 Test statistic
Define . Using the representation,
| (4.5) |
obtained by expanding the r.h.s. of (4.4), and of in (4.2), we construct an estimator of as follows, based on and . We first split the samples into and , and to and . Then, the samples and are used to estimate the covariance operator while and are used to estimate the mean elements and , respectively. Define and . Using the form of in (4.5), we estimate it using a two-sample -statistic (Hoeffding, 1992),
| (4.6) |
where
and
which is a one-sample -statistic estimator of based on , for , where . It is easy to verify that . Note that is not exactly a -statistic since it involves , but conditioned on , one can see it is exactly a two-sample -statistic. When , in contrast to our estimator which involves sample splitting, Harchaoui et al. (2007) estimate using a pooled estimator, and and through empirical estimators, using all the samples, thereby resulting in a kernelized version of Hotelling’s -statistic (Lehmann and Romano, 2006). However, we consider sample splitting for two reasons: (i) To achieve independence between the covariance operator estimator and the mean element estimators, which leads to a convenient analysis, and (ii) to reduce the computational complexity of from to . By writing (4.6) as
the following result shows that can be computed through matrix operations and by solving a finite-dimensional eigensystem.
Theorem 4.1.
Let be the eigensystem of where , , and . Define Then
where , , , , and
with and . Here
, , ,
, and .
Note that in the case of Tikhonov regularization, . The complexity of computing is given by , which is comparable to that of the MMD test if , otherwise the proposed test is computationally more complex than the MMD test.
4.2 Oracle test
Before we present the test, we make the following assumptions on which will be used throughout the analysis.
where , with the constant being called the qualification of , and , , , , are finite positive constants, all independent of . Note that () necessarily implies that as (see Lemma A.20), and controls the rate of convergence, which combined with yields upper and lower bounds on in terms of (see Lemma A.7).
Remark 4.3.
In the inverse problem literature (see Engl et al., 1996, Theorems 4.1, 4.3 and Corollary 4.4; Bauer et al., 2007, Definition 1), and are common assumptions with being replaced by . These assumptions are also used in the analysis of spectral regularized kernel ridge regression (Bauer et al., 2007). However, is less restrictive than and allows for higher qualification for . For example, when , the condition holds only for , while holds for any (i.e., infinite qualification with no saturation at ) by setting and , i.e., for all . Intuitively, the standard assumption from inverse problem literature is concerned about the rate at which approaches 1 uniformly, however in our case, it turns out that we are interested in the rate at which becomes greater than for some constant , leading to a weaker condition. is not used in the inverse problem literature but is crucial in our analysis (see Remark 4.4(iii)).
Some examples of that satisfy – include the Tikhonov regularizer, , and Showalter regularizer, , where both have qualification . Note that the spectral cutoff regularizer is defined as satisfies – with but unfortunately does not satisfy since . Now, we are ready to present a test based on where satisfies –. Define
which capture the intrinsic dimensionality (or degrees of freedom) of . appears quite heavily in the analysis of kernel ridge regression (e.g., Caponnetto and Vito, 2007). The following result provides a critical region with level .
Theorem 4.2 (Critical region–Oracle).
Let and . Suppose – hold. Then for any and ,
where Furthermore if , the above bound holds for and .
First, note that the above result yields an -level test that rejects when . But the critical level depends on which in turn depends on the unknown distributions and . Therefore, we call the above test the Oracle test. Later in Sections 4.3 and 4.4, we present a completely data-driven test based on the permutation approach that matches the performance of the Oracle test. Second, the above theorem imposes a condition on with respect to in order to control the Type-I error, where this restriction can be weakened if we further assume the uniform boundedness of the eigenfunctions, i.e., . Moreover, the condition on implies that cannot decay to zero faster than .
Next, we will analyze the power of the Oracle test. Note that
, which implies that the power is controlled by and . Lemma A.7 shows that , provided that satisfies , , and , where follows from Lemma A.18. Combining this bound with the bound on in Theorem 4.2 provides a condition on the separation boundary. Additional sufficient conditions on and are obtained by controlling to achieve the desired power, which is captured by the following result.
Remark 4.4.
(i) Note that while is lower than (see the proofs of Theorem 3.1 and Lemma A.12),
the rate at which approaches is much slower than that of (see Lemmas A.19 and A.7).
Thus one can think of this phenomenon as a kind of estimation-approximation error trade-off for the separation boundary rate.
(ii) Observe from the condition that larger corresponds to a smaller separation boundary. Therefore, it is important to work with regularizers with infinite qualification, such as Tikhonov and Showalter.
(iii) The assumption plays a crucial role in controlling the power of the test and in providing the conditions on the separation boundary in terms of . Note that for any set —we choose to be such that and are bounded in probability with —, where .
If satisfies , then it implies that , hence is invertible. Thus, . Moreover, yields that
with high probability (see Lemma A.11,
Sriperumbudur and Sterge, 2022, Lemma A.1(ii)), which when combined with Lemma A.7,
yields sufficient conditions on the separation boundary to control the power.
(iv) As aforementioned, the spectral cutoff regularizer does not satisfy . For that does not satisfy , an alternative approach can be used to obtain a lower bound on . Observe that , hence
However, the upper bound that we can achieve on is worse than the bound on , eventually leading to a worse separation boundary. Improving such bounds (if possible) and investigating this problem can be of independent interest and left for future analysis.
For the rest of the paper, we make the following assumption.
for some constant .
This assumption helps to keep the results simple and presents the separation rate in terms of . If this assumption is not satisfied, the analysis can still be carried out but leads to messy calculations with the separation rate depending on .
Theorem 4.3 (Separation boundary–Oracle).
Suppose – and hold. Let , , for some constants and , where is a constant that depends on . For any , if and satisfies
and
then
| (4.7) |
where , is a constant that depends on , and .
The above result is too general to appreciate the performance of the Oracle test. The following corollaries to Theorem 4.3 investigate the separation boundary of the test under the polynomial and exponential decay condition on the eigenvalues of .
Corollary 4.4 (Polynomial decay–Oracle).
Suppose , . Then there exists such that for all and for any ,
when
with for some constant . Furthermore, if , then
where for some constant .
Corollary 4.5 (Exponential decay–Oracle).
Suppose , . Then for any , there exists such that for all ,
when
where for some . Furthermore, if , then
where
Remark 4.5.
(i) For a bounded kernel , note that is trace class operator. With no further assumption on the decay of , it can be shown that the separation boundary has the same expression as in Corollary 4.4 for (see Remark 3.3(i) for the minimax separation). Under additional assumptions on the decay rate, the separation boundary improves (as shown in the above corollaries) unlike the separation boundary in Theorem 3.1 which does not capture the decay rate.
(ii) Suppose has infinite qualification, , then . Comparison of Corollaries 4.4 and 3.3 shows that the oracle test is minimax optimal w.r.t. in the ranges of as given in Corollary 3.3 if the eigenvalues of decay polynomially. Similarly, if the eigenvalues of decay exponentially, it follows from Corollary 4.5 and Corollary 3.4 that the Oracle test is minimax optimal w.r.t. if (resp. if ). Outside these ranges of , the optimality of the oracle test remains an open question since we do not have a minimax separation covering these ranges of .
(iii) On the other hand, if has a finite qualification, , then the test does not capture the smoothness of beyond , i.e., the test only captures the smoothness up to , which implies the test is minimax optimal only for . Therefore, it is important to use spectral regularizers with infinite qualification.
(iv) Note that the splitting choice yields that the complexity of computing the test statistic is of the order . However, it is worth noting that such a choice is just to keep the splitting method independent of and . But, in practice, a smaller order of still performs well (see Section 5). This can be theoretically justified by following the proof of Theorem 4.3 and its application to Corollaries 4.4 and 4.5, that for the polynomial decay of eigenvalues if , we can choose and still achieve the same separation boundary (up to log factor) and furthermore if and , then we can choose . Thus, as increases can be of a much lower order than . Similarly, for the exponential decay case, when , we can choose and still achieve the same separation boundary (up to factor), and furthermore if , then for , we can choose and achieve the same separation boundary.
(v) The key intuition in using the uniform bounded condition, i.e., is that it provides a reduction in the variance when applying Chebyshev’s (or Bernstein’s) inequality, which in turn provides an improvement in the separation rate, as can be seen in Corollaries 3.3, 3.4, 4.4, and 4.5, wherein the minimax optimal rate is valid for a large range of compared to the case where this assumption is not made.
4.3 Permutation test
In the previous section, we established the minimax optimality w.r.t. of the regularized test based on . However, this test is not practical because of the dependence of the threshold on which is unknown in practice since we do not know and . In order to achieve a more practical threshold, one way is to estimate from data and use the resultant critical value to construct a test. However, in this section, we resort to ideas from permutation testing (Lehmann and Romano, 2006, Pesarin and Salmaso, 2010, Kim et al., 2022) to construct a data-driven threshold. Below, we first introduce the idea of permutation tests, then present a permutation test based on , and provide theoretical results that such a test can still achieve minimax optimal separation boundary w.r.t. , and in fact with a better dependency on of the order compared to of the Oracle test.
Recall that our test statistic defined in Section 4.1 involves sample splitting resulting in three sets of independent samples, , , . Define , and . Let be the set of all possible permutations of with be a randomly selected permutation from the possible permutations, where . Define and . Let be the statistic based on the permuted samples. Let be randomly selected permutations from . For simplicity, define to represent the statistic based on permuted samples w.r.t. the random permutation . Given the samples , and , define
to be the permutation distribution function, and define
Furthermore, we define the empirical permutation distribution function based on random permutations as
and define
Based on these notations, the following result presents an -level test with a completely data-driven critical level.
Theorem 4.6 (Critical region–permutation).
For any and , if , then
Note that the above result holds for any statistic, not necessarily , thus it does not require any assumption on as opposed to Theorem 4.2. This follows from the exchangeability of the samples under and the way is defined, thus it is well known that this approach will yield an -level test when using as the threshold.
Remark 4.6.
(i) The requirement on in Theorem 4.6 is to ensure the proximity of to (refer to Lemma A.14), through an application of Dvoretzky-Kiefer-Wolfowitz (DKW) inequality (Dvoretzky et al., 1956). The parameters and introduced in the statement of Theorem 4.6 appear for technical reasons within the proof of Lemma A.14 since Lemma A.14 does not directly establish a relationship between the true quantile and the estimated quantile . Instead, it associates the true quantile with an arbitrary small shift in to the estimated quantile, hence the inclusion of these parameters. However, in practice, we rely solely on the quantile , which will be very close to the true quantile for a sufficiently large .
(ii) Another approach to construct is by using instead of the above definition, where the new definition of includes the unpermuted statistic (see Romano and Wolf 2005, Lemma 1 and Albert et al. 2022, Proposition 1). The advantage of this new construction is that the Type-I error is always smaller than for all , i.e., no condition is needed on . However, a condition on similar to that in Theorem 4.7 is anyway needed to achieve the required power. Therefore, the condition on in Theorem 4.6 does not impose an additional constraint in the power analysis. In practice, we observed that the new approach requires a significantly large to achieve similar power, leading to an increased computational requirement. Thus, we use the construction in Theorem 4.6 in our numerical experiments
Next, similar to Theorem 4.3, in the following result, we give the general conditions under which the power level can be controlled.
Theorem 4.7 (Separation boundary–permutation).
Suppose – and hold. Let , , for some constants and , where is a constant that depends on . For any , if for some , for any and satisfies
then
| (4.8) |
where is a constant that depends on , and .
The following corollaries specialize Theorem 4.7 for the case of polynomial and exponential decay of eigenvalues of .
Corollary 4.8 (Polynomial decay–permutation).
Suppose , . Then there exists such that for all and for any ,
when
with for some constant . Furthermore, if , then
where for some constant .
Corollary 4.9 (Exponential decay–permutation).
Suppose , . Then for any , there exists such that for all , when
where for some constant . Furthermore, if , then
where
These results show that the permutation-based test constructed in Theorem 4.6 is minimax optimal w.r.t. , matching the rates of the Oracle test with a completely data-driven test threshold. The computational complexity of the test increases to as the test statistic is computed times to calculate the threshold . However, since the test can be parallelized over the permutations, the computational complexity in practice is still the complexity of one permutation.
4.4 Adaptation
While the permutation test defined in the previous section provides a practical test, the choice of that yields the minimax separation boundary depends on the prior knowledge of (and in the case of polynomially decaying eigenvalues). In this section, we construct a test based on the union (aggregation) of multiple tests for different values of taking values in a finite set, , that guarantees to be minimax optimal (up to factors) for a wide range of (and in case of polynomially decaying eigenvalues).
Define where , for . Clearly is the cardinality of . Let be the optimal that yields minimax optimality. The main idea is to choose and to ensure that there is an element in that is close to for any (and in case of polynomially decaying eigenvalues). Define . Then it is easy to see that for , we have , in other words . Thus, is also an optimal choice for that belongs to . Motivated by this, in the following, we construct an -level test based on the union of the tests over that rejects if one of the tests rejects , which is captured by Theorem 4.10. The separation boundary of this test is analyzed in Theorem 4.11 under the polynomial and the exponential decay rates of the eigenvalues of , showing that the adaptive test achieves the same performance (up to a factor) as that of the Oracle test, i.e., minimax optimal w.r.t. over the range of mentioned in Corollaries 3.3, 3.4 without requiring the knowledge of .
Theorem 4.10 (Critical region–adaptation).
For any and , if , then
Theorem 4.11 (Separation boundary–adaptation).
Suppose – and hold. Let for , and . Then for any , , , , , there exists such for all , we have
provided one of the following cases hold:
(i) , , , , for some constants , where , , and
with , for some constant Furthermore, if , then the above conditions on and can be replaced by , , for some constants and
where for some constant
(ii) , , , for some , , and
where for some constant Furthermore if , then the above conditions on and can be replaced by , , for some and
where
It follows from the above result that the set which is defined by and does not depend on any unknown parameters.
Remark 4.7.
Theorem 4.11 shows that the adaptive test achieves the same performance (up to factor) as that of the Oracle test but without the prior knowledge of unknown parameters, and . In fact, following the ideas we used in the proof of Theorem 3.2 combined with the ideas in Ingster (2000) and Balasubramanian et al. (2021, Theorem 6), it can be shown that an extra factor of is unavoidable in the expression of the adaptive minimax separation boundary compared to the non-adaptive case. Thus, our adaptive test is actually minimax optimal up to a factor . This gap occurs, since the approach we are using to bound the threshold uses Bernstein-type inequality (see Lemma A.15), which involves a factor with , hence yielding the extra factor. We expect that this gap can be filled by using a threshold that depends on the asymptotic distribution of (as was done in Balasubramanian et al., 2021), yielding an asymptotic -level test in contrast to the exact -level test achieved by the permutation approach.
4.5 Choice of kernel
In the discussion so far, a kernel is first chosen which determines the test statistic, the test, and the set of local alternatives, . But the key question is what is the right kernel. In fact, this question is the holy grail of all kernel methods.
To this end, we propose to start with a family of kernels, and construct an adaptive test by taking the union of tests jointly over and to test vs. where
with being defined similar to for Some examples of include the family of Gaussian kernels indexed by the bandwidth, ; the family of Laplacian kernels indexed by the bandwidth, ; family of radial-basis functions, , where is the family of finite signed measures on ; a convex combination of base kernels, , where are base kernels. In fact, any of the kernels in the first three examples can be used as base kernels. The idea of adapting to a family of kernels has been explored in regression and classification settings under the name multiple-kernel learning and we refer the reader to Gönen and Alpaydin (2011) and references therein for details.
Let be the test statistic based on kernel and regularization parameter . We reject if for any . Similar to Theorem 4.10, it can be shown that this test has level if . The requirement of holds if we consider the above-mentioned families with a finite collection of bandwidths in the case of Gaussian and Laplacian kernels, and a finite collection of measures from in the case of radial basis functions.
Similar to Theorem 4.11, it can be shown that the kernel adaptive test is minimax optimal w.r.t. up to a factor, with the main difference being an additional factor of as illustrated in the next Theorem. We do not provide a proof since it is very similar to that of Theorem 4.11 with replaced by
Theorem 4.12 (Separation boundary–adaptation over kernel).
Suppose – and hold. Let , for , and
Then for any , , , , , , there exists such for all , we have
provided one of the following cases hold: For any and ,
(i) ,
, , , for some constants , where , , and
with , for some constant Furthermore, if , then the above conditions on and can be replaced by , , for some constants and
where for some constant
(ii) ,
, , for some , , and
where for some constant Furthermore if , then the above conditions on and can be replaced by , , for some and
where
5 Experiments
In this section, we study the empirical performance of the proposed two-sample test by comparing it to the performance of the adaptive MMD test (Schrab et al., 2021), Energy test (Szekely and Rizzo, 2004) and Kolmogorov-Smirnov (KS) test (Puritz et al., 2022; Fasano and Franceschini, 1987). The adaptive MMD test in Schrab et al. (2021) involves using a translation invariant kernel on in with bandwidth where the critical level is obtained by a permutation/wild bootstrap. Multiple such tests are constructed over , which are aggregated to achieve adaptivity and the resultant test is referred to as MMDAgg. All tests are repeated 500 times and the average power is reported.
To compare the performance, in the following, we consider different experiments on Euclidean and directional data using the Gaussian kernel, and by setting , with being the bandwidth. For our test, as discussed in Section 4.5, we construct an adaptive test by taking the union of tests jointly over and . Let be the test statistic based on and bandwidth . We reject if for any . We performed such a test for and , where . In our experiments we set , , , for all the experiments. We chose the number of permutations to be large enough to ensure the control of Type-I error (see Figure 1). We show the results for both Tikhonov and Showalter regularization and for different choices of the parameter , which is the number of samples used to estimate the covariance operator after sample splitting. All codes used for our spectral regularized test are available at https://github.com/OmarHagrass/Spectral-regularized-two-sample-test.
Remark 5.1.
(i) For our experimental evaluations of the other tests, we used the following:
For the Energy test, we used the ”eqdist.etest” function from the R Package ”energy” (for code see https://github.com/mariarizzo/energy) with the parameter indicating the number of bootstrap replicates. For the KS test, we used the R package ”fasano.franceschini.test” (for code see https://github.com/braunlab-nu/fasano.franceschini.test). For the MMDAgg test, we employed the code provided in Schrab et al. (2021). Since Schrab et al. (2021) presents various versions of the MMDAgg test, we compared our results to the version of MMDAgg that yielded the best performance on the datasets considered in Schrab et al. (2021), which include the MNIST data and the perturbed uniform. For the rest of the experiments, we compared our test to ”MMDAgg uniform” with —see Schrab et al. (2021) for details.
(ii) As mentioned above, in all the experiments, is chosen to be . It has to be noted that this choice of is much smaller than that suggested by Theorems 4.10 and 4.11 to maintain the Type-I error and so one could expect the resulting test to be anti-conservative. However, in this section’s experimental settings, we found this choice of to yield a test that is neither anti-conservative nor overly conservative. Of course, we would like to acknowledge that too small would make the test anti-conservative while too large would make it conservative, i.e., loss of power (see Figure 1 where increasing leads to a drop in the Type-I error below and therefore a potential drop in the power). Hence, the choice of is critical in any permutation-based test. This phenomenon is attributed to the conservative nature of the union bound utilized in computing the threshold of the adapted test. Thus, an intriguing future direction would be to explore methods superior to the union bound to accurately control the Type-I error at the desired level and further enhance the power.
(iii) In an ideal scenario, the choice of should be contingent upon , as evidenced in the statements of Theorems 4.10 and 4.11. However, utilizing this theoretical bound for the number of permutations would be computationally prohibitive, given the expensive nature of computing each permuted statistic. Exploring various approximation schemes such as random Fourier features (Rahimi and Recht, 2008), Nyström subsampling (e.g., Williams and Seeger, 2001; Drineas and Mahoney, 2005), or sketching (Yang et al., 2017), which are known for expediting kernel methods, could offer more computationally efficient testing approaches, and therefore could allow to choose as suggested in Theorems 4.10 and 4.11.

5.1 Bechmark datasets
In this section, we investigate the empirical performance of the spectral regularized test and compare it to the other methods.
5.1.1 Gaussian distribution
Let and , where or , , i.e., we test for Gaussian mean shift or Gaussian covariance scaling, where is the -dimensional identity matrix. Figures 2(a) and 3(a) show the results for the Gaussian mean shift and covariance scale experiments, where we used for our test. It can be seen from Figure 2(a) that the best power is obtained by the Energy test, followed closely by the proposed test, with the other tests showing poor performance, particularly in high-dimensional settings. On the other hand, the proposed test performs the best in Figure 3(a), closely followed by the Energy test. We also investigated the effect of on the test power for the Showalter method (Tikhonov method also enjoys very similar results), whose results are reported in Figures 2(b) and 3(b). We note from these figures that lower values of perform slightly better, though overall, the performance is less sensitive to the choices of . Based on these results and those presented below, as a practical suggestion, the choice is probably fine.




5.1.2 Cauchy distribution
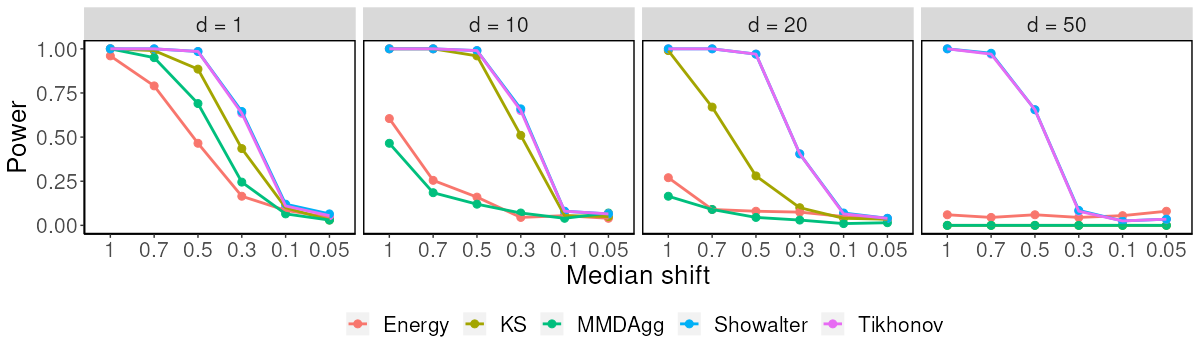
In this section, we investigate the performance of the proposed test for heavy-tailed distribution, specifically the Cauchy distribution with median shift alternatives. Particularly, we test samples from a Cauchy distribution with zero median and unit scale against another set of Cauchy samples with different median shifts and unit scale. Figure 4(a) shows that for , the KS test achieves the highest power for the majority of considered median shifts, followed closely by our regularized test which achieves better power for the harder problem when the shift is small. Moreover, for , our proposed test achieves the highest power. The effect of is captured in Figure 4(b).

5.1.3 MNIST dataset
Next, we investigate the performance of the regularized test on the MNIST dataset (LeCun et al., 2010), which is a collection of images of digits from –. In our experiments, as in Schrab et al. (2021), the images were downsampled to (i.e. ) and consider 500 samples drawn with replacement from set while testing against the set for , where consists of images of the digits
and
Figure 5(a) shows the power of our test for both Gaussian and Laplace kernels in comparison to that of MMDAgg and the other tests which shows the superior performance of the regularized test, particularly in the difficult cases, i.e., distinguishing between and for larger . Figure 5(b) shows the effect of on the test power, from which we can see that the best performance in this case is achieved for , however, the overall results are not very sensitive to the choice of .


5.1.4 Directional data
In this section, we consider two experiments with directional domains. First, we consider a multivariate von Mises-Fisher distribution (which is the Gaussian analogue on unit-sphere) given by where is the concentration parameter, is the mean parameter and is the modified Bessel function (see Figure 6(a)). Figure 7(a) shows the results for testing von Mises-Fisher distribution against spherical uniform distribution () for different concentration parameters using a Gaussian kernel. Note that the theoretical properties of MMDAgg do not hold in this case, unlike the proposed test. We can see from Figure 7(a) that the best power is achieved by the Energy test followed closely by our regularized test. Figure 7(b) shows effect of on the test power of the regularized test.
Second, we consider a mixture of two multivariate Watson distribution (which is an axially symmetric distribution on a sphere) given by , where is the concentration parameter, is the mean parameter and is Kummer’s confluent hypergeometric function. Using equal weights we drew 500 samples from a mixture of two Watson distributions with similar concentration parameter and mean parameter respectively, where and with the first coordinate changed to (see Figure 6(b)). Figure 8(a) shows the results for testing against spherical uniform distribution for different concentration parameters using a Gaussian kernel and we can see that our regularized test outperforms the other methods. Figure 8(b) shows the effect of different choices of the parameter on the test power, which like in previous scenarios, is not very sensitive to the choice of . Moreover, in Figure 8(c) we illustrate how the power changes with increasing the sample size for the case and , which shows that the regularized test power converges to one more quickly than the other methods.







5.2 Perturbed uniform distribution
In this section, we consider a simulated data experiment where we are testing a -dimensional uniform distribution against a perturbed version of it. The perturbed density for is given by
where , represents the number of perturbations being added and for ,
As done in Schrab et al. (2021), we construct two-sample tests for and , wherein we set , . The tests are constructed 500 times with a new value of being sampled uniformly each time, and the average power is computed for both our regularized test and MMDAgg. Figure 9(a) shows the power results of our test when for for both Gaussian and Laplace kernels and also when for for both Gaussian and Laplace kernels in comparison to that of other methods, where the Laplace kernel is defined as with the bandwidth being chosen as . It can be seen in Figure 9(a) that our proposed test performs similarly for both Tikhonov and Showalter regularizations, while significantly improving upon other methods, particularly in the difficult case of large perturbations (note that large perturbations make distinguishing the uniform and its perturbed version difficult). Moreover, we can also see from Figure 9(b) that the performance of the regularized test is not very sensitive to the choice of . Note that, when , it becomes really hard to differentiate the two samples for perturbations when using a sample size smaller than , thus we presented the result for this choice of sample size in order to compare with other methods. We also investigated the effect of changing the sample size when for perturbations with different choices of as shown in Figure 10, which again shows the non-sensitivity of the power to the choice of while the power improving with increasing sample size.








5.3 Effect of kernel bandwidth
In this section, we investigate the effect of kernel bandwidth on the performance of the regularized test when no adaptation is done. Figure 11 shows the performance of the test under different choices of bandwidth, wherein we used both fixed bandwidth choices and bandwidths that are multiples of the median . The results in Figures 11(a,b) are obtained using the perturbed uniform distribution data with and , respectively while Figure 11(c) is obtained using the MNIST data with —basically using the same settings of Sections 5.2 and 5.1.3. We observe from Figures 11(a,b) that the performance is better at smaller bandwidths for the Gaussian kernel and deteriorates as the bandwidth gets too large, while a too-small or too-large bandwidth affects the performance in the case of a Laplacian kernel.
In Figure 11(c), we can observe that the performance gets better for large bandwidth and deteriorates when the bandwidth gets too small. Moreover, one can see from the results that for most choices of the bandwidth, the test based on still yields a non-trivial power as the number of perturbations (or the index of in the case of the MNIST data) increases and eventually outperforms the MMDAgg test.
5.4 Unbalanced size for and
We investigated the performance of the regularized test when and report the results in Figure 12 for the 1-dimensional perturbed uniform and MNIST data set using Gaussian kernel and for fixed . It can be observed that the best performance is for as we get more representative samples from both of the distributions and , which is also expected theoretically, as otherwise the rates are controlled by .
6 Discussion
To summarize, we have proposed a two-sample test based on spectral regularization that not only uses the mean element information like the MMD test but also uses the information about the covariance operator and showed it to be minimax optimal w.r.t. the class of local alternatives defined in (1.4). This test improves upon the MMD test in terms of the separation rate as the MMD test is shown to be not optimal w.r.t. . We also presented a permutation version of the proposed regularized test along with adaptation over the regularization parameter, , and the kernel so that the resultant test is completely data-driven. Through numerical experiments, we also established the superiority of the proposed method over the MMD variant.
However, still there are some open questions that may be of interest to address. (i) The proposed test is computationally intensive and scales as where is the number of samples used to estimate the covariance operator after sample splitting. Various approximation schemes like random Fourier features (Rahimi and Recht, 2008), Nyström method (e.g., Williams and Seeger, 2001; Drineas and Mahoney, 2005) or sketching (Yang et al., 2017) are known to speed up the kernel methods, i.e., computationally efficient tests can be constructed using any of these approximation methods. The question of interest, therefore, is about the computational vs. statistical trade-off of these approximate tests, i.e., are these computationally efficient tests still minimax optimal w.r.t. ? (ii) The construction of the proposed test statistic requires sample splitting, which helps in a convenient analysis. It is of interest to develop an analysis for the kernel version of Hotelling’s -statistic (see Harchaoui et al., 2007) which does not require sample splitting. We conjecture that the theoretical results of Hotelling’s -statistic will be similar to those of this paper, however, it may enjoy a better empirical performance but at the cost of higher computational complexity. (iii) The adaptive test presented in Section 4.5 only holds for the class of kernels, for which . It will be interesting to extend the analysis for for which , e.g., the class of Gaussian kernels with bandwidth in , or the class of convex combination of certain base kernels as explained in Section 4.5.
7 Proofs
In this section, we present the proofs of all the main results of the paper.
7.1 Proof of Theorem 3.1
Define , and . Then we have
where follows from Lemma A.2 by setting and follows by writing in the last two terms. Thus we have
where , ,
and . Next, we bound the terms – as follows (similar to the technique in the proofs of Lemmas A.4, A.5, and A.6):
Combining these bounds with the fact that , and that for any , yields that
| (7.1) |
where follows from Lemma A.13.
When , we have and . Therefore under ,
| (7.2) |
where in we used . Thus using (7.2) and Chebyshev’s inequality yields
where .
Moreover using the same exchangeability argument used in the proof of Theorem 4.6, it is easy to show that
where
Bounding the power of the tests: For the threshold , we can use the bound in (7.1) to bound the power.
Let , then , for some constant . Thus
where holds when , which is implied if . follows from (7.1) and an application of Chebyshev’s inequality. The desired result, therefore, holds by taking infimum over .
For the threshold , using a similar approach to the proof of Lemma A.15 we can show that
| (7.3) |
where , for some constant Thus
where holds when , which is implied if and . follows from (7.1) with an application of Chebyshev’s inequality and using (7.3).
Thus for both thresholds and , the condition to control the power is , which in turn is implied if where in the last implication we used Lemma A.19. The desired result, therefore, holds by taking infimum over .
Finally, we will show that we cannot achieve a rate better than over . To this end, we will first show that if , then
for . Gretton et al. (2012, Appendix B.2) show that under ,
where , , , are the eigenvalues of the operator and If , then as and which is the distribution under Hence for ,
where , thus , and using the symmetry of the permutation distribution . In both cases, by the definition of , we can deduce that , which follows from the fact that the has a non-zero probability of being negative. Therefore it remains to show that when , we can construct such that To this end, let be a probability measure. Recall that . Let , where . Then Suppose , where is a strictly decreasing continuous function on (for example , and respectively correspond to polynomial and exponential decay). Let , , hence . Define
Then and thus . Define
Note that . Since , we have Next we bound in the following two cases.
Case I: and is not finite.
Note that
where in we used In we used
Case II: .
In this case,
for large enough. This implies that in both cases we can find such that and Then for such , we have .
7.2 Proof of Theorem 3.2
Let be any test that rejects when and fail to reject when . Fix some probability probability measure , and let such that . First, we prove the following lemma.
Lemma 7.1.
For , if the following hold,
| (7.4) |
| (7.5) |
then
Proof.
For any two-sample test , define a corresponding one sample test as and note that it is still an -level test since . For any , we have
where the last inequality follows by noting that
where uses the alternative definition of total variation distance using the -distance. Thus taking the infimum over yields
and the result follows. ∎
Thus, in order to show that a separation boundary will imply that , it is sufficient to find a set of distributions such that (7.4) and (7.5) hold. Note that since , it is clear that the operator is fixed for all . Recall . Let , where . Then . Furthermore, since the lower bound on is only in terms of , for simplicity, we will write as . However, since we assume , we can write the resulting bounds in terms of using Lemma A.13.
Following the ideas from Ingster (1987) and Ingster (1993), we now provide the proof of Theorem 3.2.
Case I: .
Let
and . For , define
where such that , thus . Then we have , where in we used that is a decreasing function. Thus, . Define
and
Note that . Since , we have , and
This implies that we can find such that and . Thus it remains to verify conditions (7.4) and (7.5) from Lemma 7.1.
For condition (7.4), we have
where follows from the fact that and . Similarly for (7.5), we have
where . Thus it is sufficient to show that such that if , then . To this end, consider
where . Then as argued in Ingster (1987), it can be shown for any , we have and , thus , which yields that for any , we have
Since we can choose and such that
Case II: is not finite.
Since , there exists constants and such that . Let
and . The proof proceeds similarly to that of Case I by noting that
where follows from
where follows since is a decreasing function. The rest of the proof proceeds exactly similar to that of Case I.
7.3 Proof of Corollary 3.3
If , then Theorem 3.2 yields that , if
which is equivalent to This implies the following lower bound on the minimax separation
| (7.6) |
Observe that when . Matching the upper and lower bound on by combining (7.6) with the result from Corollary 4.4 when implies that when . Similarly for the case , Theorem 3.2 yields that if
which implies that
| (7.7) |
Then combining (7.7) with the result from Corollary 4.4 when yields that when .
7.4 Proof of Corollary 3.4
If , then Theorem 3.2 yields that , if
which is implied if
for any and large enough. Furthermore if , Theorem 3.2 yields that
which is implied if for any and large enough. Thus for both cases, we can deduce that for any , then by taking supremum over yields that
| (7.8) |
Matching the upper and lower bound on by combining (7.8) with the result from Corollary 4.5 when yields the desired result.
7.5 Proof of Theorem 4.1
Define
so that
It can be shown that (Sterge and Sriperumbudur, 2022, Proposition C.1). Also, it can be shown that if is the eigensystem of where , , and , then is the eigensystem of , where
| (7.9) |
We refer the reader to Sriperumbudur and Sterge (2022, Proposition 1) for details. Using (7.9) in the definition of , we have
Define , and let be a vector of zeros with only the entry equal one. Also we define and similar to that of based on samples and , respectively. Based on Sterge and Sriperumbudur (2022, Proposition C.1), it can be shown that , , , , , and .
Based on these observations, we have
and
7.6 Proof of Theorem 4.2
Since , an application of Chebyshev’s inequality via Lemma A.12 yields,
By defining
we obtain
where follows using
and
where follows from (Sriperumbudur and Sterge, 2022, Lemma B.2(ii)), under the condition that . When , using Lemma A.17, we can obtain an improved condition on satisfying and . The desired result then follows by setting
7.7 Proof of Theorem 4.3
Let , and
where is defined in Lemma A.9. Then Lemma A.12 implies
for some constant . By Lemma A.1, if
| (7.10) |
for any , then we obtain The result follows by taking the infimum over . Therefore, it remains to verify (7.10), which we do below. Define . Consider
where follows by using , which is obtained by combining Lemma A.11 with Lemma A.7 under the assumptions , and
| (7.11) |
Note that is guaranteed since and
| (7.12) |
guarantees (7.11) since and
where follows when
| (7.13) |
and
| (7.14) |
and follows from (Sriperumbudur and Sterge, 2022, Lemma B.2(ii)), under the condition that
| (7.15) |
When , follows from Lemma A.17 by replacing (7.15) with
| (7.16) |
Below, we will show that (7.13)–(7.16) are satisfied. Using , it is easy to see that (7.12) is implied when . Using , where in the last inequality we used since and , and applying Lemma A.13, we can verify that (7.13) is implied if for some constant . It can be also verified that (7.14) is implied if and for some constants . Using , and , it can be seen that (7.15) is implied when for some constant . On the other hand, when , using , , it can be verified that (7.16) is implied when
7.8 Proof of Corollary 4.4
When , it follows from (Sriperumbudur and Sterge 2022, Lemma B.9) that
Using this bound in the conditions mentioned in Theorem 4.3, ensures that these conditions on the separation boundary hold if
where is a constant. The above condition is implied if
where and we used that , and that , when and is large enough, for any .
On the other hand when , we obtain the corresponding condition as
for some constant , which in turn is implied for large enough, if
where
7.9 Proof of Corollary 4.5
When , it follows from (Sriperumbudur and Sterge 2022, Lemma B.9) that
Thus substituting this in the conditions from Theorem 2 and assuming that
we can write the separation boundary as
which is implied if
for large enough , where and we used that implies and that implies
On the other hand when , we obtain
for some constant . We can deduce that the condition is reduced to
where , and we used when is large enough, for .
7.10 Proof of Theorem 4.6
Under , we have for any , i.e., Thus, given samples , and , we have
Taking expectations on both sides of the above inequality with respect to the samples yields
Therefore,
where we applied Lemma A.14 in , and the result follows by choosing .
7.11 Proof of Theorem 4.7
First, we show that for any , the following holds under the conditions of Theorem 4.7:
| (7.17) |
To this end, let ,
where as defined in Lemma A.9. Then Lemma A.12 implies
for some constant . By Lemma A.1, if
| (7.18) |
then we obtain (7.17). Therefore, it remains to verify (7.18) which we do below. Define
and
Thus we have
Then it follows from Lemma A.15 that there exists a constant such that
Let . Then we have
where in we assume , then it follows by using
which is obtained by combining Lemma A.11 with Lemma A.7 under the assumptions of , and (7.11). Note that is guaranteed since and (7.12) guarantees (7.11) as discussed in the proof of Theorem 4.7. follows when
| (7.19) |
follows from (Sriperumbudur and Sterge, 2022, Lemma B.2(ii)), under the condition (7.15). When , follows from Lemma A.17 by replacing (7.15) with (7.16).
As in the proof of Theorem 4.3, it can be shown that (7.11), (7.15) and (7.16) are satisfied under the assumptions made in the statement of Theorem 4.7. It can also be verified that (7.19) is implied if and for some constants . Finally, we have
where in we use (7.17) and Lemma A.14 by setting , for . Then, the desired result follows by taking infimum over .
7.12 Proof of Corollary 4.8
The proof is similar to that of Corollary 4.4. Since , we have By using this bound in the conditions of Theorem 4.7, we that the conditions on hold if
| (7.20) | ||||
where is a constant. By exactly using the same arguments as in the proof of Corollary 4.4, it is easy to verify that the above condition on is implied if
where .
On the other hand when , we obtain the corresponding condition as
| (7.21) | ||||
for some , which in turn is implied for large enough, if
where
7.13 Proof of Corollary 4.9
The proof is similar to that of Corollary 4.5. When , we have . Thus substituting this in the conditions from Theorem 4.7 and assuming that , we can write the separation boundary as
| (7.22) | |||||
where is a constant. This condition in turn is implied if
for large enough , where
and we used that implies that and that implies that On the other hand when , we obtain
for some constant . We can deduce that the condition is reduced to
where , and we used when is large enough, for .
7.14 Proof of Theorem 4.10
7.15 Proof Theorem 4.11
Using as the threshold, the same steps as in the proof of Theorem 4.7 will follow, with the only difference being replaced by . Of course, this leads to an extra factor of in the expression of in condition (7.19), which will show up in the expression for the separation boundary (i.e., there will a factor of instead of ). Observe that for all cases of Theorem 4.11, we have
For the case of , we can deduce from the proof of Corollary 4.8 (see (7.20)) that when for some , then
and the condition on the separation boundary becomes
which in turn is implied if
where for some and we used that for large enough .
Note that the optimal choice of is given by
Observe that the constant term can be expressed as for some constant that depends only on and . If , we can bound as , and as when . Therefore, for any and , the optimal lambda can be bounded as , where are constants that depend only on , , and , and .
Define . From the definition of , it is easy to see that and . Thus is an optimal choice of that will yield to the same form of the separation boundary up to constants. Therefore, by Lemma A.16, for any and any in , we have
Thus the desired result holds by taking the infimum over and .
When and , then using (7.21), the conditions on the separation boundary becomes
where . This yields the optimal to be
Using the similar argument as in the previous case, we can deduce that for any and , we have , where are constants that depend only on , , , , and . The claim therefore follows by using the argument mentioned between and .
For the case , , the condition from (7.22) becomes
where Thus
which can be bounded as for any , where are constants that depend only on , , and Furthermore when , the condition on the separation boundary becomes
where Thus
which can be bounded as
for any , where are constants that depend only on , , and The claim, therefore, follows by using the same argument as mentioned in the polynomial decay case.
Acknowledgments
The authors thank the reviewers for their valuable comments and constructive feedback, which helped to significantly improve the paper. OH and BKS are partially supported by National Science Foundation (NSF) CAREER award DMS–1945396. BL is supported by NSF grant DMS–2210775.
References
- Adams and Fournier (2003) R. A. Adams and J. J. F. Fournier. Sobolev Spaces. Academic Press, 2003.
- Albert et al. (2022) M. Albert, B. Laurent, A. Marrel, and A. Meynaoui. Adaptive test of independence based on HSIC measures. The Annals of Statistics, 50(2):858 – 879, 2022.
- Aronszajn (1950) N. Aronszajn. Theory of reproducing kernels. Trans. Amer. Math. Soc., pages 68:337–404, 1950.
- Balasubramanian et al. (2021) K. Balasubramanian, T. Li, and M. Yuan. On the optimality of kernel-embedding based goodness-of-fit tests. Journal of Machine Learning Research, 22(1):1–45, 2021.
- Bauer et al. (2007) F. Bauer, S. Pereverzev, and L. Rosasco. On regularization algorithms in learning theory. Journal of Complexity, 23(1):52–72, 2007.
- Burnashev (1979) M. V. Burnashev. On the minimax detection of an inaccurately known signal in a white Gaussian noise background. Theory of Probability & Its Applications, 24(1):107–119, 1979.
- Caponnetto and Vito (2007) A. Caponnetto and E. De Vito. Optimal rates for regularized least-squares algorithm. Foundations of Computational Mathematics, 7:331–368, 2007.
- Cucker and Zhou (2007) F. Cucker and D. X. Zhou. Learning Theory: An Approximation Theory Viewpoint. Cambridge University Press, Cambridge, UK, 2007.
- Dinculeanu (2000) N. Dinculeanu. Vector Integration and Stochastic Integration in Banach Spaces. John-Wiley & Sons, Inc., 2000.
- Drineas and Mahoney (2005) P. Drineas and M. W. Mahoney. On the Nyström method for approximating a Gram matrix for improved kernel-based learning. Journal of Machine Learning Research, 6:2153–2175, December 2005.
- Dvoretzky et al. (1956) A. Dvoretzky, J. Kiefer, and J. Wolfowitz. Asymptotic minimax character of the sample distribution function and of the classical multinomial estimator. The Annals of Mathematical Statistics, 27(3):642–669, 1956.
- Engl et al. (1996) H. W. Engl, M. Hanke, and A. Neubauer. Regularization of Inverse Problems. Kluwer Academic Publishers, Dordrecht, The Netherlands, 1996.
- Fasano and Franceschini (1987) G. Fasano and A. Franceschini. A multidimensional version of the Kolmogorov–Smirnov test. Monthly Notices of the Royal Astronomical Society, 225(1):155–170, 03 1987. ISSN 0035-8711.
- Gönen and Alpaydin (2011) M. Gönen and E. Alpaydin. Multiple kernel learning algorithms. Journal of Machine Learning Research, 12(64):2211–2268, 2011.
- Gretton et al. (2006) A. Gretton, K. Borgwardt, M. Rasch, B. Schölkopf, and A. Smola. A kernel method for the two-sample problem. In B. Schölkopf, J. Platt, and T. Hoffman, editors, Advances in Neural Information Processing Systems, volume 19, pages 513–520. MIT Press, 2006.
- Gretton et al. (2009) A. Gretton, K. Fukumizu, Z. Harchaoui, and B. K. Sriperumbudur. A fast, consistent kernel two-sample test. In Y. Bengio, D. Schuurmans, J. Lafferty, C. Williams, and A. Culotta, editors, Advances in Neural Information Processing Systems, volume 22. Curran Associates, Inc., 2009.
- Gretton et al. (2012) A. Gretton, K. M. Borgwardt, M. J. Rasch, B. Schölkopf, and A. Smola. A kernel two-sample test. Journal of Machine Learning Research, 13(25):723–773, 2012.
- Harchaoui et al. (2007) Z. Harchaoui, F. R. Bach, and E. Moulines. Testing for homogeneity with kernel fisher discriminant analysis. In J. Platt, D. Koller, Y. Singer, and S. Roweis, editors, Advances in Neural Information Processing Systems, volume 20. Curran Associates, Inc., 2007.
- Hoeffding (1992) W. Hoeffding. A class of statistics with asymptotically normal distribution. In Breakthroughs in Statistics, pages 308–334, 1992.
- Ingster (2000) Y Ingster. Adaptive chi-square tests. Journal of Mathematical Sciences, 99:1110–1119, 04 2000.
- Ingster (1987) Y. I. Ingster. Minimax testing of nonparametric hypotheses on a distribution density in the metrics. Theory of Probability & Its Applications, 31(2):333–337, 1987.
- Ingster (1993) Y. I. Ingster. Asymptotically minimax hypothesis testing for nonparametric alternatives i, ii, iii. Mathematical Methods of Statistics, 2(2):85–114, 1993.
- Kim et al. (2022) I. Kim, S. Balakrishnan, and L. Wasserman. Minimax optimality of permutation tests. The Annals of Statistics, 50(1):225–251, 2022.
- Le Cam (1986) L. Le Cam. Asymptotic Methods In Statistical Decision Theory. Springer, 1986.
- LeCun et al. (2010) Y. LeCun, C. Cortes, and C. Burges. MNIST handwritten digit database. AT &T Labs, 2010.
- Lehmann and Romano (2006) E. L. Lehmann and J. P. Romano. Testing Statistical Hypotheses. Springer Science & Business Media, 2006.
- Li and Yuan (2019) T. Li and M. Yuan. On the optimality of Gaussian kernel based nonparametric tests against smooth alternatives. 2019. https://arxiv.org/pdf/1909.03302.pdf.
- Massart (1990) P. Massart. The tight constant in the Dvoretzky-Kiefer-Wolfowitz Inequality. The Annals of Probability, 18(3):1269–1283, 1990.
- Mendelson and Neeman (2010) S. Mendelson and J. Neeman. Regularization in kernel learning. The Annals of Statistics, 38(1):526–565, 2010.
- Minh et al. (2006) H. Q. Minh, P. Niyogi, and Y. Yao. Mercer’s theorem, feature maps, and smoothing. In Gábor Lugosi and Hans Ulrich Simon, editors, Learning Theory, pages 154–168, Berlin, 2006. Springer.
- Muandet et al. (2017) K. Muandet, K. Fukumizu, B. Sriperumbudur, and B. Schölkopf. Kernel mean embedding of distributions: A review and beyond. Foundations and Trends® in Machine Learning, 10(1-2):1–141, 2017.
- Pesarin and Salmaso (2010) F. Pesarin and L. Salmaso. Permutation Tests for Complex Data: Theory, Applications and Software. John Wiley & Sons, 2010.
- Puritz et al. (2022) C. Puritz, E. Ness-Cohn, and R. Braun. fasano.franceschini.test: An implementation of a multidimensional ks test in r, 2022.
- Rahimi and Recht (2008) A. Rahimi and B. Recht. Random features for large-scale kernel machines. In J. C. Platt, D. Koller, Y. Singer, and S. T. Roweis, editors, Advances in Neural Information Processing Systems 20, pages 1177–1184. Curran Associates, Inc., 2008.
- Reed and Simon (1980) M. Reed and B. Simon. Methods of Modern Mathematical Physics: Functional Analysis I. Academic Press, New York, 1980.
- Romano and Wolf (2005) J. P. Romano and M. Wolf. Exact and approximate stepdown methods for multiple hypothesis testing. Journal of the American Statistical Association, 100(469):94–108, 2005.
- Schrab et al. (2021) A. Schrab, I. Kim, M. Albert, B. Laurent, B. Guedj, and A. Gretton. MMD aggregated two-sample test. 2021. https://arxiv.org/pdf/2110.15073.pdf.
- Simon-Gabriel and Schölkopf (2018) C. Simon-Gabriel and B. Schölkopf. Kernel distribution embeddings: Universal kernels, characteristic kernels and kernel metrics on distributions. Journal of Machine Learning Research, 19(44):1–29, 2018.
- Smola et al. (2007) A. J. Smola, A. Gretton, L. Song, and B. Schölkopf. A Hilbert space embedding for distributions. In Marcus Hutter, Rocco A. Servedio, and Eiji Takimoto, editors, Algorithmic Learning Theory, pages 13–31. Springer-Verlag, Berlin, Germany, 2007.
- Sriperumbudur (2016) B. K. Sriperumbudur. On the optimal estimation of probability measures in weak and strong topologies. Bernoulli, 22(3):1839 – 1893, 2016.
- Sriperumbudur and Sterge (2022) B. K. Sriperumbudur and N. Sterge. Approximate kernel PCA using random features: Computational vs. statistical trade-off. The Annals of Statistics, 50(5):2713–2736, 2022.
- Sriperumbudur et al. (2009) B. K. Sriperumbudur, K. Fukumizu, A. Gretton, G. R. G. Lanckriet, and B. Schölkopf. Kernel choice and classifiability for RKHS embeddings of probability distributions. In Y. Bengio, D. Schuurmans, J. Lafferty, C. K. I. Williams, and A. Culotta, editors, Advances in Neural Information Processing Systems 22, pages 1750–1758, Cambridge, MA, 2009. MIT Press.
- Sriperumbudur et al. (2010) B. K. Sriperumbudur, A. Gretton, K. Fukumizu, B. Schölkopf, and G. R. G. Lanckriet. Hilbert space embeddings and metrics on probability measures. Journal of Machine Learning Research, 11:1517–1561, 2010.
- Sriperumbudur et al. (2011) B. K. Sriperumbudur, K. Fukumizu, and G. R. Lanckriet. Universality, characteristic kernels and RKHS embedding of measures. Journal of Machine Learning Research, 12:2389–2410, 2011.
- Steinwart and Christmann (2008) I. Steinwart and A. Christmann. Support Vector Machines. Springer, New York, 2008.
- Steinwart and Scovel (2012) I. Steinwart and C. Scovel. Mercer’s theorem on general domains: On the interaction between measures, kernels, and RKHSs. Constructive Approximation, 35:363–417, 2012.
- Steinwart et al. (2006) I. Steinwart, D. R. Hush, and C. Scovel. An explicit description of the reproducing kernel hilbert spaces of gaussian rbf kernels. IEEE Transactions on Information Theory, 52:4635–4643, 2006.
- Sterge and Sriperumbudur (2022) N. Sterge and B. K. Sriperumbudur. Statistical optimality and computational efficiency of Nyström kernel PCA. Journal of Machine Learning Research, 23(337):1–32, 2022.
- Szekely and Rizzo (2004) G Szekely and M Rizzo. Testing for equal distributions in high dimension. InterStat, 5, 11 2004.
- Williams and Seeger (2001) C.K.I. Williams and M. Seeger. Using the Nyström method to speed up kernel machines. In V. Tresp T. K. Leen, T. G. Diettrich, editor, Advances in Neural Information Processing Systems 13, pages 682–688, Cambridge, MA, 2001. MIT Press.
- Yang et al. (2017) Y. Yang, M. Pilanci, and M. J. Wainwright. Randomized sketches for kernels: Fast and optimal nonparametric regression. Annals of Statistics, 45(3):991–1023, 2017.
A Technical results
In this section, we collect technical results used to prove the main results of the paper. Unless specified otherwise, the notation used in this section matches that of the main paper.
Lemma A.1.
Let be a function of a random variable , and define . Suppose for all ,
Then
Proof.
Define . Consider
where in the last step we invoked Chebyshev’s inequality: ∎
Lemma A.2.
Define where is an arbitrary function in . Then defined in (4.6) can be written as
Proof.
The proof follows by using for in as shown below:
and noting that all the terms in expansion of the inner product cancel except for the terms of the form . ∎
Lemma A.3.
Let and be independent sequences of zero-mean -valued random elements, and let f be an arbitrary function in . Then the following hold.
-
(i)
-
(ii)
-
(iii)
Proof.
(i) can be shown as follows:
For (ii), we have
Consider the last term and note that and , implies that either , or . If , then
and the same result holds when . Therefore we conclude that the third term equals zero and the result follows.
(iii) Note that
and the result follows. ∎
Lemma A.4.
Let with . Define
where with and is a bounded operator. Then the following hold.
-
(i)
-
(ii)
Proof.
For (i), we have
where we used the fact that in . On the other hand, (ii) can be written as
where follows from Lemma A.3(ii) ∎
Lemma A.5.
Let . Suppose is an arbitrary function and is a bounded operator. Define
where and . Then
-
(i)
-
(ii)
Proof.
Lemma A.6.
Let and be a bounded operator. Define
where , , and . Then
-
(i)
;
-
(ii)
Proof.
(i) Define , where with . Then it can be verified that , . Thus and . Therefore we have
(ii) follows by noting that
where follows from Lemma A.3(i). ∎
Lemma A.7.
Let and , where satisfies –. Then
Furthermore, if , and
where , then,
Proof.
Note that
where we used Lemma A.8(i) in . The upper bound therefore follows by noting that
For the lower bound, consider
Since , there exists such that . Therefore, we have
and
where are the eigenvalues and eigenfunctions of . Using these expressions we have
Thus
When , by Assumption , we have
On the other hand, for ,
where follows by Assumption . Therefore we can conclude that
where we used in . ∎
Lemma A.8.
Let satisfies –. Then the following hold.
-
(i)
;
-
(ii)
;
-
(iii)
;
-
(iv)
;
-
(v)
.
Proof.
Let be the eigenvalues and eigenfunctions of Since and , we have which implies , i.e., , where . Note that , which are the eigenfunctions of , form an orthonormal system in . Define .
(i) Using the above, we have
where follows using . On the other hand,
where follows using
(ii)
where follows from Assumptions and .
(iii) The proof is exactly same as that of (ii) but with being replaced by .
(iv)
where follows from Assumption .
(v) The proof is exactly same as that of (iv) but with being replaced by .
∎
Lemma A.9.
Define , , and where . Then the following hold:
-
(i)
-
(ii)
where can be either or , and
Proof.
Let be the eigenvalues and eigenfunctions of Since and , we have which implies , i.e., , where . Note that form an orthonormal system in . Define , thus Let . Then .
(i)
Define . Then it can be verified that , . Thus and . Therefore we have,
Next we bound the second term in the above inequality in the two cases for .
Case 1: . Define . Then we have,
where follows from
where follows from and in we used
which is proved below. Consider
Furthermore, from the definition of , we can equivalently it write as , . Thus by Mercer’s theorem (see Steinwart and Scovel 2012, Lemma 2.6), we obtain .
Case 2: Suppose is not finite. From the calculations in Case 1, we have
where we used
in .
(ii) Note that
The result therefore follows by using the bounds in part . ∎
Lemma A.10.
Let and be bounded operators on a Hilbert space, such that is bounded. Then . Also for any ,
Proof.
The result follows by noting that
and . ∎
Lemma A.11.
Let . Then
where , and .
Proof.
Lemma A.12.
Let , , and for some constant . Then
where is defined in Lemma A.9 and is a constant that depends only on , and . Furthermore, if , then
Proof.
Define , and , where . Then we have
where follows from Lemma A.2 and follows by writing in the last two terms. Thus we have
Furthermore using Lemma A.8(iii),
Next we bound the terms – using Lemmas A.4, A.5, A.6 and A.9. It follows from Lemmas A.4(ii) and A.9(i) that
and
Using Lemma A.5(ii) and A.9(ii), we obtain
and
where follows from using with in Lemma A.7. For term , using Lemma A.6 yields,
Combining these bounds with the fact that , and that for any , yields that
where follows by using Lemma A.13.
When , and using the same Lemmas as above, we have
and . Therefore,
where follows by noting that under the assumption , and follows using ∎
Lemma A.13.
For any , if for some , then for any
Proof.
Observe that using yields ∎
Lemma A.14.
Define where
is the permutation distribution function. Let be randomly selected permutations from and define
where is the statistic based on the permuted samples. Define
Then, for any , if , the following hold:
-
(i)
;
-
(ii)
Proof.
We first use the Dvoretzky-Kiefer-Wolfowitz (see Dvoretzky et al. 1956, Massart 1990) inequality to get uniform error bound for the empirical permutation distribution function, and then use it to obtain bounds on the empirical quantiles. Let
Then DKW inequality yields . Now assuming holds, we have
Furthermore, we have
Thus (i) and (ii) hold if , which is equivalent to the condition ∎
Lemma A.15.
Proof.
Let , , and
By (Kim et al., 2022, Equation 59), we can conclude that given the samples there exists a constant such that
almost surely, where
We bound as
where follows by writing then using for any , . Then following the procedure similar to that in the proof of Lemma A.12, we can bound the expectation of each term using Lemma A.4, A.5, A.6, A.7, and A.9 resulting in
where in the last inequality we used Lemma A.13. Thus using and Markov’s inequality, we obtain the desired result. ∎
Lemma A.16.
Let be a function of a random variable and some (deterministic) parameter , where has finite cardinality . Let be any function of and . If for all and , , then
Furthermore, if for some and , then
Proof.
The proof follows directly from the fact that for any sets and , :
For the second part, we have
and the result follows. ∎
Lemma A.17.
Let be an RKHS with reproducing kernel k that is defined on a separable topological space, . Define
where . Let be orthonormal eigenfunctions of with corresponding eigenvalues that satisfy . Given with , define
Then for any , and where and , the following hold:
-
(i)
;
-
(ii)
;
-
(iii)
.
Proof.
(i) Define , , . Then
Also,
| (A.1) |
where in we used that which is proved below. To this end, define so that
Therefore,
Following the same argument as in proof of Lemma A.9(i), we obtain
where , yielding
Define . Then
where the last inequality follows from (A.1). Furthermore, we have
Note that and
where follows by using . Using Theorem D.3(ii) from Sriperumbudur and Sterge (2022) , we get
where . Then using , it can be verified that , where . Note that implies This means, if and , we get
(ii) By defining , we have
where the last inequality holds whenever . Similarly,
The result therefore follows from (i).
(iii) Since
the result follows from (i). ∎
Lemma A.18.
For probability measures and ,
is a metric. Futhermore , where denotes the Hellinger distance between and .
Proof.
Observe that . Thus it is obvious that , and if . Hence, it remains just to check the triangular inequality. For that matter, we will first show that
| (A.2) |
where is a probability measure. Defining , note that . Therefore, using the convexity of the function over yields
Then by squaring (A.2) and applying Cauchy-Schwartz inequality, we get
which is equivalent to . For the relation with Hellinger distance, observe that , and . Since , the result follows. ∎
Lemma A.19.
Let and . Then
Proof.
Since , then for some . Thus,
where holds by Holder’s inequality. The desired result follows by noting that ∎
Lemma A.20.
Suppose and hold. Then for all .
Proof.
states that
where , , are positive constants all independent of . So by taking limit as on both sides of the above inequality, we get
which yields that
This implies , which implies that
for all . For the result is trivial since dictates that . ∎