[table]capposition=top
Spectral radius and spanning trees of graphs111Supported by National Natural Science Foundation of China (Nos. 11971445 and 12261032) and Natural Science Foundation of Henan Province (No. 202300410377).
Abstract
For integer a spanning -ended-tree is a spanning tree with at most leaves. Motivated by the closure theorem of Broersma and Tuinstra [Independence trees and Hamilton cycles, J. Graph Theory 29 (1998) 227–237], we provide tight spectral conditions to guarantee the existence of a spanning -ended-tree in a connected graph of order with extremal graphs being characterized. Moreover, by adopting Kaneko’s theorem [Spanning trees with constraints on the leaf degree, Discrete Appl. Math. 115 (2001) 73–76], we also present tight spectral conditions for the existence of a spanning tree with leaf degree at most in a connected graph of order with extremal graphs being determined, where is an integer.
Keywords: Spanning tree, Spectral radius, Closure, Leaf degree
AMS Classification: 05C50; 05C35
1 Introduction
In this paper, we consider simple, undirected and connected graphs. For undefined terms and notions, one can refer to [5] and [2]. Let be a graph with vertex set and edge set . The order and size of are denoted by and , respectively. We denote by , , and the vertex of degree in , the clique number, the number of isolated vertices and the complement of respectively. We use , , and to denote the path of order , the cycle of order , the complete graph of order , and the complete bipartite graph with bipartition , where and . Let and be two vertex-disjoint graphs. We denote by the disjoint union of and The join is the graph obtained from by adding all possible edges between and .
Let and be the adjacency matrix and diagonal degree matrix of . Let be the signless Laplacian matrix of . The largest eigenvalues of and , denoted by and , are called the spectral radius and the signless Laplacian spectral radius of , respectively. For convenience, Liu, Lai and Das [23] introduced the nonnegative matrix of a graph . The largest eigenvalue of is called the -spectral radius of , denoted by . It is clear that and
The concept of closure of a graph was used implicitly by Ore [25], and formally introduced by Bondy and Chvatal [4]. Fix an integer , the -closure of a graph is the graph obtained from by successively joining pairs of nonadjacent vertices whose degree sum is at least until no such pair exists. Denote by the -closure of
For integer a spanning -ended-tree of a connected graph is a spanning tree with at most leaves. Note that a spanning -ended-tree is a Hamilton path. Hence a spanning -ended-tree of a graph is a natural generalization of a Hamilton path. Fiedler and Nikiforov [14] initially proved sufficient conditions for a graph to contain a Hamilton path in terms of the spectral radius of a graph or its complement. Ning and Ge [20], Li and Ning [21] improved and extended results in [14]. As a special case of spanning -ended-tree, there are many sufficient conditions to assure a graph to contain a Hamilton path (see for example [6, 22, 24, 28, 29]). In fact, a Hamilton path can also be generalized to a spanning -tree. A spanning -tree of a connected graph is a spanning tree in which every vertex has degree at most , where is an integer. Fan et al. [11] presented spectral conditions for the existence of a spanning -tree in a connected graph.
Broersma and Tuinstra [3] showed that the problem of whether a given connected graph contains a spanning -ended tree is NP-complete. Furthermore, they presented a degree sum condition to guarantee that a connected graph has a spanning -ended tree.
Theorem 1.1 (Broersma and Tuinstra [3]).
Let be an integer, and let be a connected graph of order . If for every two nonadjacent vertices and , then has a spanning -ended tree.
Moreover, Broersma and Tuinstra [3] proved the following closure theorem for the existence of a spanning -ended-tree, which is crucial to our proof.
Theorem 1.2 (Broersma and Tuinstra [3]).
Let be a connected graph of order and be an integer with Then has a spanning -ended-tree if and only if the -closure of has a spanning -ended-tree.
Inspired by the work of Broersma and Tuinstra [3], we focus on the following interesting problem in this paper.
Problem 1.1.
Let be a connected graph of order which has no a spanning -ended-tree. What is the maximum spectral radius (or signless Laplacian spectral radius) of Moreover, characterize all the extremal graphs.
For more results on spanning -ended-tree, one can refer to [7, 8, 9, 12, 18, 19, 26, 27]. Inspired by the ideas on Hamilton path from Li and Ning [21] and using typical spectral techniques, we prove tight spectral conditions to guarantee the existence of a spanning -ended-tree in a connected graph. Let be an -regular graph with vertices.
Theorem 1.3.
Let be a connected graph of order and be an integer. Each of the following holds.
(i) If and
then has a spanning -ended-tree unless .
(ii) If and
then has a spanning -ended-tree unless .
(iii) If then has a spanning -ended-tree unless .
(iv) If and
then has a spanning -ended-tree.
Kaneko [17] introduced the concept of leaf degree of a spanning tree. Let be a spanning tree of a connected graph . The leaf degree of a vertex is defined as the number of leaves adjacent to in . Furthermore, the leaf degree of is the maximum leaf degree among all the vertices of . They posed a necessary and sufficient condition for a connected graph to contain a spanning tree with leaf degree at most . Let denote the number of isolated vertices of
Theorem 1.4 (Kaneko [17]).
Let be a connected graph and be an integer. Then has a spanning tree with leaf degree at most if and only if for every nonempty subset .
In this paper, we consider the following spectral extremal problem.
Problem 1.2.
Let be a connected graph of order which has no a spanning tree with leaf degree at most . What is the maximum spectral radius (or signless Laplacian spectral radius) of Moreover, characterize all the extremal graphs.
Motivated by Kaneko’s theorem, we present tight spectral conditions for the existence of a spanning tree with leaf degree at most in a connected graph.
Theorem 1.5.
Let be a connected graph of order , where is an integer and . If then has a spanning tree with leaf degree at most unless .
2 Proof of Theorem 1.3
Before presenting our main result, we first show that an -closed connected graph must contain a large clique if its number of edges is large enough.
Lemma 2.1.
Let be an -closed connected graph of order , where is an integer. If
then .
Proof.
For any two vertices with degree at least , we have Note that is an -closed graph. Then any two vertices of degree at least must be adjacent in . Let be the vertex set of a maximum clique of which contains all vertices of degree at least and be the subgraph of induced by Let . Then . Next we will evaluate the value of
Case 1.
Note that
Claim 1.
and for each .
Proof.
Suppose to the contrary that or for each . Assume first that . Then we have for each . Note that is an -closed graph. Then is adjacent to every vertex of and hence is a larger clique, which contradicts the maximality of . Note that . If , then and hence is adjacent to every vertex of It follows that is a larger clique, a contradiction. ∎
Case 2.
Note that
Claim 2.
for each .
Proof.
Suppose that for each . Then we have for each . Note that is -closed. Then is adjacent to every vertex of . This implies that is a larger clique, a contradiction. ∎
By Cases 1 and 2, we know that and hence . This completes the proof. ∎
With the help of Lemma 2.1, we prove a technical sufficient condition in terms of to assure that has a spanning -ended-tree.
Lemma 2.2.
Let be a connected graph of order , where is an integer. If
then has a spanning -ended-tree unless .
Proof.
Suppose that has no a spanning -ended-tree, where and . Let . It suffices to prove that
By Theorem 1.2, has no a spanning -ended-tree either. Note that . Since , then . According to Lemma 2.1, we have .
Next we will characterize the structure of . Let be a maximum clique of and be a subgraph of induced by First we claim that . If , then . Obviously, has a spanning -ended-tree, a contradiction.
Claim 3.
.
Proof.
Recall that . It suffices to prove that . Assume to the contrary that . Let be an -clique of and be a subgraph of induced by . Then because of Note that is a connected graph. Then is also connected, and hence there exists a vertex which is adjacent to a vertex in We take a path such that Note that . Therefore, has a spanning tree with at most leaves, which means that has a spanning -ended-tree, a contradiction. So we have , as we claimed. ∎
By Claim 3, we know that . Let and .
Claim 4.
is an independent set.
Proof.
Assume that is adjacent to , where . By the connectedness of , there exists a path from to . Thus, we can take the path such that . Note that . Then has a spanning tree with at most leaves. That is, has a spanning -ended-tree, a contradiction. ∎
Claim 5.
for every
Proof.
Suppose there exists a vertex with According to Claim 4, without loss of generality, we can assume that is adjacent to and , where We take the path of length .
Furthermore, we claim that must be adjacent to for each . In fact, if is adjacent to or , then there exists a path or of length . If is adjacent to , where . Then there exists a path of length . By the above proof, we can always find a path with Note that . Hence has a spanning tree with at most leaves. This implies that has a spanning -ended-tree, a contradiction. Hence must be adjacent to for every .
At this time, we can observe that has a spanning tree such that , where denotes the set of leaves of Note that . Hence has a spanning -ended-tree, a contradiction. ∎
Claim 6.
where .
Proof.
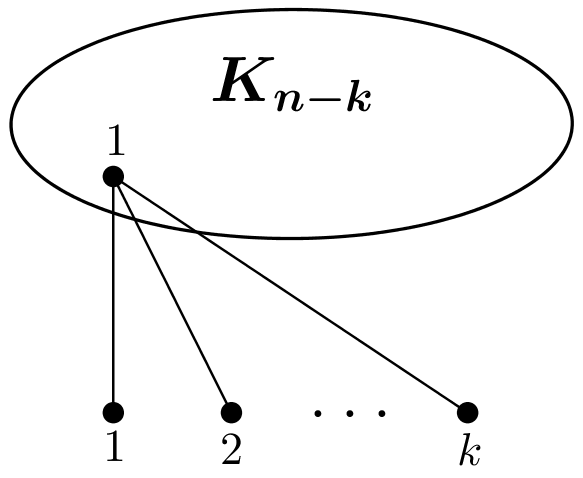
By the above claims, we know that (see Fig. 1). Note that the vertices of are only adjacent to a vertex of . Then the number of leaves of a spanning tree of is at least . This implies that has no a spanning -ended-tree. Note that and . Then we have Therefore, as desired. ∎
Next we will present important upper and lower bounds of and that will be used in our subsequent arguments.
Lemma 2.3 (Hong [16]).
Let be a connected graph with vertices. Then
Lemma 2.4 (Li and Ning [21]).
Let be a graph with non-empty edge set. Then
Moreover, if is connected, then equality holds if and only if is regular or semi-regular bipartite.
Lemma 2.6 (Li and Ning [21]).
Let be a graph with non-empty edge set. Then
Moreover, if is connected, then equality holds if and only if is regular or semi-regular bipartite.
Let and be two matrices. Define if for all and , and define if and .
Lemma 2.7 (Berman and Plemmons [1], Horn and Johnson [15]).
Let and be two matrices with the spectral radii and . If , then . Furthermore, if is irreducible and , then .
Now, we are in a position to present the proof of Theorem 1.3.
Proof of Theorem 1.3. (i) Let be a connected graph of order Suppose to the contrary that has no a spanning -ended-tree, where and By Lemma 2.7, we know that . By Lemma 2.3 and the assumption of Theorem 1.3, we have
Hence for . Let . By Lemma 2.2, we have Note that Then we have
Combining the assumption , we have From the end of the proof in Lemma 2.2, we know that has no a spanning -ended-tree. Hence as desired.
(ii) Let be a connected graph of order with Assume that has no a spanning -ended-tree, where is an integer. By Lemma 2.7, we have By Lemma 2.5 and the assumption, we have
We can deduce that for . Let . By Lemma 2.2, we have . Since , then
By the assumption, , and hence . Recall that has no a spanning -ended-tree. Hence
(iii) Let be a connected graph of order and be an integer. Let If then has a spanning -ended-tree. By Theorem 1.2, also has a spanning -ended-tree, and the result follows. Next we always assume that
Suppose to the contrary that has no a spanning -ended-tree. By Theorem 1.2, has no a spanning -ended-tree either. By Theorem 1.1, we have
for every pair of nonadjacent vertices and (always exists) of . Then we have
for every edge . Notice that every non-trivial component of has a vertex with the degree at least Then its order is at least , which implies that has exactly one non-trivial component and is the set of isolated vertices. Hence
for Since and , then we have and . Hence and That is, and . It is easy to see that
Note that is a convex function on . Then
for every edge . By the assumption and Lemma 2.4, we have
Then all the above inequalities must be equalities. This implies that , and there exists an edge such that and . Note that is a unique non-trivial component of Then
By Lemma 2.4, is regular or semi-regular bipartite.
Assume first that is semi-regular bipartite. By symmetry, we can assume that and for every edge . Hence It is easy to see that and thus since . Then we have , and hence , which contradicts that is connected.
Hence is regular. Then for each and hence . If , then is an -regular graph with vertices. Obviously, is obtained from by deleting a perfect matching of . Then is the perfect matching of which contradicts the connectedness of Next we consider . Then where . So we have . It is obvious that has no a spanning -ended-tree. Moveover, Hence .
(iv) Let By the beginning of the proof in (iii), we still assume that Suppose that has no a spanning -ended-tree. By Theorem 1.2, has no a spanning -ended-tree either. From the proof of (iii), we can obtain that has exactly one non-trivial component and
for each , where and . By the assumption and Lemma 2.6, we have
Then all the above inequalities must be equalities, which implies that , and there exists an edge such that . Furthermore, we have . By Lemma 2.6, is regular or semi-regular bipartite.
If is semi-regular bipartite, then with Since and , then we have . Hence where . Then with , which contradicts the connectedness of .
Hence is regular. Then is an -regular graph with vertices, where . It is easy to see that , and hence . Note that is an -regular graph with vertices. For convenience, let . Then we can write
where a contradiction. The proof is completed.
3 Proof of Theorem 1.5
Recall the nonnegative matrix of a graph . Let be the -spectral radius of Obviously, and Now, we are ready to present the proof of Theorem 1.5.
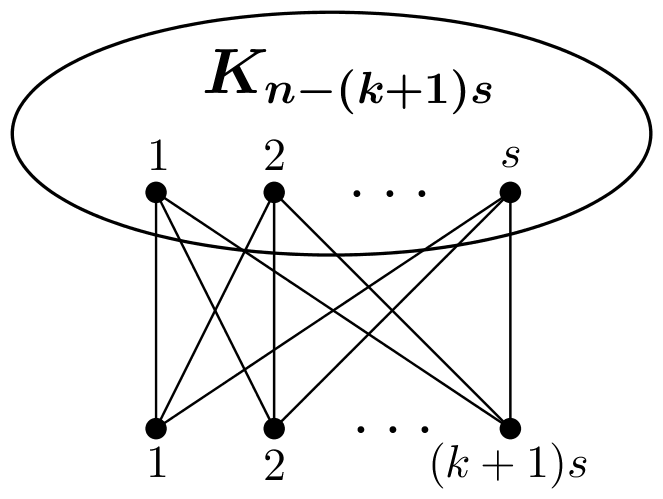
Proof of Theorem 1.5. Suppose to the contrary that has no a spanning tree with leaf degree at most for and . By Theorem 1.4, there exists some nonempty subset such that Let . Then is a spanning subgraph of (see Fig. 2). By Lemma 2.7, we have for . We distinguish the proof into the following two cases.
Case 1.
Then From the above, we know that
By the assumption , then we have Note that the vertices of are only adjacent to a vertex of . Then the leaf degree of any spanning tree of is at least . This implies that has no a spanning tree with leaf degree at most . Hence .
Case 2.
Note that and . Next we will discuss the different values of .
Subcase 2.1.
By Lemma 2.3, we have
Note that . Then Moreover, we claim that
In fact, let , by a direct calculation, we have
Note that is a monotonically increasing function on . Then
This implies that By the above proof, we have
since . On the other hand, by the assumption and Lemma 2.7, we have
a contradiction.
Subcase 2.2.
By Lemma 2.5, we have
Note that . Similar to the proof of Subcase 2.1, we can obtain that
Then
since . However, by the assumption, we have
a contradiction. We complete the proof.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- [1] A. Berman, R.J. Plemmons, Nonnegative matrices in the mathematical sciences, Academic Press, New York, 1979.
- [2] A.E. Brouwer, W.H. Haemers, Spectra of Graphs, Springer, Berlin, 2011.
- [3] H. Broersma, H. Tuinstra, Independence trees and Hamilton cycles, J. Graph Theory. 29 (1998) 227–237.
- [4] J.A. Bondy, V. Chvatal, A method in graph theory, Discrete Math. 15 (1976) 111–135.
- [5] J.A. Bondy, U.S.R. Murty, Graph Theory, Grad. Texts in Math. vol. 244, Springer, New York, 2008.
- [6] V. Chvátal, P. Erdős, A note on hamiltonian circuits, Discrete Math. 2 (1972) 111–113.
- [7] X.D. Chen, H.Q. Liu, F.L. Lu, M.D. Liu, Spanning -ended trees in quasi-claw-free graphs, Bull. Malays. Math. Sci. Soc. 43 (2020) 241–252.
- [8] Y. Chen, G.T. Chen, Z.Q. Hu, Spanning 3-ended trees in -connected -free graphs, Sci. China Math. 57 (2014) 1579–1586.
- [9] Y. Chen, P.H. Ha, D.D. Hanh, Spanning trees with at most 4 leaves in -free graphs, Discrete Math. 342 (2019) 2342–2349.
- [10] K.C. Das, Maximizing the sum of the squares of the degrees of a graph, Discrete Math. 285 (2004) 57–66.
- [11] D.D. Fan, S. Goryainov, X.Y. Huang, H.Q. Lin, The spanning -trees, perfect matchings and spectral radius of graphs, Linear Multilinear Algebra, 2021, doi.org/10.1080/03081087.2021.1985055.
- [12] E. Flandrin, T. Kaiser, R. Kužel, H. Li, Z. Ryjáček, Neighborhood unions and extremal spanning trees, Discrete Math. 308 (2008) 2343–2350.
- [13] L.H. Feng, G.H. Yu, On three conjectures involving the signless Laplacian spectral radius of graphs, Publ. Inst. Math. (Beograd) 85 (2009) 35–38.
- [14] M. Fiedler, V. Nikiforov, Spectral radius and Hamiltonicity of graphs, Linear Algebra Appl. 432 (2010) 2170–2173.
- [15] R.A. Horn, C.R. Johnson, Matrix analysis, Cambridge University Press, New York, 1986.
- [16] Y. Hong, A bound on the spectral raoius of graphs, Linear Algebra Appl. 108 (1988) 135–139.
- [17] A. Kaneko, Spanning trees with constraints on the leaf degree, Discrete Appl. Math. 115 (2001) 73–76.
- [18] A. Kyaw, Spanning trees with at most 3 leaves in -free graphs, Discrete Math. 309 (2009) 6146–6148.
- [19] A. Kyaw, Spanning trees with at most leaves in -free graphs, Discrete Math. 311 (2011) 2135–2142.
- [20] B. Ning, J. Ge, Spectral radius and Hamiltonian properties of graphs, Linear Multilinear Algebra 63 (2015) 1520–1530.
- [21] B.L. Li, B. Ning, Spectral analogues of Erdős’ and Moon-Moser’s theorems on Hamilton cycles, Linear Algebra Appl. 64 (2016) 2252–2269.
- [22] M. Lu, H.Q. Liu, F. Tian, Spectral radius and Hamiltonian graphs, Linear Algebra Appl. 437 (2012) 1670–1674.
- [23] M.H. Liu, H.-J. Lai, K.C. Das, Spectral results on Hamiltonian problem, Discrete Math. 342 (2019) 1718–1730.
- [24] R.F. Liu, W.C. Shiu, J. Xue, Sufficient spectral conditions on Hamiltonian and traceable graphs, Linear Algebra Appl. 467 (2015) 254–266.
- [25] O. Ore, Note on hamilton circuits, Amer. Math. Monthly 67 (1960) 55.
- [26] M. Tsugaki, T. Yamashita, Spanning trees with few leaves, Graphs Combin. 23 (2007) 585–598.
- [27] S. Win, On a conjecture of Las Vergnas concerning certain spanning trees in graphs, Resultate Math. 2 (1979) 215–224.
- [28] B. Zhou, Signless Laplacian spectral radius and Hamiltonicity, Linear Algebra Appl. 432 (2010) 566–570.
- [29] Q.N. Zhou, L.G. Wang, Some sufficient spectral conditions on Hamilton-connected and traceable graphs, Linear Multilinear Algebra 65 (2017) 224–234.