Spectral Bias in Practice: the Role of
Function Frequency in Generalization

Sara Fridovich-Keil
University of California, Berkeley
[email protected]
&Raphael Gontijo-Lopes
Google Brain
[email protected]
&Rebecca Roelofs
Google Brain
[email protected]
Work done as an intern and student researcher at Google Brain.

Abstract

Despite their ability to represent highly expressive functions, deep learning models seem to find simple solutions that generalize surprisingly well. Spectral bias – the tendency of neural networks to prioritize learning low frequency functions – is one possible explanation for this phenomenon, but so far spectral bias has primarily been observed in theoretical models and simplified experiments. In this work, we propose methodologies for measuring spectral bias in modern image classification networks on CIFAR-10 and ImageNet. We find that these networks indeed exhibit spectral bias, and that interventions that improve test accuracy on CIFAR-10 tend to produce learned functions that have higher frequencies overall but lower frequencies in the vicinity of examples from each class. This trend holds across variation in training time, model architecture, number of training examples, data augmentation, and self-distillation. We also explore the connections between function frequency and image frequency and find that spectral bias is sensitive to the low frequencies prevalent in natural images. On ImageNet, we find that learned function frequency also varies with internal class diversity, with higher frequencies on more diverse classes. Our work enables measuring and ultimately influencing the spectral behavior of neural networks used for image classification, and is a step towards understanding why deep models generalize well.

1 Introduction

Two fundamental questions in machine learning are why overparameterized models generalize and how to make them more robust to distribution shift and adversarial examples. Resolving both of these questions requires understanding how complex our models should be.

For instance, it is thought that overparameterized models generalize well because there are implicit regularizers that constrain the complexity of the learned functions. However, the precise nature of these implicit regularizers, and their importance in practice, remains unclear. As for how to achieve robustness, no consensus has emerged regarding function complexity. On the one hand, Cranko et al. [4] and Leino et al. [24] argue that Lipschitz smoothness of the learned function offers a guarantee of robustness; on the other, Shah et al. [37] and Madry et al. [25] argue that simplicity can be harmful and a robust model must actually be more complex than its non-robust counterpart.

One window into function complexity is spectral bias – the tendency of neural networks to learn low frequency (simple and smooth) functions first, then gradually increase the frequency (complexity) of the learned function as training proceeds. Foundational work in this area has shown theoretical evidence of spectral bias by analyzing convergence rates of neural networks towards functions of different frequencies [1, 35].

In practice, spectral bias is difficult to measure: the most direct method involves taking a Fourier transform with respect to the input, which is impractical to compute due to the high dimensionality of images. Early experimental work focused on low-dimensional synthetic data [1, 2] or used proxy measurements of spectral bias [44], for instance by inserting label noise of various frequencies during training [35]. However, the label noise method is limited to binary classification and involves modifying the training data, making it difficult to disentangle how other changes to the training data (such as augmentation) affect the spectral content of the learned function. It remains an open question whether modern neural networks exhibit spectral bias and what role it plays in generalization.

In this work, we investigate model complexity through the lens of spectral bias, by introducing experimental methods to study the frequency decomposition of the functions learned by modern image classification networks. We find that high-accuracy models learn a function that is high-frequency in regions between different image classes but low-frequency within each class, validating the intuition that a “good” model should have sharp decision boundaries to delineate different classes, but smooth behavior within each class.

Contributions.

We extend the label noise procedure of Rahaman et al. [35] to enable measuring spectral bias in multi-class classification via label smoothing, and apply this technique to understand the function frequencies present in high-accuracy models on CIFAR-10 [23]. We also introduce a second method for measuring the smoothness of a learned function via linear interpolation between test examples, and apply this method to both CIFAR-10 and ImageNet [8] models. We use this method to probe the effects of the training data on the learned function frequencies, and to distinguish the spectral content in paths between images from the same class (“within-class paths”) and paths between images from different classes (“between-class paths”).

We find that higher-test-accuracy models demonstrate greater separation in frequency content between these path types, with lower frequencies within-class and higher frequencies between-class. On CIFAR-10, this trend holds as we improve the model architecture, train longer, increase the size of the training dataset, improve the data augmentation strategy, and apply self-distillation. On ImageNet, this trend appears again as we consider models with more diverse architectures.

We also explore the relationship between image frequency and function frequency. By further extending the label noise methodology of Rahaman et al. [35] to study spectral bias in directions of interest through the input space, we find that CIFAR-10 models most readily learn functions of the low image frequencies common in natural images.

Via linear interpolation within ImageNet classes, we find that many models are higher-frequency in more internally diverse classes and lower-frequency in more internally consistent classes.

2 Related Work

Implicit bias. A common belief is that some form of implicit bias imposed by the training procedure or optimization algorithm may account for the generalization ability of overparameterized neural networks, and accordingly, much research has been directed towards understanding these implicit biases [38, 48, 22, 43, 14, 13, 15, 17, 3, 31, 29, 30, 26, 14, 20].

Spectral bias. Spectral bias, also called the frequency principle, is a form of implicit bias with much recent attention including theoretical and experimental approaches [34, 44, 35, 1, 50]. Basri et al. [1] studied spectral bias using a linear model of SGD training dynamics to show that models learn low frequency (simple) functions faster, assuming training data that is distributed uniformly on the hypersphere. Basri et al. [2] extended the analysis to consider nonuniformly spaced training data, and found that learning is faster where samples are denser; if sampling is nonuniform, then during training, the learned function will be higher frequency in regions with denser samples. Rahaman et al. [35] used a more direct analysis to show the same spectral bias toward low frequency functions and also posited that high frequency components of the learned function are most sensitive to perturbations in the model parameters, connecting back to the idea of flat optimization minima [30] or smooth loss landscape [27]. They proposed experimental methods to study spectral bias in image classification, but focused on a binary subset of the relatively simple MNIST dataset [9], with mean square error loss.

Our label smoothing experiments are a direct extension of Rahaman et al. [35] to multiclass classification with the more common cross-entropy loss. Our linear interpolation experiments are somewhat similar to the recently-proposed experimental methods in Zhang et al. [50], except that we sample along paths between images rather than in regions surrounding each image; this allows for a more global measurement of spectral bias that we apply to a broad and distinct set of training procedures beyond the double descent regime studient in Zhang et al. [50].

Model sensitivity to image frequency. While we focus on function frequency, prior research aimed to understand model sensitivity to image frequencies. Jo and Bengio [19] found that CNNs are sensitive to Fourier statistics of the training data, even those irrelevant to human viewers. Ortiz-Jiménez et al. [33] studied the image frequency bias induced by using a convolutional architecture, and Ortiz-Jiménez et al. [32] argued that models are sensitive primarily to discriminative Fourier directions in the training data. Yin et al. [46] introduced a procedure to measure the sensitivity of trained models to Fourier image perturbations, and applied it to study the effects of adversarial training and data augmentation. Our work adds to this line of research a study of the interplay between two notions of frequency: the function frequency involved in spectral bias, and the image frequencies present in the data.

3 Methodology

The goal of our work is to measure the complexity of neural network functions through the lens of frequency. In low dimensions, measuring the frequency decomposition of a function is straightforward and tractable: evaluate the function at dense, uniform sampling positions and compute its discrete Fourier transform. However, the function of interest in image classification is unavoidably high-dimensional, mapping images (with thousands of pixel values) to object classes. It would be intractable even to collect sufficient samples of this function to compute a discrete Fourier transform, let alone compute the transform itself. Instead, we employ two complementary approaches to measure informative proxies of this frequency decomposition.

3.1 Label Smoothing

The core idea for measuring function frequency introduced by Rahaman et al. [35] is to construct a sinusoid over the space of images, and to use that sinusoid as a form of label noise during training. Let $\mathcal{D}=\left\{({\bm{\mathsfit{X}}}_{i},{\bm{y}}_{i})\right\}_{i=1}^{n_{train}}$ be the training examples and $\mathcal{D_{\mathrm{valid}}}=\left\{({\bm{\mathsfit{X}}}_{j},{\bm{y}}_{j})\right\}_{j=1}^{n_{val}}$ be the validation examples, with ${\bm{\mathsfit{X}}}_{i}$ an image and ${\bm{y}}_{i}$ a one-hot class encoding, where $n_{train}$ is the number of training examples, $n_{val}$ is the number of validation examples, $d$ is the side length of an image (assumed to be square for simplicity), $c$ is the number of color channels, and $M$ is the number of classes, so ${\bm{\mathsfit{X}}}_{i}\in\mathbb{R}^{d\times d\times c}$ and ${\bm{y}}_{i}\in\mathbb{R}^{M}$ .

To extend this procedure to the multi-class setting, we add noise of various frequencies to an $M$ -dimensional label vector via label smoothing, originally introduced as a regularization approach in Szegedy et al. [39]. Intuitively, label smoothing removes some probability from the correct class and redistributes it equally among the remaining classes. Let $S:\mathbb{R}^{d\times d\times c}\rightarrow[0,1]$ be a noise function that maps an input image ${\bm{\mathsfit{X}}}_{i}$ to a scalar value between 0 and 1. We apply label smoothing to each label ${\bm{y}}_{i}$ , mapping it to $\bar{\bm{y}}_{i}={\bm{y}}_{i}(1-S({\bm{\mathsfit{X}}}_{i}))+\frac{1}{M}S({\bm{\mathsfit{X}}}_{i})$ to retain a valid probability distribution, as in Szegedy et al. [39] but with different functions $S$ . Rather than using label smoothing as a regularizer to improve performance, we use it as a form of variable frequency label noise to study spectral bias. We train from scratch using the original examples ${\bm{\mathsfit{X}}}_{i}$ and their smoothed labels $\bar{\bm{y}}_{i}$ . We evaluate on the validation images ${\bm{\mathsfit{X}}}_{j}$ , comparing to both their original one-hot labels ${\bm{y}}_{j}$ and smoothed labels $\bar{\bm{y}}_{j}={\bm{y}}_{j}(1-S({\bm{\mathsfit{X}}}_{j}))+\frac{1}{M}S({\bm{\mathsfit{X}}}_{j})$ . Our label smoothing experiments use the CIFAR-10 dataset [23], where $n_{train}=50000$ , $n_{val}=10000$ , $d=32$ , $c=3$ , and $M=10$ .

Refer to caption — Figure 1: Noise fitting shows when and how much a network fits a noise function of given frequency. At roughly epoch 150, noise fitting (Right), the difference between clean and noisy validation loss, exhibits a clear “dip” when the model begins to fit the noise function: training (Left) and validation (Center Left) loss on the perturbed function drop, while improvement stalls on clean validation data (Center Right). By comparing the minimum value of noise fitting achieved by different models throughout training (the gray line in the right plot), we can compare the relative degree to which different models fit noise functions of varying frequency. A model with higher min noise fitting more readily fits the noise function. Here, we train a wrn_32 model (wide-resnet with width 32) with radial wave label smoothing at frequency 0.04. For visual clarity, we apply exponential averaging to all curves.

This method is introduced in Figure 1. As training proceeds, we see both the training loss (between predictions and smoothed labels $\bar{\bm{y}}_{i}$ ) and noisy validation loss (between predictions and smoothed labels $\bar{\bm{y}}_{j}$ ) decrease. The clean validation loss (between predictions and one-hot labels ${\bm{y}}_{j}$ ), however, initially decreases but at some point in training plateaus or begins to increase. At this point, the model has begun to learn the noise function $S$ . Accordingly, we introduce noise fitting, defined as the difference between the validation loss on one-hot labels and the validation loss on labels smoothed with the same function $S$ that was applied to the training labels: $\textbf{noise fitting}=\textbf{clean validation loss}-\textbf{noisy validation loss}$ . We compare different models by computing the minimum noise fitting achieved throughout training. A model with higher min noise fitting more readily fits the noise function $S$ than a model with lower min noise fitting.

By choosing different functions $S$ , we can probe nuances of spectral bias. Typically (inspired by Rahaman et al. [35]) we choose a radial wave: $S({\bm{\mathsfit{X}}})=\alpha(1+\sin(2\pi f(\left\lVert{\bm{\mathsfit{X}}}\right\rVert-\mathbb{E}_{\mathcal{D}}{\left\lVert{\bm{\mathsfit{X}}}\right\rVert})))$ , where $\left\lVert{\bm{\mathsfit{X}}}\right\rVert$ denotes the Euclidean norm of the vectorized image, and $\alpha\in[0,0.5]$ to ensure that $S({\bm{\mathsfit{X}}})\in[0,1]$ . We can vary the frequency $f$ to understand spectral bias at this global scale. We can also choose more targeted functions $S$ ; for instance, if ${\bm{\mathsfit{V}}}$ is a direction of interest through the space of images (i.e. ${\bm{\mathsfit{V}}}$ is an image-shaped vector of unit norm), we can construct $S({\bm{\mathsfit{X}}})=\alpha(1+\sin(2\pi f\left\langle{\bm{\mathsfit{X}}},{\bm{\mathsfit{V}}}\right\rangle))$ . This allows us to vary both the frequency and direction of the noise function, to understand models’ learnability along different directions through image space.

However, label smoothing has a few limitations. Because it involves perturbing the training labels, it cannot directly study the interaction between the training dataset and spectral bias, such as the effects of data augmentation. It also requires retraining each model from scratch, with substantial investment of time and computational resources. We address these limitations with our linear interpolation technique in the next section.

3.2 Linear Interpolation

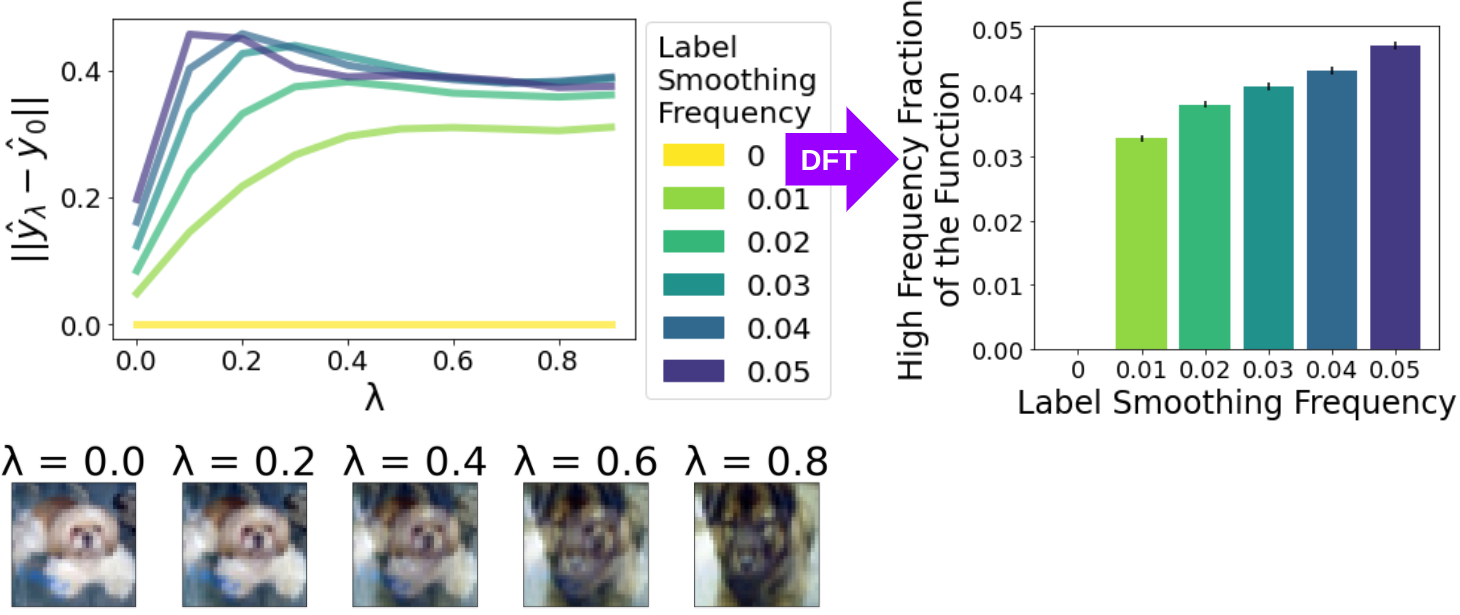
To complement the label smoothing approach, we also propose a methodology based on linear interpolation between validation images. Although we cannot take dense, regularly-spaced samples that cover the entire input (image) space, we can sample along specific paths and thereby glean glimpses into the spectral content of the learned function.

We consider two types of paths: those between images from the same class, and those between images from different classes. When considering paths between CIFAR-10 images in the same class, we choose 200 random, distinct pairs of validation images from each of the 10 CIFAR-10 classes and average over the paths defined by these pairs. We do the same for ImageNet, choosing 50 random, distinct paths for each of the 1000 ImageNet classes. When interpolating between CIFAR-10 classes, we choose 200 random, distinct validation image pairs from each of the 45 (10 choose 2) pairs of distinct classes, and average over the resulting paths; for ImageNet we choose 1000 random, distinct between-class paths, ensuring that each class is represented in exactly two paths.

For each pair of images $({\bm{\mathsfit{X}}}_{0},{\bm{\mathsfit{X}}}_{1})$ , we vary $\lambda\in[0,1]$ to trace out a path, where each image in the path is given by ${\bm{\mathsfit{X}}}_{\lambda}=\lambda{\bm{\mathsfit{X}}}_{1}+(1-\lambda){\bm{\mathsfit{X}}}_{0}$ . We choose $\lambda$ s so that the distance between adjacent images on the path is constant; each path may produce a different number of samples depending on the total distance between ${\bm{\mathsfit{X}}}_{0}$ and ${\bm{\mathsfit{X}}}_{1}$ . Figure 2 (Bottom Left) shows an illustrative example of two CIFAR-10 images and a corresponding interpolation path between them. For our experiments, we typically have 50 to 100 images along the interpolation path.

Relationship between interpolation and label smoothing experiments.

To validate our interpolation methodology, we consider the oracle function that maps directly from the interpolated image ${\bm{\mathsfit{X}}}_{\lambda}$ to the noised label used in our label smoothing experiments. We only consider within-class paths for this experiment, so that the original one-hot label (before smoothing) is fixed across the entire path, and the only change in the oracle function along the path is due to the noise function used in label smoothing. By increasing the frequency of the noise function, we create oracle functions with higher frequencies. We then verify that our interpolation measurement indeed measures higher frequencies on the higher frequency oracle functions.

In Figure 2 (Left), we show an example where we vary the label smoothing frequency from $f=0$ to $f=0.05$ . We plot the value of $\lambda$ along the interpolating path on the x axis, and the norm of the difference between the model output (softmax probabilities) on the interpolated image $\hat{{\bm{y}}}_{\lambda}$ and the model output on the original image $\hat{{\bm{y}}}_{0}$ on the y axis. This difference norm always starts at zero (although we plot it by averaging many paths over buckets in $\lambda$ , so the curves do not actually touch the axis), and tends to increase with $\lambda$ as the model predictions change along the interpolating path. The norm of the prediction difference allows us to visualize how smooth the function is along the interpolating path; smoother prediction difference norm indicates a lower frequency function.

To quantify the frequency of the oracle function along the interpolating path, we compute the per-class discrete Fourier transform (DFT). Letting $\{{\bm{\mathsfit{X}}}_{\lambda_{t}}\}_{t=1}^{T}$ denote the set of interpolated images, the DFT coefficient for frequency $f$ is given by $\hat{\textbf{Y}}_{f}[m]=\sum_{t=1}^{T}\hat{{\bm{y}}}_{\lambda_{t}}[m]\exp(-i2\pi ft)$ , where $i$ is the imaginary number and $m\in\{1,\ldots,M\}$ denotes the class. To summarize how the magnitudes of the DFT coefficients $\hat{\textbf{Y}}_{f}$ are distributed between low and high frequencies, we average the coefficient magnitudes for each of the classes and compute the fraction of the total average coefficient magnitude that is allocated to frequencies above a threshold (0.05). In Figure 2 (Right) we show this summary metric averaged over all within-class interpolating paths for the oracle functions, along with its standard error. In Figure 2 (Left), the higher frequency oracle functions have less smooth prediction norm differences, and in Figure 2 (Right), they have a higher fraction of DFT coefficient magnitudes in the high frequencies.

3.3 Data and Models

We use the CIFAR-10 [23] dataset of low-resolution (32 $\times$ 32) natural images from ten animal and object classes and the ImageNet [8] dataset of higher-resolution (224 $\times$ 224) natural images from 1000 classes. We consider a diversity of model architectures on CIFAR-10 (6 total) and ImageNet (10 total). See Section A.1 for more details on the data processing, models, and their accuracies.

4 Results on CIFAR-10

Throughout this section we show representative examples from our CIFAR-10 experiments; full results (on all six models we tested) are included in Section A.3.

4.1 Spectral Bias

We begin by applying our label smoothing methodology to find that modern image classification CNNs exhibit spectral bias, learning low frequency functions early in training and learning higher frequency functions as training proceeds. Note that Figure 3 (Left) shows spectral bias over a small but illustrative range of frequencies (the full range of frequencies we tested was 0 to 0.1); noise functions of sufficiently low frequency are fit almost immediately and noise functions of sufficiently high frequency are never learned during the 250 epochs of training we tested.

Using our linear interpolation methodology and distinguishing between within-class paths (in which both endpoint images are of the same class) and between-class paths (where the path must traverse a class boundary) in Figure 3 (Right), we find that this spectral bias is highly variable over the domain of images. In particular, while the learned function does increase in frequency for between-class paths, it decreases in frequency for within-class paths, indicating that the model is learning to cluster and separate the different classes. Throughout our CIFAR-10 experiments, we find that higher-accuracy models have greater separation between the frequencies of their within-class and between-class paths, with lower-frequency behavior inside each class and higher-frequency behavior in between.

4.2 Spectral Bias and Model Architecture

Although all models we tested exhibit spectral bias, we found that the precise nature of the bias depends on the choice of model. For example, with all else fixed, increasing the width of a model decreases its spectral bias, enabling it to more readily fit noise functions of a given frequency. This trend is evident in Figure 4 for the Wide-ResNet family (Left) and the Shake-Shake family (Center).

Although larger models learn high frequencies faster, we found that higher-accuracy models are not uniformly higher-frequency. Instead, using linear interpolation in Figure 4 (Right) we find that higher-accuracy models (ordered left to right by increasing test accuracy) are higher-frequency along between-class paths but lower-frequency along within-class paths, perhaps evident of a better class clustering.

4.3 Sensitivity to Natural Image Directions

Label smoothing with a radial wave offers a convenient global picture of spectral bias, by replacing the radial wave with other noise functions we can use the same methodology to test more localized aspects of spectral bias. We take a step in this direction by considering the family of noise functions $S({\bm{\mathsfit{X}}};k)=\alpha(1+\sin(2\pi f\left\langle{\bm{\mathsfit{X}}},{\bm{\mathsfit{F}}}_{k}\right\rangle))$ , where ${\bm{\mathsfit{F}}}_{k}$ is a diagonal Fourier basis image with frequency $k$ and the same dimensions as ${\bm{\mathsfit{X}}}$ , visualized in Figure 5 (Bottom).

We consider (a subset of) Fourier basis images because the Fourier spectra statistics of natural images are well studied (see, e.g. Tolhurst et al. [41]): natural images tend to be composed of Fourier basis images with amplitude proportional to their inverse spatial frequency. Indeed, in Figure 5 we find that shake_shake_96 is more sensitive to label smoothing in low image frequency directions.

This finding is consistent with theoretical predictions of Basri et al. [2] that models learn faster in regions of higher density of training examples: since low image frequencies are more common in natural images, the effective sampling density enjoyed by a noise function is higher in these directions. It is also possible that this bias is a byproduct of the lower Fourier magnitudes of high frequency components in natural images [36], or is inherent to the convolutional model architecture regardless of the data distribution [33], or that a combination of multiple effects is at play. Determining the precise cause of this image frequency finding is an interesting direction for further study.

4.4 Spectral Bias and Training Data

In our CIFAR-10 interpolation experiments, we consistently observed that variations in training that improve accuracy create greater disparity between the frequencies of within-class and between-class paths, with lower frequencies within-class and higher frequencies between-class. This trend is evident in Figure 3 (Right) as a model trains for more epochs and in Figure 4 (Right) as the model architecture improves. In Figure 6 we find that the same trend also holds as we train on more data (Left), apply more effective data augmentation (Center), or apply self-distillation (Right).

Training Set Size.

As shown in Figure 6 (Left) on wrn_160, we find that increasing the number of training examples increases the difference in frequency content between within-class interpolating paths and between-class interpolating paths. Training with more data makes our CIFAR-10 models behave lower-frequency within each class but higher-frequency between classes, perhaps indicating that the models are learning a better clustering of the classes as they are provided with additional data.

Data Augmentation.

Data augmentation is a common strategy to increase the effective training set size without the expense of actually collecting additional examples. In Figure 6 (Center) we consider the effects of Mixup (with strength 0.1) [49], AutoAugment [6], and RandAugment [5], each of which improves the final accuracy of the trained model (with RandAugment producing the most substantial benefits in our experiments, followed by AutoAugment and then Mixup). RandAugment and AutoAugment generate new images by applying geometric and lighting transformations, whereas Mixup linearly interpolates between pairs of existing images. Much like our experiments with training set size, we find that augmentations that improve accuracy more also produce greater frequency separation between within-class paths and between-class paths.

Mixup Strength.

Mixup augmentation [49] perturbs each batch of training data by randomly pairing the examples and perturbing each example towards its partner by an interpolation amount $\lambda$ drawn from a symmetric beta distribution (with the same $\lambda$ used for all examples in the batch). We refer to the parameter of this beta distribution as the Mixup strength, as it controls the degree to which the augmented images tend to lie close to an original training image or close to the average of two training images. A parameter of 0 corresponds to no augmentation ( $\lambda=0$ or $\lambda=1$ , always using the original images), a parameter of 1 corresponds to the uniform distribution over $\lambda\in[0,1]$ , and a parameter of $\infty$ corresponds to $\lambda=0.5$ , the exact midpoint between a pair of training images. Figure 6 (Center) compares a range of Mixup strengths and finds that relatively low values that only slightly perturb the original images tend to produce greater frequency separation (and higher test accuracy), whereas perturbing the images too much with stronger Mixup has the opposite effect on both frequency separation and accuracy. Of note, the range of Mixup strengths that increase or do not affect frequency separation in our experiments are well aligned with those recommended by the original authors [49]: 0.1 to 0.4.

Self-Distillation.

Finally, we consider the effect of self-distillation on the frequency content of the learned function. In self-distillation, a “teacher” model is trained with some form of strong regularization, in our case a combination of weight decay and early stopping based on training loss. A “student” model with the same architecture is then trained from scratch to fit the pseudolabels produced by the teacher Prior research [11] found that this procedure can train student models that outperform both their teachers and a baseline model trained as normal.

Prior research has also sought to understand the mechanism behind self-distillation. Mobahi et al. [28] finds that self-distillation acts as a regularizer by limiting the basis functions available to the student to learn. We complement their theoretical work with our interpolation experimental methodology in Figure 6 (Right), where indeed we find that the student model learns a greater frequency separation between within-class and between-class paths than its teacher, while also achieving higher test accuracy. We conjecture that this effect is analogous to low-pass prefiltering common in digital signal processing: a high-frequency noise function that we cannot adequately sample is first smoothed (in this case by being approximated by a regularized teacher) and then it can be modeled via samples without further loss in fidelity. Without this prefiltering, our samples are inadequate to capture the complexity of the noise function, so we reconstruct an imperfect version corrupted by aliasing.

5 Results on ImageNet

Finally, we apply our linear interpolation methodology to study the frequency content of a range of pretrained models on ImageNet [8]. Here we show results on ResNet50; results on all ten models we tested on ImageNet are included in Section A.4.

5.1 Training Time

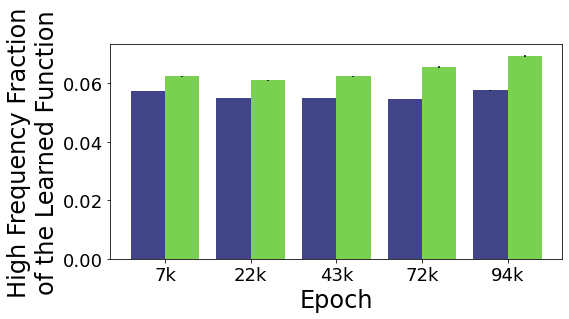
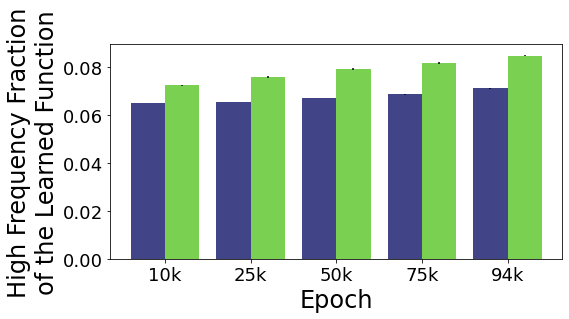
As we observed for CIFAR-10, our ImageNet models tend to increase the frequency gap between the two types of interpolating paths as training proceeds, with lower-frequencies within-class and higher-frequencies between-class. We visualize this trend for ResNet50 in Figure 7 (Left). For our CIFAR-10 models, this increase in frequency difference between path types was achieved by a combination of increasing the average high frequency content on between-class paths and decreasing the average high frequency content on within-class paths. On ImageNet, we again find that average frequency content on between-class paths increases during training, but that within-class frequencies sometimes decrease during training (e.g. for ResNets) but sometimes increase (slower than between-class paths) during training (e.g. for CoATNets). We speculate that the trend of decreasing within-class frequency as training time progresses is less consistent on ImageNet than CIFAR-10 because, as we explore in the next section, ImageNet classes are more internally diverse than CIFAR-10 classes.

5.2 Class Coherence

In addition to containing 100 $\times$ as many classes as CIFAR-10, ImageNet classes can also be more internally diverse. This notion of within-class “consistency” is captured by C-Scores [18], which assign to each training example a value between 0 and 1 denoting how typical that example is. One way of capturing the internal consistency or diversity of a class is by studying the distribution of its C-Scores. In Figure 7 (Right) we plot the mean and standard deviation of these scores for each of the 1000 ImageNet classes in gray and highlight the 10 classes whose ResNet50 interpolating paths between validation images are most high-frequency (red stars) and least high-frequency (blue squares). We find that ResNet50 is lower-frequency on more internally consistent classes and higher-frequency on more diverse classes, supporting the intuition that more diverse classes require more complex functions.

6 Conclusions

In this paper, we introduced two methods to measure spectral bias in modern image classification neural networks, and applied these methods towards the central question:

What kinds of function frequencies are needed for modern neural networks to generalize?

Specifically, we applied these methods to examine the impact of a variety of training choices on the learned frequencies. On CIFAR-10, we found that higher-accuracy models typically have greater frequency separation between within-class and between-class paths, with lower frequencies within-class and higher frequencies between-class. This trend holds regardless of whether high accuracy is achieved through longer training, choice of model architecture, increase in dataset size, data augmentation, or self-distillation. On ImageNet, we again found that this frequency separation increases during training, and noted that models are higher-frequency within more internally diverse classes. Our experimental methods offer a window onto the frequency structure of neural networks for image classification, and its relationship to model performance. In particular, although our primary goal is to improve our understanding of how neural networks generalize, our work is likely to have practical implications for improving generalization as well as robustness to image perturbations and distribution shifts. We hope that future work realizes these implications by applying our methods to study the spectral bias of robust models, and to induce model robustness directly, perhaps by incorporating our metrics as regularizers during training. Future work may also benefit from extending our methodology to interpolating paths that adhere more closely to the hypothesized manifold of natural images, such as those produced by generative networks [21, 40].

Reproducibility Statement

Our CIFAR-10 code is available at https://github.com/google-research/google-research/tree/master/spectral_bias; for ImageNet we apply the same interpolation method to pre-cropped images and pretrained model checkpoints. Our work uses the publicly-available CIFAR-10 [23] and ImageNet [8] datasets.

Acknowledgments

Many thanks to Yasaman Bahri, Ekin Dogus Cubuk, Hossein Mobahi, Michael Mozer, Maithra Raghu, Samuel Schoenholz, Jonathon Shlens, and Piotr Teterwak for productive conversations and helpful pointers.

SFK is also funded by NSF GRFP.

References

Basri et al. [2019] Ronen Basri, David W. Jacobs, Yoni Kasten, and Shira Kritchman. The convergence rate of neural networks for learned functions of different frequencies. In Hanna M. Wallach, Hugo Larochelle, Alina Beygelzimer, Florence d’Alché-Buc, Emily B. Fox, and Roman Garnett, editors, Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, pages 4763–4772, 2019. URL https://proceedings.neurips.cc/paper/2019/hash/5ac8bb8a7d745102a978c5f8ccdb61b8-Abstract.html.
Basri et al. [2020] Ronen Basri, Meirav Galun, Amnon Geifman, David W. Jacobs, Yoni Kasten, and Shira Kritchman. Frequency bias in neural networks for input of non-uniform density. In Proceedings of the 37th International Conference on Machine Learning, ICML 2020, 13-18 July 2020, Virtual Event, volume 119 of Proceedings of Machine Learning Research, pages 685–694. PMLR, 2020. URL http://proceedings.mlr.press/v119/basri20a.html.
Belkin et al. [2018] Mikhail Belkin, Siyuan Ma, and Soumik Mandal. To understand deep learning we need to understand kernel learning. In Jennifer G. Dy and Andreas Krause, editors, Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, July 10-15, 2018, volume 80 of Proceedings of Machine Learning Research, pages 540–548. PMLR, 2018. URL http://proceedings.mlr.press/v80/belkin18a.html.
Cranko et al. [2018] Zac Cranko, Simon Kornblith, Zhan Shi, and Richard Nock. Lipschitz networks and distributional robustness. CoRR, abs/1809.01129, 2018. URL http://arxiv.org/abs/1809.01129.
Cubuk et al. [2020] Ekin D. Cubuk, Barret Zoph, Jonathon Shlens, and Quoc V. Le. Randaugment: Practical automated data augmentation with a reduced search space. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR Workshops 2020, Seattle, WA, USA, June 14-19, 2020, pages 3008–3017. Computer Vision Foundation / IEEE, 2020. doi: 10.1109/CVPRW50498.2020.00359. URL https://openaccess.thecvf.com/content_CVPRW_2020/html/w40/Cubuk_Randaugment_Practical_Automated_Data_Augmentation_With_a_Reduced_Search_Space_CVPRW_2020_paper.html.
Cubuk et al. [2018] Ekin Dogus Cubuk, Barret Zoph, Dandelion Mané, Vijay Vasudevan, and Quoc V. Le. Autoaugment: Learning augmentation policies from data. CoRR, abs/1805.09501, 2018. URL http://arxiv.org/abs/1805.09501.
Dai et al. [2021] Zihang Dai, Hanxiao Liu, Quoc V. Le, and Mingxing Tan. Coatnet: Marrying convolution and attention for all data sizes. In Marc’Aurelio Ranzato, Alina Beygelzimer, Yann N. Dauphin, Percy Liang, and Jennifer Wortman Vaughan, editors, Advances in Neural Information Processing Systems 34: Annual Conference on Neural Information Processing Systems 2021, NeurIPS 2021, December 6-14, 2021, virtual, pages 3965–3977, 2021. URL https://proceedings.neurips.cc/paper/2021/hash/20568692db622456cc42a2e853ca21f8-Abstract.html.
Deng et al. [2009] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. Imagenet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition, pages 248–255. Ieee, 2009.
Deng [2012] Li Deng. The MNIST database of handwritten digit images for machine learning research [best of the web]. IEEE Signal Process. Mag., 29(6):141–142, 2012. doi: 10.1109/MSP.2012.2211477. URL https://doi.org/10.1109/MSP.2012.2211477.
Dosovitskiy et al. [2021] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, Jakob Uszkoreit, and Neil Houlsby. An image is worth 16x16 words: Transformers for image recognition at scale. In 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, Austria, May 3-7, 2021. OpenReview.net, 2021. URL https://openreview.net/forum?id=YicbFdNTTy.
Furlanello et al. [2018] Tommaso Furlanello, Zachary Chase Lipton, Michael Tschannen, Laurent Itti, and Anima Anandkumar. Born-again neural networks. In Jennifer G. Dy and Andreas Krause, editors, Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, July 10-15, 2018, volume 80 of Proceedings of Machine Learning Research, pages 1602–1611. PMLR, 2018. URL http://proceedings.mlr.press/v80/furlanello18a.html.
Gastaldi [2017] Xavier Gastaldi. Shake-shake regularization. CoRR, abs/1705.07485, 2017. URL http://arxiv.org/abs/1705.07485.
Gunasekar et al. [2018a] Suriya Gunasekar, Jason D. Lee, Daniel Soudry, and Nathan Srebro. Characterizing implicit bias in terms of optimization geometry. In Jennifer G. Dy and Andreas Krause, editors, Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, July 10-15, 2018, volume 80 of Proceedings of Machine Learning Research, pages 1827–1836. PMLR, 2018a. URL http://proceedings.mlr.press/v80/gunasekar18a.html.
Gunasekar et al. [2018b] Suriya Gunasekar, Jason D. Lee, Daniel Soudry, and Nati Srebro. Implicit bias of gradient descent on linear convolutional networks. In Samy Bengio, Hanna M. Wallach, Hugo Larochelle, Kristen Grauman, Nicolò Cesa-Bianchi, and Roman Garnett, editors, Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, December 3-8, 2018, Montréal, Canada, pages 9482–9491, 2018b. URL https://proceedings.neurips.cc/paper/2018/hash/0e98aeeb54acf612b9eb4e48a269814c-Abstract.html.
Hardt et al. [2016] Moritz Hardt, Ben Recht, and Yoram Singer. Train faster, generalize better: Stability of stochastic gradient descent. In Maria-Florina Balcan and Kilian Q. Weinberger, editors, Proceedings of the 33nd International Conference on Machine Learning, ICML 2016, New York City, NY, USA, June 19-24, 2016, volume 48 of JMLR Workshop and Conference Proceedings, pages 1225–1234. JMLR.org, 2016. URL http://proceedings.mlr.press/v48/hardt16.html.
He et al. [2016] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, June 27-30, 2016, pages 770–778. IEEE Computer Society, 2016. doi: 10.1109/CVPR.2016.90. URL https://doi.org/10.1109/CVPR.2016.90.
Hoffer et al. [2017] Elad Hoffer, Itay Hubara, and Daniel Soudry. Train longer, generalize better: closing the generalization gap in large batch training of neural networks. In Isabelle Guyon, Ulrike von Luxburg, Samy Bengio, Hanna M. Wallach, Rob Fergus, S. V. N. Vishwanathan, and Roman Garnett, editors, Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, pages 1731–1741, 2017. URL https://proceedings.neurips.cc/paper/2017/hash/a5e0ff62be0b08456fc7f1e88812af3d-Abstract.html.
Jiang et al. [2021] Ziheng Jiang, Chiyuan Zhang, Kunal Talwar, and Michael C. Mozer. Characterizing structural regularities of labeled data in overparameterized models. In Marina Meila and Tong Zhang, editors, Proceedings of the 38th International Conference on Machine Learning, ICML 2021, 18-24 July 2021, Virtual Event, volume 139 of Proceedings of Machine Learning Research, pages 5034–5044. PMLR, 2021. URL http://proceedings.mlr.press/v139/jiang21k.html.
Jo and Bengio [2017] Jason Jo and Yoshua Bengio. Measuring the tendency of cnns to learn surface statistical regularities. CoRR, abs/1711.11561, 2017. URL http://arxiv.org/abs/1711.11561.
Kalimeris et al. [2019] Dimitris Kalimeris, Gal Kaplun, Preetum Nakkiran, Benjamin L. Edelman, Tristan Yang, Boaz Barak, and Haofeng Zhang. SGD on neural networks learns functions of increasing complexity. In Hanna M. Wallach, Hugo Larochelle, Alina Beygelzimer, Florence d’Alché-Buc, Emily B. Fox, and Roman Garnett, editors, Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, pages 3491–3501, 2019. URL https://proceedings.neurips.cc/paper/2019/hash/b432f34c5a997c8e7c806a895ecc5e25-Abstract.html.
Karras et al. [2020] Tero Karras, Samuli Laine, Miika Aittala, Janne Hellsten, Jaakko Lehtinen, and Timo Aila. Analyzing and improving the image quality of stylegan. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2020, Seattle, WA, USA, June 13-19, 2020, pages 8107–8116. Computer Vision Foundation / IEEE, 2020. doi: 10.1109/CVPR42600.2020.00813. URL https://openaccess.thecvf.com/content_CVPR_2020/html/Karras_Analyzing_and_Improving_the_Image_Quality_of_StyleGAN_CVPR_2020_paper.html.
Keskar et al. [2017] Nitish Shirish Keskar, Dheevatsa Mudigere, Jorge Nocedal, Mikhail Smelyanskiy, and Ping Tak Peter Tang. On large-batch training for deep learning: Generalization gap and sharp minima. In 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings. OpenReview.net, 2017. URL https://openreview.net/forum?id=H1oyRlYgg.
[23] Alex Krizhevsky, Vinod Nair, and Geoffrey Hinton. Cifar-10 (canadian institute for advanced research). URL http://www.cs.toronto.edu/~kriz/cifar.html.
Leino et al. [2021] Klas Leino, Zifan Wang, and Matt Fredrikson. Globally-robust neural networks. In Marina Meila and Tong Zhang, editors, Proceedings of the 38th International Conference on Machine Learning, ICML 2021, 18-24 July 2021, Virtual Event, volume 139 of Proceedings of Machine Learning Research, pages 6212–6222. PMLR, 2021. URL http://proceedings.mlr.press/v139/leino21a.html.
Madry et al. [2018] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. Towards deep learning models resistant to adversarial attacks. In 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net, 2018. URL https://openreview.net/forum?id=rJzIBfZAb.
Mania et al. [2019] Horia Mania, John Miller, Ludwig Schmidt, Moritz Hardt, and Benjamin Recht. Model similarity mitigates test set overuse. In Hanna M. Wallach, Hugo Larochelle, Alina Beygelzimer, Florence d’Alché-Buc, Emily B. Fox, and Roman Garnett, editors, Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, pages 9993–10002, 2019. URL https://proceedings.neurips.cc/paper/2019/hash/48237d9f2dea8c74c2a72126cf63d933-Abstract.html.
Mehmeti-Göpel et al. [2021] Christian H. X. Ali Mehmeti-Göpel, David Hartmann, and Michael Wand. Ringing relus: Harmonic distortion analysis of nonlinear feedforward networks. In 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, Austria, May 3-7, 2021. OpenReview.net, 2021. URL https://openreview.net/forum?id=TaYhv-q1Xit.
Mobahi et al. [2020] Hossein Mobahi, Mehrdad Farajtabar, and Peter L. Bartlett. Self-distillation amplifies regularization in hilbert space. In Hugo Larochelle, Marc’Aurelio Ranzato, Raia Hadsell, Maria-Florina Balcan, and Hsuan-Tien Lin, editors, Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual, 2020. URL https://proceedings.neurips.cc/paper/2020/hash/2288f691b58edecadcc9a8691762b4fd-Abstract.html.
Neyshabur et al. [2015] Behnam Neyshabur, Ryota Tomioka, and Nathan Srebro. In search of the real inductive bias: On the role of implicit regularization in deep learning. In Yoshua Bengio and Yann LeCun, editors, 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Workshop Track Proceedings, 2015. URL http://arxiv.org/abs/1412.6614.
Neyshabur et al. [2017] Behnam Neyshabur, Srinadh Bhojanapalli, David McAllester, and Nati Srebro. Exploring generalization in deep learning. In Isabelle Guyon, Ulrike von Luxburg, Samy Bengio, Hanna M. Wallach, Rob Fergus, S. V. N. Vishwanathan, and Roman Garnett, editors, Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, pages 5947–5956, 2017. URL https://proceedings.neurips.cc/paper/2017/hash/10ce03a1ed01077e3e289f3e53c72813-Abstract.html.
Neyshabur et al. [2018] Behnam Neyshabur, Zhiyuan Li, Srinadh Bhojanapalli, Yann LeCun, and Nathan Srebro. Towards understanding the role of over-parametrization in generalization of neural networks. CoRR, abs/1805.12076, 2018. URL http://arxiv.org/abs/1805.12076.
Ortiz-Jiménez et al. [2020a] Guillermo Ortiz-Jiménez, Apostolos Modas, Seyed-Mohsen Moosavi-Dezfooli, and Pascal Frossard. Hold me tight! influence of discriminative features on deep network boundaries. In Hugo Larochelle, Marc’Aurelio Ranzato, Raia Hadsell, Maria-Florina Balcan, and Hsuan-Tien Lin, editors, Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual, 2020a. URL https://proceedings.neurips.cc/paper/2020/hash/1ea97de85eb634d580161c603422437f-Abstract.html.
Ortiz-Jiménez et al. [2020b] Guillermo Ortiz-Jiménez, Apostolos Modas, Seyed-Mohsen Moosavi-Dezfooli, and Pascal Frossard. Neural anisotropy directions. In Hugo Larochelle, Marc’Aurelio Ranzato, Raia Hadsell, Maria-Florina Balcan, and Hsuan-Tien Lin, editors, Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual, 2020b. URL https://proceedings.neurips.cc/paper/2020/hash/cff02a74da64d145a4aed3a577a106ab-Abstract.html.
Oymak et al. [2019] Samet Oymak, Zalan Fabian, Mingchen Li, and Mahdi Soltanolkotabi. Generalization guarantees for neural networks via harnessing the low-rank structure of the jacobian. CoRR, abs/1906.05392, 2019. URL http://arxiv.org/abs/1906.05392.
Rahaman et al. [2019] Nasim Rahaman, Aristide Baratin, Devansh Arpit, Felix Draxler, Min Lin, Fred A. Hamprecht, Yoshua Bengio, and Aaron C. Courville. On the spectral bias of neural networks. In Kamalika Chaudhuri and Ruslan Salakhutdinov, editors, Proceedings of the 36th International Conference on Machine Learning, ICML 2019, 9-15 June 2019, Long Beach, California, USA, volume 97 of Proceedings of Machine Learning Research, pages 5301–5310. PMLR, 2019. URL http://proceedings.mlr.press/v97/rahaman19a.html.
Schwarz et al. [2021] Katja Schwarz, Yiyi Liao, and Andreas Geiger. On the frequency bias of generative models. In Marc’Aurelio Ranzato, Alina Beygelzimer, Yann N. Dauphin, Percy Liang, and Jennifer Wortman Vaughan, editors, Advances in Neural Information Processing Systems 34: Annual Conference on Neural Information Processing Systems 2021, NeurIPS 2021, December 6-14, 2021, virtual, pages 18126–18136, 2021. URL https://proceedings.neurips.cc/paper/2021/hash/96bf57c6ff19504ff145e2a32991ea96-Abstract.html.
Shah et al. [2020] Harshay Shah, Kaustav Tamuly, Aditi Raghunathan, Prateek Jain, and Praneeth Netrapalli. The pitfalls of simplicity bias in neural networks. In Hugo Larochelle, Marc’Aurelio Ranzato, Raia Hadsell, Maria-Florina Balcan, and Hsuan-Tien Lin, editors, Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual, 2020. URL https://proceedings.neurips.cc/paper/2020/hash/6cfe0e6127fa25df2a0ef2ae1067d915-Abstract.html.
Soudry et al. [2018] Daniel Soudry, Elad Hoffer, Mor Shpigel Nacson, Suriya Gunasekar, and Nathan Srebro. The implicit bias of gradient descent on separable data. J. Mach. Learn. Res., 19:70:1–70:57, 2018. URL http://jmlr.org/papers/v19/18-188.html.
Szegedy et al. [2016] Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jonathon Shlens, and Zbigniew Wojna. Rethinking the inception architecture for computer vision. In 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, June 27-30, 2016, pages 2818–2826. IEEE Computer Society, 2016. doi: 10.1109/CVPR.2016.308. URL https://doi.org/10.1109/CVPR.2016.308.
Teterwak et al. [2021] Piotr Teterwak, Chiyuan Zhang, Dilip Krishnan, and Michael C. Mozer. Understanding invariance via feedforward inversion of discriminatively trained classifiers. In Marina Meila and Tong Zhang, editors, Proceedings of the 38th International Conference on Machine Learning, ICML 2021, 18-24 July 2021, Virtual Event, volume 139 of Proceedings of Machine Learning Research, pages 10225–10235. PMLR, 2021. URL http://proceedings.mlr.press/v139/teterwak21a.html.
Tolhurst et al. [1992] DJ Tolhurst, Y_ Tadmor, and Tang Chao. Amplitude spectra of natural images. Ophthalmic and Physiological Optics, 12(2):229–232, 1992.
Touvron et al. [2021] Hugo Touvron, Matthieu Cord, Matthijs Douze, Francisco Massa, Alexandre Sablayrolles, and Hervé Jégou. Training data-efficient image transformers & distillation through attention. In Marina Meila and Tong Zhang, editors, Proceedings of the 38th International Conference on Machine Learning, ICML 2021, 18-24 July 2021, Virtual Event, volume 139 of Proceedings of Machine Learning Research, pages 10347–10357. PMLR, 2021. URL http://proceedings.mlr.press/v139/touvron21a.html.
Wilson et al. [2017] Ashia C. Wilson, Rebecca Roelofs, Mitchell Stern, Nati Srebro, and Benjamin Recht. The marginal value of adaptive gradient methods in machine learning. In Isabelle Guyon, Ulrike von Luxburg, Samy Bengio, Hanna M. Wallach, Rob Fergus, S. V. N. Vishwanathan, and Roman Garnett, editors, Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, pages 4148–4158, 2017. URL https://proceedings.neurips.cc/paper/2017/hash/81b3833e2504647f9d794f7d7b9bf341-Abstract.html.
Xu et al. [2019] Zhi-Qin John Xu, Yaoyu Zhang, and Yanyang Xiao. Training behavior of deep neural network in frequency domain. In Tom Gedeon, Kok Wai Wong, and Minho Lee, editors, Neural Information Processing - 26th International Conference, ICONIP 2019, Sydney, NSW, Australia, December 12-15, 2019, Proceedings, Part I, volume 11953 of Lecture Notes in Computer Science, pages 264–274. Springer, 2019. doi: 10.1007/978-3-030-36708-4\_22. URL https://doi.org/10.1007/978-3-030-36708-4_22.
Yamada et al. [2019] Yoshihiro Yamada, Masakazu Iwamura, Takuya Akiba, and Koichi Kise. Shakedrop regularization for deep residual learning. IEEE Access, 7:186126–186136, 2019. doi: 10.1109/ACCESS.2019.2960566. URL https://doi.org/10.1109/ACCESS.2019.2960566.
Yin et al. [2019] Dong Yin, Raphael Gontijo Lopes, Jonathon Shlens, Ekin Dogus Cubuk, and Justin Gilmer. A fourier perspective on model robustness in computer vision. In Hanna M. Wallach, Hugo Larochelle, Alina Beygelzimer, Florence d’Alché-Buc, Emily B. Fox, and Roman Garnett, editors, Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, pages 13255–13265, 2019. URL https://proceedings.neurips.cc/paper/2019/hash/b05b57f6add810d3b7490866d74c0053-Abstract.html.
Zagoruyko and Komodakis [2016] Sergey Zagoruyko and Nikos Komodakis. Wide residual networks. In Richard C. Wilson, Edwin R. Hancock, and William A. P. Smith, editors, Proceedings of the British Machine Vision Conference 2016, BMVC 2016, York, UK, September 19-22, 2016. BMVA Press, 2016. URL http://www.bmva.org/bmvc/2016/papers/paper087/index.html.
Zhang et al. [2021a] Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. Understanding deep learning (still) requires rethinking generalization. Commun. ACM, 64(3):107–115, 2021a. doi: 10.1145/3446776. URL https://doi.org/10.1145/3446776.
Zhang et al. [2018] Hongyi Zhang, Moustapha Cissé, Yann N. Dauphin, and David Lopez-Paz. mixup: Beyond empirical risk minimization. In 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net, 2018. URL https://openreview.net/forum?id=r1Ddp1-Rb.
Zhang et al. [2021b] Xiao Zhang, Haoyi Xiong, and Dongrui Wu. Rethink the connections among generalization, memorization, and the spectral bias of dnns. In Zhi-Hua Zhou, editor, Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, IJCAI 2021, Virtual Event / Montreal, Canada, 19-27 August 2021, pages 3392–3398. ijcai.org, 2021b. doi: 10.24963/ijcai.2021/467. URL https://doi.org/10.24963/ijcai.2021/467.

Checklist

1.
For all authors…
1. (a)
  
  Do the main claims made in the abstract and introduction accurately reflect the paper’s contributions and scope? [Yes]
2. (b)
  
  Did you describe the limitations of your work? [Yes] Limitations of the label smoothing methodology are discussed at the end of Section 3.1. Limitations of the interpolation methodology are discussed in Section A.2.
3. (c)
  
  Did you discuss any potential negative societal impacts of your work? [N/A]
4. (d)
  
  Have you read the ethics review guidelines and ensured that your paper conforms to them? [Yes]
2.
If you are including theoretical results…
1. (a)
  
  Did you state the full set of assumptions of all theoretical results? [N/A]
2. (b)
  
  Did you include complete proofs of all theoretical results? [N/A]
3.
If you ran experiments…
1. (a)
  
  Did you include the code, data, and instructions needed to reproduce the main experimental results (either in the supplemental material or as a URL)? [Yes] Code is provided on GitHub.
2. (b)
  
  Did you specify all the training details (e.g., data splits, hyperparameters, how they were chosen)? [Yes] Some of these details are provided in the appendix, and the rest are evident from the code.
3. (c)
  
  Did you report error bars (e.g., with respect to the random seed after running experiments multiple times)? [Yes] Standard errors are reported for linear interpolation experiments.
4. (d)
  
  Did you include the total amount of compute and the type of resources used (e.g., type of GPUs, internal cluster, or cloud provider)? [No] These results did require substantial GPU compute, but we do not quantify the exact amount. Each point in a label smoothing figure required training a model from scratch, and each value in an interpolation figure required evaluating a pretrained model on hundreds of thousands of images.
4.
If you are using existing assets (e.g., code, data, models) or curating/releasing new assets…
1. (a)
  
  If your work uses existing assets, did you cite the creators? [Yes] We cite the creators of CIFAR-10 [23] and ImageNet [8], the image datasets we use, as well as the creators of the models we use [47, 12, 45, 6, 16, 10, 42, 7].
2. (b)
  
  Did you mention the license of the assets? [No] The licenses of each dataset and model we use are available on their websites.
3. (c)
  
  Did you include any new assets either in the supplemental material or as a URL? [N/A]
4. (d)
  
  Did you discuss whether and how consent was obtained from people whose data you’re using/curating? [N/A]
5. (e)
  
  Did you discuss whether the data you are using/curating contains personally identifiable information or offensive content? [N/A]
5.
If you used crowdsourcing or conducted research with human subjects…
1. (a)
  
  Did you include the full text of instructions given to participants and screenshots, if applicable? [N/A]
2. (b)
  
  Did you describe any potential participant risks, with links to Institutional Review Board (IRB) approvals, if applicable? [N/A]
3. (c)
  
  Did you include the estimated hourly wage paid to participants and the total amount spent on participant compensation? [N/A]

Appendix A Appendix

A.1 Data, Models, and Model Accuracies

Images are pixel-wise normalized by the mean and standard deviation of the training images for each dataset, and for ImageNet all images are center cropped and resized to 224 $\times$ 224; this preprocessing is done before any interpolating paths are constructed. For CIFAR-10, we consider six different convolutional neural networks: two Wide-ResNets [47] of different sizes (wrn_32 and wrn_160), three Shake-Shake regularized networks [12] of different sizes (shake_shake_32, shake_shake_96, and shake_shake_112), and pyramid_net, which uses the even stronger Shake-Drop regularization [45]. Our implementations are based on Cubuk et al. [6]; we use the same optimizer (stochastic gradient descent with momentum) and cosine learning rate schedule. We train without data augmentation (to ensure all models are trained on exactly the same examples), except for experiments that explicitly vary data augmentation. Without data augmentation, the test accuracies of our models are shown in Table 1.

Model	CIFAR-10 Test Accuracy (%)
wrn_32	89.4
wrn_160	90.2
shake_shake_32	92.2
shake_shake_96	93.5
shake_shake_112	93.6
pyramid_net	95.8

Table 1: Test accuracies (in increasing order) of our six CIFAR-10 models, trained without data augmentation.

For ImageNet, we consider ten different pretrained models: three ResNets [16] of different sizes (ResNet50, ResNet101, and ResNet152), two Vision Transformers [10] of different sizes (ViT and ViTSmall), three distilled transformers [42] (DeiT, DeiTSmall, and DeiTClsToken), and two CoAtNets [7] (CoAtNet0 and CoAtNet0BF16). The top-1 classification accuracies of these models are presented in Table 2.

Model	ImageNet Test Accuracy (%)
ViTSmall	64.3
ViT	75.1
ResNet50	76.1
CoAtNet0BF16	78.4
ResNet101	78.5
ResNet152	79.0
DeiTSmall	80.1
DeiTClsToken	81.5
DeiT	81.7
CoAtNet0	81.7

Table 2: Test accuracies of our ten pretrained ImageNet models, in increasing order.

A.2 Linear Interpolation: Methodological Details

For each sampled path, we compute the discrete Fourier transform (DFT) of the prediction function along the path separately for each of the $M$ class predictions, take the (real) magnitude of the resulting (complex) DFT coefficients, and average them among the $M$ classes. We then compute the fraction of this averaged DFT magnitude that is allocated to the high frequency components, and aggregate over the many paths by calculating the mean high frequency fraction and its standard error. We use a simple threshold frequency of 0.05 for both CIFAR10 and ImageNet, although our paths are sampled with a distance of 1 for CIFAR10 and 7 for ImageNet (since ImageNet images are larger and thus farther apart). This precise threshold is not critical to our qualitative results, and different tradeoffs of frequency resolution and computational expense are possible.

Limitations of linear interpolation.

Like all proxy measurements of spectral bias, linear interpolation is a coarse metric. We only measure the Fourier content of the learned function along specific paths, and aggregate results across many paths, across all classes, and only summarize frequencies into coarse "low" and "high" bins. An additional limitation is that the paths we define interpolate in pixel space, which means that there are images along our interpolating paths that are off the hypothesized manifold of natural images.

A.3 CIFAR-10 full results

A.3.1 Label Smoothing

Figure 9 shows the same results as Figure 3 (Left) on all six CIFAR-10 models we tested.

A.3.2 Sensitivity to Natural Image Directions

Figure 11 shows the same results as Figure 5 on all six CIFAR-10 models we tested.

A.3.3 Agreement Between Label Smoothing and Linear Interpolation

Varying the frequency of the radial wave label smoothing

When the frequency of the radial wave used for label smoothing increases, models take more time to fit the smoothing noise. Figure 3 (Left) and Figure 9 show this using label smoothing; the corresponding interpolation experiment is shown in Figure 13. The target frequencies between 0.035 and 0.04 are close enough that, were the model to fit each perfectly, the interpolation curves would be nearly visually indistinguishable, as we can tell from Figure 2 (Left). However, the model is actually smoother when trying to fit higher frequency label smoothing noise, because it fits this noise less well (in addition to fitting it later in training). We can see this effect, for instance, by noting that wrn_32, wrn_160, and shake_shake_32 fail to fit frequency 0.04, both in Figure 9 and Figure 13.

It is also worth noting that, in Figure 13 and repeatedly across our interpolation experiments, the learned function is smoother (lower-frequency) within-class and less smooth (higher-frequency) between-class. This is to be expected since the model must change predictions somewhere along the path between examples from different classes.

Learning low frequencies first

The label smoothing experiment presented in Figure 3 (Left) and Figure 9 shows that low frequency target functions are learned earlier than higher frequency targets; we can also confirm this finding using interpolation with model checkpoints saved at different epochs throughout training (without any label smoothing) in Figure 15. We see that spectral bias in image classification is more nuanced than simply increasing in frequency over time: as training proceeds, models become higher-frequency along between-class paths but lower-frequency along within-class paths. This may indicate that the model is learning an appropriate clustering of the data into its classes, and reducing the functional variation within each cluster.

A.3.4 Weight Decay

Figure 17 uses the label smoothing methodology on our six CIFAR-10 models to show that weight decay delays the learning of high frequencies.

A.3.5 Training Set Size

Figure 6 (Left) uses linear interpolation to show the within-class regularization (frequency reduction) effect of increasing dataset size for wrn_160. Figure 19 shows the same effect on all six CIFAR-10 models we tested.

A.3.6 Data Augmentation

Figure 6 (Center) uses linear interpolation to study the effect of common data augmentation procedures on the learned frequencies for wrn_160. Figure 21 shows the same experiment on all six models we tested.

Mixup Strength

Figure 6 (Center) uses linear interpolation to show that training with Mixup data augmentation [49] causes wrn_160 to learn a within-class lower-frequency function, but too much Mixup can produce a higher-frequency function within-class. Figure 23 repeats the experiment on all six CIFAR-10 models we tested.

A.3.7 Self-Distillation

Figure 6 (Right) uses linear interpolation to show that self-distillation with shake_shake_96 produces a student model that is lower-frequency within-class (and slightly higher-frequency between-class) than its teacher, and has higher validation accuracy than the teacher. Figure 25 shows the same result across all six CIFAR-10 models we tested.

A.4 ImageNet Full Results

A.4.1 Training Time

Figure 7 (Left) shows that ResNet50 increases in between-class frequency as training proceeds, while within-class frequencies remain constant or slightly decrease, causing increasing frequency separation between these two types of paths. In Figure 27 we show the same experiment for all ten ImageNet models we tested. We find that the overall frequency trends vary between models, but all models increase in frequency separation between path types during training.

A.4.2 Class Coherence

Figure 7 (Right) shows that ResNet50 has higher frequencies along paths within more internally diverse classes. In Figure 29 we show the same experiment for all ten ImageNet models we tested. Interestingly, the two CoATNets exhibit no clear correlation between class diversity and function frequency, and also dramatically increase in function frequency during training (Figure 27), unlike other models.