\catchline

Spectra of $\Lambda$ and $\Sigma$ Baryons under Screened Potential

CHANDNI MENAPARA¹¹1[email protected] and AJAY KUMAR RAI Department of Physics, The Maharaja Sayajirao University of Baroda, Vadodara, India
Department of Physics, Sardar Valabhbhai National Institute of Technology
Surat-395008, Gujarat, India

(Day Month Year; Day Month Year)

Abstract

The light, strange baryons have been studied through various approaches and attempted to be looked for rigorously in experiments. The screened potential has been applied to heavy baryon sector as well as meson systems in earlier works. Here, this article attempts to compare the results for linear and screened potential for light strange baryons. Also, the Regge trajectories depict the linear nature.

keywords:

Screened potential, Strange Baryon, CQM

{history}

\ccode

PACS numbers:

1 Introduction

JLab, LHC, BESIII experimental facilities have over the years looked for missing resonances from light to heavy quark systems [1, 2]. An upcoming experiment PANDA is highly focused to look for strange baryon especially ones with higher strangeness $\Xi$ and $\Omega$ [3, 4, 5, 6, 7, 8]. With every run and new upgrades in energy scale, exotic states have come up however strange quark still hasn’t revealed all its composites easily. Singly strange $\Lambda$ and its similar partner $\Sigma$ have still a sizable number of resonances but many are 1 and 2 star status [9]. A non-relativistic approach under constituent cover with different confining potential attempts to reproduce these excited states. This is the driving force for the Hadron spectroscopy field [10, 11].

Many approaches have been used throughout the years in an effort to fully comprehend the baryon sector. Internal baryon dynamics have been studied using algebraic models; a recent study used U(7) in this regard [12]. R. Bijker and group too have focused on algebraic approach with the string-like model [13]. the quark-diquark model has been examined in several variations; E. Santopinto et al. used an exchange interaction inspired by Gursey Radicati to generate both strange and non-strange baryon resonances [14, 15]. Regge phenomenology has also been employed in the study of light, strange baryons using n and J plane linear curves [16]. Other than these various models have been employed over the years [17, 22].
The screened potential term is accompanied with spin-dependent term in the present approach as detailed in section 2. The section 3 discusses mass spectra of $\Lambda$ , $\Sigma$ baryons along with the experimental and theoretical background known so far Few states need special attention regarding their actual nature. Section 4 is dedicated to Regge trajectory for (J, $M^{2}$ ) and (n, $M^{2}$ ).

2 Theoretical Framework

Hypercentral Constituent Quark Model (hCQM) has been applied in various systems and with a variety of potentials for heavy hadrons [23, 24, 25, 26, 28, 27, 29, 30, 31] and exotics. The linear potential has been employed for all octet, decuplet baryons in our earlier works [32, 33, 34, 35, 36, 37]. The screened potential now applied to strange $\Lambda$ and $\Sigma$ baryons, allows to give a vivid comparison between linear and screened potential. Our earlier works have highlighted the detailed comparison with other theoretical models.
Employing the Jacobi coordinates to describe the three body baryon system as marked by notable articles [38, 39, 40],

\vec{\rho}=\frac{\vec{r_{1}}-\vec{r_{2}}}{\sqrt{2}}\hskip 14.22636ptand\hskip 14.22636pt\vec{\lambda}=\frac{\vec{r_{1}}+\vec{r_{2}}-2\vec{r_{3}}}{\sqrt{6}}.

(1)

Hyperradias $x$ and hyperangle $\xi$ in terms of Jacobi coordinates are [41],

x=\sqrt{\rho^{2}+\lambda^{2}}\hskip 14.22636ptand\hskip 14.22636pt\xi=arctan\left(\frac{\rho}{\lambda}\right)

(2)

The Hamiltonian, presenting the three quark bound system is,

H=\frac{P^{2}}{2m}+V(x)

(3)

Here, $P$ is conjugate momentum and $m$ is the reduced mass of the system, which expressed as, $m=\frac{2m_{\rho}m_{\lambda}}{m_{\rho}+m_{\lambda}}$ . Here, the constituent quark mass $m_{u}=m_{d}=0.290GeV$ , $m_{s}=0.500GeV$ . As the hypercentral model itself suggests, $V(x)$ is non-relativistic interaction potential inside the baryonic system depending only on hyperradius x [41, 42, 43].

The screened potential is incorporated as confining potential with the color-Coulomb potential (spin independent potential $V_{SI}(x)=V_{conf}(x)+V_{Col}(x)$ ).

V_{conf}(x)=a\left(\frac{1-e^{-{\mu}x}}{\mu}\right)\hskip 14.22636ptand\hskip 14.22636ptV_{Col}(x)=-\frac{2}{3}\frac{\alpha_{s}}{x}

(4)

where, $a$ is the string tension. Based on a paper by R. Chaturvedi, the screening parameter $\mu$ has been varied over a range and 0.3 has been considered as the value obtain the spectra for all the systems considered here [44] for the case of mesons. The spin dependent part of potential $V_{SD}(x)$ is,

V_{SD}(x)=V_{SS}(x)(\vec{S_{\rho}}\cdot\vec{S_{\lambda}})+V_{\gamma S}(x)(\vec{\gamma}\cdot\vec{S})+V_{T}(x)\left[S^{2}-\frac{3(\vec{S}\cdot\vec{x})(\vec{S}\cdot\vec{x})}{x^{2}}\right]

(5)

which includes spin-spin, spin-orbit and tensor term respectively. In case of linear potential for the similar articles mentioned above, the differences for the resonances predicted for higher excited hyperfine states were more. The screened effect has shown effects in heavy baryons by reducing this splitting, which has been tried to observe in higher excited light baryons.

3 Mass Spectra

The PDG signifies the currently known resonances of $\Lambda$ with 10 four star states, 4 three star states, 2 two star states and 7 one star states. Except for four star states, there is a wide opportunity to look for the resonances in every possible reactions to know all the details. The very first excited state 1405 MeV has been under the spotlight for years. In some instances, the measurement results are consistent within a relatively narrow range. This is true not only for the well-known (1520) $\frac{3}{2}$ , but also for the (1670) $\frac{1}{2}$ , (1690) $\frac{3}{2}$ , and (1815) $\frac{5}{2}^{+}$ , all of which lie within a relatively narrow mass range. The findings of (1890) $\frac{3}{2}^{+}$ , (1830) $\frac{5}{2}$ , and (2100) $\frac{7}{2}$ are also very compelling. A Four star status has been assigned to these resonances. As it is evident that the low-lying masses i.e. S-wave the predicted mass differ by 50 MeV from PDG. Also, lower excited states for P and D-wave also, the masses are quite in the range with difference of 20-30 MeV. But for 1F, 1G the masses are under-predicted by more than 100 MeV to experimental as well as that of linear potential ones.

$\Sigma$ baryon happens to have a large number of states with 1 and 2 stars clearly marking the need to look for resonances. In the earliest studies, the resonances (1915) $\frac{5}{2}^{+}$ and (1910) $\frac{3}{2}^{-}$ emerge as the leading candidates, with additional support for (1880) $\frac{1}{2}^{+}$ and (1900) $\frac{1}{2}^{+}$ . The four star states (1670) $\frac{3}{2}^{-}$ , (1775) $\frac{5}{2}^{-}$ , (1915) $\frac{5}{2}^{+}$ , and (2030) $\frac{7}{2}^{+}$ have been established with good consistency. As here (1915) $\frac{5}{2}^{+}$ and (2030) $\frac{7}{2}^{+}$ are both assigned to 1D family, our masses are higher by 37 MeV compared to 1915. State 1660 is 2S( $\frac{1}{2}^{+}$ ) differs by 30 MeV. The three star state 2230 doesn’t have known spin-parity but here we have tentatively assigned it to be 3S( $\frac{3}{2}^{+}$ ).

Table 1:

\Lambda

Resonance mass spectra using Screened potential (in MeV)

State	$J^{P}$	$M_{scr}$	$M_{lin}$	$M_{exp}$ [9]	[18]	[19]	[20]	[21]
1S	$\frac{1}{2}^{+}$	1115	1115	1115	1115	1133	1136	1113
2S	$\frac{1}{2}^{+}$	1553	1589	1600	1615	1577	1625	1606
3S	$\frac{1}{2}^{+}$	1869	1892	1810	1901			1880
4S	$\frac{1}{2}^{+}$	2197	2220		1986			2173
5S	$\frac{1}{2}^{+}$	2536	2571		2099
$1^{2}P_{1/2}$	$\frac{1}{2}^{-}$	1554	1558		1667	1686	1556	1559
$1^{2}P_{3/2}$	$\frac{3}{2}^{-}$	1549	1544	1520	1549			1560
$1^{4}P_{1/2}$	$\frac{1}{2}^{-}$	1557	1564	1670				1656
$1^{4}P_{3/2}$	$\frac{3}{2}^{-}$	1552	1551	1690	1693
$1^{4}P_{5/2}$	$\frac{5}{2}^{-}$	1545	1533
$2^{2}P_{1/2}$	$\frac{1}{2}^{-}$	1814	1858	1800	1733			1791
$2^{2}P_{3/2}$	$\frac{3}{2}^{-}$	1808	1841		1812			1859
$2^{4}P_{1/2}$	$\frac{1}{2}^{-}$	1817	1867
$2^{4}P_{3/2}$	$\frac{3}{2}^{-}$	1811	1850
$2^{4}P_{5/2}$	$\frac{5}{2}^{-}$	1803	1827	1830	1861	1799	1778	1803
$3^{2}P_{1/2}$	$\frac{1}{2}^{-}$	2083	2186		2155
$3^{2}P_{3/2}$	$\frac{3}{2}^{-}$	2077	2166		2035
$3^{4}P_{1/2}$	$\frac{1}{2}^{-}$	2086	2196		2197
$3^{4}P_{3/2}$	$\frac{3}{2}^{-}$	2080	2176
$3^{4}P_{5/2}$	$\frac{5}{2}^{-}$	2072	2149		2136
$1^{2}D_{3/2}$	$\frac{3}{2}^{+}$	1765	1789		1854	1849		1836
$1^{2}D_{5/2}$	$\frac{5}{2}^{+}$	1755	1767	1820	1825	1849		1839
$1^{4}D_{1/2}$	$\frac{1}{2}^{+}$	1776	1814	1710*	1901	1799	1799	1764
$1^{4}D_{3/2}$	$\frac{3}{2}^{+}$	1768	1798	1890
$1^{4}D_{5/2}$	$\frac{5}{2}^{+}$	1758	1776
$1^{4}D_{7/2}$	$\frac{7}{2}^{+}$	1746	1748
$2^{2}D_{3/2}$	$\frac{3}{2}^{+}$	2032	2113	2070
$2^{2}D_{5/2}$	$\frac{5}{2}^{+}$	2022	2085	2110

State	$J^{P}$	$M_{scr}$	$M_{lin}$	$M_{exp}$ [9]	[18]	[19]	[21]
$2^{4}D_{1/2}$	$\frac{1}{2}^{+}$	2043	2144
$2^{4}D_{3/2}$	$\frac{3}{2}^{+}$	2036	2123
$2^{4}D_{5/2}$	$\frac{5}{2}^{+}$	2026	2096			2074	2008
$2^{4}D_{7/2}$	$\frac{7}{2}^{+}$	2013	2061	2085			2064
$3^{2}D_{3/2}$	$\frac{3}{2}^{+}$	2306	2459
$3^{2}D_{5/2}$	$\frac{5}{2}^{+}$	2296	2426
$3^{4}D_{1/2}$	$\frac{1}{2}^{+}$	2316	2496
$3^{4}D_{3/2}$	$\frac{3}{2}^{+}$	2309	2471
$3^{4}D_{5/2}$	$\frac{5}{2}^{+}$	2300	2438
$3^{4}D_{7/2}$	$\frac{7}{2}^{+}$	2288	2398
$1^{2}F_{5/2}$	$\frac{5}{2}^{-}$	1980	2039	2080
$1^{2}F_{7/2}$	$\frac{7}{2}^{-}$	1965	2002	2100	2097
$1^{4}F_{3/2}$	$\frac{3}{2}^{-}$	1996	2079
$1^{4}F_{5/2}$	$\frac{5}{2}^{-}$	1984	2050
$1^{4}F_{7/2}$	$\frac{7}{2}^{-}$	1969	2013
$1^{4}F_{9/2}$	$\frac{9}{2}^{-}$	1951	1969
$2^{2}F_{5/2}$	$\frac{5}{2}^{-}$	2252	2380
$2^{2}F_{7/2}$	$\frac{7}{2}^{-}$	2239	2337
$2^{4}F_{3/2}$	$\frac{3}{2}^{-}$	2267	2427	2325
$2^{4}F_{5/2}$	$\frac{5}{2}^{-}$	2256	2393
$2^{4}F_{7/2}$	$\frac{7}{2}^{-}$	2243	2350
$2^{4}F_{9/2}$	$\frac{9}{2}^{-}$	2226	2299
$1^{2}G_{7/2}$	$\frac{7}{2}^{+}$	2198	2302		2251
$1^{2}G_{9/2}$	$\frac{9}{2}^{+}$	2179	2246	2350	2360	2357
$1^{4}G_{5/2}$	$\frac{5}{2}^{+}$	2219	2363		2258
$1^{4}G_{7/2}$	$\frac{7}{2}^{+}$	2203	2316
$1^{4}G_{9/2}$	$\frac{9}{2}^{+}$	2184	2260
$1^{4}G_{11/2}$	$\frac{11}{2}^{+}$	2162	2195

Table 2:

\Sigma

resonance spectra using Screened potential (in MeV)

State	$J^{P}$	$M_{scr}$	$M_{lin}$	$M_{exp}$ [9]	[18]	[19]	[20]	[21]
1S	$\frac{1}{2}^{+}$	1193	1193	1193	1187	1170	1180	1192
	$\frac{3}{2}^{+}$	1382	1384	1385	1381	1832	1389	1383
2S	$\frac{1}{2}^{+}$	1630	1643	1660	1711	1604	1616	1664
	$\frac{3}{2}^{+}$	1809	1827	1780	1862		1865	1868
3S	$\frac{1}{2}^{+}$	2035	2099		2028			2022
	$\frac{3}{2}^{+}$	2186	2236	2230
4S	$\frac{1}{2}^{+}$	2464	2589
	$\frac{3}{2}^{+}$	2597	2693
5S	$\frac{1}{2}^{+}$	2916	3108
	$\frac{3}{2}^{+}$	3034	3189
$1^{2}P_{1/2}$	$\frac{1}{2}^{-}$	1679	1725	1620	1620	1711	1677	1657
$1^{2}P_{3/2}$	$\frac{3}{2}^{-}$	1669	1702	1670	1706	1711	1677	1698
$1^{4}P_{1/2}$	$\frac{1}{2}^{-}$	1683	1736	1750	1693		1736	1746
$1^{4}P_{3/2}$	$\frac{3}{2}^{-}$	1674	1713		1731		1736	1790
$1^{4}P_{5/2}$	$\frac{5}{2}^{-}$	1662	1683	1775	1757		1736	1743
$2^{2}P_{1/2}$	$\frac{1}{2}^{-}$	2036	2145	1900	2115	2110
$2^{2}P_{3/2}$	$\frac{3}{2}^{-}$	2025	2114	1910	2175
$2^{4}P_{1/2}$	$\frac{1}{2}^{-}$	2042	2159	2110
$2^{4}P_{3/2}$	$\frac{3}{2}^{-}$	2030	2129	2010
$2^{4}P_{5/2}$	$\frac{5}{2}^{-}$	2015	2087
$3^{2}P_{1/2}$	$\frac{1}{2}^{-}$	2417	2608
$3^{2}P_{3/2}$	$\frac{3}{2}^{-}$	2406	2571
$3^{4}P_{1/2}$	$\frac{1}{2}^{-}$	2422	2627
$3^{4}P_{3/2}$	$\frac{3}{2}^{-}$	2411	2589
$3^{4}P_{5/2}$	$\frac{5}{2}^{-}$	2396	2541
$1^{2}D_{3/2}$	$\frac{3}{2}^{+}$	1971	2057	1940	2025			1947
$1^{2}D_{5/2}$	$\frac{5}{2}^{+}$	1952	2013	1915	1991	1872		1949

State	$J^{P}$	$M_{scr}$	$M_{lin}$	$M_{exp}$ [9]	[18]	[19]	[20]	[21]
$1^{4}D_{1/2}$	$\frac{1}{2}^{+}$	1991	2107	1983		1911	1924
$1^{4}D_{3/2}$	$\frac{3}{2}^{+}$	1978	2074
$1^{4}D_{5/2}$	$\frac{5}{2}^{+}$	1959	2029
$1^{4}D_{7/2}$	$\frac{7}{2}^{+}$	1937	1974	2025	2033			2002
$2^{2}D_{3/2}$	$\frac{3}{2}^{+}$	2347	2510
$2^{2}D_{5/2}$	$\frac{5}{2}^{+}$	2329	2459
$2^{4}D_{1/2}$	$\frac{1}{2}^{+}$	2368	2568
$2^{4}D_{3/2}$	$\frac{3}{2}^{+}$	2354	2529
$2^{4}D_{5/2}$	$\frac{5}{2}^{+}$	2336	2478
$2^{4}D_{7/2}$	$\frac{7}{2}^{+}$	2313	2414	2470
$3^{2}D_{3/2}$	$\frac{3}{2}^{+}$	2747	3004	3000*
$3^{2}D_{5/2}$	$\frac{5}{2}^{+}$	2727	2945
$3^{4}D_{1/2}$	$\frac{1}{2}^{+}$	2769	3072
$3^{4}D_{3/2}$	$\frac{3}{2}^{+}$	2754	3027
$3^{4}D_{5/2}$	$\frac{5}{2}^{+}$	2735	2967
$3^{4}D_{7/2}$	$\frac{7}{2}^{+}$	2710	2892
$1^{2}F_{5/2}$	$\frac{5}{2}^{-}$	2279	2416
$1^{2}F_{7/2}$	$\frac{7}{2}^{-}$	2249	2343	2100*
$1^{4}F_{3/2}$	$\frac{3}{2}^{-}$	2311	2495		2300
$1^{4}F_{5/2}$	$\frac{5}{2}^{-}$	2287	2437		2347
$1^{4}F_{7/2}$	$\frac{7}{2}^{-}$	2258	2365		2289
$1^{4}F_{9/2}$	$\frac{9}{2}^{-}$	2223	2278		2289
$2^{2}F_{5/2}$	$\frac{5}{2}^{-}$	2681	2901
$2^{2}F_{7/2}$	$\frac{7}{2}^{-}$	2653	2819
$2^{4}F_{3/2}$	$\frac{3}{2}^{-}$	2704	2990
$2^{4}F_{5/2}$	$\frac{5}{2}^{-}$	2681	2925
$2^{4}F_{7/2}$	$\frac{7}{2}^{-}$	2653	2844
$2^{4}F_{9/2}$	$\frac{9}{2}^{-}$	2619	2746

The low-lying states are matching but higher excited states are under-predicted. However, the mass-range suggest that the given spin-parity assignment to one and two star states are well in accordance. From the resonance tables 1 and 2, it is noteworthy that for states with higher angular momentum, the under-predicted masses show the effect of screened potential. Also, the hypercentral potential leads to reversed hierarchy for hyperfine states.
The $M_{lin}$ shown in tables 1 and 2 gives the resonance masses predicted through linear potential in our earlier works for the comparison with screened potential results. It is noteworthy that linear masses have greater difference in the hyperfine states as in case of screened potential. Thus, at very high orbital states linear potential gives over prediction for the masses. This serves as a primary aim to observe the difference in application of both these potentials. Also, the tables above showcases comparison with few of the models described in section 1. The relativistic quark model studies by Faustov et al [18] have been incorporated which shows that few states predicted through screened potential are quite in accordance.

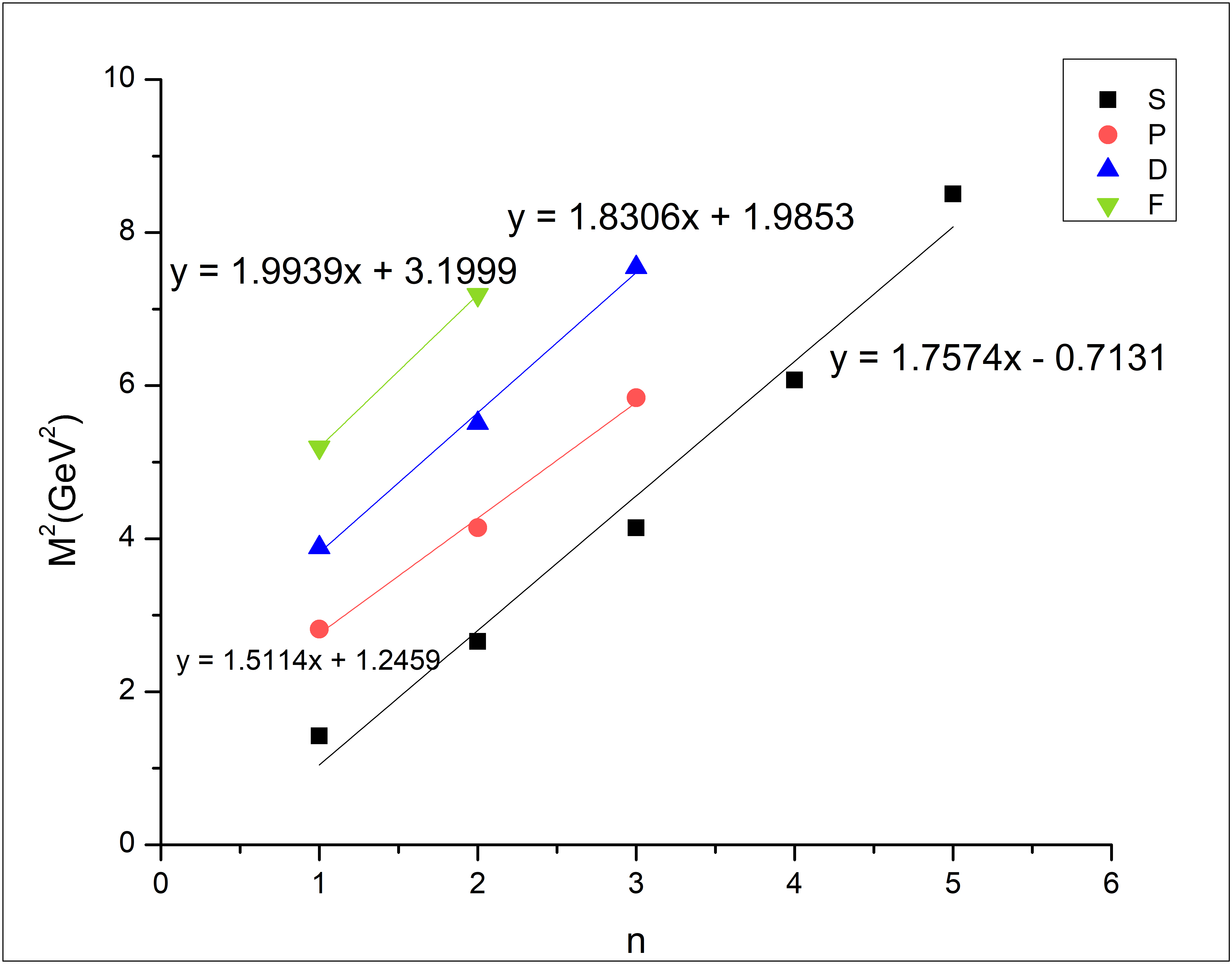
4 Regge Trajectory

A number of resonance masses to be fit for experimental comparison and observations, Regge trajectories play a significant role[45]. Regge trajectories are basically plots of total angular momentum J and principle quantum number n against the square of resonance mass as depicted by figures 1, 2, 3, 4, 5. A correct spin-parity assignment for a state can perhaps be predicted using these plots [46].


	$\displaystyle J=aM^{2}+a_{0}$		(6a)
	$\displaystyle n=bM^{2}+b_{0}$		(6b)

As it is evident that there are states in PDG whose spin-parity are not precisely known but resonance mass has been observed. Such points when put on the same line allows us to comment through the natural and unnatural parity positions. The value of slope and intercept allow us to extend it to further points to predict the higher excited states in any given baryon spectrum.

Refer to caption — Figure 1: $n$ vs $M^{2}$ for $\Lambda$ , Regge trajectory for Principle Quantum number n versus $M^{2}$ depicting the linear nature.

5 Conclusion

The present work summarizes the effect of screened type potential under hypercentral Constituent Quark Model (hCQM) for $\Lambda$ and $\Sigma$ baryons. So far, linear potential has been applied to light spectrum, whereas screened potential provided reasonable results for heavy quark systems [47]. The screening parameter plays a role in determining the spin-split and mass at higher angular momentum states. The obtained masses have been comparable with the basis of experimental known values with different star status. The masses of higher spin state for a given L value, decreases in hierarchy. The hyperfine splitting is observed to be less with screened potential than those of linear one.

Acknowledgments

C. Menapara acknowledges the support from DST under INSPIRE Fellowship. Authors are thankful to organizers of ICNFP 2022.

References

[1] R. Aaij et al. (LHCb Collaboration), Phys. Rev. Lett. 118, 052002 (2017)
[2] M. Ablikim et al. [BESIII Collaboration], Phys. Rev. D 100, 051101(R) (2019)
[3] PANDA Collaboration (G. Barruca et al.), Eur. Phys. J. A 57, 184 (2021)
[4] PANDA Collaboration (B. Singh et al.), J. Phys. G: Nucl. Part. Phys. 46, 045001 (2019)
[5] PANDA Collaboration (B. Singh et al.), Nucl. Phys. A 954, 323-340 (2016)
[6] PANDA Collaboration (B. Singh et al.), Phys. Rev. D 95, 032003 (2017)
[7] PANDA Collaboration (V. Abazov et al.) (2022), 2201.03852
[8] PANDA Collaboration (V. Abazov et al.) (2023), 2304.11977v1
[9] R. L. Workman et al. [Particle Data Group], Prog. Theor. Exp. Phys. 2022, 083C01 (2022)
[10] A. Thiel, F. Afzal, Y. Wunderlich, Prog. Part. Nucl. Phys. 125, 103949 (2022),
[11] G. Eichmann, Theory introduction to baryon spectroscopy (2022) arXiv:2202.13378
[12] N. Amiri, M. Ghapanvari and M. A. Jafarizadeh, Eur. Phys. J. Plus 141, 136 (2021)
[13] R. Bijker, J. Ferretti, G. Galata, H. Garcia-Tecocoatzi and E. Santopinto, Phys. Rev. D. 94, 074040 (2016)
[14] E. Santopinto, Phys. Rev. C 72, 022201(R) (2005)
[15] E.Santopinto and J. Ferretti, Phys. Rev. C 92, 025202 (2015)
[16] J. Oudichhya, K. Gandhi and A. K. Rai, Nucl. Phys. A; 1035, 122658 (2023)
[17] Y. Chen and B. Q. Ma, Chin. Phys. Lett. 25, 3920 (2008)
[18] R.N. Faustov and V.O. Galkin Phys. Rev. D 92, 054005 (2015)
[19] R. Bijker, F. Iachello, A. Leviatan, Annals Phys. 284, 89 (2000)
[20] T. Melde, W. Plessas, B. Sengl, Phys. Rev. D 77, 114002 (2008)
[21] Y. Chen, B.Q. Ma, Nucl. Phys. A 831, 1 (2009)
[22] E. Klempt, Phys. Rev. C 66, 058201 (2002)
[23] Z. Shah, K. Gandhi and A. K. Rai, Chin. Phys. C 43, 034102 (2019)
[24] Z. Shah and A. K. Rai, Few-Body Syst 59, 112 (2018)
[25] Z. Shah, K. Thakkar and A. K. Rai, Eur. Phys. J. C 76, 530 (2016)
[26] Z. Shah and A. K. Rai, Eur. Phys. J. A 53, 195 (2017)
[27] K. Gandhi and A. K. Rai, Eur. Phys. J. Plus 135, 213 (2020)
[28] K. Gandhi, Z. Shah and A. K. Rai, Eur. Phys. J. Plus 133 (12), 1-9 (2018)
[29] A. Kakadiya, Z. Shah, K. Gandhi and A. K. Rai Few-Body Systems 63, 29 (2022)
[30] A Kakadiya, Z Shah and A. K. Rai Int. Jour. Mod. Phys. A 37, 2250053 (2022)
[31] A Kakadiya, C. Menapara and A. K. Rai Int. Jour. Mod. Phys. A 38, 18, 234103 (2023)
[32] C. Menapara, Z. Shah and A. K. Rai, Chin. Phys. C 45, 023102 (2021)
[33] C. Menapara and A. K. Rai, Chin. Phys. C 45, 063108 (2021)
[34] C. Menapara and A. K. Rai, Chin. Phys. C 46, 103102 (2022)
[35] C. Menapara and A. K. Rai, Int. Jour. Mod. Phys. A 37, 27 2250177 (2022).
[36] C. Menapara and A. K. Rai, Int. Jour. Mod. Phys. A 38, 9, 2350053 (2023)
[37] A. Ansari, C. Menapara and A. K. Rai, Int. Jour. Mod. Phys. A 38, 21, 2350108 (2023)
[38] G. Morpurgo, Nuovo Cimento 9, 461 (1952)
[39] Yu. A. Simonov, Sov. J. Nucl. Phys. 3, 461 (1966)
[40] J. Ballot and M. Fabre de la Ripelle, Ann. of Phys. (N.Y.) 127, 62 (1980)
[41] M. M. Giannini and E. Santopinto, Chin. J. Phys. 53, 020301 (2015)
[42] M. M. Giannini, E. Santopinto, and A. Vassallo, Eur. Phys. J. A 12, 447 (2001)
[43] M. M. Giannini, E. Santopinto, and A. Vassallo, Eur. Phys. J. A 25, 241 (2005)
[44] R. Chaturvedi and A. K. Rai, Int. Jour. Theo. Phys.59, 3508-3532 (2020)
[45] K. Chen, et al., Eur. Phys. J. C 78, 20 (2018)
[46] X.-H. Guo, Ke-Wei Wei and X.-H. Wu, Phys. Rev. D 78, 056005 (2008)
[47] C. Menapara and A. K. Rai, Few-Body Syst. 65, 63 (2024)

Spectra of Λ\Lambda and Σ\Sigma Baryons under Screened Potential