This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Special least squares solutions of the reduced biquaternion matrix equation with applications 22footnotemark: 2

Sk. Safique Ahmad111 Department of Mathematics, Indian Institute of Technology Indore, Simrol, Indore-452020, Madhya Pradesh, India. email:[email protected], [email protected].    Neha Bhadala 333Research Scholar, Department of Mathematics, IIT Indore, Research work funded by PMRF (Prime Minister’s Research Fellowship). email:[email protected], [email protected]
Abstract

This paper presents an efficient method for obtaining the least squares Hermitian solutions of the reduced biquaternion matrix equation (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F). The method leverages the real representation of reduced biquaternion matrices. Furthermore, we establish the necessary and sufficient conditions for the existence and uniqueness of the Hermitian solution, along with a general expression for it. Notably, this approach differs from the one previously developed by Yuan et al. (2020)(2020), which relied on the complex representation of reduced biquaternion matrices. In contrast, our method exclusively employs real matrices and utilizes real arithmetic operations, resulting in enhanced efficiency. We also apply our developed framework to find the Hermitian solutions for the complex matrix equation (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F), expanding its utility in addressing inverse problems. Specifically, we investigate its effectiveness in addressing partially described inverse eigenvalue problems. Finally, we provide numerical examples to demonstrate the effectiveness of our method and its superiority over the existing approach.

Keywords. Least squares problem, Reduced biquaternion matrix equation, Real representation matrix, Partially described inverse eigenvalue problem.

AMS subject classification. 15B33, 15B57, 65F18, 65F20, 65F45.

1 Introduction

Matrix equations play a vital role in various fields, including computational mathematics, vibration theory, stability analysis, and control theory (for example, [2, 5, 7]). Due to their significant applications in various fields, a substantial amount of research has been dedicated to solving matrix equations. See [8, 9, 15, 17] and references therein. In this paper, we address the following matrix equation:

(A​X​B,C​X​D)=(E,F),(AXB,CXD)=(E,F), (1)

where AA, BB, CC, DD, EE, and FF are given matrices of appropriate sizes, and XX represents the unknown matrix of an appropriate size. This matrix equation has been extensively studied in the real, complex, and quaternion fields, leading to several important findings. Notably, Liao et al. [10] provided an analytical expression for the least squares solution with the minimum norm in the real field. Ding et al. [3] proposed two iterative algorithms to obtain solutions in the real field. Mitra [11] delved into the necessary and sufficient conditions for the existence of solution and presented a general formulation for the solution in the complex field. Navarra et al. [12] offered a simpler consistency condition and a new representation of the general common solution compared to Mitra [11]. They also derived a representation of the general Hermitian solution for A​X​B=CAXB=C, provided the Hermitian solution exists. Wang et al. [16] determined the least squares Hermitian solution with the minimum norm in the complex field using matrix and vector products. Zhang et al. [22] developed a more efficient method compared to [16] for finding the least squares Hermitian solution with the minimum norm by utilizing the real representation of a complex matrix. Yuan et al. [19] studied the least squares L-structured solutions of quaternion linear matrix equations using the complex representation of quaternion matrices. However, limited research has been conducted on solving matrix equations in the reduced biquaternion domain.

A reduced biquaternion, a type of 4​D4D hypercomplex number, shares with quaternions the characteristic of possessing a real part alongside three imaginary components. However, it distinguishes itself by offering notable advantages over its quaternion counterpart. One significant distinction is the commutative nature of multiplication, which streamlines fundamental operations like multiplication itself, SVD, and eigenvalue calculations [14]. This results in algorithms that are less complex and more expeditious in computational procedures. For instance, Pei et al. [13, 14] and Gai [4] demonstrated that reduced biquaternions outperform conventional quaternions for image and digital signal processing. Despite the advantage of reduced biquaternions over quaternions, limited research has been dedicated to solving reduced biquaternion matrix equations (RBMEs). Recently, Yuan et al. [18] studied the necessary and sufficient conditions for the existence of a Hermitian solution of the RBME (1) and provided a general formulation for the solution by using the method of complex representation (CR) of reduced biquaternion matrices. However, this method involves complex matrices and complex arithmetic, leading to extensive computations.

In the existing literature, several papers have employed the real representation method to solve matrix equations within the complex and quaternion domains. For instance, in [22], the authors utilized real representation of complex matrices to address the complex matrix equation (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F). In [20, 21, 24], similar approaches were taken using real representation of quaternion matrices to tackle quaternion matrix equations. These studies clearly demonstrate the superior efficiency of the real representation (RR) method compared to the complex representation (CR) method when dealing with matrix equations in the complex and quaternion domains. However, the real representation method has not yet been explored in the context of solving reduced biquaternion matrix equations. Motivated by insights from prior research, this paper introduces a more efficient approach for finding the Hermitian solution to RBME (1). Here are the highlights of the work presented in this paper:

  • •

    We explore the least squares Hermitian solution with the minimum norm of the RBME (1) using the method of real representation of reduced biquaternion matrices. The notable advantage of this method lies in its exclusive use of real matrices and real arithmetic operations, resulting in enhanced efficiency.

  • •

    We establish the necessary and sufficient conditions for the existence and uniqueness of the Hermitian solution to RBME (1) and provide a general form of the solution.

  • •

    In light of complex matrix equations being a special case of reduced biquaternion matrix equations, we utilize our developed method to find the Hermitian solution for matrix equation (1) over the complex field.

  • •

    We conduct a comparative analysis between the CR and RR methods to study the Hermitian solution of RBME (1).

Furthermore, this paper explores the application of the proposed framework in solving inverse eigenvalue problems. Inverse eigenvalue problems often involve the reconstruction of structured matrices based on given spectral data. When the available spectral data contains only partial information about the eigenpairs, this problem is termed as a partially described inverse eigenvalue problem (PDIEP). In PDIEP, two crucial aspects come to the forefront: the theory of solvability and the development of numerical solution methodologies (as detailed in [1] and related references). In terms of solvability, a significant challenge has been to establish the necessary or sufficient conditions for solvability of PDIEP. On the other hand, numerical solution methods aim to construct matrices in a numerically stable manner when the given spectral data is feasible. In this paper, by leveraging our developed framework, we successfully introduce a numerical solution methodology for PDIEP [1, Problem 5.1], which requires the construction of the Hermitian matrix from an eigenpair set.

The manuscript is organized as follows. In Section 2, notation and preliminary results are presented. Section 3 outlines a framework for solving constrained RBME. Section 4 highlights the application of our developed framework to solve PDIEP. Section 5 offers numerical verification of our developed findings.

2 Notation and preliminaries

2.1 Notation

Throughout this paper, ℚℝ\mathbb{Q}_{\mathbb{R}} denotes the set of all reduced biquaternions. ℝm×n{\mathbb{R}}^{m\times n}, ℂm×n{\mathbb{C}}^{m\times n}, and ℚℝm×n\mathbb{Q}_{\mathbb{R}}^{m\times n} represent the sets of all m×nm\times n real, complex, and reduced biquaternion matrices, respectively. We also denote 𝕊​ℝn×n{\mathbb{S}\mathbb{R}}^{n\times n}, 𝔸​𝕊​ℝn×n{\mathbb{A}\mathbb{S}\mathbb{R}}^{n\times n}, ℍ​ℂn×n\mathbb{H}\mathbb{C}^{n\times n}, and ℍ​ℚℝn×n\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} as the sets of all n×nn\times n real symmetric , real anti-symmetric, complex Hermitian, and reduced biquaternion Hermitian matrices, respectively. For a diagonal matrix A=(ai​j)∈ℚℝn×nA=(a_{ij})\in\mathbb{Q}_{\mathbb{R}}^{n\times n}, we denote it as diag​(α1,α2,…,αn)\mathrm{diag}(\alpha_{1},\alpha_{2},\ldots,\alpha_{n}), where ai​j=0a_{ij}=0 whenever i≠ji\neq j and ai​i=αia_{ii}=\alpha_{i} for i=1,…,ni=1,\ldots,n. For A∈ℂm×nA\in{\mathbb{C}}^{m\times n}, the notations A+,AT,ℜ⁡(A)A^{+},A^{T},\Re(A), and ℑ⁡(A)\Im(A) stand for the Moore-Penrose generalized inverse, transpose, real part, and imaginary part of AA, respectively. InI_{n} represents the identity matrix of order nn. For i=1,2,…,ni=1,2,\ldots,n, eie_{i} denotes the it​hi^{th} column of the identity matrix InI_{n}. 0 denotes the zero matrix of suitable size. A⊗B=(ai​j​B)A\otimes B=(a_{ij}B) represents the Kronecker product of matrices A​and​BA\;\mbox{and}\;B. The symbol ∥⋅∥F\left\lVert\cdot\right\rVert_{F} represents the Frobenius norm. ∥⋅∥2\left\lVert\cdot\right\rVert_{2} represents the 22-norm or Euclidean norm. For A∈ℚℝm×n1A\in\mathbb{Q}_{\mathbb{R}}^{m\times n_{1}} and B∈ℚℝm×n2B\in\mathbb{Q}_{\mathbb{R}}^{m\times n_{2}}, the notation [A,B]\left[A,B\right] represents the matrix [AB]∈ℚℝm×(n1+n2)\begin{bmatrix}A&B\end{bmatrix}\in\mathbb{Q}_{\mathbb{R}}^{m\times(n_{1}+n_{2})}.

Matlab command r​a​n​d​n​(m,n)randn(m,n) creates an m×nm\times n codistributed matrix of normally distributed random numbers whose every element is between 0 and 11. r​a​n​d​(m,n)rand(m,n) returns an m×nm\times n matrix of uniformly distributed random numbers. o​n​e​s​(m,n)ones(m,n) and z​e​r​o​s​(m,n)zeros(m,n) returns an m×nm\times n matrix of ones and zeros, respectively. toeplitz(1:n)toeplitz(1:n) creates a Toeplitz matrix whose first row and first column is [1,2,…,n][1,2,\ldots,n]. e​y​e​(n)eye(n) generates an identity matrix of size n×nn\times n. Let AA be any matrix of size n×nn\times n. t​r​i​u​(A)triu(A) returns the upper triangular part of a matrix AA, while setting all the elements below the main diagonal to zero. t​r​i​u​(A,k)triu(A,k) returns the elements on and above the kt​hk^{th} diagonal of AA, while setting all the elements below it as zero. We use the following abbreviations throughout this paper:
RBME : reduced biquaternion matrix equation, CME : complex matrix equation, CR : complex representation, RR : real representation.

2.2 Preliminaries

A reduced biquaternion can be uniquely expressed as a=a0+a1​i+a2​j+a3​ka=a_{0}+a_{1}\,\textit{{i}}+a_{2}\,\textit{{j}}+a_{3}\,\textit{{k}}, where ai∈ℝa_{i}\in{\mathbb{R}} for i=0,1,2,3i=0,1,2,3, and i2=k2=−1,j2=1\textit{{i}}^{2}=\textit{{k}}^{2}=-1,\;\textit{{j}}^{2}=1, ij=ji=k,jk=kj=i,ki=ik=−j\textit{{i}}\textit{{j}}=\textit{{j}}\textit{{i}}=\textit{{k}},\;\textit{{j}}\textit{{k}}=\textit{{k}}\textit{{j}}=\textit{{i}},\;\textit{{k}}\textit{{i}}=\textit{{i}}\textit{{k}}=-\textit{{j}}. The norm of aa is ∥a∥=a02+a12+a22+a32\left\lVert a\right\rVert=\sqrt{a_{0}^{2}+a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}. The Frobenius norm for A=(ai​j)∈ℚℝm×nA=(a_{ij})\in\mathbb{Q}_{\mathbb{R}}^{m\times n} is defined as follows:

∥A∥F=∑i=1m∑j=1n∥ai​j∥2.\left\lVert A\right\rVert_{F}=\sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n}\left\lVert a_{ij}\right\rVert^{2}}. (2)

Let A=A0+A1​i+A2​j+A3​k∈ℚℝm×nA=A_{0}+A_{1}\textit{{i}}+A_{2}\textit{{j}}+A_{3}\textit{{k}}\in\mathbb{Q}_{\mathbb{R}}^{m\times n}, where At∈ℝm×nA_{t}\in{\mathbb{R}}^{m\times n} for t=0,1,2,3t=0,1,2,3. The real representation of matrix AA, denoted as ARA^{R}, is defined as follows:

AR=[A0−A1A2−A3A1A0A3A2A2−A3A0−A1A3A2A1A0].A^{R}=\begin{bmatrix}A_{0}&-A_{1}&A_{2}&-A_{3}\\ A_{1}&A_{0}&A_{3}&A_{2}\\ A_{2}&-A_{3}&A_{0}&-A_{1}\\ A_{3}&A_{2}&A_{1}&A_{0}\end{bmatrix}. (3)

Let ArRA_{r}^{R} denote the first block row of the block matrix ARA^{R}, i.e., ArR=[A0,−A1,A2,−A3].A_{r}^{R}=[A_{0},-A_{1},A_{2},-A_{3}]. We have

∥A∥F=12​∥AR∥F=∥ArR∥F.\left\lVert A\right\rVert_{F}=\frac{1}{2}\left\lVert A^{R}\right\rVert_{F}=\left\lVert A_{r}^{R}\right\rVert_{F}. (4)

For matrix A=(ai​j)∈ℚℝm×nA=(a_{ij})\in\mathbb{Q}_{\mathbb{R}}^{m\times n}, let aj=[a1​j,a2​j,…,am​j]​for​j=1,2,…,na_{j}=\left[a_{1j},a_{2j},\ldots,a_{mj}\right]\;\mbox{for}\;j=1,2,\ldots,n. We have vec​(A)=[a1,a2,…,an]T\mathrm{vec}(A)=\left[a_{1},a_{2},\ldots,a_{n}\right]^{T}. Clearly, the operator vec​(A)\mathrm{vec}(A) is linear, which means that for AA, B∈ℚℝm×nB\in\mathbb{Q}_{\mathbb{R}}^{m\times n}, and α∈ℝ\alpha\in{\mathbb{R}}, we have vec​(A+B)=vec​(A)+vec​(B)​and​vec​(α​A)=α​vec​(A).\mathrm{vec}(A+B)=\mathrm{vec}(A)+\mathrm{vec}(B)\,\mbox{and}\,\mathrm{vec}(\alpha A)=\alpha\mathrm{vec}(A). Also, we have

vec​(ArR)=[vec​(A0)−vec​(A1)vec​(A2)−vec​(A3)].\mathrm{vec}(A_{r}^{R})=\begin{bmatrix}\mathrm{vec}(A_{0})\\ -\mathrm{vec}(A_{1})\\ \mathrm{vec}(A_{2})\\ -\mathrm{vec}(A_{3})\end{bmatrix}. (5)

For A∈ℂm×nA\in{\mathbb{C}}^{m\times n}, B∈ℂn×sB\in{\mathbb{C}}^{n\times s}, and C∈ℂs×tC\in{\mathbb{C}}^{s\times t}, it is well known that vec​(A​B​C)=(CT⊗A)​vec​(B)\mathrm{vec}(ABC)=\left(C^{T}\otimes A\right)\mathrm{vec}(B). Now, we present two key lemmas. The subsequent lemma can be easily deduced from the structures of ARA^{R} and ArRA_{r}^{R}.

Lemma 2.1.

Let A,B∈ℚℝm×nA,B\in\mathbb{Q}_{\mathbb{R}}^{m\times n}, C∈ℚℝn×pC\in\mathbb{Q}_{\mathbb{R}}^{n\times p}, and α∈ℝ\alpha\in{\mathbb{R}}. Then the following properties hold.

  1. (i)

    A=B⇔AR=BR⇔ArR=BrRA=B\iff A^{R}=B^{R}\iff A_{r}^{R}=B_{r}^{R}.

  2. (ii)

    (A+B)R=AR+BR(A+B)^{R}=A^{R}+B^{R}, (α​A)R=α​AR(\alpha A)^{R}=\alpha A^{R}, (A​C)R=AR​CR(AC)^{R}=A^{R}C^{R}.

  3. (iii)

    (A+B)rR=ArR+BrR(A+B)_{r}^{R}=A_{r}^{R}+B_{r}^{R}, (α​A)rR=α​ArR(\alpha A)_{r}^{R}=\alpha A_{r}^{R}, (A​C)rR=ArR​CR(AC)_{r}^{R}=A_{r}^{R}C^{R}.

Lemma 2.2.

Let X=X0+X1​i+X2​j+X3​k∈ℚℝn×nX=X_{0}+X_{1}\textit{{i}}+X_{2}\textit{{j}}+X_{3}\textit{{k}}\in\mathbb{Q}_{\mathbb{R}}^{n\times n}. Then vec​(XR)=𝒥​vec​(XrR)\mathrm{vec}(X^{R})=\mathcal{J}\mathrm{vec}(X_{r}^{R}). We have

𝒥=[𝒥0−𝒥1𝒥2−𝒥3𝒥1𝒥0𝒥3𝒥2𝒥2−𝒥3𝒥0−𝒥1𝒥3𝒥2𝒥1𝒥0],\mathcal{J}=\begin{bmatrix}\mathcal{J}_{0}&-\mathcal{J}_{1}&\mathcal{J}_{2}&-\mathcal{J}_{3}\\ \mathcal{J}_{1}&\mathcal{J}_{0}&\mathcal{J}_{3}&\mathcal{J}_{2}\\ \mathcal{J}_{2}&-\mathcal{J}_{3}&\mathcal{J}_{0}&-\mathcal{J}_{1}\\ \mathcal{J}_{3}&\mathcal{J}_{2}&\mathcal{J}_{1}&\mathcal{J}_{0}\end{bmatrix}, (6)

where 𝒥0=[𝒥01𝒥02⋮𝒥0​n]\mathcal{J}_{0}=\begin{bmatrix}\mathcal{J}_{01}\\ \mathcal{J}_{02}\\ \vdots\\ \mathcal{J}_{0n}\\ \end{bmatrix}, 𝒥1=[𝒥11𝒥12⋮𝒥1​n]\mathcal{J}_{1}=\begin{bmatrix}\mathcal{J}_{11}\\ \mathcal{J}_{12}\\ \vdots\\ \mathcal{J}_{1n}\\ \end{bmatrix}, 𝒥2=[𝒥21𝒥22⋮𝒥2​n]\mathcal{J}_{2}=\begin{bmatrix}\mathcal{J}_{21}\\ \mathcal{J}_{22}\\ \vdots\\ \mathcal{J}_{2n}\\ \end{bmatrix}, 𝒥3=[𝒥31𝒥32⋮𝒥3​n]\mathcal{J}_{3}=\begin{bmatrix}\mathcal{J}_{31}\\ \mathcal{J}_{32}\\ \vdots\\ \mathcal{J}_{3n}\\ \end{bmatrix}. 𝒥i​j\mathcal{J}_{ij} is a block matrix of size 4×n4\times n with InI_{n} at the (i+1,j)t​h(i+1,j)^{th} position, and the rest of the entries are zero matrices of size nn, where i=0,1,2,3i=0,1,2,3 and j=1,2,…,nj=1,2,\ldots,n.

The above lemma can be easily derived through direct computation; thus, we omit the proof. To enhance our understanding of the above lemma, we will examine it in the context of n=2n=2. In this scenario, we have

𝒥0=[𝒥01𝒥02]=[I20000000\hdashline​0I2000000]\mathcal{J}_{0}=\begin{bmatrix}\mathcal{J}_{01}\\ \mathcal{J}_{02}\end{bmatrix}=\begin{bmatrix}I_{2}&0\\ 0&0\\ 0&0\\ 0&0\\ \hdashline 0&I_{2}\\ 0&0\\ 0&0\\ 0&0\end{bmatrix}, 𝒥1=[𝒥11𝒥12]=[00I200000\hdashline​000I20000]\mathcal{J}_{1}=\begin{bmatrix}\mathcal{J}_{11}\\ \mathcal{J}_{12}\end{bmatrix}=\begin{bmatrix}0&0\\ I_{2}&0\\ 0&0\\ 0&0\\ \hdashline 0&0\\ 0&I_{2}\\ 0&0\\ 0&0\end{bmatrix}, 𝒥2=[𝒥21𝒥22]=[0000I2000\hdashline​00000I200]\mathcal{J}_{2}=\begin{bmatrix}\mathcal{J}_{21}\\ \mathcal{J}_{22}\end{bmatrix}=\begin{bmatrix}0&0\\ 0&0\\ I_{2}&0\\ 0&0\\ \hdashline 0&0\\ 0&0\\ 0&I_{2}\\ 0&0\end{bmatrix}, 𝒥3=[𝒥31𝒥32]=[000000I20\hdashline​0000000I2].\mathcal{J}_{3}=\begin{bmatrix}\mathcal{J}_{31}\\ \mathcal{J}_{32}\end{bmatrix}=\begin{bmatrix}0&0\\ 0&0\\ 0&0\\ I_{2}&0\\ \hdashline 0&0\\ 0&0\\ 0&0\\ 0&I_{2}\end{bmatrix}.

Now, we recall some fundamental results that are pivotal in establishing the main findings of this paper.

Definition 2.3.

For X=(xi​j)∈ℝn×nX=(x_{ij})\in{\mathbb{R}}^{n\times n}, let α1=[x11,x21,…,xn​1]\alpha_{1}=\left[x_{11},x_{21},\ldots,x_{n1}\right], α2=[x22,x32,…,xn​2]\alpha_{2}=\left[x_{22},x_{32},\ldots,x_{n2}\right], …\ldots, αn−1=[x(n−1)​(n−1),xn​(n−1)]\alpha_{n-1}=\left[x_{(n-1)(n-1)},x_{n(n-1)}\right], αn=xn​n\alpha_{n}=x_{nn}, and denote by vecS​(X)\mathrm{vec}_{S}(X) the following vector:

vecS​(X)=[α1,α2,…,αn−1,αn]T∈ℝn​(n+1)2.\mathrm{vec}_{S}(X)=\left[\alpha_{1},\alpha_{2},\ldots,\alpha_{n-1},\alpha_{n}\right]^{T}\in{\mathbb{R}}^{\frac{n(n+1)}{2}}. (7)
Definition 2.4.

For X=(xi​j)∈ℝn×nX=(x_{ij})\in{\mathbb{R}}^{n\times n}, let β1=[x21,x31,…,xn​1]\beta_{1}=\left[x_{21},x_{31},\ldots,x_{n1}\right], β2=[x32,x42,…,xn​2]\beta_{2}=\left[x_{32},x_{42},\ldots,x_{n2}\right], …\ldots, βn−2=[x(n−1)​(n−2),xn​(n−2)]\beta_{n-2}=\left[x_{(n-1)(n-2)},x_{n(n-2)}\right], βn−1=xn​(n−1)\beta_{n-1}=x_{n(n-1)}, and denote by vecA​(X)\mathrm{vec}_{A}(X) the following vector:

vecA​(X)=[β1,β2,…,βn−2,βn−1]T∈ℝn​(n−1)2.\mathrm{vec}_{A}(X)=\left[\beta_{1},\beta_{2},\ldots,\beta_{n-2},\beta_{n-1}\right]^{T}\in{\mathbb{R}}^{\frac{n(n-1)}{2}}. (8)
Lemma 2.5.

[23] If X∈ℝn×nX\in{\mathbb{R}}^{n\times n}, then

  1. (i)

    X∈𝕊​ℝn×n⇔vec​(X)=KS​vecS​(X)X\in{\mathbb{S}\mathbb{R}}^{n\times n}\iff\mathrm{vec}(X)=K_{S}\mathrm{vec}_{S}(X), where vecS​(X)\mathrm{vec}_{S}(X) is of the form (7), and the matrix KS∈ℝn2×n​(n+1)2K_{S}\in{\mathbb{R}}^{n^{2}\times\frac{n(n+1)}{2}} is represented as

    KS={blockarray}​c​c​c​c​c​c​c​c​c​c​c​c​c​c​c​{block}​[c​c​c​c​c​c​c​c​c​c​c​c​c​c​c]​e1​&​e2​e3​⋯​en−1​en​00​⋯​00​⋯​0000​e1​0​⋯​00​e2​e3​⋯​en−1​en​⋯​00000​e1​⋯​000​e2​⋯​00​⋯​000​⋮​⋮​⋮​⋮​⋮​⋮​⋮​⋮​⋮​⋮​⋮​⋮​000​⋯​e1​000​⋯​e2​0​⋯​en−1​en​0000​⋯​0​e1​00​⋯​0​e2​⋯​0​en−1​en.K_{S}=\blockarray{ccccccccccccccc}\block{[ccccccccccccccc]}e_{1}&e_{2}e_{3}\cdots e_{n-1}e_{n}00\cdots 00\cdots 000\\ 0e_{1}0\cdots 00e_{2}e_{3}\cdots e_{n-1}e_{n}\cdots 000\\ 00e_{1}\cdots 000e_{2}\cdots 00\cdots 000\\ \vdots\vdots\vdots\vdots\vdots\vdots\vdots\vdots\vdots\vdots\vdots\vdots\\ 000\cdots e_{1}000\cdots e_{2}0\cdots e_{n-1}e_{n}0\\ 000\cdots 0e_{1}00\cdots 0e_{2}\cdots 0e_{n-1}e_{n}\\ .
  2. (ii)

    X∈𝔸​𝕊​ℝn×n⇔vec​(X)=KA​vecA​(X)X\in{\mathbb{A}\mathbb{S}\mathbb{R}}^{n\times n}\iff\mathrm{vec}(X)=K_{A}\mathrm{vec}_{A}(X), where vecA​(X)\mathrm{vec}_{A}(X) is of the form (8), and the matrix KA∈ℝn2×n​(n−1)2K_{A}\in{\mathbb{R}}^{n^{2}\times\frac{n(n-1)}{2}} is represented as

    KA={blockarray}​c​c​c​c​c​c​c​c​c​c​c​{block}​[c​c​c​c​c​c​c​c​c​c​c]​e2​&​e3​⋯​en−1​en​0​⋯​00​⋯​0−e1​0​⋯​00​e3​⋯​en−1​en​⋯​00−e1​⋯​00−e2​⋯​00​⋯​0​⋮​⋮​⋮​⋮​⋮​⋮​⋮​⋮​00​⋯−e1​00​⋯−e2​0​⋯​en​00​⋯​0−e1​0​⋯​0−e2​⋯−en−1.K_{A}=\blockarray{ccccccccccc}\block{[ccccccccccc]}e_{2}&e_{3}\cdots e_{n-1}e_{n}0\cdots 00\cdots 0\\ -e_{1}0\cdots 00e_{3}\cdots e_{n-1}e_{n}\cdots 0\\ 0-e_{1}\cdots 00-e_{2}\cdots 00\cdots 0\\ \vdots\vdots\vdots\vdots\vdots\vdots\vdots\vdots\\ 00\cdots-e_{1}00\cdots-e_{2}0\cdots e_{n}\\ 00\cdots 0-e_{1}0\cdots 0-e_{2}\cdots-e_{n-1}\\ .

For any X=X0+X1​i+X2​j+X3​k∈ℍ​ℚℝn×nX=X_{0}+X_{1}\textit{{i}}+X_{2}\textit{{j}}+X_{3}\textit{{k}}\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n}, it is easy to see that

X∈ℍ​ℚℝn×n⇔X0T=X0,X1T=−X1,X2T=−X2,X3T=−X3.X\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n}\iff X_{0}^{T}=X_{0},\;X_{1}^{T}=-X_{1},\;X_{2}^{T}=-X_{2},\;X_{3}^{T}=-X_{3}.

Set

𝒬=[KS0000−KA0000KA0000−KA].\mathcal{Q}=\begin{bmatrix}K_{S}&0&0&0\\ 0&-K_{A}&0&0\\ 0&0&K_{A}&0\\ 0&0&0&-K_{A}\end{bmatrix}. (9)
Lemma 2.6.

If X=X0+X1​i+X2​j+X3​k∈ℚℝn×nX=X_{0}+X_{1}\textit{{i}}+X_{2}\textit{{j}}+X_{3}\textit{{k}}\in\mathbb{Q}_{\mathbb{R}}^{n\times n}, then

X∈ℍ​ℚℝn×n⇔vec​(XrR)=𝒬​[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)].X\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n}\iff\mathrm{vec}(X_{r}^{R})=\mathcal{Q}\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}.
Proof.

For X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n}, we have X0∈𝕊​ℝn×nX_{0}\in{\mathbb{S}\mathbb{R}}^{n\times n} and X1X_{1}, X2X_{2}, X3∈𝔸​𝕊​ℝn×nX_{3}\in{\mathbb{A}\mathbb{S}\mathbb{R}}^{n\times n}. By applying Lemma 2.5, we obtain vec​(X0)=KS​vecS​(X0)\mathrm{vec}(X_{0})=K_{S}\mathrm{vec}_{S}(X_{0}), vec​(X1)=KA​vecA​(X1)\mathrm{vec}(X_{1})=K_{A}\mathrm{vec}_{A}(X_{1}), vec​(X2)=KA​vecA​(X2)\mathrm{vec}(X_{2})=K_{A}\mathrm{vec}_{A}(X_{2}), and vec​(X3)=KA​vecA​(X3)\mathrm{vec}(X_{3})=K_{A}\mathrm{vec}_{A}(X_{3}). By utilizing (5) and (9), we achieve the desired result. ∎

Additionally, we need the following lemma for developing the main results.

Lemma 2.7.

[6] Consider the matrix equation of the form A​x=bAx=b, where A∈ℝm×nA\in{\mathbb{R}}^{m\times n} and b∈ℝmb\in{\mathbb{R}}^{m}. The following results hold:

  1. (i)

    The matrix equation has a solution xx if and only if A​A+​b=bAA^{+}b=b. In this case, the general solution is x=A+​b+(I−A+​A)​y,x=A^{+}b+\left(I-A^{+}A\right)y, where y∈ℝny\in{\mathbb{R}}^{n} is an arbitrary vector. Furthermore, if the consistency condition is satisfied, then the matrix equation has a unique solution if and only if rank​(A)=n\mathrm{rank}(A)=n. In this case, the unique solution is x=A+​bx=A^{+}b.

  2. (ii)

    The least squares solutions of the matrix equation can be expressed as x=A+​b+(I−A+​A)​y,x=A^{+}b+\left(I-A^{+}A\right)y, where y∈ℝny\in{\mathbb{R}}^{n} is an arbitrary vector, and the least squares solution with the least norm is x=A+​bx=A^{+}b.

3 Framework for solving constrained RBME

In this section, we initially investigate the least squares Hermitian solution with the least norm of RBME (1) using the RR method. The problem is formulated as follows:

Problem 3.1.

Given matrices A,C∈ℚℝm×nA,C\in\mathbb{Q}_{\mathbb{R}}^{m\times n}, B,D∈ℚℝn×sB,D\in\mathbb{Q}_{\mathbb{R}}^{n\times s}, and E,F∈ℚℝm×sE,F\in\mathbb{Q}_{\mathbb{R}}^{m\times s}, let

ℋL​E={X|X∈ℍℚℝn×n,∥(AXB−E,CXD−F)∥F=minX~∈ℍ​ℚℝn×n∥(AX~B−E,CX~D−F)∥F}.\mathcal{H}_{LE}=\left\{X\;|\;X\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n},\;\left\lVert\left(AXB-E,CXD-F\right)\right\rVert_{F}=\min_{\widetilde{X}\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n}}\left\lVert\left(A\widetilde{X}B-E,C\widetilde{X}D-F\right)\right\rVert_{F}\right\}.

Then, find XH∈ℋL​EX_{H}\in\mathcal{H}_{LE} such that

∥XH∥F=minX∈ℋL​E​∥X∥F.\left\lVert X_{H}\right\rVert_{F}=\underset{X\in\mathcal{H}_{LE}}{\min}\left\lVert X\right\rVert_{F}.

Next, by utilizing the RR method, we derive the necessary and sufficient conditions for the existence of the Hermitian solution for RBME (1), along with a general formulation for the solution if the consistency criterion is met. We also establish the conditions for a unique solution and, in such cases, provide a general form of the solution. The RR method involves transforming the constrained RBME (1) into an equivalent unconstrained real linear system.

Following that, we present a concise overview of the CR method, which is employed to find the Hermitian solution for RBME (1) as documented in [18]. Additionally, we conduct a comparative analysis between the RR and CR methods.

Before proceeding, we introduce some notations that will be used in the subsequent results. Let

𝒫=[(BR)T⊗ArR(DR)T⊗CrR],ℛ=diag​(KS,KA,KA,KA).\mathcal{P}=\begin{bmatrix}(B^{R})^{T}\otimes A_{r}^{R}\\ (D^{R})^{T}\otimes C_{r}^{R}\end{bmatrix},\;\;\mathcal{R}=\mathrm{diag}(K_{S},K_{A},K_{A},K_{A}). (10)
Theorem 3.1.

Given matrices A,C∈ℚℝm×nA,C\in\mathbb{Q}_{\mathbb{R}}^{m\times n}, B,D∈ℚℝn×sB,D\in\mathbb{Q}_{\mathbb{R}}^{n\times s}, and E,F∈ℚℝm×sE,F\in\mathbb{Q}_{\mathbb{R}}^{m\times s}, let X=X0+X1​i+X2​j+X3​k∈ℚℝn×nX=X_{0}+X_{1}\textit{{i}}+X_{2}\textit{{j}}+X_{3}\textit{{k}}\in\mathbb{Q}_{\mathbb{R}}^{n\times n}. Let 𝒫\mathcal{P} and ℛ\mathcal{R} be of the form (10), and let 𝒥\mathcal{J} and 𝒬\mathcal{Q} be of the form (6) and (9), respectively. Then, the set ℋL​E\mathcal{H}_{LE} of Problem 3.1 can be expressed as

ℋL​E={X|[vec​(X0)vec​(X1)vec​(X2)vec​(X3)]=ℛ​(𝒫​𝒥​𝒬)+​[vec​(ErR)vec​(FrR)]+ℛ​(I(2​n2−n)−(𝒫​𝒥​𝒬)+​(𝒫​𝒥​𝒬))​y},\mathcal{H}_{LE}=\left\{X\;\left|\;\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\\ \mathrm{vec}(X_{2})\\ \mathrm{vec}(X_{3})\end{bmatrix}\right.=\mathcal{R}\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}+\mathcal{R}\left(I_{(2n^{2}-n)}-\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)\right)y\right\}, (11)

where y∈ℝ(2​n2−n)y\in{\mathbb{R}}^{(2n^{2}-n)} is an arbitrary vector. Furthermore, the unique solution XH∈ℋL​EX_{H}\in\mathcal{H}_{LE} to Problem 3.1 satisfies

[vec​(X0)vec​(X1)vec​(X2)vec​(X3)]=ℛ​(𝒫​𝒥​𝒬)+​[vec​(ErR)vec​(FrR)].\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\\ \mathrm{vec}(X_{2})\\ \mathrm{vec}(X_{3})\end{bmatrix}=\mathcal{R}\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}. (12)
Proof.

By using (2), (4), and Lemma 2.1, we get

∥(A​X​B−E,C​X​D−F)∥F2\displaystyle\left\lVert\left(AXB-E,CXD-F\right)\right\rVert_{F}^{2} =\displaystyle= ∥(A​X​B−E)∥F2+∥(C​X​D−F)∥F2\displaystyle\left\lVert\left(AXB-E\right)\right\rVert_{F}^{2}+\left\lVert\left(CXD-F\right)\right\rVert_{F}^{2}
=\displaystyle= ∥(A​X​B−E)rR∥F2+∥(C​X​D−F)rR∥F2\displaystyle\left\lVert\left(AXB-E\right)_{r}^{R}\right\rVert_{F}^{2}+\left\lVert\left(CXD-F\right)_{r}^{R}\right\rVert_{F}^{2}
=\displaystyle= ∥(ArR​XR​BR−ErR)∥F2+∥(CrR​XR​DR−FrR)∥F2\displaystyle\left\lVert\left(A_{r}^{R}X^{R}B^{R}-E_{r}^{R}\right)\right\rVert_{F}^{2}+\left\lVert\left(C_{r}^{R}X^{R}D^{R}-F_{r}^{R}\right)\right\rVert_{F}^{2}
=\displaystyle= ∥vec​(ArR​XR​BR−ErR)∥F2+∥vec​(CrR​XR​DR−FrR)∥F2.\displaystyle\left\lVert\mathrm{vec}\left(A_{r}^{R}X^{R}B^{R}-E_{r}^{R}\right)\right\rVert_{F}^{2}+\left\lVert\mathrm{vec}\left(C_{r}^{R}X^{R}D^{R}-F_{r}^{R}\right)\right\rVert_{F}^{2}.

We have

vec​(ArR​XR​BR−ErR)\displaystyle\mathrm{vec}\left(A_{r}^{R}X^{R}B^{R}-E_{r}^{R}\right) =\displaystyle= ((BR)T⊗ArR)​vec​(XR)−vec​(ErR),\displaystyle\left(\left(B^{R}\right)^{T}\otimes A_{r}^{R}\right)\mathrm{vec}(X^{R})-\mathrm{vec}(E_{r}^{R}),
vec​(CrR​XR​DR−FrR)\displaystyle\mathrm{vec}\left(C_{r}^{R}X^{R}D^{R}-F_{r}^{R}\right) =\displaystyle= ((DR)T⊗CrR)​vec​(XR)−vec​(FrR).\displaystyle\left(\left(D^{R}\right)^{T}\otimes C_{r}^{R}\right)\mathrm{vec}(X^{R})-\mathrm{vec}(F_{r}^{R}).

By using Lemma 2.2 and Lemma 2.6, we get

vec​(XR)=𝒥​vec​(XrR)=𝒥​𝒬​[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)].\mathrm{vec}(X^{R})=\mathcal{J}\mathrm{vec}\left(X_{r}^{R}\right)=\mathcal{J}\mathcal{Q}\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}.

Thus,

∥(A​X​B−E,C​X​D−F)∥F2\displaystyle\left\lVert\left(AXB-E,CXD-F\right)\right\rVert_{F}^{2} =\displaystyle= ∥[(BR)T⊗ArR(DR)T⊗CrR]​vec​(XR)−[vec​(ErR)vec​(FrR)]∥F2\displaystyle\left\lVert\begin{bmatrix}\left(B^{R}\right)^{T}\otimes A_{r}^{R}\\ \left(D^{R}\right)^{T}\otimes C_{r}^{R}\end{bmatrix}\mathrm{vec}\left(X^{R}\right)-\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}\right\rVert_{F}^{2}
=\displaystyle= ∥𝒫​𝒥​𝒬​[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)]−[vec​(ErR)vec​(FrR)]∥F2.\displaystyle\left\lVert\mathcal{P}\mathcal{J}\mathcal{Q}\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}-\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}\right\rVert_{F}^{2}.

Hence, Problem 3.1 can be solved by finding the least squares solutions of the following unconstrained real matrix system:

𝒫​𝒥​𝒬​[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)]=[vec​(ErR)vec​(FrR)].\mathcal{P}\mathcal{J}\mathcal{Q}\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}=\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}. (13)

By using the fact that X∈ℍ​ℚℝn×n⇔X0∈𝕊​ℝn×n,X1∈𝔸​𝕊​ℝn×n,X2∈𝔸​𝕊​ℝn×n,X3∈𝔸​𝕊​ℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n}\iff X_{0}\in{\mathbb{S}\mathbb{R}}^{n\times n},X_{1}\in{\mathbb{A}\mathbb{S}\mathbb{R}}^{n\times n},X_{2}\in{\mathbb{A}\mathbb{S}\mathbb{R}}^{n\times n},X_{3}\in{\mathbb{A}\mathbb{S}\mathbb{R}}^{n\times n}, and using Lemma 2.5, we have

[vec​(X0)vec​(X1)vec​(X2)vec​(X3)]=ℛ​[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)].\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\\ \mathrm{vec}(X_{2})\\ \mathrm{vec}(X_{3})\end{bmatrix}=\mathcal{R}\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}. (14)

By using Lemma 2.7, the least squares solutions of matrix equation (13) is given by

[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)]=(𝒫​𝒥​𝒬)+​[vec​(ErR)vec​(FrR)]+(I(2​n2−n)−(𝒫​𝒥​𝒬)+​(𝒫​𝒥​𝒬))​y,\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}=\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}+\left(I_{(2n^{2}-n)}-\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)\right)y, (15)

where y∈ℝ(2​n2−n)y\in{\mathbb{R}}^{(2n^{2}-n)} is an arbitrary vector. Hence, we get (11) by utilizing (14) and (15).

In addition, by employing Lemma 2.7, the least squares solution with the least norm for matrix equation (13) is given by

[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)]=(𝒫​𝒥​𝒬)+​[vec​(ErR)vec​(FrR)].\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}=\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}. (16)

Hence, we get (12) by utilizing (14) and (16). ∎

Theorem 3.2.

Let 𝒫\mathcal{P} and ℛ\mathcal{R} be in the form of (10), and let X=X0+X1​i+X2​j+X3​k∈ℚℝn×nX=X_{0}+X_{1}\textit{{i}}+X_{2}\textit{{j}}+X_{3}\textit{{k}}\in\mathbb{Q}_{\mathbb{R}}^{n\times n}. Additionally, let 𝒥\mathcal{J} and 𝒬\mathcal{Q} be as in (6) and (9), respectively. Then, the RBME (1) has a Hermitian solution X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} if and only if

(I8​m​s−(𝒫​𝒥​𝒬)​(𝒫​𝒥​𝒬)+)​[vec​(ErR)vec​(FrR)]=0.\left(I_{8ms}-\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\right)\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}=0. (17)

In this case, the general solution X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} satisfies

[vec​(X0)vec​(X1)vec​(X2)vec​(X3)]=ℛ​(𝒫​𝒥​𝒬)+​[vec​(ErR)vec​(FrR)]+ℛ​(I(2​n2−n)−(𝒫​𝒥​𝒬)+​(𝒫​𝒥​𝒬))​y,\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\\ \mathrm{vec}(X_{2})\\ \mathrm{vec}(X_{3})\end{bmatrix}=\mathcal{R}\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}+\mathcal{R}\left(I_{(2n^{2}-n)}-\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)\right)y, (18)

where y∈ℝ(2​n2−n)y\in{\mathbb{R}}^{(2n^{2}-n)} is an arbitrary vector. Furthermore, if (17) holds, then the RBME (1) has a unique solution X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} if and only if

rank​(𝒫​𝒥​𝒬)=2​n2−n.\mathrm{rank}\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)=2n^{2}-n. (19)

In this case, the unique solution X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} satisfies

[vec​(X0)vec​(X1)vec​(X2)vec​(X3)]=ℛ​(𝒫​𝒥​𝒬)+​[vec​(ErR)vec​(FrR)].\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\\ \mathrm{vec}(X_{2})\\ \mathrm{vec}(X_{3})\end{bmatrix}=\mathcal{R}\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}. (20)
Proof.

By using Lemmas 2.1, 2.2, and 2.6, we have

(A​X​B,C​X​D)=(E,F)\displaystyle\left(AXB,CXD\right)=\left(E,F\right) ⇔\displaystyle\iff ((A​X​B)rR,(C​X​D)rR)=(ErR,FrR)\displaystyle\left(\left(AXB\right)_{r}^{R},\left(CXD\right)_{r}^{R}\right)=\left(E_{r}^{R},F_{r}^{R}\right)
⇔\displaystyle\iff (ArR​XR​BR,CrR​XR​DR)=(ErR,FrR)\displaystyle\left(A_{r}^{R}X^{R}B^{R},C_{r}^{R}X^{R}D^{R}\right)=\left(E_{r}^{R},F_{r}^{R}\right)
⇔\displaystyle\iff (vec​(ArR​XR​BR),vec​(CrR​XR​DR))=(vec​(ErR),vec​(FrR))\displaystyle\left(\mathrm{vec}\left(A_{r}^{R}X^{R}B^{R}\right),\mathrm{vec}\left(C_{r}^{R}X^{R}D^{R}\right)\right)=\left(\mathrm{vec}\left(E_{r}^{R}\right),\mathrm{vec}\left(F_{r}^{R}\right)\right)
⇔\displaystyle\iff [vec​(ArR​XR​BR)vec​(CrR​XR​DR)]=[vec​(ErR)vec​(FrR)]\displaystyle\begin{bmatrix}\mathrm{vec}\left(A_{r}^{R}X^{R}B^{R}\right)\\ \mathrm{vec}\left(C_{r}^{R}X^{R}D^{R}\right)\end{bmatrix}=\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}
⇔\displaystyle\iff [(BR)T⊗ArR(DR)T⊗CrR]​vec​(XR)=[vec​(ErR)vec​(FrR)]\displaystyle\begin{bmatrix}\left(B^{R}\right)^{T}\otimes A_{r}^{R}\\ \left(D^{R}\right)^{T}\otimes C_{r}^{R}\end{bmatrix}\mathrm{vec}\left(X^{R}\right)=\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}
⇔\displaystyle\iff 𝒫​𝒥​𝒬​[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)]=[vec​(ErR)vec​(FrR)].\displaystyle\mathcal{P}\mathcal{J}\mathcal{Q}\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}=\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}.

Hence, solving the constrained RBME (1) is equivalent to solving the following unconstrained real matrix system:

𝒫​𝒥​𝒬​[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)]=[vec​(ErR)vec​(FrR)].\mathcal{P}\mathcal{J}\mathcal{Q}\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}=\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}. (21)

By using the fact that X∈ℍ​ℚℝn×n⇔X0∈𝕊​ℝn×n,X1∈𝔸​𝕊​ℝn×n,X2∈𝔸​𝕊​ℝn×n,X3∈𝔸​𝕊​ℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n}\iff X_{0}\in{\mathbb{S}\mathbb{R}}^{n\times n},X_{1}\in{\mathbb{A}\mathbb{S}\mathbb{R}}^{n\times n},X_{2}\in{\mathbb{A}\mathbb{S}\mathbb{R}}^{n\times n},X_{3}\in{\mathbb{A}\mathbb{S}\mathbb{R}}^{n\times n}, and using Lemma 2.5, we have

[vec​(X0)vec​(X1)vec​(X2)vec​(X3)]=ℛ​[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)].\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\\ \mathrm{vec}(X_{2})\\ \mathrm{vec}(X_{3})\end{bmatrix}=\mathcal{R}\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}. (22)

By leveraging Lemma 2.7, we obtain the consistency condition (17). This condition establishes the criterion that ensures a solution to matrix equation (21) and a Hermitian solution for RBME (1). In this case, the solution to matrix equation (21) can be expressed as

[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)]=(𝒫​𝒥​𝒬)+​[vec​(ErR)vec​(FrR)]+(I(2​n2−n)−(𝒫​𝒥​𝒬)+​(𝒫​𝒥​𝒬))​y,\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}=\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}+\left(I_{(2n^{2}-n)}-\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)\right)y, (23)

where y∈ℝ(2​n2−n)y\in{\mathbb{R}}^{(2n^{2}-n)} is an arbitrary vector. By applying (22) and (23), we get that the Hermitian solution to RBME (1) satisfies (18).

Furthermore, if condition (17) is satisfied, applying Lemma 2.7 leads to the derivation of the condition (19). This condition signifies the criterion for ensuring a unique solution to matrix equation (21) and a unique Hermitian solution to RBME (1). In this case, the unique solution to matrix equation (21) is given by

[vecS​(X0)vecA​(X1)vecA​(X2)vecA​(X3)]=(𝒫​𝒥​𝒬)+​[vec​(ErR)vec​(FrR)].\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\\ \mathrm{vec}_{A}(X_{2})\\ \mathrm{vec}_{A}(X_{3})\end{bmatrix}=\left(\mathcal{P}\mathcal{J}\mathcal{Q}\right)^{+}\begin{bmatrix}\mathrm{vec}(E_{r}^{R})\\ \mathrm{vec}(F_{r}^{R})\end{bmatrix}. (24)

By using (22) and (24), we get that the unique Hermitian solution to RBME (1) satisfies (20). ∎

In [18], the authors investigated the Hermitian solution of RBME (1) using the CR method. They successfully established the necessary and sufficient conditions for the existence of a solution, along with providing a general expression for it. In the remainder of this section, we will present the findings from [18].
A reduced biquaternion matrix A∈ℚℝm×nA\in\mathbb{Q}_{\mathbb{R}}^{m\times n} is uniquely expressed as A=A1+A2​jA=A_{1}+A_{2}\textit{{j}}, where A1A_{1}, A2∈ℂm×nA_{2}\in{\mathbb{C}}^{m\times n}. We have ΨA=[A1,A2]∈ℂm×2​n\Psi_{A}=\left[A_{1},A_{2}\right]\in{\mathbb{C}}^{m\times 2n} and vec​(ΨA)=[vec​(A1)vec​(A2)].\mathrm{vec}(\Psi_{A})=\begin{bmatrix}\mathrm{vec}(A_{1})\\ \mathrm{vec}(A_{2})\end{bmatrix}. The complex representation of matrix AA, denoted as h​(A)h(A), is defined as

h​(A)=[A1A2A2A1].h(A)=\begin{bmatrix}A_{1}&A_{2}\\ A_{2}&A_{1}\end{bmatrix}.

Given matrices A=A1+A2​j∈ℚℝm×nA=A_{1}+A_{2}\textit{{j}}\in\mathbb{Q}_{\mathbb{R}}^{m\times n}, B=B1+B2​j∈ℚℝn×sB=B_{1}+B_{2}\textit{{j}}\in\mathbb{Q}_{\mathbb{R}}^{n\times s}, C=C1+C2​j∈ℚℝm×nC=C_{1}+C_{2}\textit{{j}}\in\mathbb{Q}_{\mathbb{R}}^{m\times n}, D=D1+D2​j∈ℚℝn×sD=D_{1}+D_{2}\textit{{j}}\in\mathbb{Q}_{\mathbb{R}}^{n\times s}, E=E1+E2​j∈ℚℝm×sE=E_{1}+E_{2}\textit{{j}}\in\mathbb{Q}_{\mathbb{R}}^{m\times s}, and F=F1+F2​j∈ℚℝm×sF=F_{1}+F_{2}\textit{{j}}\in\mathbb{Q}_{\mathbb{R}}^{m\times s}. We have

(A​X​B,C​X​D)=(E,F)⇔(vec​(ΨA​X​B),vec​(ΨC​X​D))=(vec​(ΨE),vec​(ΨF)).\left(AXB,CXD\right)=\left(E,F\right)\iff\left(\mathrm{vec}(\Psi_{AXB}),\mathrm{vec}(\Psi_{CXD})\right)=\left(\mathrm{vec}(\Psi_{E}),\mathrm{vec}(\Psi_{F})\right).

Denote

ℛ=diag​(KS,KA,KA,KA)\mathcal{R}=\mathrm{diag}(K_{S},K_{A},K_{A},K_{A}),   𝒰=[KSi​KA0000KAi​KA]\mathcal{U}=\begin{bmatrix}K_{S}&\textit{{i}}K_{A}&0&0\\ 0&0&K_{A}&\textit{{i}}K_{A}\end{bmatrix},   x=[vecS​(ℜ⁡(X1))vecA​(ℑ⁡(X1))vecA​(ℜ⁡(X2))vecA​(ℑ⁡(X2))],x=\begin{bmatrix}\mathrm{vec}_{S}(\Re(X_{1}))\\ \mathrm{vec}_{A}(\Im(X_{1}))\\ \mathrm{vec}_{A}(\Re(X_{2}))\\ \mathrm{vec}_{A}(\Im(X_{2}))\end{bmatrix},

M=h​((B1T⊗A1+B2T⊗A2)+(B1T⊗A2+B2T⊗A1)​j)M=h\left(\left(B_{1}^{T}\otimes A_{1}+B_{2}^{T}\otimes A_{2}\right)+\left(B_{1}^{T}\otimes A_{2}+B_{2}^{T}\otimes A_{1}\right)\textit{{j}}\right),

N=h​((D1T⊗C1+D2T⊗C2)+(D1T⊗C2+D2T⊗C1)​j)N=h\left(\left(D_{1}^{T}\otimes C_{1}+D_{2}^{T}\otimes C_{2}\right)+\left(D_{1}^{T}\otimes C_{2}+D_{2}^{T}\otimes C_{1}\right)\textit{{j}}\right).

According to [18, Lemma 2.3], for X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n}, the authors of [18] obtained

vec​(ΨA​X​B)\displaystyle\mathrm{vec}(\Psi_{AXB}) =\displaystyle= h​((B1T⊗A1+B2T⊗A2)+(B1T⊗A2+B2T⊗A1)​j)​𝒰​x=M​𝒰​x,\displaystyle h\left(\left(B_{1}^{T}\otimes A_{1}+B_{2}^{T}\otimes A_{2}\right)+\left(B_{1}^{T}\otimes A_{2}+B_{2}^{T}\otimes A_{1}\right)\textit{{j}}\right)\mathcal{U}x=M\mathcal{U}x,
vec​(ΨC​X​D)\displaystyle\mathrm{vec}(\Psi_{CXD}) =\displaystyle= h​((D1T⊗C1+D2T⊗C2)+(D1T⊗C2+D2T⊗C1)​j)​𝒰​x=N​𝒰​x.\displaystyle h\left(\left(D_{1}^{T}\otimes C_{1}+D_{2}^{T}\otimes C_{2}\right)+\left(D_{1}^{T}\otimes C_{2}+D_{2}^{T}\otimes C_{1}\right)\textit{{j}}\right)\mathcal{U}x=N\mathcal{U}x.

Thus, the matrix equation (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F) for X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} is equivalent to

[MN]​𝒰​x=[vec​(E1)vec​(E2)vec​(F1)vec​(F2)].\begin{bmatrix}M\\ N\end{bmatrix}\mathcal{U}x=\begin{bmatrix}\mathrm{vec}(E_{1})\\ \mathrm{vec}(E_{2})\\ \mathrm{vec}(F_{1})\\ \mathrm{vec}(F_{2})\end{bmatrix}.

Denote

Q=[MN]​𝒰,Q1=ℜ⁡(Q),Q2=ℑ⁡(Q),e=[vec​(ℜ⁡(E1))vec​(ℜ⁡(E2))vec​(ℜ⁡(F1))vec​(ℜ⁡(F2))vec​(ℑ⁡(E1))vec​(ℑ⁡(E2))vec​(ℑ⁡(F1))vec​(ℑ⁡(F2))].Q=\begin{bmatrix}M\\ N\end{bmatrix}\mathcal{U},\;Q_{1}=\Re(Q),\;Q_{2}=\Im(Q),\;e=\begin{bmatrix}\mathrm{vec}(\Re(E_{1}))\\ \mathrm{vec}(\Re(E_{2}))\\ \mathrm{vec}(\Re(F_{1}))\\ \mathrm{vec}(\Re(F_{2}))\\ \mathrm{vec}(\Im(E_{1}))\\ \mathrm{vec}(\Im(E_{2}))\\ \mathrm{vec}(\Im(F_{1}))\\ \mathrm{vec}(\Im(F_{2}))\\ \end{bmatrix}. (25)

We have

[Q1Q2]+=[Q1+−HT​Q2​Q1+,HT],[Q1Q2]+​[Q1Q2]=Q1+​Q1+R​R+,\begin{bmatrix}Q_{1}\\ Q_{2}\end{bmatrix}^{+}=\left[Q_{1}^{+}-H^{T}Q_{2}Q_{1}^{+},H^{T}\right],\;\begin{bmatrix}Q_{1}\\ Q_{2}\end{bmatrix}^{+}\begin{bmatrix}Q_{1}\\ Q_{2}\end{bmatrix}=Q_{1}^{+}Q_{1}+RR^{+}, (26)

where

H=R++(I−R+​R)​Z​Q2​Q1+​Q1+T​(I−Q2T​R+),R=(I−Q1+​Q1)​Q2T,Z=(I+(I−R+​R)​Q2​Q1+​Q1+T​Q2T​(I−R+​R))−1.}\left.\begin{aligned} H&=R^{+}+\left(I-R^{+}R\right)ZQ_{2}Q_{1}^{+}Q_{1}^{+T}\left(I-Q_{2}^{T}R^{+}\right),\;\;R=\left(I-Q_{1}^{+}Q_{1}\right)Q_{2}^{T},\\ Z&=\left(I+\left(I-R^{+}R\right)Q_{2}Q_{1}^{+}Q_{1}^{+T}Q_{2}^{T}\left(I-R^{+}R\right)\right)^{-1}.\end{aligned}\right\} (27)

As per [18], solving the constrained RBME (1) is equivalent to solving the following unconstrained real matrix system:

[Q1Q2]​x=e.\begin{bmatrix}Q_{1}\\ Q_{2}\end{bmatrix}x=e.

According to [18, Theorem 3.1], the RBME (1) has a Hermitian solution X=X0+X1​i+X2​j+X3​k∈ℍ​ℚℝn×nX=X_{0}+X_{1}\textit{{i}}+X_{2}\textit{{j}}+X_{3}\textit{{k}}\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} if and only if

(I8​m​s−[Q1Q2]​[Q1Q2]+)​e=0.\left(I_{8ms}-\begin{bmatrix}Q_{1}\\ Q_{2}\end{bmatrix}\begin{bmatrix}Q_{1}\\ Q_{2}\end{bmatrix}^{+}\right)e=0. (28)

In this case, the general solution X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} satisfies

[vec​(ℜ⁡(X1))vec​(ℑ⁡(X1))vec​(ℜ⁡(X2))vec​(ℑ⁡(X2))]=ℛ​[Q1+−HT​Q2​Q1+,HT]​e+ℛ​(I(2​n2−n)−Q1+​Q1−R​R+)​y,\begin{bmatrix}\mathrm{vec}(\Re(X_{1}))\\ \mathrm{vec}(\Im(X_{1}))\\ \mathrm{vec}(\Re(X_{2}))\\ \mathrm{vec}(\Im(X_{2}))\end{bmatrix}=\mathcal{R}\left[Q_{1}^{+}-H^{T}Q_{2}Q_{1}^{+},H^{T}\right]e+\mathcal{R}\left(I_{(2n^{2}-n)}-Q_{1}^{+}Q_{1}-RR^{+}\right)y, (29)

where y∈ℝ(2​n2−n)y\in{\mathbb{R}}^{(2n^{2}-n)} is an arbitrary vector. Furthermore, if the consistency condition is satisfied, then the RBME (1) has a unique solution X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} if and only if

rank​([Q1Q2])=2​n2−n.\mathrm{rank}\left(\begin{bmatrix}Q_{1}\\ Q_{2}\end{bmatrix}\right)=2n^{2}-n. (30)

In this case, the unique solution X∈ℍ​ℚℝn×nX\in\mathbb{H}\mathbb{Q}_{\mathbb{R}}^{n\times n} satisfies

[vec​(ℜ⁡(X1))vec​(ℑ⁡(X1))vec​(ℜ⁡(X2))vec​(ℑ⁡(X2))]=ℛ​[Q1+−HT​Q2​Q1+,HT]​e.\begin{bmatrix}\mathrm{vec}(\Re(X_{1}))\\ \mathrm{vec}(\Im(X_{1}))\\ \mathrm{vec}(\Re(X_{2}))\\ \mathrm{vec}(\Im(X_{2}))\end{bmatrix}=\mathcal{R}\left[Q_{1}^{+}-H^{T}Q_{2}Q_{1}^{+},H^{T}\right]e. (31)
Remark 3.3.

The concept behind the RR method is to transform the operations of reduced biquaternion matrices into the corresponding operations of the first row block of the real representation matrices. This approach takes full advantage of the special structure of real representation matrices, consequently minimizing the count of floating-point operations required. Moreover, our method exclusively employs real matrices and real arithmetic operations, avoiding the complexities associated with complex matrices and complex arithmetic operations used in the CR method. Consequently, our approach is more efficient and time-saving compared to the CR method.

4 Application

We will now employ the framework developed in Section 3 for finding the least squares Hermitian solution with the least norm of CME (1). The problem can be formulated as follows:

Problem 4.1.

Given matrices A,C∈ℂm×nA,C\in{\mathbb{C}}^{m\times n}, B,D∈ℂn×sB,D\in{\mathbb{C}}^{n\times s}, and E,F∈ℂm×sE,F\in{\mathbb{C}}^{m\times s}, let

ℋ~L​E={X|X∈ℍℂn×n,∥(AXB−E,CXD−F)∥F=minX~∈ℍ​ℂn×n∥(AX~B−E,CX~D−F)∥F}.\widetilde{\mathcal{H}}_{LE}=\left\{X\;|\;X\in\mathbb{H}\mathbb{C}^{n\times n},\;\left\lVert\left(AXB-E,CXD-F\right)\right\rVert_{F}=\min_{\widetilde{X}\in\mathbb{H}\mathbb{C}^{n\times n}}\left\lVert\left(A\widetilde{X}B-E,C\widetilde{X}D-F\right)\right\rVert_{F}\right\}.

Then, find X~H∈ℋ~L​E\widetilde{X}_{H}\in\widetilde{\mathcal{H}}_{LE} such that

∥X~H∥F=minX∈ℋ~L​E​∥X∥F.\left\lVert\widetilde{X}_{H}\right\rVert_{F}=\underset{X\in\widetilde{\mathcal{H}}_{LE}}{\min}\left\lVert X\right\rVert_{F}.

It is important to emphasize that complex matrix equations are particular cases of reduced biquaternion matrix equations. Let A=A0+A1​i+A2​j+A3​k∈ℚℝm×nA=A_{0}+A_{1}\textit{{i}}+A_{2}\textit{{j}}+A_{3}\textit{{k}}\in\mathbb{Q}_{\mathbb{R}}^{m\times n}, then A∈ℂm×n⇔A2=0A\in{\mathbb{C}}^{m\times n}\iff A_{2}=0, A3=0A_{3}=0. Consequently, we can apply the framework established in Section 3 to address Problem 4.1. We take the real representation of matrix A=A0+A1​i∈ℂm×nA=A_{0}+A_{1}\textit{{i}}\in{\mathbb{C}}^{m\times n} denoted by A~R\widetilde{A}^{R} as

A~R=[A0−A1A1A0],\widetilde{A}^{R}=\begin{bmatrix}A_{0}&-A_{1}\\ A_{1}&A_{0}\end{bmatrix}, (32)

and the first block row of the block matrix A~R\widetilde{A}^{R} as A~rR=[A0,−A1]\widetilde{A}^{R}_{r}=\left[A_{0},-A_{1}\right].

For matrix X=X0+X1​i∈ℂn×nX=X_{0}+X_{1}\textit{{i}}\in{\mathbb{C}}^{n\times n}, we have

vec​(X~rR)=[vec​(X0)−vec​(X1)].\mathrm{vec}(\widetilde{X}_{r}^{R})=\begin{bmatrix}\mathrm{vec}(X_{0})\\ -\mathrm{vec}(X_{1})\end{bmatrix}. (33)

At first, we need a result establishing the relationship between vec​(X~R)\mathrm{vec}(\widetilde{X}^{R}) and vec​(X~rR)\mathrm{vec}(\widetilde{X}_{r}^{R}). Following a similar approach to Lemma 2.2, we get vec​(X~R)=𝒥~​vec​(X~rR)\mathrm{vec}(\widetilde{X}^{R})=\widetilde{\mathcal{J}}\mathrm{vec}(\widetilde{X}_{r}^{R}), where

𝒥~=[𝒥~0−𝒥~1𝒥~1𝒥~0].\widetilde{\mathcal{J}}=\begin{bmatrix}\widetilde{\mathcal{J}}_{0}&-\widetilde{\mathcal{J}}_{1}\\ \widetilde{\mathcal{J}}_{1}&\widetilde{\mathcal{J}}_{0}\end{bmatrix}. (34)

We have 𝒥~0=[𝒥~01𝒥~02⋮𝒥~0​n]\widetilde{\mathcal{J}}_{0}=\begin{bmatrix}\widetilde{\mathcal{J}}_{01}\\ \widetilde{\mathcal{J}}_{02}\\ \vdots\\ \widetilde{\mathcal{J}}_{0n}\\ \end{bmatrix} and 𝒥~1=[𝒥~11𝒥~12⋮𝒥~1​n]\widetilde{\mathcal{J}}_{1}=\begin{bmatrix}\widetilde{\mathcal{J}}_{11}\\ \widetilde{\mathcal{J}}_{12}\\ \vdots\\ \widetilde{\mathcal{J}}_{1n}\\ \end{bmatrix}. 𝒥~i​j\widetilde{\mathcal{J}}_{ij} is a block matrix of size 2×n2\times n with InI_{n} at (i+1,j)t​h(i+1,j)^{th} position, and the rest of the entries are zero matrices of size nn, where i=0,1i=0,1 and j=1,2,…,nj=1,2,\ldots,n.

To enhance our understanding of above mentioned result, we will examine it in the context of n=2n=2. In this scenario, we have

𝒥~0=[𝒥~01𝒥~02]=[I2000\hdashline​0I200],𝒥~1=[𝒥~11𝒥~12]=[00I20\hdashline​000I2].\widetilde{\mathcal{J}}_{0}=\begin{bmatrix}\widetilde{\mathcal{J}}_{01}\\ \widetilde{\mathcal{J}}_{02}\end{bmatrix}=\begin{bmatrix}I_{2}&0\\ 0&0\\ \hdashline 0&I_{2}\\ 0&0\\ \end{bmatrix},\;\widetilde{\mathcal{J}}_{1}=\begin{bmatrix}\widetilde{\mathcal{J}}_{11}\\ \widetilde{\mathcal{J}}_{12}\end{bmatrix}=\begin{bmatrix}0&0\\ I_{2}&0\\ \hdashline 0&0\\ 0&I_{2}\end{bmatrix}.

Next, we will determine the expression for vec​(X~rR)\mathrm{vec}(\widetilde{X}_{r}^{R}) when X∈ℍ​ℂn×nX\in\mathbb{H}\mathbb{C}^{n\times n}. Following a similar approach to Lemma 2.6, we have X=X0+X1​i∈ℍ​ℂn×n⇔vec​(X~rR)=𝒬~​[vecS​(X0)vecA​(X1)]X=X_{0}+X_{1}\textit{{i}}\in\mathbb{H}\mathbb{C}^{n\times n}\iff\mathrm{vec}(\widetilde{X}_{r}^{R})=\widetilde{\mathcal{Q}}\begin{bmatrix}\mathrm{vec}_{S}(X_{0})\\ \mathrm{vec}_{A}(X_{1})\end{bmatrix}, where

𝒬~=[KS00−KA].\widetilde{\mathcal{Q}}=\begin{bmatrix}K_{S}&0\\ 0&-K_{A}\end{bmatrix}. (35)

Before proceeding, we introduce some notations that will be used in the subsequent results.

𝒫~=[(B~R)T⊗A~rR(D~R)T⊗C~rR],ℛ~=diag​(KS,KA).\widetilde{\mathcal{P}}=\begin{bmatrix}(\widetilde{B}^{R})^{T}\otimes\widetilde{A}_{r}^{R}\\ (\widetilde{D}^{R})^{T}\otimes\widetilde{C}_{r}^{R}\end{bmatrix},\;\;\widetilde{\mathcal{R}}=\mathrm{diag}(K_{S},K_{A}). (36)
Theorem 4.1.

Given matrices A,C∈ℂm×nA,C\in{\mathbb{C}}^{m\times n}, B,D∈ℂn×sB,D\in{\mathbb{C}}^{n\times s}, and E,F∈ℂm×sE,F\in{\mathbb{C}}^{m\times s}, let X=X0+X1​i∈ℂn×nX=X_{0}+X_{1}\textit{{i}}\in{\mathbb{C}}^{n\times n}. Let 𝒫~\widetilde{\mathcal{P}} and ℛ~\widetilde{\mathcal{R}} be of the form (36), and let 𝒥~\widetilde{\mathcal{J}} and ℚ~\widetilde{\mathbb{Q}} be of the form (34) and (35), respectively. Then, the set ℋ~L​E\widetilde{\mathcal{H}}_{LE} of Problem 4.1 can be expressed as

ℋ~L​E={X|[vec​(X0)vec​(X1)]=ℛ~​(𝒫~​𝒥~​𝒬~)+​[vec​(E~rR)vec​(F~rR)]+ℛ~​(In2−(𝒫~​𝒥~​𝒬~)+​(𝒫~​𝒥~​𝒬~))​y},\widetilde{\mathcal{H}}_{LE}=\left\{X\;\left|\;\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\end{bmatrix}\right.=\widetilde{\mathcal{R}}\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)^{+}\begin{bmatrix}\mathrm{vec}(\widetilde{E}_{r}^{R})\\ \mathrm{vec}(\widetilde{F}_{r}^{R})\end{bmatrix}+\widetilde{\mathcal{R}}\left(I_{n^{2}}-\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)^{+}\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)\right)y\right\}, (37)

where y∈ℝn2y\in{\mathbb{R}}^{n^{2}} is an arbitrary vector. Furthermore, the unique solution X~H∈ℋ~L​E\widetilde{X}_{H}\in\widetilde{\mathcal{H}}_{LE} to Problem 4.1 satisfies

[vec​(X0)vec​(X1)]=ℛ~​(𝒫~​𝒥~​𝒬~)+​[vec​(E~rR)vec​(F~rR)].\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\end{bmatrix}=\widetilde{\mathcal{R}}\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)^{+}\begin{bmatrix}\mathrm{vec}(\widetilde{E}_{r}^{R})\\ \mathrm{vec}(\widetilde{F}_{r}^{R})\end{bmatrix}. (38)
Proof.

The proof follows along similar lines as Theorem 3.1. ∎

Theorem 4.2.

Let 𝒫~\widetilde{\mathcal{P}} and ℛ~\widetilde{\mathcal{R}} be in the form of (36), and let X=X0+X1​i∈ℂn×nX=X_{0}+X_{1}\textit{{i}}\in{\mathbb{C}}^{n\times n}. Additionally, let 𝒥~\widetilde{\mathcal{J}} and ℚ~\widetilde{\mathbb{Q}} be as in (34) and (35), respectively. Then, the CME (1) has a Hermitian solution X∈ℍ​ℂn×nX\in\mathbb{H}\mathbb{C}^{n\times n} if and only if

(I4​m​s−(𝒫~​𝒥~​𝒬~)​(𝒫~​𝒥~​𝒬~)+)​[vec​(E~rR)vec​(F~rR)]=0.\left(I_{4ms}-\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)^{+}\right)\begin{bmatrix}\mathrm{vec}(\widetilde{E}_{r}^{R})\\ \mathrm{vec}(\widetilde{F}_{r}^{R})\end{bmatrix}=0. (39)

In this case, the general solution X∈ℍ​ℂn×nX\in\mathbb{H}\mathbb{C}^{n\times n} satisfies

[vec​(X0)vec​(X1)]=ℛ~​(𝒫~​𝒥~​𝒬~)+​[vec​(E~rR)vec​(F~rR)]+ℛ~​(In2−(𝒫~​𝒥~​𝒬~)+​(𝒫~​𝒥~​𝒬~))​y,\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\end{bmatrix}=\widetilde{\mathcal{R}}\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)^{+}\begin{bmatrix}\mathrm{vec}(\widetilde{E}_{r}^{R})\\ \mathrm{vec}(\widetilde{F}_{r}^{R})\end{bmatrix}+\widetilde{\mathcal{R}}\left(I_{n^{2}}-\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)^{+}\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)\right)y, (40)

where y∈ℝn2y\in{\mathbb{R}}^{n^{2}} is an arbitrary vector. Furthermore, if (39) holds, then the CME (1) has a unique solution X∈ℍ​ℂn×nX\in\mathbb{H}\mathbb{C}^{n\times n} if and only if

rank​(𝒫~​𝒥~​𝒬~)=n2.\mathrm{rank}\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)=n^{2}. (41)

In this case, the unique solution X∈ℍ​ℂn×nX\in\mathbb{H}\mathbb{C}^{n\times n} satisfies

[vec​(X0)vec​(X1)]=ℛ~​(𝒫~​𝒥~​𝒬~)+​[vec​(E~rR)vec​(F~rR)].\begin{bmatrix}\mathrm{vec}(X_{0})\\ \mathrm{vec}(X_{1})\end{bmatrix}=\widetilde{\mathcal{R}}\left(\widetilde{\mathcal{P}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)^{+}\begin{bmatrix}\mathrm{vec}(\widetilde{E}_{r}^{R})\\ \mathrm{vec}(\widetilde{F}_{r}^{R})\end{bmatrix}. (42)
Proof.

The proof follows along similar lines as Theorem 3.2. ∎

Our next step is to illustrate how our developed method can solve inverse problems. Here, we examine inverse problems where the spectral constraint involves only a few eigenpair information rather than the entire spectrum. Mathematically, the problem statement is:

Problem 4.2 (PDIEP for Hermitian matrix).

Given vectors {u1,u2,…,uk}⊂ℂn\{u_{1},u_{2},\ldots,u_{k}\}\subset\mathbb{C}^{n}, values {λ1,λ2,…,λk}⊂ℝ\{\lambda_{1},\lambda_{2},\ldots,\lambda_{k}\}\subset\mathbb{R}, find a Hermitian matrix M∈ℍ​ℂn×nM\in\mathbb{H}\mathbb{C}^{n\times n} such that

M​ui=λi​ui,i=1,2,…,k.Mu_{i}=\lambda_{i}u_{i},\;\;\;\;i=1,2,\ldots,k.

To simplify the discussion, we will use the matrix pair (Λ,Φ)\left(\Lambda,\Phi\right) to describe partial eigenpair information, where

Λ=diag​(λ1,λ2,…,λk)∈ℝk×k,and​Φ=[u1,u2,…,uk]∈ℂn×k.\Lambda=\mathrm{diag}(\lambda_{1},\lambda_{2},\ldots,\lambda_{k})\in\mathbb{R}^{k\times k},\;\mbox{and}\;\Phi=[u_{1},u_{2},\ldots,u_{k}]\in\mathbb{C}^{n\times k}. (43)

Problem 4.2 can be written as M​Φ=Φ​ΛM\Phi=\Phi\Lambda. Before moving forward, we will introduce certain notations that will be employed in the subsequent result.

𝒮~=(B~R)T⊗A~rR,R~=diag​(KS,KA),N=𝒮~​𝒥~​𝒬~,t=vec​(E~rR).\widetilde{\mathcal{S}}=(\widetilde{B}^{R})^{T}\otimes\widetilde{A}_{r}^{R},\;\;\widetilde{R}=\mathrm{diag}(K_{S},K_{A}),\;\;N=\widetilde{\mathcal{S}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}},\;\;t=\mathrm{vec}(\widetilde{E}_{r}^{R}). (44)
Corollary 4.3.

Given a pair (Λ,Φ)∈ℝk×k×ℂn×k​(k≤n)\left(\Lambda,\Phi\right)\in\mathbb{R}^{k\times k}\times\mathbb{C}^{n\times k}\left(k\leq n\right) in the form of (43). Let 𝒮~\widetilde{\mathcal{S}}, ℛ~\widetilde{\mathcal{R}}, NN, and tt be in the form of (44), and let M=M0+M1​i∈ℂn×nM=M_{0}+M_{1}\textit{{i}}\in{\mathbb{C}}^{n\times n}. Additionally, let 𝒥~\widetilde{\mathcal{J}} and ℚ~\widetilde{\mathbb{Q}} be as in (34) and (35), respectively. If rank​(N)=rank​([N,t])\mathrm{rank}(N)=\mathrm{rank}([N,t]), then the general solution to Problem 4.2 satisfies

[vec​(M0)vec​(M1)]=R~​(𝒮~​𝒥~​𝒬~)+​(vec​(E~rR))+R~​(In2−(𝒮~​𝒥~​𝒬~)+​(𝒮~​𝒥~​𝒬~))​y,\begin{bmatrix}\mathrm{vec}(M_{0})\\ \mathrm{vec}(M_{1})\end{bmatrix}=\widetilde{R}\left(\widetilde{\mathcal{S}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)^{+}\left(\mathrm{vec}(\widetilde{E}_{r}^{R})\right)+\widetilde{R}\left(I_{n^{2}}-\left(\widetilde{\mathcal{S}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)^{+}\left(\widetilde{\mathcal{S}}\widetilde{\mathcal{J}}\widetilde{\mathcal{Q}}\right)\right)y, (45)

where y∈ℝn2y\in{\mathbb{R}}^{n^{2}} is an arbitrary vector.

Proof.

By using the transformations

A=In,X=M,B=Φ,and​E=Φ​Λ,A=I_{n},\;X=M,\;B=\Phi,\;\mbox{and}\;E=\Phi\Lambda,

we can find solution to Problem 4.2 by solving matrix equation A​X​B=EAXB=E for X∈ℍ​ℂn×nX\in\mathbb{H}\mathbb{C}^{n\times n}, which is a special case of matrix equation (1) over the complex field. ∎

Remark 4.4.

We can choose yy arbitrarily in Corollary 4.3; therefore MM need not be unique.

5 Numerical Verification

In this section, we present numerical examples to verify our results. All calculations are performed on an Intel Core i​7−9700​@​3.00​G​H​z/16​G​B[email protected]/16GB computer using MATLAB R​2021​bR2021b software.

First, we present two numerical examples. In the first example, we compute the errors between the computed solution obtained through the RR method and the corresponding actual solution for Problem 3.1. The second example involves a comparison of the CPU time required to determine the Hermitian solution of RBME (1) using both the RR method and the CR method. Additionally, we compare the errors between the actual solutions and the corresponding computed solutions obtained via the RR method and the CR method for the computation of the Hermitian solution of RBME (1). In both examples, the comparison is made for various dimensions of matrices.

Example 5.1.

Let m=n=2​km=n=2k, s=ks=k, for k=1:20k=1:20. Consider the RBME (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F), where

A\displaystyle A =\displaystyle= 10∗r​a​n​d​(m,n)+r​a​n​d​(m,n)​i+r​a​n​d​(m,n)​j+r​a​n​d​(m,n)​k,\displaystyle 10*rand(m,n)+rand(m,n)\textit{{i}}+rand(m,n)\textit{{j}}+rand(m,n)\textit{{k}},
B\displaystyle B =\displaystyle= r​a​n​d​(n,s)+r​a​n​d​(n,s)​i+r​a​n​d​(n,s)​j+r​a​n​d​(n,s)​k,\displaystyle rand(n,s)+rand(n,s)\textit{{i}}+rand(n,s)\textit{{j}}+rand(n,s)\textit{{k}},
C\displaystyle C =\displaystyle= r​a​n​d​(m,n)+10∗r​a​n​d​(m,n)​i+4∗r​a​n​d​(m,n)​j+r​a​n​d​(m,n)​k,\displaystyle rand(m,n)+10*rand(m,n)\textit{{i}}+4*rand(m,n)\textit{{j}}+rand(m,n)\textit{{k}},
D\displaystyle D =\displaystyle= r​a​n​d​(n,s)+2∗r​a​n​d​(n,s)​i+r​a​n​d​(n,s)​j+r​a​n​d​(n,s)​k.\displaystyle rand(n,s)+2*rand(n,s)\textit{{i}}+rand(n,s)\textit{{j}}+rand(n,s)\textit{{k}}.

Let S0=S1=r​a​n​d​(n,n)S_{0}=S_{1}=rand(n,n), S2=5∗r​a​n​d​(n,n)S_{2}=5*rand(n,n), and S3=2∗r​a​n​d​(n,n)S_{3}=2*rand(n,n). Define

X~=(S0+S0T)+(S1−S1T)​i+(S2−S2T)​j+(S3−S3T)​k.\widetilde{X}=(S_{0}+S_{0}^{T})+(S_{1}-S_{1}^{T})\textit{{i}}+(S_{2}-S_{2}^{T})\textit{{j}}+(S_{3}-S_{3}^{T})\textit{{k}}.

Let E=A​X~​BE=A\widetilde{X}B and F=C​X~​DF=C\widetilde{X}D. Hence, X~\widetilde{X} is the unique minimum norm least squares Hermitian solution of the RBME (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F).
Next, we take matrices AA, BB, CC, DD, EE, and FF as input, and use Theorem 3.1 to calculate the unique minimum norm least squares Hermitian solution XX to Problem 3.1. Let the error ϵ=log⁡10​(∥X~−X∥F)\epsilon=\log 10\left(\left\lVert\widetilde{X}-X\right\rVert_{F}\right). The relation between the error ϵ\epsilon and kk is shown in Figure 1.

Refer to caption
Figure 1: The error in solving Problem 3.1

Based on Figure 1, the error ϵ\epsilon between the solution of Problem 3.1 obtained using Theorem 3.1 and the corresponding actual solutions, for various dimensions of matrices, consistently remains less than or equal to -11.5. This demonstrates the effectiveness of RR method in computing solution for Problem 3.1.

Example 5.2.

Let n=2​kn=2k, m=n+16m=n+16, s=n+6s=n+6, for k=1:20k=1:20. Consider the RBME (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F), where

A\displaystyle A =\displaystyle= z​e​r​o​s​(m,n)+[e​y​e​(n)z​e​r​o​s​(16,n)]​i+z​e​r​o​s​(m,n)​j+z​e​r​o​s​(m,n)​k,\displaystyle zeros(m,n)+\begin{bmatrix}eye(n)\\ zeros(16,n)\end{bmatrix}\textit{{i}}+zeros(m,n)\textit{{j}}+zeros(m,n)\textit{{k}},
B\displaystyle B =\displaystyle= z​e​r​o​s​(n,s)+z​e​r​o​s​(n,s)​i+z​e​r​o​s​(n,s)​j+[−e​y​e​(n)z​e​r​o​s​(n,6)]​k,\displaystyle zeros(n,s)+zeros(n,s)\textit{{i}}+zeros(n,s)\textit{{j}}+\begin{bmatrix}-eye(n)&zeros(n,6)\end{bmatrix}\textit{{k}},
C\displaystyle C =\displaystyle= z​e​r​o​s​(m,n)+z​e​r​o​s​(m,n)​i+[e​y​e​(n)z​e​r​o​s​(16,n)]​j+z​e​r​o​s​(m,n)​k,\displaystyle zeros(m,n)+zeros(m,n)\textit{{i}}+\begin{bmatrix}eye(n)\\ zeros(16,n)\end{bmatrix}\textit{{j}}+zeros(m,n)\textit{{k}},
D\displaystyle D =\displaystyle= z​e​r​o​s​(n,s)+z​e​r​o​s​(n,s)​i+o​n​e​s​(n,s)​j+z​e​r​o​s​(n,s)​k.\displaystyle zeros(n,s)+zeros(n,s)\textit{{i}}+ones(n,s)\textit{{j}}+zeros(n,s)\textit{{k}}.

Let S0=z​e​r​o​s​(n2,n2)S_{0}=zeros\left(\frac{n}{2},\frac{n}{2}\right), S1=e​y​e​(n2)S_{1}=eye\left(\frac{n}{2}\right), S2=r​a​n​d​n​(n,n)S_{2}=randn(n,n), and S3=r​a​n​d​n​(n,n)S_{3}=randn(n,n). Define

X~=toeplitz(1:n)+[S0S1−S1S0]i+(S2−S2T)j+(S3−S3T)k.\widetilde{X}=toeplitz(1:n)+\begin{bmatrix}S_{0}&S_{1}\\ -S_{1}&S_{0}\end{bmatrix}\textit{{i}}+(S_{2}-S_{2}^{T})\textit{{j}}+(S_{3}-S_{3}^{T})\textit{{k}}.

Let E=A​X~​BE=A\widetilde{X}B and F=C​X~​DF=C\widetilde{X}D. Clearly, the RBME (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F) is consistent and X~\widetilde{X} is its unique Hermitian solution.

Next, we input matrices AA, BB, CC, DD, EE, and FF. By employing both the RR method (Theorem 3.2) and the CR method ([18, Theorem 3.1]), we calculate the Hermitian solution for RBME (1). Let X1X_{1} and X2X_{2} denote the Hermitian solutions obtained through the RR method and the CR method, respectively. Let errors ϵ1=log⁡10​(∥X~−X1∥F)\epsilon_{1}=\log 10\left(\left\lVert\widetilde{X}-X_{1}\right\rVert_{F}\right) and ϵ2=log⁡10​(∥X~−X2∥F)\epsilon_{2}=\log 10\left(\left\lVert\widetilde{X}-X_{2}\right\rVert_{F}\right).

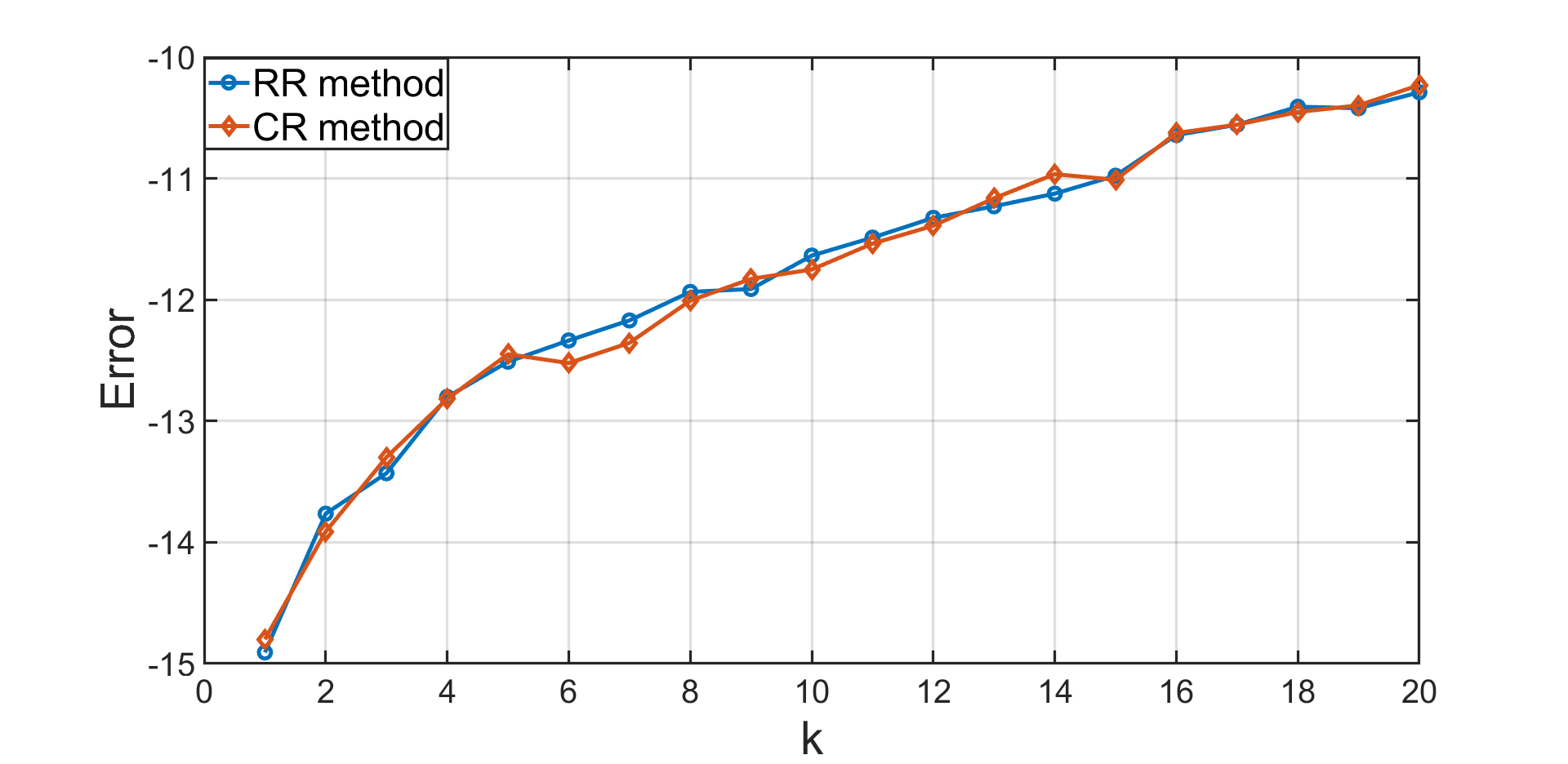
Refer to caption
Figure 2: The error in finding the Hermitian solution of RBME (1)

Figure 2 presents a comparison between ϵ1\epsilon_{1} and ϵ2\epsilon_{2}, which is obtained by taking different value of kk. Notably, the errors obtained from both methods are nearly identical and consistently remains less than −10-10. This demonstrates that the RR method is as effective as the CR method in determining Hermitian solutions for RBME (1).

Refer to caption
Figure 3: The CPU time for finding Hermitian solution of RBME (1)

Figure 3 depicts a comparison of the CPU time taken by the RR method and the CR method in finding the Hermitian solution of RBME (1). This comparison is conducted for various values of kk. Notably, the CPU time consumed by RR method is less compared to the CR method. This highlights the enhanced efficiency and time-saving nature of our proposed RR method compared to the CR method.

Next, we illustrate two examples for solving PDIEP for a Hermitian matrix.

Example 5.3.

To establish test data, we first generate a Hermitian matrix MM and compute its eigenpairs. Let S0=S1=r​a​n​d​n​(5)S_{0}=S_{1}=randn(5), M0=t​r​i​u​(S0)+t​r​i​u​(S0,1)TM_{0}=triu(S_{0})+triu(S_{0},1)^{T}, and M1=S1−S1TM_{1}=S_{1}-S_{1}^{T}. Define M=M0+M1​iM=M_{0}+M_{1}\textit{{i}}.

Reconstruction from three eigenpairs : Let the prescribed partial eigeninformation be given by (λ1,u1)\left(\lambda_{1},u_{1}\right), (λ2,u2)\left(\lambda_{2},u_{2}\right), and (λ3,u3)\left(\lambda_{3},u_{3}\right), where λ1=−5.4837\lambda_{1}=-5.4837, λ2=−1.8785\lambda_{2}=-1.8785, and λ3=−0.1774\lambda_{3}=-0.1774. Let

u1=[0.2636+0.3383​i0.4236−0.0100​i−0.4570+0.0000​i−0.1785+0.2168​i−0.5906+0.0000​i],u2=[0.1280+0.4097​i0.4292−0.3207​i0.1638−0.3434​i0.5420−0.1538​i0.2580+0.0000​i],u3=[0.0128−0.1852​i−0.4463+0.0116​i−0.0575−0.4873​i0.4944+0.3518​i−0.3964+0.0000​i].u_{1}=\begin{bmatrix}0.2636+0.3383\textit{{i}}\\ 0.4236-0.0100\textit{{i}}\\ -0.4570+0.0000\textit{{i}}\\ -0.1785+0.2168\textit{{i}}\\ -0.5906+0.0000\textit{{i}}\end{bmatrix},u_{2}=\begin{bmatrix}0.1280+0.4097\textit{{i}}\\ 0.4292-0.3207\textit{{i}}\\ 0.1638-0.3434\textit{{i}}\\ 0.5420-0.1538\textit{{i}}\\ 0.2580+0.0000\textit{{i}}\end{bmatrix},u_{3}=\begin{bmatrix}0.0128-0.1852\textit{{i}}\\ -0.4463+0.0116\textit{{i}}\\ -0.0575-0.4873\textit{{i}}\\ 0.4944+0.3518\textit{{i}}\\ -0.3964+0.0000\textit{{i}}\end{bmatrix}.

Construct the Hermitian matrix M^\widehat{M} such that M^​ui=λi​ui\widehat{M}u_{i}=\lambda_{i}u_{i} for i=1,2,3i=1,2,3. Let Φ^=[u1,u2,u3]∈ℂ5×3\widehat{\Phi}=\left[u_{1},u_{2},u_{3}\right]\in\mathbb{C}^{5\times 3} and Λ^=diag​(λ1,λ2,λ3)∈ℝ3×3\widehat{\Lambda}=\mathrm{diag}(\lambda_{1},\lambda_{2},\lambda_{3})\in\mathbb{R}^{3\times 3}. By using the transformations A=I5,X=M^,B=Φ^,and​E=Φ^​Λ^A=I_{5},\;X=\widehat{M},\;B=\widehat{\Phi},\;\mbox{and}\;E=\widehat{\Phi}\widehat{\Lambda}, we find the Hermitian solution to the matrix equation A​X​B=EAXB=E. We obtain

M^=[−0.7841+0.0000​i−0.4732−1.6515​i0.9901+0.6641​i−0.1203+0.1603​i0.9418+0.9087​i−0.4732+1.6515​i−1.2375+0.0000​i0.7154−0.0670​i−0.0395+0.7054​i1.0881+0.2186​i0.9901−0.6641​i0.7154+0.0670​i−1.0019+0.0000​i−0.7084+0.1295​i−1.9644+0.0076​i−0.1203−0.1603​i−0.0395−0.7054​i−0.7084−0.1295​i−0.8146+0.0000​i−0.8648+1.1681​i0.9418−0.9087​i1.0881−0.2186​i−1.9644−0.0076​i−0.8648−1.1681​i−1.5564+0.0000​i].\widehat{M}=\begin{bmatrix}-0.7841+0.0000\textit{{i}}&-0.4732-1.6515\textit{{i}}&0.9901+0.6641\textit{{i}}&-0.1203+0.1603\textit{{i}}&0.9418+0.9087\textit{{i}}\\ -0.4732+1.6515\textit{{i}}&-1.2375+0.0000\textit{{i}}&0.7154-0.0670\textit{{i}}&-0.0395+0.7054\textit{{i}}&1.0881+0.2186\textit{{i}}\\ 0.9901-0.6641\textit{{i}}&0.7154+0.0670\textit{{i}}&-1.0019+0.0000\textit{{i}}&-0.7084+0.1295\textit{{i}}&-1.9644+0.0076\textit{{i}}\\ -0.1203-0.1603\textit{{i}}&-0.0395-0.7054\textit{{i}}&-0.7084-0.1295\textit{{i}}&-0.8146+0.0000\textit{{i}}&-0.8648+1.1681\textit{{i}}\\ 0.9418-0.9087\textit{{i}}&1.0881-0.2186\textit{{i}}&-1.9644-0.0076\textit{{i}}&-0.8648-1.1681\textit{{i}}&-1.5564+0.0000\textit{{i}}\end{bmatrix}.

Then, M^\widehat{M} is the desired Hermitian matrix. We have ϵ1=‖M^​u1−λ1​u1‖2=2.9787×10−15\epsilon_{1}=\|\widehat{M}u_{1}-\lambda_{1}u_{1}\|_{2}=2.9787\times 10^{-15}, ϵ2=‖M^​u2−λ2​u2‖2=4.0592×10−15\epsilon_{2}=\|\widehat{M}u_{2}-\lambda_{2}u_{2}\|_{2}=4.0592\times 10^{-15}, and ϵ3=‖M^​u3−λ3​u3‖2=2.5327×10−15\epsilon_{3}=\|\widehat{M}u_{3}-\lambda_{3}u_{3}\|_{2}=2.5327\times 10^{-15}. Errors ϵ1\epsilon_{1}, ϵ2\epsilon_{2}, and ϵ3\epsilon_{3} are in the order of 10−1510^{-15} and are negligible. Clearly, M^​ui=λi​ui\widehat{M}u_{i}=\lambda_{i}u_{i} for i=1,2,3i=1,2,3.

Example 5.4.

To establish test data, we first generate a Hermitian matrix MM. Let

M=[2.30+0.00​i3.50+2.00​i1.20−1.20​i2.30−3.00​i4.50+2.00​i3.50−2.00​i8.90+0.00​i2.35−4.00​i4.35+5.20​i6.29−6.80​i1.20+1.20​i2.35+4.00​i2.00+0.00​i4.30−4.20​i6.20−7.30​i2.30+3.00​i4.35−5.20​i4.30+4.20​i1.00+0.00​i3.00−8.60​i4.50−2.00​i6.29+6.80​i6.20+7.30​i3.00+8.60​i6.40+0.00​i].M=\begin{bmatrix}2.30+0.00\textit{{i}}&3.50+2.00\textit{{i}}&1.20-1.20\textit{{i}}&2.30-3.00\textit{{i}}&4.50+2.00\textit{{i}}\\ 3.50-2.00\textit{{i}}&8.90+0.00\textit{{i}}&2.35-4.00\textit{{i}}&4.35+5.20\textit{{i}}&6.29-6.80\textit{{i}}\\ 1.20+1.20\textit{{i}}&2.35+4.00\textit{{i}}&2.00+0.00\textit{{i}}&4.30-4.20\textit{{i}}&6.20-7.30\textit{{i}}\\ 2.30+3.00\textit{{i}}&4.35-5.20\textit{{i}}&4.30+4.20\textit{{i}}&1.00+0.00\textit{{i}}&3.00-8.60\textit{{i}}\\ 4.50-2.00\textit{{i}}&6.29+6.80\textit{{i}}&6.20+7.30\textit{{i}}&3.00+8.60\textit{{i}}&6.40+0.00\textit{{i}}\end{bmatrix}.

Let (Λ,Φ)\left(\Lambda,\Phi\right) denote its eigenpairs. We have Λ=diag​(λ1,…,λ5)∈ℝ5×5\Lambda=\mathrm{diag}(\lambda_{1},\ldots,\lambda_{5})\in\mathbb{R}^{5\times 5} and Φ=[u1,u2,u3,u4,u5]∈ℂ5×5\Phi=\left[u_{1},u_{2},u_{3},u_{4},u_{5}\right]\in\mathbb{C}^{5\times 5}, where

[λ1,λ2,λ3,λ4,λ5]=[−12.0692,−6.3846, 3.8845, 8.8081, 26.3613],\left[\lambda_{1},\lambda_{2},\lambda_{3},\lambda_{4},\lambda_{5}\right]=\left[-12.0692,\,-6.3846,\,3.8845,\,8.8081,\,26.3613\right],

and their corresponding eigenvectors

u1=[−0.3035−0.1808​i0.0558−0.0876​i−0.4616+0.1624​i0.1136+0.5876​i0.5165+0.0000​i],u2=[−0.0754+0.2769​i0.3253−0.4400​i−0.1970−0.4505​i0.3006+0.2681​i−0.4628+0.0000​i],u3=[−0.1272−0.8033​i0.2812−0.1182​i−0.0469+0.2233​i0.2046−0.2034​i−0.3321+0.0000​i],\;\;\;\;\;\;\;\;\;u_{1}=\begin{bmatrix}-0.3035-0.1808\textit{{i}}\\ 0.0558-0.0876\textit{{i}}\\ -0.4616+0.1624\textit{{i}}\\ 0.1136+0.5876\textit{{i}}\\ 0.5165+0.0000\textit{{i}}\end{bmatrix},u_{2}=\begin{bmatrix}-0.0754+0.2769\textit{{i}}\\ 0.3253-0.4400\textit{{i}}\\ -0.1970-0.4505\textit{{i}}\\ 0.3006+0.2681\textit{{i}}\\ -0.4628+0.0000\textit{{i}}\end{bmatrix},u_{3}=\begin{bmatrix}-0.1272-0.8033\textit{{i}}\\ 0.2812-0.1182\textit{{i}}\\ -0.0469+0.2233\textit{{i}}\\ 0.2046-0.2034\textit{{i}}\\ -0.3321+0.0000\textit{{i}}\end{bmatrix},

u4=[−0.2920−0.1086​i−0.1898+0.5073​i−0.1913−0.5563​i0.4244−0.2667​i0.1110+0.0000​i],u5=[0.1779−0.0527​i0.3751−0.4033​i0.2429−0.2485​i0.1608−0.3452​i0.6296+0.0000​i].\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;u_{4}=\begin{bmatrix}-0.2920-0.1086\textit{{i}}\\ -0.1898+0.5073\textit{{i}}\\ -0.1913-0.5563\textit{{i}}\\ 0.4244-0.2667\textit{{i}}\\ 0.1110+0.0000\textit{{i}}\end{bmatrix},u_{5}=\begin{bmatrix}0.1779-0.0527\textit{{i}}\\ 0.3751-0.4033\textit{{i}}\\ 0.2429-0.2485\textit{{i}}\\ 0.1608-0.3452\textit{{i}}\\ 0.6296+0.0000\textit{{i}}\end{bmatrix}.

Case 1\mathbf{1}. Reconstruction from one eigenpair (k=1)(k=1): Let the prescribed partial eigeninformation be given by

Λ^=λ4∈ℝ​and​Φ^=u4∈ℂ5×1.\widehat{\Lambda}=\lambda_{4}\in\mathbb{R}\;\textrm{and}\;\;\widehat{\Phi}=u_{4}\in\mathbb{C}^{5\times 1}.

Construct the Hermitian matrix M^\widehat{M} such that M^​ui=λi​ui\widehat{M}u_{i}=\lambda_{i}u_{i} for i=4i=4. By using the transformations A=I5,X=M^,B=Φ^,and​E=Φ^​Λ^A=I_{5},\;X=\widehat{M},\;B=\widehat{\Phi},\;\mbox{and}\;E=\widehat{\Phi}\widehat{\Lambda}, we find the Hermitian solution to the matrix equation A​X​B=EAXB=E. We obtain

M^=[0.3945+0.0000​i0.0032+1.5622​i1.1249−1.3710​i−0.8515−1.1113​i−0.2523−0.0938​i0.0032−1.5622​i1.5238+0.0000​i−2.6575−2.1895​i−2.1790+1.6625​i−0.1878+0.5019​i1.1249+1.3710​i−2.6575+2.1895​i1.9423+0.0000​i0.7065−3.0186​i−0.1981−0.5762​i−0.8515+1.1113​i−2.1790−1.6625​i0.7065+3.0186​i1.2314+0.0000​i0.4061−0.2552​i−0.2523+0.0938​i−0.1878−0.5019​i−0.1981+0.5762​i0.4061+0.2552​i0.0458+0.0000​i].\widehat{M}=\begin{bmatrix}0.3945+0.0000\textit{{i}}&0.0032+1.5622\textit{{i}}&1.1249-1.3710\textit{{i}}&-0.8515-1.1113\textit{{i}}&-0.2523-0.0938\textit{{i}}\\ 0.0032-1.5622\textit{{i}}&1.5238+0.0000\textit{{i}}&-2.6575-2.1895\textit{{i}}&-2.1790+1.6625\textit{{i}}&-0.1878+0.5019\textit{{i}}\\ 1.1249+1.3710\textit{{i}}&-2.6575+2.1895\textit{{i}}&1.9423+0.0000\textit{{i}}&0.7065-3.0186\textit{{i}}&-0.1981-0.5762\textit{{i}}\\ -0.8515+1.1113\textit{{i}}&-2.1790-1.6625\textit{{i}}&0.7065+3.0186\textit{{i}}&1.2314+0.0000\textit{{i}}&0.4061-0.2552\textit{{i}}\\ -0.2523+0.0938\textit{{i}}&-0.1878-0.5019\textit{{i}}&-0.1981+0.5762\textit{{i}}&0.4061+0.2552\textit{{i}}&0.0458+0.0000\textit{{i}}\end{bmatrix}.

Then, M^\widehat{M} is the desired Hermitian matrix.

Case 2\mathbf{2}. Reconstruction from two eigenpairs (k=2)(k=2): Let the prescribed partial eigeninformation be given by

Λ^=diag​(λ2,λ5)∈ℝ2×2​and​Φ^=[u2,u5]∈ℂ5×2.\widehat{\Lambda}=\mathrm{diag}(\lambda_{2},\lambda_{5})\in\mathbb{R}^{2\times 2}\;\textrm{and}\;\;\widehat{\Phi}=\left[u_{2},u_{5}\right]\in\mathbb{C}^{5\times 2}.

Construct the Hermitian matrix M^\widehat{M} such that M^​ui=λi​ui\widehat{M}u_{i}=\lambda_{i}u_{i} for i=2,5i=2,5. By using the transformations A=I5,X=M^,B=Φ^,and​E=Φ^​Λ^A=I_{5},\;X=\widehat{M},\;B=\widehat{\Phi},\;\mbox{and}\;E=\widehat{\Phi}\widehat{\Lambda}, we find the Hermitian solution to the matrix equation A​X​B=EAXB=E. We obtain

M^=[−0.0573+0.0000​i2.9931+1.2268​i2.2043+1.6423​i0.5577+0.2617​i3.1106−0.5499​i2.9931−1.2268​i5.1050+0.0000​i4.7608−1.0023​i5.7820+2.4404​i7.6635−8.2068​i2.2043−1.6423​i4.7608+1.0023​i0.2463+0.0000​i4.4811+1.4877​i4.1500−5.1284​i0.5577−0.2617​i5.7820−2.4404​i4.4811−1.4877​i1.0747+0.0000​i3.3003−6.2445​i3.1106+0.5499​i7.6635+8.2068​i4.1500+5.1284​i3.3003+6.2445​i7.7224+0.0000​i].\widehat{M}=\begin{bmatrix}-0.0573+0.0000\textit{{i}}&2.9931+1.2268\textit{{i}}&2.2043+1.6423\textit{{i}}&0.5577+0.2617\textit{{i}}&3.1106-0.5499\textit{{i}}\\ 2.9931-1.2268\textit{{i}}&5.1050+0.0000\textit{{i}}&4.7608-1.0023\textit{{i}}&5.7820+2.4404\textit{{i}}&7.6635-8.2068\textit{{i}}\\ 2.2043-1.6423\textit{{i}}&4.7608+1.0023\textit{{i}}&0.2463+0.0000\textit{{i}}&4.4811+1.4877\textit{{i}}&4.1500-5.1284\textit{{i}}\\ 0.5577-0.2617\textit{{i}}&5.7820-2.4404\textit{{i}}&4.4811-1.4877\textit{{i}}&1.0747+0.0000\textit{{i}}&3.3003-6.2445\textit{{i}}\\ 3.1106+0.5499\textit{{i}}&7.6635+8.2068\textit{{i}}&4.1500+5.1284\textit{{i}}&3.3003+6.2445\textit{{i}}&7.7224+0.0000\textit{{i}}\end{bmatrix}.

Then, M^\widehat{M} is the desired Hermitian matrix.

Case 3\mathbf{3}. Reconstruction from three eigenpairs (k=3)(k=3): Let the prescribed partial eigeninformation be given by

Λ^=diag​(λ1,λ3,λ5)∈ℝ3×3​and​Φ^=[u1,u3,u5]∈ℂ5×3.\widehat{\Lambda}=\mathrm{diag}(\lambda_{1},\lambda_{3},\lambda_{5})\in\mathbb{R}^{3\times 3}\;\textrm{and}\;\;\widehat{\Phi}=\left[u_{1},u_{3},u_{5}\right]\in\mathbb{C}^{5\times 3}.

Construct the Hermitian matrix M^\widehat{M} such that M^​ui=λi​ui\widehat{M}u_{i}=\lambda_{i}u_{i} for i=1,3,5i=1,3,5. By using the transformations A=I5,X=M^,B=Φ^,and​E=Φ^​Λ^A=I_{5},\;X=\widehat{M},\;B=\widehat{\Phi},\;\mbox{and}\;E=\widehat{\Phi}\widehat{\Lambda}, we find the Hermitian solution to the matrix equation A​X​B=EAXB=E. We obtain

M^=[1.3834+0.0000​i3.3377−0.0836​i−0.4340−0.2088​i3.0774−1.0913​i5.1844+1.9720​i3.3377+0.0836​i5.5549+0.0000​i5.6800−1.2204​i6.9930+2.8290​i6.3976−7.2483​i−0.4340+0.2088​i5.6800+1.2204​i0.1969+0.0000​i2.5946−2.2959​i6.6286−5.5009​i3.0774+1.0913​i6.9930−2.8290​i2.5946+2.2959​i−0.6425+0.0000​i1.6758−8.5541​i5.1844−1.9720​i6.3976+7.2483​i6.6286+5.5009​i1.6758+8.5541​i6.7611+0.0000​i].\widehat{M}=\begin{bmatrix}1.3834+0.0000\textit{{i}}&3.3377-0.0836\textit{{i}}&-0.4340-0.2088\textit{{i}}&3.0774-1.0913\textit{{i}}&5.1844+1.9720\textit{{i}}\\ 3.3377+0.0836\textit{{i}}&5.5549+0.0000\textit{{i}}&5.6800-1.2204\textit{{i}}&6.9930+2.8290\textit{{i}}&6.3976-7.2483i\\ -0.4340+0.2088\textit{{i}}&5.6800+1.2204\textit{{i}}&0.1969+0.0000\textit{{i}}&2.5946-2.2959\textit{{i}}&6.6286-5.5009\textit{{i}}\\ 3.0774+1.0913\textit{{i}}&6.9930-2.8290\textit{{i}}&2.5946+2.2959\textit{{i}}&-0.6425+0.0000\textit{{i}}&1.6758-8.5541\textit{{i}}\\ 5.1844-1.9720\textit{{i}}&6.3976+7.2483\textit{{i}}&6.6286+5.5009\textit{{i}}&1.6758+8.5541\textit{{i}}&6.7611+0.0000\textit{{i}}\end{bmatrix}.

Then, M^\widehat{M} is the desired Hermitian matrix.

Case 1\mathbf{1} (k=1)(k=1) Case 2\mathbf{2} (k=2)(k=2) Case 3\mathbf{3} (k=3)(k=3)
Eigenpair ∥M^​ui−λi​ui∥2\left\lVert\widehat{M}u_{i}-\lambda_{i}u_{i}\right\rVert_{2} Eigenpairs ∥M^​ui−λi​ui∥2\left\lVert\widehat{M}u_{i}-\lambda_{i}u_{i}\right\rVert_{2} Eigenpairs ∥M^​ui−λi​ui∥2\left\lVert\widehat{M}u_{i}-\lambda_{i}u_{i}\right\rVert_{2}
(λ4,u4)\left(\lambda_{4},u_{4}\right) 3.1005×10−153.1005\times 10^{-15} (λ2,u2)\left(\lambda_{2},u_{2}\right) 1.7590×10−141.7590\times 10^{-14} (λ1,u1)\left(\lambda_{1},u_{1}\right) 2.5702×10−142.5702\times 10^{-14}
(λ5,u5)\left(\lambda_{5},u_{5}\right) 1.3918×10−141.3918\times 10^{-14} (λ3,u3)\left(\lambda_{3},u_{3}\right) 2.3303×10−152.3303\times 10^{-15}
(λ5,u5)\left(\lambda_{5},u_{5}\right) 3.1112×10−153.1112\times 10^{-15}
Table 1: Residual ∥M^​ui−λi​ui∥2\left\lVert\widehat{M}u_{i}-\lambda_{i}u_{i}\right\rVert_{2} for Example 5.4

From Table 1, we find that the residual ∥M^​ui−λi​ui∥2\left\lVert\widehat{M}u_{i}-\lambda_{i}u_{i}\right\rVert_{2}, for i=4i=4 in Case 11, for i=2,5i=2,5 in Case 22, and for i=1,3,5i=1,3,5 in Case 33, is in the order of 10−1410^{-14} and is negligible. This demonstrates the effectiveness of our method in solving Problem 4.2.

6 Conclusion

We have introduced an efficient method to obtain the least squares Hermitian solutions of the reduced biquaternion matrix equation (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F). Our method involved transforming the constrained reduced biquaternion least squares problem into an equivalent unconstrained least squares problem of a real matrix system. This was achieved by utilizing the real representation matrix of the reduced biquaternion matrix and leveraging its specific structure. Additionally, we have determined the necessary and sufficient conditions for the existence and uniqueness of the Hermitian solution, along with a general form of the solution. These conditions and the general form of the solution were previously derived by Yuan et al. (2020)(2020) using the complex representation of reduced biquaternion matrices. In comparison, our approach exclusively involved real matrices and utilized real arithmetic operations, resulting in enhanced efficiency. We have also used our developed method to solve partially described inverse eigenvalue problems over the complex field. Finally, we have provided numerical examples to demonstrate the effectiveness of our method and its superiority over the existing method.

References

  • [1] Moody Chu and Gene Golub. Inverse eigenvalue problems: theory, algorithms, and applications. OUP Oxford, 2005.
  • [2] Biswa Datta. Numerical methods for linear control systems, volume 1. Academic Press, 2004.
  • [3] Jie Ding, Yanjun Liu, and Feng Ding. Iterative solutions to matrix equations of the form Ai​X​Bi=FiA_{i}XB_{i}=F_{i}. Comput. Math. Appl., 59(11):3500–3507, 2010.
  • [4] Shan Gai. Theory of reduced biquaternion sparse representation and its applications. Expert Systems with Applications, 213:119–245, 2023.
  • [5] Feliks Rouminovich Gantmacher and Joel Lee Brenner. Applications of the Theory of Matrices. Courier Corporation, 2005.
  • [6] Gene H Golub and Charles F Van Loan. Matrix computations. JHU press, 2013.
  • [7] Dai Hua and Peter Lancaster. Linear matrix equations from an inverse problem of vibration theory. Linear Algebra Appl., 246:31–47, 1996.
  • [8] Tongsong Jiang and Musheng Wei. On solutions of the matrix equations X−A​X​B=CX-AXB=C and X−A​X¯​B=CX-A\overline{X}B=C. Linear Algebra Appl., 367:225–233, 2003.
  • [9] Peter Lancaster. Explicit solutions of linear matrix equations. SIAM Rev., 12:544–566, 1970.
  • [10] An-Ping Liao and Yuan Lei. Least-squares solution with the minimum-norm for the matrix equation (A​X​B,G​X​H)=(C,D)(AXB,GXH)=(C,D). Comput. Math. Appl., 50(3-4):539–549, 2005.
  • [11] Sujit Kumar Mitra. Common solutions to a pair of linear matrix equations A1​X​B1=C1A_{1}XB_{1}=C_{1} and A2​X​B2=C2A_{2}XB_{2}=C_{2}. Proc. Cambridge Philos. Soc., 74:213–216, 1973.
  • [12] A. Navarra, P. L. Odell, and D. M. Young. A representation of the general common solution to the matrix equations A1​X​B1=C1A_{1}XB_{1}=C_{1} and A2​X​B2=C2A_{2}XB_{2}=C_{2} with applications. Comput. Math. Appl., 41(7-8):929–935, 2001.
  • [13] Soo-Chang Pei, Ja-Han Chang, and Jian-Jiun Ding. Commutative reduced biquaternions and their Fourier transform for signal and image processing applications. IEEE Trans. Signal Process., 52(7):2012–2031, 2004.
  • [14] Soo-Chang Pei, Ja-Han Chang, Jian-Jiun Ding, and Ming-Yang Chen. Eigenvalues and singular value decompositions of reduced biquaternion matrices. IEEE Trans. Circuits Syst. I. Regul. Pap., 55(9):2673–2685, 2008.
  • [15] Sang-Yeun Shim and Yu Chen. Least squares solution of matrix equation A​X​B∗+C​Y​D∗=EAXB^{*}+CYD^{*}=E. SIAM J. Matrix Anal. Appl., 24(3):802–808, 2003.
  • [16] Peng Wang, Shifang Yuan, and Xiangyun Xie. Least-squares Hermitian problem of complex matrix equation (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F). J. Inequal. Appl., pages 1–13, 2016.
  • [17] Guiping Xu, Musheng Wei, and Daosheng Zheng. On solutions of matrix equation A​X​B+C​Y​D=FAXB+CYD=F. Linear Algebra Appl., 279(1-3):93–109, 1998.
  • [18] Shi-Fang Yuan, Yong Tian, and Ming-Zhao Li. On Hermitian solutions of the reduced biquaternion matrix equation (A​X​B,C​X​D)=(E,G)(AXB,CXD)=(E,G). Linear Multilinear Algebra, 68(7):1355–1373, 2020.
  • [19] Shi-Fang Yuan and Qing-Wen Wang. L-structured quaternion matrices and quaternion linear matrix equations. Linear Multilinear Algebra, 64(2):321–339, 2016.
  • [20] Fengxia Zhang, Weisheng Mu, Ying Li, and Jianli Zhao. Special least squares solutions of the quaternion matrix equation A​X​B+C​X​D=EAXB+CXD=E. Comput. Math. Appl., 72(5):1426–1435, 2016.
  • [21] Fengxia Zhang, Musheng Wei, Ying Li, and Jianli Zhao. Special least squares solutions of the quaternion matrix equation A​X=BAX=B with applications. Appl. Math. Comput., 270:425–433, 2015.
  • [22] Fengxia Zhang, Musheng Wei, Ying Li, and Jianli Zhao. An efficient method for special least squares solution of the complex matrix equation (A​X​B,C​X​D)=(E,F)(AXB,CXD)=(E,F). Comput. Math. Appl., 76(8):2001–2010, 2018.
  • [23] Fengxia Zhang, Musheng Wei, Ying Li, and Jianli Zhao. The minimal norm least squares Hermitian solution of the complex matrix equation A​X​B+C​X​D=EAXB+CXD=E. J. Franklin Inst., 355(3):1296–1310, 2018.
  • [24] Fengxia Zhang, Musheng Wei, Ying Li, and Jianli Zhao. An efficient method for least-squares problem of the quaternion matrix equation X−A​X^​B=CX-A\hat{X}B=C. Linear Multilinear Algebra, 70(13):2569–2581, 2022.