¹¹institutetext: Computational Imaging Research Lab, Department of Biomedical Imaging and Image-guided Therapy, Medical University of Vienna, Austria. ²²institutetext: Medical Image Analysis Laboratory, Department of Radiology, Lausanne University Hospital and University of Lausanne, Switzerland. ³³institutetext: CIBM Center for Biomedical Imaging, Switzerland. ⁴⁴institutetext: Center for Biomedical Imaging and Neuromodulation, Nathan Kline Institute, Orangeburg, NY, United States. ⁵⁵institutetext: Division of Neuroradiology and Muskulo-skeletal Radiology, Department of Biomedical Imaging and Image-guided Therapy, Medical University of Vienna, Austria.
⁵⁵email: [email protected]

Spatio-temporal motion correction and iterative reconstruction of in-utero fetal fMRI

Athena Taymourtash 11 Hamza Kebiri 2233 Ernst Schwartz 11 Karl-Heinz Nenning 1144 Sébastien Tourbier 22 Gregor Kasprian 55 Daniela Prayer 1155 Meritxell Bach Cuadra 2233 Georg Langs *1*1

Abstract

Resting-state functional Magnetic Resonance Imaging (fMRI) is a powerful imaging technique for studying functional development of the brain in utero. However, unpredictable and excessive movement of fetuses have limited its clinical applicability. Previous studies have focused primarily on the accurate estimation of the motion parameters employing a single step 3D interpolation at each individual time frame to recover a motion-free 4D fMRI image. Using only information from a 3D spatial neighborhood neglects the temporal structure of fMRI and useful information from neighboring timepoints. Here, we propose a novel technique based on four dimensional iterative reconstruction of the motion scattered fMRI slices. Quantitative evaluation of the proposed method on a cohort of real clinical fetal fMRI data indicates improvement of reconstruction quality compared to the conventional 3D interpolation approaches.

Keywords:

Fetal fMRI image reconstruction motion-compensated recovery regularization.

1 Introduction

Functional magnetic resonance imaging (fMRI) offers a unique means of observing the functional brain architecture and its variation during development, aging, or disease. Despite the insights into network formation and functional growth of the brain,in utero fMRI of living human fetuses, and the developmental functional connectivity (FC), however, remain challenging. Since the fMRI acuisition takes several minutes, unconstrained and potentially large movements of the fetuses, uterine contractions, and maternal respiration can cause severe artifacts such as in-plane blurring, slice cross-talk, and spin-history artifacts that likely vary over time. Without mitigation, motion artifacts can considerably affect the image quality, leading to a bias of subsequent conclusions about the FC of the developing brain.

Standard motion correction approaches, including frame-by-frame spatial realignment along with discarding parts of data with excessive motion, have been adopted so far to address motion artifacts of in utero fMRI [20, 10, 17]. More recently, cascaded slice-to-volume registration [13] combined with spin history correction [4], and framewise registration based on the 2^nd order edge features instead of raw intensities [11] were suggested. These studies used 3D linear interpolation of motion scattered data at each volume independently to reconstruct the entire time series. Since in utero motion is unconstrained and complex, the regular grid of observed fMRI volumes becomes a set of irregularly motion scattered points possibly out of the field-of-view of the reconstruction grid, which might contain gaps in regions with no points in close proximity. Therefore interpolation in each 3D volume cannot recover the entire reconstruction grid.

Here we propose a new reconstruction method that takes advantage of the temporal structure of fMRI time series and rather than treating each frame independently, it takes both the spatial and the temporal domains into account to iteratively reconstruct a full 4D in utero fMRI image. The proposed method relies on super-resolution techniques that attracted increasing attention in structural fetal T2-weighted imaging, aiming to estimate a 3D high-resolution (HR) volume from multiple (semi-)orthogonal low resolution scans [5, 15, 3]. In case of fMRI, orthogonal acquisitions are not available, instead the reconstruction of a 4D image from a single sequence acquired over time is desired (An illustration of the problem is shown in Figure 1). Currently, existing single-image reconstruction methods are generally proposed for 3D structural MR images with isotropic voxels, while the effect of motion is implicitly modeled via blurring the desired HR image [14]. None of these methods have been tailored for 4D fMRI with high-levels of movement such as the fetal population.

Our contribution is threefold: (1) we develop a 4D optimization scheme based on low-rank and total variation regularization to reconstruct 4D fMRI data as a whole (2) we explicitly model the effect of motion in the image degradation process since it is the main source of gaps between interpolated slices; (3) we show the performance of our algorithm on the highly anisotropic in utero fMRI images. Experiments were performed on 20 real individuals, and the proposed method was compared to various interpolation methods.

2 Method

We first describe the fMRI image acquisition model and then its corresponding inverse problem formulation to recover a 4D artifact-free fMRI from a single scan of motion corrupted image, using low-rank and total variation regularizations.

2.1 The Reconstruction Problem

fMRI requires the acquisition of a number of volumes over time (fMRI time-series, bold signal) to probe the modulation of spontaneous (or task-related) neural activity. This activity is characterized by low frequency fluctuations ( $<0.1Hz$ ) of bold signals and therefore temporal smoothing is often applied as a pre-processing step in fMRI analysis. We aim at estimating the motion-compensated reconstruction of fMRI time series ( $\mathcal{X}\in\mathbb{R}^{\hat{B}\times\hat{K}\times\hat{H}\times N}$ ) from observed motion-contaminated fMRI volumes ( $\mathcal{T}\in\mathbb{R}^{B\times K\times H\times N}$ ) that integrates temporal smoothing within a full 4D iterative framework. Both $\mathcal{X}$ and $\mathcal{T}$ are composed of $N$ 3D volumes $\mathbf{X}_{n},\mathbf{T}_{n}$ acquired over $N$ timepoints. In MR image acquisition, a degradation process yields a low-resolution image from the latent high-resolution image:

\mathbf{T}_{n}=DSM_{n}\mathbf{X}_{n}+z

(1)

where $D$ is a 3D downsampling operator, $S$ is a 3D blurring operator, $M$ is the set of estimated motion parameters (three rotation and three translation parameters for each slice $\mathbf{t}_{n,h}\in\mathbb{R}^{\textbf{B}\times K}$ of the volume $\mathbf{T}_{n}$ , estimated prior to optimization (Sec. 3.1)), and $z$ represents the observation noise. The application of $M_{n}$ in the model here is equivalent to transforming each slice by the motion followed by resampling them on a 4D regular grid. Successful recovery of $\mathcal{X}$ from the $\mathcal{T}$ not only ensures the compensation of motion but also smoother bold signals due to the implicit temporal structure present in the data. However, since the Eq.(1) is ill-posed, direct recovery of $\mathcal{X}$ is not possible without enforcing a prior. Hence, the reconstruction of the latent desired 4D image $\mathcal{X}$ is achieved by minimizing the following cost function based on the inverse problem formulation:

\min_{\mathcal{X}}\sum_{n=1}^{N}\left\|DSM_{n}\mathbf{X}_{n}-\mathbf{T}_{n}\right\|^{2}+\lambda\Re(\mathcal{X})

(2)

where $\Re(\mathcal{X})$ is a spatio-temporal regularization term, and $\lambda$ balances the contributions of the data fidelity and regularization terms. We propose two regularization terms in this context, 4D low-rank for missing data recovery and total variation for preserving local spatial consistency.

Refer to caption — Figure 1: Illustration of the image reconstruction using super-resolution technique. Oversampling exists in case of 3D structural MRI (left panel), however, there is not enough data for separate reconstruction of each 3D fMRI volume (middle panel). Here we propose to reconstruct the whole 4D fMRI at once using both spatial and temporal data structure (right panel).

2.1.1 4D Low-Rank Regularization

Rank as a measure of nondegenerateness of the matrix, is defined by the maximum number of linearly independent rows or columns in the matrix. Since self-similarity is widely observed in fMRI images, low rank prior has been successfully used in matrix completion of censored fMRI time series [1]. Here we use low rank as a regularization term to help retrieve relevant information from all image regions. To compute the rank for a 4D image $\mathcal{X}$ , we first unfold it into a 2D matrix along each dimension [7]. Specifically, suppose the size of $\mathcal{X}$ is $B\times K\times H\times N$ , we unfold it into four 2D matrices $\left\{X_{(i)},i=1,2,3,4\right\}$ with size of $B\times\left(K\times H\times N\right),K\times\left(B\times H\times N\right),H\times\left(B\times K\times N\right)$ , and $N\times\left(B\times K\times H\right)$ where X(i) means unfold $\mathcal{X}$ along dimension i. Then we compute the sum of the singular values in each matrix for their trace norms $\left\|X_{(i)}\right\|_{tr}$ . Finally, the rank of $\mathcal{X}$ is approximated as the combination of trace norms of all unfolded matrices [14]:

\Re_{rank}(\mathcal{X})=\sum_{i=1}^{4}\alpha_{i}\left\|X_{(i)}\right\|_{tr}

(3)

where $\left\{\alpha_{i}\right\}$ are parameters satisfying $\alpha_{i}\geq 0$ , and $\sum_{i=1}^{4}\alpha_{i}=1$ . By minimizing this term, we obtain a low-rank approximation of $\mathcal{X}$ . The low rank regularization is applied in the entire 4D data retrieving useful information for the reconstruction task from both spatial and temporal domains.

2.1.2 Total Variation Regularization

Total variation (TV) is defined as integrals of absolute gradient of the signal. For a 4D functional image $\mathcal{X}$ :

\Re_{tv}(\mathcal{X})=\sum_{n=1}^{N}\int\left|\nabla\mathbf{X}_{n}\right|dbdkdh

(4)

where the gradient operator is performed in 3D spatial space. TV regularization has been largely adopted in image recovery because of its powerful ability in edge preservation [15, 14]. Here, we use TV in 3D space instead of 4D space based on the notion that primarily the spatial neighborhood exhibits consistency and thus TV in temporal domain may not be effective.

2.2 Optimization

The proposed 4D single acquisition reconstruction is thus formulated as below:

\min_{\mathcal{X}}\sum_{n=1}^{N}\left\|DSM_{n}\mathbf{X}_{n}-\mathbf{T}_{n}\right\|^{2}+\lambda_{\text{rank }}\Re_{\text{rank }}(\mathcal{X})+\lambda_{tv}\sum_{n=1}^{N}\Re_{tv}\left(\mathbf{X}_{n}\right)

(5)

We employ the alternating direction method of multipliers (ADMM) algorithm to minimize the cost function in Eq.(5). ADMM has been proven efficient for solving optimization problems with multiple non-smooth terms [2]. Briefly, we first introduce redundant variables $\left\{Y_{i}\right\}_{i=1}^{4}$ with equality constraints $\mathcal{X}_{(i)}=Y_{i(i)}$ , and then use Lagrangian dual variables $\left\{U_{i}\right\}_{i=1}^{4}$ to integrate the equality constraints into the cost function:

\begin{array}[]{l}\min_{{\mathcal{X}},\left\{Y_{i}\right\}_{i=1}^{4},\left\{U_{i}\right\}_{i=1}^{4}}\sum_{n=1}^{N}\left\|DSM_{n}\mathbf{X}_{n}-\mathbf{T}_{n}\right\|^{2}+\lambda_{\text{rank }}\sum_{i=1}^{4}\alpha_{i}\left\|Y_{i(i)}\right\|_{tr}\\ {\quad+\sum_{i=1}^{4}\frac{\rho}{2}\left(\left\|\mathcal{X}-Y_{i}+U_{i}\right\|^{2}-\left\|U_{i}\right\|^{2}\right)+\lambda_{tv}\sum_{n=1}^{N}\int\left|\nabla\mathbf{X}_{n}\right|dbdkdh}\end{array}

(6)

We break the cost function into subproblems for $\mathcal{X}$ , Y, and U, and iteratively update them. The optimization scheme is summarized in Algorithm 1.

Algorithm 1 4D motion-compensated reconstruction of fMRI time series

Single scan fMRI image

\mathcal{T}

, realignment parameters

The desired

\mathcal{X}

by resampling motion-transformed image

\mathcal{T}

with linear interpolation. Set auxiliary variable

Y_{i}^{(0)}=0,U_{i}^{(0)}=0,i=1,2,3,4

while

\left\|\mathcal{X}^{k}-\mathcal{X}^{k-1}\right\|/\|\mathcal{T}\|>\varepsilon

Update

\mathcal{X}^{k}

by using gradient descent:

\arg\min_{\mathcal{X}}\sum_{n=1}^{N}\left\|DSM_{n}\mathbf{X}_{n}^{(k-1)}-\mathbf{T}_{n}\right\|^{2}+\sum_{i=1}^{4}\frac{\rho}{2}\left\|\mathcal{X}^{(k-1)}-Y_{i}^{(k-1)}+U_{i}^{(k-1)}\right\|^{2}+\lambda_{tv}\sum_{n=1}^{N}\int\left|\nabla\mathbf{X}_{n}^{(k-1)}\right|dbdhdk\lx@algorithmicx@hfill\ (7)

Update

Y_{i}^{(k)}

by using Singular Value Thresholding:

Y_{i}^{(k)}=fold_{i}\left[SVT_{\lambda_{rank}\alpha_{i}/\rho}\left(\mathcal{X}_{(i)}^{(k)}+U_{i(i)}^{(k-1)}\right)\right]\lx@algorithmicx@hfill\ (8)

with

fold_{i}\left(Y_{i(i)}\right)=Y_{i}

Update

U_{i}^{(k)}=U_{i}^{(k-1)}+\left(\mathcal{X}^{(k)}-Y_{i}^{(k)}\right)\lx@algorithmicx@hfill\ (9)

end while

3 Experiments and Results

3.1 Data

Data acquisition: Experiments in this study were performed on 20 in utero fMRI sequences obtained from fetuses between 19 and 39 weeks of gestation. None of the cases showed any neurological pathology. Pregnant women were scanned on a 1.5T clinical scanner (Philips Medical Systems, Best, Netherlands) using single-shot echo-planar imaging (EPI), and a sensitivity encoding (SENSE) cardiac coil with five elements. Image matrix size was 144 $\times$ 144, with 1.74 $\times$ 1.74 $mm^{2}$ in-plane resolution, 3 $mm$ slice thickness, a TR/TE of 1000/50 ms, and a flip angle of 90°. Each scan contains 96 volumes obtained in an interleaved slice order to minimize cross-talk between adjacent slices.

Preprocessing: For preprocessing, a binary brain mask was manually delineated on the average volume of each fetus and dilated to ensure it covered the fetal brain through all ranges of the motion. A four dimensional estimate of the bias field for spatio-temporal signal non-uniformity correction in fMRI series was obtained using N4ITK algorithm [18] as suggested previously [12]. Intensity normalization was performed as implemented in mialSRTK toolkit [16]. Finally, motion parameters were estimated by performing a hierarchical slice-to-volume registration based on the interleaved factor of acquisition to a target volume created by automatically finding a set of consecutive volumes of fetal quiescence and averaging over them [13]. Image registration software package NiftyReg [8] was used for all motion correction steps in our approach. Demographic information of all 20 subjects as well as the maximum motion parameters estimated were reported in Supplementary Table S1.

3.2 Experimental Setting and Low-Rank Representation

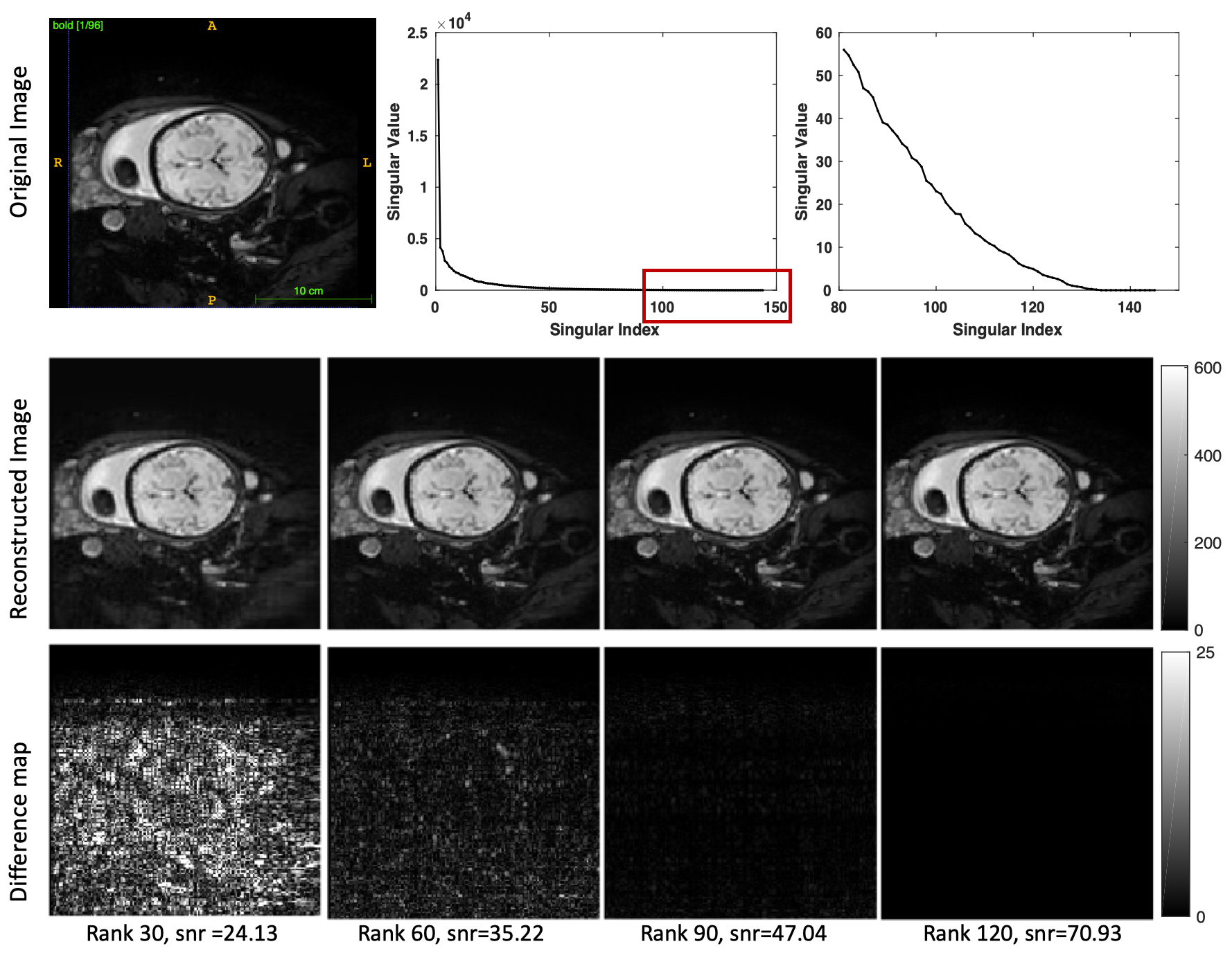
We first evaluated to which extent in utero fMRI data can be characterized by its low-rank decomposition. The rapid decay of the singular values for a representative slice of our cohort is shown in Supplementary Figure S1. We used the top 30, 60, 90, and 120 singular values to reconstruct this slice and measured signal-to-noise ratio (SNR) to evaluate the reconstruction accuracy. The number of used singular values determines the rank of the reconstructed image. Using the top 90 or 120 singular values (out of 144), the reconstructed image does not show visual differences compared to the original image while it has a relatively high SNR (Figure S1).

For the full 4D fMRI data of our cohort with the size of 144 $\times$ 144 $\times$ 18 $\times$ 96, four ranks, one for each unfolded matrix along one dimension is computed. Each is less than the largest image size 144. These ranks are relatively low in comparison to the total number of elements, implying in utero fMRI images could be represented using their low-rank approximations. We set $\alpha_{1}=\alpha_{2}=\alpha_{3}=\alpha_{4}=1/4$ as all dimensions are assumed to be equally important, $\lambda_{\text{rank}}=0.01$ , $\lambda_{\text{tv}}=0.01$ were chosen empirically. The algorithm stopped when the difference in iterations was less than $\varepsilon=1e-5$ .

3.3 Evaluation of Image Reconstruction

A number of interpolation methods was employed to be compared with our reconstructed image including linear, cubic spline, and SINC interpolation. For each method, we applied the same realignment parameters as the ones used in our model, and in accordance with standard motion correction techniques, each 3D volumes of fMRI time series was interpolated separately. We quantified sharpness [9] of the average recovered image, standard deviation of bold signal fluctuations (SD) through-out the sequence, and the Structural Similarity Index (SSIM) which correlates with the quality of human visual perception [19]. Higher values of sharpness and SSIM, and lower values of SD are indicative of better recovery.

Figure 2 shows, from left to right, the reference volume, two corresponding slices in the observed image, and the results of different reconstruction methods. Volume No.20 exhibits minor motion, volume No.65 exhibits strong motion. The motion estimate plots on the right show their respective time points. The figure shows the recovered slices of these two volumes using 3D linear, cubic, SINC, and the proposed 4D LR+TV method, respectively. In the case of excessive complex motion (30 $\degree$ out of the plane combined with in-plane rotation and translation), the 3D interpolation methods cannot recover the whole slice as they utilize information only from the local spatial neighborhoods. The reconstructed slice by the proposed 4D iterative reconstruction approach recovers the image information, is sharper, and preserves more structural detail of the brain. Figure 3 shows a qualitative and quantitative comparison of reconstruction approaches. Figure 3 (a) shows the average volume (top row), and the standard deviation of intensity changes over time (bottom row) for one subject. 4D reconstruction achieves sharper structural detail, and overall reduction of the standard deviation, which is primarily related to motion as described earlier. Although linear interpolation results in signals as smooth as the proposed method, severe blurring is observed in the obtained image by this approach. Figure 3 (b) provides the quantitative evaluation for the entire study population. The proposed method significantly (p $<$ 0.01, paired-sample t-tests for each comparison) outperforms all comparison methods. The average gain of sharpness over the observed image is 2294 in our method compared to 1521 for 3D SINC, 959 for 3D Cubic, and 294 for 3D Linear, and the average reduction of SD relative to the observed image is -17 in our method compared to -9.34 for 3D SINC, -12.70 for 3D Cubic, and -16.50 for 3D Linear. The difference between linear interpolation and our approach did not reach the statistical significance level for SSIM (p=0.28). In summary, 4D iterative reconstruction reduces standard deviation over time, while increasing sharpness and recovered structure, which the 3D approaches failed to achieve.

3.4 Functional Connectivity Analysis

Figure 4 illustrates the impact of the accurate motion correction and reconstruction for the analysis of functional connectivity (FC) in the fetal population. The details of the pipeline employed for extracting subject-specific FC maps is explained in the supplementary material. When using the time series recovered by our proposed approach for FC analysis, the number of motion-corrupted correlations decreased significantly as visible in the carpet plot of signals, and the associated connectivity matrix.

4 Conclusion

In this work, we presented a novel spatio-temporal iterative 4D reconstruction approach for in-utero fMRI acquired while there is unconstrained motion of the head. The approach utilizes the self-similarity of fMRI data in the temporal domain as 4D low-rank regularisation together with total variation regularization based on spatial coherency of neighboring voxels. Comparative evaluations on 20 fetuses show that this approach yields a 4D signal with low motion induced standard deviation, and recovery of fine structural detail, outperforming various 3D reconstruction approaches.

Acknowledgment

This work has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 765148, and partial funding from the Austrian Science Fund (FWF, P35189, I 3925-B27), in collaboration with the French National Research Agency (ANR), and the Vienna Science and Technology Fund (WWTF, LS20-065). This work was also supported by the Swiss National Science Foundation (project 205321-182602). We acknowledge access to the expertise of the CIBM Center for Biomedical Imaging, a Swiss research center of excellence founded and supported by Lausanne University Hospital (CHUV), University of Lausanne (UNIL), Ecole polytechnique fédérale de Lausanne (EPFL), University of Geneva (UNIGE) and Geneva University Hospitals (HUG).

References

[1] Balachandrasekaran, A., Cohen, A.L., Afacan, O., Warfield, S.K., Gholipour, A.: Reducing the effects of motion artifacts in fmri: A structured matrix completion approach. IEEE Transactions on Medical Imaging 41(1), 172–185 (2021)
[2] Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J., et al.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine learning 3(1), 1–122 (2011)
[3] Ebner, M., Wang, G., Li, W., Aertsen, M., Patel, P.A., Aughwane, R., Melbourne, A., Doel, T., Dymarkowski, S., De Coppi, P., et al.: An automated framework for localization, segmentation and super-resolution reconstruction of fetal brain mri. NeuroImage 206, 116324 (2020)
[4] Ferrazzi, G., Murgasova, M.K., Arichi, T., Malamateniou, C., Fox, M.J., Makropoulos, A., Allsop, J., Rutherford, M., Malik, S., Aljabar, P., et al.: Resting state fmri in the moving fetus: a robust framework for motion, bias field and spin history correction. Neuroimage 101, 555–568 (2014)
[5] Gholipour, A., Estroff, J.A., Warfield, S.K.: Robust super-resolution volume reconstruction from slice acquisitions: application to fetal brain mri. IEEE transactions on medical imaging 29(10), 1739–1758 (2010)
[6] Gholipour, A., Rollins, C.K., Velasco-Annis, C., Ouaalam, A., Akhondi-Asl, A., Afacan, O., Ortinau, C.M., Clancy, S., Limperopoulos, C., Yang, E., et al.: A normative spatiotemporal mri atlas of the fetal brain for automatic segmentation and analysis of early brain growth. Scientific reports 7(1), 476 (2017)
[7] Liu, J., Musialski, P., Wonka, P., Ye, J.: Tensor completion for estimating missing values in visual data. IEEE transactions on pattern analysis and machine intelligence 35(1), 208–220 (2012)
[8] Modat, M., Cash, D.M., Daga, P., Winston, G.P., Duncan, J.S., Ourselin, S.: Global image registration using a symmetric block-matching approach. Journal of medical imaging 1(2), 024003 (2014)
[9] Pech-Pacheco, J.L., Cristóbal, G., Chamorro-Martinez, J., Fernández-Valdivia, J.: Diatom autofocusing in brightfield microscopy: a comparative study. In: Proceedings 15th International Conference on Pattern Recognition. ICPR-2000. vol. 3, pp. 314–317. IEEE (2000)
[10] Rutherford, S., Sturmfels, P., Angstadt, M., Hect, J., Wiens, J., van den Heuval, M.I., Scheinost, D., Thomason, M., Sripada, C.: Observing the origins of human brain development: Automated processing of fetal fmri. bioRxiv p. 525386 (2019)
[11] Scheinost, D., Onofrey, J.A., Kwon, S.H., Cross, S.N., Sze, G., Ment, L.R., Papademetris, X.: A fetal fmri specific motion correction algorithm using 2 nd order edge features. In: 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018). pp. 1288–1292. IEEE (2018)
[12] Seshamani, S., Cheng, X., Fogtmann, M., Thomason, M.E., Studholme, C.: A method for handling intensity inhomogenieties in fmri sequences of moving anatomy of the early developing brain. Medical image analysis 18(2), 285–300 (2014)
[13] Seshamani, S., Fogtmann, M., Cheng, X., Thomason, M., Gatenby, C., Studholme, C.: Cascaded slice to volume registration for moving fetal fmri. In: 2013 IEEE 10th International Symposium on Biomedical Imaging. pp. 796–799. IEEE (2013)
[14] Shi, F., Cheng, J., Wang, L., Yap, P.T., Shen, D.: Lrtv: Mr image super-resolution with low-rank and total variation regularizations. IEEE transactions on medical imaging 34(12), 2459–2466 (2015)
[15] Tourbier, S., Bresson, X., Hagmann, P., Thiran, J.P., Meuli, R., Cuadra, M.B.: An efficient total variation algorithm for super-resolution in fetal brain mri with adaptive regularization. NeuroImage 118, 584–597 (2015)
[16] Tourbier, S., Velasco-Annis, C., Taimouri, V., Hagmann, P., Meuli, R., Warfield, S.K., Cuadra, M.B., Gholipour, A.: Automated template-based brain localization and extraction for fetal brain mri reconstruction. NeuroImage 155, 460–472 (2017)
[17] Turk, E.A., Luo, J., Gagoski, B., Pascau, J., Bibbo, C., Robinson, J.N., Grant, P.E., Adalsteinsson, E., Golland, P., Malpica, N.: Spatiotemporal alignment of in utero bold-mri series. Journal of Magnetic Resonance Imaging 46(2), 403–412 (2017)
[18] Tustison, N.J., Avants, B.B., Cook, P.A., Zheng, Y., Egan, A., Yushkevich, P.A., Gee, J.C.: N4itk: improved n3 bias correction. IEEE transactions on medical imaging 29(6), 1310–1320 (2010)
[19] Wang, Z., Bovik, A.C., Sheikh, H.R., Simoncelli, E.P.: Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing 13(4), 600–612 (2004)
[20] You, W., Evangelou, I.E., Zun, Z., Andescavage, N., Limperopoulos, C.: Robust preprocessing for stimulus-based functional mri of the moving fetus. Journal of Medical Imaging 3(2), 026001 (2016)