Spatio-temporal Joint Modelling on Moderate-Extreme Air Pollution in Spain
Abstract
Very unhealthy air quality is consistently connected with numerous diseases. Appropriate extreme analysis and accurate predictions are in rising demand for exploring potential linked causes and for providing suggestions for the environmental agency in public policy strategy. This paper aims to model the spatial and temporal pattern of both moderate and extremely poor PM10 concentrations (of daily mean) collected from 342 representative monitors distributed throughout mainland Spain from 2017 to 2021. We firstly propose and compare a series of Bayesian hierarchical generalized extreme models of annual maxima PM10 concentrations, including both the fixed effect of altitude, temperature, precipitation, vapour pressure and population density, as well as the spatio-temporal random effect with the Stochastic Partial Differential Equation (SPDE) approach and a lag-one dynamic auto-regressive component (AR(1)). Under WAIC, DIC and other criteria, the best model is selected with good predictive ability based on the first four-year data (2017–2020) for training and the last-year data (2021) for testing. We bring the structure of the best model to establish the joint Bayesian model of annual mean and annual maxima PM10 concentrations and provide evidence that certain predictors (precipitation, vapour pressure and population density) influence comparably while the other predictors (altitude and temperature) impact reversely in the different scaled PM10 concentrations. The findings are applied to identify the hot-spot regions with poor air quality using excursion functions specified at the grid level. It suggests that the community of Madrid and some sites in northwestern and southern Spain are likely to be exposed to severe air pollution, simultaneously exceeding the warning risk threshold.
Keywords Extreme Value Analysis Air Pollution Bayesian Joint model with sharing effects Spatio-temporal model Integrated Nested Laplace Approximation
1 Introduction
Air pollution, composed of particulate matter () and gaseous pollutants, has a substantial negative impact on the environment, ecosystem and human health. Poor air quality is one of the five most significant health risks worldwide, alongside high blood pressure, smoking, diabetes and obesity (Cohen et al.,, 2017; Daellenbach et al.,, 2020). It becomes one of the most considerable health concerns for the residents in areas of higher population density (Dias and Tchepel,, 2018), centres with dense activities, and to particular user groups (Agarwal and Kaddoura,, 2019; Singh et al.,, 2021). Among all the pollutants, the particulate matter, with an aerodynamic diameter less than or equal to 10 and 2.5 microns respectively ( and ) are most consistently connected with numerous adverse health outcomes including lung infections, cardiovascular diseases, and respiratory problems (Joseph et al.,, 2003; Martuzzi et al.,, 2006; Samoli et al.,, 2013), while appropriate regulation directly reduces the adverse health effects, increases general well-being, and improves public health (Steinle et al.,, 2015).
In Europe, although the European Environment Agency (EEA) maintains a rather dense particulate matter monitoring network to record the concentration levels across countries, huge regions of the European continent remain unmonitored. For proper assessment of population-wide exposure and appropriate formulation of pollution mitigation strategies, the responsible authorities need accurately estimate and predict the concentration levels at the unobserved locations (Chu et al.,, 2015).
The main challenge to forecasting particulate matter concentrations corresponds to the complexity of PM generation and spreading dynamics. On the one hand, the PM generation is dominated by two complicated sources, inorganic aerosol coming from the agriculture, long-range transport and energy sectors (Steinle et al.,, 2013; Daellenbach et al.,, 2020), as well as organic aerosol coming from biomass and fossil fuels burning emissions, vehicles emissions and cooking (Lenschow et al.,, 2001; Omidvarborna et al.,, 2015). On the other hand, the PM spread depends on both meteorological conditions and land use dispersion, leading the observed concentration levels to fluctuate geographically and temporally.
In the statistical literature, the Bayesian spatio-temporal model that allows modelling a complex environmental phenomenon through a hierarchy of sub-models becomes one of the most promising methodologies in air quality scientific investigations (Cameletti et al.,, 2013; Amin et al.,, 2015; Taheri Shahraiyni and Sodoudi,, 2016; Forlani et al.,, 2020; Fioravanti et al.,, 2021; Castro-Camilo et al.,, 2021). In particular, this approach allows involving the explanatory variables to explain the large-scale variability, take residual dependency into account through a space-time process with a Gaussian random field (GRF), and produce high-resolution spatial forecasts to meet the rising demand for predictive concentration maps in epidemiological studies.
According to Porcu et al., (2012), the main drawback of the Bayesian model with a GRF refers to the computational difficulty to deal with enormous amounts of data, especially applying complex spatial dependence measures (i.e., the Matérn covariance function). Some strategies have been proposed to alleviate the computational burden of fitting complex spatial and temporal models. Lindgren et al., (2011) proposed the stochastic partial differential equation (SPDE) approach, providing a method to represent a continuous Matérn field through a discretely indexed Gaussian Markov random field (GMRF) associated with a sparse precision matrix, which enjoys good computational property. Rue et al., (2009) also provided the Integrated Nested Laplace Approximation (INLA) algorithm that performs direct numerical calculations on the marginal posterior distributions, avoiding the time-consuming Markov chain Monte Carlo (MCMC) simulations. Additionally, GMRF with SPDE approach can be fitted in a Bayesian hierarchical framework through the INLA approach, with implementation in the R-INLA package available at https://www.r-inla.org/, making this methodology fast and easily implemented.
Most previous spatial and temporal studies on air pollution only concentrated on moderate (i.e., daily, monthly and annual mean) PM concentrations (Cameletti et al.,, 2013; Beloconi et al.,, 2018; Fioravanti et al.,, 2021; Saez and Barceló,, 2022). However, extreme conditions are actually more concerned with environmental quality management due to their various hazardous impacts (Amin et al.,, 2015). Numerous epidemiological studies pointed out that short-term exposures to severe particulate matter pollution can trigger serious acute cardiovascular and respiratory mortality (Orellano et al.,, 2020; Lei et al.,, 2019; Zhang et al.,, 2019; Yu et al.,, 2014; Brook et al.,, 2016) and huge economic loss in the corresponding hospitalization (Xie et al.,, 2021; Shah et al.,, 2013). In the field of extreme case spatio-temporal analysis, Sharma et al., (2012); Rodríguez et al., (2016); Amin et al., (2015); Martins et al., (2017) and Castro-Camilo et al., (2021) typically focused on a small spatial domain, making it difficult to consider the complicated orography with a variety of climatic conditions, as well as to provide general suggestions to national governments on the environmental policy formulation and health care allocation. More importantly, to our best knowledge, no studies consider the potential difference between moderate and extreme air pollution, in other words, model different scaled air pollution simultaneously to identify similarities and differences in the effects of influential factors.
In this paper, we focus on the spatial and temporal variation of both moderate and extreme air pollution (i.e., annual mean and annual maxima of daily concentration levels) in Spain from 2017 to 2021, after controlling for meteorological variables and socio-economic factors. The contribution is two-fold, the predictions of extreme pollution (excursion functions) and the investigation of similar/reverse effects of predictors in different scaled cases. Firstly, we establish several Bayesian hierarchical generalized extreme models on annual maxima and select the best model based on their predictive performance, detailed in Sections 3.1 and 4.1. Secondly, we utilize the joint Bayesian model with sharing effects in Sections 3.2 and 4.3 to model both annual mean and maxima concentrations simultaneously. We observe the comparable influence of precipitation, vapour pressure, and population density, as well as the possible opposite effects of altitude and temperature. We also generate excursion function maps (Bolin and Lindgren,, 2015) based on the joint model to highlight the regional risk ranking that simultaneously exceeds the warning risk threshold in Section 4.4. These main findings, comprehensive knowledge on the generation and spread with high-resolution spatial forecasts are expected to promote awareness of the significance of extreme air pollution research, help in the investigation of the long-term effect in epidemiological studies, and underpins air pollutants regulation and human health protection strategies for environmental agencies.
The rest of the paper is organized as follows. In Section 2, we demonstrate the dataset for response and main explanatory variables. In Section 3, we formalize spatio-temporal Bayesian generalized extreme models on moderate-extreme air pollution in the framework of Bayesian spatial analysis and extreme value theory. We present the main results, applications and potential influence in Section 4, and conclude this paper with extensional discussions in Section 5.
2 Data
2.1 PM10 concentrations and spatial domain
In mainland Spain, the concentration levels data is accessible by the Air Quality e-Reporting which is EEA’s air quality database consisting of a multi-annual time series data of air quality measurement and calculated statistics for a number of air pollutants. To work with a more robust dataset, we only retain 342 air pollution stations that have at least 60% valid observations in a year, with the geographical distribution of the stations shown in red circles embedded in the mesh constructed for the SPDE approach (Figure 1). This five-year dataset (2017–2021) with 1470 observations is divided into the training set (2017–2020; 1215 observations) and the validation set (2021; 255 observations), which are used to evaluate and compare the model fitness and predictive ability.

Figure 2 shows the temporal and spatial variations of extreme following the EEA’s air quality categories with 0–20 (Good), 20–40 (Fair), 40–50 (Moderate), 50–100 (Poor), 100–150 (Very poor), more than 150 (Extremely poor). Temporally, severe pollution seems to occur in 2017 and 2020, as indicated by the numerous monitors coloured in red (very poor) and purple (extremely poor). Spatially, compared with relatively low annual maxima recorded in the east (Valencian Community) and north (Basque Country), high concentrations are most prevalent in the centre, northwest and southeast, which correspond to the autonomous communities of Madrid, Galicia, Andalusia, and the Region of Murcia, respectively. This spatio-temporal pattern inspires our further investigation of spatio-temporal modelling taking appropriate topography covariates into account, which are stated in the following section.

2.2 Explanatory variables
A number of potential predictors are available based on prior findings in the air quality literature (Cameletti et al.,, 2013; Fioravanti et al.,, 2021; Castro-Camilo et al.,, 2021), and we choose to include a set of five main spatial and spatio-temporal varying predictors with the complete description list reported in Table 1.
| Predictors | Description | Units | Spatial Resolution |
|---|---|---|---|
| Altitude | Altitude of monitors | m | Station Specific |
| Temperature | Annual mean temperature | °C | 50km 50km |
| Precipitation | Annual mean precipitation | mm/month | 50km 50km |
| Vapour Pressure | Annual mean vapour pressure | hPa | 50km 50km |
| Population Density | Population per unit area | per | Autonomous Communities |
In the following, we describe the selected predictors in detail.
Meteorological variables. The meteorological variables (temperature, precipitation and vapour pressure) of the monthly mean are collected from the CRU TS (Climatic Research Unit gridded Time Series; Harris et al.,, 2020) dataset and aggregated to be annual mean. Accordingly, CRU TS was first published in 2000, using ADW (angular-distance weighting) to interpolate anomalies of monthly observations onto a 0.5° grid over land surfaces (excluding Antarctica) for observed and derived variables (mean, minimum and maximum temperatures, precipitation, vapour pressure, wet days and cloud cover) with no missing values in the defined domain.
Elevation. The altitude data, height over sea level, matched with locations of all air pollution monitors, is accessible in the annual aggregated air quality values dataset provided by EEA, available at https://discomap.eea.europa.eu/App/AirQualityStatistics/index.html.
Population density. The population densities are calculated in each autonomous community. The original data is collected from the statistics report (available at https://stats.oecd.org/) of the Organisation for Economic Co-operation and Development (OECD). The OECD statistics contain data and metadata for economic and education indexes of OECD countries and some selected non-member economies.
We see in Table 2 that the correlations of potential predictors to extreme and average PM10 display a similar or different direction, which also vary year by year. This will be further investigated by our spatio-temporal generalized extreme model and joint model with sharing effects, see details in both Sections 3.1 and 3.2. Furthermore, considering the correlation between location variables and meteorological variables (e.g., latitude and temperature), we adjust the location variables (longitude and latitude) as covariates to investigate the impact of meteorological factors.
| Explanatory variables | Correlation to () in each year (sample size) | |||||
|---|---|---|---|---|---|---|
| 2017 (294) | 2018 (296) | 2019 (300) | 2020 (325) | 2021 (255) | Total (1470) | |
| Altitude | ||||||
| Temperature | ||||||
| Precipitation | ||||||
| Vapour Pressure | ||||||
| Population Density | ||||||
3 Model Formulation
In Section 3.1, we provide first a brief introduction to spatio-temporal Gaussian field and extreme value models, followed by four candidate models for the annual maximum of daily PM10 in mainland Spain. Subsequently, in Section 3.2, we present the joint Bayesian Gumbel-Gaussian model for both extreme and moderate levels.
3.1 Spatio-temporal extreme value models with mixed effects
The generalized extreme value (GEV) distribution is widely employed for modelling extremes in environmental science (Reiss and Thomas,, 2007), such as temperature (Cheng et al.,, 2014), precipitation (Panagoulia et al.,, 2014), air pollution (Deng and Zhang,, 2018; Martins et al.,, 2017) and sea level (Lobeto et al.,, 2018). The GEV distribution has three parameters, location parameter (, ), scale parameter (, ) and tail parameter (, ) with the cumulative distribution function
The case is interpreted as the limit case of , leading to the Gumbel family with distribution function
Considering the potential spatial and temporal dependence among the PM10 concentrations, we use two typical approaches for measurement: Matérn covariance function (Matérn,, 1986; Guttorp and Gneiting,, 2006) with the Stochastic Partial Differential Equations approach (SPDE; Lindgren et al.,, 2011) approximation for spatial correlation and the auto-regressive dynamic model (AR; Shumway and Stoffer,, 2011) for temporal dependence. We establish two groups of generalised extreme value models with similar fixed effects and varying random effects to model the annual maxima concentrations.
Model 1: Gumbel model with fixed effect and spatio-temporal random effect. Let denote the logarithm transform of annual maxima concentrations at location and year , where is the study area and is the time period in focus. Under the assumption of constant scale () and tail () parameters, we use a linear combination of fixed effects with explanatory variables and spatio-temporal varying random effect to model the location parameter () in Gumbel model below. Suppose that
| (1) |
and
| (2) |
Here, the fixed effects are associated with the vector including an intercept and the explanatory variables of location variables, meteorological variables and human-effect variables listed in Table 1, and the vector corresponds to the regression coefficients associated with the fixed effects. The term represents a spatio-temporal varying random effect that incorporates spatio-temporal interaction (Cameletti et al.,, 2013). It temporally changes according to AR(1) dynamics with autocorrelation parameter and spatial correlated and serially independent innovations .
Given two locations and separated by (normally Euclidean) units, the Gaussian process with mean 0 and Matérn covariance function is in the form of
where is the gamma function, is the modified Bessel function of the second kind, is the range parameter, is the smoothness parameter, and for the marginal variance.
Model 2: Gumbel model with fixed effect and separated spatial and temporal random effects. Our second model is a modification of Model 1 specified in Eq.(1) with spatial and temporal random effects and separable interaction effects specified in Eq.(2), namely, we keep the Gumbel distribution assumption on as below.
| (3) |
Note that is defined the same as in Eq.(2), indicating the spatio-temporal interaction term with the Kronecker product, see e.g., Cameletti et al., (2011, 2013); Fioravanti et al., (2021). The denotes the non-linear random effect in the temporal structure of AR(), the is the spatially dependent only random effect with SPDE structure. Specifically, the implementation of the AR() model in INLA generally assumes the Gaussian white noise with mean and precision . For defined over the naturally binned covariate (Year), let denotes the time from the first year () to the last year (),
where is a numeric constant, the so-called autocorrelation, by which we multiply the lagged variable , and denotes the unpredictable error in the form of Gaussian white noise.
Model 3: GEV model with fixed effect and spatio-temporal random effect. The generalised extreme value (GEV) models are basically following the same structure as Gumbel models except the generalized extreme value distribution for the response. To be specific, we suppose that
| (4) |
where the location parameter is of the same form of mixed effects as in Eq.(1) and random effects in Eq. (2).
Model 4: GEV model with fixed effect and separated spatial and temporal random effect. Similar consideration of Model 2 modified from Model 1, we consider the following model in parallel with Model 3, i.e., we take spatial and temporal random effects with an interaction effect into the GEV model. Suppose that
| (5) |
with the location parameter is of spatio-temporal structure of the form in Eq.(3).
It is worth pointing out that the well-known limit type theorem in Coles, (2001) motivates our GEV distribution assumption of annual maxima of PM10, and its reduced case (i.e., Gumbel corresponds to GEV with ). The latter one becomes more parsimonious, and its exponential decay tail might be appropriate to fit extreme air quality (Deng and Zhang,, 2018). The Gumbel model is generally needed when the uncertainty of being non-zero arises in the GEV model with an estimate of close to zero.
3.2 Bayesian joint model with sharing effects
In order to identify the potential varied effect levels of main explanatory variables, with inspiration from applications of the joint model with sharing effects on wildfire (Koh et al.,, 2021), we model both moderate and extreme PM10 pollution simultaneously in two respective sub-models linked by the sharing effects and the sharing coefficients (scaling factors).
Let denote the logarithm transform of annual mean at location and year . We perform the Gaussian sub-model and Gumbel sub-model on annual mean and annual maxima simultaneously, with the structure of the best extreme value model as Model 1 according to the model fitness and prediction analysed in Section 4.1.
| (6) |
where the terms and with superscript denote the sharing effects, and are corresponding variables (geographical and meteorological). The term with superscript denotes the non-sharing effects with corresponding covariates which includes the intercept, location variables and human-effect variables (longitude, latitude, population density). For the selection of sharing and non-sharing variables, to avoid the potential issue of uncertainty of significant sharing effects (), we treat two significant predictors (altitude and precipitation) as sharing terms to investigate the potential similar and reverse effects by the ratios () while considering all other variables, including three non-significant ones (temperature, vapour pressure, and population density), and location variables as non-sharing terms.
Additionally, the spatio-temporal random effect is also treated as sharing effects with respect to the simplicity of computation. The sharing effects and scale the common components of covariate vector and random effect , and control how much information is shared from the average predictor towards the annual max predictor, and determine the strength of interaction between the two processes. Precisely, it allows for capturing the positive or negative correlations.
For further explanation, the sharing effects (including fixed effects and random effects) are the same in two sub-models (, ). Meanwhile, they are linked by the sharing coefficients (scaling factors) and . On the one hand, these sharing coefficients relax the strictly equal relation between the sharing effects in two sub-models. On the other hand, more importantly, their posterior distributions can also measure the similarities and differences in the effects of predictors in the sub-models. For instance, a significantly negative implies that the corresponding predictors oppositely influence the moderate and extreme air pollution cases.
3.3 Priors definition
In a Bayesian context, in order to finalize the model, we need to define prior distributions for the remaining parameters in Gumbel () and GEV distributions (, ), the regression coefficients (), the sharing coefficients in the joint model (), parameters in the Matérn covariance function (, ) and the parameters in AR(1) dynamic model (, ).
We use vague Gaussian priors for the tail parameter () in GEV distribution and the elements of coefficients (, ). The smooth parameter is treated here as a fixed value with , as in most spatial analyses. The parameters and in the Matérn function and autocorrelation parameter in AR(1) model are defined by penalized complexity (PC) priors (Simpson et al.,, 2017) with knowledge from Moraga, (2019) and Fuglstad et al., (2019). PC prior for the range parameter () is defined with , which means the probability that the range is less than is very small, and the PC prior for variance parameter as , indicating the probability for variance greater than is low. Similarly, we apply the auto-correlation () PC prior following the recommendation of .
Note that INLA often uses the precision parameter () to replace the scale parameter () by . The PC priors for all precision parameters are given by for Gumbel and GEV likelihood and for the AR model.
3.4 Model evaluation, diagnosis and cross-validation
Traditional Bayesian model performance is evaluated by two popular criteria, the deviance information criterion (DIC) and the Watanabe-Akaike information criterion (WAIC). The deviance information criterion (DIC) proposed by Spiegelhalter et al., (2002), is a popular criterion for model choice similar to the Akaike information criterion (AIC).
where is the deviance function with Bayes estimate , and is the effective number of parameters. The Watanabe-Akaike information criterion, also known as the widely applicable Bayesian information criterion, is similar to the DIC, but the effective number of parameters is computed in a different way (Watanabe,, 2013).
However, DIC may under-penalize complex models with many random effects. Alternatively, for prediction performance, INLA suggests applying the leave-one-out cross-validation criteria, conditional predictive ordinates (CPO; Pettit,, 1990) with its summative version, the Logarithmic Score (LS; Gneiting and Raftery,, 2007) and predictive integral transform (PIT; Marshall and Spiegelhalter,, 2003), which facilitates the computation of the cross-validated log-score for model choice, and enables the calibration assessment of out-of-sample predictions, respectively.
| LS | |||
where denotes the -th observation and denotes the observations with the -th component omitted. A model with a small value of LS and a standard uniform distributed PIT is preferable (Gómez Rubio,, 2020).
Note that numerical problems may occur when CPO and PIT values are computed with the complicated Gaussian process with INLA algorithm (Held et al.,, 2010). Hence, we take a few other criteria introduced in Bayesian literature into account: The coverage probability of 95% CI is computed as the proportion of the validation observations that the observed value lies between the 2.5% quantile to the 97.5% quantile of the predicted value (posterior distribution). The correlation coefficient denotes the correlation between observed values and predicted values in the validation set. The root mean square error (RMSE) is defined as the square root of the second sample moment of the differences between predicted values and observed values.
As we separate the original five-year dataset (2017–2021) into training (2017–2020) and validation (2021) sets, we decide to apply DIC, WAIC, LS, PIT and RMSE to compare the model fitness on the training set and use the coverage probability, correlation coefficient, and RMSE for predictive ability evaluation.
4 Results
In this section, we firstly compare the performance of the Bayesian generalised extreme models and select the best one with the outstanding predictive ability (Section 4.1), then summarize the corresponding posterior estimates for both fixed and random effects (Section 4.2). The analysis and interpretation of the joint model are included in Section 4.3 and followed by the excursion functions generation with severe air pollution risk ranking (Section 4.4). Note that since the explanatory variables are measured in different scales, to avoid numerical problems, each predictor is standardized to have mean zero and unit standard deviation.
4.1 Model comparison
In order to examine the fitting and prediction ability of the extreme value models, we apply some evaluation criteria (DIC, WAIC, LS, PIT and RMSE) on the training set (Table 3), and use other criteria (coverage probability, correlation and RMSE) on the validation set (Table 4). We see from Table 3 with model performance on the training set, Models 2 and 4 outperform in DIC (36.27 and 73.43, respectively), WAIC (193.67 and 223.06, respectively) and RMSE (0.24 and 0.18, respectively). However, Model 1 is preferable in the leave-one-out cross-validation criteria with LS (8019.07) and PIT plots (Figure 3). Table 4 shows that all four models are comparable in the coverage probability, correlation and RMSE.
Figure 4 shows the simultaneous visualization of model performance on both training and validation sets, where the scatters’ distribution along the line with intercept 0 and slope 1 indicates the estimated (predicted) values are best suited to the observations. All four models exhibit a strong fit for the trend.
To summarise, no model excels in all criteria. Considering the similar performance of all four models on the validation set, we choose the parsimonious model, Model 1 (the Gumbel model with fixed effects and spatio-temporal random effects defined in Eq.(1)), as the best model and bring its structure into further analysis.
| Model | DIC | WAIC | LS | RMSE |
|---|---|---|---|---|
| Model 1 | 229.78 | 356.86 | 8019.07 | 0.24 |
| Model 2 | 36.27 | 193.67 | 13140.13 | 0.20 |
| Model 3 | 277.48 | 317.67 | 12128.54 | 0.23 |
| Model 4 | 73.43 | 123.06 | 14314.97 | 0.18 |



| Model | Coverage Probability | Correlation | RMSE |
|---|---|---|---|
| Model 1 | 83.95% | 40.95% | 0.36 |
| Model 2 | 84.60% | 39.19% | 0.35 |
| Model 3 | 83.90% | 37.21% | 0.37 |
| Model 4 | 86.97% | 37.33% | 0.36 |




4.2 Summary of Model 1
The summary statistics for fixed effects are shown in Table 5. We see that altitude and population density are significantly negatively associated with annual maxima concentrations, whereas the effects of other covariates are not statistically significant. High temperature, low precipitation and low vapour pressure are likely to associate with extreme concentrations, consistent with Kalisa et al., (2018) and Li et al., (2014).
The negative association between population density and annual maxima concentrations is different from the positive correlation found in Table 2 and the positive association demonstrated by Borck and Schrauth, (2021). Together with the facts of relatively low correlation for population density (Table 2) and the phenomena that severe pollution in 2017, 2020 and 2021 (Figure 2) is usually associated with high temperature and low precipitation, our results probably imply that the generation and spread of extreme concentrations depend heavily on the climate conditions. This evidence coincides with the findings of the overwhelming role of adverse meteorology in severe air pollution events (Wang et al.,, 2020; Morawska et al.,, 2021).
The spatial and temporal dependence is accessible by spatial heat plot (Figure 5) and posterior estimates of autocorrelation coefficient ( in Table 6). Spatially, similar values of mean random effects occur in groups, especially, a large cluster of high values happens in the centre of the mainland. Temporally, the estimated mean correlation coefficient () is 0.80 with 95% credible interval (0.74, 0.85), providing evidence of relatively strong dependence between two consecutive years.
| Covariate | Mean | Stdev | 0.025 quantile | 0.5 quantile | 0.975 quantile |
|---|---|---|---|---|---|
| Intercept | 4.43 | ||||
| Longitude | 0.13 | 0.17 | |||
| Latitude | 0.13 | 0.19 | |||
| Altitude | 0.03 | ||||
| Temperature | 0.13 | 0.10 | 0.13 | 0.32 | |
| Precipitation | 0.06 | 0.09 | |||
| Vapour Pressure | 0.09 | 0.09 | |||
| Population Density | 0.03 |
| Parameter | Mean | Stdev | 0.025 quantile | 0.5 quantile | 0.975 quantile |
|---|---|---|---|---|---|
| Precision () | 25.62 | 1.64 | 22.52 | 25.57 | 28.99 |
| Range (, unit ) | 0.37 | ||||
| Stdev () | 0.58 | 0.05 | 0.48 | 0.57 | 0.69 |
| Autocorrelation () | 0.80 | 0.03 | 0.74 | 0.80 | 0.85 |


4.3 Results of the joint model with sharing effects
Combining the best extreme value model (Model 1) with the Gaussian model, we establish the joint model in Section 3.2 with sharing effects to estimate both maxima and mean concentration levels simultaneously. We keep the two significant effects of predictors (altitude and precipitation) as sharing effects, and all other effects (temperature, vapour pressure, population density and location) are treated as non-sharing ones. Table 7 summarizes the posterior estimates of these effects from the joint model. Precipitation shows significant negative associations with both annual mean and maxima concentrations, which is consistent with the notion that concentrations are generally low in wet regions (Li et al.,, 2014). In contrast, we find that altitude is negatively connected with the mean but positively connected with the maxima.
This is also supported by the detailed sharing coefficients analysed below. We see from Figure 6 that the posterior distribution of the sharing coefficients of precipitation (see detailed definition of in Section 3.2) almost lies between 0 and 1, showing that the influences of precipitation are similar on extreme and moderate air pollution. The coefficient for altitude is negative, suggesting certain evidence that altitude can impact reversely in different scaled pollution.
Furthermore, the effect of temperature is not significant with respect to 95% credible interval for mean but becomes significant for maxima. This result implies that high temperatures weakly impact the general air quality, while playing an essential role in the dispersion of extremely poor pollution. Nevertheless, considering the possibility of unmeasured confounders potentially distorting the coefficients, the strength of the aforementioned inference might be compromised.
In terms of model performance evaluation, the joint model demonstrated promising results in the validation set. In particular, the Gumbel sub-model (max sub-model) exhibited improvements in the coverage probability () and correlation (), compared with the univariate Gumbel model (Model 1), as shown in Tables 4 and 8. The insights of the joint model performance are depicted in Figure 7, where both the performance of the Gumbel model (maxima model) and the Gaussian model (mean model) are satisfied. Because of this, despite the less parsimonious nature of the joint model, which may introduce more volatility in the prediction of the Gumbel sub-model, the overall satisfying evaluation results bolster the credibility of the joint model’s findings. With this confidence, we proceed to utilize the joint model for subsequent predictions using excursion functions.
| Covariate | Annual mean model () | Annual maxima model () | ||
|---|---|---|---|---|
| Mean | 95% CI | Mean | 95% CI | |
| Altitude | ||||
| Precipitation | ||||
| Covariate | Annual mean model () | Annual maxima model () | ||
| Mean | 95% CI | Mean | 95% CI | |
| Intercept | ||||
| Longitude | ||||
| Latitude | ||||
| Temperature | ||||
| Vapour Pressure | ||||
| Population Density | ||||
| Sub-model | Coverage Probability | Correlation | RMSE |
|---|---|---|---|
| Gaussian Model (Mean) | 78.82% | 84.01% | 0.19 |
| Gumbel Model (Maxima) | 88.63% | 46.71% | 0.37 |





4.4 Annual maxima prediction and excursion functions
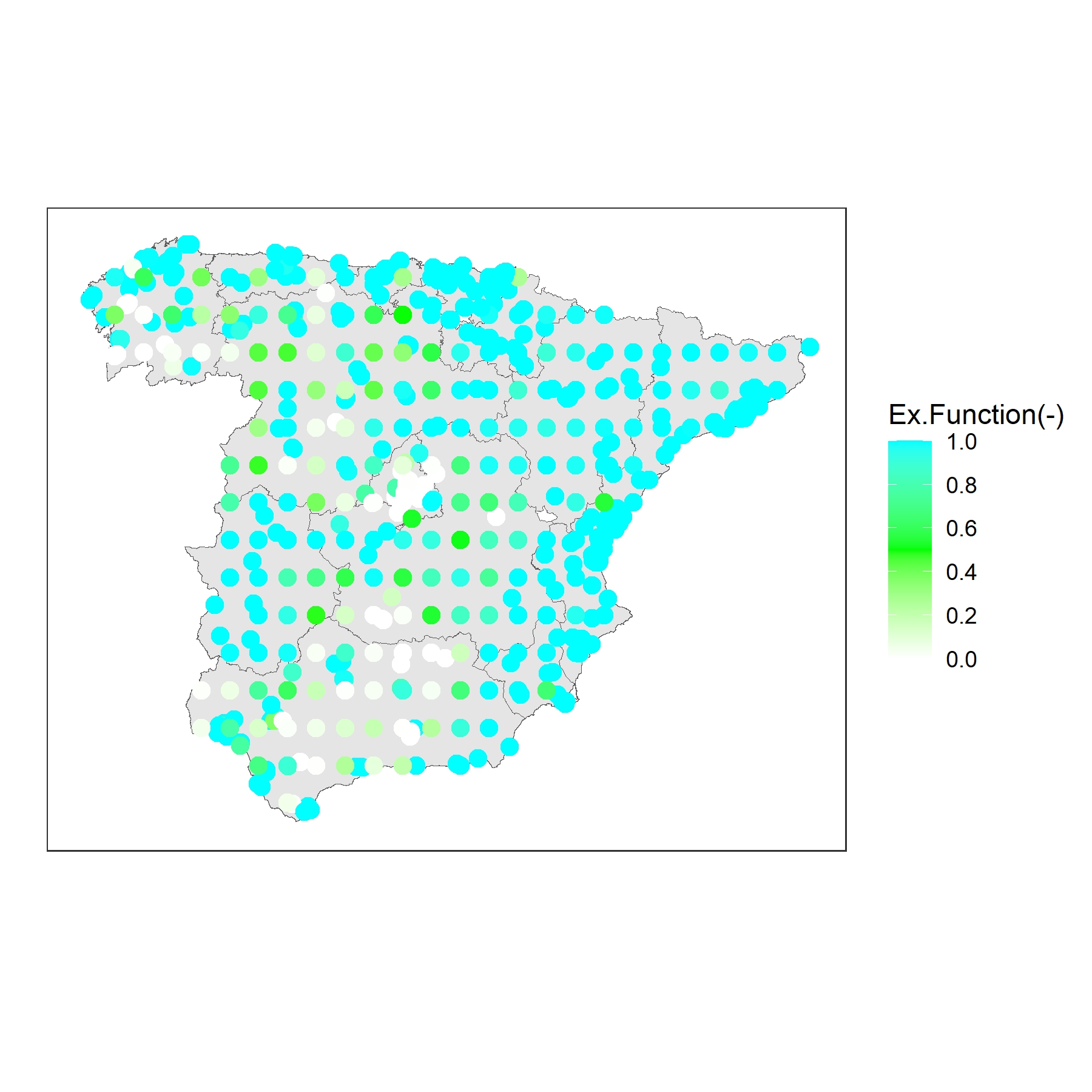
Hot-spot region identifications and predictive concentration level plots are important tools in air pollution studies, because they intuitively imply the air quality in specific regions and are easily interpreted to environmental agencies and the general public. Bolin and Lindgren, (2015) proposed the positive () and negative excursion sets () that determine the largest set that simultaneously exceeds or below the risk level () with a small error probability (), employing a parametric family and sequential importance sampling method for estimating joint probabilities. To visualize the excursion sets simultaneously, we apply the positive and negative excursion functions, and . To explain, the term denotes the ”smallest” required that the location () can be included into the positive excursion set at the first time, while the higher reported by positive excursion function generally indicates higher probabilities for the location () to exceed the risk threshold simultaneously.
In our case, to discover the areas that are most likely and most unlikely to suffer from severe pollution simultaneously, we utilize predicted concentration levels from the max sub-model of the joint model to generate both positive and negative excursion functions with the thresholds 50 (poor) and 100 (very poor) at 548 locations distributed throughout the mainland of Spain, including a set of 0.5° 0.5° (50km 50km) grids (206 locations) and locations of all stations (342 monitors).
In the case of exceeding 50 (Figure 8), the probability for simultaneously exceeding is high in the northwest, middle, and south, meaning that poor pollution probably hazard these locations during the year. In contrast, the negative excursion function with threshold 50 indicates that the regions in the north and east enjoy good or moderate air quality throughout the whole year. In the case of 100 (Figure 9), the probabilities for very poor pollution occurrence are low (in white) in most regions, but still likely to appear in certain areas in the community of Madrid, meanwhile, most areas in the north, northeast and east are expected to be below this threshold.



5 Discussions and Conclusions
In this paper, we discovered the spatio-temporal patterns of concentrations levels in mainland Spain under the framework of INLA-EVT methodology. The high-quality data-set of annual maxima and annual mean of daily PM10 concentration levels was jointly studied successfully, due to the following three reasons. Firstly, Spain is a mountainous country with a large central plateau, and this complicated orography is usually associated with a variety of climatic conditions. Secondly, the air pollution monitors distributed throughout mainland Spain provide high-quality time series data, which supports both local and national level accurate prediction and credible inference. Finally, Spain generally enjoys good air quality (low annual mean), but extreme air pollution does appear on certain days during the year (high annual maxima). This circumstance allows us to investigate the potential difference in the generation and spread of the moderate and extreme cases.
We establish a series of Bayesian spatio-temporal models on extreme concentrations in Spain, with specifically meteorological predictors, human effects, and spatio-temporal random effects following SPDE and AR(1) dynamic to account for the dependence not explained by covariates. We also provide evidence of similar and reverse connections between influential predictors and different scaled concentrations by the Bayesian joint model with sharing effects, as well as generate the annual maxima excursion functions maps specified at the grid level to highlight the regional risk ranking.
Although most statistical studies focus on moderate cases with long-term exposure, in the epidemiological field, short-term exposure to severe particulate matter is considered as an essential public health issue with major acute cardiovascular problems and health economic consequences. For example, Brook et al., (2016) emphasized that people living in highly polluted regions probably increase heart failure hospitalisations and cardiovascular mortality several folds. Shah et al., (2013) also pointed out that even modest improvements in air quality are projected to have major population health benefits and substantial health-care cost savings, preventing thousands of heart failure hospitalisations and saving millions of US dollars a year.
Combined with these health and economic hazards, the main findings in this paper are expected to provide in-depth knowledge of extreme air pollution spreading, promote awareness of extreme value studies, and provide suggestions to the national governments regarding the legislation of extremely poor air quality regulation and human health protection. In particular, the joint model incorporating sharing effects emphasizes the potential reverse or similar impacts of altitude and precipitation on both moderate and extreme cases of pollution. Moreover, the excursion functions maps indicate that the central region in Spain is more likely to experience severe pollution, which can be applied in research of long-term effects and health outcomes in epidemiological studies, such as acute cardiovascular events (Mustafić et al.,, 2012; Shah et al.,, 2013) and various types of strokes (Yu et al.,, 2014).
In conclusion, our study provides valuable insights into the generation and spreading of extreme PM10 pollution through innovative methods incorporating sharing effects in the joint model. This approach holds promise for future environmental and epidemiological studies in exploring various air pollutants and their relationship with meteorological variables and anthropogenic factors.
References
- Agarwal and Kaddoura, (2019) Agarwal, A. and Kaddoura, I. (2019). On-road air pollution exposure to cyclists in an agent-based simulation framework. Periodica Polytechnica Transportation Engineering, 48(2):117–125.
- Amin et al., (2015) Amin, N. A. M., Adam, M. B., and Aris, A. Z. (2015). Bayesian extreme for modeling high concentration in Johor. Procedia Environmental Sciences, 30:309–314.
- Basnayake et al., (2019) Basnayake, K., Mazaud, D., Bemelmans, A., Rouach, N., Korkotian, E., and Holcman, D. (2019). Fast calcium transients in dendritic spines driven by extreme statistics. PLOS Biology, 17:e2006202.
- Beirlant et al., (2005) Beirlant, J., Goegebeur, Y., Teugels, J., and Segers, J. (2005). Statistics of Extremes: Theory and Applications. Wiley.
- Beloconi et al., (2018) Beloconi, A., Chrysoulakis, N., Lyapustin, A. I., Utzinger, J., and Vounatsou, P. (2018). Bayesian geostatistical modelling of and surface level concentrations in Europe using high-resolution satellite-derived products. Environment International, 121:57–70.
- Blangiardo et al., (2013) Blangiardo, M., Cameletti, M., Baio, G., and Rue, H. (2013). Spatial and spatio-temporal models with R-INLA. Spatial and Spatio-temporal Epidemiology, 7:39–55.
- Bolin and Lindgren, (2015) Bolin, D. and Lindgren, F. (2015). Excursion and contour uncertainty regions for latent Gaussian models. Journal of the Royal Statistical Society Series B (Statistical Methodology), 77:85–106.
- Borck and Schrauth, (2021) Borck, R. and Schrauth, P. (2021). Population density and urban air quality. Regional Science and Urban Economics, 86:103596.
- Brook et al., (2016) Brook, R., Sun, Z., Brook, J., Zhao, X., Ruan, Y., Yan, J., Mukherjee, B., Rao, X., Duan, F., Sun, L., Liang, R., Lian, H., Zhang, S., Fang, Q., Gu, D., Sun, Q., Fan, Z., and Rajagopalan, S. (2016). Extreme air pollution conditions adversely affect blood pressure and insulin resistance: The air pollution and cardiometabolic disease study. Hypertension, 67(1):77—85.
- Cameletti et al., (2011) Cameletti, M., Ignaccolo, R., and Bande, S. (2011). Comparing spatio-temporal models for particulate matter in piemonte. Environmetrics, 22(8):985–996.
- Cameletti et al., (2013) Cameletti, M., Lindgren, F., Simpson, D., and Rue, H. (2013). Spatio-temporal modeling of particulate matter concentration through the SPDE approach. AStA Advances in statistical analysis: A journal of the German Statistical Society, 97(2):109–131.
- Castro-Camilo et al., (2021) Castro-Camilo, D., Huser, R., and Rue, H. (2021). Practical strategies for generalized extreme value-based regression models for extremes. Environmetrics, 33(6):e2742.
- Cheng et al., (2014) Cheng, L., AghaKouchak, A., Gilleland, E., and Katz, R. (2014). Non-stationary extreme value analysis in a changing climate. Climatic Change, 127.
- Chu et al., (2015) Chu, H., Huang, B., and Lin, C. (2015). Modeling the spatio-temporal heterogeneity in the - relationship. Atmospheric Environment, 102:176–182.
- Cohen et al., (2017) Cohen, A. J., Brauer, M., Burnett, R., Anderson, H. R., Frostad, J., Estep, K., Balakrishnan, K., Brunekreef, B., Dandona, L., Dandona, R., Feigin, V., Freedman, G., Hubbell, B., Jobling, A., Kan, H., Knibbs, L., Liu, Y., Martin, R., Morawska, L., Pope, C. A., Shin, H., Straif, K., Shaddick, G., Thomas, M., van Dingenen, R., van Donkelaar, A., Vos, T., Murray, C. J. L., and Forouzanfar, M. H. (2017). Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the global burden of diseases study 2015. The Lancet, 389(10082):1907–1918.
- Coles, (2001) Coles, S. (2001). An Introduction to Statistical Modeling of Extreme Values, volume 97. Springer.
- Daellenbach et al., (2020) Daellenbach, K., Uzu, G., Jiang, J., Cassagnes, L.-E., Leni, Z., Vlachou, A., Stefenelli, G., Canonaco, F., Weber, S., Segers, A., Kuenen, J., Schaap, M., Favez, O., Albinet, A., Aksoyoglu, S., Dommen, J., Baltensperger, U., Geiser, M., Haddad, I., and Prevot, A. (2020). Sources of particulate-matter air pollution and its oxidative potential in Europe. Nature, 587:414–419.
- Davison and Smith, (1990) Davison, A. C. and Smith, R. L. (1990). Models for exceedances over high thresholds. Journal of the Royal Statistical Society Series B-Methodological, 52:393–425.
- Deng and Zhang, (2018) Deng, L. and Zhang, Z. (2018). Assessing the features of extreme smog in China and the differentiated treatment strategy. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 474:20170511.
- Dias and Tchepel, (2018) Dias, D. and Tchepel, O. (2018). Spatial and temporal dynamics in air pollution exposure assessment. International Journal of Environmental Research and Public Health, 15(3):558.
- Fioravanti et al., (2021) Fioravanti, G., Martino, S., Cameletti, M., and Cattani, G. (2021). Spatio-temporal modelling of daily concentrations in Italy using the SPDE approach. Atmospheric Environment, 248:118192.
- Fisher and Tippett, (1928) Fisher, R. and Tippett, L. (1928). Limiting forms of the frequency distribution of the largest or smallest member of a sample. Mathematical Proceedings of the Cambridge Philosophical Society, 24:180–190.
- Forlani et al., (2020) Forlani, C., Bhatt, S., Cameletti, M., Krainski, E., and Blangiardo, M. (2020). A joint Bayesian space-time model to integrate spatially misaligned air pollution data in R-INLA. Environmetrics, 31(8):e2644.
- Fuglstad et al., (2019) Fuglstad, G.-A., Simpson, D., Lindgren, F., and Rue, H. (2019). Constructing priors that penalize the complexity of Gaussian random fields. Journal of the American Statistical Association, 114(525):445–452.
- Gandhi, (2015) Gandhi, V. (2015). Brain-Computer Interfacing for Assistive Robotics, pages 7–63. Academic Press, San Diego.
- Gelman et al., (1996) Gelman, A., Meng, X.-L., and Stern, H. (1996). Posterior predictive assessment of model fitness via realized discrepancies. Statistica Sinica, 6(4):733–760.
- Genton, (2002) Genton, M. G. (2002). Classes of kernels for machine learning: A statistics perspective. Journal of Machine Learning Research, 2:299–312.
- Gneiting and Raftery, (2007) Gneiting, T. and Raftery, A. E. (2007). Strictly proper scoring rules, prediction, and estimation. Journal of the American Statistical Association, 102(477):359–378.
- Guttorp and Gneiting, (2006) Guttorp, P. and Gneiting, T. (2006). Studies in the history of probability and statistics XLIX On the Matérn correlation family. Biometrika, 93(4):989–995.
- Gómez Rubio, (2020) Gómez Rubio, V. (2020). Bayesian Inference with INLA. Chapman & HallCRC.
- Harris et al., (2020) Harris, I., Osborn, T. J., Jones, P., and Lister, D. (2020). Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Scientific data, 7(1):109.
- Held et al., (2010) Held, L., Schrödle, B., and Rue, H. (2010). Posterior and Cross-validatory Predictive Checks: A Comparison of MCMC and INLA, pages 91–110. Physica-Verlag HD, Heidelberg.
- Joseph et al., (2003) Joseph, A., Sawant, A., and Srivastava, A. (2003). and its impacts on health - a case study in Mumbai. International Journal of Environmental Health Research, 13(2):207–214.
- Joseph et al., (2019) Joseph, M. B., Rossi, M. W., Mietkiewicz, N. P., Mahood, A. L., Cattau, M. E., St. Denis, L. A., Nagy, R. C., Iglesias, V., Abatzoglou, J. T., and Balch, J. K. (2019). Spatiotemporal prediction of wildfire size extremes with Bayesian finite sample maxima. Ecological Applications, 29(6):e01898.
- Kalisa et al., (2018) Kalisa, E., Fadlallah, S., Amani, M., Nahayo, L., and Habiyaremye, G. (2018). Temperature and air pollution relationship during heatwaves in Birmingham, UK. Sustainable Cities and Society, 43:111–120.
- Kjeldsen et al., (2018) Kjeldsen, T. R., Ahn, H., Prosdocimi, I., and Heo, J.-H. (2018). Mixture Gumbel models for extreme series including infrequent phenomena. Hydrological Sciences Journal, 63(13-14):1927–1940.
- Koh et al., (2021) Koh, J., Pimont, F., Dupuy, J., and Opitz, T. (2021). Spatiotemporal wildfire modeling through point processes with moderate and extreme marks. The Annals of Applied Statistics, in press, https://doi.org/10.48550/arXiv.2105.08004.
- Lei et al., (2019) Lei, R., Zhu, F., Cheng, H., Liu, J., Shen, C., Zhang, C., Xu, Y., Xiao, C., Li, X., Zhang, J., Ding, R., and Cao, J. (2019). Short-term effect of / on non-accidental and respiratory deaths in highly polluted area of china. Atmospheric Pollution Research, 10(5):1412–1419.
- Lenschow et al., (2001) Lenschow, P., Abraham, H.-J., Kutzner, K., Lutz, M., Preuß, J.-D., and Reichenbächer, W. (2001). Some ideas about the sources of . Atmospheric Environment, 35:S23–S33.
- Li et al., (2014) Li, L., Qian, J., Ou, C.-Q., Zhou, Y.-X., Guo, C., and Guo, Y. (2014). Spatial and temporal analysis of air pollution index and its timescale-dependent relationship with meteorological factors in Guangzhou, China, 2001–2011. Environmental Pollution, 190:75–81.
- Lindgren and Rue, (2015) Lindgren, F. and Rue, H. (2015). Bayesian spatial modelling with R-INLA. Journal of Statistical Software, 63:1–25.
- Lindgren et al., (2011) Lindgren, F., Rue, H., and Lindström, J. (2011). An explicit link between Gaussian fields and Gaussian Markov random fields: The Stochastic Partial Differential Equation approach. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73(4):423–498.
- Lobeto et al., (2018) Lobeto, H., Menendez, M., and Losada, I. J. (2018). Toward a methodology for estimating coastal extreme sea levels from satellite altimetry. Journal of Geophysical Research: Oceans, 123(11):8284–8298.
- Marshall and Spiegelhalter, (2003) Marshall, E. C. and Spiegelhalter, D. J. (2003). Approximate cross-validatory predictive checks in disease mapping models. Statistics in Medicine, 22(10):1649–1660.
- Martins et al., (2017) Martins, L., Wikuats, C., Capucim, M., de Almeida, D., da Costa, S., Albuquerque, T., Barreto Carvalho, V., de Freitas, E., de Fátima Andrade, M., and Martins, J. (2017). Extreme value analysis of air pollution data and their comparison between two large urban regions of South America. Weather and Climate Extremes, 18:44–54.
- Martuzzi et al., (2006) Martuzzi, M., Mitis, F., Iavarone, I., and Serinelli, M. (2006). Health impact of and ozone in 13 Italian cities. World Health Organization. Regional Office for Europe.
- Matérn, (1986) Matérn, B. (1986). Spatial variation, volume 36. Springer New York.
- Moraga, (2019) Moraga, P. (2019). Geospatial Health Data: Modeling and Visualization with R-INLA and Shiny. Chapman & HallCRC Biostatistics Series.
- Moraga et al., (2021) Moraga, P., Dean, C., Inoue, J., Morawiecki, P., Noureen, S., and Wang, F. (2021). Bayesian spatial modelling of geostatistical data using inla and spde methods: A case study predicting malaria risk in mozambique. Spatial and Spatio-temporal Epidemiology, 39:100440.
- Morawska et al., (2021) Morawska, L., Zhu, T., Liu, N., Amouei Torkmahalleh, M., de Fatima Andrade, M., Barratt, B., Broomandi, P., Buonanno, G., Carlos Belalcazar Ceron, L., Chen, J., Cheng, Y., Evans, G., Gavidia, M., Guo, H., Hanigan, I., Hu, M., Jeong, C. H., Kelly, F., Gallardo, L., Kumar, P., Lyu, X., Mullins, B. J., Nordstrøm, C., Pereira, G., Querol, X., Yezid Rojas Roa, N., Russell, A., Thompson, H., Wang, H., Wang, L., Wang, T., Wierzbicka, A., Xue, T., and Ye, C. (2021). The state of science on severe air pollution episodes: Quantitative and qualitative analysis. Environment International, 156:106732.
- Mustafić et al., (2012) Mustafić, H., Jabre, P., Caussin, C., Murad, M. H., Escolano, S., Tafflet, M., Périer, M.-C., Marijon, E., Vernerey, D., Empana, J.-P., and Jouven, X. (2012). Main air pollutants and myocardial infarction: A systematic review and meta-analysis. Journal of the American Medical Association, 307(7):713–721.
- Omidvarborna et al., (2015) Omidvarborna, H., Kumar, A., and Kim, D.-S. (2015). Recent studies on soot modeling for diesel combustion. Renewable and Sustainable Energy Reviews, 48:635–647.
- Opitz et al., (2018) Opitz, T., Huser, R., Bakka, H., and Rue, H. (2018). INLA goes extreme: Bayesian tail regression for the estimation of high spatio-temporal quantiles. Extremes, 21(3):441–462.
- Orellano et al., (2020) Orellano, P., Reynoso, J., Quaranta, N., Bardach, A., and Ciapponi, A. (2020). Short-term exposure to particulate matter ( and ), nitrogen dioxide (), and ozone () and all-cause and cause-specific mortality: Systematic review and meta-analysis. Environment International, 142:105876.
- Panagoulia et al., (2014) Panagoulia, D., Economou, P., and Caroni, C. (2014). Stationary and nonstationary generalized extreme value modelling of extreme precipitation over a mountainous area under climate change. Environmetrics, 25(1):29–43.
- Pettit, (1990) Pettit, L. (1990). The conditional predictive ordinate for the Normal distribution. Journal of the Royal Statistical Society: Series B (Methodological), 52(1):175–184.
- Porcu et al., (2012) Porcu, E., Montero, J., and Schlather, M. (2012). Advances and Challenges in Space-time Modelling of Natural Events. Springer.
- Reiss and Thomas, (2007) Reiss, R.-D. and Thomas, M. (2007). Statistical Analysis of Extreme Values: with Applications to Insurance, Finance, Hydrology and Other Fields. Birkhäuser Basel.
- Rodríguez et al., (2016) Rodríguez, S., Huerta, G., and Reyes, H. (2016). A study of trends for Mexico city ozone extremes: 2001-2014. Atmósfera, 29(2):107–120.
- Rue et al., (2009) Rue, H., Martino, S., and Chopin, N. (2009). Approximate Bayesian inference for latent Gaussian models by using Integrated Nested Laplace Approximations. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 71(2):319–392.
- Rue et al., (2016) Rue, H., Riebler, A., Sørbye, S., Illian, J., Simpson, D., and Lindgren, F. (2016). Bayesian computing with INLA: A review. Annual Review of Statistics and Its Application, 4.
- Saez and Barceló, (2022) Saez, M. and Barceló, M. A. (2022). Spatial prediction of air pollution levels using a hierarchical bayesian spatiotemporal model in Catalonia, Spain. Environmental Modelling & Software, 151:105369.
- Sahu, (2012) Sahu, S. K. (2012). Hierarchical Bayesian models for space-time air pollution data. Handbook of Statistics, 30:477–495.
- Samoli et al., (2013) Samoli, E., Stafoggia, M., Rodopoulou, S., Ostro, B., Declercq, C., Alessandrini, E., Díaz, J., Karanasiou, A., Kelessis, A. G., Tertre, A. L., Pandolfi, P., Randi, G., Scarinzi, C., Zauli-Sajani, S., Katsouyanni, K., and Forastiere, F. (2013). Associations between fine and coarse particles and mortality in Mediterranean cities: Results from the MED-PARTICLES Project. Environmental Health Perspectives, 121(8):932–938.
- Sario et al., (2013) Sario, M. D., Katsouyanni, K., and Michelozzi, P. (2013). Climate change, extreme weather events, air pollution and respiratory health in Europe. The European respiratory journal, 42(3):826—843.
- Sevinc et al., (2020) Sevinc, V., Kucuk, O., and Goltas, M. (2020). A Bayesian network model for prediction and analysis of possible forest fire causes. Forest Ecology and Management, 457:117723.
- Shah et al., (2013) Shah, A. S., Langrish, J. P., Nair, H., McAllister, D. A., Hunter, A. L., Donaldson, K., Newby, D. E., and Mills, N. L. (2013). Global association of air pollution and heart failure: A systematic review and meta-analysis. The Lancet, 382(9897):1039–1048.
- Sharma et al., (2012) Sharma, P., Chandra, A., Kaushik, S., Sharma, P., and Jain, S. (2012). Predicting violations of national ambient air quality standards using extreme value theory for Delhi city. Atmospheric Pollution Research, 3(2):170–179.
- Shumway and Stoffer, (2011) Shumway, R. H. and Stoffer, D. S. (2011). Time Series Analysis and Its Applications: With R Examples, volume 9. Springer Cham.
- Simpson et al., (2017) Simpson, D., Rue, H., Riebler, A., Martins, T. G., and Sørbye, S. H. (2017). Penalising model component complexity: A principled, practical approach to constructing priors. Statistical Science, 32(1):1–28.
- Singh et al., (2021) Singh, V., Meena, K. K., and Agarwal, A. (2021). Travellers’ exposure to air pollution: A systematic review and future directions. Urban Climate, 38:100901.
- Spiegelhalter et al., (2002) Spiegelhalter, D. J., Best, N. G., Carlin, B. P., and van der Linde, A. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64(4):583–639.
- Steinle et al., (2013) Steinle, S., Reis, S., and Sabel, C. E. (2013). Quantifying human exposure to air pollution—Moving from static monitoring to spatio-temporally resolved personal exposure assessment. Science of The Total Environment, 443:184–193.
- Steinle et al., (2015) Steinle, S., Reis, S., Sabel, C. E., Semple, S., Twigg, M. M., Braban, C. F., Leeson, S. R., Heal, M. R., Harrison, D., Lin, C., and Wu, H. (2015). Personal exposure monitoring of in indoor and outdoor microenvironments. Science of The Total Environment, 508:383–394.
- Taheri Shahraiyni and Sodoudi, (2016) Taheri Shahraiyni, H. and Sodoudi, S. (2016). Statistical modeling approaches for prediction in urban areas; a review of 21st-Century studies. Atmosphere, 7:15.
- Wang et al., (2020) Wang, P., Chen, K., Zhu, S., Wang, P., and Zhang, H. (2020). Severe air pollution events not avoided by reduced anthropogenic activities during COVID-19 outbreak. Resources, Conservation and Recycling, 158:104814.
- Watanabe, (2013) Watanabe, S. (2013). A widely applicable Bayesian information criterion. Journal of Machine Learning Research, 14(1):867–897.
- Xie et al., (2021) Xie, Y., Li, Z., Zhong, H., Feng, X. L., Lu, P., Xu, Z., Guo, T., Si, Y., Wang, J., Chen, L., Wei, C., Deng, F., Baccarelli, A. A., Zheng, Z., Guo, X., and Wu, S. (2021). Short-term ambient particulate air pollution and hospitalization expenditures of cause-specific cardiorespiratory diseases in China: A multicity analysis. The Lancet Regional Health - Western Pacific, 15:100232.
- Yu et al., (2014) Yu, X., Su, J., Li, X., and Chen, G. (2014). Short-term effects of particulate matter on stroke attack: Meta-regression and meta-analyses. The Public Library of Science, 9:e95682.
- Zhang et al., (2017) Zhang, H., Wang, Y., Park, T.-W., and Deng, Y. (2017). Quantifying the relationship between extreme air pollution events and extreme weather events. Atmospheric Research, 188:64–79.
- Zhang et al., (2019) Zhang, J., Chen, Q., Wang, Q., Ding, Z., Sun, H., and Xu, Y. (2019). The acute health effects of ozone and on daily cardiovascular disease mortality: A multi-center time series study in China. Ecotoxicology and Environmental Safety, 174:218–223.