Space charge fields in azimuthally symmetric beams: integrated Green’s function approach

The space charge effect is a basic collective phenomenon in Accelerator Physics that plays an important role both in electron and proton machines. In high current regimes, self-generated electromagnetic fields become so strong that they lead to significant emittance growth a:Chasman:1969 ; a:Lapostolle:1971 ; a:Hofmann:1981 ; a:Kim:1989 , slice energy change, and the microbunching instability a:Huang:2004 , which is especially detrimental in the context of free electron laser linacs a:Borland:2002 ; a:Huang:2004 . In the case of x-ray free electron lasers with periodic enhancement of electron peak current a:Zholents:2005 ; a:Kur:2011 ; a:Tanaka:2013 , strong longitudinal current modulation may result in large space charge forces which, in turn, may limit the performance of these schemes.

Compact analytical expressions for the space charge induced fields are currently available in the limits of either large- or small-scale current variations. The first limit provides a local description b:Chao:1993 while the second limit requires an impedance based description tr:Rosenzweig:1996 that is non-local as it depends on the Fourier spectrum of the current. This latter approach allows for semi-analytical treatment and is implemented in the Elegant numerical code tr:Borland:2000 in order to include longitudinal space charge effects on a beam axis.

An alternative approach adopted in many numerical codes, such as OPAL tr:OPAL:2008 , Astra web:Floettmann:2011 , and Parmela tr:Billen:1996 . This approach uses a Poison solver in order to find the space charge induced fields. However it is very time consuming and a semi-analytic description for the space charge induced fields applicable in the full range of current variations is highly desired.

In this paper we provide a semi-analytical description of the space charge problem in the case of an axially symmetric beam in a round pipe. The derived expressions for components of the induced field are valid in the full range of current variations. They also can be efficiently evaluated by the method of Integrated Green’s functions (IGF).

We present our approach in Section II, where we find that the Green’s function for a charged disk in a round pipe fully determines the components of the induced fields. In Section III, we express the Green’s function in terms of an on-axis potential from a charged disk in a round pipe and find a compact analytical approximation for this potential. Section IV uses the compact analytical expression for the Green’s function in order to present the field components in a form suitable for the IGF approach. In Section V we suggest how to improve a semi-analytical description of the space charge fields in numerical codes such as Elegant by providing a step-by-step instructions of IGF approach with our Green’s function. We finally summarize our findings in the conclusion.

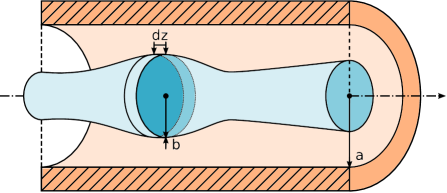
The most general approach considers an electron beam with charge density $\rho(\mathbf{r})$ that travels on axis of a perfectly conducting pipe of radius $a$ at a speed $v_{z}$ (see Fig. 1). It starts in the beam frame, $\mathbf{R}$, where the electrostatic potential induced by the space charge, $\varrho(\mathbf{R})$, is a solution of the Poisson equation:

where $\Gamma(\mathbf{R}|\mathbf{R^{\prime}})$ is the Green’s function for the Laplace’s equation inside a perfectly conducting pipe. The corresponding Green’s function is derived in Appendix as an expansion in terms of radial-azimuthal eignenfunctions that can be used in systems without translational symmetry.

In this paper, we will consider axially symmetric densities in the lab frame, $\mathbf{r}$, of the form $\rho(\mathbf{r})=\rho_{\perp}(r)\lambda(z)$ with normalization $\int\rho_{\perp}(r^{\prime})d^{2}\mathbf{r^{\prime}}=1$. In this case, the electrostatic potential in the beam frame is expressed as

where $\Lambda(Z^{\prime})=\gamma^{-1}\lambda(Z^{\prime}/\gamma)$ and

with $c_{n}=\int\rho_{\perp}(r^{\prime})J_{0}(\mu_{0,n}r^{\prime}/a)d^{2}\mathbf{r^{\prime}}$ that has to be individually calculated for different transverse density profiles. In the particular case of $c_{n}=1$, one recovers a result for an electrostatic potential of a point charge on the axis of a perfectly conducting pipe (see Eq. (27) in Ref. a:Bouwkamp:1947 ).

The electrostatic potential in the beam reference frame results in the electric field with longitudinal and transverse components that have the following expressions in the lab frame

in terms of transformed to the lab frame Green’s function, $g(r,z-z^{\prime})=G(r,\gamma z-\gamma z^{\prime})$. Additionally, in the lab frame, there is also an azimuthal magnetic field $B_{\phi}(r,z)=\frac{v_{z}}{c^{2}}E_{r}(r,z)$, which reduces the overall transverse space charge force acting on charged particles in the beam by $\gamma^{-2}$.

In the previous section, we have reduced the problem of space charge induced fields to the finding Green’s function, $G(R,Z-Z^{\prime})$, — the electrostatic potential from a charge distribution, $\varrho(\mathbf{R})=\rho_{\perp}(R)\delta(Z-Z^{\prime})$. Due to the axial symmetry of the charge distribution, one can use the Poisson representation a:Poisson:1823 in order to the potential outside the axis of symmetry once the potential on the axis has been found:

where

Sometimes, however, the integral cannot be taken analytically or potential has to be found near the axis. Therefore, we propose an alternative approach here based on the formal separation of variables:

where a function of a derivative is defined via its Taylor series expansion ¹¹1Consider the following on axis potential, $G(0,Z-Z^{\prime})=1/|Z-Z^{\prime}|$. Using the Poisson representation, one can show that $G(R,Z-Z^{\prime})=1/\sqrt{(Z-Z^{\prime})^{2}+R^{2}}$, which is a free space potential of a point charge in cylindrical coordinates. In order to apply our approach, one start with the Taylor series expansion, $J_{0}(x)=1-\frac{x^{2}}{4}+O(x^{4})$, and arrives to $G(R,Z-Z^{\prime})=1/|Z-Z^{\prime}|-\frac{R^{2}}{4}\frac{\partial^{2}}{\partial Z^{2}}1/|Z-Z^{\prime}|+O(R^{4})$. Carrying out the derivatives leads to $G(R,Z-Z^{\prime})=1/|Z-Z^{\prime}|\left(1-\frac{R^{2}}{2(Z-Z^{\prime})^{2}}+O(R^{4})\right)$, which is a series expansion of a free space potential of a point charge in cylindrical coordinates for small $R$. . As a consequence of our approach, one can confirm, based on a formal substitution $x\to R\frac{\partial}{\partial Z}$ into the Bessel differential equation, $\left(x^{2}\frac{d^{2}}{dx^{2}}+x\frac{d}{dx}+x^{2}\right)J_{0}\left(x\right)=0$, that the derived Green’s function is indeed a solution of the Laplace equation, $\left(\frac{\partial^{2}}{\partial R^{2}}+\frac{1}{R}\frac{\partial}{\partial R}+\frac{\partial^{2}}{\partial Z^{2}}\right)G(R,Z-Z^{\prime})=0$.

As the transformed Green’s function is $g(r,z-z^{\prime})=G(r,\gamma z-\gamma z^{\prime})$, we have just reduced the space charge problem to finding electrostatic potential on the pipe axis, $G(0,Z-Z^{\prime})$, which is shown in Fig. 2, in the case of a uniform transverse distribution, $\rho_{\perp}(r<b)=1/\pi b^{2}$, for different values of $b/a$. It shows that there are two distinct regions with different behaviors of the Green’s function. The first region corresponds to the far zone, $|Z-Z^{\prime}|\gg b$, where the Green’s function is just a potential of a point charge in a pipe. The second region corresponds to the vicinity of the source, $|Z-Z^{\prime}|\ll a$, in which case the free space approximation can be used. Both of these regions allow for accurate and compact analytical expressions for $G(0,Z-Z^{\prime})$. Furthermore, we can be combined these expressions together in a single analytical expression due to a broad overlap region, $b\ll|Z-Z^{\prime}|\ll a$, which corresponds to a point charge in a free space.

In the first region, $|Z-Z^{\prime}|\gg b$, the sum in Eq. (7) converges rapidly due to vanishing exponential factors $\exp(-\mu_{0,n}|Z-Z^{\prime}|/a)$. The actual number of terms contributing to the sum can be estimated as $\mu_{0,n}|Z-Z^{\prime}|/a\sim 1$. Under this condition, $c_{n}\simeq 1$, resulting in the expression for the on-axis potential from a point charge on the pipe axis a:Bouwkamp:1947 . A compact form representation for the on-axis Green’s function in the far zone is hence a sum of the geometric series:

where we have used that $\mu_{0,n}-\mu_{0,1}\approx\pi(n-1)$ and $\mu_{0,n}J_{1}(\mu_{0,n})^{2}\approx 2/\pi$.

The second region is in the vicinity of the source, $|Z-Z^{\prime}|\ll a$. Hence, one can ignore a boundary effect of the pipe surface but has to account for an actual transverse charge density, $\rho_{\perp}(r)$. In the absence of the boundary effect the convergence of the sum in Eq. (7) is defined by $c_{n}$ rather than by the exponent. Hence, one can replace summation with integration. We chose the integration variable to be $x=\mu_{0,n}$ with the Jacobian of this transformation $dn/dx\simeq 1/\pi$:

Carrying out one integration results in the following compact form representation of the on-axis Green’s function

which is indeed the on-axis potential from a charged disk in free space. The Table 1 provides examples of this potential for different transverse charge distributions.

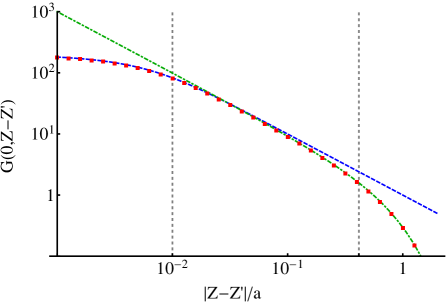
So far, we have found two analytical representations for the on-axis Green’s function that describe two physical limits. Figure 3 compares these approximate representations given by Eqs. (9) and (11) with values of the on-axis Green’s function given in Eq. (7). It shows that approximate expressions describe the on-axis Green’s function well within their applicability regions. We note that there is an overlap region where two physical limits have common domain of mutual applicability, $b\ll|Z-Z^{\prime}|\ll a$. This region is well defined when the beam size is sufficiently smaller than the pipe radius, $b<a$, and correspond to the case where the charge distribution can be already approximated by a point charge yet the presence of pipe walls can be still ignored. In this region, both expressions result in the same asymptotic form for the on-axis Green’s function and coincide with the expression for the point charge potential in free space:

This allows matching of the two analytical representations as their product divided by their mutual asymptotic expression. As a result, the on-axis Green’s function in a perfectly conducting pipe can be approximated with:

for $b<a$ and $|Z-Z^{\prime}|\in(0,\infty)$.

The main advantage of using the compact form expression is its simplicity. In contrast, evaluation of an exact Green’s function described with Eq. (7) requires summation of a large number of terms and takes a significant amount of time. Figure 4 shows the comparison between these two approaches for the uniform transverse charge distribution with $b/a=0.01$. The inset shows the relative error of using the approximate Green’s function instead of exact. The absolute error is the largest at $Z=Z^{\prime}$ but does not exceed $0.87069/a$ based on a simple method of summing Bessel series proposed by Greenwood in Ref. a:Greenwood:1968 .

In the previous section, we have provided a compact form for the Green’s function that describes an axially symmetric space charge problem. Using this result, the longitudinal space charge field takes on the following form for the translationally invariant transverse distributions

with $g_{z}(r,z-z^{\prime})=J_{0}\left(\frac{r}{\gamma}\frac{\partial}{\partial z}\right)g(0,z-z^{\prime})$. The operational form for the Green’s function suggested in Eq. 8 also allows for a similar representation for the transverse component of the space charge induced field

with $g_{r}(r,z-z^{\prime})=-J_{1}\left(\frac{r}{\gamma}\frac{\partial}{\partial z}\right)g(0,z-z^{\prime})$ ²²2Here we substituted $\frac{\partial}{\partial r}g(r,z-z^{\prime})=-\frac{\partial}{\gamma\partial z}J_{1}\left(\frac{r}{\gamma}\frac{\partial}{\partial z}\right)g(0,z-z^{\prime})$ based on the formal definition of the function that contains a derivative.. This solution for the space charge problem allows for efficient numerical evaluation based on the Integrated Green’s function approach ip:Ryne:2003 ; ip:Abell:2007 ; a:Qiang:2007 .

For the purposes of providing a recipe for numerical evaluation of the Eqs. 14 and 15, we will use the Integrated Green’s function approach in a constant function basis. This approach approximates the charge density as $\lambda(z^{\prime})=\left(\lambda_{j+1}+\lambda_{j}\right)/2$ within a cell of the computational domain, $z^{\prime}\in\left[z_{j},z_{j+1}\right]$ for $z_{j}=jh$, and arrives to the following discrete convolution

with normalization constants $A_{r}=1/4\pi\varepsilon_{0}$ and $A_{z}=A_{r}/\gamma$.

The Green’s functions derived in this paper behave differently near the source. Namely, the longitudinal Green’s function, $g_{z}(r,z-z^{\prime})$, is a continuous function of $z$, while the radial Green’s function, $g_{r}(r,z-z^{\prime})$, has a discontinuity at $z=z^{\prime}$. Taking this into account, leads to the following integrated Green’s function for the longitudinal component

with $\zeta=h(i-j)$; and for the radial component:

where $w_{r}(h)$ uses the Green’s function defined for $z\geq z^{\prime}$ in order to evaluate $g_{r}(r,0)$, while $w_{r}(-h)$ and $g_{r}(r,0^{-})$ use $z\leq z^{\prime}$ definition.

Equation 13 is the main result of the paper that has allowed us to express the space charge induced fields in terms of the Green’s functions that have simple analythical representation. Equations 14 and 15 with the corresponding Green’s function are the next important result of this paper. These expressions for the components of the field can be efficiently evaluated using the Integrated Green’s functions, Eqs. 17 and 18.

It is often a case that the transverse beam size is a smallest scale of the problem and that only the space charge induced fields within the beam are of interest. Thus, the particle accelerator codes, similar to Elegant, include only the effects of the space charge induced fields at $r=0$. X-ray free electron lasers often operate in a space charge dominated regime and a more diligent treatment of the space charge induced fields is in order. In what follows we will illustrate the steps required to obtain the off-axis behavior for the components of the space charge induces field.

The radial component of the space charge induced field, evaluated on $z_{i}=ih$ grid, is equal to $E_{r}(z_{i})=hA_{r}\sum_{j}\lambda_{j}w_{r}^{i-j}$, where $\lambda_{j}$ is a space charge distribution on the same grid and $A_{r}=1/4\pi\varepsilon_{0}$. Equation 18 defines the integrated Green’s function, $w_{r}(\zeta)$, in terms of

where we have kept the leading term in the Taylor series expansion of $J_{1}(x)$ for the purpose of illustration only. In order to evaluate the derivation of the on-axis Green’s function, we can apply the logic used in deriving the analythical representation of the on-axis Green’s function itself and arrive to the following expression:

Evaluation of the longitudinal component of the space charge induced field follows the same steps but uses $A_{z}=A_{r}/\gamma$ and $w_{z}(\zeta)$ as defined in Eq. 17 in terms of

where we have kept the first two leading terms in the Taylor series expansion of $J_{0}(x)$ for the purpose of illustration only. The second term requires the second derivative of the on-axis Green’s function that has the following form:

From the provided illustration, the solution of the space charge problem at $r=0$ requires a single evaluation of a discreet convolution. An additional convolution provides a linear contribution to the radial component of the space charge induced field. The third convolution can be also carried out in order to find a next order correction to the longitudinal component of the space charge induced field. One can apply the illustrated approach in order to find the next order corrections with computational effort that scales linearly with number of corrections.

We have studied the space charge problem for the beam with axially symmetric charge distribution in a smooth perfectly conducting pipe. We have develop a Green’s function-based description for the space charge induced fields that is valid in the full range of current variations and applicable to beams with varying beam radius. The Green’s function discussed in the paper corresponds to the electrostatic potential of a charged disk in a pipe and is completely defined by its behavior on the pipe axis due to axial symmetry.

We have found a compact analytical approximation for the on-axis Green’s function that allows for analytical calculation of the Green’s function off axis. Having a compact representation of the on-axis behavior of the response function can improve semi-analytical codes, such as Elegant, as it offers a significant advantage over numerical evaluation of the exact solution.

Finally, we have provided a detail prescription based on the Integrated Green’s function approach for efficient numerical evaluation of the fields in the case of translational symmetry. This approach describes transverse as well as longitudinal component of the space charge induced field and scales linearly with the number of radial corrections.

We gratefully acknowledge the support of the U.S. Department of Energy through the LANL/LDRD Program for this work.