Solutions of the Multivariate Inverse Frobenius–Perron Problem

A deterministic map $x_{n+1}=M(x_{n})$ defines a map on probability distributions over state, called the transfer operator KlusKoltaiSchutte2016 . Consider the case where the initial state $x_{0}\sim\rho_{0}(\cdot)$ ($x_{0}$ is distributed as $\rho_{0}$) for some distribution $\rho_{0}$ and let $\rho_{n}$ denote the $n$-step distribution, i.e., the distribution over $x_{n}=M^{n}(x_{0})$ at iteration $n$. The transfer operator that maps $\rho_{n}\mapsto\rho_{n+1}$ induced by $M$ is given by the Frobenius–Perron operator associated with $M:x\mapsto y$ dorfman1999introduction ; LasotaMackey ; Gaspard1998

$$\rho_{n+1}(y)=\sum_{x\in M^{-1}(y)}\frac{\rho_{n}\left(x\right)}{|J(x)|}$$

(2)

where $|J(x)|$ denotes the Jacobian determinant ²²2We have used the language of differential maps, as all the maps that we display in this paper are differentiable almost everywhere varberg1971change. More generally, $|J(x)|^{-1}$ denotes the density of $\rho_{n}M^{-1}$ with respect to $\rho_{n+1}$, see, e.g., (LasotaMackey, , Remark 3.2.4.). of $M$ at $x$, and the sum is over inverse images of $y$.

The equilibrium distribution $\rho$ of $M$ satisfies

$$\rho(y)=\sum_{x\in M^{-1}(y)}\frac{\rho(x)}{|J(x)|}$$

(3)

and we say that $\rho$ is invariant under $M$.

The inverse problem that we address is finding an iterative map $M$ that has a given distribution $\rho$ as its equilibrium distribution. We do this by performing the inverse Frobenius–Perron problem (IFPP) of finding $M$ that satisfies (3) to ensure that $\rho$ is an invariant distribution of $M$. Establishing chaotic hence ergodic behaviour is a separate calculation.

We will assume throughout that $\rho$ is absolutely continuous with respect to the underlying measure so that a probability density function $\rho(x)$ exists, and, furthermore, that $\rho(x)>0$, $\forall x\in X$.

The Lyapunov exponent $h$ of an iterative map gives the average exponential rate of divergence of trajectories. We define the (maximal) Lyapunov exponent $h$ as dorfman1999introduction ; LasotaMackey

$$h=\lim_{N\to\infty}\frac{1}{N}\log\left|\frac{\mathrm{d}x_{N}}{\mathrm{d}x_{0}}\right|=\lim_{N\to\infty}\frac{1}{N}\sum^{N-1}_{n=0}\log|J(x_{n})|$$

(4)

that features the starting value $x_{0}$. For ergodic maps the dependency on $x_{0}$ is lost as $N\to\infty$ and the Lyapunov exponent may be written

$$h=\int_{X}\log|J(x)|\rho(x)\,\mathrm{d}x$$

(5)

where $\rho(x)$ is the invariant density. A positive Lyapunov exponent $h$ indicates that the map is chaotic.

The theoretical value for the Lyapunov exponent may be obtained using (5), while (4) provides an empirical value obtained by iterating the map $M$. For example, the Lyapunov exponent of the logistic map evaluated by (5) is $h_{\text{log}}=\log 2\approx 0.693147$ while (4) evaluated over an orbit with $10000$ iterations gave $h_{\text{log}}\approx 0.693140$.

For chaotic maps, any uncertainty in initial value means that an orbit cannot be precisely predicted, since initial states with any separation become arbitrarily far apart, within $X$, as iterations increase. Hence it is useful to characterize the orbit statistically, in terms of the equilibrium distribution over states in the orbit.

It is interesting to note that theoretical chaotic and ergodic behaviour does not necessarily occur when iterations of a map are implemented on a finite-precision computer. For example, when the logistic map, above, on $[0,1]$ is iterated on a binary computer the multiplication by $4$ corresponds to a shift left by two bits and all subsequent operations maintain lowest order bits that are zero. Repeated iterations eventually produce the number zero, no matter the starting value. While it is simple to correct this non-ideal behaviour, as was done to give the numerical Lyapunov exponent, above, it is important to note that computer implementation can have very different dynamics to the mathematical model.

We first note, almost trivially, that the identity map $M=I$, where $I(x)=x$, has $\rho$ as an invariant distribution, so solves the IFPP for any $\rho$. Somewhat less trivial is to derive this simplest solution by assuming that $M$ is monotonic increasing and $M(0)=0$, so that there is just one inverse image in (6). Writing $|M^{\prime}(x)|=\mathrm{d}M/\mathrm{d}x$ gives the differential equation with separated variables

$$\rho(M)\mathrm{d}M=\rho(x)\mathrm{d}x$$

(7)

that has solution

$$F(M)=F(x)$$

where $F(x)=\int_{0}^{x}\rho(x^{\prime})\,\mathrm{d}x^{\prime}$ is the cumulative distribution function (CDF) for $\rho$. If $F$ is invertible denote the inverse by $F^{-1}$, called the the inverse distribution function (IDF), otherwise let $F^{-1}$ denote the generalized inverse distribution function, $\displaystyle F^{-1}(p)=\inf\{x\in X:F(x)\geq p\}$. Then, $M=F^{-1}(F(x))=x$, or $M(x)=x$, almost everywhere. Hence the identity map is the unique monotonic increasing map that has $\rho$ as its invariant distribution. Clearly, the identity map is not ergodic for $\rho$.

We may generalize this solution by setting $M(0)=k$, for some $k\in[0,1)$, and also only requiring $M$ to be piecewise continuous. Allowing one discontinuity in $M$ we write the integral of the separated differential equation (7) as

$$F(M)=F(x)+k\mod 1$$

giving the solution to the IFPP

$$M(x)=\left(F^{-1}\circ T^{c}\circ F\right)(x)$$

(8)

where $c=F^{-1}(k)$. Here $T^{c}$ denotes the operator that translates by $c$ with wrap-around on $[0,1)$ ³³3Hence $T^{c}$ is the translation operator on the unit circle $S^{1}$

$$T^{c}(y)=y+c-\lfloor y+c\rfloor,$$

(9)

where $\displaystyle\lfloor\,\ \rfloor$ denotes the floor function; see Figure 1 (left). The identity map is recovered when $k=c=0$.

It is easily seen that the Lyapunov exponent of the map in (8) is $h=0$, so the map is not chaotic. However, interestingly, this map can generate a sequence of states that produce a numerical integration rule with respect to $\rho$, since appropriate choices of $c$ and number of iterations $N$ can produce a rectangle rule quadrature or a quasi Monte Carlo lattice rule; see Sec. IV.3.

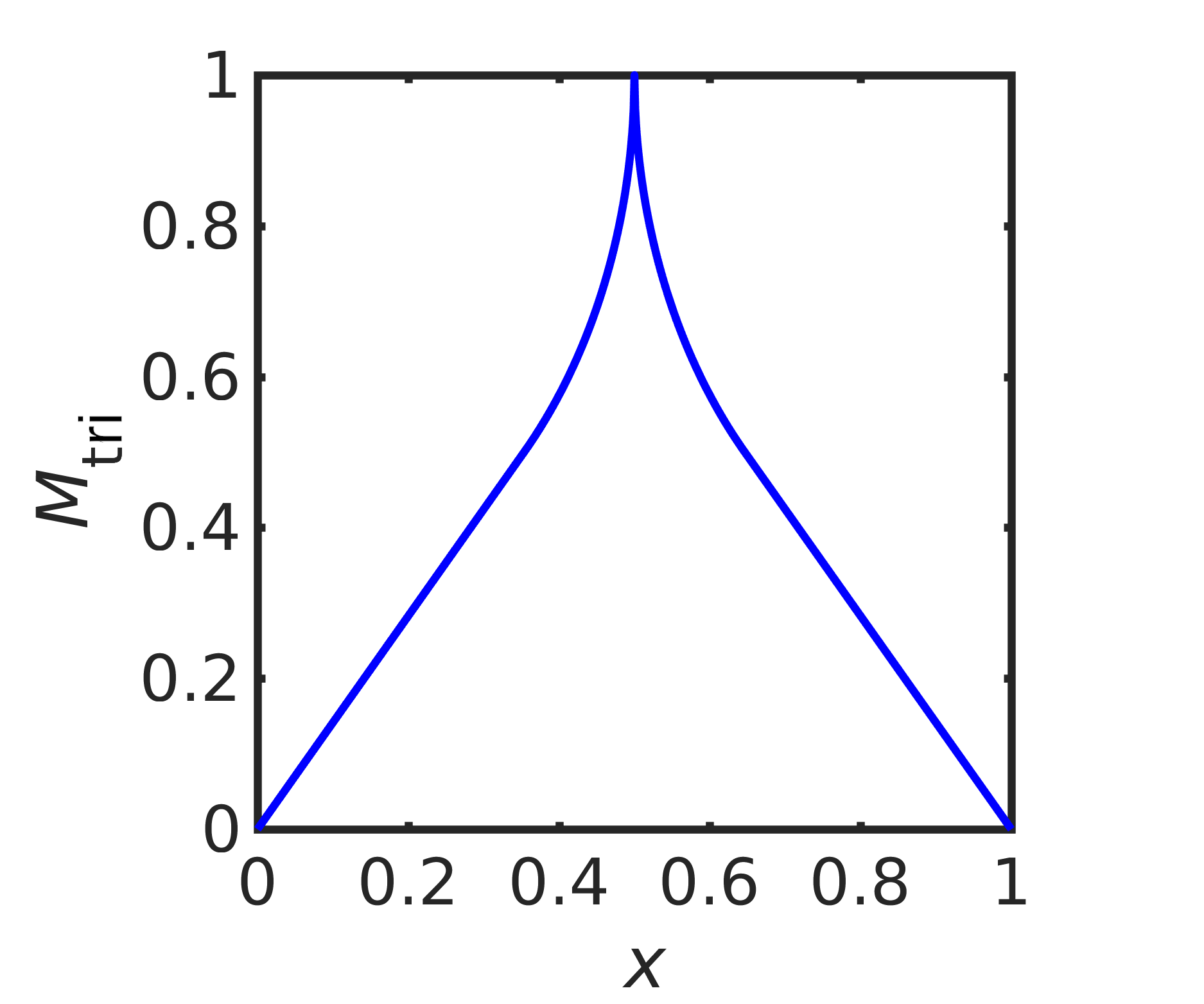
When the PDF $\rho$ has reflexive symmetry about $1/2$, i.e. $\rho(x)=\rho(1-x)$, we can simplify the FP equation (6) by assuming that the map $M$ has the same symmetry. Specifically, we write the triangle map (see Figure 1 (right))

$$t_{1}(x)=1-2\left|x-1/2\right|$$

(10)

that has reflexive symmetry about $1/2$, and write

$$M(x)=m(t_{1}(x))$$

(11)

where $m(x):[0,1]\to[0,1]$ is a monotonic increasing map with $m(0)=0$ (and, it will turn out, $m(1)=1$). Hence the FP equation simplifies to

$$\rho(y)=2\frac{\rho\left(x\right)}{|M^{\prime}(x)|},\quad x\in M^{-1}(y),$$

(12)

that we can write as the separated equations

	$\displaystyle\rho(M)\,\mathrm{d}M=2\rho(x)\mathrm{d}x,\quad$	$\displaystyle x<1/2,$
	$\displaystyle\rho(M)\,\mathrm{d}M=-2\rho(x)\mathrm{d}x,\quad$	$\displaystyle x>1/2,$

that has the continuous solution

$$F(M)=t_{1}(F(x))$$

giving the continuous solution to the IFPP

$$M(x)=\left(F^{-1}\circ t_{1}\circ F\right)(x).$$

(13)

One can solve for $m(x)=F^{-1}(2F(x/2))$, though we do not further consider the function $m$.

The approach we have used here simplifies the approach in diakonos1996construction , while ‘doubly symmetric’ maps of the form (11) were considered in gyorgyi1984fully , and again in pingel1999theory ; diakonos1999stochastic .

To give a concrete example of the solution in (13), we consider the symmetric triangular distribution on $[0,1]$ with PDF

$$\rho_{\text{tri}}(x)=2-4\left|x-\frac{1}{2}\right|$$

(14)

that has reflexive symmetry about $x=\frac{1}{2}$. The CDF is

$$F_{\text{tri}}(x)=\begin{cases}2x^{2}&0\leq x\leq\frac{1}{2}\\ \frac{1}{2}+4x-2x^{2}&\frac{1}{2}\leq x\leq 1\end{cases}$$

giving the unimodal map, after substituting into (13),

$$M_{\text{tri}}(x)=\left\{\begin{array}[]{rl}\sqrt{2}x&0\leq x\leq\frac{1}{\sqrt{8}}\\ 1-\sqrt{\frac{1}{2}-2x^{2}}&\frac{1}{\sqrt{8}}\leq x\leq\frac{1}{2}\\ 1-\sqrt{\frac{1}{2}-2(1-x)^{2}}&\frac{1}{2}\leq x\leq 1-\frac{1}{\sqrt{8}}\\ \sqrt{2}(1-x)&1-\frac{1}{\sqrt{8}}\leq x\leq 1\end{array}\right.$$

(15)

shown in Figure 2 (left). The same map was derived in grossmann1977invariant . Figure 2 (right) shows a normalized histogram of $10^{6}$ iterates of $M_{\text{tri}}$ starting at $x=0.3$, confirming that the orbit of $M_{\text{tri}}$ converges to the desired triangular distribution. The numerical implementation avoids finite-precision effects, as discussed later.

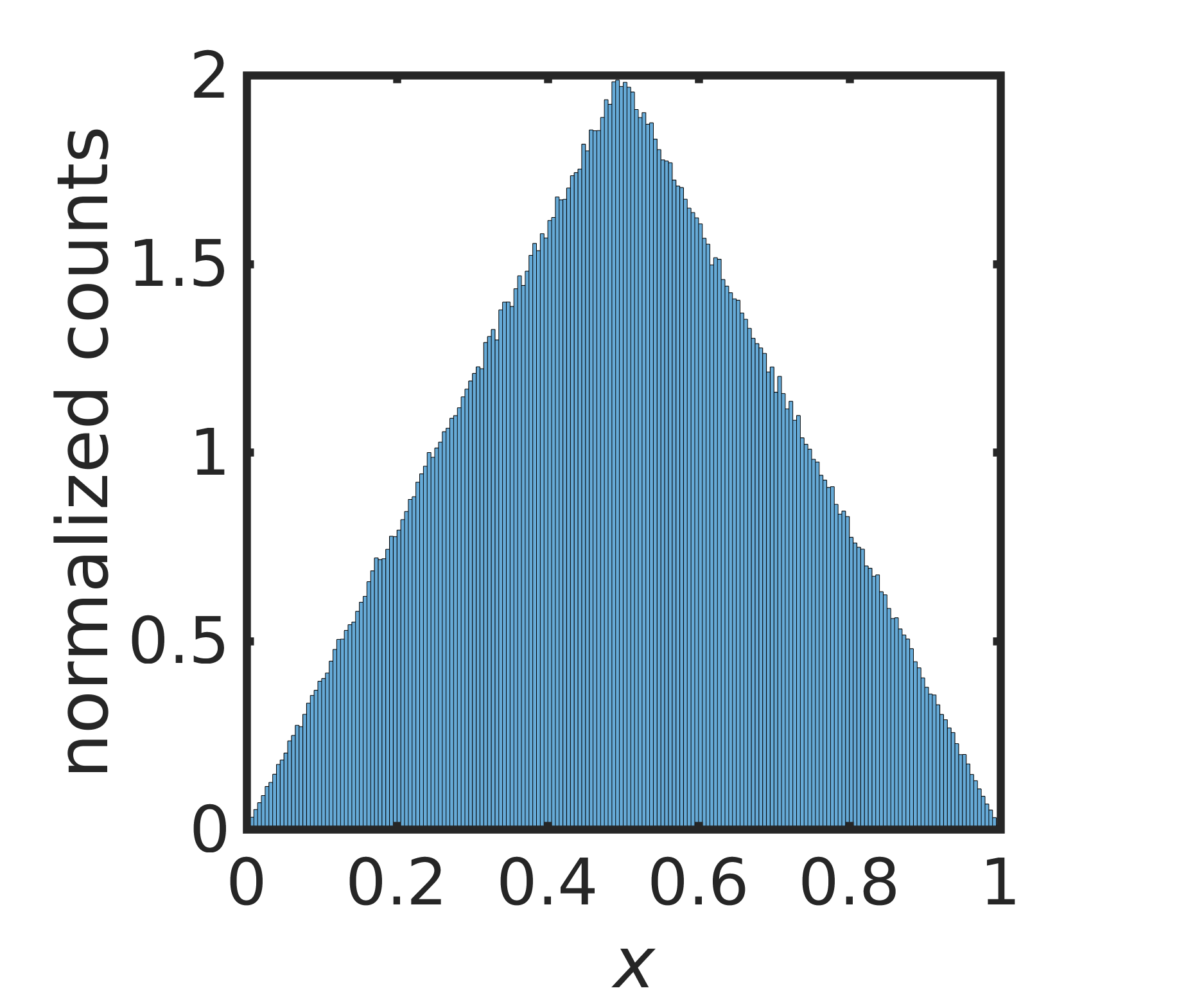
The theoretical Lyapunov exponent for $M_{\text{tri}}$ is $h_{\text{tri}}=\log 2\approx 0.693147$ while (4) evaluated over an orbit with $10^{6}$ iterations gave $h_{\text{tri}}\approx 0.693148$.

A simple transformation of an absolutely continuous $d$-variate distribution into the uniform distribution on the $d$-dimensional hypercube was introduced by Rosenblatt rosenblatt-1952 , as follows. The joint PDF can be written as a product of conditional densities,

$$\rho(x_{1},\ldots,x_{d})=\rho_{1}(x_{1})\rho_{2}(x_{2}|x_{1})\cdots\rho_{d}(x_{d}|x_{1}\ldots,x_{d-1}),$$

where $\rho_{k}(x_{k}|x_{1}\ldots,x_{k-1})$ is a conditional density given by

$$\rho_{k}(x_{k}|x_{1}\ldots,x_{k-1})=\frac{p_{k}(x_{1},\ldots,x_{k})}{p_{k-1}(x_{1}\ldots,x_{k-1})},$$

(16)

in terms of the marginal densities,

$$p_{k}=\int\rho(x_{1},\ldots,x_{d})\,\mathrm{d}x_{k+1}\cdots\mathrm{d}x_{d},$$

(17)

where $k=1,\ldots,d$.

Let $z=(z_{1},\ldots,z_{d})=R(x_{1},\ldots,x_{d})$ where $R$ is the Rosenblatt transformation rosenblatt-1952 from the state-space $X\subseteq\mathbb{R}^{d}$ of $\rho$ to the $d$-dimensional unit cube $[0,1]^{d}$, defined in terms of the (cumulative) distribution function $F$ by

	$\displaystyle z_{1}$	$\displaystyle=F_{1}(x_{1})=\int_{-\infty}^{x_{1}}\rho_{1}(x_{1}^{\prime})\,\mathrm{d}x_{1}^{\prime},$
	$\displaystyle z_{2}$	$\displaystyle=F_{2}(x_{2}|x_{1})=\int_{-\infty}^{x_{2}}\rho_{2}(x_{2}^{\prime}|x_{1})\,\mathrm{d}x_{2}^{\prime},$
		$\displaystyle\vdots$
	$\displaystyle z_{d}$	$\displaystyle=F_{d}(x_{2}|x_{1},\ldots,x_{d-1})=\int_{-\infty}^{x_{d}}\rho_{d}(x_{d}^{\prime}|x_{1},\ldots,x_{d-1})\,\mathrm{d}x_{d}^{\prime}.$

As noted in rosenblatt-1952 , there are $d!$ transformations of this type, corresponding to the $d!$ ways of ordering the coordinates. Further multiplicity is introduced by considering coordinate transformations, such as rotations.

Notice that in $1$-dimension, the Rosenblatt transformation $R(x)$ is simply the CDF $F(x)$.

It follows that if $x\sim\rho$ then $z=R(x)\sim\operatorname{Unif}([0,1]^{d})$, i.e., $z$ is uniformly distributed on the $d$-dimensional unit cube rosenblatt-1952 . When $\rho(x)>0$, $\forall x\in X$ the distribution functions are strictly monotonic increasing and the inverse of the Rosenblatt transformation $R^{-1}$ is well defined, otherwise let $R^{-1}$ denote the generalized inverse as in Sec. III.1. Then, if $z\sim\operatorname{Unif}([0,1]^{d})$ it follows that $x=R^{-1}(z)\sim\rho$, i.e., $x$ is distributed as the desired target distribution $\rho$ johnson1987multivariate ; this is the basis of the conditional distribution method for generating multi-variate random variables, that generalizes the inverse cumulative transformation method for univariate distributions devroye-rvgen-1986 ; johnson1987multivariate ; hormann-rvgen-2004 ; dolgov2020approximation . These results may also be established by substituting $R$ or $R^{-1}$ into the the FP equation (2), noting that there is a single inverse image and that the Jacobian determinant of $R$ equals the target PDF $\rho(x)$.

In the remainder of this paper, we refer to any map $R$ satisfying $x\sim\rho\Rightarrow R(x)\sim\operatorname{Unif}([0,1]^{d})$ as a Rosenblatt transformation, with (generalized) inverse as defined above.

The following theorem characterizes solutions to the IFPP.

The first part of the proof shows that any uniform map $U$ induces a solution to the IFPP, though the particular solution depends on the particular Rosenblatt transformation. The second part of the proof shows that different solutions to the IFPP effectively differ only by the choice of the uniform map $U$, once the Rosenblatt transformation is determined, that is, a coordinate system is chosen with an ordering of those coordinates.

Grossmann and Thomae grossmann1977invariant called dynamical systems $M$ and $U$ related by a formula of the form (18) as ‘related by conjugation’, or just ‘conjugate’, and the map $R^{-1}$ in (18) is a ‘conjugating function’. Thus, in the language of grossmann1977invariant , Theorem 1 shows that the IFPP for any distribution $\rho$ has a solution (actually, it shows that there are infinitely many solutions), every solution map is conjugate to a uniform map, and the conjugating function is precisely the inverse Rosenblatt transformation.

Notice that both the translation operator $T^{c}$ in (9) and the triangle map in (10) are uniform maps on the unit interval $[0,1]$. Thus, the solutions to the IFPP given in Eqs (8) and (13) are examples of the general solution form in (18). In particular, while the solution to the IFPP in (13) was derived assuming symmetry of the target density $\rho(\cdot)$, (13) actually gives a solution of the IFPP for any density $\rho(\cdot)$. Unimodal maps of this form were derived in ershov1988solution .

Computed examples of solutions to the IFPP given by the factorization (18) are presented in Sec. V, in one dimension, and in Sec VI in two dimensions. High dimensional calculations are discussed in Sec. VII.

Many properties of the map $M$ are inherited from the uniform map $U$.

When $R$ and $R^{-1}$ are continuous, $M$ is continuous iff $U$ is continuous. In one dimension, monotonicity of the CDF and IDF imply that the number of modes of $U$ equals the number of modes of $M$; in particular, $M$ is unimodal iff $U$ is unimodal.

Constructing iterative maps with specific periodicity of the orbit is possible through the use of translation operators $T^{c}$ as uniform maps, defined in Eq. (9). Consider, first, maps in one dimension on $[0,1]$. If the shift $c\neq 0$ and $c\notin\mathbb{Q}$, the map is aperiodic. However, in the case that $c\neq 0$ and $c\in\mathbb{Q}$ such that

$$c=\frac{N}{D}$$

(19)

with $N,D\in\mathbb{N}$ and $\gcd(N,D)=1$, then the map is periodic with periodicity $D$, and iterative maps constructed with $U=T^{c}$ exhibit the same periodicity. These properties may be extended to multi-dimensional settings when the translation constant $c$ is a vector of shifts in each coordinate direction, as used in rank-one lattice rules for quasi-Monte Carlo integration dick2013high .

The factorization in Theorem 1 also shows that performing an iteration $x_{n+1}=M(x_{n})$ with an iterative map $M$ on the space $X$ is equivalent to applying the corresponding uniform map $z_{n+1}=U(z_{n})$ on the space $[0,1]^{d}$ through the transformations $R$ and $R^{-1}$, as indicated in the following (commuting) diagram.

Using this commuting property, it is straightforward to prove the following lemma.

Hence, instead of iterating $M$ on the space $X$ to produce the sequence $\{x_{1},x_{2},x_{3},\ldots\}$, Eq. (20) shows that one can iterate the map $U$ on the space $[0,1]^{d}$ to produce the sequence $\{z_{1},z_{2},z_{3},\ldots\}$ and then evaluate $x_{n}=R^{-1}z_{n}$, $n=1,2,\ldots$, to produce exactly the same sequence on $X$. Since the map $M$ is mixing or ergodic iff the uniform map $U$ is mixing or ergodic, respectively, in this sense mixing and ergodicity of $M$ is inherited from $U$.

Using the expansion in Eq. (20), we see that $M$ is deterministic or stochastic iff $U$ is deterministic or stochastic, respectively. Even though we are not considering stochastic maps here, we note that, for stochastic maps, iterations of $M$ are correlated or independent iff iterations of $U$ are correlated or independent, respectively.

Some other properties that are, and are not, preserved by the transformation from $U$ to $M$ are discussed in grossmann1977invariant .

We have already encountered three uniform maps on the interval $[0,1]$, namely the identity map $I(x)=x$ (Figure 3 (top, left)) and the translation operator (9) (Figure 1 (left)), that have Lyapunov exponent $h=0$, and the triangle map (Figure 1 (right)) with Lyapunov exponent $h=\log 2$.

Some further elementary uniform maps on $[0,1]$, and associated Lyapunov exponents, are:

• •

  $\ell$ periods of a sawtooth function on $[0,1]$ (Figure 3, top-right, for $l=3$ periods) ⁵⁵5The two period sawtooth map $s_{2}$ is also called the Bernoulli map, and its orbit $\mathcal{O}^{+}(x)$ is the dyadic transformation.

  $$s_{\ell}(x)=\ell*x-\lfloor\ell*x\rfloor,$$

  (21)

  with Lyapunov exponent $h=\log\ell$,

• •

  $\ell$ periods of a triangle function on $[0,1]$ (Figure 3 (bottom, left) for $l=3$ periods) ⁶⁶6This is the ‘broken linear transformation’ in grossmann1977invariant of order $p=2\ell$.

  $$t_{\ell}(x)=1-2\left|s_{\ell}(x)-1/2\right|.$$

  (22)

  with Lyapunov exponent $h=\log 2\ell$,

• •

  and the asymmetric triangle, for $c\in(0,1)$ (Figure 3 (bottom, right) for $c=0.3$)

  $$t^{c}(x)=\begin{cases}\displaystyle\frac{x}{c}&0\leq x\leq c\\[10.00002pt] \displaystyle\frac{1-x}{1-c}&c\leq x\leq 1\end{cases}$$

  (23)

  with Lyapunov exponent $0\leq h=-c\log c-(1-c)\log(1-c)\leq\log 2$.

Obviously, many more uniform maps are possible. Further examples can be formed by partitioning the domain and range of any uniform map, and then permuting the subintervals. Many existing ‘matrix-based’ methods for constructing solutions to the IFPP, can be viewed as examples of such a partition-and-permute of an elementary uniform map rogers2004synthesizing . Uniform maps of other forms are developed in huang2005characterizing from two-segmental Lebesgue processes, producing uniform maps that are curiously non-linear.

An example is $t_{\ell}$, that can be constructed as the composition $t_{\ell}=s_{\ell}\circ t_{1}$.

We mentioned the numerical artifacts that can occur with finite-precision arithmetic, particularly when implementing maps on a binary computer and when the endpoints of the interval $X$ and constants in the maps have exact binary representations. We avoided these artifacts by composing the stated uniform map with the translation $T^{c}$ for $c=1/3\times 10^{-9}$ that does not have finite binary representation ⁷⁷7Computation was performed in MatLab that implements IEEE Standard 754 for double-precision binary floating-point format.. This small shift is indiscernible in the graphs of the maps.

To give a concrete example of the solution in (13) for a distribution without reflexive symmetry, we consider the ramp distribution with PDF

$$\rho_{\text{ramp}}(x)=2x$$

(24)

that has CDF

$$F_{\text{ramp}}(x)=x^{2}.$$

We produce a unimodal, continuous map by choosing the uniform map $t_{1}$, as in (13), to give

$$M_{\text{ramp}}=\begin{cases}\sqrt{2}x&0\leq x\leq\frac{1}{\sqrt{2}}\\ \sqrt{2}\sqrt{1-x^{2}}&\frac{1}{\sqrt{2}}\leq x\leq 1\end{cases}$$

(25)

shown in Figure 4 (left). Figure 2 (right) shows a normalized histogram of $10^{6}$ iterates of $M_{\text{ramp}}$ starting at $x=0.3$, confirming that the orbit of $M_{\text{ramp}}$ converges to the desired ramp distribution, as guaranteed by Theorem 1. The numerical implementation avoids finite-precision effects, as discussed earlier.

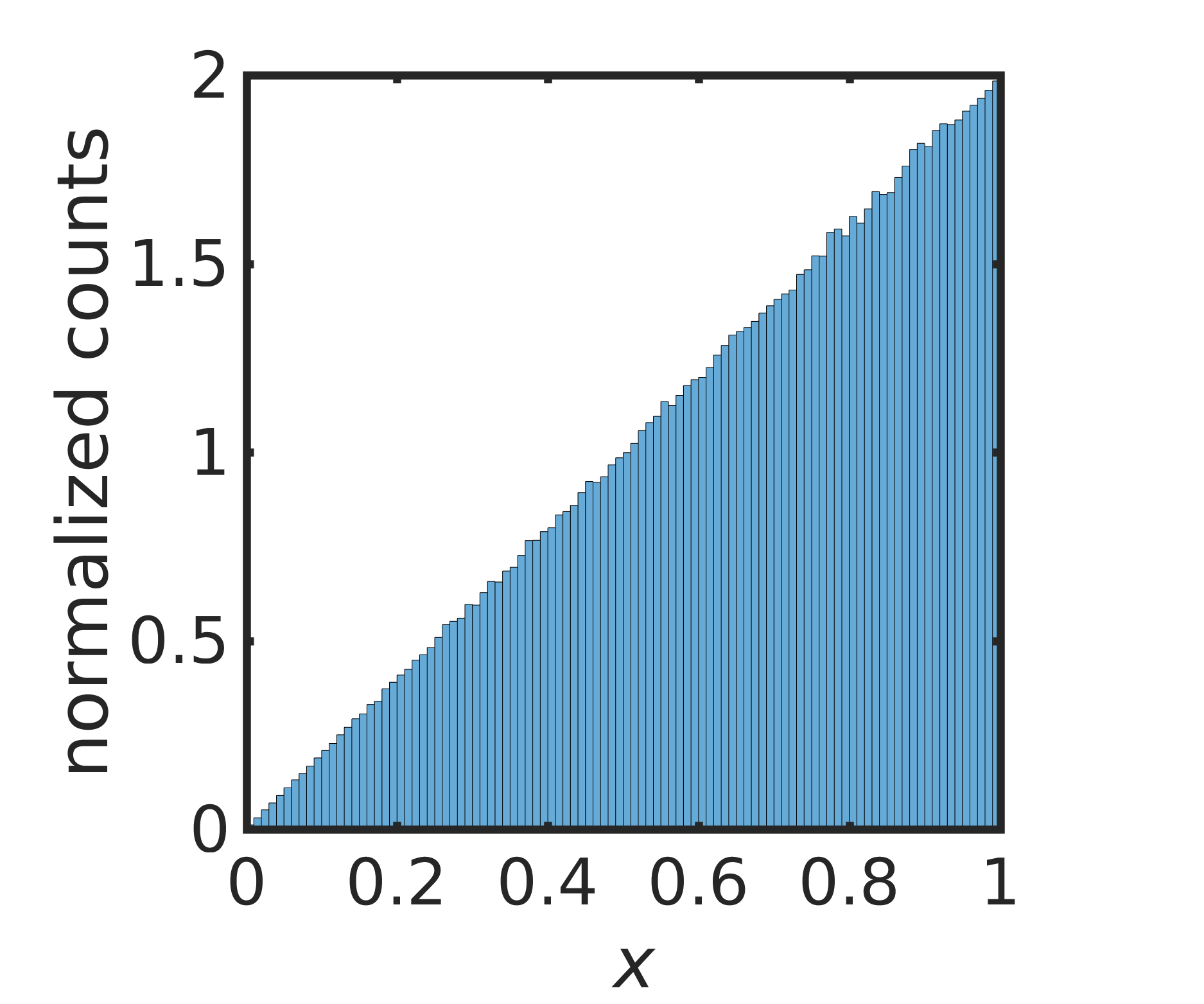
The estimated Lyapunov exponent for this map is $h\approx 1.040035$, which is greater than the Lyapunov exponent for the inducing triangular map $t_{1}$ which is $\log 2\approx 0.693147$.

Using a different uniform map gives a different solution to the IFPP. For example, choosing $s_{3}$ gives the map $M=F^{-1}\circ s_{3}\circ F$ shown in Figure 5 (left). A normalized histogram over an orbit of $10^{6}$ iterations is shown in Figure 5 (right), confirming that this map is also ergodic for $\rho_{\text{ramp}}$.

The estimated Lyapunov exponent for this map is $h\approx 1.098612$, which is the same numerical value as the Lyapunov exponent for the sawtooth map $s_{3}$ which is $\log 3\approx 1.098612$. Comparing with the result for the map induced by $t_{1}$, this shows that the Lyapunov exponent of a map is not generally equal to the Lyapunov exponent of the inducing uniform map.

The logistic map, mentioned in the introduction, is

$$M_{\text{log}}(x)=4x(1-x).$$

(26)

The equilibrium distribution of this map

$$\rho_{\text{log}}(x)=\frac{1}{\pi\sqrt{x(1-x)}},$$

(27)

can be easily verified by substituting into the FP equation (6). The CDF of $\rho_{\text{log}}(x)$ is

$$F_{\text{log}}(x)=\int_{0}^{x}\rho_{\text{log}}(x^{\prime})dx^{\prime}=\frac{2}{\pi}\arcsin(\sqrt{x}),$$

(28)

and the IDF is

$$F_{\text{log}}^{-1}(x)=\sin^{2}(\frac{\pi x}{2})=\frac{1}{2}(1-\cos(\pi x)).$$

(29)

The logistic map (26) is induced by the factorization (18) by choosing the triangle map $t_{1}$ as uniform map, i.e., substituting the CDF (28) and IDF (29) into (13); see Figure 6 (left). Equivalently, one may note that the logistic map (26) is transformed into the triangle map $t_{1}$ by the change of variables $z=F^{-1}(x)$; in the language of grossmann1977invariant , $M_{\text{log}}$ and $t_{1}$ are conjugate dynamical laws.

Other iterative maps which preserves the same equilibrium distribution (27) can be constructed by choosing another uniform map, such as $\ell$ periods of a triangle function (22). This gives the iterative maps

$$M_{\ell}=F_{\text{log}}^{-1}\circ t_{\ell}\circ F_{\text{log}}=\sin^{2}(2\ell\arcsin(\sqrt{x})),\ell\geq 1,$$

(30)

that coincide with the $n^{\text{th}}$ power of the logistic map (26) for $\ell=2^{n-1}$. Figure 6 (right) shows the map which preserves the same equilibrium distribution as the logistic map but induced by the uniform map $t_{3}$. Since $3$ is not of the form $2^{n-1}$, this map is not simply a power of the logistic map.

The theoretical value of the Lyapunov exponent of the map in (30) is $\log 2\ell$, using (5). Table 1 gives the theoretical values of the Lyapunov exponent and experimentally calculated values using $10000$ iterations, as in (4), for some values of $\ell$.

Two well-known examples of uniform maps in the two-dimensional unit square, $X=[0,1]^{2}$, are the baker’s map

$$U_{\text{b}}(x_{1},x_{2})=\left(2x_{1}\mod 1,\frac{x_{2}+u\left(x_{1}-\frac{1}{2}\right)}{2}\right),$$

(31)

where $u$ is the unit step function, and the Arnold cat map

$$U_{\text{A}}(x_{1},x_{2})=\left((2x_{1}+x_{2})\mod 1,(x_{1}+x_{2})\mod 1\right).$$

(32)

Other uniform maps in $d>1$ dimensions may be formed by $1$-dimensional uniform maps acting on each coordinate, giving the coordinate-wise uniform map

$$U(x)=\left(U_{1}(x_{1}),U_{2}(x_{2}),\ldots,U_{n}(x_{d})\right)$$

(33)

where $U_{i}(x)$, $i=1,2,\ldots,d$, are uniform maps in one dimension. We will use the baker’s map (31) and a coordinate-wise uniform map in the $2$-dimensional examples that follow.

This example demonstrates construction of a map in two-dimensions that targets the checker board distribution, shown in Figure 8 (bottom-left) and Figure 9 (bottom-left), using the factorization (18).

The first step in constructing a solution to the IFPP for this distribution is to construct the forward and inverse Rosenblatt transformations, which requires the marginal density functions (17) that may be evaluated analytically in this case. A plot of the two components of the functions $R$ and $R^{-1}$ is shown in Figure 7.

We construct two solutions to the IFPP, each induced by choosing a particular uniform map: the first is the baker’s map (31); the second is a component-wise uniform map (33) with an asymmetric triangle map (23) acting on each component,

$$U(x_{1},x_{2})=\left(U_{1}(x_{1}),U_{2}(x_{2})\right)$$

(34)

where $U_{1}=t^{c}$ for $c=0.3$ and $U_{2}=t^{c}$ with $c=0.9$.

Figure 8 (top row) shows the two components of the map induced by the baker’s map, the checker-board distribution (bottom-left), and a histogram of $10^{6}$ iterates (bottom-right) showing that the map does indeed converge in distribution to the desired distribution.

Figure 9 (top row) shows the two components of the map constructed using the two component-wise asymmetric triangular maps, the checker-board distribution (bottom-left), and a histogram of $10^{6}$ iterates (bottom-right) showing that the map also converges in distribution to the desired distribution, and hence is also a solution to the IFPP.

Numerical implementation of the factorized solution (18) is not difficult in few dimensions. In this section we present an example of numerical implementation using a normalized greyscale image of a coin ⁸⁸8A pre-2006 New Zealand $50$ cent coin., piecewise constant over pixels, as the target distribution; see Figure 10 (left). The marginal distributions (17) are evaluated as linear interpolation of cumulative sums over pixel values, and hence the CDF and then forward and inverse Rosenblatt transformations follow as in section IV.1. The uniform map was produced as component-wise univariate translation maps, specifically

$$U(x_{1},x_{2})=\left(U_{1}(x_{1}),U_{2}(x_{2})\right)$$

where $U_{1}=T^{c}$ for $c=0.6$ and $U_{2}=T^{c}$ with $c=0.2$. The resulting map is given by Eq. (18).

Figure 10 (right) shows a normalized histogram, binned to pixels, of $10^{6}$ iterations of this map. As can be seen, the estimated PDF from the orbit of this map does reproduce the image of the coin. However, there are also obvious artifacts near the edge of the image showing that mixing could be better. We conjecture that a chaotic uniform map would produce better mixing and fewer numerical artifacts.