Solute-mediated colloidal vortex in a microfluidic T-junction
Abstract
Solute gradients next to an interface drive a diffusioosmotic flow, the origin of which lies in the intermolecular interactions between the solute and the interface. These flows on the surface of colloids introduce an effective slip velocity, driving their diffusiophoretic migration. In confined environments, we expect the interplay between diffusiophoretic migration and diffusioosmotic flows near the walls to govern the motion of colloids. These near-wall osmotic flows are, however, often considered weak and neglected. Here, using microfluidic experiments in a T-junction, numerical simulations, and theoretical modeling, we show that the interplay between osmotic and phoretic effects leads to unexpected outcomes: forming a colloidal vortex in the absence of inertial effects, and demixing and focusing of the colloids in the direction opposite to what is commonly expected from diffusiophoresis alone. We show these colloidal vortices to be persistent for a range of salt types, salt gradients, and flow rates, and establish a criterion for their emergence. Our work sheds light on how boundaries modulate the solute-mediated transport of colloids in confined environments.
The discovery of colloidal migration in response to solute gradients dates back to the works of Derjaguin more than half a century ago [1] and the later developments by Prieve, Anderson and others [2, 3, 4, 5, 6]. While sophisticated technologies for manipulation of colloids and biomolecules in microfluidics using external electric/magnetic fields have been developed over the past two decades [7, 8, 9, 10], using a “pinch of salt” to guide the motion of colloids offers a tempting alternative [11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 29, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70] that biology seems to have benefited from as evidenced by the role of diffusiophoresis in cargo transport and phase separation within the living cells [71, 72, 73, 74, 75, 76, 77].
Solute gradients in confined and crowded environments also drive diffusioosmotic flows next to the confining surfaces. These flows have been utilized for directional pumping and trapping of DNA and exosomes [78, 79, 80]. However, they are often considered weak, leading to small changes to the diffusiophoretic migration of colloids, and therefore neglected. A few recent studies have reported on the emergence of solute-driven vortices and convection rolls near surfaces, leading to the trapping and entrainment of colloids [81, 82, 83]. Yet, how and under what circumstances diffusiophoresis and diffusioosmosis conspire to lead to these reported behaviors has remained elusive.
Here, we use microfluidic experiments and 3D numerical simulations to demonstrate that solute-driven colloidal vortices emerge due to a subtle interplay between solutal gradients perpendicular to the walls, driving the phoretic migration of colloids toward the walls, and solutal gradients parallel to the walls, sweeping the colloids by the diffusioosmotic flows. We show the universality of these vortices for a range of salt types, salt gradients, and flow rates, and demonstrate that the vortex location, which coincides with the colloidal focusing line scales as , where with as the flow velocity, as the channel height, and as the solute diffusivity. We finally demonstrate that the competition between diffusioosmotic mobility and diffusiophoretic mobility governs the formation of these colloidal vortices.
We use a microfluidic T-junction setup, which is schematically shown in Fig. 1 (a), with height , width , and length . The mid-channel width is set as to keep the mean flow velocity constant. We inject solutions with salt concentrations and from the left and right sides, respectively; colloids are introduced from the right branch [84]. In the absence of solute gradients, i.e., the control case, colloids occupy half the channel and move downstream without any noticeable diffusion (Fig. 1 (b)). We use particles with 1 micron diameter, with diffusivity , which should be contrasted with the solute diffusivity of . For the experiments shown in Fig. 1 (b), the particle Peclet number is therefore , indicating the dominance of advection over diffusion for the particles.
Adding a “pinch of salt” to either channel, however, changes the picture completely. We expect the negatively-charged colloids to migrate toward the higher salt concentration for the salts we use (LiCl, NaCl, KCl) [11]. Surprisingly, however, we observe the focusing of colloids in the lower salt concentration region, i.e., when , colloids move to the right side, and when , a focusing line emerges on the left side (Fig. 1 (b)), in contrast to what is expected [11].
To gain insight into this unexpected focusing, we conducted 3D numerical simulations of the flow, solute, and particle transport. The flow field is governed by the Stokes equations:
| (1) | ||||
| (2) |
where is the flow velocity, represents the fluid pressure, and is the fluid viscosity. The solute and colloid fields are governed by advection-diffusion equations:
| (3) | ||||
| (4) |
where the colloid diffusiophoretic velocity is with as the diffusiophoretic mobility [3, 6, 35, 84]. The flow velocity on the walls of the channel is determined by the diffusioosmotic slip velocity , where is the unit normal vector on the boundary. We solve these equations using the open-source software OpenFoam [85, 84].
In a Lagrangian frame, the colloidal transport can be described as , where represents the particle location at time . Following the trajectories of particles obtained from the simulations, we gain insight into the focusing mechanism (Fig. 2). In the control case, where solute gradients are absent, colloids simply follow the flow streamlines as evident from the absence of mixing of the colored particles introduced upstream in the four quadrants (Fig. 2 (a, b)), which remain in their corresponding quadrants as they travel along the channel (Fig. 2 (c)). In this case, there is no colloidal motion in the z direction, perpendicular to the fluid flow.
In the presence of salt gradients, both diffusiophoretic migration of colloids and diffusioosmotic flows emerge. To disentangle these two effects, we first turn-off the osmotic flows near the walls, setting . In this case, colloids deviate from the flow streamlines, and move toward the higher salt concentration side due to diffusiophoresis (Fig. 2 (d)). This behavior is consistent with the observations of Abécassis et al. [11]; however, opposite of what we observed in our experiments (Fig. 1). We therefore conclude that diffusiophoresis alone cannot explain our observations.
Accounting for the diffusioosmotic flows near the channel walls changes the particle trajectories drastically (Fig. 2 (e)). The colloids move out-of-plane in the direction, and get dragged along the walls due to the diffusioosmotic flows, leading to their spiraling motion, and focusing on the right side of the channel, opposite of what diffusiophoresis alone does (Fig. 2 (f)). The presence of diffusioosmosis, therefore, does not simply lead to a weak quantitative drift in the colloidal trajectories, but leads to significant qualitative changes, and an effective demixing of the colloidal field that certainly cannot be described using a diffusive framework.
The out-of-plane motion of colloids is driven by the solute gradients in the direction. The presence of shear near the wall and its absence in the mid-plane leads to a differential solute diffusion and is the reason for the emergence of solute gradients in the direction, driving the motion of colloids both within and perpendicular to the x-y plane (Fig. 3 (a-c)). In the mid-plane of the channel, solute diffusion competes with advection along the channel (), leading to scaling for the solute diffusion width . Near the walls, however, the presence of shear fow changes this scaling (), leading to scaling for the diffusion width [86, 87, 84].
Once near the walls, the colloids experience the competing effects of diffusiophoresis and diffusioosmosis. These osmotic flows create a fluid vortex, which is responsible for the spiral-like motion of the colloids [84]. To identify these osmotic near-wall vortices, we rely on the second invariant of the velocity gradient tensor, , known as the Q criterion [88]. The eigenvalues of the velocity gradient tensor satisfy the characteristic equation , where , , and are the invariants [89]. These invariants can be written in terms of the symmetric rate-of-strain tensor and antisymmetric vorticity tensor , where for incompressible flows, , and
| (5) |
with identifying a vortex as the region, where vorticity dominates over the rate of strain [84] (Fig. 3 (d)). The colloid focusing can therefore be understood as the interplay between the diffusiophoretic migration of colloids away from the mid-plane toward the walls and entrainment by the diffusioosmotic vortex near the walls.
The focusing of colloids near the walls creates a local maximum in the colloid density field, where . The colloid evolution equation near this local maximum can therefore be simplified to
| (6) |
which balances the colloid accumulation due to the effective compressibility with the colloid diffusion away from the peak, where (Fig. 3 (e,f)). This effective compressibility of the colloid density field creates an effective particle source near the mid-plane and an effective particle sink near the walls [46].
The competition between diffusioosmosis and diffusiophoresis modulates the focusing location of colloids near the wall. At steady state and neglecting particle diffusion, this balance can be written as , which further simplifies to
| (7) |
leading to the following scaling for the particle focusing location
| (8) |
which suggests that the solute diffusion width near the walls sets the length scale for the colloidal focusing (Fig. 4 (a)). The dependence of the focusing location on the strength of solute gradients can be inferred from the evolution of colloids in the Lagrangian frame near the wall, which can be written as , suggesting . This scaling argument for the colloid focusing location is supported by our experimental observations and numerical simulations (Fig. 4 (b-c)), where is defined as the distance between the central line and the focusing band at location . In the experiments, is obtained by averaging a series of steady-state snapshots of the colloid field, and the error bars represent the standard deviation of measurements [84]. We further demonstrate in the Supplementary Materials that this scaling is consistent with self-similarity arguments for the solute and colloid fields [84].
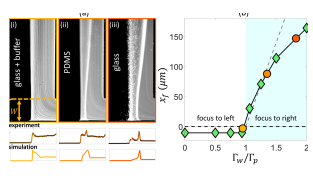
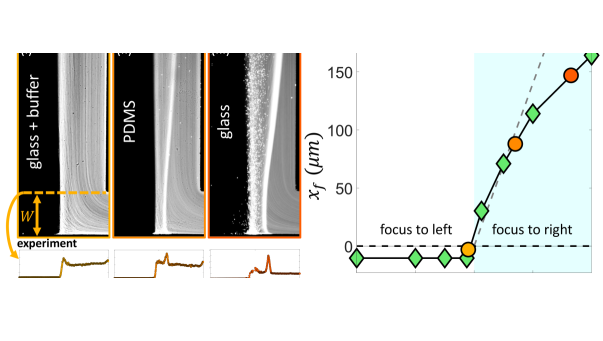
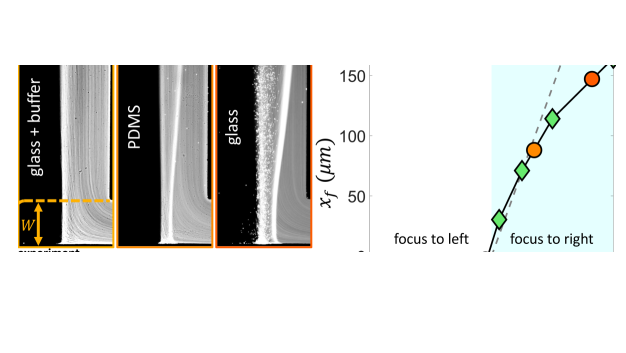
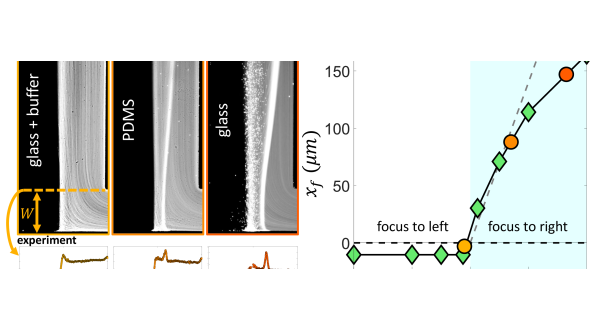
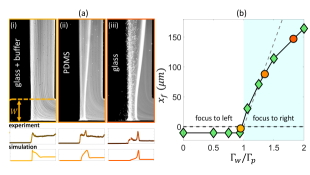
Our scaling argument suggests that the focusing side is determined by the ratio : when osmotic mobility is stronger than the phoretic mobility (), focusing occurs on the lower concentration side as we have shown. However, when phoretic mobility dominates (), we expect the focusing on the higher concentration side. For a colloid with a given value, we can modulate the diffusioosmotic mobility of the surfaces by using different materials (glass versus PDMS) or by adding a buffer solution [84]. We observe that adding the buffer solution completely eliminates the diffusioosmotic flows, explaining why the early work of Abécassis et al. [11] had not observed these flows (Fig. 5 (a,i)). On a PDMS-coated channel, we do observe focusing to the right, but weaker than that of the glass (Fig. 5 (a,ii-iii)). While we cannot directly measure the diffusioosmotic mobility of these surfaces, we can infer them from the comparison of the colloid focusing location in the experiments and simulations (Fig. 5 (b)). Our simulations show that for , the focusing location becomes insensitive to the value of diffusioosmotic mobility. However, for , the focusing location keeps moving further to the right; this increase is initially almost linear, before plateauing to an upper limit, which is determined by the solute diffusion width [84]. We note here that we have used a constant zeta potential in all our simulations so far; considering variable zeta potential models leads to quantitative changes in our simulation results as discussed in the Supplementary Materials [84].
Our observations suggest that the subtle interplay between diffusiophoresis and diffusioosmosis can be utilized to infer the diffusioosmotic mobility of the surfaces, or separate particles based on their zeta potential or size. Beyond microfluidic applications for particle sorting and separation, our findings point to the importance of accounting for the often-ignored diffusioosmotic flows in the solute-mediated transport of colloids in complex environments, from contaminant removal in porous materials to cargo delivery in living cells [90, 91, 72, 73, 75]. We further expect these osmotic flows to play role in modulating reactions in subsurface flows [92, 93], phase separation in living cells [76, 77], and ionic transport in porous electrodes [94, 95, 96, 97, 98, 99, 100, 101].
References
- B. V. Derjaguin, S. S. Dukhin and A. A. Korotkova [1961] B. V. Derjaguin, S. S. Dukhin and A. A. Korotkova, Diffusiophoresis in electrolyte solutions and its role in mechanism of film formation from rubber latexes by method of ionic deposition, Kolloidn. Zh. 23, 53 (1961).
- Anderson et al. [1982] J. Anderson, M. Lowell, and D. Prieve, Motion of a particle generated by chemical gradients part 1. non-electrolytes, J. Fluid Mech. 117, 107 (1982).
- Prieve et al. [1984] D. Prieve, J. Anderson, J. Ebel, and M. Lowell, Motion of a particle generated by chemical gradients. part 2. electrolytes, J. Fluid Mech. 148, 247 (1984).
- Ebel et al. [1988] J. P. Ebel, J. L. Anderson, and D. C. Prieve, Diffusiophoresis of latex particles in electrolyte gradients, Langmuir 4, 396 (1988).
- Staffeld and Quinn [1989] P. O. Staffeld and J. A. Quinn, Diffusion-induced banding of colloid particles via diffusiophoresis: 1. electrolytes, Journal of Colloid and Interface Science 130, 69 (1989).
- Anderson [1989] J. L. Anderson, Colloid transport by interfacial forces, Annu. Rev. Fluid Mech. 21, 61 (1989).
- Rousselet et al. [1994] J. Rousselet, L. Salome, A. Ajdari, and J. Prostt, Directional motion of brownian particles induced by a periodic asymmetric potential, Nature 370, 446 (1994).
- Stone et al. [2004] H. A. Stone, A. D. Stroock, and A. Ajdari, Engineering flows in small devices: microfluidics toward a lab-on-a-chip, Annu. Rev. Fluid Mech. 36, 381 (2004).
- Matsunaga et al. [2017] D. Matsunaga, F. Meng, A. Zöttl, R. Golestanian, and J. M. Yeomans, Focusing and sorting of ellipsoidal magnetic particles in microchannels, Phys. Rev. Lett. 119, 198002 (2017).
- Dreyfus et al. [2005] R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone, and J. Bibette, Microscopic artificial swimmers, Nature 437, 862 (2005).
- Abécassis et al. [2008] B. Abécassis, C. Cottin-Bizonne, C. Ybert, A. Ajdari, and L. Bocquet, Boosting migration of large particles by solute contrasts, Nat. Mater. 7, 785 (2008).
- Palacci et al. [2010] J. Palacci, B. Abécassis, C. Cottin-Bizonne, C. Ybert, and L. Bocquet, Colloidal motility and pattern formation under rectified diffusiophoresis, Phys. Rev. Lett. 104, 138302 (2010).
- Palacci et al. [2012] J. Palacci, C. Cottin-Bizonne, C. Ybert, and L. Bocquet, Osmotic traps for colloids and macromolecules based on logarithmic sensing in salt taxis, Soft Matter 8, 980 (2012).
- Khair [2013] A. S. Khair, Diffusiophoresis of colloidal particles in neutral solute gradients at finite péclet number, Journal of Fluid Mechanics 731, 64 (2013).
- Florea et al. [2014] D. Florea, S. Musa, J. M. R. Huyghe, and H. M. Wyss, Long-range repulsion of colloids driven by ion exchange and diffusiophoresis, Proceedings of the National Academy of Sciences 111, 6554 (2014).
- Deseigne et al. [2014] J. Deseigne, C. Cottin-Bizonne, A. D. Stroock, L. Bocquet, and C. Ybert, How a “pinch of salt” can tune chaotic mixing of colloidal suspensions, Soft matter 10, 4795 (2014).
- Volk et al. [2014] R. Volk, C. Mauger, M. Bourgoin, C. Cottin-Bizonne, C. Ybert, and F. Raynal, Chaotic mixing in effective compressible flows, Phys. Rev. E 90, 013027 (2014).
- Kar et al. [2015] A. Kar, T.-Y. Chiang, I. Ortiz Rivera, A. Sen, and D. Velegol, Enhanced transport into and out of dead-end pores, ACS Nano 9, 746 (2015).
- Velegol et al. [2016] D. Velegol, A. Garg, R. Guha, A. Kar, and M. Kumar, Origins of concentration gradients for diffusiophoresis, Soft Matter 12, 4686 (2016).
- Banerjee et al. [2016] A. Banerjee, I. Williams, R. N. Azevedo, M. E. Helgeson, and T. M. Squires, Soluto-inertial phenomena: Designing long-range, long-lasting, surface-specific interactions in suspensions, Proceedings of the National Academy of Sciences 113, 8612 (2016).
- Keh [2016] H. J. Keh, Diffusiophoresis of charged particles and diffusioosmosis of electrolyte solutions, Current Opinion in Colloid & Interface Science 24, 13 (2016).
- Shin et al. [2016] S. Shin, E. Um, B. Sabass, J. T. Ault, M. Rahimi, P. B. Warren, and H. A. Stone, Size-dependent control of colloid transport via solute gradients in dead-end channels, Proc. Natl. Acad. Sci. U.S.A. 113, 257 (2016).
- Shi et al. [2016] N. Shi, R. Nery-Azevedo, A. I. Abdel-Fattah, and T. M. Squires, Diffusiophoretic focusing of suspended colloids, Phys. Rev. Lett. 117, 258001 (2016).
- Mauger et al. [2016] C. Mauger, R. Volk, N. Machicoane, M. Bourgoin, C. Cottin-Bizonne, C. Ybert, and F. Raynal, Diffusiophoresis at the macroscale, Phys. Rev. Fluids 1, 034001 (2016).
- Schmidt et al. [2016] L. Schmidt, I. Fouxon, D. Krug, M. van Reeuwijk, and M. Holzner, Clustering of particles in turbulence due to phoresis, Phys. Rev. E 93, 063110 (2016).
- Shin et al. [2017a] S. Shin, J. T. Ault, P. B. Warren, and H. A. Stone, Accumulation of colloidal particles in flow junctions induced by fluid flow and diffusiophoresis, Phys. Rev. X 7, 041038 (2017a).
- Shukla et al. [2017] V. Shukla, R. Volk, M. Bourgoin, and A. Pumir, Phoresis in turbulent flows, New Journal of Physics 19, 123030 (2017).
- Sear and Warren [2017] R. P. Sear and P. B. Warren, Diffusiophoresis in nonadsorbing polymer solutions: The asakura-oosawa model and stratification in drying films, Phys. Rev. E 96, 062602 (2017).
- Shin et al. [2017b] S. Shin, O. Shardt, P. B. Warren, and H. A. Stone, Membraneless water filtration using co2, Nat. Commun. 8, 15181 (2017b).
- Nery-Azevedo et al. [2017] R. Nery-Azevedo, A. Banerjee, and T. M. Squires, Diffusiophoresis in ionic surfactant gradients, Langmuir 33, 9694 (2017).
- Ault et al. [2018] J. T. Ault, S. Shin, and H. A. Stone, Diffusiophoresis in narrow channel flows, J. Fluid Mech. 854, 420 (2018).
- Shin et al. [2018] S. Shin, P. B. Warren, and H. A. Stone, Cleaning by surfactant gradients: Particulate removal from porous materials and the significance of rinsing in laundry detergency, Phys. Rev. Appl. 9, 034012 (2018).
- Lee et al. [2018] H. Lee, J. Kim, J. Yang, S. W. Seo, and S. J. Kim, Diffusiophoretic exclusion of colloidal particles for continuous water purification, Lab Chip 18, 1713 (2018).
- Raynal et al. [2018] F. Raynal, M. Bourgoin, C. Cottin-Bizonne, C. Ybert, and R. Volk, Advection and diffusion in a chemically induced compressible flow, Journal of Fluid Mechanics 847, 228 (2018).
- Marbach and Bocquet [2019] S. Marbach and L. Bocquet, Osmosis, from molecular insights to large-scale applications, Chem. Soc. Rev. 48, 3102 (2019).
- Gupta et al. [2019] A. Gupta, B. Rallabandi, and H. A. Stone, Diffusiophoretic and diffusioosmotic velocities for mixtures of valence-asymmetric electrolytes, Phys. Rev. Fluids 4, 043702 (2019).
- Battat et al. [2019] S. Battat, J. T. Ault, S. Shin, S. Khodaparast, and H. A. Stone, Particle entrainment in dead-end pores by diffusiophoresis, Soft Matter 15, 3879 (2019).
- Banerjee and Squires [2019] A. Banerjee and T. M. Squires, Long-range, selective, on-demand suspension interactions: Combining and triggering soluto-inertial beacons, Science Advances 5, eaax1893 (2019).
- Raynal and Volk [2019] F. Raynal and R. Volk, Diffusiophoresis, batchelor scale and effective péclet numbers, Journal of Fluid Mechanics 876, 818 (2019).
- Ault et al. [2019] J. T. Ault, S. Shin, and H. A. Stone, Characterization of surface–solute interactions by diffusioosmosis, Soft Matter 15, 1582 (2019).
- Gandhi et al. [2020] T. Gandhi, J. Mac Huang, A. Aubret, Y. Li, S. Ramananarivo, M. Vergassola, and J. Palacci, Decision-making at a t-junction by gradient-sensing microscopic agents, Phys. Rev. Fluids 5, 104202 (2020).
- Gupta et al. [2020] A. Gupta, S. Shim, and H. A. Stone, Diffusiophoresis: from dilute to concentrated electrolytes, Soft Matter 16, 6975 (2020).
- Williams et al. [2020] I. Williams, S. Lee, A. Apriceno, R. P. Sear, and G. Battaglia, Diffusioosmotic and convective flows induced by a nonelectrolyte concentration gradient, Proceedings of the National Academy of Sciences 117, 25263 (2020).
- Warren [2020] P. B. Warren, Non-faradaic electric currents in the nernst-planck equations and nonlocal diffusiophoresis of suspended colloids in crossed salt gradients, Phys. Rev. Lett. 124, 248004 (2020).
- Shimokusu et al. [2020] T. J. Shimokusu, V. G. Maybruck, J. T. Ault, and S. Shin, Colloid separation by co2-induced diffusiophoresis, Langmuir 36, 7032 (2020).
- Singh et al. [2020] N. Singh, G. T. Vladisavljević, F. m. c. Nadal, C. Cottin-Bizonne, C. Pirat, and G. Bolognesi, Reversible trapping of colloids in microgrooved channels via diffusiophoresis under steady-state solute gradients, Phys. Rev. Lett. 125, 248002 (2020).
- Shin [2020] S. Shin, Diffusiophoretic separation of colloids in microfluidic flows, Phys. Fluids. 32, 101302 (2020).
- Jotkar and Cueto-Felgueroso [2021] M. Jotkar and L. Cueto-Felgueroso, Particle separation through diverging nanochannels via diffusiophoresis and diffusioosmosis, Phys. Rev. Appl. 16, 064067 (2021).
- Alessio et al. [2021] B. M. Alessio, S. Shim, E. Mintah, A. Gupta, and H. A. Stone, Diffusiophoresis and diffusioosmosis in tandem: Two-dimensional particle motion in the presence of multiple electrolytes, Phys. Rev. Fluids 6, 054201 (2021).
- Chu et al. [2021] H. C. W. Chu, S. Garoff, R. D. Tilton, and A. S. Khair, Macrotransport theory for diffusiophoretic colloids and chemotactic microorganisms, Journal of Fluid Mechanics 917, A52 (2021).
- Shim et al. [2021a] S. Shim, M. Baskaran, E. H. Thai, and H. A. Stone, Co2-driven diffusiophoresis and water cleaning: similarity solutions for predicting the exclusion zone in a channel flow, Lab Chip 21, 3387 (2021a).
- Shim et al. [2021b] S. Shim, S. Khodaparast, C.-Y. Lai, J. Yan, J. T. Ault, B. Rallabandi, O. Shardt, and H. A. Stone, Co2-driven diffusiophoresis for maintaining a bacteria-free surface, Soft Matter 17, 2568 (2021b).
- Tan et al. [2021] H. Tan, A. Banerjee, N. Shi, X. Tang, A. Abdel-Fattah, and T. M. Squires, A two-step strategy for delivering particles to targets hidden within microfabricated porous media, Sci. Adv. 7, eabh0638 (2021).
- Doan et al. [2021] V. S. Doan, S. Chun, J. Feng, and S. Shin, Confinement-dependent diffusiophoretic transport of nanoparticles in collagen hydrogels, Nano Letters 21, 7625 (2021).
- Shim [2022] S. Shim, Diffusiophoresis, diffusioosmosis, and microfluidics: Surface-flow-driven phenomena in the presence of flow, Chem. Rev. 122, 6986 (2022).
- Chu et al. [2022] H. C. W. Chu, S. Garoff, R. D. Tilton, and A. S. Khair, Tuning chemotactic and diffusiophoretic spreading via hydrodynamic flows, Soft Matter 18, 1896 (2022).
- Volk et al. [2022] R. Volk, M. Bourgoin, C.-É. Bréhier, and F. Raynal, Phoresis in cellular flows: from enhanced dispersion to blockage, Journal of Fluid Mechanics 948, A42 (2022).
- Alessio et al. [2022] B. M. Alessio, S. Shim, A. Gupta, and H. A. Stone, Diffusioosmosis-driven dispersion of colloids: a taylor dispersion analysis with experimental validation, Journal of Fluid Mechanics 942, A23 (2022).
- McKenzie et al. [2022] B. E. McKenzie, H. C. W. Chu, S. Garoff, R. D. Tilton, and A. S. Khair, Drop deformation during diffusiophoresis, Journal of Fluid Mechanics 949, A17 (2022).
- Migacz and Ault [2022] R. E. Migacz and J. T. Ault, Diffusiophoresis in a taylor-dispersing solute, Phys. Rev. Fluids 7, 034202 (2022).
- Somasundar et al. [2023] A. Somasundar, B. Qin, S. Shim, B. L. Bassler, and H. A. Stone, Diffusiophoretic particle penetration into bacterial biofilms, ACS Applied Materials & Interfaces 15, 33263 (2023).
- Akdeniz et al. [2023] B. Akdeniz, J. A. Wood, and R. G. H. Lammertink, Diffusiophoresis and diffusio-osmosis into a dead-end channel: Role of the concentration-dependence of zeta potential, Langmuir 39, 2322 (2023).
- Ghosh et al. [2023] S. Ghosh, S. Lee, M. V. Johnson, J. Hardin, V. S. Doan, S. Shin, S. R. Kalidindi, J. Lee, J. T. Ault, and Y. L. Kong, Diffusiophoresis-enhanced particle deposition for additive manufacturing, MRS Communications 13, 1053 (2023).
- Lee et al. [2023] S. Lee, J. Lee, and J. T. Ault, The role of variable zeta potential on diffusiophoretic and diffusioosmotic transport, Colloids and Surfaces A: Physicochemical and Engineering Aspects 659, 130775 (2023).
- Teng et al. [2023] J. Teng, B. Rallabandi, and J. T. Ault, Diffusioosmotic dispersion of solute in a long narrow channel, Journal of Fluid Mechanics 977, A5 (2023).
- Yang et al. [2023] A. Yang, B. E. McKenzie, Y. Yi, A. S. Khair, S. Garoff, and R. D. Tilton, Effect of polymer/surfactant complexation on diffusiophoresis of colloids in surfactant concentration gradients, Journal of Colloid and Interface Science 642, 169 (2023).
- Sambamoorthy and Chu [2023] S. Sambamoorthy and H. C. W. Chu, Diffusiophoresis of a spherical particle in porous media, Soft Matter 19, 1131 (2023).
- Williams et al. [2024] I. Williams, P. B. Warren, R. P. Sear, and J. L. Keddie, Colloidal diffusiophoresis in crossed electrolyte gradients: Experimental demonstration of an “action-at-a-distance” effect predicted by the nernst-planck equations, Phys. Rev. Fluids 9, 014201 (2024).
- Migacz et al. [2024] R. E. Migacz, M. Castleberry, and J. T. Ault, Enhanced diffusiophoresis in dead-end pores with time-dependent boundary solute concentration, Phys. Rev. Fluids 9, 044203 (2024).
- Yang et al. [2024] A. Yang, B. E. McKenzie, B. Pavlat, E. S. Johnson, A. S. Khair, S. Garoff, and R. D. Tilton, Diffusiophoretic transport of charged colloids in ionic surfactant gradients entirely below versus entirely above the critical micelle concentration, Langmuir 40, 10143 (2024).
- Sear [2019] R. P. Sear, Diffusiophoresis in cells: A general nonequilibrium, nonmotor mechanism for the metabolism-dependent transport of particles in cells, Phys. Rev. Lett. 122, 128101 (2019).
- Ramm et al. [2021] B. Ramm, A. Goychuk, A. Khmelinskaia, P. Blumhardt, H. Eto, K. A. Ganzinger, E. Frey, and P. Schwille, A diffusiophoretic mechanism for atp-driven transport without motor proteins, Nat. Phys. 17, 850 (2021).
- Burkart et al. [2022] T. Burkart, M. C. Wigbers, L. Würthner, and E. Frey, Control of protein-based pattern formation via guiding cues, Nature Reviews Physics 4, 511 (2022).
- Alessio and Gupta [2023] B. M. Alessio and A. Gupta, Diffusiophoresis-enhanced turing patterns, Sci. Adv. 9, eadj2457 (2023).
- Shandilya et al. [2024] E. Shandilya, B. Rallabandi, and S. Maiti, In situ enzymatic control of colloidal phoresis and catalysis through hydrolysis of atp, Nature Communications 15, 3603 (2024).
- Häfner and Müller [2024] G. Häfner and M. Müller, Reaction-driven diffusiophoresis of liquid condensates: Potential mechanisms for intracellular organization, ACS Nano 18, 16530 (2024).
- Doan et al. [2024] V. S. Doan, I. Alshareedah, A. Singh, P. R. Banerjee, and S. Shin, Diffusiophoresis promotes phase separation and transport of biomolecular condensates., bioRxiv (2024).
- Hatlo et al. [2011] M. M. Hatlo, D. Panja, and R. van Roij, Translocation of dna molecules through nanopores with salt gradients: the role of osmotic flow, Phys. Rev. Lett. 107, 068101 (2011).
- Lee et al. [2014] C. Lee, C. Cottin-Bizonne, A.-L. Biance, P. Joseph, L. Bocquet, and C. Ybert, Osmotic flow through fully permeable nanochannels, Phys. Rev. Lett. 112, 244501 (2014).
- Rasmussen et al. [2020] M. K. Rasmussen, J. N. Pedersen, and R. Marie, Size and surface charge characterization of nanoparticles with a salt gradient, Nat. Commun. 11, 2337 (2020).
- Shin et al. [2020] S. Shin, J. T. Ault, K. Toda-Peters, and A. Q. Shen, Particle trapping in merging flow junctions by fluid-solute-colloid-boundary interactions, Phys. Rev. Fluids 5, 024304 (2020).
- Chakra et al. [2023] A. Chakra, N. Singh, G. T. Vladisavljević, F. Nadal, C. Cottin-Bizonne, C. Pirat, and G. Bolognesi, Continuous manipulation and characterization of colloidal beads and liposomes via diffusiophoresis in single- and double-junction microchannels, ACS Nano 17, 14644 (2023).
- Migacz et al. [2023] R. E. Migacz, G. Durey, and J. T. Ault, Convection rolls and three-dimensional particle dynamics in merging solute streams, Phys. Rev. Fluids 8, 114201 (2023).
- [84] H. Liu and A. A. Pahlavan, Supplementary Materials, .
- Weller et al. [1998] H. G. Weller, G. Tabor, H. Jasak, and C. Fureby, A tensorial approach to computational continuum mechanics using object-oriented techniques, Computers in physics 12, 620 (1998).
- Ismagilov et al. [2000] R. F. Ismagilov, A. D. Stroock, P. J. A. Kenis, G. Whitesides, and H. A. Stone, Experimental and theoretical scaling laws for transverse diffusive broadening in two-phase laminar flows in microchannels, Appl. Phys. Lett. 76, 2376 (2000).
- Salmon and Ajdari [2007] J.-B. Salmon and A. Ajdari, Transverse transport of solutes between co-flowing pressure-driven streams for microfluidic studies of diffusion/reaction processes, J. Appl. Phys. 101, 074902 (2007).
- Hunt et al. [1988] J. C. Hunt, A. A. Wray, and P. Moin, Studying turbulence using numerical simulation databases, 2. Proceedings of the 1988 summer program (1988).
- Jeong and Hussain [1995] J. Jeong and F. Hussain, On the identification of a vortex, J. Fluid Mech. 285, 69 (1995).
- Park et al. [2021] S. w. Park, J. Lee, H. Yoon, and S. Shin, Microfluidic investigation of salinity-induced oil recovery in porous media during chemical flooding, Energy & Fuels 35, 4885 (2021).
- Jotkar et al. [2024] M. Jotkar, P. de Anna, M. Dentz, and L. Cueto-Felgueroso, The impact of diffusiophoresis on hydrodynamic dispersion and filtration in porous media, Journal of Fluid Mechanics 991, A8 (2024).
- Kar et al. [2016] A. Kar, M. McEldrew, R. F. Stout, B. E. Mays, A. Khair, D. Velegol, and C. A. Gorski, Self-generated electrokinetic fluid flows during pseudomorphic mineral replacement reactions, Langmuir 32, 5233 (2016).
- Plümper et al. [2017] O. Plümper, A. Botan, C. Los, Y. Liu, A. Malthe-Sørenssen, and B. Jamtveit, Fluid-driven metamorphism of the continental crust governed by nanoscale fluid flow, Nature Geoscience 10, 685 (2017).
- Newman and Tiedemann [1975] J. Newman and W. Tiedemann, Porous-electrode theory with battery applications, AIChE Journal 21, 25 (1975).
- Biesheuvel et al. [2011] P. M. Biesheuvel, Y. Fu, and M. Z. Bazant, Diffuse charge and faradaic reactions in porous electrodes, Phys. Rev. E 83, 061507 (2011).
- Ferguson and Bazant [2012] T. R. Ferguson and M. Z. Bazant, Nonequilibrium thermodynamics of porous electrodes, Journal of The Electrochemical Society 159, A1967 (2012).
- Mirzadeh et al. [2014] M. Mirzadeh, F. Gibou, and T. M. Squires, Enhanced charging kinetics of porous electrodes: Surface conduction as a short-circuit mechanism, Phys. Rev. Lett. 113, 097701 (2014).
- Alizadeh and Mani [2017] S. Alizadeh and A. Mani, Multiscale model for electrokinetic transport in networks of pores, part i: Model derivation, Langmuir 33, 6205 (2017).
- Smith and Bazant [2017] R. B. Smith and M. Z. Bazant, Multiphase porous electrode theory, Journal of The Electrochemical Society 164, E3291 (2017).
- Maggiolo et al. [2020] D. Maggiolo, F. Picano, F. Zanini, S. Carmignato, M. Guarnieri, S. Sasic, and H. Ström, Solute transport and reaction in porous electrodes at high schmidt numbers, Journal of Fluid Mechanics 896, A13 (2020).
- Henrique et al. [2024] F. Henrique, P. J. Żuk, and A. Gupta, A network model to predict ionic transport in porous materials, Proceedings of the National Academy of Sciences 121, e2401656121 (2024).