Solar Radio-Frequency Reflectivity and Localization of FRB from Solar Reflection
Abstract
The radiation of a Fast Radio Burst (FRB) reflects from the Moon and Sun. If a reflection is detected, the time interval between the direct and reflected signals constrains the source to a narrow arc on the sky. If both Lunar and Solar reflections are detected these two arcs intersect, narrowly confining the location on the sky. A previous paper calculated reflection by the Moon. Here we calculate the reflectivity of the Sun in the “flat Sun” approximation as a function of angle of incidence and frequency. The reflectivity is high at low frequencies (MHz) and grazing incidence (angles ), but exceeds 0.1 for frequencies MHz at all angles. However, the intense thermal emission of the Solar corona likely precludes detection of the Solar reflection of even MJy Galactic bursts like FRB 200428.
keywords:
radio continuum, transients: fast radio bursts, Sun: atmosphere1 Introduction
The all-sky FRB rate, above a threshold Jy-ms at 1400 MHz, is /sky-year (Cordes & Chatterjee, 2019; Petroff, Hessels & Lorimer, 2022). Despite this, until recently only distinct FRB sources had been observed (Petroff et al., 2016; Transient Name Server, ) because most radio telescopes have very limited fields of view. For example, an individual Parkes beam has a width of about sterad at this frequency; its 13 beams together cover about of the sky. CHIME/FRB (Ng et al., 2017; CHIME/FRB Collaboration, 2021a) has the comparatively large field of view of 200 square degrees and discovered 536 distinct FRB sources above a 400–800 MHz fluence threshold of about 5 Jy-ms in about a year (CHIME/FRB Collaboration, 2019b; Fonseca et al., 2020; CHIME/FRB Collaboration, 2021b). STARE2, consisting of a network (providing interferometric localization information) of choke-ring (essentially dipole) feeds (Bochenek et al., 2020a), has a field of view of about 3.6 sterad, about 30% of the sky, at the price of the very high L-band detection threshold of kJy-ms.
It has long been realized (Katz, 2014) that a “cosmological” FRB in our Galaxy would be bright enough to be observed by a single half-wave dipole antenna, and that a small network of such dipoles could localize it. STARE2 observed (Bochenek et al., 2020b) the first (at the time of writing, only) Galactic FRB 200428, even though it was less energetic than any observed extra-Galactic FRB. It was also, more fortuitously, observed by CHIME/FRB (CHIME/FRB Collaboration, 2020a). More FRB with accurate positions, as well as observations with full-sky sensitivity, could identify future Galactic FRB.
A radio telescope whose beam is approximately matched to the angular size of the Moon or the somewhat larger (Mercier & Chambe, 2015) radio size of the Sun (telescope diameter about 22 m in L-band) and staring at that object could detect reflected radiation from a FRB anywhere in the sky, with sensitivity about one order of magnitude less than that of a dipole or a single element of STARE2. Although insufficiently sensitive to detect FRB at cosmological distances, this was proposed (Katz, 2020) as a method to detect Galactic micro-FRB, and anticipated the the first such event discovered, FRB 200428.
Greater sensitivity could be provided by a larger telescope with a multi-beam feed covering the Moon or Sun. Comparing the phases of the signals from such telescopes with that from STARE2 or a similar instrument would provide two very long interferometric baselines, one equal to the projected Earth-Moon separation and one equal to the projected Earth-Sun separation, and would therefore enable precise localization on the sky. At the lower frequencies at which the Solar reflectivity is high, the resolution-matched telescope would be much larger than 22 m and its sensitivity higher, but even a 22 m telescope could have useful sensitivity.
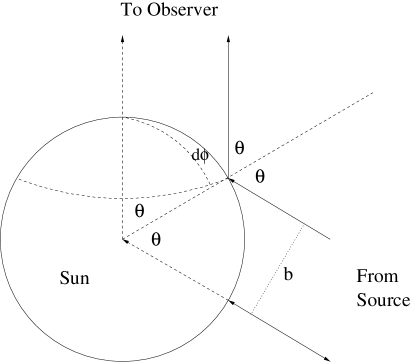
This paper calculates the reflectivity of the Sun as a function of frequency and angle of incidence using a known model of the Solar atmosphere and corona. The reflectivity must be known to evaluate the feasiblity of observing FRB reflected by the Sun. The geometry is shown in Fig. 1. Qualitative refracted ray paths were shown by Newkirk (1961) before the development of modern quantitative coronal models.
2 Reflectivity
Katz (2020) estimated that the radio-frequency reflectivity of the Sun is low at frequencies MHz, but high at lower frequencies. FRB have not generally been observed at low frequencies, in part because dispersion delays and scattering broadening are much greater at low frequencies, the former scaling (and the derivative that measures the differential arrival time across a channel ), and . However, FRB 20180916B was detected by LOFAR at frequencies as low as 120 MHz (, 2020; Pleunis et al., 2021), demonstrating that at least some FRB may be observed at these low frequencies at which the Solar reflectivity is expected to be high.
Radar measurements of the Solar reflectivity only measure it at normal incidence, but most FRB specularly reflected by the Sun to the Earth will have angles of incidence far from normal, so their rays do not penetrate the denser and more absorptive lower layers of the Solar atmosphere.
Radio telescopes operating at lower frequencies ( MHz), such as the Murchison Widefield Array (Tingay et al., 2013; Wayth et al., 2018), LOFAR (van Haarlem et al., 2013) and the planned SKA LFAA (, 2020), are generally phased arrays of dipoles. Focusing is electronic (beams are synthesized) so the telescope can effectively “stare” at the Sun without imposing a focussed visible and infrared light heat load on the receiving elements. The older Giant Metrewave Radio Telescope (Ananthakrishnan, 1995) uses parabolic dishes to focus radio waves, but its dishes are made of an open (7% filled) wire mesh that does not efficiently focus visible light because the wires are cylindrical and much thicker than the wavelength of visible light. If necessary, the receiver can be protected from focussed sunlight with a thin sheet of opaque (to visible and infrared light) plastic.
Synthesized beams have complex angular structure, rather than being simply matched to the angular size of the Sun, as would be possible for a parabolic dish at shorter wavelengths and proposed for parabolic reflectors staring at the Moon at higher frequencies. Despite this, they are sensitive to FRB scattered by the Sun; aside from radio frequency interference (generally narrowly confined in frequency), there is little radiation with the temporal characteristics of FRB in any direction, other than FRB themselves. At low frequencies the dispersion and scatter broadening characteristic of FRB are large, making them easy to discriminate from any other transients in a synthesized beam. Solar-scattered FRB would be distinguishable from unscattered FRB simultaneously observed in other lobes of the beam by different dispersion measures and by the possible earlier direct path observation of flux from the FRB by instruments like STARE2.
The reflectivity
| (1) |
where is the wave frequency and is determined by the direction to the FRB. The absorption optical depth along the ray path
| (2) |
where is the opacity, the electron density and the temperature are found from a model (Newkirk, 1967) of the Solar corona.
The path of a ray of radiation is found, in the geometrical optics limit, from the eikonal equation (Brau, 2004)
| (3) |
where is an element of path length, the refractive index
| (4) |
and the plasma frequency
| (5) |
For a specified , we integrate Eq. 3 numerically to find the path. In a “flat Sun” approximation the initial condition is the angle of incidence at an altitude far above the Solar surface, where and refraction is negligible. This is related to the impact parameter by . In general this relation is non-trivial, but in a “flat Sun” approximation , where is the Solar radius and is replaced by an altitude . This approximation is justified because a 150 MHz ray at near-normal incidence penetrates, fitting the profile of Newkirk (1967), to an altitude above the photosphere, where the scale height of the Solar atmosphere . At shallower angles of incidence the penetration is shallower, the attenuation less, and its quantitative calculation less important.
There is an extensive literature on the properties of the Solar corona (e.g. Saito, Poland & Munro (1977); Geryaev et al. (2014); McCauley, Cairns & Morgan (2018); Zhang, Wang & Kontar (2021)). Unfortunately, only a fraction of this literature is concerned with the background Solar corona (as opposed to phenomena such as coronal streamers or Type III radio bursts) and apparently none provides both the density and the temperature in the inner coronal region relevant here. Instead, we fit the smooth density profile of an isothermal quiet Solar corona
| (6) |
to the classic results of Newkirk (1967), where the molecular weight per particle is taken as , where is the proton mass, appropriate to fully ionized hydrogen and helium. A good fit is obtained for K, a value we adopt to calculate the opacity.
More detailed modern studies (Mercier & Chambe, 2015) show that even the quiet corona is both very variable and not spherically symmetric. Because the present work is only a feasibility study whose purpose is to estimate whether Solar-reflected FRB may be observable, we do not need very accurate temperature and density profiles; the variability of the corona makes any model profile only approximately applicable at any particular time and for any particular direction to a FRB. If reflected FRB are observed the quantity of interest will be the time delay between the direct and reflected signals, not their comparative amplitudes.
The opacity (Spitzer, 1962), including the effect of stimulated emission,
| (7) |
where is the density of ions with charge (allowing for multiply ionized atoms in the hotter regions), is the Boltzmann constant and is the Gaunt factor. The Gaunt factor depends only logarithmically on the parameters, except where and the group velocity is significantly less than (Spitzer, 1962), and is typically about 15 (van Hoof et al., 2014). Rays whose angles of incidence are not small do not closely approach . Eqs. 1, 2 are then used to find the reflectivity.
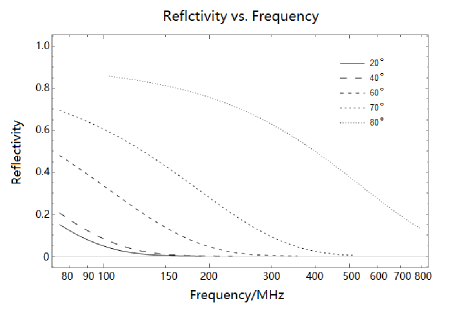
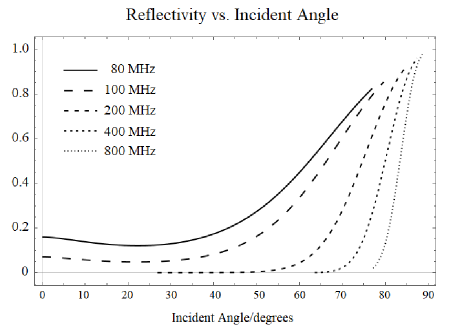
The results for several angles of incidence are shown as functions of the frequency in Fig. 2 and as functions of the angle of incidence in Fig. 3.
3 Solar Background
In addition to scattered FRB, a telescope pointed at the Sun receives Solar radiation, with which the FRB signal must compete. At the frequencies of interest, 100–200 MHz, the quiet Sun is nearly a thermal emitter at its coronal temperature with a brightness temperature K, corresponding to a flux Jy (Kraus, 1966). During periods of Solar activity may be much higher; scattered FRB cannot be detected at such times. If the Sun fills the field of view (or the resolution element of a larger telescope), the background quiet Sun antenna temperature K. A telescope staring at the Moon has K, its mean surface temperature.
A FRB (or other distant source) with direct flux produces a scattered flux at the Earth (Katz, 2020)
| (8) |
where is the reflectivity calculated in Sec. 2, is the angle of incidence, the radius of the scattering object, AU its distance and is the unscattered flux ( is nearly the same for the Moon and the Sun).
For a telescope matched to the angular size of the Sun with diameter , the antenna temperature produced by the scattered radiation
| (9) |
or
| (10) |
For a matched telescope the antenna temperature is independent of the angular size of the scatterer. At MHz such a telescope would have m, which is not feasible. For a more feasible telescope with m
| (11) |
The limiting factor in observations in the direction of the Sun is not the receiver noise temperature but the thermal emission from the corona, that may be approximated as a black body of temperature K, where the physical temperature K is multiplied by the emissivity . Integrated over a bandwidth and a time (such as the duration of a FRB) , the signal to (background) noise ratio of detection
| (12) |
In addition, scattering in the turbulent corona would temporally broaden a FRB, reducing (more than it would increase ), and . Zhang, Wang & Kontar (2021) estimate scattering widths s at 150 MHz, that would reduce by an additional factor in comparison to an unbroadened ms.
It is evident that a Galactic FRB would have to have flux for its Solar reflection to be detectable above the coronal thermal emission. Although such an event would be unprecedented, a 1 Jy FRB at would have a flux at 10 kpc, indicating that such events may occur. Events producing 0.01–0.1 Jy at “cosmological” distances would be 1–10 GJy at Galactic distances, are more frequent than the most extreme events, and their Solar reflections are likely detectable.
4 Discussion
Figs. 2 and 3 show that for frequencies MHz the reflectivity the reflectivity is substantial only for angles of incidence . The fraction of the sky with angles of incidence is , which is 0.25 for but only 0.12 for . Unlike the Moon, the Sun is a far-from-isotropic reflector at those frequencies and effectively reflects only a fraction of isotropically distributed sources, such as FRB. At lower frequencies MHz, the Sun is a good reflector, better than the Moon (Katz, 2020), at all angles of incidence.
The results of this study were disappointing because of the intense background of Solar coronal thermal emission. This is in contrast to the results of our earlier study of Lunar scattering; the Lunar surface is only a weak source of thermal emission at radio frequencies.
Acknowledgement
We thank an anonymous reviewer for several rounds of constructive criticism and for pointers to the Solar physics literature with which we were unfamiliar. In particular, we appreciate his calling to our attention the intense thermal coronal background that determines the observability of Solar reflections.
Data Availability
This theoretical study did not generate any new data.
References
- Ananthakrishnan (1995) Ananthakrishnan, S. 1995 J. Astrophys. Astr. 16, 427.
- Bochenek et al. (2020a) Bochenek, C., McKenna, D. L., Belov, K. V. et al 2020a PASP 132, 4202.
- Bochenek et al. (2020b) Bochenek, C., Ravi, V., Belof, K. V. et al. 2020b Nature 587, 59.
- Brau (2004) Brau, C. A. Modern Problems in Classical Electrodynamics 2004 Oxford U. Press, New York.
- CHIME/FRB Collaboration (2019b) CHIME/FRB Collaboration, Andersen, B. C., Bandura, K. et al. 2019b ApJ 885, L24.
- CHIME/FRB Collaboration (2020a) CHIME/FRB Collaboration, Andersen, B. C., Bandura, K. et al. 2020a Nature 587, 54.
- CHIME/FRB Collaboration (2021a) CHIME/FRB Collaboration 2021a http://chime-experiment.ca/en accessed Oct. 27, 2021.
- CHIME/FRB Collaboration (2021b) CHIME/FRB Collaboration, Amiri, M. et al. 2021b arXiv:2106.04352.
- Cordes & Chatterjee (2019) Cordes, J. M. & Chatterjee, S. 2019 ARA&A 57, 417.
- Fonseca et al. (2020) Fonseca, E., Andersen, B. C., Bhardwaj, M. et al. 2020 ApJ 891, L6.
- Geryaev et al. (2014) Geryaev, F., Slamzin, V., Vainshtein, L. & Williams, D. R. 2014 ApJ 781, 200.
- Katz (2014) Katz, J. I. 2014 Phys. Rev. D 89, 103009.
- Katz (2020) Katz, J. I. 2020 MNRAS 494, 3464 arXiv:2002.03506.
- Kraus (1966) Kraus, J. D. 1966 Radio Astronomy McGraw-Hill, New York.
- (15) de Lera Acedo, E., Pienaar, H., Ghods, N. R. et al. 2020 arXiv:2003.12744v2.
- McCauley, Cairns & Morgan (2018) McCauley, P. I., Cairns, I. H. & Morgan, J. 2018 Solar Phys. 293, 132.
- Mercier & Chambe (2015) Mercier, C. & Chambe, G. 2015 A&A 583, A101.
- Mondal, Oberoi & Mohan (2020) Mondal, S., Oberoi, D. & Mohan, A. 2020 ApJ 895, L39.
- Newkirk (1961) Newkirk, G. Jr. 1961 ApJ 133, 983.
- Newkirk (1967) Newkirk, G. Jr. 1967 ARA&A 5, 213.
- Ng et al. (2017) Ng, C., Vanderlinde, K., Paradise, A. et al. 2017 arXiv:1702.04728.
- (22) Pastor-Marazuela, I., Connor, L., van Leeuwen, J. et al. 2020 arXiv:2010.14334.
- Petroff et al. (2016) Petroff, E., Barr, E. D., Jameson, A. et al. 2016 http://www.frbcat.org; see also Transient Name Server.
- Petroff, Hessels & Lorimer (2022) Petroff, E., Hessels, J. W. T. & Lorimer, D. R. 2022 Astron. & Ap. Rev. in press arXiv:2107.10113.
- Pleunis et al. (2021) Pleunis, Z., Michilli, D., Bassa, C. G. et al. 2021 ApJ 911, L3.
- Saito, Poland & Munro (1977) Saito, K., Poland, A. I. & Munro, R. H. 1977 Solar Phys. 55, 121.
- Spitzer (1962) Spitzer, L. Physics of Fully Ionized Gases 1962 (Interscience, New York).
- Tingay et al. (2013) Tingay, S. J., Goeke, R., Bowman, J. D. et al. 2013 Pub. Astr. Soc. Australia 30, e007.
- (29) Transient Name Server 2021 https://wis-tns.weizmann.ac.il accessed October 27, 2021.
- van Haarlem et al. (2013) van Haarlem, M. P., Wise, M. W., Gunst, A. W. et al. 2013 A&A 556, A2.
- van Hoof et al. (2014) van Hoof, P. A. M., Williams, R. J. R., Volk, K. et al. 2014 MNRAS 444, 420.
- Wayth et al. (2018) Wayth, R. B., Tingay, S. J., Trott, C. M. et al. 2018 Pub. Astro. Soc. Australia 35, e033.
- Zhang, Wang & Kontar (2021) Xhang, P., Wang, C. B. & Kontar, E. P. 2021 ApJ 909, 195.