Soft Truncation: A Universal Training Technique of
Score-based Diffusion Model for High Precision Score Estimation

In the family of linear SDEs, the gradient of the log transition probability satisfies $\nabla\log{p_{0t}(\mathbf{x}_{t}|\mathbf{x}_{0})}=-\frac{\mathbf{x}_{t}-\mu(t)\mathbf{x}_{0}}{\sigma^{2}(t)}=-\frac{\mathbf{z}}{\sigma(t)}$, where $\mathbf{x}_{t}$ is given to $\mu(t)\mathbf{x}_{0}+\sigma(t)\mathbf{z}$ with $\mathbf{z}\sim\mathcal{N}(0,\mathbf{I})$. The denominator of $\sigma(t)$ converges to zero as $t\rightarrow 0$, which leads $\|\mathbf{s}_{\bm{\theta}}(\mathbf{x}_{t},t)-\nabla\log{p_{0t}(\mathbf{x}_{t}|\mathbf{x}_{0})}\|_{2}$ to diverge as $t\rightarrow 0$, as illustrated in Figure 1-(a), see Appendix A.2 for details. Therefore, the Monte-Carlo estimation of the NCSN loss is under high variance, which prevents stable training of the score network. In practice, therefore, previous research truncates the diffusion time range to $[\tau,T]$, with a positive truncation hyperparameter, $\tau=\epsilon>0$.

For the analysis for density estimation in Section 3.3, this section derives the variational bound of the log-likelihood when a diffusion model has a positive truncation because Inequality (5) holds only with zero truncation ($\tau=0$). Lemma 1 provides a generalization of Inequality (5), proved by applying the data processing inequality (Gerchinovitz et al., 2020) and the Girsanov theorem (Pavon & Wakolbinger, 1991; Vargas et al., 2021; Song et al., 2021a).

Lemma 1 is a generalization of Inequality (5) in that Inequality (6) collapses to Inequality (5) under the zero truncation: $\mathcal{L}_{NCSN}(\bm{\theta};\lambda)=\mathcal{L}(\bm{\theta};\lambda,\tau=0)$. If the time range is truncated to $[\tau,T]$ for $\tau\in[0,T]$, then from the variational inference, the log-likelihood becomes

where

with $p_{\bm{\theta}}(\mathbf{x}_{0}|\mathbf{x}_{\tau})$ being the probability distribution of $\mathbf{x}_{0}$ given $\mathbf{x}_{\tau}$ and the score estimation with $\mathbf{s}_{\bm{\theta}}$ at $\tau$. For any $\tau$, we apply Lemma 1 to the right-hand-side of Inequality (7) to obtain the variational bound of the log-likelihood as

To avoid the diverging issue introduced in Section 3.1, previous works in VPSDE (Song et al., 2021a; Vahdat et al., 2021) modify the loss by truncating the integration on $[\tau,T]$ with a fixed hyperparameter $\tau=\epsilon>0$ so that the score network does not estimate the score function on $[0,\epsilon)$. Analogously, previous works in VESDE (Song et al., 2021b; Chen et al., 2022) approximate $\sigma_{VE}^{2}(t)\approx\sigma_{min}^{2}(\frac{\sigma_{max}}{\sigma_{min}})^{2t}$ to truncate the minimum variance of the transition probability to be $\sigma_{min}^{2}$. Truncating diffusion time at $\epsilon$ in VPSDE is equivalent to truncating diffusion variance ($\sigma_{min}^{2}$) in VESDE, so these two truncations on VE/VP SDEs have the identical effect on bounding the diffusion loss. Henceforth, this paper discusses the argument of truncating diffusion time (VPSDE) and diffusion variance (VESDE) exchangeably.

Figure 1 illustrates the significance of truncation in the training of diffusion models. With the truncation of strictly positive $\epsilon=10^{-5}$, Figure 1-(a) shows that the integrand of $\mathcal{L}(\bm{\theta};g^{2},\tau)$ in the Bits-Per-Dimension (BPD) scale is still extremely imbalanced. It turns out that such extreme imbalance appears to be a universal phenomenon in training a diffusion model, and this phenomenon lasts from the beginning to the end of training.

Figure 1-(b) with the green line presents the variational bound of the log-likelihood (right-hand-side of Inequality (8)) on the $y$-axis, and it indicates that the variational bound is sharply decreasing near the small diffusion time. Therefore, if $\epsilon$ is insufficiently small, the variational bound is not tight to the log-likelihood, and a diffusion model fails at MLE training. In addition, Figure 2 indicates that insufficiently small $\epsilon$ (or $\sigma_{min}$) would also harm the microscopic sample quality. From these observations, $\epsilon$ becomes a significant hyperparameter that needs to be selected carefully.

Figure 1-(c) reports test performances on density estimation. Figure 1-(c) illustrates that both Negative Evidence Lower Bound (NELBO) and NLL monotonically decrease by lowering $\epsilon$ because NELBO is largely contributed by small diffusion time at test time as well as training time. Therefore, it could be a common strategy to reduce $\epsilon$ as much as possible to reduce test NELBO/NLL.

On the contrary, there is a counter effect on FID for $\epsilon$. Table 1, trained on CIFAR-10 (Krizhevsky et al., 2009) with NCSN++ (Song et al., 2021b), presents that FID is worsened as we take smaller hyperparameter $\sigma_{min}$ for the training. It is the range of small diffusion time that significantly contributes to the variational bound in the blue line of Figure 1-(b), so the score network with a small truncation hyperparameter, $\sigma_{min}$ or $\epsilon$, remains unoptimized on large diffusion time. In the lens of Figure 2, therefore, the inconsistent result of Table 1 is attributed to the inaccurate score on large diffusion time.

We design an experiment to validate the above argument in Table 2. This experiment utilizes two types of score networks: 1) three alternative networks (As) with diverse $\sigma_{min}\in\{10^{-3},10^{-4},10^{-5}\}$ trained in Table 1 experiment; 2) a network (B) with $\sigma_{min}=10^{-5}$ (the last row of Table 1). With these score networks, we denoise the noises by either one of the first-typed As from $\sigma_{max}$ to a common and fixed $\sigma_{tr}(=1)$, and we use B to further denoise from $\sigma_{tr}$ to $\sigma_{min}=10^{-5}$. This further denoising step with model B enables us to compare the score accuracy on large diffusion time for models with diverse truncation hyperparameters in a fair resolution setting. Table 2 presents that the model with $\sigma_{min}=10^{-3}$ has the best FID, implying that the training with too small truncation would harm the sample fidelity.

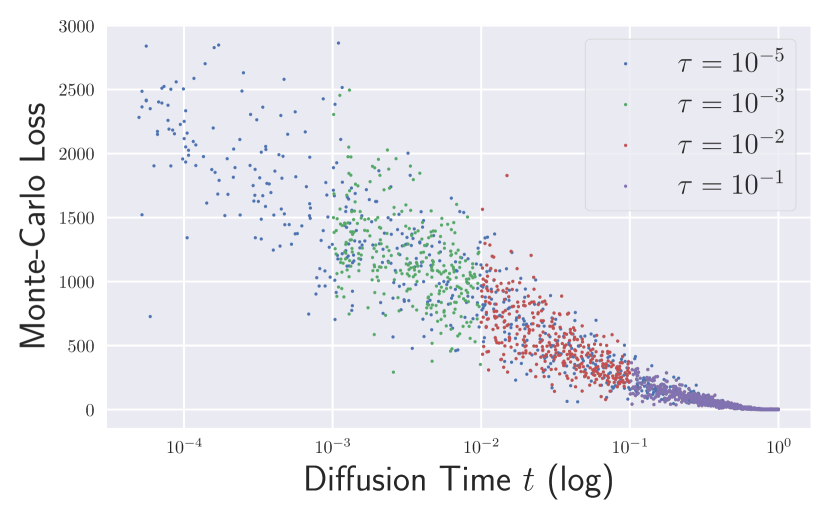
Specifically, Figure 4 shows the Euclidean norm of $g^{2}(t)\mathbf{s}_{\bm{\theta}}(\mathbf{x}_{t},t)$, where each dot represents for a Monte-Carlo sample from $p_{t}(\mathbf{x}_{t})$. Here, $g^{2}(t)\mathbf{s}_{\bm{\theta}}(\mathbf{x}_{t},t)$ is in the reverse drift term of the generative process, $\mathop{}\!\mathrm{d}\mathbf{x}_{t}^{\bm{\theta}}=[\mathbf{f}(\mathbf{x}_{t}^{\bm{\theta}},t)-g^{2}(t)\mathbf{s}_{\bm{\theta}}(\mathbf{x}_{t}^{\bm{\theta}},t)]\mathop{}\!\mathrm{d}\bar{t}+g(t)\mathop{}\!\mathrm{d}\mathbf{\bar{w}}_{t}$. Figure 4 illustrates that it is the large diffusion time that dominates the sampling process. Therefore, a precise score network on large diffusion time is particularly important in sample generation.

The imprecise score mainly affects the global sample context, as the denoising on small diffusion time only crafts the image in its microscopic details, illustrated in Figures 3 and 5. Figure 3 shows how the global fidelity is damaged: a man synthesized in the second row has unrealistic curly hair on his forehead, constructed on the large diffusion time. Figure 5 deepens the importance of learning a good score estimation on large diffusion time. It shows the regenerated samples by solving the generative process time reversely, starting from $\mathbf{x}_{\tau}$ (Meng et al., 2021).

In this section, we fix a truncation hyperparameter to be $\tau=\epsilon$. For every batch $\{\mathbf{x}_{0}^{(b)}\}_{b=1}^{B}$, the Monte-Carlo estimation of the variational bound in Inequality (6) is $\mathcal{L}(\bm{\theta};g^{2},\epsilon)\approx\mathcal{\hat{L}}(\bm{\theta};g^{2},\epsilon)=\frac{1}{2B}\sum_{b=1}^{B}g^{2}(t^{(b)})\|\mathbf{s}_{\bm{\theta}}(\mathbf{x}_{t^{(b)}},t^{(b)})-\nabla\log{p_{0t^{(b)}}(\mathbf{x}_{t^{(b)}}|\mathbf{x}_{0})}\|_{2}^{2}$, up to a constant irrelevant to $\bm{\theta}$, where $\mathbf{x}_{t^{(b)}}=\mu(t^{(b)})\mathbf{x}_{0}+\sigma(t^{(b)})\bm{\epsilon}^{(b)}$ with $\{t^{(b)}\}_{b=1}^{B}$ and $\{\bm{\epsilon}^{(b)}\}_{b=1}^{B}$ be the corresponding Monte-Carlo samples from $t^{(b)}\sim[\epsilon,T]$ and $\bm{\epsilon}^{(b)}\sim\mathcal{N}(0,\mathbf{I})$, respectively. Note that this Monte-Carlo estimation is tractably computed from the analytic form of the transition probability as $\nabla\log{p_{0t^{(b)}}(\mathbf{x}_{t^{(b)}}|\mathbf{x}_{0})}=\frac{\bm{\epsilon}^{(b)}}{\sigma(t^{(b)})}$ under linear SDEs.

Previous works (Song et al., 2021a; Huang et al., 2021) apply the importance sampling with the importance distribution of $p_{iw}(t)=\frac{g^{2}(t)/\sigma^{2}(t)}{Z_{\epsilon}}1_{[\epsilon,T]}(t)$, where $Z_{\epsilon}=\int_{\epsilon}^{T}\frac{g^{2}(t)}{\sigma^{2}(t)}\mathop{}\!\mathrm{d}t$. It is well known (Goodfellow et al., 2016) that the Monte-Carlo variance of $\hat{\mathcal{L}}$ is minimum if the importance distribution is $p_{iw}^{*}(t)\propto g^{2}(t)L(t)$ with $L(t)=\mathbb{E}_{\mathbf{x}_{0},\mathbf{x}_{t}}[\|\mathbf{s}_{\bm{\theta}}(\mathbf{x}_{t},t)-\nabla\log{p_{0t}(\mathbf{x}_{t}|\mathbf{x}_{0})}\|_{2}^{2}]$, but sampling of Monte-Carlo diffusion time from $p_{iw}^{*}(t)$ at every training iteration would incur $2\times$ slower training speed, at least, because the importance sampling requires the score evaluation. Therefore, previous research approximates $L(t)$ by $\hat{L}(t)=\mathbb{E}_{\mathbf{x}_{0},\mathbf{x}_{t}}[\|\nabla\log{p_{0t}(\mathbf{x}_{t}|\mathbf{x}_{0})}\|_{2}^{2}]\propto 1/\sigma^{2}(t)$, and $p_{iw}(t)$ becomes the approximate importance weight. This approximation, at the expense of bias, is cheap because the closed-form of the inverse Cumulative Distribution Function (CDF) is known. Unless we train the variance directly as in Kingma et al. (2021), we believe $p_{iw}(t)$ is the maximally efficient sampler as long as the training speed matters. The importance weighted Monte-Carlo estimation becomes

where $\{t_{iw}^{(b)}\}_{b=1}^{B}$ is the Monte-Carlo sample from the importance distribution, i.e., $t_{iw}^{(b)}\sim p_{iw}(t)\propto\frac{g^{2}(t)}{\sigma^{2}(t)}$.

The importance sampling is advantageous in both NLL and FID (Song et al., 2021a) over the uniform sampling, as the importance sampling significantly reduces the estimation variance. Figure 6-(a) illustrates the sample-by-sample loss, and the importance sampling significantly mitigates the loss scale by diffusion time compared to the scale in Figure 1-(a). However, the importance distribution satisfies $p_{iw}(t)\rightarrow\infty$ as $t\rightarrow 0$ in Figure 6-(c) blue line, and most of the importance weighted Monte-Carlo time is concentrated at $t\approx\epsilon$ in Figure 7. Hence, the use of the importance sampling has a trade-off between the reduced variance (Figure 6-(a)) versus the over-sampled diffusion time near $t\approx\epsilon$ (Figure 7). Regardless of whether to use the importance sampling or not, therefore, the inaccurate score estimation on large diffusion time appears sampling-strategic-independently, and solving this pre-matured score estimation becomes a nontrivial task.

Instead of the likelihood weighting, previous works (Ho et al., 2020; Nichol & Dhariwal, 2021; Dhariwal & Nichol, 2021) train the denoising score loss with the variance weighting, $\lambda(t)=\sigma^{2}(t)$. With this weighting, the importance distribution becomes the uniform distribution, $p_{iw}(t)=\frac{\lambda(t)}{\sigma^{2}(t)}\equiv 1$, so it significantly alleviates the trade-off of using the likelihood weighting. However, the variance weighting favors FID at the sacrifice in NLL because the loss is no longer the variational bound of the log-likelihood. In contrast, the training with the likelihood weighting is leaning towards NLL than FID, so Soft Truncation is for the balanced NLL and FID, using the likelihood weighting.

Soft Truncation releases the truncation hyperparameter from a static variable to a random variable with a probability distribution of $\mathbb{P}(\tau)$. In every mini-batch update, Soft Truncation optimizes the diffusion model with $\mathcal{\hat{L}}_{iw}(\bm{\theta};g^{2},\tau)$ in Eq. (9) for a sampled $\tau\sim\mathbb{P}(\tau)$. In other words, for every batch $\{\mathbf{x}_{0}^{(b)}\}_{b=1}^{B}$, Soft Truncation optimizes the Monte-Carlo loss

with $\{t_{iw}^{(b)}\}_{b=1}^{B}$ sampled from the importance distribution of $p_{iw,\tau}(t)=\frac{g^{2}(t)/\sigma^{2}(t)}{Z_{\tau}}1_{[\tau,T]}(t)$, where $Z_{\tau}:=\int_{\tau}^{T}\frac{g^{2}(t)}{\sigma^{2}(t)}\mathop{}\!\mathrm{d}t$.

Soft Truncation resolves the oversampling issue of diffusion time near $t\approx\epsilon$, meaning that Monte-Carlo time is not concentrated on $\epsilon$ anymore. Figure 7 illustrates the quantiles of importance weighted Monte-Carlo time with Soft Truncation under $\tau=\epsilon$ and $\tau=0.1$. The score network is trained more equally on diffusion time when $\tau=0.1$, and as a consequence, the loss imbalance issue in each training step is also alleviated as in Figure 6-(b) with purple dots. This limited range of $[\tau,T]$ provides a chance to learn a score network more balanced on diffusion time. As $\tau$ is softened, such truncation level will vary by mini-batch updates: see the loss scales change by blue, green, red, and purple dots according to various $\tau$s in Figure 6-(b). Eventually, the softened $\tau$ will provide a fair chance to learn the score network from small as well as large diffusion time.

In the original diffusion model, the loss estimation, $\mathcal{\hat{L}}(\bm{\theta};g^{2},\epsilon)$, is just a batch-wise approximation of a population loss, $\mathcal{L}(\bm{\theta};g^{2},\epsilon)$. However, the target population loss of Soft Truncation, $\mathcal{L}(\bm{\theta};g^{2},\tau)$, is depending on a random variable $\tau$, so the target population loss itself becomes a random variable. Therefore, we derive the expected Soft Truncation loss to reveal the connection to the original diffusion model:

up to a constant, where $g^{2}_{\mathbb{P}}(t)=\big{(}\int_{0}^{t}\mathbb{P}(\tau)\mathop{}\!\mathrm{d}\tau\big{)}g^{2}(t)$, by exchanging the orders of the integrations. Therefore, we conclude that Soft Truncation reduces to a diffusion model with a general weight of $g_{\mathbb{P}}^{2}(t)$, see Appendix A.3:

As explained in Section 4.3, Soft Truncation is a diffusion model with a general weight, in the expected sense. Reversely, this section analyzes a diffusion model with a general weight in view of Soft Truncation. Suppose we have a general weight $\lambda$. Theorem 1 implies that this general weighted diffusion loss, $\mathcal{L}(\bm{\theta};\lambda,\epsilon)$, is the variational bound of the perturbed KL divergence expected by $\mathbb{P}_{\lambda}(\tau)$. Theorem 1 collapses to Lemma 1 if $\lambda(t)=cg^{2}(t)$ for any $c>0$¹¹1If $\lambda(t)=cg^{2}(t)$, the probability satisfies $\mathbb{P}([a,b])=1_{[a,b]}(\epsilon)$, which is a probability distribution of one mass at $\epsilon$.. See Appendix B for the detailed statement and proof.

The meaning of Soft Truncation becomes clearer in view of Theorem 1. Instead of training the general weighted diffusion loss, $\mathcal{L}(\bm{\theta};\lambda,\epsilon)$, we optimize the truncated variational bound, $\mathcal{L}(\bm{\theta};g^{2},\tau)$. This truncated loss upper bounds the perturbed KL divergence, $D_{KL}(p_{\tau}\|p_{\tau}^{\bm{\theta}})$ by Lemma 1, and Figure 1-(c) indicates that the Inequality (6) is nearly tight. Therefore, Soft Truncation could be interpreted as the Maximum Perturbed Likelihood Estimation (MPLE), where the perturbation level is a random variable. Soft Truncation is not MLE training because the Inequality 8 is not tight as demonstrated in Figure 1-(b) unless $\tau$ is sufficiently small.

Old wisdom is to minimize the loss variance if available for stable training. However, some optimization methods in the deep learning era (e.g., stochastic gradient descent) deliberately add noises to a loss function that eventually helps escape from a local optimum. Soft Truncation is categorized in such optimization methods that inflate the loss variance by intentionally imposing auxiliary randomness on loss estimation. This randomness is represented by the outmost expectation of $\mathbb{E}_{\mathbb{P}_{\lambda}(\tau)}$, which controls the diffusion time range batch-wisely. Additionally, the loss with a sampled $\tau$ is the proxy of the perturbed KL divergence by $\tau$, so the auxiliary randomness on loss estimation is theoretically tamed, meaning that it is not a random perturbation.

We parametrize the probability distribution of $\tau$ by

where $Z_{k}=\int_{\epsilon}^{T}\frac{1}{\tau^{k}}\mathop{}\!\mathrm{d}\tau$ with sufficiently small enough truncation hyperparameter. Note that it is still beneficial to remain $\epsilon$ strictly positive because a batch update with $\tau\approx 0<\epsilon$ would drift the score network away from the optimal point. Figure 6-(c) illustrates the importance distribution of $\lambda_{\mathbb{P}_{k}}$ for varying $k$. From the definition of Eq. (11), $\mathbb{P}_{k}(\tau)\rightarrow\delta_{\epsilon}(\tau)$ as $k\rightarrow\infty$, and this limiting delta distribution corresponds to the original diffusion model with the likelihood weighting. Figure 6-(c) shows that the importance distribution of $\mathbb{P}_{k}$ with finite $k$ interpolates the likelihood weighting and the variance weighting.

With the current simple form, we experimentally find that the sweet spot is $k\approx 1.0$ in VPSDE and $k=2.0$ in VESDE with the emphasis on the sample quality. For VPSDE, the importance distribution in Figure 6-(c) is nearly equal to that of the variance weighting if $k\approx 1.0$, so Soft Truncation with $k\approx 1.0$ improves the sample fidelity, while maintaining low NLL. On the other hand, if $k$ is too small, no $\tau$ will be sampled near $\epsilon$, so it hurts both sample generation and density estimation. We leave further study on searching for the optimal distribution of $\tau$ as future work.