Soft-Minimum and Soft-Maximum Barrier Functions for
Safety with Actuation Constraints
Abstract
This paper presents two new control approaches for guaranteed safety (remaining in a safe set) subject to actuator constraints (the control is in a convex polytope). The control signals are computed using real-time optimization, including linear and quadratic programs subject to affine constraints, which are shown to be feasible. The first control method relies on a soft-minimum barrier function that is constructed using a finite-time-horizon prediction of the system trajectories under a known backup control. The main result shows that the control is continuous and satisfies the actuator constraints, and a subset of the safe set is forward invariant under the control. Next, we extend this method to allow from multiple backup controls. This second approach relies on a combined soft-maximum/soft-minimum barrier function, and it has properties similar to the first. We demonstrate these controls on numerical simulations of an inverted pendulum and a nonholonomic ground robot.
keywords:
Control of constrained systems, Optimization-based controller synthesis, Nonlinear predictive control, Safety,
1 Introduction
Robots and autonomous systems are often required to respect safety-critical constraints while achieving a specified task [1, 2]. Safety constraints can be achieved by determining a control that makes a designated safe set forward invariant with respect to the closed-loop dynamics [3], that is, designing a control for which the state is guaranteed to remain in . Approaches that address safety using set invariance include reachability methods [4, 5], model predictive control [6, 7, 8], and barrier function (BF) methods (e.g., [9, 10, 11, 12, 13, 14, 15]).
Barrier functions are employed in a variety of ways. For example, they are used for Lyapunov-like control design and analysis [9, 10, 11, 12]. As another example, the control barrier function (CBF) approaches in [13, 14, 15] compute the control signal using real-time optimization. These optimization-based methods can be modular in that they often combine a nominal performance controller (which may not attempt to respect safety) with a safety filter that performs a real-time optimization using CBF constraints to generate a control that guarantees safety. This real-time optimization is often formulated as an instantaneous minimum-intervention problem, that is, the problem of finding a control at the current time instant that is as close as possible to the nominal performance control while satisfying the CBF safety constraints.
Barrier-function methods typically rely on the assumption that is control forward invariant (i.e., there exists a control that makes forward invariant). For systems without actuator constraints (i.e., input constraints), control forward invariance is satisfied under relatively minor structural assumptions (e.g., constant relative degree). In this case, the control can be generated from a quadratic program that employs feasible CBF constraints (e.g., [13, 14, 15]). In contrast, actuator constraints can prevent from being control forward invariant. In this case, it may be possible to compute a control forward invariant subset of using methods such as Minkowski operations [16], sum-of-squares [17, 18], approximate solutions of a Hamilton-Jacobi partial differential equation [19], or sampling [20]. However, these methods may not scale to high-dimensional systems.
Another approach to address safety with actuator constraints is to use a prediction of the system trajectories into the future to obtain a control forward invariant subset of . For example, [21] uses the trajectory under a backup control. However, [21] uses an infinite time horizon prediction, which limits applicability. In contrast, [22, 23] determine a control forward invariant subset of from a BF constructed from a finite-horizon prediction under a backup control. This BF uses the minimum function, which is not continuously differentiable and cannot be used directly to form a BF constraint for real-time optimization. Thus, [22, 23] replace the original BF by a finite number of continuously differentiable BFs. However, the number of substitute BFs (and thus optimization constraints) increases as the prediction horizon increases, and these multiple BF constraints can be conservative. It is also worth noting that [22, 23] do not guarantee feasibility of the optimization with these multiple BF constraints. Related approaches are in [24, 25, 26].
This paper makes several new contributions. First, we present a soft-minimum BF that uses a finite-horizon prediction of the system trajectory under a backup control. We show that this BF describes a control forward invariant (subject to actuator constraints) subset of . Since the soft-minimum BF is continuously differentiable, it can be used to form a single non-conservative BF constraint regardless of the prediction horizon. The soft-minimum BF facilitates the paper’s second contribution, namely, a real-time optimization-based control that guarantees safety with actuator constraints. Notably, the optimization required to compute the control is convex with guaranteed feasibility. Next, we extend this approach to allow from multiple backup controls by using a novel soft-maximum/soft-minimum BF. In comparison to the soft-minimum BF, the soft-maximum/soft-minimum BF (with multiple backup controls) can yield a larger control forward invariant subset of . Some preliminary results on the soft-minimum BF appear in [27].
2 Notation
Let , and consider defined by
which are the soft minimum and soft minimum. The next result relates soft minimum and soft maximum to the minimum and maximum.
Proposition 1.
Let . Then,
and
Proposition 1 shows that as , and converge to the minimum and maximum. Thus, and are smooth approximations of the minimum and maximum. Note that if , then the soft minimum is strictly less than the minimum.
For a continuously differentiable function , let be defined by . The Lie derivatives of along the vector field of is . Let , , denote the interior, boundary, and closure of the set . Let . If each element of is less than or equal to the corresponding element of , then we write .
3 Problem Formulation
Consider
| (1) |
where and are continuously differentiable on , is the state, is the initial condition, and is the control. Let and , and define
| (2) |
which we assume is bounded and not empty. We call an admissible control if for all , .
Let be continuously differentiable, and define the safe set
| (3) |
Note that is not assumed to be control forward invariant with respect to (1) where is an admissible control. In other words, there may not exist an admissible control such that if , then for all , .
Next, consider the nominal desired control designed to satisfy performance specifications, which can be independent of and potentially conflict with safety. Thus, is not necessarily forward invariant with respect to (1) where . We also note that is not necessarily an admissible control.
The objective is to design a full-state feedback control such that for all initial conditions in a subset of , the following hold:
-
(O1)
For all , .
-
(O2)
For all , .
-
(O3)
For all , is small.
4 Barrier Functions Using the Trajectory Under a Backup Control
Consider a continuously differentiable backup control . Let be continuously differentiable, and define the backup safe set
| (4) |
We assume and make the following assumption.
Assumption 1.
If and , then for all , .
Assumption 1 states that is forward invariant with respect to (1) where . However, may be small relative to .
Consider defined by
| (5) |
which is the right-hand side of the closed-loop dynamics (1) with . Next, let satisfy
| (6) |
which implies that is the solution to (1) at time with and initial condition .
Let be a time horizon, and consider defined by
| (7) |
and define
| (8) |
For all , the solution (6) under does not leave and reaches by time . The next result relates to and . The result is similar to [22, Proposition 6].
Proposition 2.
Assume that satisfies Assumption 1. Then, .
Let . Assumption 1 implies for all , , which implies for all , and . Thus, it follows from (7) and (8) that , which implies . Therefore, .
Let , and (7) implies . Thus, , which implies .
The next result shows that is forward invariant with respect to (1) where . In fact, this result shows that the state converges to by time .
Proposition 3.
To prove (a), since , it follows from (7) and (8) that , which implies . Since , Assumption 1 implies for all , , which confirms (a).
To prove (b), let and consider 2 cases: , and . First, let , and it follows from (a) that for all , . Since, in addition, for all , , it follows from (7) and (8) that , which implies . Next, let . Since , it follows from (7) and (8) that for all , , which implies for all , . Since, in addition, for all , , it follows from from (7) and (8) that , which implies .
Proposition 3 implies that for all , the backup control satisfies (O1) and (O2). However, does not address (O3). One approach to address (O3) is to use as a BF in a minimum intervention quadratic program. However, is not continuously differentiable. Thus, it cannot be used directly to construct a BF constraint because the constraint and associated control would not be well-defined at the locations in the state space where is not differentiable. This issue is addressed in [22] by using multiple BFs—one for each argument of the minimum in (7). However, (7) has infinitely many arguments because the minimum is over . Thus, [22] uses a sampling of times. Specifically, let be a positive integer, and define and . Then, consider defined by
| (9) |
and define
| (10) |
The next result relates to and .
Proposition 4.
.
Let , and (9) implies . Thus, , which implies .
The next result shows that for all , the backup control causes the state to remain in at the sample times and converge to by time .
Proposition 5.
To prove (a), since , it follows from (9) and (10) that , which implies . Since , Assumption 1 implies for all , , which confirms (a).
To prove (b), let . Since , it follows from (9) and (10) that for all , , which implies for all , . Since, in addition, for all , , it follows from (9) and (10) that , which implies .
Proposition 5 does not provide any information about the state in between the sample times. Thus, Proposition 5 does not imply that is forward invariant with respect to (1) where . However, we can adopt an approach similar to [22] to determine a superlevel set of such that for all initial conditions in that superlevel set, keeps the state in for all time. To define this superlevel set, let be the Lipschitz constant of with respect to the two norm, and define , which is finite if is bounded. Define the superlevel set
| (11) |
Proposition 6.
.
Together, Propositions 3 and 6 imply that for all , the backup control keeps the state in for all time. However, does not address (O3).
Since is not continuously differentiable, [22] addresses (O3) using a minimum intervention quadratic program with BFs—one for each of the arguments in (9). However, this approach has 3 drawbacks. First, the number of BFs increases as the time horizon increases or the sample time decreases (i.e., as increases). Thus, the number of affine constraints and computational complexity increases as increases. Second, although imposing an affine constraint for each of the BFs is sufficient to ensure that remains positive, it is not necessary. These affine constraints are conservative and can limit the set of feasible solutions for the control. Third, [22] does not guarantee feasibility of the optimization used to obtain the control.
The next section uses a soft-minimum BF to approximate and presents a control synthesis approach with guaranteed feasibility and where the number of affine constraints is fixed (i.e., independent of ).
5 Safety-Critical Control Using Soft-Minimum Barrier Function with One Backup Control
This section presents a continuous control that guarantees safety subject to the constraint that the control is admissible (i.e., in ). The control is computed using a minimum intervention quadratic program with a soft-minimum BF constraint. The control also relies on a linear program to provide a feasibility metric, that is, a measure of how close the quadratic program is to becoming infeasible. Then, the control continuously transitions to the backup control if the feasibility metric or the soft-minimum BF are less than user-defined thresholds.
Let , and consider defined by
| (12) |
which is continuously differentiable. Define
| (13) |
Proposition 1 implies that for all , . Thus, . Proposition 1 also implies that for sufficiently large , is arbitrarily close to . Thus, is a smooth approximation of . However, if is large, then is large at points where is not differentiable. Thus, selecting is a trade-off between the conservativeness of and the size of .
Next, let and . Consider defined by
| (14) |
where exists because is not empty. Define
| (15) |
Proposition 7.
For all , there exists such that .
Let and consider defined by
| (16) |
and define
| (17) |
Note that . For all , define
| (18a) | |||
| subject to | |||
| (18b) | |||
Since , Proposition 7 implies that for all , the quadratic program (18) has a solution.
Consider a continuous function such that for all , ; for all , ; and is strictly increasing on . The following example provides one possible choice for .
Example 1.
Consider given by
Finally, define the control
| (19) |
Since is continuously differentiable, the quadratic program (18) requires only the single affine constraint (18b) as opposed to the constraints used in [22]. Since (18) has only one affine constraint, we can define the feasible set as the zero-superlevel set of , which is the solution to the linear program (14). Since there is only one affine constraint, we can use the homotopy in (19) to continuously transition from to as leaves .
Remark 1.
The control (12)–(19) is designed for the case where the relative degree of (1) and (12) is one (i.e., ). However, this control can be applied independent of the relative degree. If , then it follows from (14)–(18) that for all , the solution to the quadratic program (18) is the unconstrained minimizer, which is the desired control if . In this case, (19) implies that is determined from a continuous blending of and based on (i.e., feasibility of (18) and safety). We also note that the control (12)–(19) can be generalized to address the case where the relative degree exceeds one. In this case, the linear program (14) for feasibility and the quadratic program constraint (18b) are replaced by the appropriate higher-relative-degree Lie derivative expressions (see [28, 29, 30]).
The next theorem is the main result on the control (12)–(19) that uses the soft-minimum BF approach.
Theorem 1.
To prove (a), we first show that is continuous on . Define and . Let , and Proposition 7 implies is not empty. Since, in addition, is strictly convex, is convex, and (18b) with is convex, it follows that is unique. Next, since for all , is bounded, it follows that is bounded. Thus, is compact. Next, since is a convex polytope and (18b) is affine in , it follows from [31, Remark 5.5] that is continuous at . Finally, since exists and is unique, is compact, is continuous at , and is continuous on , it follows from [32, Corollary 8.1] that is continuous at . Thus, is continuous on .
Define , and note that (14) implies . Since is continuous on and is compact, it follows from [32, Theorem 7] that is continuous on . Thus, (17) implies is continuous on .
For all , define . Since , , and are continuous on , and is continuous on , it follows that is continuous on . Next, let . Since is bounded, it follows from (16) and (17) that . Since is continuous on , is continuous on , and for all , , it follows from (19) that is continuous on .
To prove (b), let . Since , it follows from (2) that and . Since, in addition, , it follows that
| (20) | |||
| (21) |
Next, summing (20) and (21) and using (19) yields , which implies .
To prove (c), assume for contradiction that for all , . Since, in addition, , it follows from (10) that for all , . Thus, Proposition 1 implies for all , , which combined with (16) and (17) implies . Next, (19) implies the for all , . Hence, Proposition 5 implies , which is a contradiction.
To prove (d), let , and (16) and (17) impliy . Since, in addition, Proposition 1 implies , it follows that . Thus, (11) implies , which implies .
Let , and assume for contradiction that . Since, in addition, and , it follows that there exists such that and for all , . Thus, (19) implies for all , . Since, in addition, , Proposition 3 implies , which is a contradiction.
Parts (a) and (b) of Theorem 1 guarantee that the control is continuous and admissible. Part (d) states that if , then is forward invariant under the control and is in for all time. Part (c) shows that for any choice of , is in the safe set at sample times .
The control (12)–(19) relies on the Lie derivatives in (14) and (18b). To calculate and , note that
| (22) |
where is defined by . Differentiating (6) with respect to yields
| (23) |
Next, differentiating (23) with respect to yields
| (24) |
Note that for all , is the solution to (24), where the initial condition is . Thus, for all , and can be calculated from (5), where is the solution to (1) under on the interval with , and is the solution to (24) on the interval with . In practice, these solutions can be computed numerically at the time instants where the control algorithm (12)–(19) is executed (i.e., the time instants where the control is updated). Algorithm 1 summarizes the implementation of (12)–(19), where is the time increment for a zero-order-hold on the control.
The control (12)–(19) involves the user-selected parameters . Recall that large improves the soft-minimum approximation of the minimum but can also result in large , which can tend to cause to be large. The quadratic program (18) shows that small results in more conservative behavior; specifically, deviates more from the desired control in order to keep the state trajectory farther away from . The homotopy (19) and definition (16) of show that large or cause the control to deviate more from the optimal control to the backup control if either the feasibility metric or the barrier function are small.
Example 2.
Consider the inverted pendulum modeled by (1), where
and is the angle from the inverted equilibrium. Let and . The safe set is given by (3), where , is the -norm, and . The backup control is , where . The backup safe set is given by (4), where Lyapunov’s direct method can be used to confirm that Assumption 1 is satisfied. The desired control is , which implies that the objective is to stay in using instantaneously minimum control effort. We implement the control (12)–(19) using , , , and given by Example 1. We let s, and s, which implies that the time horizon is s.
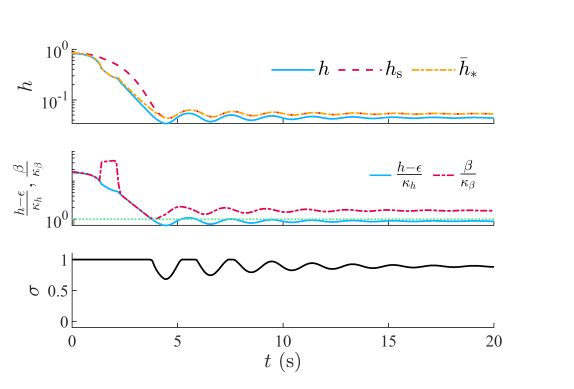
Figure 1 shows , , , and . Note that . Figure 1 also provides the closed-loop trajectories for 8 initial conditions, specifically, , where . We let for the initial conditions with , and we let for , which are the reflection of the first 4 across the origin. For the cases with , Theorem 1 implies that is forward invariant under the control (19). The trajectories with are more conservative than those with .
Figure 2 and 3 provide time histories for the case where and . Figure 2 shows , , , , , and . The first row of Figure 3 shows that , , and are nonnegative for all time. The second row of Figure 3 shows and . Note that is positive for all time, which implies that (18) is feasible at all points along the closed-loop trajectory. Since is positive for all time but is less than in steady state, it follows from (19) that in steady state is a blend of and .


Example 3.
Consider the nonholonomic ground robot modeled by (1), where
and is the robot’s position in an orthogonal coordinate system, is the speed, and is direction of the velocity vector (i.e., the angle from to ). Let , , and
Define , and , where , and note that is the position of a point-of-interest on the robot. Consider the map shown in Figure 4, which has 6 obstacles and a wall. For , the area outside the th obstacle is modeled as the zero-superlevel set of
where specify the location and dimensions of the th obstacle. The area inside the wall is modeled as the zero-superlevel set of
where specify the dimension of the space inside the wall. The safe set is given by (3), where . The safe set projected into the – plane is shown in Figure 4. Note that is also bounded in speed , specifically, for all , .
The backup control is , where . The backup safe set is given by (4), where . Lyapunov’s direct method can be used to confirm that Assumption 1 is satisfied. Figure 4 shows the projection of into the – plane.
Let be the goal location, that is, the desired location for . Next, the desired control is , where
where . Note that the desired control is designed using a process similar to [33, pp. 30–31].
Figure 4 shows the closed-loop trajectories for with 3 different goal locations , , and . In all cases, the robot position converges to the goal location while satisfying safety and the actuator constraints.
Figures 5 and 6 show the trajectories of the relevant signals for the case where . Figure 6 shows that is positive for all time, which implies that (18) is feasible at all points along the closed-loop trajectory. Since is positive for all time and is greater than for , it follows from (19) that in steady state is equal to (as shown in Figure 2).



6 Soft-Maximum/Soft-Minimum Barrier Function with Multiple Backup Controls
This section extends the method from the previous section to allow for multiple backup controls by adopting a soft-maximum/soft-minimum BF. The following example illustrates the limitations of a single backup control and motivates the potential benefit of considering multiple backup controls.
Example 4.
We revisit the inverted pendulum from Example 2, where the safe set is given by (3), where . We let , and . Everything else is the same as in Example 2.
Figure 7 shows , and . We note that increasing does not change . In other words, was selected to yield the largest possible under the backup control and safe set considered. Thus, with only one backup control, cannot always be expanded by increasing .

This section presents a method to expand by using multiple backup controls. Let be a positive integer, and consider the continuously differentiable backup controls . Let be continuously differentiable, and define the backup safe set
| (25) |
We assume and make the following assumption.
Assumption 2.
For all , if and , then for all , .
Assumption 2 states that is forward invariant with respect to (1) where . This is equivalent to Assumption 1 for each backup control.
Let be defined by (5), where and are replaced by and . Similarly, let be defined by (6), where and are replaced by and . Thus, is the solution to (1) at time with and initial condition .
Let , and consider defined by
and define and . The next result examines forward invariance of and is a consequence of Proposition 3.
Proposition 8.
Next, let be a positive integer, and define and . Then, consider defined by
| (26) | ||||
| (27) |
and define
| (28) | ||||
| (29) |
The next result is a consequence of Proposition 5.
Proposition 9.
Part (b) of Proposition 9 does not provide information regarding the state in between sample times. Thus, we adopt an approach similar to that in Section 5. Specifically, define the superlevel sets
| (30) | ||||
| (31) |
where is the Lipschitz constant of with respect to the two norm and . The next result is analogous to Proposition 6, and its proof is similar.
Proposition 10.
The following statements hold:
-
(a)
For , .
-
(b)
.
Next, we use the soft minimum and soft maximum to define continuously differentiable approximations to and . Let , and consider defined by
| (32) | ||||
| (33) |
and define
| (34) |
Proposition 1 implies that .
Let , , and . Furthermore, let , , , , and be given by (14)–(18) where is given by (33) instead of (12).
We cannot use the control (19) because there are different backup controls rather than just one. Next, define
| (35) |
and for all , define
| (36) |
Then, for all , define the augmented backup control
| (37) |
which is a weighted sum of the backup controls for which . Note that (35) implies that for all , is not empty and thus, is well-defined.
Proposition 11.
is continuous on .
It follows from (36) and (37) that , where
Since and are continuous on , it follows that and are continuous on . Since, in addition, for all , , it follows that is continuous on .
Proposition 12.
.
Next, for all , define
| (38) |
which is the same as the homotopy in (19) except that is replaced by the augmented backup control .
Finally, consider the control
| (39) |
where satisfies
| (40) |
where and is the value of after an instantaneous change. It follows from (40) that if , then the index is constant. In this case, the same backup control is used in (39) until the state reaches . This approach is adopted so that switching between backup controls (i.e., switching in (40)) only occurs on .
If there is only one backup control (i.e., ), then and . In this case, the control in this section simplifies to the control (12)–(19) in Section 5.
The following theorem is the main result on the soft-maximum/soft-minimum BF approach.
Theorem 2.
To prove (a), note that the same arguments in the proof to Theorem 1(a) imply that and are continuous on . Next, Propositions 11 and 12 imply that is continuous on . Since, in addition, is continuous on , it follows from (38) that is continuous on . Next, let . Since is bounded, it follows from (16), (17), and (38) that . Since is continuous on , is continuous on , and for all , , it follows from (19) that is continuous on . Next, (40) implies for , is constant. Since, in addition, is continuous on , it follows from (39) that is continuous on . Thus, is continuous on , which confirms (a).
To prove (b), let , and we consider 2 cases: , and . First, let , and (39) implies . Next, let . Since for , , it follows from (37) that . Since , the same arguments in the proof to Theorem 1(b) with replaced by imply that , which confirms (b).
To prove (c), assume for contradiction that for all , , and it follows from (29) and (35) that for all , . Next, we consider two cases: (i) there exists such that , and (ii) for all , .
First, consider case (i), and it follows that there exists such that and for all , . Hence, (40) and (39) imply that there exists such that for all , and . Next, let be the positive integer such that , and define . Since and for all , , it follows from Proposition 9 that , which is a contradiction.
Next, consider case (ii), and it follows that for all for all , . Hence, (40) and (39) imply that for all , and . Next, let be the positive integer such that , and define . Since and for all , , it follows from Proposition 9 that , which is a contradiction.
To prove (d), since , it follows from (31), (35), and Proposition 10 that . Define , and it follows from (30) and Proposition 10 that .
Let , and assume for contradiction that , which implies . Next, we consider two cases: (i) there exists such that , and (ii) for all , .
First, consider case (i), and it follows that there exists such that and for all , . Thus, (40) and (39) imply that there exists such that for all , and . Since, in addition, , it follows from Proposition 8 that , which is a contradiction.
Next, consider case (ii), and (39) and (40) imply that for all , and . Since, in addition, , Proposition 8 implies , which is a contradiction.
Theorem 2 provides the same results as Theorem 1 except is not necessarily continuous on because there are multiple backup controls. Specifically, is not continuous on ; however, the following remark illustrates a condition under which is continuous at a point on .
Remark 2.
Let such that , and let and denote times infinitesimally before and after . If , , and is a singleton, then is continuous at .
The control (14)–(18) and (32)–(40) can be computed using a process similar to the one described immediately before Example 2. Algorithm 2 summarizes the implementation of (14)–(18) and (32)–(40).
Example 5.
We revisit the inverted pendulum from Example 4 but use multiple backup controls to enlarge in comparison to Example 4. The safe set is the same as in Example 4. For , the backup controls are , where , , , and . The backup safe sets are given by (25), where
and for ,
Note that and are the backup control and backup safe set used in Example 4. Lyapunov’s direct method can be used to confirm that Assumption 2 is satisfied. The desired control is .
We implement the control (14)–(18) and (32)–(40) using and the same parameters as in Example 4 except rather than 150. We selected rather than 150 because this example has 3 backup controls, so was reduced by 1/3 to obtain a computational complexity that is comparable to Example 4,
Figure 8 shows , , , , . Note that using multiple backup controls is larger than that from Example 4, which uses only one backup control and has a comparable computational cost. Figure 8 also shows the closed-loop trajectories under Algorithm 2 for 2 initial conditions, specifically, and . Example 4 shows that the closed-loop trajectory leaves under Algorithm 1 with . In contrast, Figure 8 shows that Algorithm 2 keeps the state in .
Figure 9 provides time histories for the case where . The last row of Figure 9 shows that and nonnegative for all time and that the soft maximum in is initially an approximation of and then becomes an approximation of as the trajectory moves closer to . Note that, is positive for all time but is less than in steady state, it follows from (39) that in steady state is a blend of and .


References
- [1] U. Borrmann, L. Wang, A. D. Ames, M. Egerstedt, Control barrier certificates for safe swarm behavior, IFAC-PapersOnLine (2015) 68–73.
- [2] Q. Nguyen, K. Sreenath, Safety-critical control for dynamical bipedal walking with precise footstep placement, IFAC-PapersOnLine (2015) 147–154.
- [3] F. Blanchini, Set invariance in control, Automatica (1999) 1747–1767.
- [4] M. Chen, C. J. Tomlin, Hamilton–Jacobi reachability: Some recent theoretical advances and applications in unmanned airspace management, Ann. Rev. of Contr., Rob., and Auton. Sys. (2018) 333–358.
- [5] S. Herbert, J. J. Choi, S. Sanjeev, M. Gibson, K. Sreenath, C. J. Tomlin, Scalable learning of safety guarantees for autonomous systems using hamilton-jacobi reachability, in: Int. Conf. Rob. Autom., IEEE, 2021, pp. 5914–5920.
- [6] K. P. Wabersich, M. N. Zeilinger, Predictive control barrier functions: Enhanced safety mechanisms for learning-based control, IEEE Trans. Autom. Contr.
- [7] T. Koller, F. Berkenkamp, M. Turchetta, A. Krause, Learning-based model predictive control for safe exploration, in: Proc. Conf. Dec. Contr., IEEE, 2018, pp. 6059–6066.
- [8] J. Zeng, B. Zhang, K. Sreenath, Safety-critical model predictive control with discrete-time control barrier function, in: Proc. Amer. Contr. Conf., 2021, pp. 3882–3889.
- [9] S. Prajna, A. Jadbabaie, G. J. Pappas, A framework for worst-case and stochastic safety verification using barrier certificates, IEEE Trans. Autom. Contr. (2007) 1415–1428.
- [10] D. Panagou, D. M. Stipanović, P. G. Voulgaris, Distributed coordination control for multi-robot networks using Lyapunov-like barrier functions, IEEE Trans. Autom. Contr. (2015) 617–632.
- [11] K. P. Tee, S. S. Ge, E. H. Tay, Barrier Lyapunov functions for the control of output-constrained nonlinear systems, Automatica (2009) 918–927.
- [12] X. Jin, Adaptive fixed-time control for MIMO nonlinear systems with asymmetric output constraints using universal barrier functions, IEEE Trans. Autom. Contr. (2018) 3046–3053.
- [13] A. D. Ames, J. W. Grizzle, P. Tabuada, Control barrier function based quadratic programs with application to adaptive cruise control, in: Proc. Conf. Dec. Contr., 2014, pp. 6271–6278.
- [14] A. D. Ames, X. Xu, J. W. Grizzle, P. Tabuada, Control barrier function based quadratic programs for safety critical systems, IEEE Trans. Autom. Contr. (2016) 3861–3876.
- [15] M. Jankovic, Robust control barrier functions for constrained stabilization of nonlinear systems, Automatica 96 (2018) 359–367.
- [16] S. V. Rakovic, P. Grieder, M. Kvasnica, D. Q. Mayne, M. Morari, Computation of invariant sets for piecewise affine discrete time systems subject to bounded disturbances, in: Proc. Conf. Dec. Contr., 2004, pp. 1418–1423.
- [17] M. Korda, D. Henrion, C. N. Jones, Convex computation of the maximum controlled invariant set for polynomial control systems, SIAM J. Contr. and Opt. (2014) 2944–2969.
- [18] X. Xu, J. W. Grizzle, P. Tabuada, A. D. Ames, Correctness guarantees for the composition of lane keeping and adaptive cruise control, IEEE Trans. Auto. Sci. and Eng. (2017) 1216–1229.
- [19] I. M. Mitchell, A. M. Bayen, C. J. Tomlin, A time-dependent Hamilton-Jacobi formulation of reachable sets for continuous dynamic games, IEEE Trans. Autom. Contr. (2005) 947–957.
- [20] J. H. Gillula, S. Kaynama, C. J. Tomlin, Sampling-based approximation of the viability kernel for high-dimensional linear sampled-data systems, in: Proc. Int. Conf. Hybrid Sys.: Comp. and Contr., 2014, pp. 173–182.
- [21] E. Squires, P. Pierpaoli, M. Egerstedt, Constructive barrier certificates with applications to fixed-wing aircraft collision avoidance, in: Proc. Conf. Contr. Tech. and App., 2018, pp. 1656–1661.
- [22] T. Gurriet, M. Mote, A. Singletary, P. Nilsson, E. Feron, A. D. Ames, A scalable safety critical control framework for nonlinear systems, IEEE Access (2020) 187249–187275.
- [23] Y. Chen, A. Singletary, A. D. Ames, Guaranteed obstacle avoidance for multi-robot operations with limited actuation: A control barrier function approach, IEEE Contr. Sys. Letters (2020) 127–132.
- [24] W. Xiao, C. A. Belta, C. G. Cassandras, Sufficient conditions for feasibility of optimal control problems using control barrier functions, Automatica (2022) 109960.
- [25] A. Singletary, A. Swann, Y. Chen, A. D. Ames, Onboard safety guarantees for racing drones: High-speed geofencing with control barrier functions, IEEE Rob. and Autom. Letters 7 (2) (2022) 2897–2904.
- [26] A. Singletary, A. Swann, I. D. J. Rodriguez, A. D. Ames, Safe drone flight with time-varying backup controllers, in: Int. Conf. Int. Rob. and Sys., IEEE, 2022, pp. 4577–4584.
- [27] P. Rabiee, J. B. Hoagg, Soft-minimum barrier functions for safety-critical control subject to actuation constraints, in: Proc. Amer. Contr. Conf., 2023.
- [28] P. Rabiee, J. B. Hoagg, A closed-form control for safety under input constraints using a composition of control barrier functions, arXiv preprint arXiv:2406.16874.
- [29] P. Rabiee, J. B. Hoagg, Composition of control barrier functions with differing relative degrees for safety under input constraints, arXiv preprint arXiv:2310.00363.
- [30] W. Xiao, C. Belta, High-order control barrier functions, IEEE Trans. Autom. Contr. 67 (7) (2021) 3655–3662.
- [31] F. Borrelli, A. Bemporad, M. Morari, Predictive control for linear and hybrid systems, Cambridge University Press, 2017.
- [32] W. W. Hogan, Point-to-set maps in mathematical programming, SIAM review (1973) 591–603.
- [33] A. De Luca, G. Oriolo, M. Vendittelli, Control of wheeled mobile robots: An experimental overview, RAMSETE (2002) 181–226.