Sobolev extensions over Cantor-cuspidal graphs

Let $1\leq q\leq p\leq\infty$. If $\psi$ is a Lipschitz function on $\mathbb{R},$ then the upper and lower domains determined by the graph of $\psi$ are extension domains for all the first order Sobolev spaces $W^{1,p}$ by the works of Calderón and Stein [11]: if $\Omega$ is either one of these domains, then there is a linear bounded extension operator from $W^{1,p}(\Omega)$ into $W^{1,p}(\mathbb{R}^{2}).$ In fact, it is not hard to check that one can obtain such an extension operator via a bi-Lipschitz reflection that switches the upper and lower domains: the bi-Lipschitz map $f(x,y)=(x,y-\psi(x))$ maps the two domains onto half-planes and one can use the usual reflection with respect to the first coordinate axes, modulo $f$ and its inverse.

If $\psi$ is Hölder-continuous, one cannot necessarily extend from $W^{1,p}(\Omega)$ to $W^{1,p}(\mathbb{R}^{2})$ since the graph of $\psi$ can contain cusps. In this case, under the correct assumptions on $p,q$ and the Hölder-exponent, one can nevertheless extend from $W^{1,p}(\Omega)$ to $W^{1,q}(\mathbb{R}^{2}),$ see [2], in the sense that the extension belongs to $W^{1,q}_{{\mathop{\mathrm{missing}}{\,loc\,}}}(\mathbb{R}^{2})$ with

More precisely, if $1/2<\alpha<1$ and $p>\frac{\alpha}{2\alpha-1}$ then any $1\leq q<\frac{\alpha p}{\alpha+(1-\alpha)p}$ can be obtained. For a single cusp, the sharp exponents for the interior are $p>\frac{1+\alpha}{2\alpha}$ and $q<\frac{2\alpha}{(1+\alpha)p}$ and for the exterior $p>1$ and $q<\frac{(1+\alpha)p}{2\alpha+(1-\alpha)p}$ or $p=1=q$. This follows from more general work of Gol’dshtein and Sitnikov [3] who showed that for certain cusp-like domains with Hölder boundaries one can obtain an extension via a reflection which in this case is not anymore bi-Lipschitz. For an exposition and more historical references for the theory of Sobolev spaces on non-smooth domains, we refer the reader to [10].

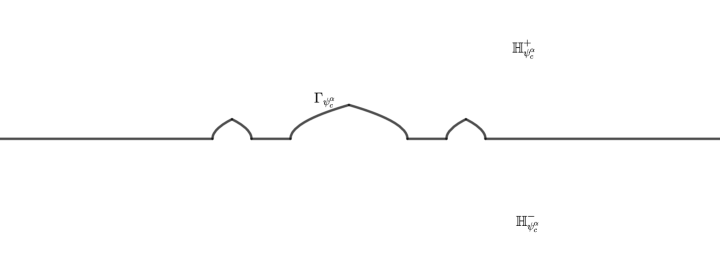
In this paper we consider the above extension problem in a model case in oder to gain better insight to the problem. Towards our model case, let $\mathcal{C}\subset[0,1]\times\{0\}\subset\mathbb{R}^{2}$ be the standard ternary Cantor set, obtained by removing a sequence of ‘centrally located” open intervals from $[0,1]\times\{0\}$: at stage $j$ we have $2^{j}$ closed intervals, each of length $3^{-j},$ from the middle of each we remove an open interval of length $3^{-j-1}.$ For $\alpha\in(0,1)$, we define $\psi^{\alpha}_{c}:{\mathbb{R}}\to{\mathbb{R}}$ by setting

Then $\psi^{\alpha}_{c}$ is Hölder continuous with exponent $\alpha.$ Define the corresponding graph by setting

and let $\Omega^{+}_{\psi^{\alpha}_{c}}$ be the domain above the “Cantor-cuspidal” graph $\Gamma_{\psi^{\alpha}_{c}}:$

and $\Omega^{-}_{\psi^{\alpha}_{c}}$ be the domain below the “Cantor-cuspidal” graph $\Gamma_{\psi^{\alpha}_{c}}:$

See Figure $1$ below. Notice that

for all $x_{1}\in\mathcal{C}\setminus\{0,1\}.$ Hence the common boundary of both of these domains is ‘cusp-like” in a set of Hausdorff dimension $\frac{\log 2}{\log 3}.$

Towards our results, we call a homeomorphism $\mathcal{R}:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ a reflection over $\Gamma_{\psi^{\alpha}_{c}}$ if $\mathcal{R}(\Omega^{+}_{\psi^{\alpha}_{c}})=\Omega^{-}_{\psi^{\alpha}_{c}}$ and $\mathcal{R}(x)=x$ for all $x\in\Gamma_{\psi^{\alpha}_{c}}.$ Let $\Omega$ be one of the domains $\Omega^{+}_{\psi^{\alpha}_{c}},\Omega^{-}_{\psi^{\alpha}_{c}}.$ We say that a reflection $\mathcal{R}$ over $\Gamma_{\psi^{\alpha}_{c}}$ induces a bounded linear extension operator from $W^{1,p}(\Omega)$ to $W_{\rm loc}^{1,q}({\mathbb{R}}^{2})$ if for every $u\in W^{1,p}(\Omega),$ the function $v$ defined by setting $v=u$ on $\Omega$ and $v=u\circ\mathcal{R}$ on ${\mathbb{R}}^{2}\setminus\overline{{\Omega}}$ has a representative that belongs to $W_{\rm loc}^{1,q}({\mathbb{R}}^{2})$ such that for every bounded open set $U\subset{\mathbb{R}}^{2}$, we have

for a positive constant $C$ independent of $u$. In our setting, this conclusion easily implies that one can find an extension $Eu$ with

The following theorem is the main result of the article.

The following proposition shows the sharpness of Theorem 1.1.

We would like to know if Theorem 1.1 exhibits a general principle: could it be the case that for graphs the Sobolev extension problem is equivalent to the existence of a suitable reflection? For partial results in this direction see [3, 9]. The symmetry in Theorem 1.1 cannot hold in general as follows by the results in [3], our reflection has better properties that one would in general expect [6, 7].

We close this introduction with a comment regarding the case $p=1=q.$ A domain ${\Omega}\subset{{{\mathbb{R}}}^{n}}$ is called quasiconvex, if there exists a positive constant $C>1$ such that for every pair of points $x,y\in{\Omega}$, there exists a rectifiable curve $\gamma\subset{\Omega}$ joining $x,y$ with

For every $0<\alpha<1$, one can easily see that neither $\Omega^{+}_{\psi^{\alpha}_{c}}$ nor $\Omega^{-}_{\psi^{\alpha}_{c}}$ is quasiconvex. Then the corollary in [8] with a bit of work implies that neither $\Omega^{+}_{\psi^{\alpha}_{c}}$ nor $\Omega^{-}_{\psi^{\alpha}_{c}}$ is a Sobolev $(1,1)$-extension domain. Hence, in the proof to Proposition 1.1 below, we will only discuss the case for $p>1$.

The notation $x=(x_{1},x_{2})\in{\mathbb{R}}^{2}$ means a point in the Euclidean plane ${\mathbb{R}}^{2}$. Typically $C$ will be a constant that depends on various parameters and may differ even on the same line of inequalities. The notation $A\lesssim B$ means there exists a finite constant $C$ with $A\leq CB$ , and $A\sim_{C}B$ means $\frac{1}{C}A\leq B\leq CA$ for a constant $C>1$. The Euclidean distance between points $x,x^{\prime}$ in the Euclidean plane $\mathbb{R}^{2}$ is denoted by $|x-x^{\prime}|$. The open disk of radius $r$ centered at $x$ is denoted by $D(x,r)$. $\mathcal{H}^{2}(A)$ means the $2$-dimensional Lebesgue measure for a measurable set $A\subset\mathbb{R}^{2}$.

To obtain the classical ternary Cantor set in the unit interval $[0,1]\subset{\mathbb{R}}$, we remove a class of pairwise disjoint open intervals step by step. At the first step, we remove the middle $\frac{1}{3}$-interval $I_{1}^{1}:=(\frac{1}{3},\frac{2}{3})$ from the unit interval $I:=[0,1]$. At the second step, we remove the middle $\frac{1}{9}$-intervals $I_{2}^{1}:=(\frac{1}{9},\frac{2}{9})$ and $I_{2}^{2}:=(\frac{7}{9},\frac{8}{9})$ from the two intervals of length $\frac{1}{3}$ obtained from the first step. By induction, at the $n$-th step, we remove the middle $\frac{1}{3^{n}}$-intervals from the $2^{n-1}$ intervals $\{I_{n}^{k}\}_{k=1}^{2^{n-1}}$ of length $\frac{1}{3^{n-1}}$ obtained from the $(n-1)$-th step. Finally, we obtain the classical ternary Cantor set

Let us denote the removed open intervals by $I_{n}^{k}:=(a_{n}^{k},b_{n}^{k})$. Then, the function $\psi^{\alpha}_{c}$ defined in (1.1) can be rewritten as

Let us give the definition of Sobolev spaces.

Although the Cantor-cuspidal graph $\Gamma_{\psi^{\alpha}_{c}}$ has a plethora of singularities, the corresponding upper and lower domains $\Omega^{+}_{\psi^{\alpha}_{c}}$ and $\Omega^{-}_{\psi^{\alpha}_{c}}$ still enjoy some nice geometric properties. For example, they satisfy the following so-called segment condition.

For domains which satisfy the segment condition, we have the following density result. See [1, Theorem 3.22].

By combining the theorems in [12, 13, 14, 15], also see [4, 5], we obtain the following lemma.

In this section, we always assume $\frac{\log 2}{2\log 3}<\alpha<1$. To begin, we define a class of sets $\{\mathsf{R}_{n,k};k=1,...,2^{n-1}\}_{n=1}^{\infty}$ by setting

We also define $\mathsf{R}^{+}_{n,k}$ and $\mathsf{R}^{-}_{n,k}$ to be the corresponding upper and lower parts of $\mathsf{R}_{n,k}$ with respect to $\Gamma_{\psi^{\alpha}_{c}}$ by setting

and

Fix $x_{1}\in I_{n}^{k}$ for some $n\in\mathbb{N}$ and $k\in\{1,2,\cdots,2^{n-1}\}.$ Then

is a vertical line segment in $\mathsf{R}^{+}_{n,k}$ and

is a vertical line segment in $\mathsf{R}^{-}_{n,k}$.

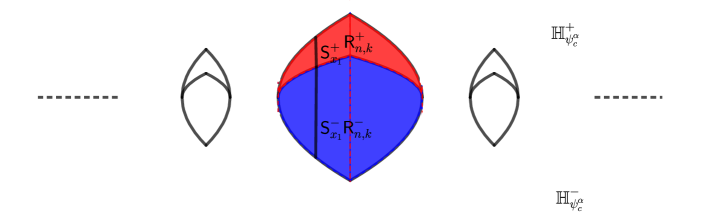
Now, we are ready to define our reflection $\mathcal{R}:{\mathbb{R}}^{2}\to{\mathbb{R}}^{2}$ over $\Gamma_{\psi^{\alpha}_{c}}$. Our reflection will map the segment $\mathsf{S}^{+}_{x_{1}}$ onto the segment $\mathsf{S}^{-}_{x_{1}}$ affinely for every $x_{1}\in I_{n}^{k}$. To be precise, we define the reflection $\mathcal{R}$ on $\Omega^{+}_{\psi^{\alpha}_{c}}$ by setting

where $x=(x_{1},x_{2})$. It is easy to check that $\mathcal{R}$ maps $\mathsf{R}^{+}_{n,k}$ onto $\mathsf{R}^{-}_{n,k}$, for every $n\in\mathbb{N}$ and $k\in\{1,2,\cdots,2^{n-1}\}$. On $\Omega^{-}_{n,k}$, we simply let $\mathcal{R}$ be the inverse of (3.6). Since $\mathcal{R}(\Omega^{+}_{\psi^{\alpha}_{c}})=\Omega^{-}_{\psi^{\alpha}_{c}}$, $\mathcal{R}(\Omega^{-}_{\psi^{\alpha}_{c}})=\Omega^{+}_{\psi^{\alpha}_{c}}$ and $\mathcal{R}(x)=x$ for every $x\in\Gamma_{\psi^{\alpha}_{c}}$, $\mathcal{R}$ is a reflection over $\Gamma_{\psi^{\alpha}_{c}}$. For every $x_{1}\in I_{n}^{k}$ with $n\in\mathbb{N}$ and $k\in\{1,2,\cdots,2^{n-1}\}$, the reflection $\mathcal{R}$ maps $\mathsf{S}^{+}_{x_{1}}$ onto $\mathsf{S}^{-}_{x_{1}}$ affinely.

By a simple computation, at every point $x\in\mathsf{R}^{+}_{n,k}$ for some $n\in\mathbb{N}$ and $k\in\{1,2,\cdots,2^{n-1}\}$, the differential matrix $D\mathcal{R}(x)$ is

By another simple computation, there exists a positive constant $C>0$ such that for every $x\in\mathsf{R}^{+}_{n,k}$, we have

and

Next, let us estimate the analog of $(2)$ of Lemma 2.2 for $\mathcal{R}$:

whenever $\frac{(1+\alpha)-\frac{\log 2}{\log 3}}{2\alpha-\frac{\log 2}{\log 3}}<p<\infty$ and $1\leq q<\frac{((1+\alpha)-\frac{\log 2}{\log 3})p}{(1+\alpha)-\frac{\log 2}{\log 3}+(1-\alpha)p}$.

By a simple computation, we can rewrite the reflection $\mathcal{R}$ on $\Omega^{-}_{\psi^{\alpha}_{c}}$ as

where $x=(x_{1},x_{2})$. At every point $x\in\mathsf{R}^{-}_{n,k}$ for $n\in\mathbb{N}$ and $k\in\{1,2,\cdots,2^{n-1}\}$, the differential matrix $D\mathcal{R}(x)$ is

There exists a positive constant $C>1$ such that

and

Hence, we have

whenever $\frac{(1+\alpha)-\frac{\log 2}{\log 3}}{2\alpha-\frac{\log 2}{\log 3}}<p<\infty$ and $1\leq q<\frac{((1+\alpha)-\frac{\log 2}{\log 3})p}{(1+\alpha)-\frac{\log 2}{\log 3}+(1-\alpha)p}$.

Finally, it is easy to see that the reflection $\mathcal{R}$ is bi-Lipschitz on every open set $U\subset{\mathbb{R}}^{2}$ with $d(U,\Gamma_{\psi^{\alpha}_{c}})>0$.