Smoothers Based on Nonoverlapping Domain Decomposition Methods for Problems: A Numerical Study
Abstract.
This paper presents a numerical study on multigrid algorithms of –cycle type for problems posed in the Hilbert space in three dimensions. The multigrid methods are designed for discrete problems originated from the discretization using the hexahedral Nédélec edge element of the lowest-order. Our suggested methods are associated with smoothers constructed by substructuring based on domain decomposition methods of nonoverlapping type. Numerical experiments to demonstrate the robustness and the effectiveness of the suggested algorithms are also provided.
Key words and phrases:
multigrid method, Nédélec finite element, , nonoverlapping domain decomposition2020 Mathematics Subject Classification:
65N30, 65N55, 65F081. Introduction
Let be a domain that is bounded in . We will work with the Hilbert space which consists of vector fields in the space with curl also in and vanishing tangential components on the boundary (cf. [12]). We will consider the following variational problem: Find such that
| (1) |
where
| (2) |
Here, is the standard inner product on and we assume that is nonnegative and is strictly positive. We also assume that is a square integrable vector field on , i.e., . In this manuscript, we will provide a multigrid framework for solving our model problem (1).
The model problem (1) is originated from the applications in Maxwell’s equation; see [21]. Relevant fast solvers, such as multigrid methods and domain decomposition methods, for problems connected with have been discussed in [14, 15, 17, 4, 24, 25, 9, 10, 16, 11, 26, 18].
It is well-known that the traditional smoothers for solving the scalar elliptic problems do not work well for vector field problems related to and ; see [8]. Hence, a special smoothing technique is necessary for vector field problems. Function space splitting methods based on Helmholtz type decompositions pioneered by Hiptmair [14, 13] and Hiptmair and Xu [15] have been considered. In [2, 4, 3], an overlapping type domain decomposition preconditioner has been applied. We also note that the author and Brenner considered smoothers associated with nonoverlapping type domain decomposition methods for problems in [5, 6].
In this paper, we propose a –cycle multigrid method with nonoverlapping domain decomposition smoothers and mainly consider the numerical study that is not covered by theories in [23]. In [23], the author provided the convergence analysis with the assumptions, i.e., convex domain and constant material parameters in (1). We test our method with less strict conditions, e.g., jump coefficients for and , nonconvex domain. We note that our multigrid method is an counterpart of the method in [5, 6] and a nonoverlapping alternative of the method in [4], which requires less computational costs when applying the smoother.
2. The Discrete Problem
We first consider a triangulation of into hexahedral elements. The lowest order hexahedral Nédélec element [20, 22] has the following form:
on each hexahedral mesh, where the ’s, ’s and ’s are constants. We note that the twelve degrees of freedom can be completely recovered by the average tangential component on each edge of the element. Using the finite elements, we obtain the following discretized problem for (1): Find such that
| (3) |
where is the Nédélec finite element space of the lowest order.
We define the operator in the following way:
| (4) |
Here, is the canonical bilinear form on . We then have the following discrete problem:
| (5) |
where defined by
3. -Cycle Multigrid Method
In a multigrid setting, we construct a nested sequence of triangulations, starting with the initial triangulation consisting of few hexahedral elements. We assume that is obtained by uniform subdivision from . We then define which is the lowest order Nédélec space related to the level mesh and the corresponding discrete problem: Find such that
| (6) |
Here, is defined by
In order for solving the discrete problem (6) using multigrid methods, we need two essential ingredients, intergrid transfer operators and smoothers. We note that everything else can be constructed in a standard way.
Since we are dealing with the nested finite element spaces, the natural injection can be used as the coarse-to-fine operator . The fine-to-coarse operator is then defined by
| (7) |
We now focus on the missing piece, smoother. As we are interested in designing nonoverlapping type domain decomposition smoothers, we borrow the standard two level domain decomposition framework, i.e., the coarse level and the fine level that are associated with and , respectively.
Before we construct the smoothers, we set up notations for the geometric substructures. Let , , and be the sets of interior edges, interior faces, and interior vertices of the triangulation , respectively.
We first consider the interior space. Given any coarse element , let us define the subspace by
| (8) |
Let denote the natural injection from into . The operator is constructed by
| (9) |
For a coarse edge , there are four coarse elements, , in and four coarse faces, , in , that are sharing . The edge space of is defined as follow:
| (10) | ||||
Let be the natural injection and the operator be defined by
| (11) |
Finally, we define the vertex space of . For each coarse vertex , there are eight elements, , in , twelve faces, , in , and six edges, , in , that have the point in common. We define the vertex space by
| (12) | ||||
The natural injection and the operator are obtained by a similar way to and , respectively.
We now define two smoothers, the edge-based and the vertex-based preconditioners. The edge-based smoother is constructed as follow:
| (13) |
Similarly, the vertex-based smoother is obtained by
| (14) |
Here, and are damping factors and , , and are the transposes of , , and , respectively. We can decide the damping factors such that
| (15) |
where and are the spectral radii of and , respectively. We note that the conditions in (15) are satisfied if and .
Putting all together, we can completely determine the multigrid framework. The output of the level (symmetric) multigrid -cycle algorithm for , with initial guess and smoothing steps, is defined as follows:
For , the result is obtained by using a direct solver:
For , we set
The output of is . The smoother is either or defined earlier in the current section.
In order to check the efficiency of the algorithm, we consider the following error propagation operator:
| (16) |
The operator is affiliated with the error after one multigrid sweep with smoothing steps. For more detail, see [7, Chapter 6].
4. Numerical Results
We note that a part of the finite element discretizations has been implemented with the MFEM library [1, 19]. The codes used for the experiments are available at the repository https://github.com/duksoon-open/MG_ND.
4.1. Jump Coefficients
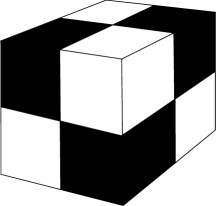
The first experiment is for the cube . The domain is decomposed into eight identical cubical subdomains and set the subregions as the initial triangulation . We assume that the coefficients and are constants in each subdomain in a checkerboard pattern; see Fig. 1. We apply the multigrid algorithms, edge-based method and vertex-based method, introduced in Section 3. We report the contraction numbers by calculating the largest eigenvalue of the operators in (16), for and for . The results are presented in Table 1 and Table 2. We see that the multigrid methods provide contraction and are robust to the jump between the interface of the initial mesh.
| 0.905 | 0.827 | 0.762 | 0.709 | 0.663 | |
| 0.940 | 0.908 | 0.872 | 0.841 | 0.811 | |
| 0.967 | 0.952 | 0.935 | 0.917 | 0.902 | |
| 0.981 | 0.970 | 0.960 | 0.955 | 0.942 | |
| 0.905 | 0.827 | 0.763 | 0.710 | 0.666 | |
| 0.941 | 0.910 | 0.875 | 0.844 | 0.807 | |
| 0.967 | 0.954 | 0.937 | 0.92 | 0.905 | |
| 0.980 | 0.971 | 0.961 | 0.956 | 0.945 | |
| 0.907 | 0.831 | 0.769 | 0.719 | 0.677 | |
| 0.944 | 0.917 | 0.885 | 0.858 | 0.830 | |
| 0.970 | 0.959 | 0.944 | 0.930 | 0.917 | |
| 0.981 | 0.972 | 0.965 | 0.963 | 0.956 | |
| 0.909 | 0.836 | 0.777 | 0.729 | 0.690 | |
| 0.948 | 0.924 | 0.896 | 0.872 | 0.853 | |
| 0.972 | 0.965 | 0.952 | 0.941 | 0.931 | |
| 0.982 | 0.974 | 0.971 | 0.969 | 0.966 | |
| 0.910 | 0.837 | 0.778 | 0.731 | 0.693 | |
| 0.949 | 0.926 | 0.898 | 0.875 | 0.857 | |
| 0.973 | 0.966 | 0.954 | 0.943 | 0.934 | |
| 0.982 | 0.975 | 0.972 | 0.970 | 0.968 | |
| 0.790 | 0.624 | 0.493 | 0.390 | 0.308 | |
| 0.792 | 0.627 | 0.495 | 0.393 | 0.312 | |
| 0.791 | 0.625 | 0.494 | 0.391 | 0.310 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.317 | |
| 0.790 | 0.624 | 0.493 | 0.390 | 0.308 | |
| 0.791 | 0.626 | 0.494 | 0.392 | 0.310 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.310 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.311 | |
| 0.790 | 0.624 | 0.493 | 0.390 | 0.308 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.310 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.311 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.311 | |
| 0.790 | 0.624 | 0.493 | 0.390 | 0.308 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.311 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.311 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.311 | |
| 0.790 | 0.624 | 0.493 | 0.390 | 0.308 | |
| 0.791 | 0.626 | 0.495 | 0.392 | 0.311 | |
| 0.791 | 0.626 | 0.495 | 0.393 | 0.318 | |
| 0.791 | 0.632 | 0.524 | 0.483 | 0.429 | |
4.2. Nonconvex Domain
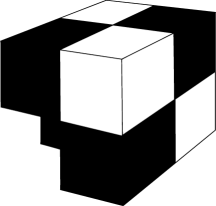
In the second set of numerical tests, we consider the domain , which is nonconvex. We begin with the initial mesh which consists of seven identical cubes as in Figure 2 and inductively define the level mesh by a uniform subdivision. Other general settings are similar to those of Section 4.1. We apply our multigrid algorithm for the problem (1) on the domain and report the contraction numbers computed in the same manner with the first experiment. As we see the results in the Table 3 and Table 4, the uniform convergences and robustness are observed except for the problem with using the vertex-based smoother.
| 0.835 | 0.702 | 0.576 | 0.471 | 0.420 | |
| 0.940 | 0.881 | 0.828 | 0.785 | 0.749 | |
| 0.967 | 0.940 | 0.918 | 0.892 | 0.869 | |
| 0.982 | 0.969 | 0.957 | 0.948 | 0.934 | |
| 0.823 | 0.682 | 0.542 | 0.436 | 0.390 | |
| 0.943 | 0.887 | 0.832 | 0.796 | 0.757 | |
| 0.966 | 0.941 | 0.918 | 0.892 | 0.870 | |
| 0.983 | 0.970 | 0.958 | 0.948 | 0.936 | |
| 0.799 | 0.627 | 0.511 | 0.419 | 0.338 | |
| 0.945 | 0.894 | 0.844 | 0.802 | 0.768 | |
| 0.970 | 0.942 | 0.920 | 0.896 | 0.876 | |
| 0.984 | 0.974 | 0.961 | 0.950 | 0.941 | |
| 0.802 | 0.646 | 0.523 | 0.420 | 0.348 | |
| 0.946 | 0.896 | 0.851 | 0.804 | 0.773 | |
| 0.972 | 0.943 | 0.924 | 0.902 | 0.881 | |
| 0.986 | 0.976 | 0.964 | 0.954 | 0.945 | |
| 0.804 | 0.651 | 0.529 | 0.424 | 0.354 | |
| 0.947 | 0.896 | 0.851 | 0.805 | 0.774 | |
| 0.972 | 0.944 | 0.924 | 0.903 | 0.882 | |
| 0.986 | 0.976 | 0.965 | 0.955 | 0.946 | |
| 0.912 | 0.835 | 0.765 | 0.683 | 0.648 | |
| 0.905 | 0.825 | 0.758 | 0.689 | 0.622 | |
| 0.912 | 0.834 | 0.765 | 0.697 | 0.626 | |
| 0.896 | 0.808 | 0.726 | 0.622 | 0.598 | |
| 0.878 | 0.789 | 0.710 | 0.629 | 0.535 | |
| 0.890 | 0.792 | 0.703 | 0.577 | 0.518 | |
| 0.869 | 0.758 | 0.660 | 0.576 | 0.504 | |
| 0.837 | 0.705 | 0.593 | 0.497 | 0.425 | |
| 0.827 | 0.689 | 0.570 | 0.479 | 0.407 | |
| 0.863 | 0.766 | 0.666 | 0.591 | 0.503 | |
| 0.844 | 0.725 | 0.613 | 0.495 | 0.453 | |
| 0.829 | 0.706 | 0.574 | 0.498 | 0.420 | |
| 0.865 | 0.772 | 0.675 | 0.602 | 0.515 | |
| 0.849 | 0.735 | 0.626 | 0.509 | 0.471 | |
| 0.833 | 0.717 | 0.590 | 0.519 | 0.447 | |
Acknowledgement
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1F1A1A01072168).
References
- [1] R. Anderson, J. Andrej, A. Barker, J. Bramwell, J.-S. Camier, J. C. V. Dobrev, Y. Dudouit, A. Fisher, T. Kolev, W. Pazner, M. Stowell, V. Tomov, I. Akkerman, J. Dahm, D. Medina, and S. Zampini. MFEM: A modular finite element library. Computers & Mathematics with Applications, 81:42–74, 2021.
- [2] D. N. Arnold, R. S. Falk, and R. Winther. Preconditioning in and applications. Math. Comp., 66(219):957–984, 1997.
- [3] D. N. Arnold, R. S. Falk, and R. Winther. Multigrid preconditioning in on non-convex polygons. Comput. Appl. Math., 17(3):303–315, 1998.
- [4] D. N. Arnold, R. S. Falk, and R. Winther. Multigrid in and . Numer. Math., 85(2):197–217, 2000.
- [5] S. C. Brenner and D.-S. Oh. Multigrid methods for in three dimensions with nonoverlapping domain decomposition smoothers. Numer. Linear Algebra Appl., 25(5):e2191, 14, 2018.
- [6] S. C. Brenner and D.-S. Oh. A smoother based on nonoverlapping domain decomposition methods for problems: a numerical study. In Domain decomposition methods in science and engineering XXIV, volume 125 of Lect. Notes Comput. Sci. Eng., pages 523–531. Springer, Cham, 2018.
- [7] S. C. Brenner and L. R. Scott. The mathematical theory of finite element methods, volume 15 of Texts in Applied Mathematics. Springer, New York, third edition, 2008.
- [8] Z. Q. Cai, C. I. Goldstein, and J. E. Pasciak. Multilevel iteration for mixed finite element systems with penalty. SIAM J. Sci. Comput., 14(5):1072–1088, 1993.
- [9] J. G. Calvo. A two-level overlapping Schwarz method for in two dimensions with irregular subdomains. Electron. Trans. Numer. Anal., 44:497–521, 2015.
- [10] J. G. Calvo. A new coarse space for overlapping Schwarz algorithms for problems in three dimensions with irregular subdomains. Numer. Algorithms, 83(3):885–899, 2020.
- [11] C. R. Dohrmann and O. B. Widlund. A BDDC algorithm with deluxe scaling for three-dimensional problems. Comm. Pure Appl. Math., 69(4):745–770, 2016.
- [12] V. Girault and P.-A. Raviart. Finite element methods for Navier-Stokes equations, volume 5 of Springer Series in Computational Mathematics. Springer-Verlag, Berlin, 1986. Theory and algorithms.
- [13] R. Hiptmair. Multigrid method for in three dimensions. Electron. Trans. Numer. Anal., 6(Dec.):133–152, 1997. Special issue on multilevel methods (Copper Mountain, CO, 1997).
- [14] R. Hiptmair. Multigrid method for Maxwell’s equations. SIAM J. Numer. Anal., 36(1):204–225, 1999.
- [15] R. Hiptmair and J. Xu. Nodal auxiliary space preconditioning in and spaces. SIAM J. Numer. Anal., 45(6):2483–2509, 2007.
- [16] Q. Hu and J. Zou. A nonoverlapping domain decomposition method for Maxwell’s equations in three dimensions. SIAM J. Numer. Anal., 41(5):1682–1708, 2003.
- [17] T. V. Kolev and P. S. Vassilevski. Parallel auxiliary space AMG for problems. J. Comput. Math., 27(5):604–623, 2009.
- [18] Y.-J. Lee, J. Wu, J. Xu, and L. Zikatanov. Robust subspace correction methods for nearly singular systems. Math. Models Methods Appl. Sci., 17(11):1937–1963, 2007.
- [19] MFEM: Modular finite element methods [Software]. mfem.org.
- [20] P. Monk. Finite element methods for Maxwell’s equations. Numerical Mathematics and Scientific Computation. Oxford University Press, New York, 2003.
- [21] P. B. Monk. A mixed method for approximating Maxwell’s equations. SIAM J. Numer. Anal., 28(6):1610–1634, 1991.
- [22] J.-C. Nédélec. Mixed finite elements in . Numer. Math., 35(3):315–341, 1980.
- [23] D.-S. Oh. Multigrid methods for 3 problems with nonoverlapping domain decomposition smoothers, 2022. submitted, arXiv:2205.05840.
- [24] A. Toselli. Overlapping Schwarz methods for Maxwell’s equations in three dimensions. Numer. Math., 86(4):733–752, 2000.
- [25] A. Toselli. Domain decomposition methods of dual-primal FETI type for edge element approximations in three dimensions. C. R. Math. Acad. Sci. Paris, 339(9):673–678, 2004.
- [26] S. Zampini. Adaptive BDDC deluxe methods for . In Domain decomposition methods in science and engineering XXIII, volume 116 of Lect. Notes Comput. Sci. Eng., pages 285–292. Springer, Cham, 2017.