Sliding ferroelectricity in a bulk misfit layer compound (PbS)_1.18VS₂

The group of possible two-dimensional (2D) ferroelectric materials has been significantly expanded by the recent theoretical prediction [1, 2, 3, 4] and experimental confirmation [5, 6, 7, 8, 9, 10] of sliding ferroelectricity. For certain stacking configurations in bi- and multilayer 2D materials, the inversion and/or mirror symmetry is broken and thereby an in- and/or out-of-plane polarization are induced. Due to the weak interlayer interaction in van der Waals multilayers, the polarization can be reversed via in-plane lattice sliding.

Experimentally, a sliding ferroelectric material can be created by manual stacking of 2D van der Waals materials on top of each other with a defined twist angle $\theta$ [11, 12, 13, 14]. Unfortunately, manual stacking can create difficulties with device reproducibility [15]. Sliding ferroelectricity can also be observed in bulk van der Waals crystals, as long as there is no inversion symmetry between the layers, as was recently shown for the amphidynamic crystal (15-crown-5)Cd₃Cl₆ [16]. In the case of transition metal dichalcogenides (TMD) crystals, the centrosymmetric 2H-form is the most common stable form and rarely a 3R-stacked bilayer can be found [14]. Nevertheless, bulk crystals with a broken inversion symmetry can be grown, such as 3R-MoS₂ [17] or graphene polytypes with stacking faults or twins [4, 10]. Also in van der Waals epitaxy of 2D materials on (quasi)-2D substrates, the formation of stacking faults and twins is often observed, due to very similar binding energies for the different stacking configurations [18].

In this work, instead of manually stacking a van der Waals heterostructure with a certain twist angle, we searched for a class of 2D materials where twins having a small twist angle with respect to each other can be easily induced during the growth. A member of the TMD class are the misfit layer compounds (MLCs) with the general formula (MX)_1+m(TX₂)_n, where M = Sn, Pb, Sb, Bi, or a rare earth element; T = Ti, V, Cr, Nb, or Ta; X = S, or Se; 0.08 $<$ m $<$ 0.28; and n = 1, 2, or 3 [19]. MLCs, characterized by the alternating stacking of a TMD layer and a post-transition metal chalcogenide monolayer (TMM), are the ideal class of 2D materials which should favor the creation of twins. During the growth, each next layer of 2D TMD(TMM) is grown on a TMM(TMD) substrate layer, which should be similar as with van der Waals epitaxy of thin films, result in the creation of twins.

Using a combination of single crystal X-ray diffraction analysis (XRD), scanning electron microscopy (SEM), photoemission electron microscopy (PEEM) and scanning probe microscopy (SPM), we show that within (PbS)_1.18VS₂ bulk crystals, twins are present. The twist angle between different twins is small and that twins with 3R-stacking show the characteristic properties of a sliding ferroelectric material.

The crystal structure of a MLC (also called composite) is formed by two or more distinct columns or layers, where each of them is called a subsystem. Two subsystems $\textbf{A}^{(1)}$ and $\textbf{A}^{(2)}$ are related by an interlattice matrix $\sigma$ via $\textbf{A}^{(2)}=\sigma\textbf{A}^{(1)}$ [20, 21]. The interaction between the subsystems corresponds to a perturbing potential that modulates the columns or layers and generates satellite reflections on the diffraction pattern of the composite. The intensities of the satellite reflections depend on the modulation. Since the diffraction pattern of a composite contains the contribution of each subsystem and the satellites, at least four indices are necessary to index it.

(PbS)_1.18VS₂ crystals were grown using chemical vapor transport according to a modified recipe of Gotoh et al. [23, 24]. They crystallize as a layer composite structure (see Figs. LABEL:fgr:fig_s1 – LABEL:fgr:fig_s3 in the Supplemental Material [24]), where subsystems 1 and 2 are PbS and VS₂, respectively. Subsystems 1 and 2 have parallel sublattice parameters a and c, while b is the incommensurate axis. Using the superspace formalism, indices $\textbf{a}^{*}$, $\textbf{b}_{1}^{*}$, $\textbf{c}^{*}$, and $\textbf{b}^{*}_{2}$ [21] are necessary to index both reciprocal sublattices of (PbS)_1.18VS₂, where $\textbf{b}_{1}^{*}$ is the modulation vector of sublattice 2, and $\textbf{b}_{2}^{*}$ is the modulation vector of sublattice 1.

A diffraction vector Q is given by $\textbf{Q}=h\textbf{a}^{*}+k\textbf{b}_{1}^{*}+l\textbf{c}^{*}+m\textbf{b}^{*}_{2}$, where $hklm$ are the reflection indices containing information from both subsystems;

• •

  $k=m=0$, main reflections common for both subsystems;

• •

  $k\neq 0$ $m=0$, main reflections for the first subsystem, $k^{th}$ order satellites for the second subsystem;

• •

  $k=0$, $m\neq 0$, main reflection for the second subsystem, $m^{th}$ order satellites;

• •

  $k\neq 0$, $m\neq 0$, pure satellite reflection of $k^{th}$ order and $m^{th}$ order for the first and second subsystem, respectively.

In a previous attempt to elucidate the crystal structure of (PbS)_1.18VS₂, Gotoh et al. [23, 25] observed satellites on electron diffraction photographs, but not by single crystal XRD. Hence, the structure was analyzed using the superspace formalism without observed satellites.

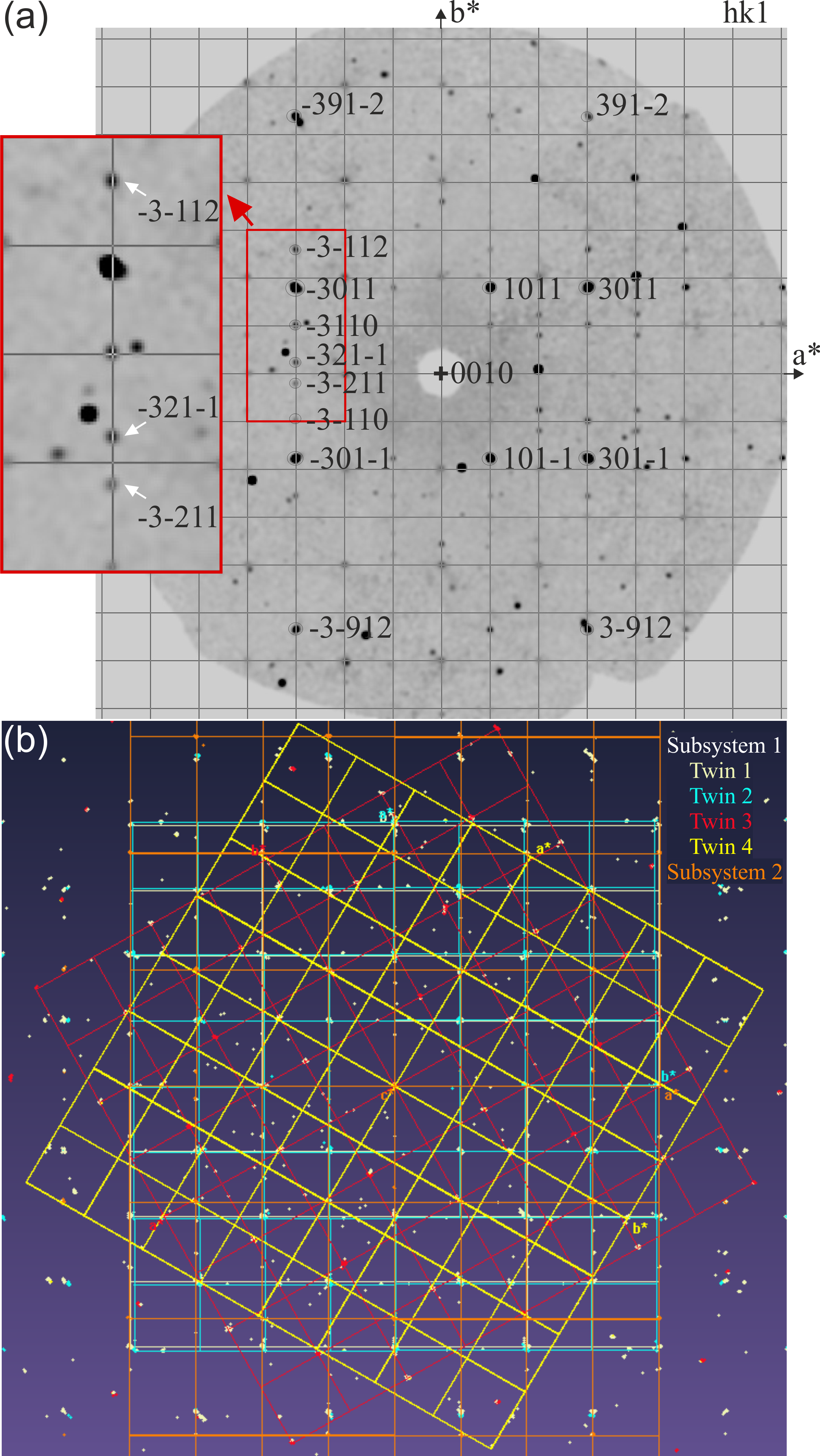
In our case, not only satellites were observed by single crystal X-ray diffraction, but also twins were present in the data, as shown in the reconstructed reciprocal space section $(hk1)$ (Fig. 1). Using a monoclinic unit cell to index both subsystems, the $a$ and $c$ parameters are common to both subsystems: subsystem 1 (PbS) has unit cell parameters $a=5.7062(5)$, $b=5.7674(7)$, $c=23.691(2)$  Å, and $\beta=94.878(8)\degree$. Subsystem 2 (VS₂) has $b=3.204$  Å. Figure 1(a) contains reflections belonging to subsystems 1 and 2, weak satellites, and several reflections that are not indexed. The extra reflections can be indexed, if other twins are included during the data integration. Since the two subsystems have either a distorted cubic or a hexagonal subcell, there are several possible configurations of layer organization, which allows for a range of twin orientations. Figure 1(b) shows the reciprocal space map containing four possible twins from the PbS subsystem: twin 1 has 30.8$\%$ of indexation, twin 2 has 26.6$\%$ of indexation, twin 3 has 24.5$\%$ of indexed peaks, and twin 4 has 4.8$\%$ of indexed peaks. The second subsystem is shown in orange and has 19.7$\%$ of indexed peaks. Each twin has part of the indexed peaks overlapped with other components. Data integrated for the structure analysis [26] includes three twins, which can be seen in Fig. LABEL:fgr:fig_s3(a) in the Supplemental Material [24]. The first twin is the one with the highest percentage of indexed reflections and has the main reflections from subsystems 1 and 2, plus satellites (Fig. LABEL:fgr:fig_s3(b) in the Supplemental Material [24]). Even though the relation between twins 2, 3, and 4 to twin 1 seems to be a rotation of approximately 180$\degree$, 30$\degree$, and 60$\degree$ around $c^{*}$, respectively (see Fig. 1(b)), the real rotation is along all the three axes $a^{*}$, $b^{*}$, and $c^{*}$.

From a crystallographic point of view, a variety of twin angles can be expected, but the dominant twist angles here, have a preference angle of approximately 0 and $\pm$180$\degree$ with respect to the twin with the highest indexation. Table. LABEL:tab:tab_s1 in the Supplemental Material [24] shows this effect in more detail. This is probably no coincidence, as the difference between the twist angle of two twins being approximately 0$\degree$ twins would result in an 3R-type alignment and 60 or 180$\degree$ twins would result in an 2H-type alignment [13] of the VS₂-layer, respectively. This indicates that these two configurations are local energy minima, similar as has been observed in exfoliated van der Waals heterostructures [13].

To investigate the possible presence of sliding ferroelectricity between the different twins, secondary electrons imaging (SE) in a SEM was used to map the surface electrical potential and spatial variations of topography [27, 28, 29]. In Fig. 2, SE images of the (PbS)_1.18VS₂ surface cleaved in ambient conditions are shown. Clearly visible is the presence of a complex domain structure, where the shape of the domains is either preferentially aligned stripes or triangular-like. Similar domain shapes were observed before in exfoliated TMD-based van der Waals heterostructures, which were stacked on top of each other with a small twist angle between the layers. Those domains were shown to be ferroelectric [5, 6, 7, 8]. The triangular domain indicates that the layers in those areas have a 3R-type alignment, and the triangular moiré is induced by the distorted hexagonal VS₂ layer. SE imaging of a 2H-type alignment is shown in Fig. LABEL:fgr:fig_s6 in the Supplemental Material [24].

The period $l$ of the domain network is for very small twist angles $\theta$ equal to $a/\theta$, where $a$ is the lateral lattice constant of VS₂ [7]. The largest observed triangular shape domains with lateral dimensions around 30 $\mu$m suggest that the smallest twist angles present between the hexagonal lattices of the VS₂ layers are of the order 10^-4 rad.

As recently shown, the ferroelectric domains in van der Waals moiré materials can be straightforwardly imaged using electric force microscopy (EFM) [9, 30]. Even in standard tapping mode atomic force microscopy (TM-AFM), the phase and even topography can be used for imaging moiré interlayer modulation of the van der Waals potential [31]. Our TM-AFM and EFM measurements were performed on freshly cleaved single crystals. Like the SEM images presented in Fig. 2, domain structures with similar shapes and sizes were found, depending on the position at the sample surface. In Fig. 3, the topography and phase of the TM-AFM and EFM’s phase are shown. When Fig. 3(a) and (b) are compared, two different features can be seen in both the topography and TM-AFM phase contrast; the terrace step going through the whole image, marked by the arrow, and the domains. In the topography image, the features appear as approximately 1 nm high steps. In the TM-AFM phase image, the domains induce a constant phase shift, resulting from different energy dissipation due to the modulation of van der Waals forces in the moiré structures [31] while the terraces are visible only as lines along the step edges.

The domains are also visible in the EFM phase image in Fig. 3(c) (lift height 15 nm, zero bias voltage). The domains show a large contrast, while the terrace edge is barely visible. When a bias voltage is applied, the phase difference between both domains becomes larger, and the contrast can be switched when an opposite bias voltage is applied (not shown). This effect is similar to measurements on der Waals heterostructures [31, 7, 6, 9]. However, in our case, the domains are much more pronounced in the topography than reported. This is probably due to the samples’ bulk character and surface quality.

Energy-filtered PEEM imaging can provide spatial information on the elemental composition, but also on changes in the work function caused by the different alignment of the electric polarization, as already shown in the early 1970s by Le Bihan [32, 33] and Morlon et al. [34] for ferroelectric domains in BaTiO₃.

In Fig. 4(a), an energy-filtered PEEM image is shown acquired using a Hg lamp and an analyzer kinetic energy setting of 4 eV. In this mode, the image is dominated by secondary electrons and reflects differences in the work function. The work function contrast reveals a domain structure similar to what was also observed using SEM and SPM. To verify if these domains are not caused by alternations of either a PbS or VS₂ termination of the crystal, an elemental map of the same area was measured using energy-filtered PEEM of the Pb 4f core spectrum (see Fig. LABEL:fgr:fig_s4 in the Supplemental Material [24] for the complete XPS spectrum). As the intensity of the PEEM imaging is very sensitive to the stacking of the final layers of the crystal, a different termination of the sample should result in the appearance of PbS and VS₂ domains. As shown in Fig. 4(b), no contrast is visible, so it can be concluded that the termination of the whole area is the same.

Subsequently, spatially resolved ultraviolet photoelectron spectroscopy (UPS) was used to measure the work function of both domains. In Fig. 4(c), the UPS spectra of the two polarized regions are shown for low binding energies, [-0.5 - +0.5 eV], and high binding energies, [16 - 18 eV]. The low energy window reflects the density of states at the valence band maximum, whereas the high energy window reflects the drop in intensity due to the cut-off energy of secondary electrons. Comparing the data of both domains, it is visible that the Fermi edge remains at the same position. The fit by a Fermi function, dashed lines in Fig. 4(c), gives a Fermi energy position $E_{b}=(0.00\pm 0.02)$ eV. In contrast, the secondary electron energy cut-off around 17.5 eV, derived from the tangential fit, is downshifted by 0.11 eV between the two domains. This indicates that the change in the UPS spectra is due to a different work function of both domains.

In the following part, we discuss the consequences of the observed twins and domains in the (PbS)_1.18VS₂ crystals. In contrast to ‘traditional’ electrically isolating ferroelectrics, (PbS)_1.18VS₂ crystals are semiconducting [19], according to electric transport measurements, or even metallic, according to UPS or UV-VIS absorption spectroscopy [35]. The comparably large conductivity makes the ‘traditional’ electrical characterization used to identify ferroelectric materials and to switch the ferroelectric domains very challenging. Nevertheless, here we show using the combination of the structural data obtained with single crystal XRD and the observed domains obtained using various technique that sliding ferroelectricity is present in bulk MLC crystals .

Generally, the crystal structure refinement of MLCs using single crystal XRD is challenging [36]. However, moiré patterns in van der Waals heterostructures, which work as a magnifying glass [37], provide essential information for the structural refinement of the very small twist angle and strain variations between the different layers.

The presence of moiré structures in (PbS)_1.18VS₂ make this class of materials a possible next platform to explore the physics of strong electronic correlations and possible non-trivial band topology. A first hint of such strongly correlated physics can be found in low-temperature studies which were performed in the past on the MLC LaS_1.17VS₂, which can be either electron or hole-doped using Pb and Sr [38, 39].

To conclude, sliding ferroelectricity has been observed in bulk (PbS)_1.18VS₂ crystals. The mutual interaction between the PbS and VS₂ subsystems is the key mechanism, which introduces well-defined groups of twins in the (PbS)_1.18VS₂ bulk crystal, where the stacking of the twins determines if there is locally a 2H- or 3R-type alignment. The possibility to steer interaction-driven twist angles in bottom-up growth can provide a new pathway to create large-scale moiré landscapes, twintronics, both in thin films and bulk crystals and might remove the problems with manual stacked devices [15].

We thank Peter Minárik for the FIB lamella preparation and Jan Michalička for the support during the HRTEM measurement. The authors acknowledge the support provided by the Czech Science Foundation (project No. 22-04816S) and from the Czech Ministry of Education, Youth, and Sports (MEYS) project SOLID21 (Project No. CZ.02.1.01/0.0/0.0/16_-019/0000760). Single-crystal growth and characterization were performed in MGML, within the program of Czech Research Infrastructures (project no. LM2023065). CzechNanoLab (project no. LM2023051) funded by MEYS CR is acknowledged for the financial support of the TEM measurements at CEITEC Nano Research Infrastructure.