Size-Reduction of Rydberg collective excited states in cold atomic system

The collective effect of large amounts of atoms exhibit an enhanced interaction between light and atoms. This holds great interest in quantum optics, and quantum information. When a collective excited state of a group of atoms during Rabi oscillation is varying, the oscillation exhibits rich dynamics. Here, we experimentally observe a size-reduction effect of the Rydberg collective state during Rabi oscillation in cold atomic dilute gases. The Rydberg collective state was first created by the Rydberg quantum memory, and we observed a decreased oscillation frequency effect by measuring the time traces of the retrieved light field amplitude, which exhibited chirped characteristics. This is caused by the simultaneous decay to the overall ground state and the overall loss of atoms. The observed oscillations are dependent on the effective Rabi frequency and detuning of the coupling laser, and the dephasing from inhomogeneous broadening. The reported results show the potential prospects of studying the dynamics of the collective effect of a large amount of atoms and manipulating a single-photon wave-packet based on the interaction between light and Rydberg atoms.

The interaction of light with an atomic media containing a large number of particles causes a collective effect W. Guerin and Kaiser (2016), which is at the focus of intense research in different areas in quantum metrology, quantum optics, and quantum information. The single collective excitation shared among a large number of ground-state atoms results in a coherent superposition state Dicke (1954); Honer et al. (2011). In contrast to the single atom coupled to the light field this state can still carry only a single excitation; however, the light matter interaction is enhanced owing to a large number of ground state atoms, as predicted by Dicke’s theory. When the single excitation corresponds to the Rydberg excitation, Rydberg-state super atoms were formed Gaëtan et al. (2009); Urban et al. (2009); Dudin et al. (2012); Zeiher et al. (2015); Weber et al. (2015); Beterov et al. (2016); Paris-Mandoki et al. (2017); Busche et al. (2017) consisting of a single Rydberg excitation and many ground state atoms. Because of the exaggerated properties of the Rydberg atom, it is a valuable resource for numerous potential applications in quantum computing Lukin et al. (2001); Saffman (2016), quantum optics Firstenberg et al. (2016), and many-body physics Schauß et al. (2012); Labuhn et al. (2016); Ding et al. (2020, 2021) etc.

Storing photons to Rydberg super atoms can be realized by the technology of quantum memory Bussieres et al. (2013); Ding et al. (2016a), in which an interface between light and Rydberg atoms is created that allows for the storage and retrieval of the optical field. Demonstrating a Rydberg-mediated quantum memory could enable the implementation of quantum computation and information processing with the advantages of Rydberg super atoms, for example, by converting a Rydberg super atom to a single photon, the demonstration of a deterministic single-photon generator can be realized Dudin and Kuzmich (2012); Ripka et al. (2018). Coherently preparing and manipulating the Rydberg super atom based on quantum memory holds promise in quantum information science; it should be studied. When the stored collective excited state is driven by the read field, a Rabi oscillation dynamics of the quantum reading process as studied in a double-$\varLambda$ system Du et al. (2008); Mendes et al. (2013); de Oliveira et al. (2014), however, an anomalous reduction-frequency oscillation with a varying frequency has never been reported before.

In this work, we prepared a Rydberg super atom through quantum memory in the Rydberg electromagnetically induced transparency (Rydberg EIT) configuration. Rabi oscillation between the low-lying collective excited-state and high-lying Rydberg-state super atom is realized by driving the coupling laser in the reading process. The retrieved probe pulse exhibits chirped characteristics because of the reduction of the effective size of the Rydberg super atom. Combining the two-level atoms dephasing model extracted from inhomogeneous broadening, we model our experimental observations with a decreased-frequency Rabi oscillation function. The coherent Rabi oscillation in the Rydberg quantum memory process is a new representation for combining the collective dynamical behavior of Rydberg atoms and the radiation of a single photon, which is crucial for the applications of Rydberg atoms in quantum information processing Saffman et al. (2010) and for providing a versatile interface between light and atoms.

Experimental setup

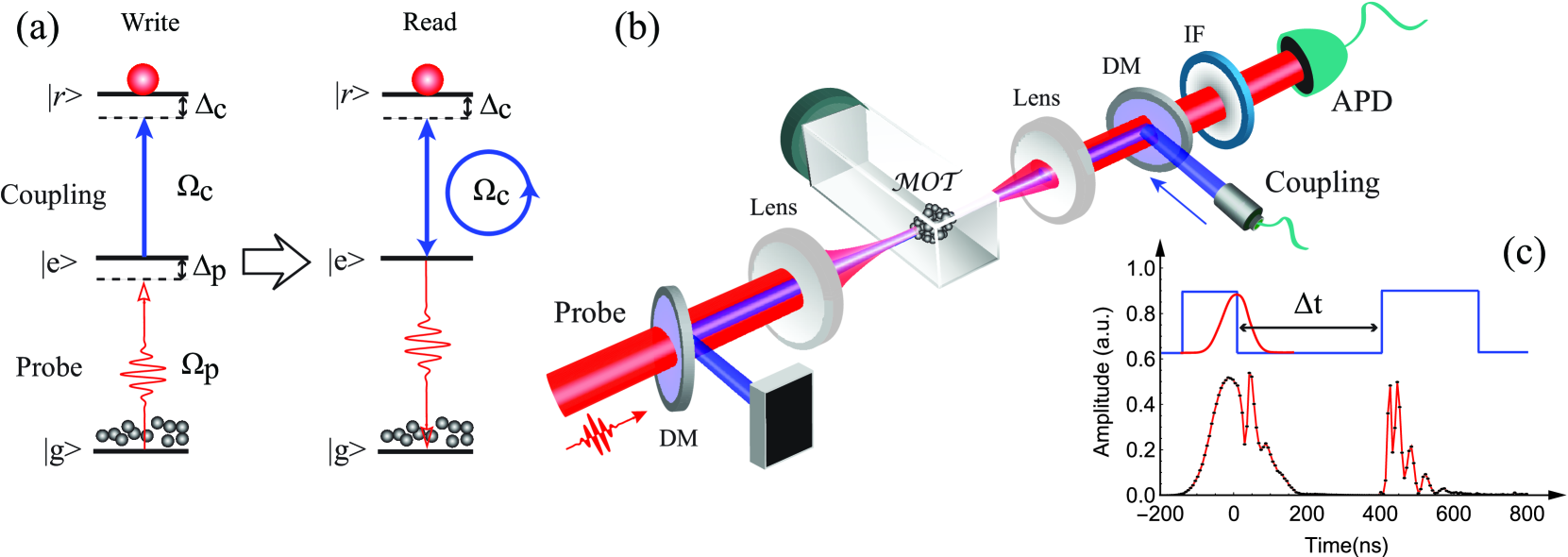
The schematics of the energy levels, experimental setup, and time sequence are shown in figure 1(a)–(c). The sample media is an optically thick atomic ensemble of Rubidium 85 trapped in MOT. This atomic cloud has a size of $500\leavevmode\nobreak\ \mu$m with a temperature $\sim$ 20 $\mu$K and an average density of $\sim 1.0\times 10^{11}\textrm{c$\textrm{m}^{-3}$}$ at the center of the cloud. The optical depth (OD) in MOT is approximately $20$. The probe field is then input into the atomic cloud using a beam waist $\sim 5$ $\mu\textrm{m}$ in the center of the MOT estimated by fluorescence imaging, which is covered by the coupling beam with a beam waist of 16 $\mu\textrm{m}$. With a coupling laser beam, we demonstrate the quantum memory via Rydberg-EIT in the ladder-type atomic configuration, consisting of a ground state $\left|g\right\rangle$, an excited state $\left|e\right\rangle$, and a highly-excited Rydberg state $\left|r\right\rangle$; here, $n=50$. The probe and coupling fields are counter-propagating, and couple the two-photon transitions $\left|g\right\rangle\rightarrow\left|e\right\rangle\rightarrow\left|r\right\rangle$, forming a Ladder-type EIT. The bandwidth of the transparency window of Rydberg-EIT is measured as $\delta w\sim 2\pi\times 5$ MHz.

The probe field has a pulse width of 200 ns. The coupling field is modulated into double rectangular pulses with a width of 400 ns to demonstrate the write and read operations. The amplitudes and frequencies of the write and read pulses are tuned individually by an electro-optic modulator (EOM, LM 0202, Germany) and an acoustic-optic modulator (AOM) respectively; therefore, we can turn on/off the coupling field with fast rising and falling time. This guarantees that the probe is efficiently converted into the Rydberg polariton. We adiabatically switch off the coupling field, and a stored high-lying Rydberg-state super atom is obtained given by $1/\sqrt{N_{m}}\sum e^{i\mathbf{\mathit{\mathbf{k}}}_{S}\mathbf{\cdot\mathit{\mathbf{r}}}_{i}}\left|g\right\rangle_{1}\cdot\cdot\cdot\left|r\right\rangle_{i}\cdot\cdot\cdot\left|g\right\rangle_{N_{m}}$ Fleischhauer et al. (2005); Ding et al. (2013, 2015a, 2015b), also referred to as a Rydberg polariton. $\mathbf{\mathrm{\mathit{k}}}_{S}=\mathbf{\mathrm{\mathit{k}}}_{c}-\mathbf{\mathrm{\mathit{k}}}_{p}$ is the wave vector of the atomic polariton, $\mathbf{\mathrm{\mathit{k}}}_{c}$ and $\mathbf{\mathit{k}}_{p}$ are the vectors of the coupling and probe fields and $\mathbf{\mathit{\mathbf{r}}}_{i}$ denotes the position of the $i$-th atom in atomic cloud. After a programmed storage time, the polariton is converted back into photonic excitation by switching on the coupling laser again. Figure 1(c) shows the storage sequence for the probe pulse; the leaked and retrieved probe fields both exhibit oscillation.

The repetition rate of our experiment is $200$ Hz, and the MOT trapping time is 4.71 ms. Moreover, the experimental window is 290 $\mu$s. The probe field is collected into a single-mode fiber and detected by a single-photon detector (avalanche diode, PerkinElmer SPCM-AQR-16-FC, 60% efficiency, maximum dark count rate of 25/s). The two detectors are gated by an arbitrary function generator. The signal from the single-photon detector and the triggered signal from the arbitrary function generator are then sent to a time-correlated single-photon counting system (TimeHarp 260) to measure the probe temporal profile.

Results

Theoretical analysis

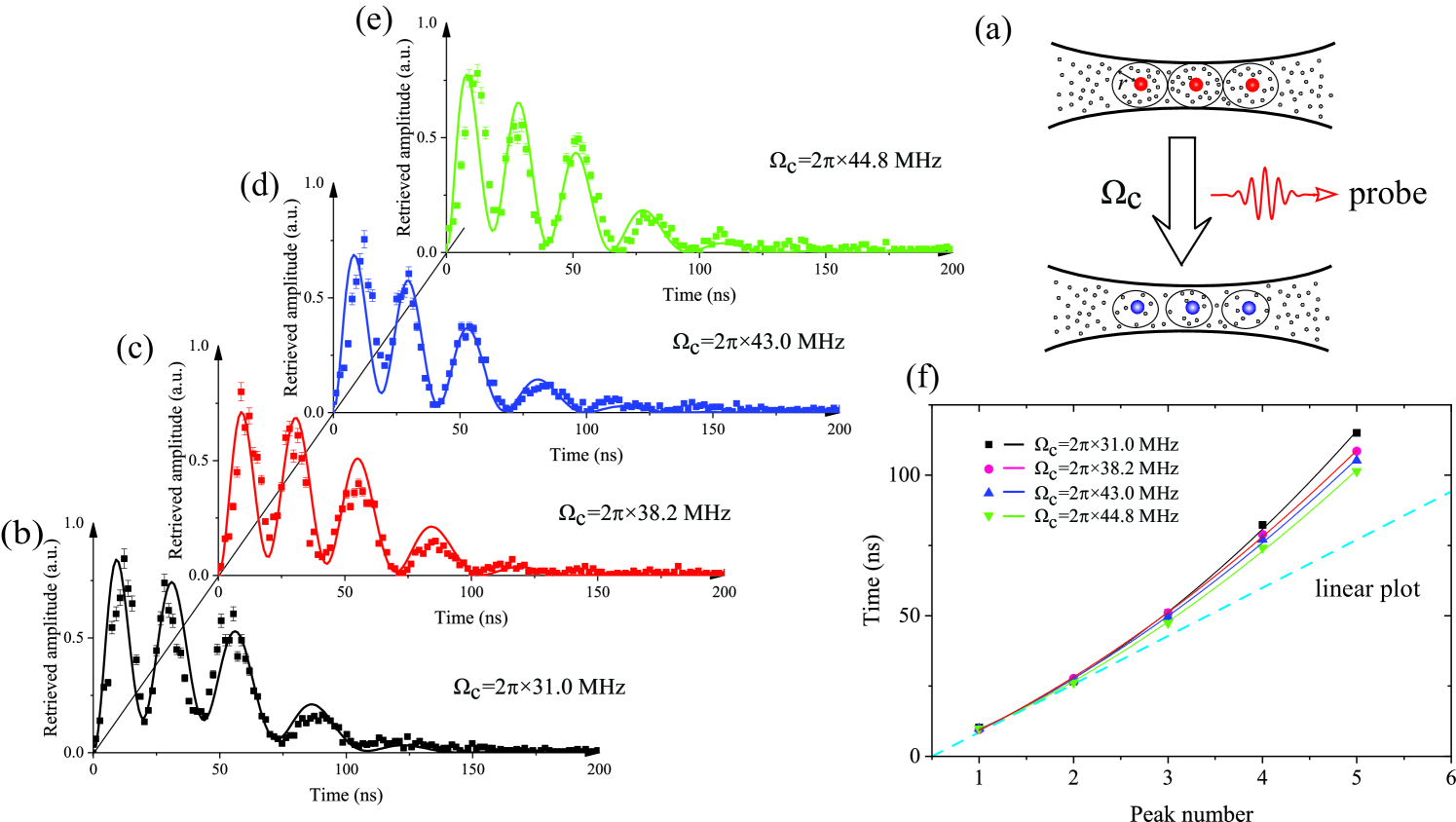
In the storage process, the input probe field contains approximately 10 photons per pulse, and the efficiency of converting the photons to Rydberg polaritons is measured as $\sim 0.04$, guaranteeing one polariton excitation in the one storage process. The probe field illuminates the entire ensemble and excites all atoms with equal probability. Owing to the $L$-length cylinder mesoscopic atomic ensemble along the direction of probe beam, our system can be regarded as quasi-one-dimensional mesoscopic atomic ensemble, see the schematic diagram in Fig. 2(a). After storing the probe pulse in this medium, the converted Rydberg polariton can be expressed as follows:

$$\displaystyle\left|R_{m}\right\rangle=\frac{{\rm 1}}{\sqrt{\mathcal{N}_{m}}}\sum\limits_{i=1}^{i=\mathcal{N}_{m}}e^{i\Delta\mathbf{k}\cdot\mathbf{r}_{i}}\left|g_{1}\cdots r_{i}\cdots g_{\mathcal{N}_{m}}\right\rangle$$

(1)

where $\mathcal{N}_{m}$ is the atom number in interacted area $m$, $\mathbf{\Delta\mathbf{k}}$ is the wave-vector mismatch between the probes, and coupling fields, $\mathbf{r}_{i}$ is the position of atom $i$. Accordingly, the low-lying collective excited state is given

$$\left|E_{m}\right\rangle=\frac{{\rm 1}}{\sqrt{\mathcal{N}_{m}}}\sum\limits_{i=1}^{i=\mathcal{N}_{m}}e^{i\mathbf{k_{p}}\cdot\mathbf{r}_{i}}\left|g_{1}\cdots e_{i}\cdots g_{\mathcal{N}_{m}}\right\rangle$$

(2)

Owing to the atoms loss and nonlinear conversion in the reading process, the size of the collective states $\left|E_{m}\right\rangle$ or $\left|R_{m}\right\rangle$ decreased. This reduction can be observed by observing the populations $\left|E_{m}\right\rangle$ or $\left|R_{m}\right\rangle$ under the driving of the coupling laser beam. The low-lying collective excited state is converted into the $\mathbf{k}_{\mathbf{p}}$-photon pulse with an efficiency of $\eta$, $\left|E_{m}\right\rangle\rightarrow\sqrt{\eta}\left|G_{m}\right\rangle+\sqrt{1-\eta}\left|E_{m}\right\rangle$, here $\left|G_{m}\right\rangle=\left|g_{1}\cdots g_{i}\cdots g_{\mathcal{N}_{m}}\right\rangle$ which is the ground state with multiple atoms. In this process, the loss of atoms is influenced by driving the coupling laser beam, in which there is no emitted probe field. The nonlinear converted efficiency $\eta$ is dependent on the experimental parameters, such as OD, $\gamma_{e}$, $\Omega_{c}$ and $\Delta_{c}$ in the reading process, as the quantum memory is regarded as a delayed four-wave mixing process Ripka et al. (2018). Consequently, the collective Rabi frequency coupling the collective state $\left|R_{m}\right\rangle$ and $\left|E_{m}\right\rangle$ becomes Tresp (PhD Thesis, 2017)

	$\displaystyle\Omega_{\mathrm{coll}}$	$\displaystyle=-\frac{e\varepsilon}{\hbar}\left\langle E_{m}\right|\mathbf{r}\left|R_{m}\right\rangle$		(3)
		$\displaystyle=-\frac{e\varepsilon}{\hbar}\frac{{\rm\sqrt{\eta}}}{\sqrt{\mathcal{N}_{m}}}\sum\limits_{i=1}^{i=\mathcal{N}_{m^{\prime}}}\left\langle g_{1}\cdots g_{i}\cdots g_{\mathcal{N}_{m^{\prime}}}\right|\mathbf{r}\left|g_{1}\cdots r_{i}\cdots g_{\mathcal{N}_{m}}\right\rangle$
		$\displaystyle-\frac{e\varepsilon}{\hbar}\frac{{\rm\sqrt{1-\eta}}}{\mathcal{N}_{m}}\sum\limits_{i=1}^{i=\mathcal{N}_{m^{\prime}}}\left\langle g_{1}\cdots e_{i}\cdots g_{\mathcal{N}_{m^{\prime}}}\right|\mathbf{r}\left|g_{1}\cdots r_{i}\cdots g_{\mathcal{N}_{m}}\right\rangle$
		$\displaystyle=\frac{N_{m^{\prime}}}{\sqrt{N_{m}}}{\rm\sqrt{\eta}}\Omega_{g}+\frac{N_{m^{\prime}}}{N_{m}}{\rm\sqrt{1-\eta}}\Omega$

Here, $N_{m^{\prime}}$ is the remaining number of ground state atoms owing to the loss induced by blue laser driving. $\Omega_{g}=-\frac{e\varepsilon}{\hbar}\left\langle g\right|\mathbf{r}\left|r\right\rangle$, corresponds to the Rabi frequency of a two-level single atom between the ground state $\left|g\right\rangle$ and Rydberg state $\left|r\right\rangle$ and $\Omega=-\frac{e\varepsilon}{\hbar}\left\langle e\right|\mathbf{r}\left|r\right\rangle$ corresponds to the Rabi frequency of a two-level single atom between the excited state $\left|e\right\rangle$ and Rydberg state $\left|r\right\rangle$. The first term corresponds to the enhanced effective Rabi frequency, which was not considered in our experiment (we detected only the transition process between $\left|e\right\rangle$ and $\left|r\right\rangle$). The equation Eq.(3) gives rise to an anomalous oscillation between the residual low-lying collective excited state $\left|E_{m}\right\rangle$ and the high-lying Rydberg-state super atom $\left|R_{m}\right\rangle$, with a decreased Rabi frequency $N_{m^{\prime}}\Omega{\rm\sqrt{1-\eta}}/N_{m}$. Because the quantum state $\left|E_{m}\right\rangle$ is continuously converted to $\left|G_{m}\right\rangle$ and the ground state atoms are lost during the reading process, the effective Rabi frequency $\Omega_{\mathrm{coll}}$ decreases with time during the oscillation as stated.

The reading process in our system can be modeled using a two-level atomic system with a varying effective Rabi frequency because the super atom could be regarded as a quasi-single particle. In the state evolution, as we consider the inhomogeneous broadening in our system, the broadening width can be embodied by the transparency bandwidth of the Rydberg-EIT. The probability of the retrieved signal is distributed as a Gaussian profile owing to the time reversal in the writing and reading processes Novikova et al. (2007); Everett et al. (2018); Ding et al. (2016a) $\sim$ $e^{-C^{2}t^{2}}$. The probability of the retrieved probe pulse under Rabi oscillation is expressed by Stanojevic and Côté (2009):

$$P_{r}(\beta,\Delta,C,t_{0},\Omega_{n},t)\\ =e^{-\beta^{2}(t-t_{0})^{2}}(1-\mathrm{Cos}(\sqrt{\frac{e^{-C^{2}t^{2}}+1}{2}}\Omega t))$$

(4)

The term $e^{-\beta^{2}(t-t_{0})^{2}}$ is the fitted emission rate from a low-lying collective excited state to a photon; $C^{2}$ is the chirped coefficient, and $t_{0}$ is a parameter that fits the temporal profile of the probe intensity. The Rabi frequency $\Omega=\sqrt{\varDelta^{2}+\Omega_{n}^{2}}$. $\Omega_{n}$ is the effective Rabi frequency of the atomic transitions $\left|r\right\rangle$ and $\left|e\right\rangle$ involving $\Omega_{c}$ and $\Delta_{c}$. The temporal profile of the retrieved probe field can be simulated by integrating the inhomogeneous shift $\varDelta$:

$$P_{s}(\beta,C,t_{0},\Omega_{n},t)\\ =\int_{-\infty}^{+\infty}\sqrt{\pi/\alpha}e^{-\alpha\Delta^{2}}P(\beta,\Delta,C,t_{0},\Omega_{n},t)d\varDelta$$

(5)

here, we consider the energy broadening effect, which is distributed with a Gaussian function $\sqrt{\pi/\alpha}e^{-\alpha\varDelta^{2}}$; here $\alpha$ is the broadening coefficient.

Size-reduction of Rabi oscillations

To explore the chirped character of the observed Rabi oscillations, we measure the temporal profile of the retrieved probe field with varying $\Omega_{c}$. Here, we set $\Delta_{p}=-2\pi\times 2.7$ MHz and $\Delta_{c}=2\pi\times 14.79$ MHz to write the Rydberg polariton and set $\Delta_{c}=2\pi\times 23.4$ MHz to read the Rydberg polariton out. We record the retrieved probe field, and deduce that the oscillation exhibits a period of gradual increase, which corresponds to a chirped pulse; the results are shown in Fig. 2(b-e). The effective Rabi frequency, $\Omega_{n}$, was fitted as $2\pi\times 46.1$ MHz, $2\pi\times 47.7$ MHz, $2\pi\times 49.3$ MHz, and $2\pi\times 50.9$ MHz, as shown in Fig. 2(b-e), which tend to be consistent with $\Omega_{n}^{exp}$ at large $\Omega_{c}$ by considering the effective Rabi frequency $\Omega_{n}^{exp}=\sqrt{\Omega_{c}^{2}+\varDelta_{c}^{2}}$. The different peaks against time are plotted in Fig. 2(f), which are fitted by the polynomial function $y=y_{0}+bx+cx^{2}$ different from the normal fixed oscillation period with linear behavior. The collective state $\left|E_{m}\right\rangle$ is continuously converted to $\left|G_{m}\right\rangle$ during the reading process and the collective Rabi frequency gradually decreased over time. This observation differs from previous works Dudin et al. (2012). The Rabi oscillation is demonstrated with fixed $N_{m}$ and $\Omega$, thus the Rabi frequency is a constant of $\sqrt{N_{m}}$$\Omega$.

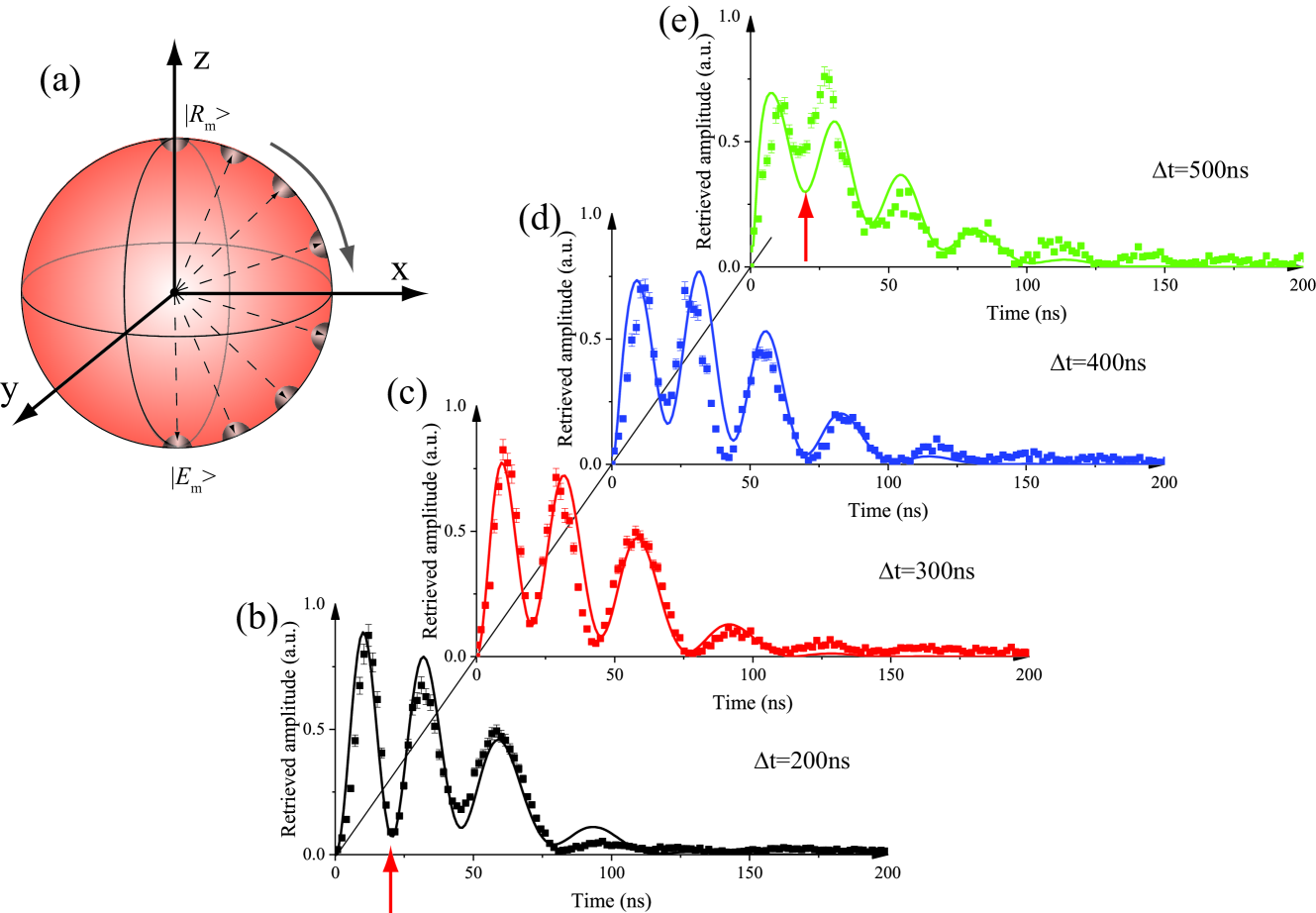
This process can be regarded as shaping a light pulse; the advantage of shaping a light pulse with this method is that the shaping operation is on-demand. Next, we change the storage time $\Delta t$ and record the retrieved probe field; the results are shown in Fig. 3(b-e). Dephasing also occurs during the storage process, which affects the coherence of the Rabi oscillations between the collective $\left|R_{m}\right\rangle$ and $\left|E_{m}\right\rangle$. In the Bloch sphere given in Fig. 3(a), the trajectory of rotations driven by the coupling field do not express a curve but a surface because the point on the Bloch sphere is replaced by a sphere surface. The size of the sphere surface is determined by the broadening coefficient $\alpha$. The broadening effect reduces the visibility of the Rabi oscillations and may even suppress them significantly as decoherence in the storage process de Léséleuc et al. (2018); Levine et al. (2018). As observed in Fig. 3(b), the retrieved probe pulse shows an obviously decreased visibility which is marked by the red arrow. When increasing the storage time from $\Delta t=200$ ns to $\Delta t=500$ ns, the visibility is further reduced, as shown in Fig. 3(b-e) because of the increased $\alpha$. This is because the collective state is dephased during storage, which generates a finite storage lifetime. The atoms in the MOT are not spin-polarized, and the absence of spin polarization with respect to light leads to an inhomogeneous broadening of the Rabi frequencies and, therefore, to dephasing. Additionally, the inhomogeneous $\Omega_{c}$ caused by the transverse differentiated intensity distribution of the coupling field induce additional dephasing. The broadening effect reflects the broadened bandwidth of the transparency window of the Rydberg EIT, as given in Ref. Yu et al. (2020).

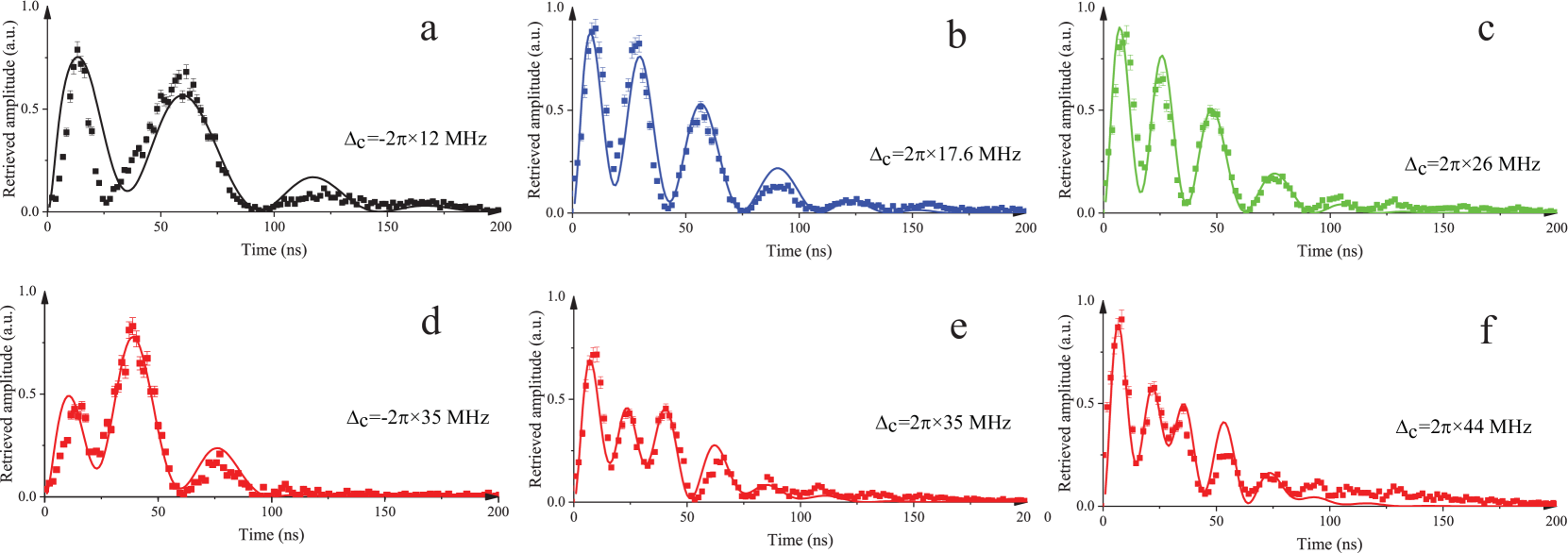
Moreover, we changed the detuning $\Delta_{c}$ to explore the evolution of the collective state. In this process, we write the high-lying Rydberg-state super atom under the optimized condition $\Delta_{p}=-2\pi\times 2.7$ MHz and $\Delta_{c}=2\pi\times 14.8$ MHz. In the read process, the temporal profile of the retrieved probe field is changed by varying $\Delta_{c}$. The results are given in Fig. 4(a-e), in which the detuning $\Delta_{c}$ is changed to $-2\pi\times 12$ MHz, (b) $2\ pi\ times17.6$ MHz, and (c) $2\pi\times 26$ MHz (c) respectively. The periods of these oscillations are clearly increased as the effective Rabi frequencies are increased versus $\Delta_{c}$. The theoretical function fits the results in Fig. 4(b) and Fig. 4(c) but with uncertainty deviations for the red detuning of $\Delta_{c}$ as shown in the example in Fig. 4(a).

When the detuning $\Delta_{c}$ is large enough, we can evaluate more complex oscillations shown in Fig. 4(e-f). In these two cases, we set the detuning $\Delta_{c}=2\pi\times 35$ MHz and $\Delta_{c}=2\pi\times 44$ MHz, respectively. The constructive and destructive interference appeared alternately along the time axis in Fig. 4(e) and (f) supports a superposition of two Rabi oscillations, with fitted Rabi frequencies $\Omega_{n}=2\pi\times 41.4$, $2\pi\times 62.1$ MHz for Fig. 4(e) and $\Omega_{n}=2\pi\times 49.3$, $2\pi\times 68.4$ MHz for Fig. 4(f). Accordingly, the system is described by state $\left|\psi\right\rangle=c_{1}\left|R_{m1}\right\rangle+c_{2}\left|R_{m2}\right\rangle+c_{3}\left|E_{m}\right\rangle$. The coefficients $c_{1}$, $c_{2}$ and $c_{3}$ are the time-dependent complex amplitudes, here $\left|R_{m1}\right\rangle$ and $\left|R_{m2}\right\rangle$ correspond to the states of high-lying Rydberg-state super atoms. However, for the red detuning $\Delta_{c}=-2\pi\times 35$ MHz in Fig. 4(d) completely opposite to the case in Fig. 4(e), there is a single oscillation with fitted Rabi frequencies $\Omega_{n}=2\pi\times 41.4$ MHz. The measured data with $\Delta_{c}=\pm 2\pi\times 35$ MHz with asymmetric Rabi oscillations supports that an enhanced Rabi oscillation process occurs under blue detuning.

Conclusion

In summary, the entire process of the Rydberg-quantum memory with Rabi oscillation can be considered as manipulating a Rydberg super atom to shape the photon wave-packet. The unique technology to modulate the photon wave-packet presented here is based on the Rabi oscillation between different collective excited states. This is significantly different from the progresses of using electro-optical modulators to directly modulate the amplitude of single-photon wave packets Kolchin et al. (2008); Specht et al. (2009) or modulating the properties of pump fields by electro-optical modulators and spatial light modulation to change the temporal quantum waveform of narrowband biphotons in cold atoms Chen et al. (2010); Zhao et al. (2015), or modulating photonic bandwidth through sum frequency generation Rakher et al. (2011); Lavoie et al. (2013). The anomalous Rabi oscillations hint that the arbitrary photonic wave-packet could be constructed via superposing multi-polaritons with more tunable detunings. The reported results combined the techniques of quantum memory and the anomalous Rabi oscillations have potential in modulating the single photon wave-packet Dudin and Kuzmich (2012) and provide a perspective approach of constructing an interface between light and the atoms to study collective effect. Additionally, this can be regarded as a tool to realize the manipulation of the quantum state towards the study of quantum mechanics in the microscopic field.

Acknowledgments

Dong-Sheng Ding and Yi-Chen Yu contributed equally to the study. The authors would like to thank Prof. Wei Zhang, Jin-Ming Cui, and Prof. Xiang-Dong. Chen for the initial discussions on the results, Prof. Lin Li. from Huazhong University Of Science and Technology and Prof. Yuan Sun from the National University of Defense Technology for their valued discussions. This study was supported by the National Key R&D Program of China (2017YFA0304800). the National Natural Science Foundation of China (Grant Nos. U20A20218, 61525504, 61435011), and Fundamental Research Funds for the Central Universities, and the Youth Innovation Pro motion Association of CAS under Grant No. 2018490.

Conflict of interest The authors declare no conflict of interest.