SIS: Seam-Informed Strategy for T-shirt Unfolding
Abstract
Seams are information-rich components of garments. The presence of different types of seams and their combinations helps to select grasping points for garment handling. In this paper, we propose a new Seam-Informed Strategy (SIS) for finding actions for handling a garment, such as grasping and unfolding a T-shirt. Candidates for a pair of grasping points for a dual-arm manipulator system are extracted using the proposed Seam Feature Extraction Method (SFEM). A pair of grasping points for the robot system is selected by the proposed Decision Matrix Iteration Method (DMIM). The decision matrix is first computed by multiple human demonstrations and updated by the robot execution results to improve the grasping and unfolding performance of the robot. Note that the proposed scheme is trained on real data without relying on simulation. Experimental results demonstrate the effectiveness of the proposed strategy. The project video is available at https://github.com/lancexz/sis.
I INTRODUCTION
Garment unfolding remains an open challenge in robotics. Existing research utilizes folds [1, 2, 3], edges [4, 5], outline points, and structural regions [6, 7] as primary references for selecting grasping points, or uses a value map calculated using models trained in simulators [8, 9, 10, 11, 12]. However, none of these methods have utilized seam information. Seams are usually located in the contour position of the garment when fully unfolded. Consequently, the desirable grasping points for unfolding the garment tend to fall near the seams.
We believe that the introduction of seam information could improve the efficiency of the garment unfolding process for the following reasons:
-
•
Seams can be used as a universal garment feature due to their prevalence in different types of garments.
-
•
Seams are more visible than other features when the garment is randomly placed, facilitating the perception process without additional reconfiguration of the garment.
-
•
The introduction of seam information makes it possible to select the grasping points without explicitly using the garment structure, resulting in efficient garment handling.

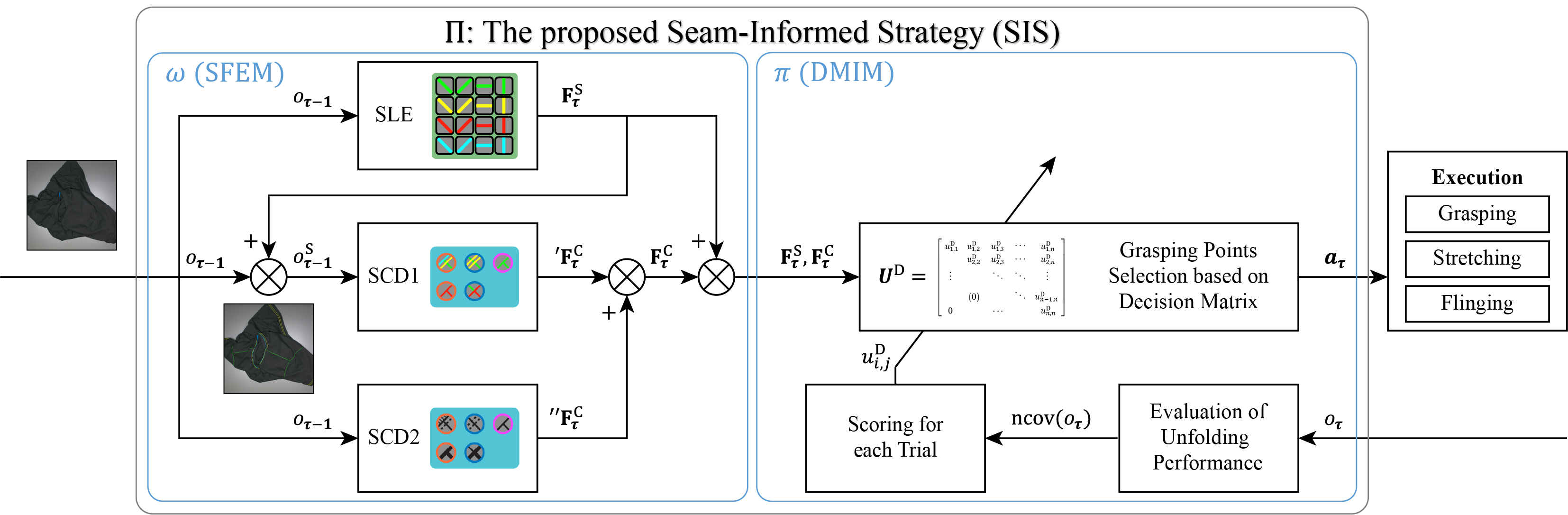
This paper presents Seam-Informed Strategy (SIS), a novel scheme for selecting actions that can be used for automatic garment handling, such as dual-arm robotic T-shirt unfolding. We use the seam segments and their crossings as reference information to limit the search space for selecting grasping points, as shown in Fig. 1.
To facilitate the SIS, we propose a Seam Feature Extraction Method (SFEM) and a Decision Matrix Iteration Method (DMIM). The SFEM is used to extract seam features as candidates for a pair of dual-arm grasping points. The DMIM is used as a comprehensive grasping points selection policy from the extracted candidates for dual-arm unfolding motion planning. This motion involves a sequence of robot motion primitives including grasping, stretching, and flinging to flatten and align the T-shirt.
We train the networks in SFEM with real data annotated by humans. The decision matrix in DMIM is initially computed with human demonstrations and updated with real robot execution results. Using the decision matrix, the robot can also align the orientation of the unfolded T-shirt. We evaluate the efficiency of our scheme on the real robot system through extensive experiments.
In summary, our contributions include:
-
•
We propose SIS, a novel strategy for selecting grasping points for T-shirt unfolding using the seam information. SFEM and DMIM are proposed for this strategy.
-
•
In the proposed SFEM, we formulate the extraction of seam lines as an oriented line object detection problem. This formulation allows the use of any object detection network to efficiently handle curved/straight seam lines.
-
•
We solve the grasping points selection as a scoring problem for combinations of seam segment types using a proposed DMIM, a low-cost solution for unfolding a garment.
-
•
Experimental results demonstrate that the performance of unfolding the T-shirt is promising in terms of obtaining high evaluation metrics with few episode steps.
II Related Work
Unfolding and flattening is the first process that enables various garment manipulation tasks. However, the selection of grasping points remains a challenging aspect of garment unfolding. Much work has been done so far.
II-A Grasping Points Selection Strategies
There are three main types of strategies for selecting grasping points in garment unfolding or other garment handling tasks: heuristic-based strategy, matching-based strategy, and value-map-based strategy.
II-A1 Heuristic-based Strategy
II-A2 Matching-based Strategy
This strategy first maps the observed garment configuration to a canonical configuration and then obtains the grasping points based on the canonical configuration [15]. The method proposed in [16] estimates the garment pose and the corresponding grasping point by searching a database constructed for each garment type.
II-A3 Value-map-based Strategy
II-B Datasets for Learning-based Methods
One of the key issues for learning-based methods is the lack of data sets when dealing with garments due to the difficulty of annotation. To address this problem, most researchers [8, 9, 10, 11, 12, 18] train their networks using simulators. SpeedFolding[17] uses real data annotated by humans together with self-supervised learning. In [4] and [6], the use of color-marked garments is proposed to automatically generate annotated depth maps. The use of transparent fluorescent paints and ultraviolet (UV) light is proposed by [19] to generate RGB images annotated by the paints observed under UV light.
II-C Unfolding Actions Strategies
In addition to the commonly used Pick&Place, the Flinging proposed by FlingBot[8] is widely used for unfolding actions. FabricFolding[12] introduces a Pick&Drag action to improve the unfolding of sleeves. Meanwhile, DextAIRity[20] proposes the use of airflow provided by a blower to indirectly unfold the garment, thereby reducing the workspace of robots. UniFolding[11] uses a Drag&Mop action to reposition the garment when the grasping points are out of the robot’s reach.
III Problem statement
This paper focuses on automating the process of unfolding a T-shirt from arbitrary configurations by a sequence of grasping, stretching, and flinging motions using a dual-arm manipulator system under the following assumptions:
-
•
Seams are always present on the target T-shirt.
-
•
The shirt is not in an inside-out configuration.
-
•
The shirt does not have pockets attached with seams.
The desired outcomes include reducing the number of necessary steps of robot actions (episode steps) to unfold a T-shirt and increasing the normalized coverage of the final unfolded garment. We also consider the final orientation of the unfolded garment. This section describes the problem to be solved in this paper.
III-A Problem Formulation
Given an observation , captured by an RGB camera with resolution of at episode step , our goal is to develop a policy mapping to an action , i.e. , to make the garment converge to a flattened configuration. The action can be described by the pair of grasping points for the left and right hands, and , w.r.t the image frame .
III-B Outline of the Proposed Scheme
Existing strategies try to map the to a canonical space or a value map to select grasping points pixel-wise. This paper proposes a new Seam-Informed Strategy (SIS) to select grasping points based on seam information. To implement the mapping policy based on SIS, we divide the policy into two policies, and , as shown in Fig. 2.
The policy , which uses the Seam Feature Extraction Method (SFEM), is proposed to extract seam line segments and their crossings from . We use the extracted set of seam line segments and the set of seam crossing segments as candidates for grasping points. The policy is formulated as follows:
| (1) |
The policy using the Decision Matrix Iteration Method (DMIM) is proposed to select a pair of grasping points from the candidates obtained above for the unfolding action of the dual-arm robot. The decision matrix takes into account both human prior knowledge and the results of real robot executions. The policy is formulated as follows:
| (2) |
IV METHOD
As outlined in Section III-B, this paper primarily addresses two challenges. In Section IV-A, we will explain how to extract sets of grasping point candidates and from an RGB image input using the proposed SFEM at each episode step . In Section IV-B, we will explain how to select a pair of grasping points and from the candidates and using the proposed DMIM at each episode step .
IV-A Seam Feature Extraction Method (SFEM)
The proposed SFEM consists of a seam line-segment extractor (SLE) and two seam crossing-segment detectors (SCD1 and SCD2) as shown in Fig. 2 which are designed based on the YOLOv3 [21]. Extracting seams as segments allows them to be used as grasping point candidates.
IV-A1 Seam Line-segment Extractor (SLE)
The YOLOv3 was originally designed for object detection and has proven to be accurate and computationally efficient. For the SLE, we formulate the extraction of curvedstraight seams as an oriented line object detection problem since the YOLOv3 cannot be used directly for seam line segment extraction. The proposed formulation allows any object detection network to extract seam line features.
To extract seams using the object detection network, we first approximate the continuous curved seam as a set of straight line segments. Each straight line segment is described by the seam segment category and its endpoint positions and w.r.t the image frame , i.e. . In this paper, the seam segments are categorized into four categories, namely solid (), dotted (), inward (), and neckline (), as shown in Fig. 3 (a) and (b), based on the seam types of the T-shirt used in the experiments.
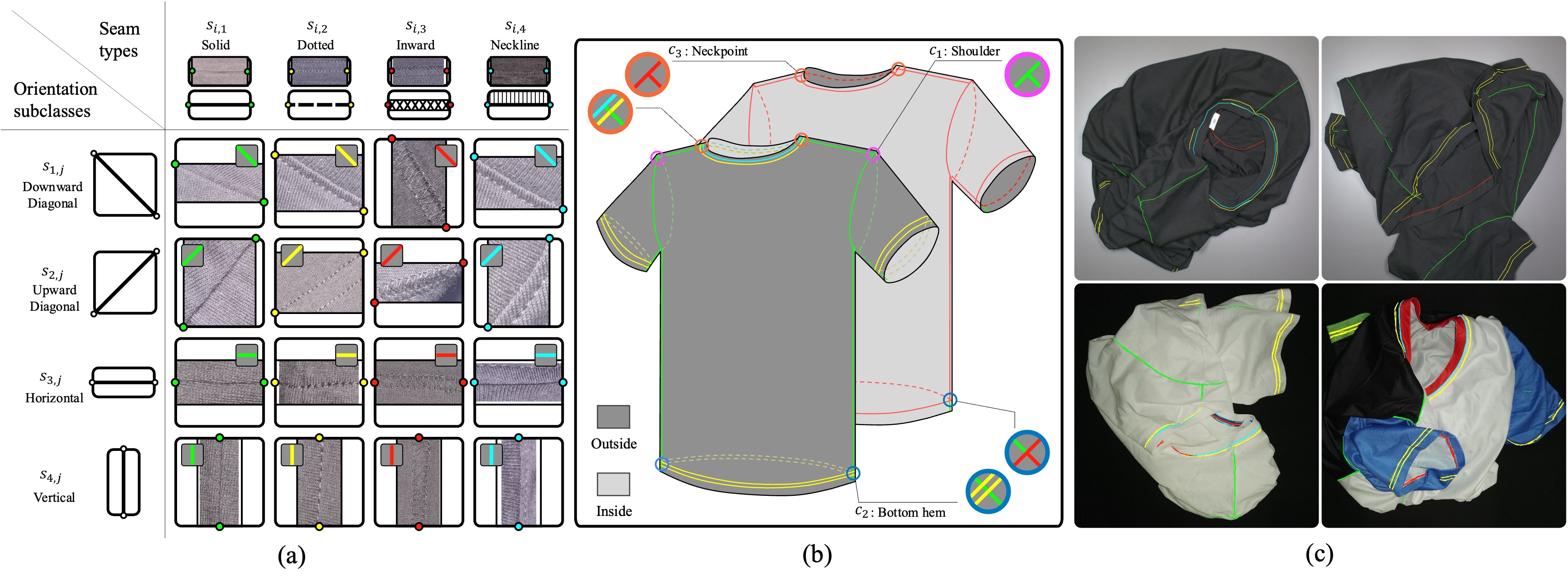
We then convert the straight line segment into a bounding box by using the two endpoints as the diagonal vertices of the bounding box. To represent the orientation of the straight line segment in the bounding box , we divide each seam segment category into four orientation subclasses , namely downward diagonal (), upward diagonal (), horizontal (), and vertical (), as shown in Fig. 3 (a). This quadrupled the number of seam segment categories. Consequently, each oriented seam line segment is defined by the oriented seam segment category and the parameters of the bounding box, i.e. , where denote the coordinate of the center of the bounding box. denote the width and height of the bounding box.
This bounding-box-based categorization of the seam line segment is used as the labeling rule for the SLE shown in Algorithm 1. To implement the SLE, we introduce:
-
•
, a threshold for the width and height of the bounding box in pixels: Note that the computation of the loss function during network training is very sensitive to a tiny or thin object whose area is very small. is introduced in Algorithm 1 to guarantee a minimum size of the bounding box.
-
•
Data augmentation of with recategorization: The orientation subclass is not invariant if the image is flipped or rotated during data augmentation. Recategorization is carried out using Algorithm 1 when the image is flipped or rotated.
The proposed SLE can extract both curved and straight seams as a set of seam line segments. The predicted seam segments are superimposed onto the original observation to generate the seam map , as shown in Fig. 3 (c)
IV-A2 Seam Crossing-segment Detectors (SCDs)
As shown in Fig. 3 (b), three types of seam crossing segments, namely shoulder (), bottom hem (), and neck point () of the T-shirt, are detected by using both SCD1 and SCD2 to increase the recall of the predictions. The inputs of SCD1 and SCD2 are the original image observation and the corresponding seam map , respectively, as shown in Fig. 2.
Note that the outputs of SCD1 and SCD2 are merged considering the maximum number of each type of crossing segments according to the confidence of the predictions, since the number of each type of seam crossing segments on the T-shirt is limited.
IV-B Decision Matrix Iteration Method (DMIM)
The idea of DMIM is proposed based on the following observations of human unfolding actions using a flinging motion:
-
•
The combination of seam segment types (CSST) of two selected grasping points affects the unfolding performance. For example, grasping two points both at the shoulders results in a higher unfolding quality than the other CSSTs.
-
•
The first step of the unfolding action affects the final performance of the unfolding since an appropriate first step action simplifies the complexity of the subsequent steps. Fig. 4 shows some of the intermediate configurations that appear after the first episode step. The grasping points for the next step can be easily obtained for these intermediate configurations. To obtain such intermediate configurations, we intuitively select two grasping points that are empirically far apart.

Based on these observations, we extract the human skill of unfolding by scoring the performance of each CSST through human demonstrations. The DMIM proposed in this paper represents the grasping strategy using a decision matrix. The performance score of each CSST is implemented by initializing the decision matrix with human demonstrations and updating it with robot demonstrations.
IV-B1 Decision Matrix
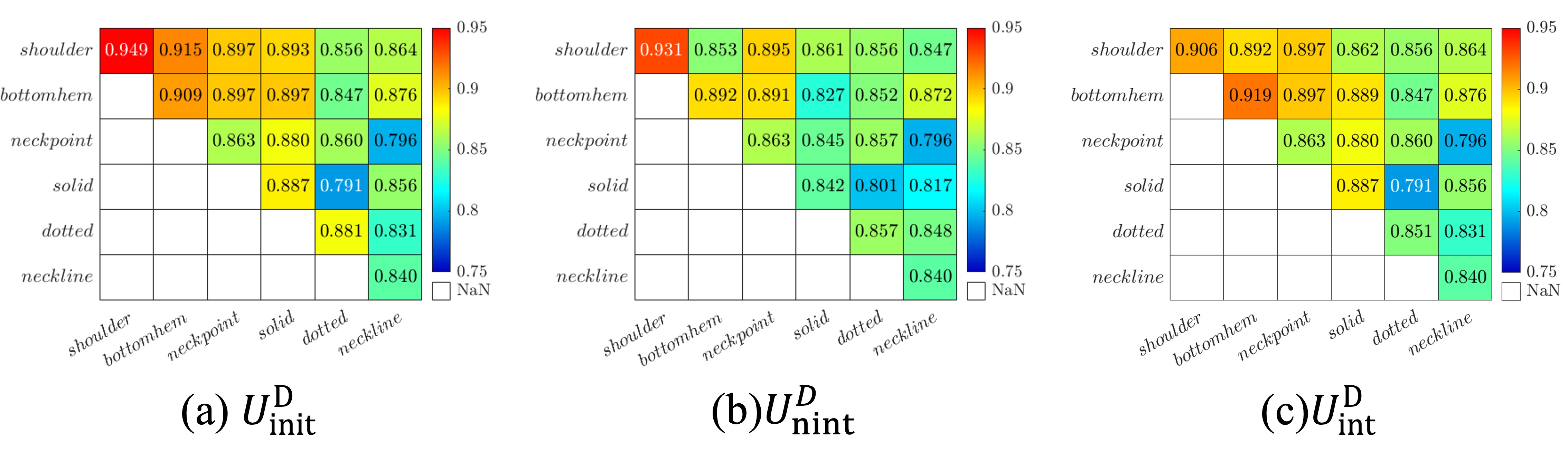
As shown in Fig. 5, the proposed decision matrix is constructed as an upper triangular matrix. In this paper, six types of seam segments are considered, including shoulder, bottom hem, neck point, solid, dotted, and neckline (the inward seam line type is treated as the dotted type in this paper for simplicity). The element of , , is the performance score of the combination of the and the seam segment types, and expressed as follows:
| (4) |
where is the total number of trials of unfolding demonstrations performed by both human and robot. Note that and . For each trial, the average normalized coverage is expressed as follows:
| (5) |
where is the number of episode steps in a trial and is the normalized coverage of the T-shirt from an overhead camera observation at episode step during a trial, similar to [8, 17], and [20]. The normalized coverage is calculated by:
| (6) |
where the coverage is calculated by counting the pixel number of segmented mask output by the Segment Anything Model (SAM) [22]. The maximum coverage is obtained from an image of a manually flattened T-shirt.
The decision matrix is used to select grasping points from the seam segments extracted by SFEM. Based on the score of in the decision matrix and the types of extracted seam segments, the CSST with the highest score is selected. If there are multiple combinations of candidates belonging to each seam segment type of the selected CSST, the most distant candidate pair is selected as the grasping points.
IV-B2 Initialization with Human Demonstrations and Updating with Robot Executions
The initial decision matrix is computed using only the human demonstration data by (4). The same equation is then used to update the decision matrix with subsequent robot executions.
Human hands exhibit more dynamic and flexible movements that allow fine-tuning of the resulting garment configuration, a capability that the robot manipulators lack. In other words, there is a human-to-robot gap in garment manipulation. To bridge this gap, we perform real robot trials to update the decision matrix. This iterative method ensures that the grasping strategy integrates the learned human experience and the real robot explorations.
Note that the unfolding performance can be improved by using two decision matrices based on the normalized coverage of the T-shirt, as shown in Section V-C. Using the same initialized decision matrix, we update the two matrices for intermediate and non-intermediate configurations using robot executions. The decision matrix in Fig. IV-B (c) is for the intermediate configurations with normalized coverage equal to or greater than 0.4, and the decision matrix in Fig. IV-B (b) is for the non-intermediate configurations with normalized coverage less than 0.4. The is also used for the initial configurations.
V EXPERIMENT
The garment unfolding dual-arm manipulator system consists of two Denso VS087 manipulators mounted on a fixed frame, a Basler ACE4096 RGB camera equipped with an 8 mm Basler lens, an Azure Kinect DK depth camera, two ATI Axia80-M20 Force Torque (FT) sensors, and two Taiyo EGS2-LS-4230 electric grippers. The robot control system is constructed based on ROS2 Humble [23] installed on a PC equipped with an RTX3090 GPU, an i9-10900KF CPU, and 64 GB of memory.
V-A Motion Primitives Used for Experiments
Below are the major motion primitives associated with the T-shirt unfolding experiments.
| Exp Name | Dual Matrix (DM) | Seam Information (SI) | Matrix Iteration (MI) | Average evaluation metric at each step over 20 trials (coverage, IoU) | ||||
| 1 | 2 | 3 | 4 | 5 | ||||
| SIS | 0.704, 0.489 | 0.883, 0.783 | 0.933, 0.883 | 0.904, 0.862 | 0.907, 0.871 | |||
| Ab-DM | 0.735, 0.587 | 0.762, 0.642 | 0.725, 0.592 | 0.734, 0.604 | 0.793, 0.687 | |||
| Ab-SI | 0.609, 0.480 | 0.814, 0.728 | 0.891, 0.820 | 0.924, 0.880 | 0.914, 0.881 | |||
| Ab-MI | 0.692, 0.514 | 0.832, 0.759 | 0.878, 0.835 | 0.901, 0.871 | 0.903, 0.873 | |||
V-A1 Grasp&Fling Motion Primitive
Similar to [8], we implement a Grasp&Fling motion primitive to speed up the process of unfolding the garment. After grasping, the T-shirt is stretched by the robot arms until the stretching force reaches a predefined 1.4 N using the wrist FT sensors attached to both manipulators. The robot then generates a flinging motion that mimics the human flinging motion based on fifth-order polynomial interpolation.
V-A2 Randomize Motion Primitive
To generate initial configurations of the T-shirt that are fair enough for comparison, we randomly select a grasping point from the garment area and release it from a fixed position 0.78 m above the table using one of the robot arms. During the experiments described in Section V-C and V-D, the robot repeats this motion before each trial until the normalized coverage of the initial configuration is less than 0.4.
V-B Training/Updating of SFEM and DMIM
V-B1 Training of SFEM
The dataset used to train the SLE consists of 360 images with manually annotated labels of seam line segments. Using data augmentation by image rotation and flipping, we obtain 2304 images for training and 576 images for validation with annotated labels.
The dataset used to train SCD1 consists of 1481 original images with manually annotated labels of seam crossing segments. The dataset used to train SCD2 consists of the same 1481 images overlaid with the seam lines extracted by the trained SLE.
The original images in all datasets are captured by the Basler camera. The resolution of the images used for training is 1280 1024, obtained by resizing the original images.
V-B2 Initialization and Updating of DMIM
The decision matrix is initialized with human demonstrations. For each human trial, we set the maximum number of episode steps to , although two to three steps are usually enough to flatten the T-shirt. Once the T-shirt is flattened, we skip the remaining steps and use the same as in this step for the remaining steps.
To initialize a for each CSST, the demonstrator is asked to randomize the T-shirt until at least one point pair in the CSST appears. The demonstrator then selects the furthest pair of points as grasping points. In the following steps of this trial, the demonstrator selects grasping points based on the demonstrator’s intuition, and the of the CSST is calculated. The matrix is initialized as shown in Fig. 5 (a). Each is computed using (4) with the number of trials .
The DMIM is a simple, yet efficient and easy to implement scheme for selecting grasping points from candidate grasping points extracted by SFEM. As shown in Section V-C, we found that using two decision matrices based on the normalized coverage of the T-shirt significantly improves the unfolding performance. is used for intermediate configurations when and is used for non-intermediate configurations when . is updated from with (5) when and a trial is completed. is updated from with (5) when and an episode step is completed.
V-C Ablation Studies of the Proposed Strategy
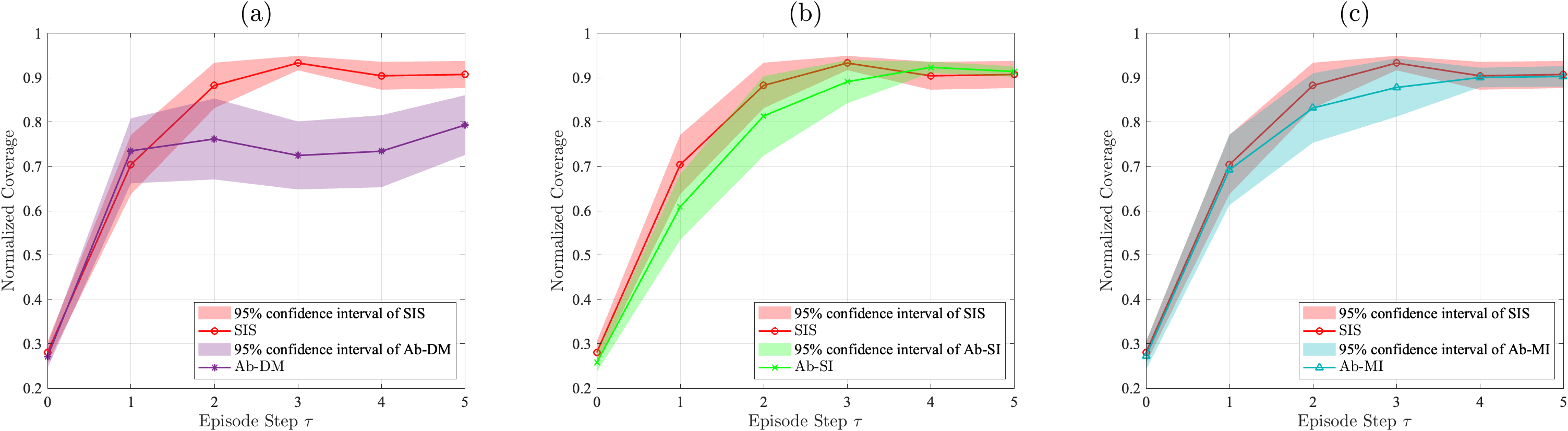
In this section, ablation studies are conducted for our proposed strategy. In the following experiments, 20 trials of experiments are performed, with each trial consisting of five episode steps. The results are shown in Table I and Fig. 6. We use normalized coverage [8, 17, 20] and IoU between the current configuration and the manually unfolded configuration [9] as evaluation metrics, as shown in Table I. Fig. 6 shows the distribution of the evaluation results with 95% confidence interval shading.
In Table I, the SIS is the scheme proposed in this paper based on seam information and DMIM using and .
The Ab-DM was performed using only one updated matrix to unfold the T-shirt in both non-intermediate and intermediate configurations. The unfolding performance of the SIS is better than that of the Ab-DM, as shown in Fig. 6 (a). This shows the effectiveness of introducing two decision matrices based on normalized coverage.
The Ab-SI is performed without the seam information extracted by the SLE and uses only the crossings detected by the SCD2 as grasping point candidates, while and are used. The difference between the Ab-SI and the SIS in Fig. 6 (b) shows that the seam information significantly speeds up the convergence process of the normalized coverage, especially during the first two episode steps.
The Ab-MI is performed to show the effectiveness of the proposed iteration method. In this experiment, is used without updating. The results of Ab-MI show that removing the iteration of increases the variance of the normalized coverage compared to the SIS as shown in Fig. 6 (c). This demonstrates that updating the decision matrix bridges the human-to-robot gap and speeds up the convergence of the normalized coverage.
Note that the following hardware-related failures are excluded from the statistical data since they are not relevant to the performance of our proposed strategy.
-
•
Grasping failures: We consider a grasp to have failed if either one or both of the grippers failed to grasp the selected grasping points on the T-shirt. We also consider the grasp to have failed if the T-shirt falls off the gripper(s) during the robot motion.
Note that similar to [8], we have not filtered out the data when the T-shirt is grasped in its crumpled state, which makes the flinging motion ineffective.
-
•
Motion failures: These occur when the grasping points exceed the working space of the robot, or when an emergency stop is triggered due to robot singularity.
-
•
Releasing failures: We consider a garment release to have failed if the garment remains in the gripper after the gripper fingers open.
V-D Comparison with Existing Research
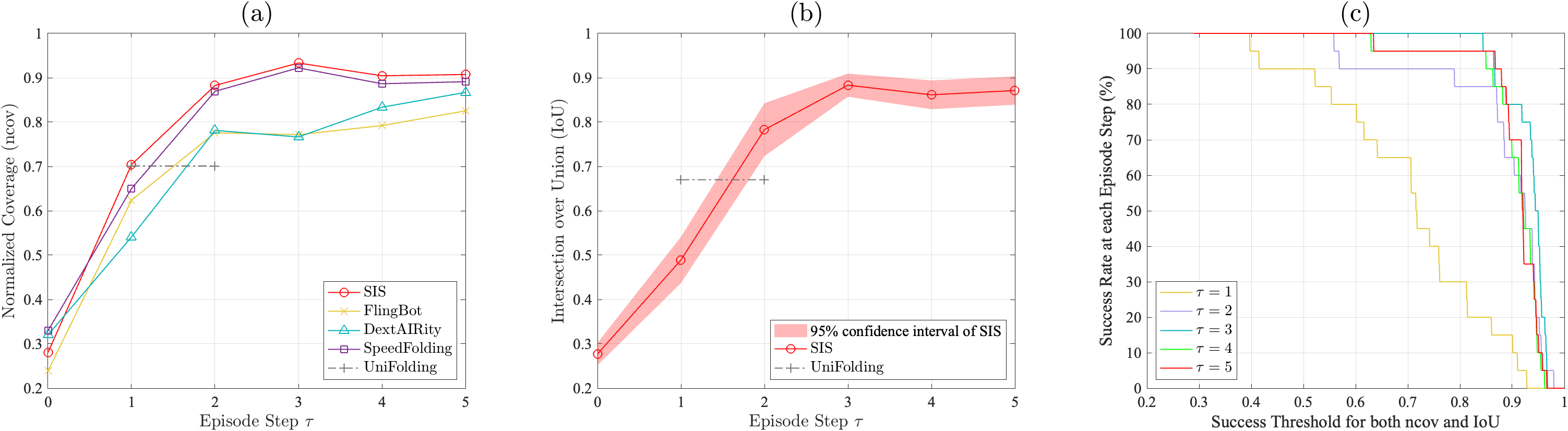
We compare the proposed method in this paper with those presented in [8][17][20], utilizing normalized coverage as the evaluation metric. The results are shown in Fig. 7 (a). Our SIS scheme, which uses only one type of Grasp&Fling motion, outperforms existing methods. The SIS demonstrates faster convergence compared to others, highlighting the effectiveness of our method.
The performance of SpeedFolding is close to the proposed SIS. However, SpeedFolding does not consider the alignment of the orientation of the unfolded T-shirt. The proposed SIS aligns the T-shirt to a specific goal configuration, similar to ClothFunnels [9], which handles a long-sleeved shirt.
Fig. 7 (b) compares the evaluation of orientation alignment of SIS with that of UniFolding [11]. UniFolding shows the IoU results within one or two steps. Our SIS achieves over 0.85 average IoU within three episode steps.
We consider a success unfolding at episode step if both the normalized coverage and the IoU metrics exceed a certain threshold. Fig. 7 (c) plots the success rate under different thresholds for each episode step. Using a threshold of 0.85 for determining a successful unfolding, our scheme achieves 20%, 85%, 90%, 95%, and 95% success rates in 20 trials at episode steps and , respectively. Fig. 8 illustrates ten examples of qualitative results captured during these 20 trials. In most cases, both the normalized coverage and the IoU exceed 0.85 within three episode steps.

VI CONCLUSION
In this paper, we propose a Seam-Informed Strategy (SIS) that uses seam information to select a pair of grasping points for a dual-arm robot system to unfold a T-shirt.
We propose a Seam Feature Extraction Method (SFEM) to extract seam line segments and seam crossing segments as grasping point candidates in our strategy. The proposed formulation in the seam line-segment extractor (SLE) allows any object detection network to handle curvedstraight seam lines.
We propose a Decision Matrix Iteration Method (DMIM) for selecting a pair of grasping points from the candidates extracted by SFEM. The decision matrix is initialized with human demonstrations and updated with robot executions, thus bridging the Human-to-Robot gap. The proposed DMIM is a low-cost solution to align the unfolded T-shirt orientation.
The experimental results have shown that the proposed SIS effectively solves the problem of T-shirt unfolding. The performance of T-shirt unfolding is promising in terms of obtaining high evaluation metrics with few episode steps.
The generalization performance of the proposed SIS will be further investigated in our future work.
Acknowledgment
This work was supported in part by the Innovation and Technology Commission of the HKSAR Government under the InnoHK initiative. The research work described in this paper was in part conducted in the JC STEM Lab of Robotics for Soft Materials funded by The Hong Kong Jockey Club Charities Trust.
References
- [1] D. Triantafyllou, I. Mariolis, A. Kargakos, S. Malassiotis, and N. Aspragathos, “A geometric approach to robotic unfolding of garments,” Robot. Auton. Syst. (RAS), vol. 75, pp. 233–243, 2016.
- [2] A. Doumanoglou, J. Stria, G. Peleka, I. Mariolis, V. Petrik, A. Kargakos, L. Wagner, V. Hlaváč, T.-K. Kim, and S. Malassiotis, “Folding clothes autonomously: A complete pipeline,” IEEE Trans. Robot. (TRO), vol. 32, no. 6, pp. 1461–1478, 2016.
- [3] J. Stria, V. Petrík, and V. Hlaváč, “Model-free approach to garments unfolding based on detection of folded layers,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst. (IROS), 2017, pp. 3274–3280.
- [4] A. Gabas and Y. Kita, “Physical edge detection in clothing items for robotic manipulation,” in Proc. IEEE Int. Conf. Robot. Autom. (ICRA), 2017, pp. 524–529.
- [5] X. Lin, Y. Wang, Z. Huang, and D. Held, “Learning visible connectivity dynamics for cloth smoothing,” in Proc. Mach. Learn. Res. (PMLR), vol. 164, 08–11 Nov 2022, pp. 256–266.
- [6] W. Chen, D. Lee, D. Chappell, and N. Rojas, “Learning to grasp clothing structural regions for garment manipulation tasks,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst. (IROS), 2023.
- [7] R. Wu, H. Lu, Y. Wang, Y. Wang, and H. Dong, “Unigarmentmanip: A unified framework for category-level garment manipulation via dense visual correspondence,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), June 2024, pp. 16 340–16 350.
- [8] H. Ha and S. Song, “Flingbot: The unreasonable effectiveness of dynamic manipulation for cloth unfolding,” in Proc. Conf. Robot. Learn. (CoRL), 2021.
- [9] A. Canberk, C. Chi, H. Ha, B. Burchfiel, E. Cousineau, S. Feng, and S. Song, “Cloth funnels: Canonicalized-alignment for multi-purpose garment manipulation,” in Proc. IEEE Int. Conf. Robot. Autom. (ICRA), 2023, pp. 5872–5879.
- [10] N.-Q. Gu, R. He, and L. Yu, “Learning to unfold garment effectively into oriented direction,” IEEE Robot. Autom. Lett. (RAL), 2023.
- [11] H. Xue, Y. Li, W. Xu, H. Li, D. Zheng, and C. Lu, “Unifolding: Towards sample-efficient, scalable, and generalizable robotic garment folding,” arXiv:2311.01267, 2023.
- [12] C. He, L. Meng, Z. Sun, J. Wang, and M. Q.-H. Meng, “Fabricfolding: learning efficient fabric folding without expert demonstrations,” Robotica, vol. 42, no. 4, pp. 1281–1296, 2024.
- [13] F. Osawa, H. Seki, and Y. Kamiya, “Unfolding of massive laundry and classification types by dual manipulator,” J. Adv. Comput. Intell. Intell. Inform. (JACIII), vol. 11, no. 5, pp. 457–463, 2007.
- [14] A. Doumanoglou, T.-K. Kim, X. Zhao, and S. Malassiotis, “Active random forests: An application to autonomous unfolding of clothes,” in Proc. Eur. Conf. Comput. Vis. (ECCV). Springer, 2014, pp. 644–658.
- [15] C. Chi and S. Song, “Garmentnets: Category-level pose estimation for garments via canonical space shape completion,” in Proc. IEEE/CVF Int. Conf. Comput. Vis. (ICCV), 2021, pp. 3324–3333.
- [16] Y. Li, D. Xu, Y. Yue, Y. Wang, S.-F. Chang, E. Grinspun, and P. K. Allen, “Regrasping and unfolding of garments using predictive thin shell modeling,” in IEEE Int. Conf. Robot. Autom. (ICRA), 2015, pp. 1382–1388.
- [17] Y. Avigal, L. Berscheid, T. Asfour, T. Kröger, and K. Goldberg, “Speedfolding: Learning efficient bimanual folding of garments,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst. (IROS), 2022, pp. 1–8.
- [18] D. Tanaka, S. Arnold, and K. Yamazaki, “Emd net: An encode–manipulate–decode network for cloth manipulation,” IEEE Robot. Autom. Lett. (RAL), vol. 3, no. 3, pp. 1771–1778, 2018.
- [19] L. Y. Chen, B. Shi, D. Seita, R. Cheng, T. Kollar, D. Held, and K. Goldberg, “Autobag: Learning to open plastic bags and insert objects,” in Proc. IEEE Int. Conf. Robot. Autom. (ICRA), 2023, pp. 3918–3925.
- [20] Z. Xu, C. Chi, B. Burchfiel, E. Cousineau, S. Feng, and S. Song, “Dextairity: Deformable manipulation can be a breeze,” arXiv:2203.01197, 2022.
- [21] J. Redmon and A. Farhadi, “Yolov3: An incremental improvement,” arXiv:1804.02767, Apr. 2018.
- [22] A. Kirillov, E. Mintun, N. Ravi, H. Mao, C. Rolland, L. Gustafson, T. Xiao, S. Whitehead, A. C. Berg, W.-Y. Lo, P. Dollár, and R. Girshick, “Segment anything,” 2023.
- [23] S. Macenski, T. Foote, B. Gerkey, C. Lalancette, and W. Woodall, “Robot operating system 2: Design, architecture, and uses in the wild,” Sci. Robot., vol. 7, no. 66, p. eabm6074, 2022.