Single-shot measurement of a Rydberg superatom via collective photon burst

Quantum internet [1] aims to connect remote quantum nodes efficiently that enables a number of profound applications [2], such as distributed quantum computing, multi-party quantum communication and quantum repeater. The physical realization of quantum internet requires a system that can couple with single photons efficiently. An ensemble of atoms very suits for this purpose [3], due to the collectively enhanced atom-photon interaction. A qubit in an atomic ensemble is usually measured via converting to a single-photon field and performing photon counting. This approach has limited overall efficiency, due to inefficiencies in retrieval, transmission and detection. When photon detection fails, no measurement result can be given, making a commonly single-shot measurement impossible. State-dependent fluorescence detection is ubiquitously used for detecting single-atom qubits [4, 5, 6], while its adoption for an atomic ensemble qubit is very challenging due to off-scattering of reservoir atoms. An effective way is pushing off the reservoir atoms [7] and applying traditional single-atom fluorescence detection. Nevertheless, such an approach is destructive and requires atom reloading for subsequent experimental trials. Similar to single atoms, a strongly coupled cavity-QED system [8] also provides a route for lossless detection of collective atomic excitations, albeit requiring a technically demanding setup.

Rydberg interactions [9] in an atomic ensemble enable the realization of a vast range of new quantum optical phenomena, such as single-photon interactions  [10, 11, 12, 13], transistor [14, 15, 16], contactless nonlinear optics [17], and photon-photon gate [18]. If the size is small enough (typically $<10$ $\upmu$m), an ensemble of atoms can behave like a two-level atom [9]. Such a superatom has many benefits. In comparison with single atoms, the interaction with single photons are collectively enhanced. In comparison with traditional ensemble approach, it has the benefit of deterministic entanglement preparation. Besides, the long-range dipole interaction also provides a promising interface [19, 20, 21] for quantum computers with single atoms in arrayed optical tweezers [22], and the interaction with microwave photons also enables a promising interface [23] for super-conducting quantum computers [24, 25]. Significant experimental progresses have been achieved so far, such as the observation collective Rabi oscillation [26], on demand single-photon source [27] and atom-photon entanglement [28]. It was also reported of creating multiple superatoms and interfering them for entanglement production [29, 30]. With these developments, targeting advanced quantum applications (e.g. constructing a quantum network of multiple superatoms), it becomes more and more urgent to extend the experimental toolbox of superatom manipulation, such as improving the single-photon retrieval efficiency and developing the technology of deterministic single-shot measurement. In previous studies of single-photon transistor [14, 15, 16], a single photon can control the transmission of many photons with an achievable gain as high as 100, and probabilistic collective excitations were measured. Nevertheless, these realizations have not reached the superatom regime and did require additional experimental setups.

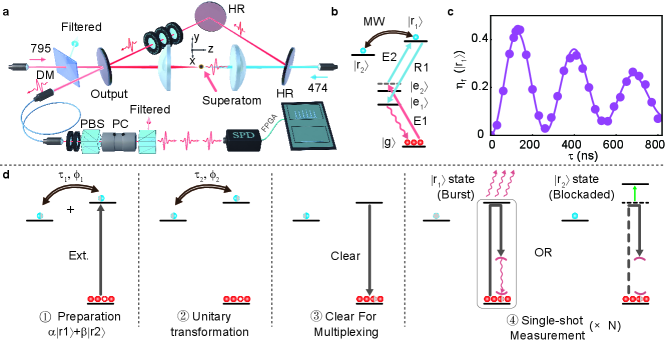
In this article, we report the experimental realization of single-shot measurement for a Rydberg superatom qubit via photon burst. Our scheme is shown in Fig. 1d. We make use of Rydberg blockade [9] between $|r_{1}\rangle$ and $|r_{2}\rangle$ to probe the population in $|r_{2}\rangle$ via controlled multi-photon generation. If there is no population in $|r_{2}\rangle$, we can repeat the process of excitation and retrieving for $|r_{1}\rangle$ to create a sequence of single photons. While if $|r_{2}\rangle$ is populated, this process will not generate any photon. Therefore, by counting the number of photons, we can measure the population in $|r_{2}\rangle$. Furthermore, by applying a microwave (MW) field that couples the transition $|r_{1}\rangle\leftrightarrow|r_{2}\rangle$, we can prepare an arbitrary single qubit state and perform measurements in arbitrary bases. This scheme simply makes use of the build-in single-photon interface for qubit measurement, which is advantageous experimentally. Then in order to obtain a high fidelity in a short measurement duration, it is crucially important to improve photon detection efficiency. By making use of a low-finesse cavity to further enhance the collective atom-photon interaction, we achieve a high in-fiber retrieval efficiency $\eta_{f}$ = 44%. By repeating the exciting and retrieving process for 12 times in 4.8 $\upmu$s, we detect 2.63 photons for a superatom in $|r_{1}\rangle$ and 0.19 photons for a superatom in $|r_{2}\rangle$, which gives a single-shot measurement fidelity of 91.3%. After correcting the preparation infidelity, the single-shot fidelity reaches 93.2%. Then for a qubit in the superposition of $|r_{1}\rangle$ and $|r_{2}\rangle$, we achieve a close tomography fidelity.

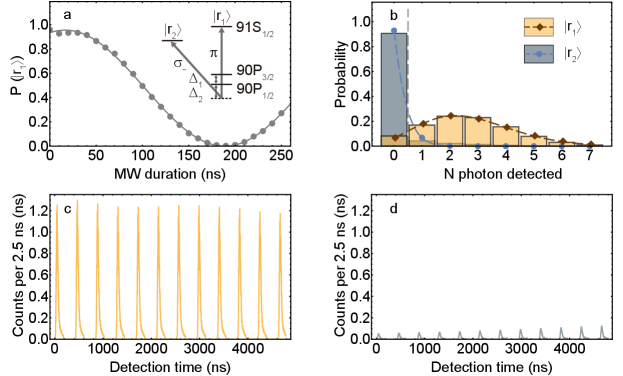
Our detailed experimental setup is sketched in Fig. 1. In order to reach the superatom regime, we capture a tiny atomic ensemble with the thickness of $\sim$3 $\upmu$m, using a 852 nm optical trap. Then we deterministically prepare a Rydberg single excitation making use of two-photon excitation with the E1 and E2 pulses shown in Fig. 1b, to restrict the $1/e^{2}$ radius of excitation area within 6.5 $\upmu\rm{m}$. Then we observe the collective Rabi oscillation as shown in Fig. 1c with the collective Rabi frequency of 2$\pi\times$2.9 MHz. The blockade radius is estimated to be $\sim$ 9.0 $\upmu$m, which is much larger than the excitation area. By setting the $\pi$ pulse excitation period, we realize the deterministic superatom preparation. We choose firstly preparing the superatom into the qubit state of $\ket{r_{1}}=\ket{91S_{1/2},m_{j}=1/2}$ and $\ket{r_{2}}=\ket{91S_{1/2},m_{j}=-1/2}$. With two independent MW pulses, we realize high fidelity MW Raman operation between $\ket{r_{1}}$ and $\ket{r_{2}}$ state, and prepare them into arbitrary qubit state by setting different pulse areas and phases in the 1st operation of Fig. 1d. Then in order to perform single-shot measurement of the qubit state, we make use of the Rydberg interaction between $\ket{r_{1}}$ and $\ket{r_{2}}$, and collective photon burst with the Rydberg superatom combined with an optical cavity as shown in Fig. 1a. Benefitting from the deterministic preparation, we can clear $\ket{r_{1}}$ state, then the population of $\ket{r_{2}}$ will identify the qubit state. Afterwards the cleared $\ket{r_{1}}$ channel will be multiplexed to implement collective photon burst.

The high efficiency photon-superatom interface is of great significance in quantum internet and our single-shot measurement scheme. Due to the limited optical depth (OD) of the superatom, we set up a ring cavity [31, 32] around the superatom to enhance the superatom-photon coupling strength, to realize efficiently emission and detection of photons in a short period which is defined as collective photon burst. Until now, although optical cavity has been used to achieve strong coupling with Rydberg atoms [33], performing high efficiency photon collection and detection is still missing. In our platform, the caivty is built with three customized planar mirrors, and two aspherical lens to create the cavity waist radius of 6.5 $\upmu$m. The left mirror in Fig. 1a is the output mirror with 78$\%$ reflectivity. Due to the intra-cavity loss of $\sim$7%, we choose to use higher output proportion to make sure of high output efficiency of 80%, with the other two mirrors designed as high-reflectivity mirrors. The cavity has a finesse of $\mathscr{F}$ = 19.5, realizing intrinsic enhancement of $2\mathscr{F}/\pi$=12.4 [34, 31] of the cooperativity, and then the photons leaving the cavity are collected into the single mode fiber (SMF) with the efficiency of 85.9$\%$, and detected with a SPD with the efficiency $\eta_{SPD}$ of 68%.

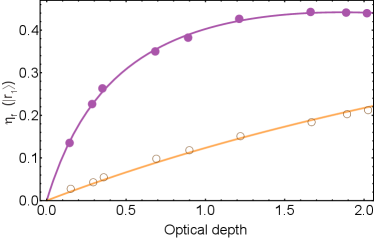
The retrieval efficiencies with and without cavity enhancement are shown in Fig. 2. We test different results by changing the OD. At each point, we prepare a superatom, and detect the retrieved single photons. There we measure the single-photon retrieval efficiency $\eta$ with the SPD, then we get the in-fiber efficiency $\eta_{f}=\eta/\eta_{SPD}$. As shown in Fig. 2, the efficiency increases linearly with OD in freespace, but in cavity it gradually shows saturation with large OD. And we get the highest $\eta_{f}$ of 21$\%$ in freespace (with collection efficiency of 90%), and 44% in cavity. So we get the intrinsic retrieval efficiencies of 24% in freespace and 64% in cavity with OD=1.9. After fitting the intrinsic retrieval efficiencies with the $k\cdot OD/(k\cdot OD+1)$ model (see Supplemental Material), we find the result in cavity seems to be 17.7% lower than the theoretical prediction. We infer that the main reason comes from the limited size of the Read beam, which will cause dephasing because of the inhomogeneous AC stark shift. [34]

With MW operations and the high efficiency collective photon burst, we prepare the qubit respectively in $\ket{r_{1}}$ and $\ket{r_{2}}$, and performing single-shot measurements. The main results are shown in Fig. 3. In order to measure $\ket{r_{1}}$, we make use of photon burst, by repeating excitation and retrieving of 12 times, and detecting 2.63 photons in 4.8 $\upmu$s with the photons profile in temporal domain shown in Fig. 3c. Similarly we prepare the superatom into $\ket{r_{2}}$ but with the MW $\pi$ pulse as shown in Fig. 3a, with the transfer fidelity of 99.7%. Then we get the contrastive result in Fig. 3d, in which the photon emission is intensely suppressed to 0.19 photons by $\ket{r_{2}}$. Furthermore, except the mean photon numbers, we also analyse the statistical distributions of detecting different photon numbers, as shown in Fig. 3b. As we can see, for the $\ket{r_{1}}$ state it has the intrinsic noise of Poisson distribution (zero photon percentage of $e^{-N_{photon}}$), thus there is 8.2$\%$ zero photon events. As for the $\ket{r_{2}}$ state, although it is almost fully suppressed to zero, we still have tiny chance to detect one photon. The reason is from the dark count noise of 1.2$\%$ due to residual excitation noise. If divided by $N$ = 0 photon and $N\geqslant$ 1 photon (dashed vertical line), the probability of detecting the superatom in $\ket{r_{i}}$ when prepared in $\ket{r_{i}}$ is calculated to be 90.8% ($\ket{r_{2}}$) and 91.8% ($\ket{r_{1}}$), with the average value of 91.3% defined as the raw fidelity of single-shot measurement. After correcting the preparation infidelity of 4.5% (see Supplemental Material), the photon emission of $\ket{r_{2}}$ is calculated to be actually suppressed to 0.08 photons, and the corrected fidelity is calculated to be 93.2% with the respective probability of 94.6% ($\ket{r_{2}}$) and 91.8% ($\ket{r_{1}}$). Better fidelity can be achieved by harnessing a superconducting single-photon detector with much higher efficiency, and confining atom movement in Rydberg state [28, 35, 36] with optical dipole trap etc.

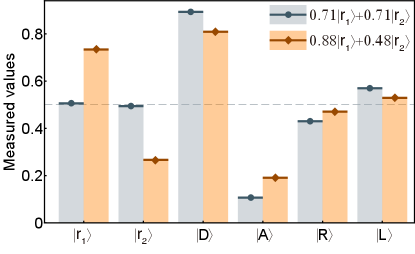
Finally, we prepare the superatom into the superposition states of $\alpha\ket{r_{1}}+\beta\ket{r_{2}}$. With unitary transformation and single-shot measurement, we can demonstrate the qubit state tomography by perform projective measurements in arbitrary bases. Firstly, the superposition states $(\ket{r_{1}}+\ket{r_{2}})/\sqrt{2}$ is prepared with a $\pi/2$ MW pulse. Then we bring in another independent MW pulse with different pulse durations and relative phases to perform arbitrary unitary transformation. Without the second pulse, we can directly measure in the eigenstate bases of $\ket{r_{2}}$ or $\ket{r_{1}}$. Then with the $\pi$/2 pulse and different relative phase of 0 and $\pi$/2, we can measure in (anti)diagonal and circular bases of $(\ket{r_{1}}\pm\ket{r_{2}})/\sqrt{2}$ and $(\ket{r_{1}}\pm i\ket{r_{2}})/\sqrt{2}$ The projective measurements results are shown in Fig. 4. By calculating the Stokes parameters and rebuilding the density matrix [37], we get a fidelity of 89.3$\%$ for $(\ket{r_{1}}+\ket{r_{2}})/\sqrt{2}$ state. Similarly, for another initial state $0.88\ket{r_{1}}+0.47\ket{r_{2}}$, we get a fidelity of 88.6%. We infer that the slight decrease of the fidelity compared with Fig. 3b mainly comes from the infidelity of the $\pi/2$ MW pulse, limited by the mechanical delay line which is used here to adjust the relative phase, which has low precision, and unstable insertion loss when adjusting the phases. It can be replaced by electronic elements in the future.

To summarize, we have realized the single-shot measurement of a Rydberg superatom qubit by making use of its efficient single-photon interface. Blockade between two Rydberg levels enables the controlled generation of sequential single photons. MW Raman coupling further enables the ability of measuring in a super-positional basis. And the enhancement via a low-finesse cavity boosts the single-photon retrieval efficiency significantly, which will not only benefit entangling rate between remote quantum nodes, but also plays an essential role in achieving high-fidelity measurement in a short duration. The technologies developed will enable a series of new capabilities that are not possible for traditional large atomic ensembles, such as performing device-independent quantum key distribution, deterministic entanglement swapping [38] for quantum repeater and quantum networking.

This work was supported by National Key R&D Program of China (No. 2017YFA0303902), Anhui Initiative in Quantum Information Technologies, National Natural Science Foundation of China, and the Chinese Academy of Sciences.