Single-qubit measurement of two-qubit entanglement in generalized Werner states
Abstract
Conventional methods of measuring entanglement in a two-qubit photonic mixed state require the detection of both qubits. We generalize a recently introduced method which does not require the detection of both qubits, by extending it to cover a wider class of entangled states. Specifically, we present a detailed theory that shows how to measure entanglement in a family of two-qubit mixed states — obtained by generalizing Werner states — without detecting one of the qubits. Our method is interferometric and does not require any coincidence measurement or postselection. We also perform a quantitative analysis of anticipated experimental imperfections to show that the method is experimentally implementable and resistant to experimental losses.
I Introduction
Traditional methods of characterizing entanglement in two-photon mixed states (e.g., the violation of Bell’s inequalities Freedman and Clauser (1972); Aspect et al. (1982); Ou et al. (1992); Giustina et al. (2015), quantum state tomography James et al. (2001), etc.) require detection of both photons (see, for example, Gühne and Tóth (2009); Friis et al. (2019) and references therein). These methods, therefore, involve coincidence measurement or postselection. Methods that do not require detection of both photons rely on the assumption that the quantum state is pure (see, for example, Walborn et al. (2006); Sahoo et al. (2020); Bhattacharjee et al. (2022); Di Lorenzo Pires et al. (2009); Just et al. (2013); Sharapova et al. (2015)).
Recently, it has been demonstrated theoretically Lahiri et al. (2021) and experimentally Lemos et al. (2023) that it is possible to measure entanglement of a special class of two-photon mixed states — obtained by generalizing Bell states — without detecting one of the photons and without employing coincidence measurement or postselection. Density matrices representing such states have two generally non-vanishing coherence terms (off-diagonal elements). The states are entangled if and only if these coherence terms are nonzero. Furthermore, these two coherence terms are complex conjugate of each other. Therefore, entanglement of the states considered in Refs. Lahiri et al. (2021); Lemos et al. (2023) is fully characterized by one coherence term of the corresponding density matrix. However, entanglement of most two-qubit states are not dependent on their density matrix elements in such a trivial manner, e.g., the Werner state that can be entangled without violating Bell’s inequalities Werner (1989). Whether the entanglement of any two-qubit photonic mixed state can be verified by detecting one qubit remains an open question of fundamental importance.
Here, we take an important step toward answering this question by extending the method to two-qubit mixed states that can be obtained by generalizing Werner states. We find that albeit the same principle introduced in Refs. Lahiri et al. (2021); Lemos et al. (2023) applies, the measurement procedure requires considerable modifications. Our results also suggest that the method to account for experimental losses would require significant adaptation (Supplementary Material).
The article is organized as follows: In Sec. II, we discuss the class of quantum state we address and their entanglement. In Sec. III, we provide an outline of the entanglement measurement scheme. In Sec. IV we present a detailed theoretical analysis and our main results. We also illustrate the results by numerical examples. In Sec. V we compare our results with existing ones. In Sec. VI, we discuss the effect of anticipated experimental imperfections. Finally, we summarize and conclude in Sec. VII.
II Two-Qubit Generalized Werner State and Its Entanglement

We work with a two-photon polarization state that is a common test bed for two-qubit systems. Throughout this paper, we call the two photons forming a pair signal () and idler (). We use , and to represent horizontal, vertical, diagonal, antidiagonal, right-circular, and left-circular polarization, respectively. The ket, , represents a photon pair where the idler photon has polarization and the signal photon has polarization .
The quantum state considered here is obtained by generalizing the Werner state. The density matrix takes the following form in the computational basis :
| (1) |
where , , , , and represents a phase. It can be immediately checked that this state becomes a Werner state when and . For , and , it reduces to Bell states and when and , respectively. Therefore, the state given by Eq. (1) can also be obtained by the convex combination of a fully mixed state with the generalization of Bell states considered in Refs. Lahiri et al. (2021); Lemos et al. (2023).
The entanglement of this state can be verified by testing the positive partial transpose (PPT) criterion Peres (1996). A partial transposition of the density matrix () is a transposition taken with respect to only one of the photons. The density matrix has a positive partial transpose if and only if its partial transposition does not have any negative eigenvalues. Since we have a system, according to the PPT criterion the state is entangled if and only if it does not have a positive partial transpose Horodecki (1997).
By determining the eigenvalues of a partial transpose of the density matrix given by Eq. (1), we find that three of them are always positive (see Appendix A). The only eigenvalue that can be negative is given by
| (2) |
Figure 1 illustrates entanglement of generalized Werner states () characterized by the PPT criterion for various choices of state parameters , , and .
III Outline of the Entanglement Measurement Scheme
The principle of our method is based on a unique quantum interference phenomenon that was first demonstrated by Zou, Wang, and Mandel Zou et al. (1991); Wang et al. (1991) and is sometimes called the interference by path identity Hochrainer et al. (2022). The method employs a nonlinear interferometer Chekhova and Ou (2016) that contains two identical twin-photon sources. Each source produces the same quantum state [Eq. (1)].
A conceptual arrangement of the entanglement measurement scheme is illustrated in Fig. 2. The two photon-pair sources are denoted by and . A photon pair is in superposition of being created at the two sources — for sources made of nonlinear crystals, such a situation can be achieved by weakly pumping them with mutually coherent laser beams. The sources do not produce the states simultaneously, i.e., the probability of having more than one photon pair in the system between an emission and a detection is negligible. That is, in this situation the effect of stimulated (induced) emission is negligible Zou et al. (1991); Wang et al. (1991); Wiseman and Mølmer (2000); Liu et al. (2009); Lahiri et al. (2019).

Signal beams ( and ) from the two sources are superposed by a balanced beamsplitter and the single-photon counting rate (intensity) is measured at one of the outputs of the beamsplitter. The idler beam from is sent through and is aligned with the idler beam generated by . (Such an alignment was originally suggested by Z. Y. Ou Zou et al. (1991).) This alignment makes it impossible to know from which source the signal photon originated. Consequently, a single-photon interference pattern appears at a detector placed at an output of the beamsplitter. Details of experimental conditions to obtain the interference pattern have been discussed in numerous publications (see, for example, Wang et al. (1991); Lemos et al. (2022a, b)).
We apply a unitary transformation on the field representing the idler photon between the two sources. Such transformations can readily be implemented in a laboratory using quarter- and half-wave plates. We choose a unitary transformation that is characterized by two controllable parameters ( and ) and has the following form in the basis:
| (4) |
where and can be understood as two half-wave plate angles.
The fact that we can fully control the choice of and plays crucial role in our measurement scheme. We show below that the effect of this unitary transformation appears in the interference patterns generated by the signal photon after it is projected onto appropriate polarization states. We also show how the entanglement of can be fully characterized from these single-photon interference patterns with the knowledge of the unitary transformation. For simplicity, we initially assume that there is no experimental loss. In the supplementary material, we provide a detailed description of how to treat dominant experimental losses and imperfections. We discuss the effects of experimental imperfections in Sec. VI.
We emphasize that the signal photon never interacts with the device performing the unitary transformation and the idler photon is never detected. These are two unique features of our entanglement measurement scheme in addition to the fact that no postselection or coincidence measurement is required.
IV Theoretical Analysis
IV.1 Determining the quantum state
We use the standard bra-ket notation for the convenience of analysis. The generalized Werner state [Eq. (1)] in the bra-ket notation takes the form
| (5) |
where represents a matrix element; for example, .
Equation (5) [or equivalently, Eq. (1)] is the state generated by an individual source. While determining the quantum state generated by the two sources jointly, one needs to use the fact that the probability of emission of more than one photon pair is negligible, that is, the total occupation number of photons in the state is always two.
We first consider the scenario in which the idler beams are not aligned. In this case, a signal photon is in a superposition of being in modes and that emerges from two sources. Likewise, an idler photon is in a superposition of being in modes and . Consequently, the density matrix representing the quantum state produced jointly by the two sources becomes an matrix. We determine this matrix following the approach introduced in Ref. Lahiri et al. (2021) and represent it by bra-ket notation [Appendix C, Eq. (Appendix C: The two-photon density matrix)].
We now analytically represent the alignment of idler beams. Modes and becomes identical due to this alignment. The alignment, together with the unitary transformation [Eq. (4)] applied on the idler photon, results in the following transformations of kets:
| (6a) | |||
| (6b) | |||
where is the phase acquired by propagation from to .
Finally, we obtain the density matrix, , representing the photon pair in our system (before arriving at ) by substituting from Eqs. (6a) and (6b) into the density matrix [Appendix C, Eq. (Appendix C: The two-photon density matrix)] mentioned above. An expression for is given by Eq. (Appendix C: The two-photon density matrix) in Appendix C. The probability of detecting a signal photon at one of the outputs of (Fig. 2) can be determined using this density matrix or from the reduced density matrix () obtained by taking partial trace of over the subspace of the idler photon. Here, we take the later approach. The reduced density matrix representing a signal photon before arriving at is given by
| (7) |
where is the probability of emission from source , H.c. represents the Hermitian conjugation, , , , and
| (8a) | ||||
| (8b) | ||||
with and . We observe that all state parameters (, , and ) and the unitary transformation parameters ( and ) appear in the density matrix representing a signal photon.
IV.2 Information of entanglement in Interference Patterns
As mentioned in Sec. III, signal beams and are superposed by a balanced beamsplitter (BS), one of the outputs of BS is projected onto a particular polarization state, and then sent to a detector. Therefore, the positive-frequency part of the quantized electric field at the detector is given by
| (9) |
where and is the annihilation operator corresponding to signal photon with polarization emitted by source . The probability of detecting a signal photon with polarization is obtained by the standard formula Glauber (1963)
| (10) |
where and is given by Eq. (IV.1). The single-photon counting rate (intensity) at the detector is linearly proportional to the probability . We show below that these photon counting rates represent interference patterns. The state parameters () that characterize the entanglement appear in the expressions for these interference patterns.
We first determine the photon counting rate at the detector when the signal photon is projected onto the horizontally polarized (H) state. It follows from Eqs. (IV.1) – (10) that (Appendix D)
| (11) |
where =, , , and ; the explicit form of is not required for our purpose. It is evident from Eq. (IV.2) that the value of changes sinusoidally as is varied, i.e., Eq. (IV.2) represents an interference pattern. Here, we have chosen to maximize the contribution from the interference term (general expressions are given in Appendix D).
Equation (IV.2) shows that the visibility depends on the parameter that one can fully control in an experiment. We set such that the visibility attains its minimum non-zero value, i.e, . The expression for then becomes
| (12) |
and consequently, the visibility is given by 111The visibility is determined by the standard formula .
| (13) |
Likewise, we find that the visibility of the single-photon interference pattern for polarization is
| (14) |
where plays the same role as in Eq. (13).
| State | () | PPT Criterion | Concurrence | ||||
|---|---|---|---|---|---|---|---|
| (0.0, –, –) | 0.00 | 0.00 | 0.00 | 0.00 | Separable | 0.00 | |
| (0.2, 1.0, 0.5) | 0.08 | 0.18 | 0.20 | 0.20 | Separable | 0.00 | |
| (0.6, 0.8, 0.3) | 0.17 | 0.41 | 0.67 | 0.47 | Entangled | 0.24 | |
| (0.7, 1.0, 0.5) | 0.27 | 0.64 | 0.70 | 0.70 | Entangled | 0.55 | |
| (1.0, 1.0, 0.5) | 0.38 | 0.92 | 1.00 | 1.00 | Entangled | 1.00 |
We now consider the remaining cases where the signal photon is projected onto diagonal (D), antidiagonal (A), right-circular (R), and left-circular (L) polarizations. General expressions for single-photon counting rates for all these cases are given in Appendix D. Using those expressions [Eqs. (D5a)–(D5d)], we obtain the corresponding formulas for visibility as
| (15) |
and
| (16) |
where is given in Appendix D (its explicit form is not required for our purpose).
Equations (13)–(16) show that all parameters that characterize the entanglement appear in the expressions for visibility for , , , , , and polarizations. That is, the information about the entanglement is contained in the single-photon interference patterns obtained by detecting one of the qubits only.
IV.3 Entanglement Verification and Measurement
We now show how to test the PPT criterion and to measure the concurrence from the single-photo interference patterns. It follows from Eqs. (2) and (3) that it is enough to represent and in terms of experimentally measurable quantities. We show below that these two quantities can be directly obtained from the expressions for visibilities given in Sec. IV.2. That is, we do not need to determine all state parameters (, , and ) individually.
We first express in terms of experimentally measurable quantities. We recall that and are probabilities of emission from sources and , respectively. Suppose that is the probability of detecting a signal photon with polarization () when signal beam, , emerging from is blocked. Likewise, is the detection-probability when signal beam is blocked. We thus have
| (17) |
We now apply Eqs. (13) and (14) to determine and find that
| (18) |
It can be checked that when , the right-hand side of Eq. (18) becomes equal to 1 in the limit and . In this limit, the generalized Werner state [Eq. (1)] reduces to the generalization of Bell states considered in Refs. Lahiri et al. (2021); Lemos et al. (2023), for which . Using Eqs. (17) and (18) one can immediately express in terms of experimentally measurable quantities.
To determine the quantity , we eliminate the cosine terms from Eqs. (15) and (16) by squaring and adding them. It then immediately follows that
| (19) |
Using Eqs. (17) and (19), we can readily express in terms of photon counting rates and visibilities of single-photon interference patterns.
To test the PPT criterion, we express the eigenvalue, [Eq. (2)], in terms of experimentally measurable quantities. Using Eq. (2) and Eqs. (17)–(19), we find that
| (20) |
where we have denoted the right-hand sides of Eqs. (18) and (19) by and , respectively. According to the PPT criterion, the state [Eq. (1)] is entangled if and only if , that is, the state is entangled if and only if
| (21) |
We illustrate the PPT criterion by choosing five quantum states () in Table 1. The criterion is tested using Eq. (21). For simplicity, we assume that . To compute visibilities for and polarization, we chose . It is to be noted that the entanglement does not depend on the value of [see Eqs. (15)–(19)].
The state is chosen to be fully mixed. (Note that in this case and values of and are irrelevant.) Applying Eq. (21), we find that is separable as one would expect. The state is chosen as a Werner state with and this state is found to be separable as expected. We choose as an entangled mixed state and we find that Eq. (21) verifies that it is entangled. The density matrix represents a Werner state for which . We find this state to be entangled. Finally, the state is chosen to be the Bell state, . As expected, the state is entangled according to Eq. (21).
In order to express the concurrence in terms of experimentally measurable quantities, we substitute from Eqs. (19) and (18) into Eq. (3) and find that
| (22) |
where and represent right-hand sides of Eqs. (18) and (19), respectively. Equation (22) shows that the concurrence of the two-qubit mixed state can be determined from visibilities of the interference patterns obtained by detecting only one of the qubits.
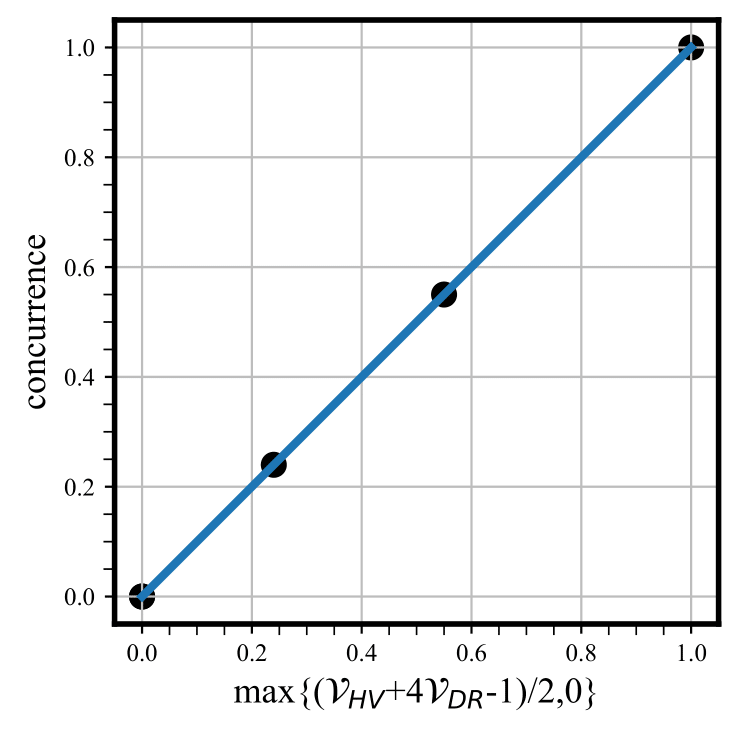
To illustrate Eq. (22), we consider the five quantum states () given in Table 1 and choose for simplicity. We determine the concurrence of these states using two methods: (i) using the state-parameters [i.e., using Eq. (3); the corresponding values of the concurrence are given in Table 1], and (ii) using the values of visibilities [i.e, the formula ]. In Fig. 3 we plot the values of concurrence obtained by method (i) against the values obtained by method (ii), and find that they lie on the straight line predicted by Eq. (22).
We have thus shown that it is possible to test the PPT criterion and measure concurrence for a two-qubit generalized Werner state without detecting one of the qubits.
We have expressed the PPT criterion and the concurrence in terms of interference visibilities to be consistent with existing results Lahiri et al. (2021). We note that they can be equivalently expressed in terms of detection probabilities [see Appendix E, Eqs. (E5) and (E6)]. The latter approach results in simpler theoretical treatment of the problem in the presence of experimental losses (Supplementary Material).
We stress that all state parameters (, , and ) are not required to be determined for verifying and measuring entanglement, albeit they can be determined from the single-photon interference patterns. Equation (18) [or, equivalently, Eq. (E2) of Appendix E] provides an expression for . Expressions for and are given by Eqs. (F1) and (F2) in Appendix F.
V Comparison with Existing Results
In order to put our work into context with existing work, we now compare our results to those presented in Refs. Lahiri et al. (2021); Lemos et al. (2023). The entanglement of quantum states considered in Refs. Lahiri et al. (2021); Lemos et al. (2023) is fully characterized by one coherence term (off-diagonal element) of the density matrix. Consequently, such states are entangled if or and vice versa Lahiri et al. (2021); Lemos et al. (2023). This is no longer the case for generalized Werner states as illustrated by state in Table 1. State is characterized by state parameters , , and . We find that this state is separable (not entangled) even if and . Furthermore, for the states considered in Refs. Lahiri et al. (2021); Lemos et al. (2023), one does not require to measure visibilities for and polarized signal photons to characterize entanglement in a loss-less scenario: measurements in the basis are required only to account for experimental losses. On the contrary, our results show that measurements in the basis are absolutely essential for characterizing entanglement of a generalized Werner state even in the absence of experimental losses.
VI Treating Experimental Imperfections
In an experiment, numerous imperfections may appear. However, results of Ref. Lemos et al. (2023) show that most dominant ones are the misalignment of idler beams and loss of idler photons between the two sources. These imperfections need separate attention because they result in the loss of interference-visibility that cannot be compensated in any way.
In the Supplementary Material, we provide a detailed analysis showing how to treat such experimental imperfections. We represent the PPT criterion and the concurrence in terms of experimentally measurable quantities by taking these imperfections into account. Equations (G4) and (G5) of Appendix G display the corresponding formulas. Considering the five quantum states given by Table 1, we test the PPT criterion and determine their concurrence in the presence of high experimental loss (Supplementary Material, Table S1) and find that the results are identical to those presented in Table 1 and Fig. 3. Our analysis thus shows that the proposed method is experimentally implementable and resistant to experimental losses.
VII Summary and Conclusions
It is a common perception that one must detect both photons to measure entanglement of a two-photon mixed state. Only recently it has been demonstrated that by the application of “quantum indistinguishability by path identity” Hochrainer et al. (2022) it is possible to measure entanglement in a special class of two-qubit mixed states without detecting one of the qubits Lahiri et al. (2021); Lemos et al. (2023). We have generalized the method to cover a wider class of states. In particular, we have shown how to measure entanglement in a two-qubit generalized Werner state without detecting one of the qubits and without employing coincidence measurement or postselection. Our analysis shows that the generalization requires non-trivial adaptation of the previously introduced measurement procedure, especially when experimental imperfections are present. Our work also marks an important step toward the generalization of this unique method to an arbitrary two-qubit mixed state.
In a recent publication Zhan (2021), Zhan has proposed to extend the measurement procedure introduced in Refs. Lahiri et al. (2021); Lemos et al. (2023) to mixed high-dimensional Bell states. We expect that our work will inspire novel proposals to measure entanglement in high-dimensional generalized Werner states, which would not require detection of all entangled particles. We hope that such a generalization will contribute toward reducing the resource requirement for entanglement measurement of high-dimensional entangled states.
Finally, since our analysis is based on quantum field theory, it can in principle be applied to non-photonic quantum states. As the method relies on detection of only one of the two entangled particles, it can be practically advantageous when adequate detectors are not available for both entangled particles.
Acknowledgments
This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-23-1-0216.
Appendix A : The PPT criterion eigenvalues
We obtain a partial transposition of the density matrix, [Eq. (1)], by taking the transposition with respect to only one of the photons. It can be readily found that the eigenvalues of the resulting matrix are
| (A1a) | ||||
| (A1b) | ||||
| (A1c) | ||||
| (A1d) | ||||
We show below that only can take negative values and the remaining eigenvalues must be non-negative.
Since and , we must have . Furthermore, since , we obtain the condition
| (A2) |
Applying condition (A2) to Eq. (A1a), we immediately find that
| (A3) |
The expression on the left of inequality (A3), is negative when , that is, the lower bound of can be negative. For example, if one sets , , and , one finds from Eq. (A1a) that .
We now consider eigenvalue . We note that and . It now becomes evident from Eq. (A1b) that .
Using Eq. (A1c), we can express in the following form
| (A4) |
Since and , it immediately follows that .
Finally, since and , we readily obtain from Eq. (A1d) that .
Appendix B: Derivation of Eq. (3)
The concurrence is determined following the prescription given in Wootters (1998). First, the spin flipped density matrix is determined using the formula
| (B1) |
where is the second Pauli matrix, represents the Kronecker product, the asterisk implies complex conjugation, and is given by Eq. (1). It is well known that has only non-negative eigenvalues Wootters (1998). We denote these eigenvalues by , , , and . We find these eigenvalues to be given by
| (B2a) | |||
| (B2b) | |||
| (B2c) | |||
where
| (B3a) | |||
| (B3b) | |||
It is evident from Eqs. (B3a) and (B3b) that and . Therefore, we have from Eqs. (B2a)–(B2c) that and . Consequently, the standard formula for the concurrence, Wootters (1998), becomes
| (B4) |
where are positive square-roots of .
Appendix C: The two-photon density matrix
We briefly discuss the procedure of obtaining the two-photon density matrix generated by our system. We start with the generalized Werner state [Eq. (5)]:
| (C1) |
Without any loss of generality, an arbitrary element of this density matrix can be expressed in the form
| (C2) |
where each quantity on the right-hand side is defined as follows. The real and non-negative quantity, , represents the square-root of a diagonal element of . The quantity is also non-negative and given by the properties: (i) , (ii) for all diagonal elements, i.e., for and , (iii) for , , and , it takes the following form:
| (C3) |
and (iv) for the remaining cases. Phases in Eq. (C2) obey the following relations: , , and values of for other choices of are irrelevant since the corresponding matrix elements are zero. The quantum state given by Eqs. (C1)-(C3) is generated by an individual source.
We first consider the case in which the idler beams are not aligned. In our system, the two sources are mutually coherent and they emit in such a way that there are never more than one photon pair simultaneously. A prescription to write down the quantum state in such a scenario is given in Ref. Lahiri et al. (2021). Following this prescription, we find that the state jointly generated by the two sources is represented by the density matrix
| (C4) |
where and label the two sources, is the probability of emission from source (i.e., ), quantities and are defined below Eq. (C2), , and .
When the idler beams are aligned and the unitary transformation [Eq. (4)] is performed on the state of the idler photon between and , the transformation of kets are given by Eqs. (6a) and (6b). We rewrite these equations in the following form:
| (C5) |
where represents matrix elements of the unitary transformation given by Eq. (4).
The two-photon quantum state () generated by our system is obtained by substituting from Eq. (C5) into Eq. (Appendix C: The two-photon density matrix) and it is given by
| (C6) |
Appendix D: General expressions for signal photon detection probabilities (photon counting rates)
We obtain the detection probability, , of a signal photon with polarization (where ) at an output of (Fig. 2) using Eqs. (IV.1)-(10). When the signal photon is projected onto polarization state, we have from these equations
| (D1) |
where . We now note the following trigonometric identity:
| (D2) |
where . Now using Eqs. (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)) and (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)), we find that
| (D3) |
where , and is analogous to in Eq. (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)). It can readily checked that Eq. (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)) reduces to Eq. (IV.2) when .
Following the same procedure, we determine the detection probability (i.e., the single-photon counting rate) when the signal photon is projected onto the polarization state. We find it to be given by
| (D4) |
where , , and is analogous to in Eq. (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)).
Likewise, using Eqs. (IV.1)-(10), we determine the photon counting rates corresponding to the polarization states , , and
| (D5a) | |||
| (D5b) | |||
| (D5c) | |||
| (D5d) | |||
where , , and are analogous to in Eq. (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)), and
| (D6) |
expressions for visibility for , , , and polarizations [Eqs. (15) and (16)] are obtained by setting in Eqs. (D5a)-(D5d), followed by application of the standard formula for visibility.
Appendix E: Alternative Expressions for the PPT Criterion and Concurrence
Here we express the PPT Criterion and Concurrence in terms of single-photon detection probabilities. In Eqs. (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)) and (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)), we set to maximize the contribution from the interference term and choose and such that and . Let us define
| (E1a) | ||||
| (E1b) | ||||
where and the maximum and minimum values of are obtained by varying the interferometric phase . It readily follows from Eqs. (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)), (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)), (E1a) and (E1b) that
| (E2) |
where can be replaced by and an expression for in terms of single-photon detection probabilities is given by Eq. (17).
Likewise, for , , , and polarizations, we define
| (E3) |
where . Using Eqs. (D5a)-(D5d) and Eq. (E3), we find that
| (E4) |
where is given by Eq. (17). From Eqs. (2), (E2), and (E4), we have
where we have denoted the right-hand sides of Eqs. (E2) and (E4) by and respectively. According to the PPT criterion, the state [Eq. (1)] is entangled if and only if , that is, if and only if
| (E5) |
where , , and can be replaced by , , and respectively.
Appendix F: Expressions for and
In this appendix, we express state-parameters and in terms of experimentally measurable quantities. Using Eqs. (Appendix D: General expressions for signal photon detection probabilities (photon counting rates)), (E1a), and (E1b), we find that
| (F1) |
where an expression for in terms of experimentally measurable quantities is given by Eq. (17).
Using Eqs. (E2) and (E4), we find that
| (F2) |
where and are right-hand sides of Eqs. (E2) and (E4) respectively and we have used the relation . Now substituting from Eq. (F1) into Eq. (F2), we can obtain an expression for in terms of experimentally measurable quantities. Equation (F2) shows that when (i.e., ) and/or , no meaningful value of can be obtained. This is because in these cases all off-diagonal terms of the density matrix [Eq. (1)] are zero for all values of , that is, obtaining a value for becomes irrelevant in these cases.
Appendix G: Effects of Experimental Imperfections
Both the misalignment of idler beams and polarization-dependent loss of idler photons between the two sources can be effectively modeled by the action of an attenuator (e.g., neutral density filter or any absorptive plate) that has polarization dependent transmissivity. Suppose that the amplitude transmission coefficient of the attenuator for horizontal () and vertical () polarizations are and , respectively. Without any loss of generality it can be assumed that and are real quantities obeying relations and . A detailed analysis of the problem considering experimental imperfections is given in the supplementary material. Our analysis shows that both and can be determined from experimental data. Therefore, we treat and as experimentally measurable quantities.
We show in the Supplementary Material that
| (G1) |
and
| (G2) |
Here , , , and are the same physical quantities introduced in Appendix E. However, their analytical expressions now involve and (Supplementary Material).
Now using Eq. (2), (G1), and (G2), we get
| (G3) |
where and are right-hand sides of Eqs. (G1) and (G2) respectively. According to the PPT criterion, the state [Eq. (1)] is entangled if and only if . Thus the PPT criterion in the presence of experimental imperfections can be expressed as
| (G4) |
References
- Freedman and Clauser (1972) S. J. Freedman and J. F. Clauser, Phys. Rev. Lett. 28, 938 (1972).
- Aspect et al. (1982) A. Aspect, P. Grangier, and G. Roger, Phys. Rev. Lett. 49, 91 (1982).
- Ou et al. (1992) Z. Y. Ou, S. F. Pereira, H. J. Kimble, and K. C. Peng, Physical Review Letters 68, 3663 (1992).
- Giustina et al. (2015) M. Giustina, M. A. M. Versteegh, S. Wengerowsky, J. Handsteiner, A. Hochrainer, K. Phelan, F. Steinlechner, J. Kofler, J.-A. Larsson, C. Abellán, et al., Phys. Rev. Lett. 115, 250401 (2015).
- James et al. (2001) D. F. V. James, P. G. Kwiat, W. J. Munro, and A. G. White, Phys. Rev. A 64, 052312 (2001).
- Gühne and Tóth (2009) O. Gühne and G. Tóth, Physics Reports 474, 1 (2009).
- Friis et al. (2019) N. Friis, G. Vitagliano, M. Malik, and M. Huber, Nature Reviews Physics 1, 72 (2019).
- Walborn et al. (2006) S. Walborn, P. S. Ribeiro, L. Davidovich, F. Mintert, and A. Buchleitner, Nature 440, 1022 (2006).
- Sahoo et al. (2020) S. N. Sahoo, S. Chakraborti, A. K. Pati, and U. Sinha, Physical Review Letters 125, 123601 (2020).
- Bhattacharjee et al. (2022) A. Bhattacharjee, N. Meher, and A. K. Jha, New Journal of Physics 24, 053033 (2022).
- Di Lorenzo Pires et al. (2009) H. Di Lorenzo Pires, C. H. Monken, and M. P. van Exter, Phys. Rev. A 80, 022307 (2009).
- Just et al. (2013) F. Just, A. Cavanna, M. V. Chekhova, and G. Leuchs, New Journal of Physics 15, 083015 (2013).
- Sharapova et al. (2015) P. Sharapova, A. M. Pérez, O. V. Tikhonova, and M. V. Chekhova, Phys. Rev. A 91, 043816 (2015).
- Lahiri et al. (2021) M. Lahiri, R. Lapkiewicz, A. Hochrainer, G. B. Lemos, and A. Zeilinger, Phys. Rev. A 104, 013704 (2021).
- Lemos et al. (2023) G. B. Lemos, R. Lapkiewicz, A. Hochrainer, M. Lahiri, and A. Zeilinger, Phys. Rev. Lett. 130, 090202 (2023).
- Werner (1989) R. F. Werner, Phys. Rev. A 40, 4277 (1989).
- Peres (1996) A. Peres, Phys. Rev. Lett. 77, 1413 (1996).
- Horodecki (1997) P. Horodecki, Physics Letters A 232, 333 (1997), ISSN 0375-9601.
- Wootters (1998) W. K. Wootters, Phys. Rev. Lett. 80, 2245 (1998).
- Zou et al. (1991) X. Zou, L. J. Wang, and L. Mandel, Physical review letters 67, 318 (1991).
- Wang et al. (1991) L. Wang, X. Zou, and L. Mandel, Physical Review A 44, 4614 (1991).
- Hochrainer et al. (2022) A. Hochrainer, M. Lahiri, M. Erhard, M. Krenn, and A. Zeilinger, Rev. Mod. Phys. 94, 025007 (2022).
- Chekhova and Ou (2016) M. Chekhova and Z. Ou, Advances in Optics and Photonics 8, 104 (2016).
- Wiseman and Mølmer (2000) H. Wiseman and K. Mølmer, Physics Letters A 270, 245 (2000).
- Liu et al. (2009) B. Liu, F. Sun, Y. Gong, Y. Huang, Z. Ou, and G. Guo, Physical Review A 79, 053846 (2009).
- Lahiri et al. (2019) M. Lahiri, A. Hochrainer, R. Lapkiewicz, G. B. Lemos, and A. Zeilinger, Phys. Rev. A 100, 053839 (2019).
- Lemos et al. (2022a) G. B. Lemos, V. Borish, G. D. Cole, S. Ramelow, R. Lapkiewicz, and A. Zeilinger, Nature 39, 2200 (2022a).
- Lemos et al. (2022b) G. B. Lemos, M. Lahiri, S. Ramelow, R. Lapkiewicz, and W. Plick, Journal of the Optical Society of America B 512, 409 (2022b).
- Glauber (1963) R. J. Glauber, Physical Review 130, 2529 (1963).
- Zhan (2021) X. Zhan, Phys. Rev. A 103, 032437 (2021).
Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections
Synopsis. Although numerous imperfections may appear in an experimental scenario, the experiment reported in Ref. Lemos et al. (2023) shows that most dominant ones are the misalignment of idler beams and polarization-dependent loss of idler photons between the two sources. Here, we take these experimental imperfections into account to show that the proposed method is resistant to experimental losses and imperfections. In particular, we represent the PPT criterion and the concurrence in terms of experimentally measurable quantities by taking these imperfections into account. We numerically illustrate the results by considering the five quantum states given by Table I of the main text.
Theoretical Analysis Obtaining an Expression of the Density Matrix.— Since the detailed description of the setup is given in the main paper, we skip it here for brevity. Instead, we focus on treating the key experimental imperfections quantitatively.

We recall from the main paper that the two-qubit generalized Werner state takes the following matrix form in the computational basis :
| (S6) |
where , , , , and represents a phase. This state is generated by an individual source used in the setup. When both sources are considered together and the idler beams are not aligned, the quantum state produced by our system is given by Eq. (C4) in Appendix C of the main paper.
We also recall from the main paper that the unitary transformation performed on the idler photon between the two sources has the following form in the basis:
| (S7) |
where and can be understood as two half-wave plate angles. Calculations up to this step are identical to those in the case with no experimental imperfections.
As mentioned above, the two main imperfections are: (i) misalignment of the idler beams and (ii) polarization-dependent loss of idler photons between the two sources. Both of these imperfections can be effectively modeled by the action of an attenuator (e.g., neutral density filter or any absorptive plate) that has polarization dependent transmissivity (Fig. S4). Suppose that the amplitude transmission coefficient of the attenuator for horizontal () and vertical () polarizations are and , respectively. Without any loss of generality it can be assumed that and are real quantities obeying relations and . It was shown in Ref. Zou et al. (1991) that the action of an attenuator on the idler-field is mathematically equivalent to that of a beamsplitter with a single input. Therefore, the imperfections in idler beam alignment together with the unitary transformation [Eq. (S7)] result in the following transformation of the quantum field representing an idler photon (see also Lahiri et al. (2021)):
| (S8a) | ||||
| (S8b) | ||||
where represents a photon annihilation operator such that with and , the operator can be interpreted as the field of a lost photon, , and is the phase change due to propagation from to . Equations (S8a) and (S8b) result in the following transformation of kets:
| (S9a) | ||||
| (S9b) | ||||
where represents the absorbed photon with polarization . It can be readily checked that Eqs. (S9a) and (S9b) reduce to Eqs. (6a) and (6b), respectively, of the main paper when and , i.e., when there is no experimental imperfections.
In order to obtain the quantum state, , generated by our system (before reaching the beamsplitter ) we substitute from Eqs. (S9a) and (S9b) into Eq. (C4) in Appendix C of the main paper (i.e., the density matrix in the case with unaligned idler beams) and we find that
| (S10) |
It can be verified that when and , Eq. (Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections) reduces to Eq. (C6) in Appendix C of the main paper.
The reduced density matrix, , representing a signal photon before reaching the beamsplitter , is obtained by taking partial trace of over the subspace of the idler photon and the loss modes. The reduced density matrix is found to be
| (S11) |
where H.c. represents the Hermitian conjugation, , , , and
| (S12a) | |||
| (S12b) | |||
with and . It can once again be checked that Eqs. (Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections) and (S12) reduce to Eqs. (7) and (8), respectively, of the main paper when there is no experimental imperfections (i.e., and ).
Obtaining Detection Probability of a Signal Photon.— The probability of detecting a signal photon emerging from the beamsplitter (BS) is obtained following the same procedure described in the main paper. In particular, we apply Eqs. (9) and (10) from the main paper and use Eq. (Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections) for the expression for the density matrix.
When the signal photon is projected onto polarization state, the probability of its detection is given by
| (S13) |
where =, , and is analogous to in Eq. (D2) in Appendix D of the main paper. It can be readily checked that Eq. (Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections) reduces to Eq. (D3) of Appendix D in the main paper when .
Similarly, when the signal photon is projected onto polarization state, the probability of its detection is given by
| (S14) |
where is given below Eq. (Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections), , , and is analogous to .
For , , , and polarizations, we get likewise
| (S15a) | ||||
| (S15b) | ||||
| (S15c) | ||||
| (S15d) | ||||
where
| (S16) |
It can be checked that all the expressions for detection probabilities are fully consistent with those obtained assuming no experimental imperfections in the main paper.
The term appearing in the expressions for single-photon counting rates can be expressed in terms of experimentally measurable quantities and is given by [Eq. (17) of the main paper]
| (S17) |
where .
Testing the PPT criterion and Determining the Concurrence.— We set in Eqs. (Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections) and (Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections) to maximize the contribution from the interference term. We then choose and for these two equations so that and , respectively. Let us now define,
| (S18a) | ||||
| (S18b) | ||||
where and the maximum and minimum values of are obtained by varying the interferometric phase . Likewise, we can choose and so that and , and then define
| (S19) |
where .
Using Eqs. (Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections), (Supplementary Material: Entanglement Measurement in the Presence of Dominant Experimental Imperfections), (S18a), (S18b), and (S19), we obtain
| (S20a) | ||||
| (S20b) | ||||
| (S20c) | ||||
| (S20d) | ||||
| (S20e) | ||||
| (S20f) | ||||
where we recall that .
From the set of equations (S20a)–(S20f), we can always find four linearly independent equations [e.g., (S20b), (S20d), (S20e), and (S20f)] that involve four unknowns, , , , and . Therefore, it is always possible to obtain unique solutions for and , i.e., experimental imperfections can be quantitatively characterized from the measurement data. We, however, do not go into the details of finding and since it is an experimental problem. The fact that and can be determined is enough for our purpose. We treat and as experimentally measurable quantities.
If , we find using Eqs. (S17), (S20a), and (S20b) that
| (S21) |
Similarly, if , we obtain the following expression using Eqs. (S17), (S20c), and (S20d) as follows,
| (S22) |
It can be checked using Eqs. (S20a)–(S20d) that when , Eqs. (S21) and (S22) become identical to each other. Combining Eqs. (S21) and (S22), we express in terms of experimentally measurable quantities as
| (S23) |
where an expression for in terms of experimentally measurable quantities is given by Eq. (S17).
| State | () | PPT Criterion | Concurrence | ||
|---|---|---|---|---|---|
| (0.0, –, –) | 0.00 | 0.00 | Separable | 0.00 | |
| (0.2, 1.0, 0.5) | 0.20 | 0.10 | Separable | 0.00 | |
| (0.6, 0.8, 0.3) | 0.6 | 0.22 | Entangled | 0.24 | |
| (0.7, 1.0, 0.5) | 0.69 | 0.35 | Entangled | 0.55 | |
| (1.0, 1.0, 0.5) | 1.00 | 0.50 | Entangled | 1.00 |
We now set in Eqs. (S15a)–(S15d). In analogy with Eq. (S18b), we define
| (S30) |
where . Now from Eqs. (S15a)–(S15d) and (S30), we have
| (S31a) | |||
| (S31b) | |||
Solving Eqs. (S31a) and (S31b), we get
| (S32) |
where is given by Eq. (S17).
To test the PPT criterion, we express the eigenvalue [Eq. (2) in main paper] in terms of experimentally measurable quantities. Using Eq. (2) from the main paper and Eqs. (S17), (S23), and (S32), we find that
| (S33) |
where and are right-hand sides of Eqs. (S23) and (S32) respectively. According to the PPT criterion, the state [Eq. (S6)] is entangled if and only if , that is, the state is entangled if and only if
| (S34) |
It can be readily checked that Eq. (S34) reduces to Eq. (E6) of the main paper when . That is it becomes equivalent to Eq. (21) of the main text when there is no experimental imperfections.
To numerically illustrate our results, we choose the same five quantum states () considered in Table I of the main paper. We consider a high loss scenario in which and . We test whether these states are entangled using Eq. (S34) and present the results in Table S2. We find that the results are identical to those found assuming the absence of experimental imperfections.
In order to express the concurrence in terms of experimentally measurable quantities, we substitute from Eqs. (S17), (S32) and (S23) into Eq. (3) of the main paper and find that
| (S35) |
where and are right-hand sides of Eqs. (S23) and (S32) respectively. It can be readily checked that when , Eq. (S35) reduces to Eq. (E7) of Appendix E of the main paper. That is, it is fully equivalent to Eq. (22) of the main paper in absence of experimental imperfections.
We numerically illustrate the formula for the concurrence using the same five quantum states used for testing the PPT criterion. Using Eq. (S35), we determine the concurrence of these states for and . The results are displayed in the rightmost column of Table S2. They are identical to those obtained assuming no experimental imperfections in the main paper.
Our results thus establish that the technique is resistant to experimental imperfections.