Single-photon synchronization with a room-temperature atomic quantum memory
Abstract
Efficient synchronization of single photons that are compatible with narrowband atomic transitions is an outstanding challenge, which could prove essential for photonic quantum information processing. Here we report on the synchronization of independently-generated single photons using a room-temperature atomic quantum memory. The photon source and the memory are interconnected by fibers and employ the same ladder-level atomic scheme. We store and retrieve the heralded single photons with end-to-end efficiency of and final anti-bunching of . Our synchronization process results in over tenfold increase in the photon-pair coincidence rate, reaching a rate of more than detected synchronized photon pairs per second. The indistinguishability of the synchronized photons is verified by a Hong-Ou-Mandel interference measurement.
Multi-photon states are an important resource for photonic quantum information processing, with potential applications in quantum computation, communication, and metrology [1, 2, 3, 4]. It is beneficial that these photons interact coherently with atomic ensembles, to enable the implementation of deterministic two-photon gates [5] and quantum repeaters for long-distance communication [6]. Efficient, well-established, room-temperature platforms for generating such photons are based on parametric processes such as spontaneous parametric down-conversion (SPDC) and four-wave mixing (FWM) [7]. These processes give rise to stochastic emission of photon pairs and are therefore utilized as heralded single-photon sources [8, 9, 10, 11]. However, they are probabilistic, rendering the construction of larger multi-photon states exponentially slow [12]. At present, the demonstrated rate for generating a 12-photon entangled state from six stochastic emission events is one per hour [13].
The exponential scaling of the rate with the number of photons can be mitigated by using quantum memories to synchronize the probabilistically generated photons [12]. Particularly, the quantum memory can support a time-multiplexing scheme, generating a string of quasi-deterministic photons at pre-determined clock cycles [14, 15, 16]. Alternatively, stochastic photon sources with memories can be used to generate a synchronous -photon state [12, 17]. Most works focus on , and we do so as well.
For , we identify several key metrics. The first is the rate enhancement factor , which is the accomplishment of the synchronization, the ratio between the detection rate of photon pairs after the synchronization compared to the stochastic (accidental) pair detection rate before synchronization . The second is , which should be high for practical applications. A third metric is the anti-bunching of the synchronized photons , which is the normalized autocorrelation of the retrieved signal field conditioned on heralding. Ideally, , and any undesired multi-photon component, e.g., due to noise, increases .
There are two types of memories: those containing an internal source [18, 19, 20], and input-output memories accepting photons from outside [21, 22, 23]. The natural advantage of input-output memories is that they can be used to synchronize and delay photons that have already undergone some processing, including photons that are part of larger entangled states. Photon synchronization has been demonstrated with cold [24, 25, 26, 27] and hot [28] atomic ensembles, employing internal-source memories [24, 25, 26, 28] and input-output memories [27]. However, all these demonstrations suffer from a low photon-pair synchronization rate [ counts per second (cps)] and moderate photon antibunching (). For a comparison of different experiments, see Supplemental Material (SM).
A successful, competing approach to atomic memories uses all-optical setups, namely cavities [29, 30] and storage loops [14, 15, 17, 16, 31, 32, 33]. Cavity systems have achieved good performance with narrowband photons, and cps [30], but these are internal-source systems. Storage loops, which are input-output systems, have reached and cps with broadband SPDC photons [17, 16, 32] but inferior performance with narrowband photons [31]. Notably, interfacing the broadband photons generated from SPDC with atomic ensembles remains an outstanding challenge.
Here we demonstrate for the first time single-photon synchronization using an input-output memory that combines substantial rate enhancement , high pair detection rates cps, low-noise operation with , and compatibility with atomic ensembles. We achieve these at room temperature by employing the ladder orbital scheme in rubidium vapor for the photon source [34, 35, 36] and for the quantum memory [37, 38]. This scheme has three main benefits. First, the all-orbital fast ladder memory (FLAME) provides high-bandwidth operation, low noise, and high end-to-end memory efficiency [39, 37, 38] which are key for high-rate single-photon synchronization. Second, the small wavelength mismatch within the two-photon transition enables a nearly Doppler-free operation and thus a long coherence time between the ground and doubly-excited state. This provides a memory lifetime of over ns [38] and single-photon generation with high rate and low noise [34, 35, 36]. Third, by employing the same level scheme for the photon source and quantum memory, the generated photons are inherently compatible with the memory, enabling an end-to-end memory efficiency of . This also maintains the indistinguishability of the synchronized photons, as quantified by the Hong-Ou-Mandel (HOM) interference visibility .
Synchronization scheme.— The synchronization experiment comprises a spatially-multiplexed single-photon source, a quantum memory, and electronic triggering of the memory operation, as shown schematically in Fig. 1. The photon source is based on FWM in rubidium vapor with two continuous-wave pump fields [35, 36]. The pump fields, at wavelengths of 780 nm and 776 nm, counter-propagate through an isotopically purified vapor cell and excite the and transitions, respectively. The detection of a spontaneously emitted idler photon heralds the generation of a collective state comprising a single excitation that is shared among all atoms, and the signal photon emission to the ground state is thus collectively enhanced into the phase-matched direction [40]. We utilize the cylindrical symmetry of the phase-matching condition to set collection channels on both sides of the optical axis, effectively realizing two sources in the same vapor cell. We denote the generated photons in channel as idler- and signal- (). Additional details on the photon source are given in SM and in Refs. [35, 36].
The quantum memory is based on the FLAME scheme in vapor [37, 38]. Initially, the atoms in the memory cell are optically pumped to the maximal spin state. An input signal-1 photon, which couples to the transition, is stored on the doubly-excited state by sending the first (storage) control pulse. At a controllable time later, a second (retrieval) control pulse releases the signal-1′ photon from the memory (1′ marks post-memory). We use an auxiliary dressing field (not shown in Fig. 1) that weakly couples the storage state to a high-lying orbital in order to counteract the residual Doppler broadening of the two-photon transition [41] and prolong the memory lifetime [38]. The overall transmission of the memory module from the input fiber to the output fiber is (including the 4% loss on exiting the input fiber). Further details on the memory are given in SM and in Ref. [38].
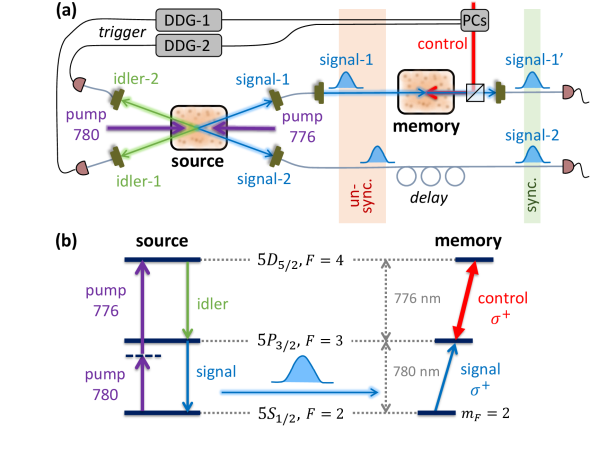
The detection of idler photons triggers digital delay generators (DDG) that set off the control pulses for the memory via free-space Pockels cells (PCs). DDG-1, triggered by idler-1, sends a control pulse that stores the heralded signal-1 in the memory. Subsequently, DDG-2, triggered by idler-2, sends a second control pulse that retrieves signal-1′. This protocol synchronizes signal-1′ and signal-2. We find that the memory efficiency is optimal when the control field is on resonance, indicating that signal-1 is emitted from the source on resonance, as expected [36]. As our PCs’ maximal average repetition rate is limited to operations per second, we devise a logical scheme that operates them only if idler-1 and idler-2 were both detected within a 100-ns time window, set by the memory lifetime. Details on the electronic triggering, timing sequence, and fiber routing are given in SM.
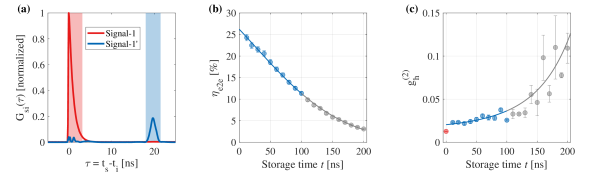
Storage and retrieval of heralded single photons.— We begin by characterizing the storage and retrieval of signal-1. Figure 2(a) shows the count histogram [signal-idler correlation ] for a storage time of ns. We compare the histogram of signal-1 (i.e. directly after the photon source) to that of signal-1′ (i.e. after storage and retrieval in the memory, including the overall transmission of the memory module). The 3.5-ns-long shaded areas indicate the integration windows used for calculating , , , , and ; This window captures over of the pulse energy.
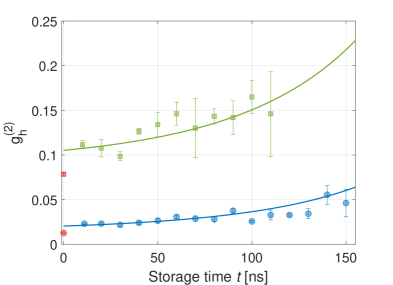
The memory efficiency versus the storage time is shown in Fig. 2(b). Here, we directly measure the end-to-end efficiency by connecting the optical fiber of signal-1 either to the memory input fiber ( coupling) or directly to the detector input fiber ( coupling). Comparing between the detection rates of signal-1 and signal-1′, after correcting for the different couplings, provides . Note particularly that includes all fiber/free-space couplings. We measure . By fitting the data to a decoherence model with homogeneous () and inhomogeneous () decoherence times, we extract the zero-time memory efficiency . The memory lifetime is ns. Here the errors are 1 standard deviation (s.d.) of the fit uncertainty. Given the overall transmission , the memory internal efficiency, comprising only the mapping of the light to and from the atoms, is .
We verify that the memory preserves the quantum statistics of the stored single photons, as shown in Fig. 2(c). For ns, the multi-photon component of signal-1′ is , which is higher than of signal-1 but still at the few-percent level.
The increase in is due to noise photons originating in either the memory or the source. In our system, the former is negligible: the memory generates only noise photons per operation. These photons govern the short-time signal-to-noise ratio , where is the heralding efficiency of the source, and indeed . Therefore, we attribute the increase in predominantly to noise photons arriving from the source at the time of retrieval and detected in coincidence with signal-1′. The dominant contribution comes from photons that scatter directly from the continuous, off-resonant, 780-nm pump field, which are transmitted well through the memory module. Further increase of at larger is explained solely by the decrease of . Our model of this mechanism, shown in Fig. 2(c) and detailed in SM, agrees well with the data.
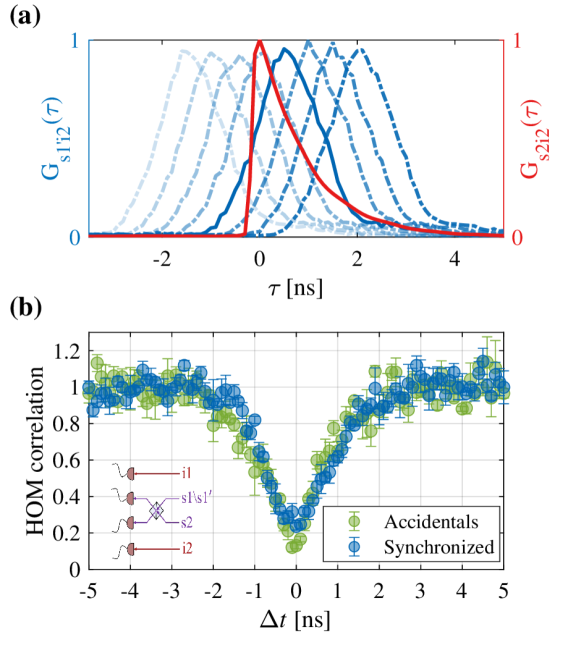
Photon synchronization.— We now turn to demonstrate the synchronization of photon pairs using the memory. Figure 3(a) shows temporal profiles of the retrieved signal-1′ photons (signal-1′-idler-2 correlation conditioned on memory operation, ) in comparison to the profile of signal-2 (signal-2-idler-2 correlation, ) for varying timing settings. Note that the data do not correspond to a specific memory time but rather represent an average over ns, stochastically ‘sampled’ by the regular operation of the synchronization protocol. We control the exact relative timing between signal-1′ and signal-2 by electronically tuning the trigger delay, which controls the memory retrieval time. Figure 3(a) demonstrates, for arbitrary 500-ps intervals, our capability of on-demand, continuous tuning of the retrieval time.
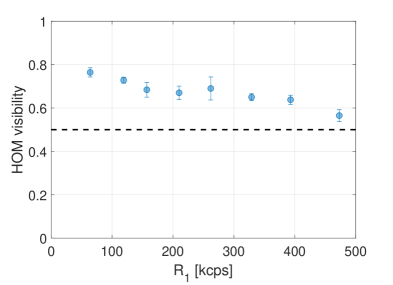
To optimize the relative timing and to characterize the fidelity of the synchronized photons, we perform HOM interference measurements [42]. These measurements attest to the indistinguishability of the synchronized photon pair. Figure 3(b) shows the HOM correlation of signal-1′ and signal-2 for varying triggering delays. The HOM visibility (the interference contrast), quantifying the indistinguishability, is . We use the position of the minimum to define and to set the optimal delays in the system. For reference, we show in Fig. 3(b) the HOM measurement of accidental pairs without the memory, exhibiting %. Notably, the acquisition time per data point for synchronized pairs is 100 times shorter than for accidental pairs, illustrating the importance of synchronization for efficiently manipulating multi-photon states.
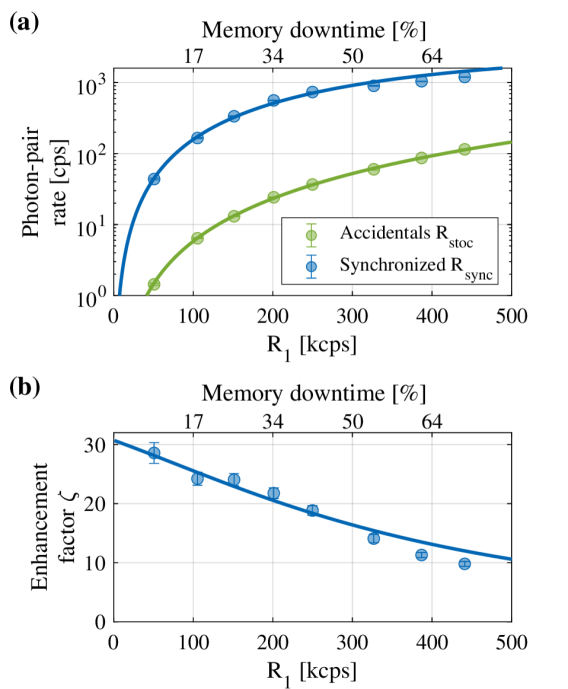
Finally, we show the merit of synchronization in terms of the enhanced two-photon coincidence rate in Fig. 4(a). We study as a function of the heralded single-photon rate , which we control by tuning the strength of the pumps in the source module. We cover the range kilo-cps (kcps), for which the accidental coincidence rates are cps. Here, we consider an accidental coincidence if idler-1 and idler-2 are detected within ps of each other. This time interval is chosen based on the HOM correlation measurement, which exhibits within ps around the minimum (this is a conservative choice, generous in terms of ). As shown in Fig. 4(a), the coincidence rates after synchronization grow to cps, a substantial enhancement compared to .
The rate enhancement is shown in Fig. 4(b). The maximal enhancement is obtained at low . As increases, the system is triggered more often, and each triggering event is followed by s during which the memory cannot handle additional photons (see SM for details). This leads to technical saturation of the system, which we quantify by the relative memory downtime, shown as top axes in Fig. 4. A second issue occurring at high is a moderate increase of and a corresponding decrease of (see SM). We attribute this partially to a degradation of the pulses generated by the PCs at a high triggering rate. Nevertheless, even at the highest rate, we obtain a tenfold increase in the pair coincidence rate and a non-classical HOM visibility .
The rates of accidental and synchronized photon pairs and their dependence on the rate of single photons can be calculated from the parameters of the source, memory, and electronics, all of which we have independently characterized. Our model, based solely on these parameters without fitting (see SM for details), is presented by the solid lines in Fig. 4. The model correctly predicts and and confirms that the decrease of with is due only to the memory downtime. We attribute the slight deviation of the model from the data at large to the PCs’ pulse degradation noted above.
Discussion.— There are several factors limiting the increase of the two-photon coincidence rate. The main ones are the end-to-end efficiency of the memory, the limited operation rate of the PCs, and the heralding efficiency of the photon source. All these factors can be improved.
First, as discussed in Ref. [38], practicable technical improvements of the memory module can increase the internal memory efficiency to %. This, in addition to raising the setup transmission by anti-reflection coating of the optical fiber-to-free-space interfaces, will substantially raise the end-to-end efficiency. Second, the heralding efficiency of the photon source can be increased by using etalon filters to block the direct scattering of photons from the pump fields into the idler modes. Third, the PCs can be replaced by an amplitude electro-optic modulator seeding a tapered amplifier [23]. This will enable both a higher repetition rate and a higher memory efficiency by optimizing the control temporal shape to that of the signal photons [43, 44].
In conclusion, we demonstrate synchronization of single photons with a high rate and low noise using a quantum memory and a photon source, both based on a ladder-level scheme in rubidium vapor. Our synchronized photons are well-suited for quantum information protocols requiring efficient interaction with atomic ensembles, such as Rydberg-mediated deterministic two-photon gates. The scheme presented here can be used to efficiently generate synchronous few-photon states, and, with feasible improvements, larger multi-photon states.
We acknowledge financial support from the Israel Science Foundation, the US-Israel Binational Science Foundation (BSF) and US National Science Foundation (NSF), the Minerva Foundation with funding from the Federal German Ministry for Education and Research, the Estate of Louise Yasgour, and the Laboratory in Memory of Leon and Blacky Broder.
References
- [1] Fulvio Flamini, Nicolò Spagnolo, and Fabio Sciarrino. Photonic quantum information processing: a review. Reports on Progress in Physics, 82(1):016001, nov 2018.
- [2] E. Knill, R. Laflamme, and G. J. Milburn. A scheme for efficient quantum computation with linear optics. Nature, 409:46–52, 2001.
- [3] Koji Azuma, Kiyoshi Tamaki, and Hoi-Kwong Lo. All-photonic quantum repeaters. Nature Communications, 6(1):6787, Apr 2015.
- [4] Jonathan P. Dowling. Quantum optical metrology – the lowdown on high-n00n states. Contemporary Physics, 49(2):125–143, Mar 2008.
- [5] O Firstenberg, C S Adams, and S Hofferberth. Nonlinear quantum optics mediated by rydberg interactions. Jr. Phys. B: At. Mol. Opt. Phys., 49(15):152003, 2016.
- [6] L. M. Duan, M. D. Lukin, J. I. Cirac, and P. Zoller. Long-distance quantum communication with atomic ensembles and linear optics. Nature, 414:413, 2001.
- [7] M. D. Eisaman, J. Fan, A. Migdall, and S. V. Polyakov. Invited review article: Single-photon sources and detectors. Review of Scientific Instruments, 82(7):071101, 2011.
- [8] Hanna Le Jeannic, Varun B. Verma, Adrien Cavaillès, Francesco Marsili, Matthew D. Shaw, Kun Huang, Olivier Morin, Sae Woo Nam, and Julien Laurat. High-efficiency wsi superconducting nanowire single-photon detectors for quantum state engineering in the near infrared. Opt. Lett., 41(22):5341–5344, 2016.
- [9] Chih-Hsiang Wu, Tsung-Yao Wu, Yung-Chin Yeh, Po-Hui Liu, Chin-Hsuan Chang, Chiao-Kai Liu, Ting Cheng, and Chih-Sung Chuu. Bright single photons for light-matter interaction. Phys. Rev. A, 96:023811, 2017.
- [10] Daniel Llewellyn, Yunhong Ding, Imad I. Faruque, Stefano Paesani, Davide Bacco, Raffaele Santagati, Yan-Jun Qian, Yan Li, Yun-Feng Xiao, Marcus Huber, Mehul Malik, Gary F. Sinclair, Xiaoqi Zhou, Karsten Rottwitt, Jeremy L. O’Brien, John G. Rarity, Qihuang Gong, Leif K. Oxenlowe, Jianwei Wang, and Mark G. Thompson. Chip-to-chip quantum teleportation and multi-photon entanglement in silicon. Nature Physics, 16(2):148–153, 2020.
- [11] Gurpreet Kaur Gulati, Bharath Srivathsan, Brenda Chng, Alessandro Cerè, Dzmitry Matsukevich, and Christian Kurtsiefer. Generation of an exponentially rising single-photon field from parametric conversion in atoms. Phys. Rev. A, 90:033819, 2014.
- [12] J. Nunn, N. K. Langford, W. S. Kolthammer, T. F. M. Champion, M. R. Sprague, P. S. Michelberger, X.-M. Jin, D. G. England, and I. A. Walmsley. Enhancing multiphoton rates with quantum memories. Phys. Rev. Lett., 110:133601, Mar 2013.
- [13] Han-Sen Zhong, Yuan Li, Wei Li, Li-Chao Peng, Zu-En Su, Yi Hu, Yu-Ming He, Xing Ding, Weijun Zhang, Hao Li, Lu Zhang, Zhen Wang, Lixing You, Xi-Lin Wang, Xiao Jiang, Li Li, Yu-Ao Chen, Nai-Le Liu, Chao-Yang Lu, and Jian-Wei Pan. 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion. Phys. Rev. Lett., 121:250505, Dec 2018.
- [14] T. B. Pittman, B. C. Jacobs, and J. D. Franson. Single photons on pseudodemand from stored parametric down-conversion. Phys. Rev. A, 66:042303, Oct 2002.
- [15] Fumihiro Kaneda, Bradley G. Christensen, Jia Jun Wong, Hee Su Park, Kevin T. McCusker, and Paul G. Kwiat. Time-multiplexed heralded single-photon source. Optica, 2(12):1010–1013, Dec 2015.
- [16] F. Kaneda and P. G. Kwiat. High-efficiency single-photon generation via large-scale active time multiplexing. Science Advances, 5(10):eaaw8586, 2019.
- [17] Fumihiro Kaneda, Feihu Xu, Joseph Chapman, and Paul G. Kwiat. Quantum-memory-assisted multi-photon generation for efficient quantum information processing. Optica, 4(9):1034–1037, Sep 2017.
- [18] Shuai Chen, Yu-Ao Chen, Thorsten Strassel, Zhen-Sheng Yuan, Bo Zhao, Jörg Schmiedmayer, and Jian-Wei Pan. Deterministic and storable single-photon source based on a quantum memory. Phys. Rev. Lett., 97:173004, 2006.
- [19] Erwan Bimbard, Rajiv Boddeda, Nicolas Vitrant, Andrey Grankin, Valentina Parigi, Jovica Stanojevic, Alexei Ourjoumtsev, and Philippe Grangier. Homodyne tomography of a single photon retrieved on demand from a cavity-enhanced cold atom memory. Phys. Rev. Lett., 112:033601, 2014.
- [20] Karsten B. Dideriksen, Rebecca Schmieg, Michael Zugenmaier, and Eugene S. Polzik. Room-temperature single-photon source with near-millisecond built-in memory. Nature Communications, 12(1):3699, Jun 2021.
- [21] Yunfei Wang, Jianfeng Li, Shanchao Zhang, Keyu Su, Yiru Zhou, Kaiyu Liao, Shengwang Du, Hui Yan, and Shi-Liang Zhu. Efficient quantum memory for single-photon polarization qubits. Nature Photonics, 13(5):346–351, May 2019.
- [22] Mingtao Cao, Félix Hoffet, Shuwei Qiu, Alexandra S. Sheremet, and Julien Laurat. Efficient reversible entanglement transfer between light and quantum memories. Optica, 7(10):1440–1444, Oct 2020.
- [23] Gianni Buser, Roberto Mottola, Björn Cotting, Janik Wolters, and Philipp Treutlein. Single-photon storage in a ground-state vapor cell quantum memory. PRX Quantum, 3:020349, Jun 2022.
- [24] D. Felinto, C. W. Chou, J. Laurat, E. W. Schomburg, H. de Riedmatten, and H. J. Kimble. Conditional control of the quantum states of remote atomic memories for quantum networking. Nature Physics, 2(12):844–848, Dec 2006.
- [25] Zhen-Sheng Yuan, Yu-Ao Chen, Shuai Chen, Bo Zhao, Markus Koch, Thorsten Strassel, Yong Zhao, Gan-Jun Zhu, Jörg Schmiedmayer, and Jian-Wei Pan. Synchronized independent narrow-band single photons and efficient generation of photonic entanglement. Phys. Rev. Lett., 98:180503, May 2007.
- [26] Yun-Fei Pu, Sheng Zhang, Yu-Kai Wu, Nan Jiang, Wei Chang, Chang Li, and Lu-Ming Duan. Experimental demonstration of memory-enhanced scaling for entanglement connection of quantum repeater segments. Nature Photonics, 15(5):374–378, May 2021.
- [27] Keyu Su, Yunfei Wang, Shanchao Zhang, Zhuoping Kong, Yi Zhong, Jianfeng Li, Hui Yan, and Shi-Liang Zhu. Synchronization and phase shaping of single photons with high-efficiency quantum memory. Chinese Physics Letters, 38(9):094202, oct 2021.
- [28] Chao-Ni Zhang, Hang Li, Jian-Peng Dou, Feng Lu, Hong-Zhe Yang, Xiao-Ling Pang, and Xian-Min Jin. Hong-ou-mandel interference linking independent room-temperature quantum memories. Photon. Res., 10(10):2388–2393, Oct 2022.
- [29] Jun-ichi Yoshikawa, Kenzo Makino, Shintaro Kurata, Peter van Loock, and Akira Furusawa. Creation, storage, and on-demand release of optical quantum states with a negative wigner function. Phys. Rev. X, 3:041028, Dec 2013.
- [30] Kenzo Makino, Yosuke Hashimoto, Jun ichi Yoshikawa, Hideaki Ohdan, Takeshi Toyama, Peter van Loock, and Akira Furusawa. Synchronization of optical photons for quantum information processing. Science Advances, 2(5):e1501772, 2016.
- [31] Xiao-Ling Pang, Ai-Lin Yang, Jian-Peng Dou, Hang Li, Chao-Ni Zhang, Eilon Poem, Dylan J. Saunders, Hao Tang, Joshua Nunn, Ian A. Walmsley, and Xian-Min Jin. A hybrid quantum memory-enabled network at room temperature. Science Advances, 6(6):eaax1425, 2020.
- [32] Evan Meyer-Scott, Nidhin Prasannan, Ish Dhand, Christof Eigner, Viktor Quiring, Sonja Barkhofen, Benjamin Brecht, Martin B. Plenio, and Christine Silberhorn. Scalable generation of multiphoton entangled states by active feed-forward and multiplexing. Phys. Rev. Lett., 129:150501, Oct 2022.
- [33] Zhibo Hou, Jun-Feng Tang, Chang-Jiang Huang, Yun-Feng Huang, Guo-Yong Xiang, Chuan-Feng Li, and Guang-Can Guo. Entangled-state time multiplexing for multiphoton entanglement generation. Phys. Rev. Appl., 19:L011002, Jan 2023.
- [34] Yoon-Seok Lee, Sang Min Lee, Heonoh Kim, and Han Seb Moon. Highly bright photon-pair generation in doppler-broadened ladder-type atomic system. Opt. Express, 24(24):28083–28091, 2016.
- [35] O Davidson, R Finkelstein, E Poem, and O Firstenberg. Bright multiplexed source of indistinguishable single photons with tunable ghz-bandwidth at room temperature. New Journal of Physics, 23(7):073050, jul 2021.
- [36] Omri Davidson, Ohad Yogev, Eilon Poem, and Ofer Firstenberg. Bright, low-noise source of single photons at 780 nm with improved phase-matching in rubidium vapor. arXiv:2301.06049, 2023.
- [37] Ran Finkelstein, Eilon Poem, Ohad Michel, Ohr Lahad, and Ofer Firstenberg. Fast, noise-free memory for photon synchronization at room temperature. Science Advances, 4(1), 2018.
- [38] Omri Davidson, Ohad Yogev, Eilon Poem, and Ofer Firstenberg. Fast, noise-free atomic optical memory with 35 end-to-end efficiency. arXiv:2212.04263, 2022.
- [39] K. T. Kaczmarek, P. M. Ledingham, B. Brecht, S. E. Thomas, G. S. Thekkadath, O. Lazo-Arjona, J. H. D. Munns, E. Poem, A. Feizpour, D. J. Saunders, J. Nunn, and I. A. Walmsley. High-speed noise-free optical quantum memory. Phys. Rev. A, 97:042316, Apr 2018.
- [40] H. H. Jen. Positive- phase-space-method simulation of superradiant emission from a cascade atomic ensemble. Phys. Rev. A, 85:013835, 2012.
- [41] R. Finkelstein, O. Lahad, I. Cohen, O. Davidson, S. Kiriati, E. Poem, and O. Firstenberg. Continuous protection of a collective state from inhomogeneous dephasing. Phys. Rev. X, 11:011008, Jan 2021.
- [42] C. K. Hong, Z. Y. Ou, and L. Mandel. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett., 59:2044–2046, 1987.
- [43] Alexey V. Gorshkov, Axel André, Michael Fleischhauer, Anders S. Sørensen, and Mikhail D. Lukin. Universal approach to optimal photon storage in atomic media. Phys. Rev. Lett., 98:123601, Mar 2007.
- [44] Alexey V. Gorshkov, Axel André, Mikhail D. Lukin, and Anders S. Sørensen. Photon storage in -type optically dense atomic media. ii. free-space model. Phys. Rev. A, 76:033805, Sep 2007.
- [45] Martin J. Stevens. Chapter 2 - photon statistics, measurements, and measurements tools. In Alan Migdall, Sergey V. Polyakov, Jingyun Fan, and Joshua C. Bienfang, editors, Single-Photon Generation and Detection, volume 45 of Experimental Methods in the Physical Sciences, pages 25–68. Academic Press, 2013.
- [46] P. Grangier, G. Roger, and A. Aspect. Experimental evidence for a photon anticorrelation effect on a beam splitter: A new light on single-photon interferences. EPL (Europhysics Letters), 1(4):173, 1986.
Supplementary material
The supplementary material contains the following sections:
S1 Comparison of photon synchronization experiments
Table S1 compares different photon-synchronization experiments. We only consider experiments that perform active photon-synchronization with a quantum memory.
| Ref. | Source | Memory | Synchronization rate [cps] | Enhancement factor | HOM visibility [%] | |
| This work | Hot atoms | Hot atoms | 1200 | 28.6 | 0.023 | 76 |
| [24] | Cold atoms | Cold atoms | 0.03 | 28 | 0.17 | 77 |
| [25] | Cold atoms | Cold atoms | 0.08 | 136 | 0.17 | 80 |
| [26] | Cold atoms | Cold atoms | 0.167 | 300 | - | - |
| [27] | Cold atoms | Cold atoms | 0.89 | 15 | 0.43 | 76 |
| [28] | Hot atoms | Hot atoms | 0.0056 | 15 | 0.33 | 75 |
| [30] | SPDC | Cavity | 90 | 25 | - | 82 |
| [31] | Hot atoms | Storage loop | 1.3 | - | - | - |
| [17] | SPDC | Storage loop | 14 | 30.5 | - | 91 |
| [32] | SPDC | Storage loop | 450 | 9.7 | - | 94.5 |
| [33] | SPDC | Storage loop | 6 | 7.5 | - | 91.7 |
| [16] | SPDC | Storage loop | - | 27.9 | 0.007 | 91 |
-
a
Here the source is internal to the memory in a combined system.
-
b
The enhancement factor is calculated, not measured.
-
c
The synchronization rate is estimated from Fig. 4(b) in the main text of Ref. [31].
-
d
The visibility was derived by adding the measured background.
-
e
Here the storage loop was used not for photon synchronization, but in a time multiplexing scheme to enhance the photon generation probability in a pre-detrmined clock-cycle.
S2 Experimental setup
S2.1 Photon source
We use the photon source described in Ref. [35] and improved in Ref. [36]. The pumping powers used are W for pump-780 and mW for pump-776, corresponding to a heralded single-photon detection rate from kilo-counts per second (kcps) up to kcps, in each of the channels of the source. Pump-780 detuning is set to GHz, and pump-776 is set to two-photon resonance. At the optical depth of the photon source, the photons’ temporal full-width at half maximum is ns and slightly increasing with the increase of the pump fields’ power.
The detected heralding efficiency, defined as , where is the detection rate of idler- photons, is and . The main reason for the lower heralding efficiency in channel 2 is the higher noise originating from a direct scattering of photons from pump-776 into the idler modes. This scattering can be reduced by rotating the vapor cell holder [35], but it is generally different for the two idler modes. Additionally, is higher than by , which we attribute to a slightly better phase-matching of signal-1 and idler-1.
can be easily increased to the value of by employing photon sources from two different vapor cells instead of one multiplexed source from a single vapor cell, and optimizing each vapor cell orientation to reduce pump-776 scattering noise into the corresponding idler mode. This will also enable slightly further increasing the heralding efficiency [36], as the vapor cells orientation can be chosen to optimize the scattering noise into a single spatial mode, instead of a trade-off of the noise into two different modes.
S2.2 Memory
Our quantum memory is based on the system described in Ref. [38]. We change the vapor cell used in Ref. [38] to a similar one (same size and same type; Precision Glassblowing) with a higher transmission of at 780 nm. The higher transmission is obtained by a different cleaning procedure of immersing the cell into an Acetone bath before inserting it into the setup. The total memory setup transmission, from after the input fiber, is thus increased from in Ref. [38] to in this work. Considering an extra 4% loss in the input fiber to free-space coupling, the overall memory setup transmission is . The vapor cell temperature (C) and (with optical pumping) are the same as in Ref. [38].
The detuning of the control field that optimizes the storage efficiency is MHz, which corresponds to storing and retrieving signal photons on-resonance [38]. The control field’s peak power at the vapor cell which optimizes the storage efficiency is 1.2 W. The atoms are optically pumped within the ground-state manifold to the maximal spin state using pump and repump fields. The pump beams have an annular shape and are inserted at a slight angle to the optical axis, as described in Ref. [38].
We use an auxiliary dressing field that weakly couples the level to the level with a detuning of MHz and power of 80 mW. This field counteracts the residual Doppler broadening of the two-photon transition [41] and prolongs the memory lifetime [38]. Using a memory storage time of up to 100 ns as in our demonstration, the rate of synchronized photon pairs increases with the dressing field by compared to without the dressing field. Using longer memory storage times increases the benefit of employing the dressing field.
S2.3 Electronics and timing
The maximal average repetition rate of our PCs is limited to sec and the minimal time between pulse operations is 1.5 s. Therefore, we only operate the memory if the two idler photons are detected within a ns time window. Figure S1 shows the electronic triggering scheme of the experiment. Upon detection of idler-2 photon, DDG-2 (T564, Highland technology) is triggered and starts the electronic control sequence. Following a 22-ns insertion delay, DDG-2 outputs a gating pulse of length ns to DDG-1. After another ns, it outputs a trigger to PC-2 which operates the retrieval pulse. This time delay is set to accommodate the electronic delays and memory lifetime, and is controlled with 10-ps resolution. DDG-1 is triggered only if an idler-1 detection is received within the ns ‘Gate’ pulse from DDG-2. After the 22-ns insertion delay, it sends a trigger pulse with a 15-ns delay (to match the arrival time of signal-1 to the memory) to PC-1, which operates the control storage pulse. It also sends a Gate pulse to the logic Buffer (T860, Highland technology) that transmits the trigger of DDG-2 to PC-2 only if the Gate is on, ensuring PC-2 is operated only when both idler photons were detected within .

The DDGs ignore any input trigger while they output pulses. We use this feature to suppress the PCs triggering in times shorter than 1.5 s. For DDG-1, we set a trigger acceptance downtime of s (after each accepted trigger), which ensures that the PCs are not operated within this time. For DDG-2, we set a trigger acceptance downtime of ns, which is set slightly longer than required for photon synchronization in order to ensure that the Gate from DDG-1 to the Buffer does not overlap with the trigger pulse from DDG-2 in different memory operation realizations. The average duty cycle of the experiment, accounting for the acceptance downtime of the DDGs, is defined as the memory downtime used in Fig. 4 of the main text.
S2.4 Optical fibers and photon detection
Signal-2 photons generated by the source are coupled to a 60-m-long delay-line optical fiber. This fiber length is, on the one hand, long enough to accommodate the electronics delays and memory lifetime and, on the other hand, short as possible in order to minimize the photon loss ( dB/km) and the forced downtime of the electronics. A slightly longer (shorter) fiber can be chosen to enable working with a longer (shorter) idler photons’ detection time window . For given generation rates , different choices of optimize the synchronized photon-pair rate . This is due to a trade-off between the probability for two idler photons to be generated within , and the average memory efficiency within and the electronics downtime. The model for given in Sec. S3 can be used to find the optimal .
Signal-1 photons generated by the source are coupled to a 25-m-long optical fiber that is coupled with a mating-sleeve connection to a 5-m-long fiber that is input to the memory, or to a different fiber that goes directly to a photon detector. The combined 30-m-long fiber from the source to the memory is used as a delay line to accommodate the electronic latencies and the propagation of the idler photons and control pulses through the optical fibers. The mating sleeve connection enables us to characterize the source without the memory and to input classical light into the memory for characterization and alignment. The coupling efficiency of the mating sleeve connection is () to the memory fiber (detector fiber).
We detect the photons using superconducting nanowire single-photon detectors (Quantum Opus) with detection efficiency and -ps detection time jitter. These detectors are sensitive to the polarization of the light fields, and therefore we couple the signal and idler photons from polarization-maintaining fibers to single-mode fibers in polarization controllers (Thorlabs FPC030) using mating-sleeve connectors. The single-mode fibers are then coupled to the detectors. In order to minimize the loss in the mating-sleeve connectors, we use low-loss key-aligned fiber optical patch cables (Oz Optics) with transmission.
S3 Model for photon coincidence rate
The accidental photon-coincidence rate is given by the signal-2 detection rate multiplied by the probability that a signal-1 photon is detected within a small time window . As explained in the main text, we consider ps. Therefore,
| (S1) |
For the coincidence rate after synchronization , we first examine the triggering rate of DDG-2. The rate at which idler-2 photons are detected is . However, the actual triggering rate is lower due to the set downtime of DDG-2 after an accepted input trigger. Next, we define the probability that, within the time window , idler-1 is detected and triggers DDG-1. The rate of DDG-1 output pulses (which corresponds to the number of synchronization attempts) is also reduced due to its electronics downtime . Therefore, the rate of synchronization attempts is
| (S2) |
Using , we calculate the memory downtime, given by
| (S3) |
Here we subtract the rate of synchronization attempts from the trigger rate of DDG-2 so as not to double-count the electronics downtime.
The average memory efficiency in the synchronization experiment is , which in our experiment is () before (after) correcting for the different transmissions of signal-1 through the two fiber alternatives, i.e., memory fiber or detector fiber. Note that here we neglect the probability of a photon arriving earlier within , as it is small for our experimental parameters. The synchronized photon coincidence count rate is finally given by
| (S4) |
and the coincidence enhancement factor is .
Figure 4 in the main text shows the calculated and , exhibiting an excellent agreement with the measured data. We attribute the small reduction of the measured compared to the model at high average downtime to a degradation of the amplitude of the control pulses when they are generated within 2 s from one another, which slightly reduces .
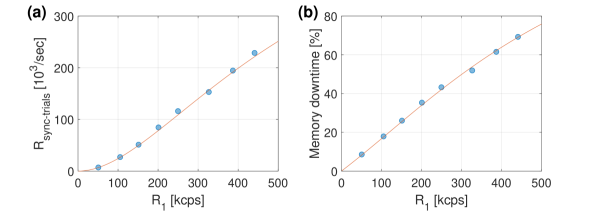
Figure S2 shows the memory operation rate and downtime versus . The model correctly predicts for all (with ), which further confirms that the slight degradation of the coincidence count rate is due to the reduced control-pulse amplitude.
S4 Model for
In the Fock state basis, the heralded single-photon state before the memory is given by
| (S5) |
where is the conditional, same-time, auto-correlation of signal-1 (before the memory). Here we assume that , where is the probability that contains photons, such that [45].
After the memory, the amplitude of the single-photon component reduces to due to the finite memory efficiency. We assume that the two-photon component is comprised of one heralded single photon (i.e. the signal photon) and one noise photon. The signal photon is stored and retrieved from the memory with efficiency . The noise photon may arrive from three different sources: (1) A (second) signal photon emitted at the same time as the (first) signal photon and stored with efficiency ; (2) A (second) signal photon emitted during the retrieval time of the memory, which may be partially transmitted through the memory module with transmission ; (3) An off-resonant photon scattered from pump-780 into the signal mode at the time of retrieval, transmitted through the memory module with transmission . While for the on-resonance photons, , for the off-resonance photons, the transmission is high (the 0.9 correction originates from residual absorption in the Autler-Townes splitting of the atomic absorption line, estimated from a comprehensive simulation of our system).
With these three sources for the noise photon, the photonic state after storage and retrieval at time is given by
| (S6) |
and the conditional auto-correlation after the memory is
| (S7) |
Here is the probability that the noise photon originates from the scattered off-resonant pump-780, which we independently measure.
We fit Eq. (S7) to the measured after the memory with as the only fit parameter. As shown in Fig. S3, we simultaneously fit the model to with kcps [as shown in Fig. 2(c) in the main text] and with kcps. The probability is independently measured to be () for (). Here the difference arises from different ratios between the powers of pump-780 and pump-776. We extract from the fit .
S5 Data analysis
Here we provide details on the data analysis used to compile the figures of the main text. Throughout the analysis, we consider a heralded single-photon detection if a signal photon is detected within 3.5-ns of the idler photon, or within a similar time window shifted due to the memory operation, as shown in Fig. 2(a) in the main text. This window accounts for of the photon-pulse energy. We consider only detected photon events and do not subtract any background.
The memory end-to-end efficiency is calculated by integrating the photons’ energy directly after the photon source and after storage and retrieval in the memory. Due to the lower transmission of signal-1 in the fiber coupling to the detector (see Sec. S2.4), we multiply the measured memory efficiency and enhancement factor by , so as not to overestimate our memory performance. The error bars in Figs. 2(c), 3(b), and 4(a) are calculated from the standard deviation of the mean (STDM) of repeated measurements. Due to a uncertainty in the fiber transmissions and detection efficiency, we calculate the error bars of as
| (S8) |
with a corresponding expression for the error bars of .
The signal photon auto-correlation , conditioned on an idler photon detection, is measured using a Hanburry Brown and Twiss setup, where the signal photon is split in a fiber beam splitter and detected in the output modes and . The conditional auto-correlation is given by [46], where is the three-photon coincidence count rate in a 3.5 ns time window, and and are the two-photon coincidence count rates in the same time window.
We measure the indistinguishability of signal-1 and signal-2 using a HOM interference measurement [42], with the two photons entering a symmetric fiber BS from different input ports. For the HOM measurement without synchronization, the time axis in Fig. 3(b) of the main text is given by the difference in detection times of the idler photons . We consider a double-heralded-single-photon event if and are both detected within the 3.5-ns window shown in Fig. 2(a) of the main text, or and are detected within the time window. Here and are the detection times of the signal photons at the output of the beam splitter in modes and , respectively.
For the synchronized HOM measurement, is defined by the different controlled retrieval times of signal-1′ from the memory. Here we consider a double-heralded-single-photon event if and were both detected within the 3.5-ns time window, or and were detected within the time window. Here is idler-2 detection time, conditioned on the memory operation, which ensures that idler-1 (now with uncorrelated timing to signal-1) was also detected.
For Fig. 4(a) in the main text, a double-heralded-single-photon coincidence for is considered if and are both detected within a 3.5-ns window, and ps. We consider a double-heralded-single-photon coincidence for if and are both detected within a 3.5-ns window, where is defined above.
S6 Additional experimental data
Figure S4 shows the HOM interference visibility versus . As increases, decreases due to the increase in the multi-photon component . is reduced compared to partially due to the increase of and partially due to the temporal distortion of the retrieved photon. To evaluate the latter, we calculate the temporal overlap of signal-1′ and signal-2 [21] , where , using the red and solid-blue profiles in Fig. 3(a) in the main text. We find , making it the dominant source of the visibility reduction at low , while the increased is the dominant source of the visibility reduction at high . For all data points presented in the paper, exceeds the classical bound.