This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs

T. Shang [email protected] Laboratory for Multiscale Materials Experiments, Paul Scherrer Institut, Villigen CH-5232, Switzerland Physik-Institut, Universität Zürich, Winterthurerstrasse 190, CH-8057 Zürich, Switzerland    M. Smidman Center for Correlated Matter and Department of Physics, Zhejiang University, Hangzhou 310058, China    A. Wang Center for Correlated Matter and Department of Physics, Zhejiang University, Hangzhou 310058, China    L. -J. Chang Department of Physics, National Cheng Kung University, Tainan 70101, Taiwan    C. Baines Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institut, CH-5232 Villigen PSI, Switzerland    M. K. Lee Department of Physics, National Cheng Kung University, Tainan 70101, Taiwan    Z. Y. Nie Center for Correlated Matter and Department of Physics, Zhejiang University, Hangzhou 310058, China    G. M. Pang Center for Correlated Matter and Department of Physics, Zhejiang University, Hangzhou 310058, China    W. Xie Center for Correlated Matter and Department of Physics, Zhejiang University, Hangzhou 310058, China    W. B. Jiang Center for Correlated Matter and Department of Physics, Zhejiang University, Hangzhou 310058, China    M. Shi Swiss Light Source, Paul Scherrer Institut, Villigen CH-5232, Switzerland    M. Medarde Laboratory for Multiscale Materials Experiments, Paul Scherrer Institut, Villigen CH-5232, Switzerland    T. Shiroka Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institut, CH-5232 Villigen PSI, Switzerland Laboratorium für Festkörperphysik, ETH Zürich, CH-8093 Zurich, Switzerland    H. Q. Yuan [email protected] Center for Correlated Matter and Department of Physics, Zhejiang University, Hangzhou 310058, China Collaborative Innovation Center of Advanced Microstructures, Nanjing Univeristy, Nanjing 210093, China
Abstract

By employing a series of experimental techniques, we provide clear evidence that CaPtAs represents a rare example of a noncentrosymmetric superconductor which simultaneously exhibits nodes in the superconducting gap and broken time-reversal symmetry (TRS) in its superconducting state (below TcT_{c} ≈\approx 1.5 K). Unlike in fully-gapped superconductors, the magnetic penetration depth λ​(T)\lambda(T) does not saturate at low temperatures, but instead it shows a T2T^{2}-dependence, characteristic of gap nodes. Both the superfluid density and the electronic specific heat are best described by a two-gap model comprising of a nodeless gap and a gap with nodes, rather than by single-band models. At the same time, zero-field muon-spin spectra exhibit increased relaxation rates below the onset of superconductivity, implying that TRS is broken in the superconducting state of CaPtAs, hence indicating its unconventional nature. Our observations suggest CaPtAs to be a new remarkable material which links two apparently disparate classes, that of TRS-breaking correlated magnetic superconductors with nodal gaps and the weakly-correlated noncentrosymmetric superconductors with broken TRS, normally exhibiting only a fully-gapped behavior.

††preprint: Preprint: , 5:08.

When entering the superconducting state, the breaking of extra symmetries in addition to U​(1)U(1) gauge symmetry is normally an indication of unconventional superconductivity (SC) Sigrist and Ueda (1991); Tsuei and Kirtley (2000). In a growing number of superconductors, time-reversal symmetry (TRS) breaking has been proved via the detection of spontaneous magnetic fields below the onset of superconductivity by means of zero-field muon-spin relaxation measurements. Notable examples include Sr2RuO4 Luke et al. (1998), UPt3 Luke et al. (1993), PrOs4Sb4 Aoki et al. (2003), LaNiGa2 Hillier et al. (2012), LaNiC2, La7T3T_{3}, and ReTT (TT = transition metal) superconductors Hillier et al. (2009); Barker et al. (2015); Singh et al. (2018, 2014); Shang et al. (2018a, b); Singh et al. (2017). The first two are well-known examples of SC in strongly-correlated systems with unconventional pairing mechanisms Mackenzie and Maeno (2003); Joynt and Taillefer (2002), while the latter three are examples of noncentrosymmetric superconductors (NCSCs), where the lack of inversion symmetry gives rise to an antisymmetric spin-orbit coupling (ASOC) leading to spin-split Fermi surfaces. Consequently, their pairing states are not constrained to be purely singlet or triplet, and mixed-parity pairing may occur Bauer and Sigrist (2012); Sungkit (2014); Smidman et al. (2017). Owing to such mixed pairing and/or the influence of ASOC, NCSCs may exhibit significantly different properties from their conventional counterparts, e.g., superconducting gaps with nodes Yuan et al. (2006); Nishiyama et al. (2007); Bonalde et al. (2005); Pang et al. (2015); Adroja et al. (2015), upper critical fields exceeding the Pauli limit Bauer et al. (2004); Carnicom et al. (2018); Shang et al. (2018a); Kimura et al. (2007); Chen et al. (2011) or, as recently proposed, even topological superconductivity Kim et al. (2018); Sun et al. (2015); Ali et al. (2014); Sato and Fujimoto (2009); Tanaka et al. (2010).

In general, the relationship between the breaking of TRS and a lack of inversion symmetry in the crystal structure is unclear. In many NCSCs such as Mo3Al2C, LaTTSi3, Mg10Ir19B16, or Mo3P Bauer et al. (2010); Anand et al. (2011, 2014); Smidman et al. (2014); Aczel et al. (2010); Shang et al. (2019), no spontaneous magnetic fields have been observed and thus TRS is preserved in the superconducting state. A notable feature of most of the weakly correlated NCSCs with broken TRS is the presence of fully opened superconducting gaps. In the case of LaNiC2, inconsistent results, including both fully-opened and nodal gap structures, have been found from measurements of the order parameter Lee et al. (1996); Chen et al. (2013); Hirose et al. (2012); Chen et al. (2013); Bonalde et al. (2011); Landaeta et al. (2017)111In an early report of the specific heat of LaNiC2, a T2T^{2}-dependence of C/T was observed (indicating nodal SC) Lee et al. (1996), but more recently exponential behavior of C/TC/T was reported, consistent with a fully-gapped superconducting state Chen et al. (2013); Hirose et al. (2012). Similar inconsistencies are also found from magnetic penetration depth λ​(T)\lambda(T) measurements, where both a T2T^{2}- and an exponential temperature dependence have been reported Chen et al. (2013); Bonalde et al. (2011); Landaeta et al. (2017), consistent with the presence of point nodes and fully gapped behavior, respectively.. The nodeless superconductivity of weakly correlated NCSCs is not only in contrast to the general expectations for strong singlet-triplet mixing, but also sets these systems apart from the strongly correlated superconductors Sr2RuO4 and UPt3 Luke et al. (1998, 1993), where the presence of unconventional pairing mechanisms is more unambiguously determined.

In LaNiC2, as well as in centrosymmetric LaNiGa2, the observed TRS breaking has been accounted for by non-unitary triplet pairing Hillier et al. (2009); Quintanilla et al. (2010); Hillier et al. (2012). This was reconciled with nodeless multigap SC by the proposal of even-parity triplet pairing, between electrons on different orbitals Weng et al. (2016). On the other hand, the ReTT superconductors, which have a relatively large ASOC compared to LaNiC2, appear to exhibit single fully-opened gaps, more consistent with a predominantly singlet pairing. The recent observation of TRS breaking in centrosymmetric elemental Re strongly suggests that the local electronic structure of Re is crucial for understanding the TRS breaking in the ReTT family Shang et al. (2018b). The broken TRS in weakly correlated systems, which otherwise appear to behave as conventional superconductors, has led to proposals to account for this behavior with a conventional pairing mechanism Agterberg et al. (1999), such as the loop-Josephson-current state, based on a model with onsite singlet pairing Ghosh et al. (2018).

To date, there are scarcely any examples of NCSC which clearly exhibit broken TRS and nodal-gap SC. In this Letter, we show that CaPtAs, a newly discovered NCSC Xie et al. (2020), is a rare candidate to display both such unconventional features. Our key observations of a nodal-gap and of spontaneous magnetic fields (concomitant with the onset of SC) indicate that CaPtAs represents a new remarkable example of a weakly-correlated NCSC encompassing both broken TRS and nodal SC.

Polycrystalline CaPtAs was synthesized via a solid-state reaction method Xie et al. (2020). Magnetic susceptibility, electrical resistivity, and specific-heat measurements were performed on a Quantum Design MPMS and PPMS, respectively. The muon-spin relaxation/rotation (μ\muSR) measurements were carried out on the low-temperature facility (LTF) spectrometers of the π\piM3 beamline at the Paul Scherrer Institut, Villigen, Switzerland. The temperature-dependent shift of the magnetic penetration depth, which is proportional to the frequency shift, i.e., Δ​λ=G​Δ​f\Delta\lambda=G\Delta f (with GG a geometry related constant), was measured by using a tunnel-diode oscillator (TDO) based technique at an operating frequency of 7 MHz Chen et al. (2013); Pang et al. (2015); Chen et al. (2011).

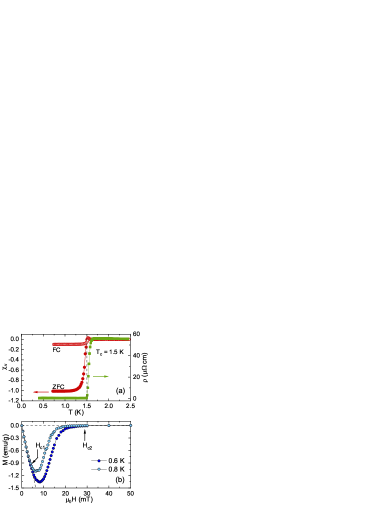
Refer to caption
Figure 1. : (a) Temperature dependent ZFC- and FC magnetic susceptibilities of CaPtAs (left axis), measured in an applied field of 1 mT, and zero-field electrical resistivity (right axis). The magnetic susceptibility data were corrected after considering the demagnetization factor. (b) Magnetization vs. applied magnetic field in the superconducting state. The lower critical field μ0​Hc1\mu_{0}H_{\mathrm{c1}} was determined as the value where M​(H)M(H) starts deviating from linearity (see dashed-line), while the upper critical field μ0​Hc2\mu_{0}H_{\mathrm{c2}} was identified with the field where the diamagnetic signal disappears.

CaPtAs crystallizes in a tetragonal noncentrosymmetric structure with space group I​41​m​dI4_{1}md (No. 109) Xie et al. (2020). The SC of CaPtAs was characterized by magnetic susceptibility, measured using both field-cooling- (FC) and zero-field-cooling (ZFC) protocols. As shown in Fig. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(a), the ZFC-susceptibility (after accounting for the demagnetization factor) indicates SC below Tc=1.5T_{c}=1.5 K, where the electrical resistivity (right axis) drops to zero, both being consistent with the specific-heat data Sup . The lower-critical-field, estimated from the field-dependent magnetization, is μ0​Hc​1=4.8​(1)\mu_{0}H_{c1}=4.8(1) mT [see Fig. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(b)].

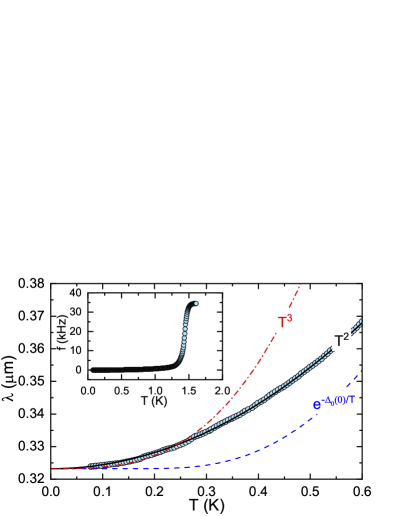
Refer to caption
Figure 2. : The magnetic penetration depth λ​(T)\lambda(T) of CaPtAs, measured using the TDO-based method in zero field at T≲1/3​TcT\lesssim 1/3T_{c}. The inset shows the TDO frequency up to temperatures above TcT_{c}. The black- and red lines represent fits to λ​(T)∼\lambda(T)\sim T2T^{\mathrm{2}} and T3T^{\mathrm{3}}, respectively, while the blue line indicates an exponential temperature dependence. λ\lambda was calculated as λ0+Δ​λ\lambda_{0}+\Delta\lambda, where λ0\lambda_{0} was derived from TF-μ\muSR measurements.

Figure Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs shows the temperature dependent magnetic penetration depth λ​(T)\lambda(T) measured by the TDO method and the corresponding exponential- and power-law fits. The TDO data over the full temperature range (see inset) illustrate the superconducting transition near Tc=1.5T_{c}=1.5 K. Clearly, λ​(T)\lambda(T) follows a quadratic temperature dependence [λ​(T)\lambda(T) ∼\sim T2T^{\mathrm{2}}], as expected for superconductors with point nodes. In contrast, a power-law with a larger exponent [λ​(T)\lambda(T) ∼\sim T3T^{\mathrm{3}}] or an exponential temperature dependence [λ​(T)\lambda(T) ∼\sim e−Δ0​(0)/Te^{-\Delta_{0}(0)/T}], the latter indicating fully-gapped behaviour, both deviate significantly from the experimental data.

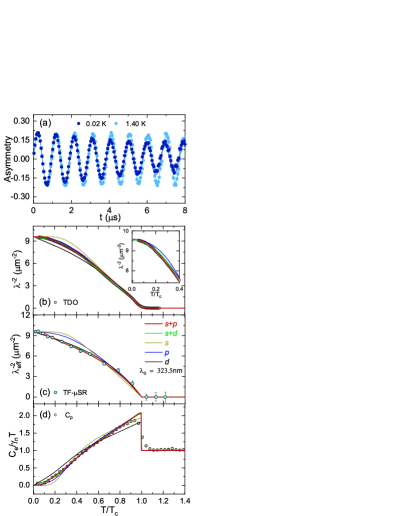
Refer to caption
Figure 3. : (a) Time-domain TF-μ\muSR spectra in the superconducting (0.02 K) and normal (1.4 K) states of CaPtAs. Superfluid density as estimated from (b) The TDO-based method and (c) TF-μ\muSR vs. the reduced temperature TT/TcT_{c}. The inset shows the enlarged plot of the TDO low-TT region. (d) Zero-field electronic specific heat vs. TT/TcT_{c}. The different lines represent fits to the various models (see text for details). The fit parameters are listed in Table SI Sup .

Figure Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(a) shows two typical transverse-field (TF) μ\muSR spectra collected at temperatures above and below TcT_{c} at 8 mT (Tc8​mTT_{c}^{\mathrm{8\,mT}} = 1.15 K) Sup , here corresponding to nearly twice μ0​Hc​1​(0)\mu_{0}H_{c1}(0). The TF-μ\muSR asymmetry data were analyzed using:

ATF=As​e−σ2​t2/2​cos⁡(γμ​Bs​t+ϕ)+Abg​cos⁡(γμ​Bbg​t+ϕ).A_{\mathrm{TF}}=A_{\mathrm{s}}e^{-\sigma^{2}t^{2}/2}\cos(\gamma_{\mu}B_{\mathrm{s}}t+\phi)+A_{\mathrm{bg}}\cos(\gamma_{\mu}B_{\mathrm{bg}}t+\phi). (1)

Here AsA_{\mathrm{s}} (50%) and AbgA_{\mathrm{bg}} (50%) represent the asymmetry of the sample and background (e.g., sample holder), respectively. γμ/2​π=135.53\gamma_{\mu}/2\pi=135.53 MHz/T is the muon gyromagnetic ratio, BsB_{\mathrm{s}} and BbgB_{\mathrm{bg}} are the local fields sensed by implanted muons in the sample and sample holder, ϕ\phi is the shared initial phase, and σ\sigma is a Gaussian relaxation rate. σ\sigma includes contributions from both the flux-line lattice (σsc\sigma_{\mathrm{sc}}) and a temperature-invariant relaxation due to nuclear moments (σn\sigma_{\mathrm{n}}). By subtracting the nuclear contribution in quadrature, one can extract σsc\sigma_{\mathrm{sc}}, i.e., σsc\sigma_{\mathrm{sc}} = σ2−σn2\sqrt{\sigma^{2}-\sigma^{2}_{\mathrm{n}}}. The upper critical field of CaPtAs is relatively small compared to the field applied during the TF-μ\muSR measurements (Hc​2H_{c2}/HapplH_{\mathrm{appl}} ∼\sim 4.3) Tinkham (1996); Werthamer et al. (1966); Sup . Hence, the effective penetration depth λeff\lambda_{\mathrm{eff}} had to be calculated from σsc\sigma_{\mathrm{sc}} by considering the overlap of vortex cores Brandt (2003):

σsc​(h)=0.172​γμ​Φ02​π​(1−h)​[1+1.21​(1−h)3]​λeff−2.\sigma_{\mathrm{sc}}(h)=0.172\frac{\gamma_{\mu}\Phi_{0}}{2\pi}(1-h)[1+1.21(1-\sqrt{h})^{3}]\lambda^{-2}_{\mathrm{eff}}. (2)

Here, h=Happl/Hc2h=H_{\mathrm{appl}}/H_{\mathrm{c2}}, is the reduced magnetic field.

Figures Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(b)-(c) show the superfluid density (ρsc∝λ−2\rho_{\mathrm{sc}}\propto\lambda^{-2}) measured by μ\muSR and TDO vs. the reduced temperature T/TcT/T_{c}, respectively. The superfluid density clearly varies with temperature down to the lowest TT, i.e., well below T/Tc=0.3T/T_{c}=0.3. This non-constant behavior again indicates the presence of low energy excitations and, hence, of nodes in the superconducting gap. To get further insight into the pairing symmetry, the temperature-dependent superfluid density was analyzed using different models. Considering a superconducting gap Δk\Delta_{\mathrm{k}}, the superfluid density ρsc​(T)\rho_{\mathrm{sc}}(T) can be calculated as:

ρsc=1+2​⟨∫Δk∞EE2−Δk2​∂f∂E​𝑑E⟩FS,\rho_{\mathrm{sc}}=1+2\Bigg{\langle}\int^{\infty}_{\Delta_{\mathrm{k}}}\frac{E}{\sqrt{E^{2}-\Delta_{\mathrm{k}}^{2}}}\frac{\partial f}{\partial E}dE\Bigg{\rangle}_{\mathrm{FS}}, (3)

where f=(1+eE/kB​T)−1f=(1+e^{E/k_{\mathrm{B}}T})^{-1} is the Fermi function and ⟨⟩FS\langle\rangle_{\mathrm{FS}} represents an average over the Fermi surface. The gap function can be written as Δk​(T)=Δ0​(T)​gk\Delta_{\mathrm{k}}(T)=\Delta_{0}(T)g_{\mathrm{k}}, where Δ0\Delta_{0} is the maximum gap value and gkg_{\mathrm{k}} is the angular dependence of the gap (see details in Table SI) Sup . The temperature dependence of the gap was assumed to follow Δ0​(T)=Δ0​(0)​tanh​{1.82​[1.018​(Tc/T−1)]0.51}\Delta_{0}(T)=\Delta_{0}(0)\mathrm{tanh}\{1.82[1.018(T_{\mathrm{c}}/T-1)]^{0.51}\}, where Δ0​(0)\Delta_{0}(0) is the gap value in the zero-temperature limit.

Five different models, single-gap ss-, pp-, dd-, and two-gap s+ps+p- and s+ds+d-wave, were used to analyze the superfluid density. The marked temperature dependence of the superfluid density at low-TT clearly rules out a fully-gapped ss-wave model [see yellow lines in Figs. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(b)-(c)]. Also in the case of a pure pp-wave, we find a poor agreement with the low-TT data (blue lines). A dd-wave model with line nodes, can reproduce reasonably well the TF-μ\muSR data, but it fails to follow the low-TT λ−2​(T)\lambda^{-2}(T) data obtained via TDO [see black lines in Figs. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(b)-(c)]. The slight difference between the TDO and TF-μ\muSR data below T/Tc∼0.5T/T_{c}\sim 0.5 is most likely due to the applied external field (8 mT) during the TF-μ\muSR measurements, which is not neglible comparedto the small Hc2H_{\mathrm{c2}} value of CaPtAs.

Conversely, the superfluid density is best fitted by a two-component s+ps+p- or s+ds+d-wave model [red and green lines in Figs. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(b)-(c)]. The good agreement with data of these models indicates the presence of multiple gaps, of which at least one has nodes on the Fermi surface. Although both models fit the superfluid density satisfactorily well across the full temperature range (T<TcT<T_{c}), the s+ps+p-wave model agrees better with the λ−2​(T)\lambda^{-2}(T) data measured using the TDO method [see inset of Fig. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(b)]. This is also strongly evidenced by both its smaller deviation from the data (see Table SI) and the quadratic low-TT dependence of λ​(T)\lambda(T) Sup .

To further validate the above conclusions, the zero-field electronic specific heat Ce/TC_{\mathrm{e}}/T was also analyzed using the above models Tinkham (1996); Padamsee et al. (1973); Bouquet et al. (2001). Ce/TC_{\mathrm{e}}/T was obtained by subtracting the phonon- and nuclear contributions from the measured data (see Fig. S2) Sup and it is shown in Fig. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(d) as Ce/γn​TC_{\mathrm{e}}/\gamma_{\mathrm{n}}T, with γn\gamma_{\mathrm{n}} the normal-state electronic specific-heat coefficient. Again, the single-gap ss-, pp-, and dd-wave models deviate significantly from the data. Conversely, both multigap models exhibit a good agreement with the experimental data across the full temperature range, with the s+ps+p-wave model showing the smallest deviation Sup , hence providing further evidence for nodal-gap SC in CaPtAs. The fit of the s+ps+p-wave model to the superfluid density and the electronic specific heat [including the ss-(∼\sim15%) and pp-wave (∼\sim85%) components] is shown in Fig. S3 Sup .

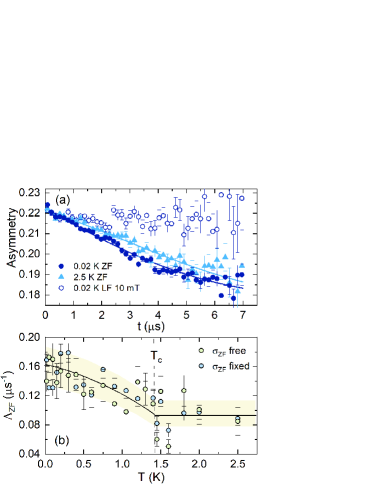
Refer to caption
Figure 4. : (a) Representative zero-field μ\muSR time spectra collected in the superconducting- (0.02 K) and normal (2.5 K) state of CaPtAs. Additional data were collected at 0.02 K in a 10-mT longitudinal field. The solid lines are fits to Eq. (4). (b) Derived Lorentzian relaxation rate ΛZF\Lambda_{\mathrm{ZF}} (using either a free- or a fixed-σZF\sigma_{\mathrm{ZF}} analysis) versus temperature. The solid line through the data is a guide to the eyes.

To search for spontaneous fields below TcT_{c}, signaling possible TRS breaking in CaPtAs, we performed zero field (ZF)-μ\muSR measurements. The clear increase in relaxation rate in the superconducting state [see Fig. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(a)] hints at the breaking of TRS. For non-magnetic materials, the depolarization is generally described by a Gaussian Kubo-Toyabe relaxation function Kubo and Toyabe (1967); Yaouanc and de Réotier (2011). For CaPtAs, the ZF-μ\muSR spectra were fitted by considering an additional Lorentzian relaxation component, with AsA_{\mathrm{s}} and AbgA_{\mathrm{bg}} being the same as in the TF-μ\muSR case:

AZF=As​[13+23​(1−σZF2​t2)​e(−σZF2​t22)]​e−ΛZF​t+Abg.A_{\mathrm{ZF}}=A_{\mathrm{s}}\left[\frac{1}{3}+\frac{2}{3}(1-\sigma_{\mathrm{ZF}}^{2}t^{2})\,\mathrm{e}^{(-\frac{\sigma_{\mathrm{ZF}}^{2}t^{2}}{2})}\right]\mathrm{e}^{-\Lambda_{\mathrm{ZF}}t}+A_{\mathrm{bg}}. (4)

Fits using the above model yield an almost temperature-independent Gaussian relaxation rate (σZF\sigma_{\mathrm{ZF}}) across the measured temperature range [see Fig. S4(b)] Sup . Hence, the Lorentzian relaxation rate (ΛZF\Lambda_{\mathrm{ZF}}) was estimated by fixing σZF\sigma_{\mathrm{ZF}} to its average value (σZFavg\sigma_{\mathrm{ZF}}^{\mathrm{avg}} = 0.13 μ\mus-1). As shown in Fig. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(b), a small yet measurable increase of ΛZF\Lambda_{\mathrm{ZF}} below TcT_{c} and a temperature-independent relaxation above TcT_{c}, reflect the onset of spontaneous magnetic fields. The latter can be considered as the signature of TRS breaking in the superconducting state of CaPtAs, with similarly enhanced ΛZF\Lambda_{\mathrm{ZF}} having also been found in other TRS breaking NCSCs Hillier et al. (2009); Barker et al. (2015). Both free- and fixed-σZF\sigma_{\mathrm{ZF}} analyses show a robust increase in ΛZF​(T)\Lambda_{\mathrm{ZF}}(T) below TcT_{c}, demonstrating that the signal of spontaneous magnetic fields is an intrinsic effect, rather than an artifact of correlated fit parameters. This is further confirmed in Fig. S5, where we show the cross correlations between the different fit parameters Sup . Finally, longitudinal-field (LF)-μ\muSR measurements were performed at base temperature (0.02 K) to rule out additional extrinsic effects such as defect/impurity induced relaxation. As shown in Fig. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs(a), a small field of 10 mT is sufficient to fully decouple the muon spins from the weak spontaneous magnetic fields, indicating that the fields are static on the time scale of the muon lifetime.

To date, most NCSCs with broken TRS exhibit nodeless superconductivity, indicating that the spin-singlet channel dominates the pairing. These include the α\alpha-Mn-type ReTT Singh et al. (2014, 2017); Shang et al. (2018a, b) and Th7Fe3-type La7T3T_{3} Barker et al. (2015); Singh et al. (2018). As for CeNiC2-type NCSCs, the recently discovered ThCoC2 exhibits nodal SC, but no evidence of broken TRS has been found Bhattacharyya et al. (2019). In LaNiC2 instead, the low symmetry of its orthorhombic crystal structure means that the breaking of TRS at TcT_{c} necessarily implies nonunitary triplet pairing, and rules out the mixed singlet-triplet state described below Hillier et al. (2009); Quintanilla et al. (2010). However, measurements of the gap symmetry have yielded inconsistent results, where both fully-opened and nodal gap structures have been reported Lee et al. (1996); Chen et al. (2013); Hirose et al. (2012); Chen et al. (2013); Bonalde et al. (2011); Landaeta et al. (2017). Compared to the above cases, CaPtAs represents a new remarkable NSCS, which accommodates both broken TRS and nodal SC.

One possibility is that the observed multigap superconductivity corresponds to different gaps on distinct electronic bands, which would be consistent with band-structure calculations showing multiple bands crossing the Fermi level Xie et al. (2020). An alternative scenario is that in NCSCs, the admixture of singlet- ψ​(𝒌)\psi(\boldsymbol{k}) and triplet 𝒅​(𝒌)\boldsymbol{d}(\boldsymbol{k}) order parameters leads to gap structures with Δ​(𝒌)±=ψ​(𝒌)±|𝒅​(𝒌)|\Delta(\boldsymbol{k})_{\pm}=\psi(\boldsymbol{k})\pm\left|\boldsymbol{d}(\boldsymbol{k})\right|  Bauer and Sigrist (2012); Sungkit (2014); Smidman et al. (2017). Clearly, if the triplet component is small, the gaps on the spin-split Fermi surfaces will both be nodeless and of nearly equal magnitude, making this case hardly distinguishable from a single-gap ss-wave superconductor. On the other hand, if the triplet component dominates, there can be one nodeless gap, and another with nodes. Such a scenario can explain well, for instance, the multigap nodeless SC in Li2Pd3B and the nodal SC in Li2Pt3B, since the triplet-component increases with the enhanced ASOC upon the substitution of Pt for Pd Yuan et al. (2006). We find that the superfluid density of CaPtAs is best described by models with one nodeless and one nodal gap, which also corresponds to that expected for significant singlet-triplet mixing.

According to band-structure calculations, the estimated band splitting due to ASOC is about 50–100 meV, which gives EsocE_{\mathrm{soc}}/kBk_{\mathrm{B}}TcT_{c} ∼\sim 400-800 Xie et al. (2020). Though much smaller than the band splitting of CePt3Si (EsocE_{\mathrm{soc}}/kBk_{\mathrm{B}}TcT_{c} ∼\sim 3095) Samokhin et al. (2004), it is comparable to that of Li2Pt3B (∼\sim 831) Lee and Pickett (2005), and much larger than that of most other NCSCs. Since the above two Pt compounds are believed to exhibit mixed pairing Frigeri et al. (2004); Yuan et al. (2006), the presence of large band splitting due to ASOC, in addition to nodal multigap SC, suggests that CaPtAs is a good candidate for large singlet-triplet mixing. However, whether in this crystal structure there is a TRS-breaking mixed singlet-triplet state compatible with the ASOC, requires further theoretical analysis. We note that, if one considers TRS breaking states corresponding to the two-dimensional irreducible representations of the point group C4​vC_{4v}, the simplest one is a chiral pp-wave state Smidman et al. (2017), originally applied to Sr2RuO4 Mackenzie and Maeno (2003). The pp-wave model and pp-component of s+ps+p-wave model we use in Fig. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs correspond to this chiral pp-wave state. A specific attribution of the pairing symmetry requires further measurements on single crystals, together with microscopic calculations based on the band structure. Different from the proposed topological NCSCs Kim et al. (2018); Sun et al. (2015), CaPtAs exhibits simultaneously nodal SC and broken TRS. This suggests that it could be a possible exotic-type of topological superconductor, a suitable candidate material in which to search for Majorana zero modes Schnyder and Brydon (2015); Sato and Ando (2017). Due to its high stability and the availability of single crystals Xie et al. (2020), CaPtAs is very promising for future investigations using other techniques, such as scanning tunneling microscopy (STM), or angle-resolved photoemission spectroscopy (ARPES).

In summary, we find that CaPtAs is an example of an NCSC exhibiting both TRS breaking and nodal superconductivity. Its superfluid density and specific heat are best described by a two-gap model, with one gap being fully open and the other being nodal. The presence of multigap nodal superconductivity and sizeable band splitting due to ASOC makes CaPtAs a good candidate for hosting mixed singlet- and triplet pairing. While further theoretical calculations and measurements are necessary to determine the nature of the order parameter and pairing mechanism, this system may offer new insights for bridging the gap between different classes of TRS-breaking superconductors, namely strongly correlated superconductors with magnetically mediated pairing and nodal gaps (such as Sr2RuO4 and UPt3) and the more recently discovered weakly-correlated NCSCs.

This work was supported by the National Key R&D Program of China (Grants no. 2016YFA0300202 and 2017YFA0303100), the National Natural Science Foundation of China (Grants no. U1632275, 11874320 and 11974306), the Schweizerische Nationalfonds zur Förderung der Wissenschaftlichen Forschung, SNF (Grants no. 200021-169455 and 206021-139082). L. J. C. thanks the MOST Funding for the support under the projects 104-2112-M-006-010-MY3 and 107-2112-M-006-020. We also acknowledge the assistance from other beamline scientists on LTF μ\muSR spectrometers at PSI.

References

  • Sigrist and Ueda (1991) M. Sigrist and K. Ueda, Phenomenological theory of unconventional superconductivity, Rev. Mod. Phys. 63, 239 (1991).
  • Tsuei and Kirtley (2000) C. C. Tsuei and J. R. Kirtley, Pairing symmetry in cuprate superconductors, Rev. Mod. Phys. 72, 969 (2000).
  • Luke et al. (1998) G. M. Luke, Y. Fudamoto, K. M. Kojima, M. I. Larkin, J. Merrin, B. Nachumi, Y. J. Uemura, Y. Maeno, Z. Q. Mao, Y. Mori, H. Nakamura, and M. Sigrist, Time-reversal symmetry-breaking superconductivity in Sr2RuO4, Nature 394, 558 (1998).
  • Luke et al. (1993) G. M. Luke, A. Keren, L. P. Le, W. D. Wu, Y. J. Uemura, D. A. Bonn, L. Taillefer, and J. D. Garrett, Muon spin relaxation in UPt3, Phys. Rev. Lett. 71, 1466 (1993).
  • Aoki et al. (2003) Y. Aoki, A. Tsuchiya, T. Kanayama, S. R. Saha, H. Sugawara, H. Sato, W. Higemoto, A. Koda, K. Ohishi, K. Nishiyama, and R. Kadono, Time-reversal symmetry-breaking superconductivity in heavy-fermion PrOs4Sb12 detected by muon-spin relaxation, Phys. Rev. Lett. 91, 067003 (2003).
  • Hillier et al. (2012) A. D. Hillier, J. Quintanilla, B. Mazidian, J. F. Annett, and R. Cywinski, Nonunitary triplet pairing in the centrosymmetric superconductor LaNiGa2, Phys. Rev. Lett. 109, 097001 (2012).
  • Hillier et al. (2009) A. D. Hillier, J. Quintanilla, and R. Cywinski, Evidence for time-reversal symmetry breaking in the noncentrosymmetric superconductor LaNiC2, Phys. Rev. Lett. 102, 117007 (2009).
  • Barker et al. (2015) J. A. T. Barker, D. Singh, A. Thamizhavel, A. D. Hillier, M. R. Lees, G. Balakrishnan, D. M. Paul, and R. P. Singh, Unconventional superconductivity in La7Ir3 revealed by muon spin relaxation: Introducing a new family of noncentrosymmetric superconductor that breaks time-reversal symmetry, Phys. Rev. Lett. 115, 267001 (2015).
  • Singh et al. (2018) D. Singh, M. S. Scheurer, A. D. Hillier, and R. P. Singh, Time-reversal-symmetry breaking and unconventional pairing in the noncentrosymmetric superconductor La7Rh3 probed by μ\muSR, arXiv preprint arXiv:1802.01533  (2018).
  • Singh et al. (2014) R. P. Singh, A. D. Hillier, B. Mazidian, J. Quintanilla, J. F. Annett, D. M. Paul, G. Balakrishnan, and M. R. Lees, Detection of time-reversal symmetry breaking in the noncentrosymmetric superconductor Re6Zr using muon-spin spectroscopy, Phys. Rev. Lett. 112, 107002 (2014).
  • Shang et al. (2018a) T. Shang, G. M. Pang, C. Baines, W. B. Jiang, W. Xie, A. Wang, M. Medarde, E. Pomjakushina, M. Shi, J. Mesot, H. Q. Yuan, and T. Shiroka, Nodeless superconductivity and time-reversal symmetry breaking in the noncentrosymmetric superconductor Re24Ti5, Phys. Rev. B 97, 020502(R) (2018a).
  • Shang et al. (2018b) T. Shang, M. Smidman, S. K. Ghosh, C. Baines, L. J. Chang, D. J. Gawryluk, J. A. T. Barker, R. P. Singh, D. M. Paul, G. Balakrishnan, E. Pomjakushina, M. Shi, M. Medarde, A. D. Hillier, H. Q. Yuan, J. Quintanilla, J. Mesot, and T. Shiroka, Time-reversal symmetry breaking in Re-based superconductors, Phys. Rev. Lett. 121, 257002 (2018b).
  • Singh et al. (2017) D. Singh, J. A. T. Barker, A. Thamizhavel, D. M. Paul, A. D. Hillier, and R. P. Singh, Time-reversal symmetry breaking in the noncentrosymmetric superconductor Re6Hf: Further evidence for unconventional behavior in the α\alpha-Mn family of materials, Phys. Rev. B 96, 180501(R) (2017).
  • Mackenzie and Maeno (2003) A. P. Mackenzie and Y. Maeno, The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing, Rev. Mod. Phys. 75, 657 (2003), and reference therein.
  • Joynt and Taillefer (2002) R. Joynt and L. Taillefer, The superconducting phases of UPt3, Rev. Mod. Phys. 74, 235 (2002), and reference therein.
  • Bauer and Sigrist (2012) E. Bauer and M. Sigrist, eds., Non-Centrosymmetric Superconductors, Vol. 847 (Springer Verlag, Berlin, 2012).
  • Sungkit (2014) Y. Sungkit, Noncentrosymmetric superconductors, Annu. Rev. Condens. Matter Phys. 5, 15 (2014).
  • Smidman et al. (2017) M. Smidman, M. B. Salamon, H. Q. Yuan, and D. F. Agterberg, Superconductivity and spin–orbit coupling in non-centrosymmetric materials: A review, Rep. Prog. Phys. 80, 036501 (2017).
  • Yuan et al. (2006) H. Q. Yuan, D. F. Agterberg, N. Hayashi, P. Badica, D. Vandervelde, K. Togano, M. Sigrist, and M. B. Salamon, S-wave spin-triplet order in superconductors without inversion symmetry: Li2Pd3B and Li2Pt3B, Phys. Rev. Lett. 97, 017006 (2006).
  • Nishiyama et al. (2007) M. Nishiyama, Y. Inada, and G.-q. Zheng, Spin triplet superconducting state due to broken inversion symmetry in Li2Pt3B, Phys. Rev. Lett. 98, 047002 (2007).
  • Bonalde et al. (2005) I. Bonalde, W. Brämer-Escamilla, and E. Bauer, Evidence for line nodes in the superconducting energy gap of noncentrosymmetric CePt3Si from magnetic penetration depth measurements, Phys. Rev. Lett. 94, 207002 (2005).
  • Pang et al. (2015) G. M. Pang, M. Smidman, W. B. Jiang, J. K. Bao, Z. F. Weng, Y. F. Wang, L. Jiao, J. L. Zhang, G. H. Cao, and H. Q. Yuan, Evidence for nodal superconductivity in quasi-one-dimensional K2Cr3As3, Phys. Rev. B 91, 220502(R) (2015).
  • Adroja et al. (2015) D. T. Adroja, A. Bhattacharyya, M. Telling, Y. Feng, M. Smidman, B. Pan, J. Zhao, A. D. Hillier, F. L. Pratt, and A. M. Strydom, Superconducting ground state of quasi-one-dimensional K2Cr3As3 investigated using μ​SR\mu\text{SR} measurements, Phys. Rev. B 92, 134505 (2015).
  • Bauer et al. (2004) E. Bauer, G. Hilscher, H. Michor, C. Paul, E. W. Scheidt, A. Gribanov, Y. Seropegin, H. Noël, M. Sigrist, and P. Rogl, Heavy fermion superconductivity and magnetic order in noncentrosymmetric CePt3Si, Phys. Rev. Lett. 92, 027003 (2004).
  • Carnicom et al. (2018) E. M. Carnicom, W. w. Xie, T. Klimczuk, J. J. Lin, K. Górnicka, Z. Sobczak, N. P. Ong, and R. J. Cava, The chiral non-centrosymmetric superconductors TaRh2B2 and nbrh NbRh2B2, Sci. Adv. 4, eaar7969 (2018).
  • Kimura et al. (2007) N. Kimura, K. Ito, H. Aoki, S. Uji, and T. Terashima, Extremely high upper critical magnetic field of the noncentrosymmetric heavy fermion superconductor CeRhSi3, Phys. Rev. Lett. 98, 197001 (2007).
  • Chen et al. (2011) J. Chen, M. B. Salamon, S. Akutagawa, J. Akimitsu, J. Singleton, J. L. Zhang, L. Jiao, and H. Q. Yuan, Evidence of nodal gap structure in the noncentrosymmetric superconductor Y2C3, Phys. Rev. B 83, 144529 (2011).
  • Kim et al. (2018) H. Kim, K. Wang, Y. Nakajima, R. Hu, S. Ziemak, P. Syers, L. Wang, H. Hodovanets, J. D. Denlinger, P. M. R. Brydon, D. F. Agterberg, M. A. Tanatar, R. Prozorov, and J. Paglione, Beyond triplet: Unconventional superconductivity in a spin-3/23/2 topological semimetal, Sci. Adv. 4, eaao4513 (2018).
  • Sun et al. (2015) Z. X. Sun, M. Enayat, A. Maldonado, C. Lithgow, E. Yelland, D. C. Peets, A. Yaresko, A. P. Schnyder, and P. Wahl, Dirac surface states and nature of superconductivity in noncentrosymmetric BiPd, Nat. Commun. 6, 6633 (2015).
  • Ali et al. (2014) M. N. Ali, Q. D. Gibson, T. Klimczuk, and R. J. Cava, Noncentrosymmetric superconductor with a bulk three-dimensional Dirac cone gapped by strong spin-orbit coupling, Phys. Rev. B 89, 020505(R) (2014).
  • Sato and Fujimoto (2009) M. Sato and S. Fujimoto, Topological phases of noncentrosymmetric superconductors: Edge states, Majorana fermions, and non-Abelian statistics, Phys. Rev. B 79, 094504 (2009).
  • Tanaka et al. (2010) Y. Tanaka, Y. Mizuno, T. Yokoyama, K. Yada, and M. Sato, Anomalous Andreev bound state in noncentrosymmetric superconductors, Phys. Rev. Lett. 105, 097002 (2010).
  • Bauer et al. (2010) E. Bauer, G. Rogl, X.-Q. Chen, R. T. Khan, H. Michor, G. Hilscher, E. Royanian, K. Kumagai, D. Z. Li, Y. Y. Li, R. Podloucky, and P. Rogl, Unconventional superconducting phase in the weakly correlated noncentrosymmetric Mo3Al2C compound, Phys. Rev. B 82, 064511 (2010).
  • Anand et al. (2011) V. K. Anand, A. D. Hillier, D. T. Adroja, A. M. Strydom, H. Michor, K. A. McEwen, and B. D. Rainford, Specific heat and μ\musr study on the noncentrosymmetric superconductor LaRhSi3, Phys. Rev. B 83, 064522 (2011).
  • Anand et al. (2014) V. K. Anand, D. Britz, A. Bhattacharyya, D. T. Adroja, A. D. Hillier, A. M. Strydom, W. Kockelmann, B. D. Rainford, and K. A. McEwen, Physical properties of noncentrosymmetric superconductor LaIrSi3: A μ\muSR study, Phys. Rev. B 90, 014513 (2014).
  • Smidman et al. (2014) M. Smidman, A. D. Hillier, D. T. Adroja, M. R. Lees, V. K. Anand, R. P. Singh, R. I. Smith, D. M. Paul, and G. Balakrishnan, Investigations of the superconducting states of noncentrosymmetric LaPdSi3 and LaPtSi3, Phys. Rev. B 89, 094509 (2014).
  • Aczel et al. (2010) A. A. Aczel, T. J. Williams, T. Goko, J. P. Carlo, W. Yu, Y. J. Uemura, T. Klimczuk, J. D. Thompson, R. J. Cava, and G. M. Luke, Muon spin rotation/relaxation measurements of the noncentrosymmetric superconductor Mg10Ir19B16, Phys. Rev. B 82, 024520 (2010).
  • Shang et al. (2019) T. Shang, J. Philippe, J. A. T. Verezhak, Z. Guguchia, J. Z. Zhao, L.-J. Chang, M. K. Lee, D. J. Gawryluk, E. Pomjakushina, M. Shi, M. Medarde, H.-R. Ott, and T. Shiroka, Nodeless superconductivity and preserved time-reversal symmetry in the noncentrosymmetric Mo3P superconductor, Phys. Rev. B 99, 184513 (2019).
  • Lee et al. (1996) W. H. Lee, H. K. Zeng, Y. D. Yao, and Y. Y. Chen, Superconductivity in the Ni based ternary carbide LaNiC2, Physica C 266, 138 (1996).
  • Chen et al. (2013) J. Chen, L. Jiao, J. L. Zhang, Y. Chen, L. Yang, M. Nicklas, F. Steglich, and H. Q. Yuan, Evidence for two-gap superconductivity in the non-centrosymmetric compound LaNiC2, New J. Phys. 15, 053005 (2013).
  • Hirose et al. (2012) Y. Hirose, T. Kishino, J. Sakaguchi, Y. Miura, F. Honda, T. Takeuchi, E. Yamamoto, Y. Haga, H. Harima, R. Settai, and Y. Ōnuki, Fermi Surface and Superconducting Properties of Non-centrosymmetric LaNiC2, J. Phys. Soc. Jpn. 81, 113703 (2012).
  • Bonalde et al. (2011) I. Bonalde, R. L. Ribeiro, K. J. Syu, H. H. Sung, and W. H. Lee, Nodal gap structure in the noncentrosymmetric superconductor LaNiC2 from magnetic-penetration-depth measurements, New J. Phys. 13, 123022 (2011).
  • Landaeta et al. (2017) J. F. Landaeta, D. Subero, P. Machado, F. Honda, and I. Bonalde, Unconventional superconductivity and an ambient-pressure magnetic quantum critical point in single-crystal LaNiC2, Phys. Rev. B 96, 174515 (2017).
  • Note (1) In an early report of the specific heat of LaNiC2, a T2T^{2}-dependence of C/T was observed (indicating nodal SC) Lee et al. (1996), but more recently exponential behavior of C/TC/T was reported, consistent with a fully-gapped superconducting state Chen et al. (2013); Hirose et al. (2012). Similar inconsistencies are also found from magnetic penetration depth λ​(T)\lambda(T) measurements, where both a T2T^{2}- and an exponential temperature dependence have been reported Chen et al. (2013); Bonalde et al. (2011); Landaeta et al. (2017), consistent with the presence of point nodes and fully gapped behavior, respectively.
  • Quintanilla et al. (2010) J. Quintanilla, A. D. Hillier, J. F. Annett, and R. Cywinski, Relativistic analysis of the pairing symmetry of the noncentrosymmetric superconductor LaNiC2, Phys. Rev. B 82, 174511 (2010).
  • Weng et al. (2016) Z. F. Weng, J. L. Zhang, M. Smidman, T. Shang, J. Quintanilla, J. F. Annett, M. Nicklas, G. M. Pang, L. Jiao, W. B. Jiang, Y. Chen, F. Steglich, and H. Q. Yuan, Two-gap superconductivity in LaNiGa2 with nonunitary triplet pairing and even parity gap symmetry, Phys. Rev. Lett. 117, 027001 (2016).
  • Agterberg et al. (1999) D. F. Agterberg, V. Barzykin, and L. P. Gor’kov, Conventional mechanisms for exotic superconductivity, Phys. Rev. B 60, 14868 (1999).
  • Ghosh et al. (2018) S. Ghosh, J. F. Annett, and J. Quintanilla, Time-reversal symmetry breaking in superconductors through loop Josephson-current order, arXiv preprint arXiv:1803.02618  (2018).
  • Xie et al. (2020) W. Xie, P. R. Zhang, B. Shen, W. B. Jiang, G. M. Pang, T. Shang, C. Gao, M. Smidman, and H. Q. Yuan, CaPtAs: a new noncentrosymmetric superconductor, Sci. China-Phys. Mech. Astron. 63, 237412 (2020).
  • (50) See the Supplemental Material at http://link.aps.org/supplemental/xxx/PhysRevLett.xxxxx for details on the measurements of the upper critical field, the analyses of superfluid density, specific heat, and ZF-μ\muSR data, and Refs. [43–44, 46–47] therein.
  • Tinkham (1996) M. Tinkham, Introduction to Superconductivity, 2nd ed. (Dover Publications, Mineola, NY, 1996).
  • Werthamer et al. (1966) N. R. Werthamer, E. Helfand, and P. C. Hohenberg, Temperature and purity dependence of the superconducting critical field, Hc​2{{H}}_{c2}. III. Electron spin and spin-orbit effects, Phys. Rev. 147, 295 (1966).
  • Brandt (2003) E. H. Brandt, Properties of the ideal Ginzburg-Landau vortex lattice, Phys. Rev. B 68, 054506 (2003).
  • Padamsee et al. (1973) H. Padamsee, J. E. Neighbor, and C. A. Shiffman, Quasiparticle phenomenology for thermodynamics of strong-coupling superconductor, J. Low Temp. Phys. 12, 387 (1973).
  • Bouquet et al. (2001) F. Bouquet, Y. Wang, R. A. Fisher, D. G. Hinks, J. D. Jorgensen, A. Junod, and N. E. Phillips, Phenomenological two-gap model for the specific heat of MgB2, Europhys. Lett. 56, 856 (2001).
  • Kubo and Toyabe (1967) R. Kubo and T. Toyabe, A stochastic model for low field resonance and relaxation, in Magnetic Resonance and Relaxation, edited by R. Blinc (North-Holland, Amsterdam, 1967) pp. 810–823.
  • Yaouanc and de Réotier (2011) A. Yaouanc and P. D. de Réotier, Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter (Oxford University Press, Oxford, 2011).
  • Bhattacharyya et al. (2019) A. Bhattacharyya, D. T. Adroja, K. Panda, S. Saha, T. Das, A. J. S. Machado, O. V. Cigarroa, T. W. Grant, Z. Fisk, A. D. Hillier, and P. Manfrinetti, Evidence of a nodal line in the superconducting gap symmetry of noncentrosymmetric ThCoC2, Phys. Rev. Lett. 122, 147001 (2019).
  • Samokhin et al. (2004) K. V. Samokhin, E. S. Zijlstra, and S. K. Bose, CePt3Si: An unconventional superconductor without inversion center, Phys. Rev. B 69, 094514 (2004).
  • Lee and Pickett (2005) K.-W. Lee and W. E. Pickett, Crystal symmetry, electron-phonon coupling, and superconducting tendencies in Li2Pd3B and Li2Pt3B, Phys. Rev. B 72, 174505 (2005).
  • Frigeri et al. (2004) P. A. Frigeri, D. F. Agterberg, A. Koga, and M. Sigrist, Superconductivity without inversion symmetry: MnSi versus CePt3​Si{\mathrm{C}\mathrm{e}\mathrm{P}\mathrm{t}}_{3}\mathrm{S}\mathrm{i}, Phys. Rev. Lett. 92, 097001 (2004).
  • Schnyder and Brydon (2015) A. P. Schnyder and P. M. R. Brydon, Topological surface states in nodal superconductors, J. Phys.: Condens. Matter 27, 243201 (2015).
  • Sato and Ando (2017) M. Sato and Y. Ando, Topological superconductors: a review, Rep. Prog. Phys. 80, 076501 (2017).