XXXX-XXXX
1]Graduate School of Science and Technology, University of Tsukuba, Tsukuba, Ibaraki, 305-8571, Japan
2]Institute of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Ibaraki, 305-8571, Japan
3]Center for Computational Sciences, University of Tsukuba, Tsukuba, Ibaraki, 305-8577, Japan
4]Division of Science and Technology, Tokushima University, 2-1 Minami Josanjima-cho Tokushima city, Tokushima, 770-8506, Japan
5]Department of Human Science, Obihiro University of Agriculture and Veterinary Medicine, Obihiro, Hokkaido, 080-8555, Japan 6]Research Center for Neutrino Science, Tohoku University, Sendai, 980-8578, Japan
7]New Industry Creation Hatchery Center, Tohoku University, 6-6-10 Aramaki Aza Aoba, Aoba-ku, Sendai, Miyagi, 980-8579, Japan 8]C&A Corporation, 1-16-23 Ichibancho, Aoba-ku, Sendai, Miyagi, 980-0811, Japan
9]Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency, Sagamihara, Kanagawa, 252-5210, Japan
Simulation Tool Development and Sensitivity Analysis of 160Gd Double Beta Decay Search by the PIKACHU Project
Abstract
Neutrinoless double beta decay (02) has been investigated as a physical process that can provide evidence for the Majorana nature of neutrinos. The theoretical predictions of the 02 rate are subject to significant uncertainty, primarily due to nuclear matrix elements (NME). To reduce this uncertainty, experimental measurements of the half-lives of two-neutrino double beta decay (22) in various nuclei are essential as a benchmark for NME calculations. The PIKACHU (Pure Inorganic scintillator experiment in KAmioka for CHallenging Underground sciences) project searches for the previously unobserved 22 of 160Gd, employing Ce-doped Gd3Ga3Al2O12 (GAGG) single crystals. In the Phase 1 experiment, we aim to improve the current lower limit on the 22 half-life of 160Gd, set at 1.9 1019 years (90 C.L.) by a prior study using a Ce-doped Gd2SiO5 (GSO) crystal. Ultimately, in Phase 2, the project seeks to achieve a sensitivity surpassing the theoretical prediction of 7.4 1020 years, enabling the potential discovery of the 160Gd 22. Understanding and evaluating backgrounds are crucial to determining the experimental sensitivity. In this paper, we describe the development of background models based on GEANT4 simulations. The modeled backgrounds are contributions from uranium and thorium decay chains, 40K present in GAGG, and 40K -rays from outside of GAGG. Additionally, we developed models for both 22 and 02 by implementing the theoretical kinematics of two-electron emission in double beta decay in the GEANT4 simulation. As a result, our background models successfully reproduced the measured background spectrum through fitting. By generating pseudo background spectra expected in Phase 1 and analyzing them with the combined background and 22 models, we evaluated the 22 sensitivity of Phase 1 to be 2.78 1019 years (90 C.L.). This paper presents the development of these simulation models and the expected sensitivities for both Phase 1 and Phase 2 based on the pseudo data analyses.
xxxx, xxx
1 Introduction
The neutrinoless double beta decay (02) is a physical process beyond the framework of the Standard Model that violates the lepton number conservation. The 02 provides conclusive evidence for the Majorana nature of neutrinos, wherein neutrinos are identical to their own antiparticles. The half-life of 02 () is inversely proportional to the square of the effective electron neutrino mass (), offering crucial insights into the neutrino’s absolute mass. In contrast, the two-neutrino double beta decay (22), a process allowed within the Standard Model, has been experimentally observed in several nuclei 2nbb . Many research groups are actively measuring the half-lives of 22 () in various candidate nuclei, as these measurements play a key role in improving the precision of nuclear matrix elements (NME) calculations NME . NME, a nuclide-specific theoretical parameters connecting and , carries significant uncertainties depending on the calculation method employed. Reducing these uncertainties is essential for enhancing the reliability of theoretical predictions and experimental interpretations in 02 studies.
The PIKACHU (Pure Inorganic scintillator experiment in KAmioka for CHallenging Underground sciences) project focuses on investigating the double beta decay (2) of 160Gd. 160Gd is a 2 candidate with a high natural abundance (21.9) and a low -value (1.730 MeV Qval ) compared to other candidates. These characteristics suggest that an abundance of 160Gd can be utilized in experiments, highlighting the critical need to suppress background radiation with the energy near the 160Gd -value, arising from environmental radioactivity. The most sensitive 2 search for 160Gd to date was conducted in Ukraine using a 2-inch square Ce-doped Gd2SiO5 (GSO) crystal containing 103.6 g of 160Gd Ukraine . The sensitivity of this search was limited by background noise from uranium and thorium (U/Th) decay chains present in the GSO crystal. Consequently, while the 22 was not observed, the lower limits for the and were set at 1.9 1019 years and 2.3 1021 years, respectively.
The PIKACHU project utilizes Ce-doped Gd3Ga3Al2O12 (GAGG) scintillator crystals for the 2 search. GAGG is an inorganic scintillator for which large single crystal growth up by Czochralski method has been well-established Kochurikhin . A GAGG crystal with dimensions of 65 mm in diameter and 145 mm in length contains approximately 355 g of 160Gd. Furthermore, GAGG has a superior light yield ( 50,000 photons/MeV) compared to GSO ( 10,000 photons/MeV), and its pulse shape discrimination (PSD) capability for particle identification Tamagawa allows for effective removal of -ray background. However, the development of low-radioactivity GAGG remains an ongoing and critical research challenge.
The theoretical prediction of the 2 half-life is associated with substantial uncertainty primarily due to NME. There are two typical predictions for the in 160Gd: 9.6 1021 years derived from the NME calculated in Ref. Hirsch , and 7.4 1020 years derived from the NME calculated using the quasiparticle random-phase approximation (QRPA) method Hinohara . In these calculation, we use the phase space factor shown in Phase Space . Therefore, if our experimental sensitivity exceeds that of previous study by approximately an order of magnitude, we can expect either the detection of 22 in 160Gd, or feedback on the NME value giving the shorter half-life prediction through an improved lower limit on the half-life.
The PIKACHU project is planned in two experimental phases: Phase 1 aims to search for 2 with higher sensitivity than that of the previous study. Phase 2 seeks to either discover 22 or constrain the theoretical value of NME by searching for 22 with sensitivity comparable to the theoretical prediction mentioned above. We estimated that Phase 1 can be carried out using GAGG crystals with the current level of purity PIKACHU . However, the feasibility of Phase 2 requires GAGG crystals with at least an order of magnitude higher purity than the currently used one. In both phases, it is essential to understand the radioactive background that competes with the 2 signal, especially for 160Gd which has a low -value. This paper describes the development of the background and signal models for the PIKACHU project using Monte-Carlo simulations, and their verification against the measured background spectrum. In addition, we evaluated the Phase 1 sensitivity by fitting the pseudo spectra with the background combined with signal model spectra.
2 Monte-Carlo simulation
The background and signal models are essential for evaluating the 2 of 160Gd from the measured energy spectrum. We obtained all model spectra described in this paper, by applying the energy resolution to the energy loss of radiations in GAGG calculated with GEANT4-11.0.2. The Reference PhysicsList library used in GEANT4 is “Shielding,” which includes standard and spontaneous nuclear decay physics as well as electromagnetic interactions, including , decays and -rays from nuclear de-excitation. The simulated detector model consists of two physical volumes: the crystal and the light guide. The crystal model is a cylinder with a diameter of 65 mm and a height of 145 mm. Its material is GAGG, defined as a mixture of atoms according to the composition formula Gd3Ga3Al2O12, with a density of 6.63 g/cm3. The light guide model is a trapezoidal cone with a top diameter of 65 mm, a bottom diameter of 50 mm and a height of 100 mm. Its material is defined as G4PLEXIGLASS prepared in the GEANT4 material database.
2.1 Background model
We considered two types of background sources: nuclides in 232Th, 238U, and 235U decay chains contaminated in GAGG, and 40K present in both GAGG and photomultiplier tube (PMT).
, , and decay chains in GAGG crystal
It has been confirmed through background measurement in Kamioka underground facility that high-purity GAGG contains 232Th, 238U, and 235U decay chains PIKACHU . On the other hand, the investigations using a high purity germanium detector demonstrated that the purity of crystal’s raw materials is higher than that of high-purity GAGG. This suggests that radioactive impurities may also be introduced from the environment during the crystal growth process.
In GEANT4, we generated the stationary parent nuclide for each decay chain, corresponding to 232Th, 238U, and 235U, uniformly within the volume of the crystal model. Each parent nuclide was generated 1,500,000 times in this study. GEANT4 then simulated their chain decays until the parent nuclide reached the most stable nuclide in each chain and the behavior of resulting radiations in the crystal model. The energy losses of the radiations in the crystal model were recorded, along with the names of the decayed nuclide and the daughter nuclide. However, the recorded energy losses do not reflect the effect of quenching or the detector’s energy resolution. These effects are artificially incorporated into analysis as follows.
Quenching is the effect in which -rays are detected with lower energies than their original energies. The ratio of the -ray energy calibrated by -rays to the original -ray energy (the / ratio) is known to depend proportionally on the original -ray energy in GAGG quenching . Therefore, we approximated the correlation between the -ray energy before and after quenching using a quadratic function, as shown in Fig. 1 (b). The red line represents the quadratic fit function () to the blue filled points with error bars. The blue points are obtained by fitting the measured -ray spectrum of high-purity GAGG PIKACHU with Gaussian functions (red lines) in Fig. 1 (a). Based on the curve in Fig. 1 (b), we corrected the energy losses of the -rays calculated by GEANT4 to the -equivalent energies. Then, by applying the detector’s resolution to the corrected energy losses, we reproduced the measured -ray spectrum. The resolution was measured using -ray sources and approximated with an offset of 0.148 MeV in Ref. PIKACHU . For this reason, the resolution cannot be applied to -equivalent energies less than 0.148 MeV in the model spectra presented in this paper. However, the effect of this offset is negligible because it is sufficiently lower than both the threshold of the data acquisition and the energy region of interest in our analysis.
Radioactive nuclides are present in GAGG in a state of radioactive equilibrium in relation to half-lives as shown in Table 1. We classified the 238U decay chain into five sections: 238Uup, 234U, 230Th, 238Umid, and 238Udown, with 238U, 234U, 230Th, 226Ra, and 210Pb as the parent nuclides, respectively. 235U decay chain was divided into 235Uup, 231Pa, and 235Udown with 235U, 231Pa, and 227Ac as the parent nuclides, respectively. We developed the -ray and ()-ray background model spectra for each equilibrium section, as shown in Figs. 2 and 3.

| Chain | Section name | Parent nucleus ( [Yr]) | Last nucleus |
| 232Th | 232Th | 232Th () | 208Pb |
| 238U | 238Uup | 238U () | 234Pa |
| 234U | 234U () | - | |
| 230Th | 230Th () | - | |
| 238Umid | 226Ra () | 214Po, 210Tl | |
| 238Udown | 210Pb (22.3) | 206Hg, 206Pb | |
| 235U | 235Uup | 235U () | 231Th |
| 231Pa | 231Pa () | - | |
| 235Udown | 227Ac (21.8) | 207Pb |


in GAGG and PMT
40K is an environmental isotope with a natural abundance of 0.0117. The most common disintegration mode is the beta-minus decay to the ground state of 40Ca, with a of 1.31 MeV, occurring with a branching ratio of 89.25. The next dominant mode is the electron capture, which converts 40K to the excited state of 40Ar, followed by the de-excitation to the ground state with the emission of a 1.46 MeV -ray, occurring with a branching ratio of 10.55. There are also other modes with branching ratios on the order of less than 0.1 40K . Based on the above, the energy spectrum of 40K has a photoelectric peak at 1.46 MeV and a continuous beta spectrum up to around 1.31 MeV. Therefore, the radiation emitted from 40K can contribute to the background in the 22 search because its spectrum is continuous up to around 1.73 MeV. In contrast, 40K would not contribute significantly to the background for the search of 02, which is expected to produce a peak spectrum at 1.73 MeV.
40K is present in both PMT (40Kext.) and GAGG (40Kint.). The 40Kext. emits 1.46 MeV -ray, which is detected as background when it enters and deposits the energy in GAGG. Assuming that 40K is contained on the photocathode surface of the PMT, we simulated spherically symmetric emissions of 1.46 MeV -rays from a uniform positions on the 500 mm-diameter surface of the light guide model, which is the joint surface with the PMT. For 40Kint., we generated stationary 40K uniformly in the crystal model and simulated the aforementioned disintegration scheme.
Consequently, we obtained the background model spectra for 40K, as shown in Fig. 4. The energy resolution was applied as described in the previous section.

2.2 Signal model
The 2 in GAGG can be simulated by generating two electrons from the same position, with their energies governed by theoretical probability distributions. The kinematics of the emitted electrons are described in terms of phase space factors. Reference Phase Space calculated phase space factors for various nuclear candidates across a broad range of mass numbers, from 48Ca to 238U. Reference Phase Space also provides a list of combinations of each electron energy () minus rest mass energy () emitted in the 22, denoted as (, ), along with their corresponding probabilities of occurrence, given at intervals of 0.001 MeV. By summing the probabilities in the list specific to 160Gd, we produced a discrete cumulative distribution function (CDF) of (, ). The CDF can then be used to determine (, ) based on uniform random numbers between 0 and 1, like an inversion method inversion .
The blue histograms in Fig. 5 represent the energy distributions of the summed electrons, (Left) and each individual electron, (Center) and (Right), calculated 700,000 times using the CDF. Figure 5 shows that the CDF can determine the energies of the two electrons in accordance with the theoretical distributions represented by the red lines. In GEANT4, we defined two primary electrons emitted with energies and obtained from the CDF, emitted in random directions from a random position in the crystal model. The resulting 22 model spectrum is shown on the left in Fig. 6.
The theoretical energy distribution for a single electron of the two electrons emitted in 02 is also provided by Ref. Phase Space . In this case, we determined only from the CDF, and calculated by subtracting from the -value. The 02 model spectrum is shown on the right in Fig. 6. It has a peak at the -value (1.73 MeV) and also has a tail on the low-energy side due to the escape of electrons from the crystal model. The energy resolution was applied as described in Section 2.1.


3 Sensitivity study using the background and signal models
The purpose of Phase 1 of the PIKACHU project is to update the lower limits of and for 160Gd. Based on the performance evaluation of high-purity GAGG PIKACHU , Phase 1 experiment is planned to last for two years, using two large GAGG single crystals with purity equivalent to that of high-purity GAGG. In this section, we have estimated the sensitivity that Phase 1 can achieve.
The background models developed as described in Section 2.1 can reproduce the measured background, as shown in Fig. 7. The black points represent high-purity GAGG’s -ray (Fig. 7(a)) and ()-ray (Fig. 7(b)) background spectrum measured for 56,448 seconds in Kamioka. This measurement was made using a setup consisting of high-purity GAGG, an acrylic light guide, and a PMT (R6231-100 manufactured by Hamamatsu Photonics r6231 ) PIKACHU . The thick red lines represent the total of background model spectra fitted to the data, while the thin lines in different colors represent the breakdown of the background components, as indicated in the legends. The amount of U/Th impurities in GAGG is evaluated from the fitting results of the -ray spectrum, as the -ray backgrounds arise solely from decays in the U/Th decay chains present in GAGG. Therefore, the model spectra of the U/Th chains in the ()-ray spectrum (Fig. 7(b)) are fixed to the values obtained from the -ray spectrum fitting (Fig. 7(a)). The fitting parameters in Fig. 7(b) are limited to the 40Kint. and 40Kext., represented by the dashed pink and gray lines, respectively.
To evaluate the sensitivity in Phase 1, we scaled the best-fit background model spectrum (thick red lines in Fig. 7) to the Phase 1 exposure of 1.43 kg year, and determined the number of events for each bin according to the Poisson distribution, with averages set to the values of the scaled best-fit at corresponding bins. The spectrum generated pseudo-randomly in this way is referred to as the pseudo spectrum in the present paper. We generated 10,000 sets of the pseudo spectrum for each -ray and ()-ray background, and evaluated the sensitivity using two different methods, as described below.


Method 1
In this method, we fitted all the pseudo spectra with the background models combined with each 2 signal model. We regarded the error in the signal parameter as the upper limits for the number of observed signals (). We then calculated the lower limits of and using
| (1) |
where the Avogadro constant () is 6.02 1023 atoms/mol, the natural abundance of 160Gd () is 0.219, the atomic mass of 160Gd () is 0.157 kg/mol, the detection efficiency () is assumed to be 1.00, the amount of Gd contained in two GAGG crystals () is 3.25 kg, and the search period () is 2.00 years. Figures 8(a) and 8(b) show the distributions of the lower limits of and at 90 C.L., respectively, calculated for all the pseudo spectra. As shown in Fig. 8, the lower limits of and expected in Phase 1 are 2.78 1019 years and 1.68 1021 years, respectively.


Method 2
In this method, we investigated the -- () for the pseudo -ray spectrum by increasing signal rate from zero. The amount of U/Th impurities in GAGG was determined from each -ray pseudo spectrum. 40Kint. and 40Kext. are fitting parameters associated with each signal rate. The is given by
| (2) |
where and represent the values of model and data in the -th bin Baker Cousins . The final term of the right-hand side in Eq. (2) is zero for bins with no data ( = 0). Figures 9(a) and 9(b) show the and as a function of each signal rate [events/day/kg] () for a particular pseudo -ray spectrum, respectively. The provides the Probability at a certain signal rate () by
| (3) |
The red lines in Figs. 9(a) and 9(b) are drawn at and , where Probability equals 0.9, indicating the upper limits of 2 rate at 90 C.L., respectively.
Substituting the 22 and 02 rates evaluated for all the pseudo spectra into in Eq. (1), we obtained the distribution of the lower limits of and at 90 C.L., as shown in Figs. 10(a) and 10(b), respectively. The arrows in Fig. 10 indicate the lower limits of and set by the previous study Ukraine . We obtained the lower limits of and exceeding previous limits for 8,509 and 7,560 sets of pseudo spectra, respectively. In conclusion, we obtained representative (median) values of 2.78 1019 years for and 1.70 1021 years for , respectively.
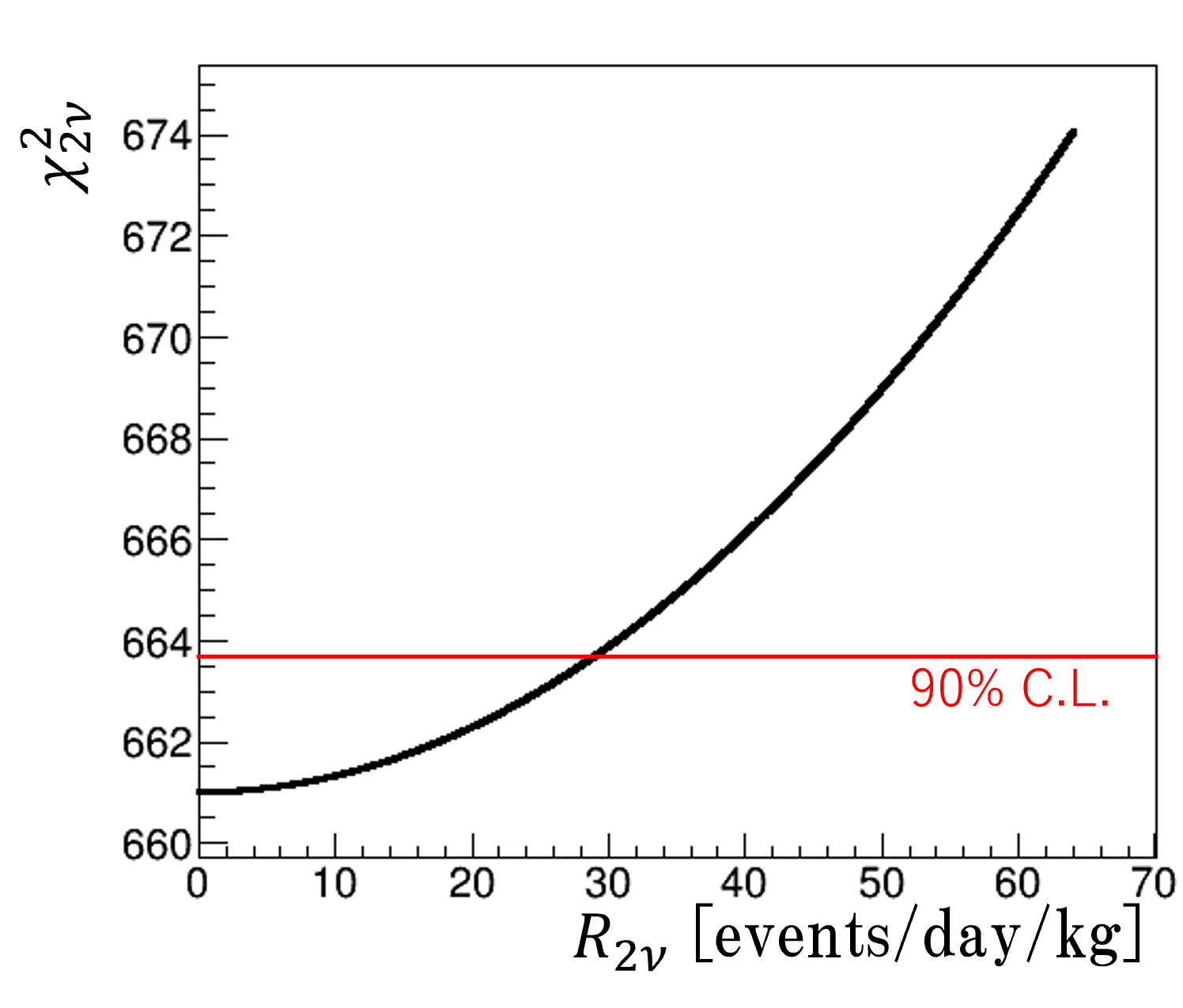



Table 2 summarizes the lower limits of and in Phase 1, estimated by two different approaches, along with the limits from the previous study. As shown in Table 2, both and were consistently evaluated for Method 1 and Method 2, and they exceed the limits from the previous study.
| Experiment | Method | [Yr] | [Yr] |
|---|---|---|---|
| Phase 1 | Method 1 | 2.78 (4.57) 1019 | 1.68 (2.76) 1021 |
| Method 2 | 2.78 (4.59) 1019 | 1.70 (2.85) 1021 | |
| Ref. Ukraine | 1.9 (3.1) 1019 | 1.3 (2.3) 1021 |
4 Discussion
4.1 The purity of GAGG crystal required for Phase 2
The goal of Phase 2 is to either discover 22 or constrain the theoretical model for NME, by searching for 2 with a sensitivity more than 7.4 1020 years, which is the theoretical prediction Hinohara as described in Section 1. For the 22 search, the main radioactive background sources in GAGG are currently 125 2 mBq/kg of 238Uup, 14.3 1.1 mBq/kg of 232Th, and 13.0 1.6 mBq/kg of 40Kint. (see Fig. 7(b)). In contrast, the Gd2O3, which is the main raw material for GAGG, has been measured to contain 16.3 mBq/kg, 0.96 mBq/kg and 2.7 mBq/kg of 238Uup, 232Th, and 40Kint., respectively, as measured by a high purity germanium detector PIKACHU . Other raw materials have also been confirmed to exhibit significantly higher purity than the crystal itself. These discrepancies suggest the contamination from the materials installed in the crystal growing furnace, but they also indicate the potential to develop GAGG with a purity at least an order of magnitude higher than the current level. If such an appropriate purification can be achieved, 40Kext. would become a dominant background in the 22 search. We will address this issue through the strategies as described in the next section.
Suppose Phase 2 experiment is conducted for 5 years, using a hundred of GAGG crystals with an order of magnitude lower concentrations of 238Uup, 232Th, and 40Kint. compared to those in high-purity GAGG, and utilizing ideal photodetectors without 40Kext.. Under these assumptions, the background spectrum of Phase 2 is expected to be as shown in Fig. 11, which represents one of the -ray pseudo spectrum generated in the same way as described in Section 3. By the Method 2 analysis for the 10,000 data-set of the Phase 2 pseudo spectra, we obtained 1.91 (2.84) 1021 years as the lower limit of at 90 (68) C.L., providing sufficient sensitivity to meet the objectives of Phase 2.

4.2 Strategies to reduce the -ray background from in photodetectors
Crystal purification, including a reassessment of the crystal growth environment and optimization of growth conditions, will remain as a long-term challenge. However, the reduction of 40Kext. can effectively contribute to the indirect improvement of the 22 sensitivity, and the strategies for achieving this are relatively straightforward.
40Kint. will be a critical background source in the 22 search because the beta-minus decay events of 40Kint. with a of 1.31 MeV are distributed within the 22 energy region, resembling the shape of the 22 spectrum. Indeed, their negative correlation can be seen in Fig. 12 (a), which shows the 22 rate and the 40Kint. radioactivity obtained through the best-fit of all the pseudo data. Therefore, an accurate evaluation of 40Kint. is desirable for the precise 22 analysis. Additionally, 40Kext. is also negatively correlated with 40Kint. due to the similarity of the shape of their model spectra, as shown in Fig. 12 (b), which contributes to the uncertainty of 40Kint.. In other words, if the detection rate of 40Kext. can be sufficiently suppressed relative to the radioactivity of 40Kint., the 40Kint. content can be estimated accurately from the photoelectron peak at 1.46 MeV.

Two main strategies are being considered to reduce 40Kext., the -ray background from 40K in the photodetectors. One is to use low radioactivity PMT, while the other is to use multi-pixel photon counter (MPPC) to detect the GAGG scintillation.
Low radioactivity PMTs, such as the R8778 used in the XMASS-I experiment r8778 , have been developed for the dark matter search in low background environments. The R6231-100 was measured to contain 5.58 0.05 Bq/PMT of 40K, as determined by a high purity germanium detector, while the R8778 contains 140 20 mBq/PMT of 40K r8778 , which can suppress the rate of 40Kext. by more than an order of magnitude compared to the current level. However, the quantum efficiency (Q.E.) of R8778 is optimized for about 178 nm wavelength of liquid xenon scintillation Xe . For Q.E. at around 520 nm, corresponding to the wavelength of GAGG scintillation GAGG , the Hamamatsu R6231-04 can be a suitable candidate, as its Bialkali photocathode is sensitive to wavelengths around 300 650 nm. Furthermore, due to its input window being made of potassium-free glass, the 40K content is suppressed to 1.15 0.07 Bq/PMT, as confirmed by measurement using the high purity germanium detector.
MPPC can also be considered as a photodetector candidate in our experiment, because its peak sensitivity wavelength of it is typically around 450 nm. In fact, GAGG scintillation has been successfully read out using an MPPC array MPPC . The MPPC is composed of fewer materials than the PMT, and in particular, it does not include glass, which typically contains the majority of 40K among the PMT components. In this strategy, the MPPC must be arrayed to extend the photosensitive area, thereby covering the cross-sectional area of the GAGG crystal. Additionally, the signal readout circuit must be designed to accommodate the arrayed MPPC.
Acknowledgments
This work was supported by JSPS KAKENHI Grant No. 22H04570 and 23H01196, and the Inter-University Cooperative Research Program of the Institute for Materials Research, Tohoku University (Proposal No. 202112-RDKGE-0005 and 202012-RDKGE-0016). This experiment was conducted in a part of the area provided by Research Center for Neutrino Science, Tohoku University.
References
- (1) Ruben Saakyan, Annual Review of Nuclear and Particle Science, Vol. 63, num. 1, pages 503-529 (2013). 10.1146/annurev-nucl-102711-094904
- (2) Jonathan Engel and Javier Menéndez, 2017 Rep. Prog. Phys. 80 046301 10.1088/1361-6633/aa5bc5
- (3) G. Audi, A.H. Wapstra, The 1995 update to the atomic mass evaluation, Nuclear Physics A, Vol.595, Iss.4 (1995) Pages 409-480. 10.1016/0375-9474(95)00445-9
- (4) F. A. Danevich, V. V. Kobychev, O. A. Ponkratenko, V. I. Tretyak and Yu. G. Zdesenko, Nucl. Phys. A 694, 375-391 (2001). 10.1016/S0375-9474(01)00983-6
- (5) V. Kochurikhin, K. Kamada, K. Jin Kim, M. Ivanov, L. Gushchina, Y. Shoji, M. Yoshino, A. Yoshikawa., J. Cryst. Growth, 531 (2020) 125384. 10.1016/j.jcrysgro.2019.125384
- (6) Y. Tamagawa, Y. Inukai, I. Ogawa, M. Kobayashi, Nucl. Instrum. Methods Phys. Res. A. 795 (2015) 192–195. 10.1016/j.nima.2015.05.052
-
(7)
J. G. Hirsch, O. Castaos and P. O. Hess, Phys. Rev. C. 66, 015502 (2002).
https://doi.org/10.1103/PhysRevC.66.015502
- (8) N. Hinohara and Jonathan Engel, Phys. Rev. C 105, 044314 (2022). 10.1103/PhysRevC.105.044314
- (9) J. Kotila and F. Iachello. Phys. Rev. C 85, 034316 (2012) and nucleartheory.yale.edu. 10.1103/PhysRevC.85.034316
- (10) S.G. Henderson and B.L. Nelson. Handbook in OR MS, Vol. 13, Chapter 4 (2006). 10.1016/S0927-0507(06)13004-2
- (11) T. Omori et al. Prog. Theor. Exp. Phys. 033D01 (2024). 10.1093/ptep/ptae026
- (12) T. Furuno, A. Koshikawa, T. Kawabata, M. Itoh, S. Kurosawa, T. Morimoto, M. Murata, K. Sakanashi, M. Tsumura and A. Yamaji. JINST. 16 P10012 (2021). 10.1088/1748-0221/16/10/P10012
- (13) X. Mougeot, R. G. Helmer. LNHB, INEEL. http://www.lnhb.fr/nuclides/K-40_tables.pdf
- (14) PHOTOMULTIPLIER TUBES AND ASSEMBLIES FOR SCINTILLATION COUNTING & HIGH ENERGY PHYSICS, Hamamatsu Photonics K.K., https://www.hamamatsu.com/content/dam/hamamatsu-photonics/sites/documents/99_SALES_LIBRARY/etd/High_energy_PMT_TPMZ0003E.pdf
- (15) S. Baker and R. D. Cousins, Nucl. Instrum. Meth. 221, 437 (1984). 10.1016/0167-5087(84)90016-4
- (16) K. Abe et al. Nucl. Instrum. Meth. A 922, 171-176 (2019). 10.1016/j.nima.2018.12.083
- (17) Akira Hitachi. Astroparticle Physics 24, Pages 247–256 (2005). 10.1016/j.astropartphys.2005.07.002
- (18) K. Kamada et al. Journal of Crystal Growth, 452, Pages 81-84 (2016). 10.1016/j.jcrysgro.2016.04.037
- (19) D. Nobashi, K. Yamaoka, H. Tajima and K. Ito. Nucl. Instrum. Meth. A 986, 684811 (2021). 10.1016/j.nima.2020.164811