Signature of Anomalous Andreev bound states in magnetic Josephson junction of noncentrosymmetric superconductor on a topological insulator
Abstract
We study the Josephson effect in a clean noncentrosymmetric superconductor/half-metal/noncentrosymmetric superconductor junction, which is grown on the surface of a three-dimensional Topological Insulator (TI) in the ballistic limit. We find the signature of anomalous Andreev Bound States (ABS) and band splitting for a spin-active barrier whose barrier magnetic moment is misaligned with the bulk moment. The chiral Majorana mode and 4 periodic ABS are found to exist on the surface of TI for parallel orientation of the moments in the normal incidence condition. But for anti-parallel misalignment, we observe the 2 periodic ABS. There exist a gap in ABS for oblique incidence. We find the splitting of Andreev levels in the presence of RSOC and also for unequal mixing of singlet-triplet correlations present in NCSC. The Majorana mode, ABS and Josephson supercurrent can be controlled by the ratio of barrier magnetic and non-magnetic moments. The critical current is found to be maximum for singlet or triplet dominated NCSC, while it is minimum in the equal mixing condition. The ABS is found to be barrier thickness dependent and is suppressed for an opaque barrier. We observe a monotonic decay in critical current with a finite length of the junction for all the singlet-triplet mixings and magnetic moments. The current-phase relation is found to be sinusoidal with no phase shift in the half-metallic limit, however, for different orientations of the bulk moment, an anomalous characteristic is also observed.
pacs:
67.30.hj, 85.75.-d, 74.90.+nI Introduction
Topological Insulators (TI) are a new class of material that exhibit non-trivial band topology due to a strong spin-orbit coupling fu1 ; fu2 ; moore2 ; roy ; moore1 ; hasan1 ; qi ; hasan2 . They remain insulating in bulk, but the most intriguing characteristic of them is the presence of gapless conducting edge states (in two dimensions) and surface states (in three dimensions). In 3D TIs, the spin of a moving particle is helically locked to the momentum at their surface beidenkopf ; roushan ; liu ; dyrdal ; li ; yang ; chen12 . Due to spin-momentum locking, it is possible to induce new phases when a magnetic or superconducting element is brought in close proximity with the 3D TIs. Previous works indicate that when a conventional s-wave superconductor is coupled with 3D TIs then the superconducting correlation is induced at their surface fu3 ; fu4 ; sochnikov ; kohda . In contrast to the conventional spin-singlet Cooper pairing, the induced superconductivity is an admixture of both singlet and triplet correlations due to spin lifted degeneracy at their surface gorkov1 ; tkachov ; gong . Moreover, the Andreev Bound States (ABS) formed in superconductor-topological insulator-superconductor (STIS) Josephson junctions can exhibit zero energy crossing, when the phase difference between the superconductor is . Thus it can host Majorana quasiparticle gorkov1 ; tkachov ; sochnikov ; kohda ; gong ; fu3 ; fu4 ; tanaka1 , which is a fermionic mode of its own antiparticle. Though in conventional SNS junctions, a weak backscattering can splits the spin degeneracy at , however, due to non-trivial topology, STIS junctions can support -periodic Josephson supercurrent. Recently, their is a growing interest to understand the robust phenomena like, zero-energy Majorana modes gorkov1 ; tkachov ; sochnikov ; kohda ; gong ; fu3 ; fu4 ; tanaka1 and topological superconductivity frolov ; chen11 ; linder11 ; hsieh ; nakhmedov ; trang on the surface of 3D TIs. Experimentally it is very challenging to distinguish topologically trivial and non-trivial modes. It is due to the reason that most of the TIs discovered till now are not perfectly insulating in bulk. But recently, it is reported that the majority of helical supercurrent is due to its surface and only a feeble contribution arises due to the bulk veldhorst ; cho ; stehno . Moreover, some exotic TIs are also discovered which display insulating bulk at low temperatures kayyalha ; jauregui ; xu11 ; xu12 .
Many theoretical and experimental efforts are made to demonstrate helical ABS, Current Phase Relation (CPR) and temperature dependence of critical current in various STIS Josephson junctions kwon ; olund ; burset ; ghaemi ; tkachov1 ; snelder1 ; snelder2 ; kurter ; schrade ; linder12 . However, the ABS and the supercurrent formed on the helical surface states due to Non Centrosymmetric Superconductors (NCSC) are yet to be understood. The reasons for considering NCSC are: (i) Coexistence of spin-singlet and spin-triplet superconducting correlations and (ii) the existence of strong Antisymmetric Spin-Orbit Coupling (ASOC) due to the absence of inversion symmetry bauer1 ; bauer2 ; bauer3 ; motoyama ; kawasaki ; akazawa ; anand1 ; smidman ; anand2 ; yuan ; togano ; badica ; matthias ; singh ; pecharsky ; hillier ; bonalde ; yogi ; ali ; xu ; acharjee2 ; acharjee3 ; acharjee1 ; linder15 ; frigeri . Earlier studies indicate that due to the presence of the Rashba Spin-Orbit Coupling (RSOC) the pairing symmetry and hence the transport properties drastically get influenced in NCSC heterostructure yuan ; togano ; badica ; acharjee2 ; acharjee3 ; linder15 ; frigeri . Moreover, it is also reported that the RSOC and singlet-triplet mixing ratio of NCSC play very significant roles in the formation of ABS and supercurrent vorontsov ; klam ; zhang11 ; smidman1 ; duckheim ; sun ; iniotakis . So it is necessary to study the interplay of RSOC and singlet-triplet correlation in helical ABS and also to understand the Majorana modes in NCSC Josephson junctions.
Josephson junctions with a magnetic material as an intermediate layer can exhibit unconventional spin-triplet proximity effect bobkova ; saxena ; aoki ; pfleiderer ; huy ; buzdin ; rahnavard ; zutic . As spin-triplet correlations are long-ranged keizer1 ; eschrig ; khaire ; linder14 , so the supercurrent in the magnetic element of such heterostructures can be carried by spin-triplet Cooper pairs. The long-range nature of spin-triplet correlation is due to a combination of two mechanisms: (i) spin-flip scattering eschrig2 ; galaktionov ; eschrig and (ii) spin-active interfacial phase shifts of the wave functions of electrons millis ; hubler ; galaktionov . Thus the superconductor-ferromagnet heterostructures gained a lot of research interest in the present era. Also, with the development of spintronic devices, Half Metallic (HM) ferromagnets have attracted a particular attention due to high spin polarization eschrig2 ; galaktionov ; eschrig ; millis ; hubler . Previously, the dc Josephson effect and its dependence on spin-flip parameters have been studied considering a spin active barrier in SHMS Josephson junctions galaktionov . In the present work, we consider an NCSCHMNCSC Josephson junction grown on the surface of 3D TI (See Fig. 1). The goal of this work is to understand the magnetic-superconducting correlations, the interplay between spin-dependent interfacial properties, RSOC and superconducting pairing in the bulk NCSC with regard to (i) helical ABS, (ii) Josephson supercurrent and (iii) Majorana modes on the surface of 3D TI.
The paper is organized as follows: In Section II, we present our theoretical model of the proposed system and present an explicit form of the Hamiltonian. We calculate the ABS and supercurrent both analytically and numerically in Section III. In Section IV, we discuss the numerical as well as some approximated analytic results. Finally, we summarize our work with conclusions in Section V.
II Model and formulation
We employ Bogoliubov-de Gennes (BdG) formalism to study the bound states and Josephson supercurrent (JSC) for the proposed setup as shown in Fig. 1. In Nambu basis
| (1) |
the Hamiltonian for the surface of a 3D TI with induced superconducting and magnetic proximity due to NCSC and HM can be defined as snelder1 ; snelder2 ; linder12 ; tanaka1
| (2) |
where, and are defined as
| (3) |
| (4) |




where, is the Fermi velocity, are the chemical potentials of the respective layers, is the magnetization of the bulk HM and () are Pauli’s spin matrices. The last term of Eq. (3) represents the interacting potential defined as
| (5) |
where, gives the intrinsic spin independent barrier potential while represent the spin dependent the barrier potential. We define the spin dependent potential as linder12
where, represent the effective ratio between the barrier magnetic and non-magnetic moments. The last term in the first square backet of Eq. (5) is the contribution due to the RSOC, with being the strength of the RSOC and it arises due to the asymmetry of the interface as well as due to NCSC acharjee2 ; acharjee3 ; badica ; linder15 ; frigeri .
Since both even and odd frequency correlations are present in NCSC at the same time, so the gap matrix appearing in Eq. (2) can be represented as a superposition of the singlet and triplet components acharjee2 ; acharjee3 ; linder15 , i.e.
| (6) |
where, and are contributions due to the singlet (S) and triplet (T) components respectively. Here, () represents the macroscopic phase of left(right) superconductor. Considering the RSOC vector for CePt3Si linder15 ; frigeri ; acharjee2 , the gap vectors can be defined as
| (7) |
and . We define a parameter to characterize singlet-triplet mixing as and . So, in view of Eqs. (3), (4), (5) and (6), the Hamiltonian (2) can be written as
| (8) |
where, , , , and
.
Assuming as the incident angle of the quasi particle in the left NCSC, the trajectory of the particle can be expressed using the momentum components, and . Thus the total wave function of an electron injected in the left NCSC with an angle can be written as
| (9) |
where, is the momentum parallel to the interface and , , are the quasi particle wave functions in the left NCSC, half metal and right NCSC respectively. The wave functions in different layers are obtained by diagonalizing the Hamiltonian (8) and can be written as acharjee3
| (10) |
The wave function in the right NCSC region in a similar way can be written as
| (11) |
Here we define, , , and . Here, () are the reflection coefficients for up(down) spin electrons, while () are the reflection coefficients for the up(down) spin holes. () are the transmission coefficients for up(down) spin electrons, while () are the transmission coefficients for the up(down)spin holes in right NCSC region. and are the superconducting phase factor for the left and right NCSC respectively. gives the momenta of the electron (hole) in NCSC with represent spin up and down particles. The momenta of the electron and the hole are defined as
| (12) |
where, is the chemical potential and is strength of RSOC in NCSC region. The factor is defined as
| (13) |
The quasi particle amplitudes and appearing in Eqs. (10) and (11) are defined as
| (14) | |||
| (15) |
In a similar way the wave function in the half metallic region is linder12
| (16) |
where, , , , are the transmission coefficients for electron and hole in half metallic region. The quasi particle momenta in this region is given by
| (17) |
where, and is the chemical potential of TI. In most of the TIs, chemical potential lies closer to the valence band as they are not perfectly insulating. So in experiment beenakker , the chemical potential has larger value than the superconducting gap. The band dispersion at the surface of topological insulator is plotted using Eq. (17) and displayed in Fig. (2). It is noted that there exist a gap in the band energy when both bulk and barrier magnetic moment are parallel to each other along z-direction with . However, the energy gap disappears for the anti-parallel orientation. This signifies that the band dispersion at the surface of 3D TIs depends on the alignment angle of the magnetic moment due to bulk HM and barrier. The boundary conditions that are to be satisfied by the wavefunctions at two junctions are as follows:
| (18) | ||||
| (19) | ||||
| (20) | ||||
| (21) |
where, is defined as klam
| (22) |
with where, and are the parameters characterizing spin independent barrier strength and RSOC. The matrix gives the contribution due to spin active interacting potential and has the following form linder16 :
| (23) |
where, and .
III Andreev Bound States and Josephson Supercurrent
The wave functions must satisfy the boundary conditions defined in Eqs. (18), (19), (20) and (21). This leads to a system of linear equations connecting the coefficients defined as , where is a matrix and . The Andreev Bound States (ABS) can be calculated by the condition . The solution for these equations needed several lengthy calculations. However, under some limiting cases they are expressible in analytic form. Considering the limiting cases, like normal interface (), transparent barrier (), Rashba free case () and small length scale (), the Andreev levels can be expressed as
| (24) |
where, for left and right moving Cooper pairs respectively, is the helicity index and . The parameters , and are defined as
| (25) |
| (26) |
| (27) |
with
| (28) |
Using the approximated analytical expression in Eq. (24), we study the formation of ABS and its dependence on the parameters like barrier spin-dependent parameters (, , ) and singlet-triplet mixing parameter (). However, if we consider the barrier thickness (), RSOC strength () and oblique incident angle (), then the calculations become a too cumbersome and the analytical expression for the same is too hard to obtain. So numerical approach is followed to obtain ABS and the results are also displayed in the later sections.
The angle-averaged Josephson supercurrents of the ABS are evaluated using the standard expression linder12 ,
| (29) |
where, . We obtain the numerical plots of Josephson supercurrents by considering with being the critical temperature. We set, , , and as beenakker , so we consider and for all our analysis.










IV Results and Discussions
IV.1 Andreev Bound States
First, we consider the ABS corresponding to the different angles of incidence of the injected particles. The results are displayed in Fig. 3 for different misalignment angles considering two different length scales viz., and . We consider , and for this analysis. We find a gapless dispersion with periodic ABS for perpendicular incidence as represented by the solid curves of Fig. 3(a). It indicates the presence of Majorana at for perpendicular incidence. More interestingly result in Fig. 3(a) signifies that Majorana is present in a spin-active barrier. However, for oblique incidence, a gap is always observed for all cases, as shown by the dotted and dashed lines of Figs. 3(a)-3(j). It is to be noted that the gap opens up further for larger the angle of incidence as seen for indicated by the dotted lines. The presence of a gap at oblique incidence is due to non-zero backscattering at a finite angle. To realize the impact of barrier magnetic moment, we have plotted ABS in Figs. 3(a)-3(j) for different values of with and . It is seen that the Andreev levels split corresponding to spin helicity and for non-vanishing values of . The wave vector mismatch occurs for the misalignment of the polar angle of magnetic moments. Thus the two degenerate energy bands split into two more branches, as seen in Figs. 3(b)-3(d) and Figs. 3(g)-3(i). We also find that the two sets of ABS depart away from each other with the increase in misalignment angle . This results in the formation of a junction for non-vanishing values of corresponding to normal incidence. Similar behavior is also observed for oblique incidence. However, the gap remains constant in this situation also. It is seen that the periodicity of the ABS will not present for non-vanishing values of and finally for anti-parallel orientation , the system resides in -ABS branches as seen from Figs. 3(e) and 3(j). Thus, interaction with the barrier magnetic moments results in the system to reside in the lower Andreev energy branches. The Andreev levels are found to display similar characteristics in Figs. 3(f)-3(j) for in normal incidence condition. However, for oblique incidence, the gap is significantly reduced for this length scale. It may be due to the reason that with increasing length, induced magnetic proximity on the surface of 3D TI gets weaker and hence the effect of barrier and bulk moment is reduced. Thus, the system is found to display periodicity for the parallel alignment while it shows anomalous characteristics and periodicity for the misalignment of the barrier and bulk moments.
In Figs. 4(a)-4(j), we show the dependence of ABS on the ratio of barrier magnetic to non-magnetic moment () in perpendicular incidence condition. We study the ABS spectra for different polar angles (). The plots in the top panel are for azimuthal angle while the plots in bottom panel are for . We find that the Majorana modes appear at in parallel configuration for all choices of and as seen in Figs. 4(a) and 4(f). Andreev levels shrinks with the increasing values of and maximum contraction is observed for as seen from the dashed curves of Figs. 4(a) and 4(b). However, for , and the ABS grows more for and a opposite characteristic is seen. It signifies that for anti-parallel alignment ABS energy becomes maximum when magnitude of barrier magnetic moment approaches to non-magnetic moment. This behaviour is seen in Figs. 4(c)-4(e) for . The ABS depart again for non-vanishing values of . However, the Andreev levels for and are found to display nearly same characteristics for . The ABS shrinks further for with as seen from Fig. 4(d). Though a similar characteristic is seen for and with , but for the Andreev energy levels are found to be independent of as seen from Fig. 4(h). For and with , the Andreev levels grows for all choices of . Thus, although the Andreev energy levels becomes anomalous for nonzero values of but the magnitude of the Andreev levels can significantly change for different azimuthal angle as seen from Fig. 4. This indicate that the ABS not only depends on the polar angle but also on azimuthal angle .










We study the effect of barrier transparency on ABS as shown in Figs. 5(a)-5(e) considering a -like barrier at and . We make this analysis by considering a quasi-magnetic barrier with and the barrier moment is misaligned by an angle for all plots of Fig. 5. We also set , and . For a nearly transparent barrier the Andreev levels are found to be nearly similar to that obtained in Figs. 4(b), 4(g), 5(a) and 5(b). In this scenario, the ABS depart again due to non-vanishing values of . For , the Andreev levels shrinks but the splitting is still present as seen in Fig. 5(b). With the further increase in barrier transparency , the energy of the ABS significantly decreases as seen from the Figs. 5(c)-5(e). It is seen that the pattern of ABS is found to be significantly different in Figs. 5(a) and Fig. 5(e) characterize by an anticrossing at and is due to finite value of . However, the splitting of the Andreev levels still present in the system.
The plots in the middle panel of Fig. 5 display the effect of RSOC on Andreev energy levels. In the presence of RSOC, the four degenerate energy bands of the TI further split into four branches, as seen in Figs. 5(f)-5(j). In this situation, the wave vectors of the NCSC are different from that of TI. Due to the mismatch of the wave vector, an additional gap appears at . However, it is seen from Figs. 5(g)-5(i) that the four energy branches grow while the other four shrinks simultaneously with an increase in the strength of RSOC. For , four Andreev energy branches grow to their maximum value while the other four branches shrink completely, as seen in Fig. 5(j). In this scenario, thus the supercurrent is carried by only one branch of Andreev energy levels. Furthermore, it is noted that though the RSOC splits the energy bands, it does not create a phase shift. It indicates that there exist Majorana modes at for normal incidence even in the presence of RSOC. Thus, the main effect of RSOC on the Andreev levels are, (i) shift of energy bands and (ii) presence of an additional gap at . So, it can be concluded that RSOC plays a very significant role on the ABS spectrum.
We show ABS spectra for different values of singlet-triplet mixing parameter in the bottom panel of Fig. 5. We set , and for this analysis. The mixing parameter plays a very significant role in NCSC with correspond to majority of singlet and correspond to majority of triplet correlations. We find that the system exhibit exactly same behaviour for and as seen from Figs. 5(k) and 5(o). We encounter band splitting again for unequal mixing of the singlet-triplet components. For unequal mixing, the Andreev levels corresponding to shrinks while the levels corresponding to remains unchanged as seen from Fig. 5(l) and 5(n). Moreover, the helical ABS spectra for is found to be exactly same as that of . For equal mixing, the Andreev energy levels corresponding to die out completely while the levels corresponding to remains unchanged as seen from Fig. 5(m). Thus the supercurrent is only due to the component, while the contribution of the supercurrent from is zero for equal mixing conditions. We find that the magnitude of ABS energy is dependent on gap while it is totally independent of . Furthermore, the crossing of the energy levels and the phase are totally independent of the gap parameter . It signifies that Majorana modes can exist at the surface of 3D TI in a -NCSC Josephson junction.















IV.2 Josephson Supercurrent
The magnetic tunability of the Andreev energy levels and its effects on the superconducting phase indicates the presence of a non-trivial Josephson current in the proposed setup. Experimentally, Josephson junctions made up of Superconductor-Topological Insulator-Superconductor (STIS) has been realized recently veldhorst . The work indicates the anomalous characteristics of the supercurrent. Moreover, presently there is a great interest in the experimental realization of ferromagnetic topological insulator hybrids (FTI). It can be achieved by random doping of transition metal elements like Cr or V on the surface of 3D TI chang11 ; chang12 . This result in magnetic proximity on the surface of TI. Recently it is found that due to the presence of magnetic material in the NCSC Josephson junction, the system displays anomalous Josephson current zhang11 . It arises due to the different orientation of the exchange field. However, the Josephson current in an NCSC corresponding to an HM ferromagnet is not studied yet. Also, as NCSCHMNCSC Josephson junctions hold Majorana modes at in parallel orientation for half-metallic limit, so it is necessary to understand the behaviour of supercurrent flowing at the surface of 3D TI. We initially calculated the Josephson supercurrent for an HM with bulk magnetic moments and the barrier magnetic moments . The results in the half-metallic limit are displayed in Figs. 6, 7, 8 and 9. However, we also plotted the supercurrent for a general ferromagnet in Fig. 10. For simplicity of our calculations, we ignore the continuum states of asymmetric contact junction and we only focus on the discrete states. This approximation does not drastically change the effective current phase relation and hold good to simplify the calculations as seen from the previous works klam .
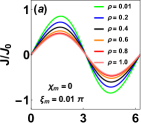












In Fig. 6, we have plotted the Josephson supercurrent for different values of the effective ratio of magnetic and non-magnetic barrier potentials. We find that for parallel orientation of the barrier and bulk moments with , the magnitude of supercurrent is maximum for . It decreases with the increasing values of as seen from Fig. 6(a). This signifies that in this situation, a non-magnetic barrier offers more supercurrent than the magnetic barrier. It is also noted that the supercurrent is found to be 2 periodic. If the barrier and the bulk moments are misaligned to an angle , then the supercurrent significantly reduces for all choices of . However, in this condition also non-magnetic barrier offer more supercurrent than the magnetic barrier and the supercurrents still found to display periodic phase as seen from Fig. 6(b). This is due to the presence of symmetric branches in ABS spectra in HM limit, which is significantly different for a bulk ferromagnet zhang11 . The magnitude of the supercurrent further decreases for the perpendicular misalignment of the barrier and bulk moments characterize by . In this case, all the magnetic barrier corresponding to non-zero values of display exactly the same characteristics. As the misalignment angle increases further to and , the supercurrents display phase shift. But in this case, the component display critical current while it is found to be minimum for . Thus the magnetic barriers enhance the supercurrent while the non-magnetic barriers suppress the supercurrent, as seen from Figs. 6(d) and 6(e). It is to be noted that the magnitude of the supercurrent is found to be maximum for the anti-parallel misalignment of the barrier and the bulk moments. To understand the effect of azimuthal angle on the supercurrent, we plotted the CPR for in Figs. 6(f)-6(j). It is seen that the nature of the supercurrent remains quite similar for the case as seen from Fig. 6(f). However, for we find that the supercurrent corresponding to and enhances while it suppressed further for and as seen from Fig. 6(g). Supercurrent is found to be independent of the strength of the magnetic barrier for . However, it is still found to be maximum for non-magnetic barrier that is seen from Fig. 6(h). The CPR for from Fig. 6(i) is found to drastically different from Fig. 6(d). In this condition, the magnitude of the supercurrent corresponding to the magnetic barrier drastically increases while it suppressed for a non-magnetic barrier. It indicates that CPR is also dependent on the azimuthal angle of the barrier moment. For the anti-parallel misalignment, we find exactly similar characteristics from Figs. 6(e) and 6(j). Thus these results indicate that supercurrent is dependent on the misalignment of barrier and bulk magnetic moments. Depending upon the orientations, both magnetic and non-magnetic barriers offer critical current in certain orientations.
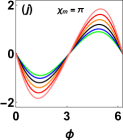
We study the CPR of the total supercurrent for different singlet-triplet correlations in Fig. 7. We set , , , and 1 for this analysis. We find that the CPR corresponding to coinciding with that for which is in accordance with Fig. 5. It is to be noted that the critical current is observed for the majority of either singlet or triplet components represented by and respectively. The critical current is found to be minimum for equal mixing of the singlet-triplet parameter for all possible misalignment angles. It is due to the reason that for equal mixing, the supercurrent is only due to the component while it is completely suppressed for the component represented by solid black lines of Fig. 7. However, the critical current display a moderate value for unequal mixing of the singlet-triplet parameter represented by solid orange lines of Fig. 7. In this condition, though the ABS is suppressed due to the component, some supercurrent still presents due to the non-vanishing value of . Moreover, the CPR is found to execute nearly sinusoidal characteristics as the contribution from the higher harmonics are very much suppressed.






From Figs. 6 and 7, we have seen that the characteristics of Josephson supercurrent are dependent on the effective ratio between magnetic and non-magnetic moments, misalignment angle between the barrier and bulk magnetic moment and singlet-triplet mixing parameter. So to understand the interplay between them, we have plotted supercurrent as a function of in Fig. 8 for different singlet-triplet mixing parameter. We find that for , the critical current is observed at and the supercurrent decreases monotonically with the increasing values of for all choices of singlet-triplet mixing parameter as seen from Fig. 8(a). The maximum critical current is observed for and while the minimum critical current is observed for as seen earlier from Figs. 6 and 7. The characteristics of the critical current remain the same for as seen from Fig. 8(b). However, the critical current is found to be decreased in all mixing scenarios for . For , the Josephson current is found to be totally independent of for all values as seen from Fig. 8(c). We find an exactly opposite behaviour characterized by the negative critical current for anti-parallel misalignment. In this case also and display maximum critical current as seen from Fig. 8(d).
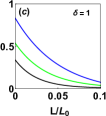
We study the dependence of the critical Josephson current on the length of the Josephson junction in Fig. 9. It is a quantity that represents the maximum supercurrent and often measured in magnetic Josephson junctions linder12 ; snelder1 ; snelder2 . We consider , and for this analysis. We find that the critical current monotonically decays for all choices of mixing parameter . The misalignment angle can only split the energy bands but not transfer any finite centre of mass momentum to the Cooper pairs. This results in a monotonous decay of the critical current. From Fig. 9 we see that provides the maximum critical currents in all three scenarios, while minimum critical current is observed for . It is also seen that the magnitude of critical current is dependent on the mixing parameter . The critical current is found on decaying rapidly in an equal mixing scenario as seen from Fig. 9(a). For unequal mixing and , the critical current decays comparatively slower than that for as seen from Figs. 9(b) and 9(c). The decay rate of critical current is found to be minimum for . Thus it can be concluded that the decay rate of the critical current is dependent on the singlet-triplet mixing parameter.





Figs. 4, 5 and 6 indicate that the presence of a spin-active barrier drastically changes the characteristics of Andreev energy levels and Josephson supercurrent in an HM ferromagnet. For all our analysis, we consider the magnetization of the bulk HM ferromagnet is along z-direction and contribution due to xy-component is zero, i.e., . However, it is natural to address the scenario of a general ferromagnet which can be represented by random orientation of the bulk moments. Though many similar works tanaka1 ; zhang11 ; linder12 is done before but the interplay of the bulk moment with spin-active barrier moments on the surface of a TI is yet to be studied. So, we have plotted ABS energy levels as a function of and in Fig. 10. We consider three different bulk moments. In Fig. 10(a), we consider the scenario where no barrier and bulk moment is present, i.e., , . In this scenario, we observe a 4 periodic ABS and a band crossover at and specif by the darker region of the density plot of Fig. 10(a). In this condition, the Andreev energy levels are found to be symmetric with respect to and Majorana modes are observed at . However, for , the band crossing will not appear at and . Thus the ABS spectra are found to be asymmetric in this condition seen from Fig. 10(b). In Fig. 10(c), we display the ABS for . In this condition, the crossover of the Andreev energy bands will appear at , which signify the -periodic ABS. The ABS spectra and CPR for all the choices of are shown in Figs. 10(d) and 10(e). We find that there exists a phase shift in Josephson supercurrent for random orientation of the bulk magnetic moments.
It is very worthwhile to mention that experimentally transport properties of heterostructures are studied in the diffusive limit. In the diffusive limit, one needs to use quasi-classical Usadel equations to obtain the Andreev levels and supercurrent. However, an analytic equation for ABS energy considering all contributing parameters is too hard to obtain for heterostructure like NCSCHMNCSC. So in that case also we need to use a numerical approach. Though we perform all our calculations considering BdG equations in the ballistic limit, our results are quite adequate in diffusive limits also because of two reasons: (1) The anomalous Andreev energy levels and the -states are generated due to chiral spin symmetry breaking along with scattering from the spin-active barrier. It is to be noted that these effects pertain uniquely to both ballistic and diffusive limits. (2) We find that CPR for low and moderate interface transparency is close to sinusoidal in nature. It is due to the suppression of the higher harmonics. As in diffusive limit, first harmonics give the most important contribution. So our results will be quite adequate in diffusive limits also. There may be some difference in ballistic and diffusive limits qualitatively. But it is expected to have no dramatic alteration of the results in diffusive limit.
V Conclusions
In summary, we have studied the transport in NCSCHMNCSC Josephson junction grown on a 3D TI. Our model predicts the formation of the helical Andreev Bound States, Majorana mode and Josephson supercurrent on the surface of a 3D TI. We employ Bogoliubov de-Gennes equations to obtain ABS and CPR. We investigated the role of the spin-active barrier by considering different alignments of barrier magnetic moment on Andreev levels and supercurrent. It is seen that a 4-periodic ABS is formed for parallel alignment of barrier and bulk magnetic moments for all incidence angles. However, for anti-parallel alignment, the system resides in 2 in Andreev levels. It is seen that Majorana modes exist at for parallel alignment in normal incidence, while they disappear in oblique incidence condition. We find that the degenerate Andreev bands split into their corresponding branches for misalignments of the barrier and bulk moments. In this condition, a phase shift is observed, which results in -junction. It is seen that the Andreev energy levels are suppressed for a strongly magnetic barrier in parallel orientation conditions, while a reverse scenario is observed for anti-parallel orientation. The magnitude of ABS energy decreases with the increase in barrier width. It is found that there exists an anti-crossing at in the ABS spectra for a finite barrier thickness. In the presence of RSOC, the degenerate sub-bands further split into their respective branches. It is seen that with the increasing strength of RSOC, the Andreev levels corresponding to positive spin helicity grow, while the other shrinks. For an NCSC with very strong RSOC, the ABS branches corresponding to negative spin helicity shrinks completely result in no supercurrent for these branches. We find that the band splits for unequal mixing of singlet-triplet parameter even in the absence of RSOC. However, no splitting is observed for equal mixing or singlet/triplet dominated scenarios. We also find that for parallel alignment of the moments, a non-magnetic barrier offers more supercurrent than a magnetic barrier. However, an opposite scenario is observed in anti-parallel orientation. So depending on the orientations, both magnetic and non-magnetic barriers offer critical current in certain orientations. The decay rate of the critical current is found to be dependent on the singlet-triplet mixing parameter. We also find an anomalous characteristic of Josephson supercurrent for random orientation of the bulk magnetic moment, but it is not observed in the half-metallic limit. These results would be a significant guiding background for innovating novel TI based sprintronics appliances.
References
- (1) L. Fu, C. L. Kane and E. J. Mele, Phys. Rev. Lett. 98, 106803 (2007).
- (2) L. Fu and C. L. Kane, Phys. Rev. B 76, 045302 (2007).
- (3) J. E. Moore and L. Balents, Phys. Rev. B 75, 121306 (2007).
- (4) R. Roy, Phys. Rev. B 79, 195322 (2009).
- (5) J. Moore, Nat. Phys. 5, 378 (2009).
- (6) M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010).
- (7) X.-L. Qi and S. -C. Zhang, Rev. Mod. Phys. 83, 1057 (2011).
- (8) M. Z. Hasan and J. E. Moore, Annu. Rev. Cond. Mat. Phys. 2, 55 (2011).
- (9) R. Roushan, et al., Nature (London) 460, 1106 (2009).
- (10) H. Beidenkopf, et. al., Nat. Phys. 7, 939 (2011).
- (11) L. Liu, et al., Phys. Rev. B 91, 235437 (2015).
- (12) P. Li, et al., Nat. Commun. 9, 3990 (2018).
- (13) A. Dyrdał, J. Barnaś, and A. Fert, Phys. Rev. Lett. 124, 046802 013903 (2020).
- (14) Z. Q. Yang, et al., Phys. Rev. Lett. 125, 013903 (2020).
- (15) J. R. Chen, et al., Nanoscale 12, 22958 (2020).
- (16) L. Fu and C. L. Kane, Phys. Rev. Lett. 100, 096407 (2008).
- (17) L. Fu and C. L. Kane, Phys. Rev. B 79, 161408 (2009).
- (18) I. Socnikov, et al., Phys. Rev. Lett. 114, 066801 (2015).
- (19) M. Kohda, T. Okayasu and J. Nitta, Sci. Rep. 9, 1909 (2019).
- (20) L. P. Gor’kov and E. I. Rashba, Phys. Rev. Lett. 87, 037004 (2001).
- (21) G. Tkachov and E. M. Hankiewickz, Phys. Rev. B 88, 075401 (2013).
- (22) X. Gong, et al., Sci. Adv 3, 1602579 (2017).
- (23) Y. Tanaka, T. Yokoyama and N. Nagaosa Phys. Rev. Lett. 103, 107002 (2009).
- (24) J. Linder, et al., Phys. Rev. Lett. 104, 067001 (2010).
- (25) T. H. Heish and L. Fu, Phys. Rev. Lett. 108, 107005 (2012).
- (26) E. Nakhmedov, et al., Phys. Rev. B 96, 014519 (2017).
- (27) A. Chen, et al., Nat. Commun. 9, 3478 (2018).
- (28) S. M. Frolov, M. J. Manfra and J. D. Sau, Nat. Phys. 16, 718 (2020).
- (29) C. X. Trang, et al., Nat. Commun. 11, 159 (2020).
- (30) M. Veldhorst, et al., Nat. Mater, 11, 417 (2012).
- (31) S. Cho, et al., Nat. Commun. 4, 1689 (2013).
- (32) M. P. Stehno, et al., Phys. Rev. B 93, 035307 (2016).
- (33) L. A. Jauregui, et al., Appl. Phys. Lett. 112, 093105 (2018).
- (34) Y. Xu, et al., Nat. Phys. 10, 956 (2014).
- (35) Y. Xu, I. Miotkowski and Y. P. Chen, Nat. Commun. 7, 11434 (2016).
- (36) M. Kayyalha, et al., Phys. Rev. Lett. 122, 047003 (2019).
- (37) H. -J. Kwon, K. Sengupta and V. M, Yakovenko, Eur. Phys. J. B 37, 349 (2004).
- (38) C. T. Olund and E. Zhao, Phys. Rev. B 86, 214515 (2012).
- (39) P. Burset, et al., Phys. Rev. B 90, 085438 (2014).
- (40) P. Ghaemi and V. P. Nair, Phys Rev. Lett. 116, 037001 (2016).
- (41) G. Tkachov, Phys Rev. Lett. 118, 016802 (2017).
- (42) J. Linder, et al., Phys. Rev. B 81, 184525 (2010).
- (43) M. Snelder, et al., Phys. Rev. B 87, 104507 (2013).
- (44) M. Snelder, et al., J. Phys. Condens Matter 27, 315701 (2015).
- (45) C. Kurter, et al., Nat. Commun. 6, 7130 (2015).
- (46) C. Schrade, et al., Phys Rev. Lett. 115, 237001 (2015).
- (47) E. Bauer, et al., Phys. Rev. Lett. 92, 027003 (2004).
- (48) E. Bauer, I. Bonalde, and M. Sigrist., Low Temp. Phys. 31, 748 (2005).
- (49) E. Bauer, et al., J. Phys.Soc. Jpn. 76, 051009 (2007).
- (50) G. Motoyama, et al., J. Phys. Conf. Ser. 400, 022079 (2012).
- (51) I. Kawasaki, et al., J. Phys. Soc. Jpn 82, 084713 (2013).
- (52) T. Akazawa, et al., J. Phys. Cond. Matter 16, L29 (2009).
- (53) V. K. Anand, et al., Phys. Rev. B. 83, 064522 (2011).
- (54) M. Smidman, et al., Phys. Rev. B. 89, 094509 (2014).
- (55) V. K. Anand, et al., Phys. Rev. B. 90, 041513 (2014).
- (56) K. Togano, et al., Phys. Rev. Lett. 93, 247004 (2004).
- (57) H. Q. Yuan, et al., Phys. Rev. Lett. 97, 017006 (2006).
- (58) P. Badica, et al., J. Phys. Soc. Jpn. 74, 1014 (2005).
- (59) P. A. Frigeri, et al., Phys. Rev. Lett. 92, 097001 (2004).
- (60) J. Linder and A. Sudbø, Phys. Rev. B 76, 054511 (2007).
- (61) S. Acharjee and U. D. Goswami, Supercond. Sci. Technol. 32, 085004 (2019).
- (62) S. Acharjee and U. D. Goswami, J. Magn. Magn. Mater. 495, 165844 (2020).
- (63) S. Acharjee and U. D. Goswami, J. Appl. Phys. 120, 263902 (2016).
- (64) B. T. Matthias, V. B. Compton and E. Corenzwit, J. Phys. Chem. Solids 19, 130 (1961).
- (65) R. P. Singh, et al., Phys. Rev. Lett. 112, 107002 (2014).
- (66) V. K. Pecharsky, L. L. Miller and K. A. Gschneidner, Phys. Rev. B 58, 497 (1998).
- (67) A. D. Hillier, J. Quintanilla and R. Cywinski, Phys. Rev. Lett. 102, 117007 (2009).
- (68) I. Bonalde et al., New J. Phys. 13, 123022 (2011).
- (69) M. Yogi, et al., Phys. Rev. Lett. 93, 027003 (2004).
- (70) M. N. Ali, et al., Phys. Rev. B 89, 020505(R) (2014).
- (71) C. Q. Xu, et al., Phys. Rev. B 96, 064528 (2017).
- (72) A. B. Vorontsov, I. Vekhter and M. Eschrig, J. Phys. Soc. Jpn. 77, 165 (2007).
- (73) C. Iniotakis, et al., Phys. Rev. B 76, 012501 (2007).
- (74) M. Duckheim and P. W. Brouwer, Phys. Rev. B 83, 054513 (2011).
- (75) L. Klam, et al., Phys. Rev. B 89, 174505 (2014).
- (76) Z. Sun, et al., Nat. Commun., 6, 6633 (2015).
- (77) H. Zhang, J. Wang and J. F. Liu, Appl. Phys. Lett. 108, 102601 (2016).
- (78) M. Smidman, et al., Rep. Prog. Phys. 80, 036501 (2017).
- (79) S.S. Saxena, et al., Nature (London) 406, 587 (2005).
- (80) D. Aoki, et al., Nature (London) 413, 613 (2001).
- (81) C. Pfleiderer et al., Nature (London) 412, 58 (2001).
- (82) N.T. Huy et al., Phy. Rev. Lett. 99, 067006 (2007).
- (83) A.I. Buzdin, Rev. Mod. Phys. 77, 935 (2005).
- (84) I. Zutic, J. Fabian and S. Das. Sarma, Rev. Mod. Phys. 76, 323 (2004).
- (85) Y. Rahnavard, D. Manske and G. Annunziata, Phys. Rev. B. 89, 214501 (2014).
- (86) I. V. Bobkova, et al., Phys. Rev. B. 102, 134505 (2020).
- (87) R. S. Keizer, et al., Nature (London) 439, 825 (2006).
- (88) T. S. Khaire, et al., Phys. Rev. Lett. 104, 137002 (2010).
- (89) J. Linder and A. Sudbø, Phys. Rev. B 82, 020512(R) (2010).
- (90) M. Eschrig and T. Löfwander, Nat. Phys. 4, 138 (2008).
- (91) M. Eschrig, et al., Phys. Rev. Lett. 90, 137003 (2003).
- (92) A. V. Galaktionov, M. S. Kalenkov and A. D. Zaikin, Phys. Rev. B 77, 094520 (2008).
- (93) A. Millis, D. Rainer, and J. A. Sauls, Phys. Rev. B 38, 4504 (1988).
- (94) F. Hübler, et al., Phys. Rev. Lett. 109, 087004 (2012).
- (95) J. Linder, M. Cuoco and A. Sudbø, Phys. Rev. B 81, 174526 (2010).
- (96) C. W. J. Beenakker, Phys. Rev. Lett. 97, 067007 (2006).
- (97) C. Z. Chang, et al., Adv. Mater. 25, 1065 (2013).
- (98) C. Z. Chang, et al., Nat. Mater. 14, 473 (2015).