Signature-inverse Theorem in Mesh Group-planes
Abstract
This is the second paper devoted to the numerical version of Signature-inverse Theorem in terms of the underlying joint invariants. Signature Theorem and its Inverse guarantee any application of differential invariant signature curves to the invariant recognition of visual objects. We first show the invalidity of Curvature-inverse and Signature-inverse theorems, meaning non-congruent meshes may have the same joint invariant numerical curvature or signature. Then by classifying three and five point ordinary meshes respectively in the Euclidean and affine cases, we look for conditions in terms of the associated joint invariant signatures which make these theorems correct. Additionally, we bring forward The Host Theorem to provide a simpler version of Signature-inverse Theorem for closed ordinary meshes.
Mathematical subject classification 2010: 53A55, 53A04, 53A15, 14L24, 65D18.
Keywords: Invariants theory, Differential invariant signature curves, Joint invariant numerical signatures, Curvature-inverse and Signature-inverse theorems, and Curve analysis.
I 1 Introduction
Geometric invariants play a crucial role in object recognition where the object of interest is affected by a transformation group. They were studied by Halphen hal , Wilczynski wil1 ; wil2 , Čech and Fubini fub , Weyl wey , Cartan car , Nagata nag , and Mumford mum who developed the theory of the invariants of transformation groups. A more modern approach has being studied by Calabi et al. cal3 by introducing the invariant signatures of planar curves, which later modified by Boutin bou , Aghayan et al. agh , and Aghayan agh1 ; agh2 ; agh3 ; agh4 ; agh5 . In agh ; agh1 ; bru3 ; bru2 ; bru4 ; bou ; fen ; cal3 ; hof2 , differential and integral signatures were applied to invariant recognition of object boundaries and detecting symmetries.
Throughout this paper refers to the special Euclidean motions , the Euclidean group , the equiaffine transformations , and the extended equiaffine group . Also, a -plane means the plane with the geometry induced by acting on E.
Curvature Theorem and its Inverse sap indicates that a in and in curve is uniquely represented, up to the transformation group , by its -invariant curvature as a function of the -invariant arc length . To avoid the ambiguity caused by the choice of initial point from where the arc length is measured, Calabi et al. cal3 brought forward differential invariant signature curves (DISCs) or classifying curves as a new scheme of the invariant recognition for visual objects.
Definition 1.1 agh . A in and in curve is regular if and its first derivative are defined and analytic over . Then, the -invariant signature set of the regular curve is parameterized by
Moreover, if is nonsingular, i.e. its signature set is a nondegenerate curve, is called the -DISC of . Nonsingularity is guaranteed by .
Signature Theorem in olv3 . Let be two congruent curves, i.e. for some . Then, their DISCs are identical: .
Signature-inverse Theorem in olv3 . All smooth nonsingular curves with the same DISC are congruent.
Accordingly, DISCs can be applied to program a computer to recognize curves modulo a certain transformation group. However, one major difficulty has been the noise sensitivity of standard differential invariants owing to their dependence on high order derivatives. Aiming to obtain less sensitive approximations, Calabi et al. cal3 suggested numerical expressions for and in terms of joint invariants and introduced “joint invariant numerical signatures” (JINSs). Later, Boutin bou corrected and Aghayan et al. agh generalized the original formulae and recently Aghayan agh1 illustrated the resulting formulation depends on the viewpoint and introduced ‘orientation-invariant’ JINSs, leading to the same signature for congruent meshes - named “the current formulation”.
In the first paper in this series agh3 , we proved that Signature-inverse theorem is not correct in terms of the current formulation and therefore non-congruent meshes may have the same JINS. To deal with the problem, we introduced “the new formulation” for JINSs and showed that, compared to the current expressions, the new ones are not only closer to -DISCs but for ordinary meshes are also more stable.
This paper is organized as follows. Section 2 provides a brief survey of the framework of the new formulation. Section 3 shows that Curvature-inverse Theorem and Signature-inverse Theorem are not valid in terms of the new expressions, therefore, non-congruent meshes may have identical numerical curvatures or JINSs. Section 4 first classifies equally and unequally spaced three-point ordinary meshes with respect to their curvatures and side lengths, then, we look for conditions in terms of the new formulas to make the Euclidean Signature-inverse Theorem correct. Next, we bring forward The Host Theorem to give simpler versions of this theorem for closed meshes. Section 5 goes through the same process for the equi-affine case by classifying five-point ordinary meshes. Finally, Section 6 present our conclusions.
II 2 K-point -signatures - The new formulation
According to agh2 , the following subsection does a brief survey of the new formulation.
In a mesh of points , a cusp is a point where the moving point starts to move backward - in other word, . An ordinary mesh point refers to a set of successive points with no cusp. An ordinary mesh is fine if it approximates a in and in curve and all angles are obtuse - in this case, the JINS of approximates the DISC of .
Also, the n-neighborhood of means the 2n+1 successive points:
In addition, a “k-point invariant” of is a function such that for each and every k-point subset we have
II.1 2.1 Two-point -signatures
Consider the Euclidean geometry of curves in the plane where the underlying group of transformations is the special Euclidean group , containing all translations and rotations. One can also include reflections, leading to the Euclidean group .
Definition 2.1. The 2-point -curvature of an ordinary mesh is the function given by , where are the Euclidean distances in the one-neighborhood of and is the area of the triangle whose vertices are the one-neighborhood of given by
Then the 2-point -signature of an ordinary mesh is parameterized as follows.
- Where is equally spaced:
| (1) |
or, in terms of a centered difference quotient
| (2) |
- Where is unequally spaced:
| (3) |
or, in terms of a centered difference quotient
| (4) |
In which denotes their Euclidean distance and .
II.2 2.2 Three-point -signatures
Affine geometry is the study of geometric properties of the objects in the plane which remain unchanged by signed area-preserving affine transformations and - called the equiaffine group . One can include reflections, leading to the extended equiaffine group .
Definition 2.2 agh2 . The 3-point -curvature of an ordinary convex (no three are collinear) mesh is the real-valued function given by , where F and S are the first and second affine invariants of .
Moreover, the 3-point affine arc lengths of are obtained as follows.
Theorem 2.3 agh2 . In the five-neighborhood of any point , the 3-point -arc length from to is computed as follows.
-If , then
and equals the signed area of the parallelogram whose sides are and .
-If , then
and A, B, C, D, and E are the affine functions of . Moreover, .
Then the 3-point -signature of the convex mesh is obtained as follows.
- Where is equally spaced:
| (5) |
or, in terms of a centered difference quotient
| (6) |
- Where is unequally spaced:
| (7) |
Or, in terms of a centered difference quotient
| (8) |
III 3. Counterexamples in the space of ordinary meshes
Consider the space of all planar ordinary meshes affected by , called the Mesh -plane . Two n-point ordinary meshes and in are congruent if and only if there exists a and a permutation such that
| (9) |
This identity introduces an equivalence relation on , called the -congruent classes. From now on, without loss of generality, we suppose that and are congruent if and only if there exists such that for all .
III.1 3.1 Counterexamples for Curvature-inverse Theorem in
According to agh ; agh1 , Curvature Theorem is correct in , meaning congruent meshes have the same k-point -curvature . Now, we are going to investigate its inverse.
Example 1. Let and be two 3-point ordinary meshes of the unit circle as shown in Figure 1.
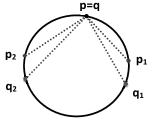
These meshes have the following identical -curvatures, while they are clearly non-congruent:
Example 2. Let and be two equally spaced 3-point ordinary meshes in , see FIG. 2, and their circumcircles have the same radius .
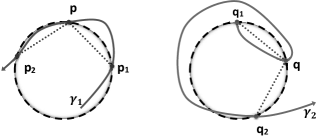
and are clearly non-congruent, while they have the same 2-point -curvature:
Now consider two approximating meshes of with the same resolution (number of points) in which one is equally and the other one is unequally spaced. They have the same 2-point -curvatures, while they are not congruent, meaning Curvature-inverse Theorem is not correct even for fine partitions.
Just like the Euclidean case, it is also easy to give some counterexamples in , therefore, we have the following proposition.
proposition 3.1. Non-congruent meshes may have identical k-point -curvatures.
III.2 3.2 Counterexample for Signature-inverse Theorem in
According to agh1 , to validate Signature Theorem in terms of the current formulation, one just needs to consider the orientation-invariant version of it, meaning congruent meshes have the same orientation-invariant JINS. Now, we investigate the correctness of its inverse.
Let be the radius of the circumcircle passing through the one-neighborhood of a point on an ordinary mesh .
Example 3. Let and denote two equally spaced ordinary meshes with , see FIG. 3. Also, let
and .
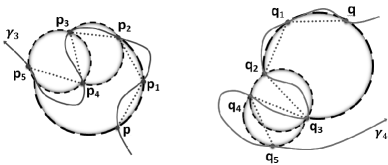
From identity (2)
and
Thus and have the same 2-point -signature, while they are not clearly congruent.
Just like the Euclidean case, it is also easy to give some counterexamples in , therefore, we have the following corollary.
Proposition 3.2. Signature-inverse Theorem is not correct in .
Remark. There are theorems with very simple conditions for Signature-inverse Theorem in , but they are not in terms of the resulting JINSs. For example, the following theorem is the simplest.
Theorem 3.3. Let denote ordinary meshes with the same Euclidean distance between any two corresponding successive points and have also identical corresponding signed angles. Then, and are congruent.
From now on, this paper looks for conditions in terms of the resulting signatures to make Signature-inverse Theorem correct in .
IV 4 Signature-inverse Theorem in
Definition 4.1. Let denote an ordinary mesh point.
a) The signature-sign of is the function given at any point by: where denotes the 2d-cross product.
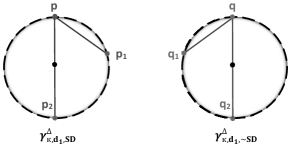
b) is in the signature-direction if its one-neighborhood are in counterclockwise order on their circumcircle. Otherwise, we say is in .
Besides, two ordinary meshes and are in the same signature-direction if and only if for the corresponding points and are both in or in .
Proposition 4.2. Rotations do not change the signature-directions while reflections do. In other words, for a mesh point
a) is in SD iff are in SD, where ,
b) is in SD iff are in , where ,
meaning the signature-direction makes a distinction between rotations and reflections.
IV.1 4.1 Equally spaced meshes in
A mesh point is equally spaced, if all edges (two successive points) have the same Euclidean length. Also, in a 3-point equally spaced mesh, let and denote respectively the -length of each edge and the -distances between the first and end points. In addition, for a n-point equally spaced mesh, let and be respectively and in the one-neighborhood of its point (in open meshes ).
The following lemma plays a central role in our investigations.
Lemma 4.3 fel2 . The 2-point action given by
is free on , where .
Signature-inverse Theorem in terms of (1)
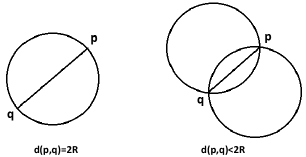
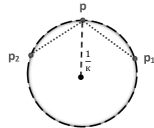
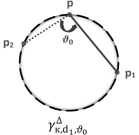
Lemma 4.4. For any , there are at most 2 circles with a given radius passing through them, see FIG. 4.
Let denote a 3-point equally spaced ordinary mesh with -curvature and side length , see FIG. 5.
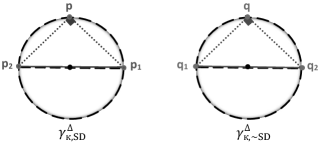
By Lemma 4.4, there exists only one class of 3-point equally spaced meshes with the same and and non-congruent with , which is its mirror reflection - denoted by , see FIG. 6.
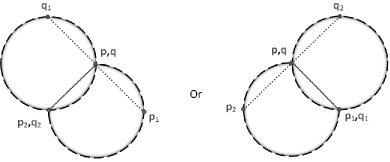
We, therefore, have the following results.
Theorem 4.5. In , there exist two congruent classes of equally spaced 3-point ordinary meshes with the same curvature and side length . One in and another in denoted respectively by and , see FIG. 7. Also, there is a unique class of them in .
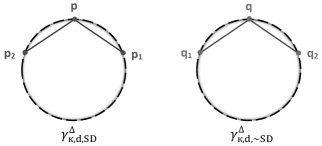
Corollary 4.6. There exists a unique -congruent class of 3-point equally spaced ordinary meshes with total length , -curvature , and being in the same signature-direction.
Corollary 4.7. Two equally spaced ordinary meshes and in with the same total length, signature-direction, and 2-point curvature are congruent.
However, it is not in terms of the -JINSs. It is also easy to check the following result.
Theorem 4.8. In , there exist two congruent classes of equally spaced 3-point meshes with curvature , angle , and the same signature-direction denoted by and , see FIG. 8. Moreover, there is a unique equivalence class of them in .
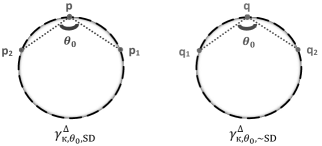
Theorem 4.9, Signature-inverse Theorem. Equally spaced ordinary meshes and in with the same signature-direction and identical JINSs given by (1) are congruent.
Proof. Let and . Also, without loss of generality, we assume that for . By identity (1)
which result
Hence
| (10) |
where To show that for all , consider the one-neighborhoods of a point . From (10)
| (11) |
On the other hand, Corollary 4.6 and Lemma 4.3 give
which, along with (11), results in
In other words, and are -congruent.
It is not also hard to check that Theorem 4.9 and Theorem 3.3 are the same.
Signature-inverse Theorem in terms of (2) - version 1
Definition 4.10. Two ordinary meshes have the same “angle-type” iff any pair of angles and are both acute, obtuse, or right.
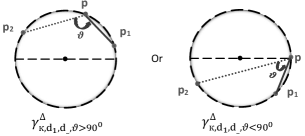
Theorem 4.11. In , there exist at most 4 congruent classes of 3-point equally spaced ordinary meshes with curvature and distance as follows:
- If ; there are 2 congruent classes: one in denoted by and another in denoted by , see FIG. 9.
- If ; there are 4 congruent classes: two in denoted by , and the other two in denoted by , see FIG. 10.
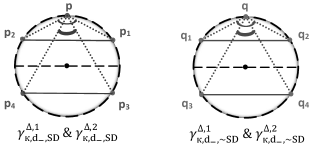
We, therefore, established the following results.
Theorem 4.12. In , there exist 2 congruent classes of 3-point equally spaced ordinary meshes with curvature , distance , and also the same angle-type . One in and another in denoted respectively by and , see FIG. 11. Moreover, there is a unique congruent class of them in .
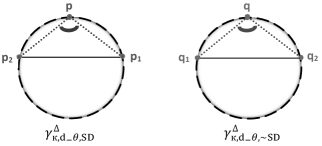
Corollary 4.13. There exists a unique congruent class of 3-point equally spaced ordinary meshes with the same , , and angle-type which are also in the same signature-direction.
Theorem 4.14, Signature-inverse Theorem. Equally spaced ordinary meshes and in with the same signature-direction and angle-type which also have identical 2-point signatures in terms of (2) are congruent.
Proof. According to (2) and just like the Theorem 4.9 we have
| (12) |
| (13) |
Since, additionally, and are equally spaced of the same angle-type and are in the same signature-direction, by Corollary 4.13
| (14) |
To prove that s are equal, consider the one-neighborhoods of two successive points and . From (14)
.
Hence, according to Lemma 4.3, for . In other words
Finally, Corollary 4.6 extends this result to the whole points of the meshes, meaning and are -congruent.
We indeed established the following theorem for fine meshes as well.
Theorem 4.15, Signature-inverse Theorem. Two equally spaced ordinary fine meshes in the same signature-direction and with identical 2-point JINS, parameterized by (2), are congruent.
Signature-inverse Theorem in terms of (2) - version 2
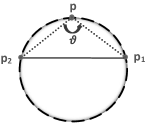
Definition 4.16. Let denote an ordinary mesh. By “the signed angle” at a point we mean where .
Also, two ordinary meshes and have the same “signed angle-type” if the corresponding angles and are both signed-acute, signed-obtuse, or signed-right.
Definition 4.16, along with Corollary 4.13 and Theorem 4.14, gives the following results.
Theorem 4.17. There exists a unique congruent class of equally spaced 3-point ordinary meshes with -curvature , distance , and the same signed angle-type , see FIG. 12.
Theorem 4.18, Signature-inverse Theorem. Equally spaced ordinary meshes and in with the same signed angle-type and 2-point signature obtained from (2) are congruent.
Now, we rewrite Theorem 4.8 in terms of the signed angles as follows.
Theorem 4.19. There is a unique congruent class of 3-point equally spaced meshes with Euclidean curvature and signed-angle .
Theorem 4.19 establishes the following result.
Theorem 4.20. Equally spaced ordinary meshes and in with identical signed angles and 2-point Euclidean curvatures are congruent.
IV.2 4.2 Unequally spaced meshes in
Definition 4.21 agh . Let be an ordinary mesh.
a) The -neighborhood of a point means .
b) The 2-point -curvature of is the real-valued function -, given by Definition 2.1 rewritten in the -neighborhood of each point.
c) - denotes the 2-point -signature of parameterized by (1)-(4) where they are rewritten in the -neighborhood of each point in terms of the -.
d) The -angle at refers to - along . In addition, the signed -angle at means --.
Moreover, if then “-” will be denoted by “”.
Theorem 4.22, Signature Theorem in agh ; agh1 ; agh2 . Congruent ordinary meshes have the same (orientation-invariant) 2-point -signature.
Signature-inverse Theorem in terms of (3) and (4)
In an unequally spaced 3-point mesh, let and denote, respectively, the -distances between the first and middle points, the end and middle points, and the first and end points. Besides for an unequally spaced n-point mesh, let -, - and - denote, respectively, the -distances between the first and middle points, the end and middle points, and the first and end points of the -neighborhood of the point (for open meshes where ). We also suppose that --.
Lemma 4.23. There are at most 4 congruent classes of 3-point unequally spaced meshes with -curvature and the side lengths and classified as follows.
a) If ;111footnotetext: meaning that the bigger side is the diameter of the circumcircle there exist 2 equivalent classes: one in denoted by and another in denoted by , see FIG. 13.
b) If ; there exist 4 congruent classes: two in denoted by and the other two in denoted by , see FIG. 14.
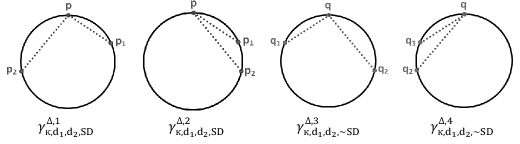
We, therefore, have the following theorem.
Theorem 4.24. In , there exists a unique congruent class of unequally spaced 3-point ordinary meshes with the following conditions.
a) With the same , , and signed angle , denoted by , see FIG. 15.
b) With the same , , and signed angle-type , denoted by .
c) With the same , , , and signed angle-type , denoted by , see FIG. 16.
Theorem 4.25, Signature-inverse Theorem. Unequally spaced ordinary meshes and in with identical lengths , the same signed (1,2)-angle type, and the same 2-point -signature in terms of (3) are congruent.
Proof. According to the definition of -signatures in terms of (3)
where . Therefore
| (15) |
| (16) |
Additionally, and the signed angles and have the same type, therefore, according to Theorem 4.24-part c)
| (17) |
Now, consider the corresponding triangles and . From (17)
which, with regard to the Lemma 4.3, results in for . In other words
showing the congruence of and where they are closed. It also proves that for the open meshes the congruence satisfies where . In this case, if and have the same -, the result extends to their whole points.
Theorem 4.26, Signature-inverse Theorem. Let denote two unequally spaced ordinary meshes with the same -curvature and signed angle -. Let also they have the same signed 3-angle type, identical lengths , and identical 2-point -signatures in terms of (4). Then, and are congruent.
Proof. With regard to the definition of -signatures in terms of (4)
where . As a result
| (18) |
| (19) |
Besides, and the signed angles and have the same type, therefore, according to Theorem 4.24-part c)
| (20) |
Now, through the following steps, we prove that s are identical.
Step 1.
By (20)
which, according to Lemma 4.3, result in and thus there would be only the following three group transformations:
| (21) |
which we need to show they are equal.
Step 2.
Let . From (20), we have and additionally
- -- -.
Therefore, with regard to Theorem 4.24-part a)
| (22) |
Identity (22), along with (20), indicates that
which, according to Lemma 4.3, results in . Hence, by (22)
| (23) |
Step 3.
Consider now the triangles and . From (20) and (23)
Accordingly, (1,2)-triangles at and are congruent, where , resulting
| (24) |
and
| (25) |
which, along with (23), result in
.
In other words, we have
| (26) |
Step 4.
From (23) and (26)
which, according to Lemma 4.3, result in .
Similarly, we can prove . Thus
showing the congruence of and where they are closed. It also proves that for the open meshes the congruence satisfies where . In this case, adding extra conditions for the first and end points in the open case, for example or and have identical corresponding 3-angles and , extends the result to the whole points.
IV.3 4.3 The Host Theorem and Signature-inverse Theorem
40 guests are supposed to sit around a dinner table. The host has asked the party planner to provide 3, 4, or 5 different types of rare wildflowers and put them on the table in front of each guest between the dinner and dessert so that the following conditions must be met.
Depending on the variety in the selected flowers (2, 3, or 5), every second, third, or fourth person would receive the same type of flower.
The party planner must not look at the guests. He should just step forward and put each flower on the table with his right hand.
In addition, each gust must have one and only one flower.
Below we bring a general mathematical setting for this problem.
The Host Problem. Let be a closed ordinary mesh and 1mn. We start from and connect every point by a straight line until getting back to . The question is for what “m” we meet all points of the mesh uniquely on our way.
According to the group of primitive residue classes modulo m in modular arithmetic, we bring in the following theorem.
The Host Theorem. In The Host Problem, the whole points of the given mesh are met iff after n steps we return to the start point iff . 11footnotetext: gcd refers to the greatest common divisor.
We, therefore, have the following corollary.
Corollary. The party planner can fulfill the task by ways where denotes Euler’s totient (phi) function.
As an example, consider a 10-point mesh and let and . Since gcd(3,10)=1, every point will be met, see FIG. 17-left, and since gcd, there is no way one meets all points on their way, see FIG. 17-right.
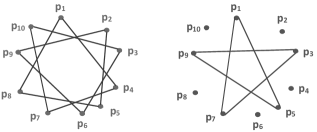
As a result, since gcd(3,40)=1, the party planner must provide 3 different types of flowers and place them in different baskets behind the host and do his task with no worries.
The Host Theorem results in the following Signature-inverse Theorem for closed meshes.
The Host Theorem and Signature-inverse Theorem. Let be two n-point unequally spaced ordinary closed meshes, where . Let they have the same signed angle-type , corresponding length , and 2-point -signature resulted from identity (4). Then, and are congruent.
V 5. Signature-inverse Theorem in
Definition 5.1. Let be a convex ordinary mesh. A is in -signature direction if its two-neighborhood is counterclockwise on the unique conic section passing through it. Otherwise, we say is in .
In addition, two n-point convex meshes and are in the same -signature direction iff for the corresponding points and are in or in .
Definition 5.2. Let denote a n-point ordinary convex mesh. For , the -arc length set of at a point is the ordered set given by Theorem 2.3 in the two-neighborhood of .
Also, ordinary convex meshes and have the same -arc length set if their corresponding points have the same -arc length set.
Definition 5.3. Let be an ordinary convex mesh point.
a) A positive -curvature point has the fine-area if the area if its approximating ellipse is not less than the area of the elliptical sector surrounded by the two-neighborhood of .
b) A negative -curvature point is in the fine-position if the points in its two-neighborhood are located on the same branch of the approximating hyperbola. In other words, the Euclidean distance between every two successive points of this neighborhood is less than (twice the semi-major axis of the approximating hyperbola), where F and S are the first and second -invariants of and is the large root of the equation in which A and C are the affine-functions of .
Definition 5.4. An ordinary convex mesh is called -fine if each point with a positive -curvature has the fine-area and with a negative -curvature, is in the fine-position.
It is not hard to demonstrate the following classifications in the affine case.
Lemma 5.5 a) In , there are 2 congruent classes of five-point ordinary convex meshes with -curvature , -arc length set L, and also their middle points have the fine-area. One in denoted by and another in denoted by .
b) In , there exist 2 congruent classes of five-point ordinary convex meshes with , L, and their middle points are in the fine-position. One in denoted by and another in denoted by .
c) In , there exist 2 congruent classes of five-point ordinary convex meshes with and -arc length set L. One in and another in denoted respectively by and .
Lemma 5.6 fel2 . The 3-point action defined by
is free on , where and are collinear .
Now, we present Signature-inverse Theorem in terms of identity (6).
Theorem 5.7, Signature-inverse Theorem. Ordinary -fine convex meshes and in with never-zero -curvatures and the same -arc length set and 3-point -signature are congruent.
Proof. According to (6) and just like the Theorem 4.9
where . Hence
| (27) |
| (28) |
In addition, in the two-neighborhoods of each corresponding points and , we have
which, along with (27), gives
Therefore
| (29) |
On the other hand, with regard to the hypothesis, Lemma 5.5 indicates that
| (30) |
at any point .
Identities (29) and (30) along with Lemma 5.6 result in . Hence
which means the congruence of and .
Similarly, we can prove the following theorem in terms of (6).
Theorem 5.8, Signature-inverse Theorem. Let be two ordinary -fine convex meshes with the same area in the one-neighborhoods of the corresponding points with zero -curvatures. Also, let they have the same -arc length set and 3-point -signatures. Then, and are congruent.
The preceding theorem in terms of fine meshes is written as follows.
Corollary 5.9, Signature-inverse Theorem. Let denote two fine convex meshes having the same area in the one-neighborhoods of the corresponding points with zero -curvatures. Let also they have the same -arc length set and 3-point -signatures. Then, and are congruent.
Just like the Euclidean case, more versions of Signature-inverse theorems can be presented in terms of -signatures parameterized by the identities (5), (7), and (8).
VI 6. Conclusions
This paper has considered the new formulation for -JINSs introduced in the first paper in this series. We first provided several counterexamples for Curvature-inverse Theorem and Signature-inverse Theorem in , meaning that non-congruent meshes may have the same -curvature or -JINS. To give a numerical version of Euclidean Signature-inverse Theorem in terms of the associated JINSs, we first classified equally and unequally spaced three-point meshes with respect to their curvatures and side lengths, then, we looked for conditions that make this theorem correct. Next, we brought forward The Host Theorem to prove a simpler version of Signature-inverse Theorem for closed meshes. Finally, we went through the same process for the equiaffine case by classifying five-point ordinary meshes.
VII References
References
- (1) Aghayan, R., Ellis, T., and Dehmeshki, J., Planar numerical signature theory applied to object recognition, J. Math. Imaging Vision, vol. 48, no. 3, pp. 583-605, 2014.
- (2) Aghayan, R., Orientation-invariant numerically invariant joint signatures in curve analysis, International Journal of Computer Mathematics, vol 3, issue 1, pp. 13-30, 2018.
- (3) Aghayan, R., Visual groups and their Structural Equations, in: Proceedings of the 49th Annual Iranian Mathematics Conference - Geometry Section, Tehran, IRAN, August 23-26, pp. 21-35, 2018.
- (4) Aghayan, R., Signature-inverse Theorem in Mesh Group-planes The new formulation, in: Proceedings of the 49th Annual Iranian Mathematics Conference - Computer Science Section, Tehran, IRAN, August 23-26, pp. 2310-2332, 2018.
- (5) Aghayan, R., Generating visual invariants applied to curve analysis, submitted and revised, 2020.
- (6) Aghayan, R., Joint invariant level set formulation with unique segmentation results, submitted, 2020.
- (7) Boutin, M., Numerically invariant signature curves, Int. J. Comput. Vision, vol 40, no. 3, pp. 235-248, 2000.
- (8) Bruckstein, A.M., Katzir, N., Lindenbaum, M., and Porat, M., Similarity invariant signatures and partially occluded planar shapes, Int. J. Comput. Vision, vol 7, no. 3, pp. 271-285, 1992.
- (9) Bruckstein, A.M., Halt, R.J., Netravali, A.N., and Richardson, T.J., Invariant signatures for planar shape recognition under partial occlusion, CVGIP: Image Understanding, 58, pp. 49-65, 1993.
- (10) Bruckstein, A.M., and Netravali, A.N., On differential invariants of plannar curves and recog-nizing partially occluded planar shapes, Ann. Math. Artificial Intel., vol. 13, pp. 227-250, 1995.
- (11) Bruckstein, A.M. and Shaked, D,. Skew symmetry detection via invariant signatures, Pattern Recognition, vol. 31, no. 2, pp. 181-192, 1998.
- (12) Calabi, E., Olver, P.J., Shakiban, C., Tannenbaum, A., and Haker, S., Differential and numeri-cally invariant signature curves applied to object recognition, Int. J. Comput. Vision, vol. 26, pp. 107-135, 1998.
- (13) Cartan, É., La méthode du repére mobile, la théorie des groupes continus et les espaces généra-lisés, Exposés de Géométrie, no. 5, Paris, Hermann et cie, 1935.
- (14) Čech, E., and Fubini, G., Geometria Proiettiva Differenziale, Bologna, Nicola Zanichelli, 1927.
- (15) Faugeras, O., Cartan’s moving frame method and its application to the geometry and evolution of curves in the Euclidean, affine and projective planes, Applications of Invariance in Computer Vision, vol. 825, no. 2053, Springer-Verlag, pp. 11-16, 1994.
- (16) Feng, S., Kogan, I., and Krim, H., Classification of curves in 2D and 3D via affine integral signatures, Acta Appl. Math., vol. 109, no. 3, pp. 903-937, 2010.
- (17) Fels, M., Olver, P.J., Moving coframes II. Regularization and theoretical foundations, Acta Appl. Math., vol. 55, pp. 127-208, 1999.
- (18) Halphen, G.,-H., Sure les invariants différentiels, in Oeuvres, vol. 2, Gauthier-Villars, Paris, 1913, pp. 197-253.
- (19) Hoff, D., and Olver, P.J., Automatic solution of jigsaw puzzles, J. Math. Imaging Vision, vol. 49, pp. 234-250, 2014.
- (20) Mumford, D., Fogarty, J., and Kirwan, F., Geometric invariant theory, edition, Ergebnisse Math. 34, Springer-Verlag, Berlin, 1994 (the 1st edition published in 1965).
- (21) Musso, E., and Nicolodi, L., Invariant signature of closed Planar curves, J. Math. Imaging Vision, vol. 35, pp. 68-85, 2009.
- (22) Nagata, M., Complete reducibility of rational representations of a matric group, J. Math. Kyoto Univ., vol. 1, no. 1, pp. 87-99, 1961.
- (23) Olver, P.J., Classical Invariant Theory, Cambridge Univ. Press, New York, 1999.
- (24) Pauwels, E., Moons, T., Van Gool, L.J., Kempenaers, P., and Oosterlinck, A., Recognition of planar shapes under affine distortion, Int. J. Comput. Vision, vol. 14, pp. 49-65, 1995.
- (25) Rathi, Y., Olver, P.J., Sapiro, G., and Tannenbaum, A.R., Affine invariant surface evolutions for 3D image segmentation, Image Processing: Algorithms and Systems, Neural Network, and Machine Learning, Editors: Dougherty, E.R., Nasrabadi, N.M., Rizv, S.A., Proc. Of SPIE-IS&T Electronic Imaging, SPTE Press, vol. 6064, pp. 606401, 2006.
- (26) Sapiro, G., Geometrical Partial Differential Equations and Image Analysis, Cambridge University Press, 2001.
- (27) Weyl, H., The Classical groups: Their Invariants and Representations, Princeton University Press, N. J., 1946.
- (28) Weiss, I., Geometric invariants and object recognition, Int. J. Comput. Vision, vol. 10, no. 3, June 1993.
- (29) Wilczynski, E.J., Projective differential geometry of curves and Ruled Surfaces, Leipzig, B. G. Teubner, New York, 1906.
- (30) Wilczynski, E.J., Projective differential geometry of curved surface (Second Memoir), Amer. Math. Soc. Trans., vol. 9, no. 1, Jan. 1908.