Signals of quark combination at hadronization in collisions at GeV
Abstract
We find signals of quark combination at hadronization from the experimental data of spectra of hadrons at mid-rapidity in collisions at GeV. The first is the constituent quark number scaling property for spectra of and and that for spectra of and . The second is that spectra of , , and can be self-consistently described using the spectrum of strange quarks from data and that of up/down quarks from data in the equal-velocity combination mechanism. The third is that experimental data for spectrum of are also well described using the spectrum of up/down quarks from data and that of charm quarks from perturbative QCD calculations. These results indicate a similarity between hadron production in collisions at GeV and that at LHC energies. We predict spectra of single-charm hadrons and their spectrum ratios. We suggest systematic measurements in collisions at GeV in future so as to better understand the property of small parton system created in collisions at different collision energies.
I Introduction
Hadronization refers to the process of the formation of hadrons from final state quarks and gluons created in high energy reactions. Hadronization is a non-perturbative quantum chromodynamics (QCD) process and is described by phenomenological models at present. String fragmentation (Andersson et al., 1983), cluster fragmentation (Webber, 1984) and quark recombination (Bjorken and Farrar, 1974; Das and Hwa, 1977) are three kinds of popular models which are often used to describe the hadron production in high energy reactions.
Experimental data of hadron production in high energy reactions often provide new inspiration on the understanding of hadronization. We recall that heavy-ion collision experiments at Relativistic Heavy Ion Collider (RHIC) in the 2000s found several surprising phenomena such as the enhanced ratio of baryon to meson (Adcox et al., 2002; Abelev et al., 2006; Adams et al., 2006a) and number-of-constituent quark scaling (NCQ) property for hadronic elliptic flow (Adams et al., 2004a, 2005a; Adare et al., 2007) in intermediate range. These observations prompt the study of quark (re-)combination or parton coalescence mechanism (Greco et al., 2003; Fries et al., 2003; Hwa and Yang, 2003; Molnar and Voloshin, 2003; Chen and Ko, 2006; Shao et al., 2009) for the hadronization of bulk quark matter created in relativistic heavy-ion collisions. On the other hand, the hadronization of parton jet with high and small parton system is still usually described by fragmentation mechanism.
In the last decade, experiments of and pA collisions at energies available at Large Hadron Collider (LHC) found a series of new phenomena in hadron production in high multiplicity events such as ridge or long-range correlation (Khachatryan et al., 2010; Chatrchyan et al., 2013), collectivity (Khachatryan et al., 2015, 2017), enhanced ratio of baryon to meson (Adam et al., 2017; Abelev et al., 2014; Adam et al., 2016a, b). These phenomena have been observed in relativistic heavy-ion collisions and are usually regarded to be closely related to the formation of quark-gluon plasma (QGP). Observation of these phenomena in and A collisions therefore invoke an interesting question, i.e., the possible creation of mini-QGP. This attracts intensive theoretical studies from different aspects (Liu and Werner, 2011; Bzdak et al., 2013; Bozek and Broniowski, 2013; Prasad et al., 2010; Avsar et al., 2011; Zhao et al., 2018). Our recent studies (Shao et al., 2017; Song et al., 2017; Gou et al., 2017; Zhang et al., 2020; Li et al., 2018; Song et al., 2018; Li et al., 2021) found that an equal-velocity combination (EVC) mechanism of constituent quarks and antiquarks can systematically describe spectra of light-flavor and single-charm hadrons. Compared with the traditional viewpoint that fragmentation mechanism is often applied to small parton system and usually successful, our studies indicate the new feature of hadron production in and A collisions at LHC energies. This may be related to the possible formation of mini-QGP in and A collisions at LHC energies.
The production of identified hadrons in collisions at 200 GeV was systematically measured by STAR collaboration in early years of RHIC experiments (Adams et al., 2005b, 2004b, c; Abelev et al., 2007; Adams et al., 2006b; Adamczyk et al., 2012; Qiu, 2016). Experimental data were usually compared with calculations of event generators such as PHTHIA with tuned parameters. In view of our findings in collisions at LHC energies (Shao et al., 2017; Song et al., 2017; Gou et al., 2017; Zhang et al., 2020; Li et al., 2018; Song et al., 2018; Li et al., 2021), it is interesting to study the performance of quark combination in collisions at 200 GeV so as to find the similarity or difference in hadron production in collisions at two collision energy scales. The study of spectra of identified hadrons in this paper gives a surprising indication.
II Quark number scaling of hadronic spectra
In our EVC model (Song et al., 2017; Gou et al., 2017), a hadron is formed by the combination of (anti-)quarks with the equal velocity. distribution of a hadron () is the product of those of (anti-)quarks
| (1) | ||||
| (2) |
Here, (anti-)quarks are constituent (anti-)quarks so that their equal velocity combination can correctly construct the on-shell hadron. Moment fractions satisfy with ( in baryon formation and with ( in meson formation. is constituent mass of quark . Coefficients and are independent of but dependent on numbers of quarks and antiquarks (Gou et al., 2017).
For hyperon which only consists of strange quarks, its distribution has a simple expression
| (3) |
distribution of meson also has a simple expression
| (4) |
where the approximation at mid-rapidity is taken. From Eqs. (3) and (4), we obtain a relationship
| (5) |
which is called the constituent quark number scaling of hadronic spectra. Coefficient is independent of . For spectra of proton and , we obtain a similar relationship
| (6) |
where approximations and at mid-rapidity are taken. We run PYTHIA 8 with default parameter values and find that calculation results do not exhibit properties in Eqs. (5) and (6).
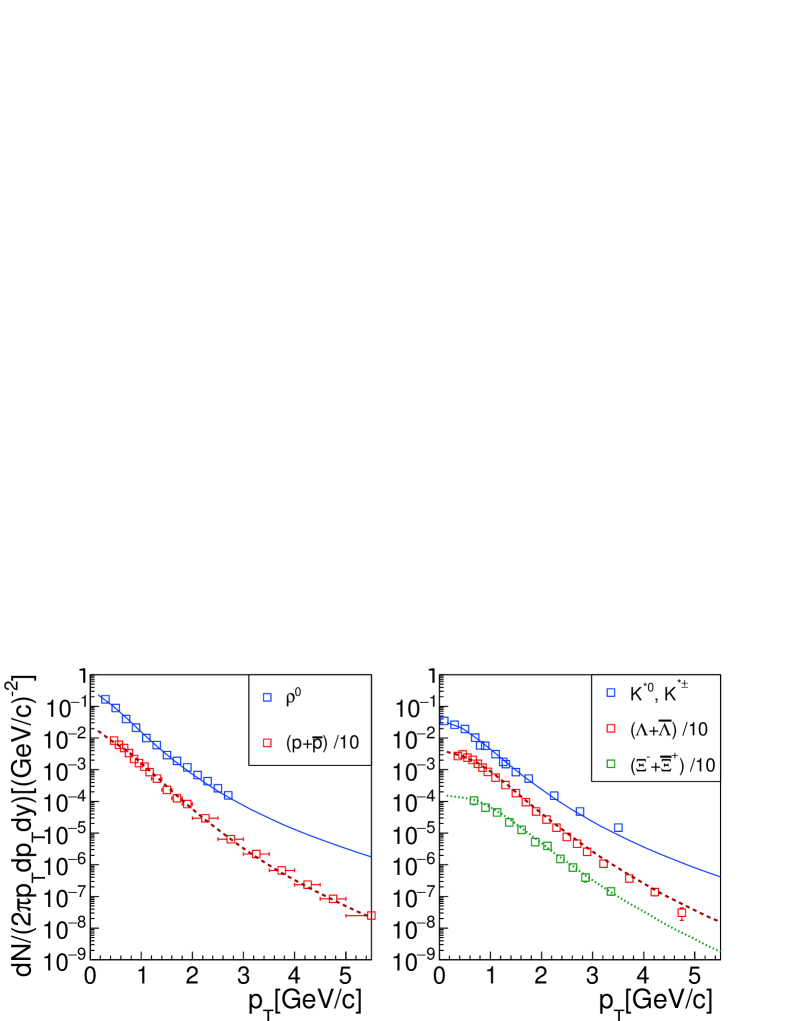
In Fig. 1 (a), we test the scaling property Eq. (5) using experimental data of and at mid-rapidity in inelastic collisions at 200 GeV (Adams et al., 2005b; Abelev et al., 2007). is taken as 1.88. has only three datum points and we see that they are almost coincident with the scaled data of . In Fig. 1 (b), we test Eq. (6) using experimental data of proton and (Adams et al., 2006b, 2004b). is taken as 1.10. Except for the first datum point at GeV/c, we see that other datum points of are very close to the scaled data of proton. We emphasize that values of two coefficients and can be reproduced in our model by considering quark number distributions at hadronization. Therefore, these two scaling tests positively indicate quark combination mechanism at hadronization in collisions even at GeV.
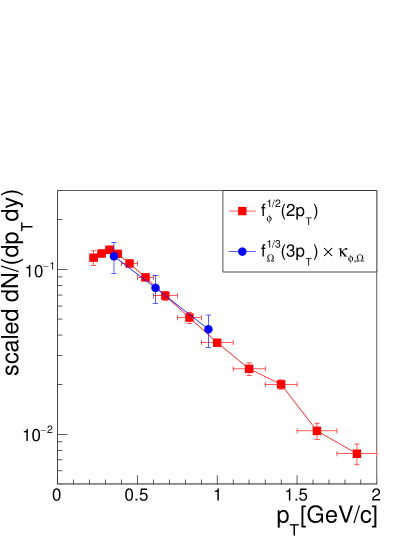

III spectra of mixing-flavor hadrons
Subsequently, we understand the experimental data for spectra of , and (Adams et al., 2005c; Abelev et al., 2007). These hadrons consist of strange quarks and up/down quarks. By Eqs. (1) and (2), their spectra at hadronization are given as
| (7) | ||||
| (8) | ||||
| (9) |
where is the relative momentum ratio of strange quark to up quark. We take by considering constituent quark masses GeV and GeV in constituent quark model. To calculate Eqs. (7)-(9), quark distributions and at hadronization are needed. We obtain them by using our EVC model to fit experimental data of and proton (Adams et al., 2005b; Abelev et al., 2007). Here, the decay contributions of decuplet baryons in ground state to octet baryons are included. The detailed derivation of coefficient in the EVC model can be found in Refs. (Gou et al., 2017; Zhang et al., 2020; Li et al., 2021).
In Fig. 2 (a), we firstly show spectrum of based on fitted from proton data. We see that result is in good agreement with experimental data (Adams et al., 2004b). We note that the consistency between and proton here is better than the scaling test in Fig. 1(b). This is because final-state protons receive certain decay contamination of decuplet baryons , which will weakly influence spectrum of proton. and hardly contain decay contributions and therefore their spectra do not have this contamination.
In Fig. 2(b), we show results for spectra of , and . We see a good agreement with experimental data of three hadrons (Adams et al., 2005c; Abelev et al., 2007). Combining results of Figs. 1 and 2, we see that experimental data of , , , proton, , and can be self-consistently explained by a set of quark spectra at hadronization and under equal-velocity combination mechanism. This is the explicit signal of quark combination at hadronization in collisions at GeV.
IV spectrum of single-charm hadron
We extend the above study to the combination of charm quark and light-flavor quarks. Because constituent mass of charm quark is larger than those of light-flavor quarks, a charm quark with momentum will hadronize by combining a light-flavor antiquark or two light-flavor quarks with momentum where (). We take and by considering the constituent mass of charm quark GeV. In our EVC model, distribution of is
| (10) |
where we assume at mid-rapidity.
Since is already known by fitting data of proton, spectrum of can be calculated when is also known. Here, we consider the calculation result of perturbative QCD for differential cross-section of charm quark in FONLL scheme (Cacciari et al., 1998, 2001). Because FONLL calculation has relatively large uncertainties at low , we firstly fit the FONLL calculation in Fig. 3(a) with a Lévy-Tsallis function to get the normalized distribution and then take mb at mid-rapidity which is located in the range of theoretical uncertainties.

In Fig. 3(b), we show model result of differential cross-section of and compare it with available experimental data (Adamczyk et al., 2012; Qiu, 2016). We see a good agreement. This provides a significant indication on the equal velocity combination of charm quark with light-flavor (anti-)quarks as an effective hadronization mechanism in collisions at 200 GeV.
V Prediction of single-charm hadrons
Similarly, we study the combination of charm quark with a strange antiquark to form a . The calculation results for differential cross-section of and the spectrum ratio as the function of are shown in Fig. 4. Compared with , production of is suppressed. As we known, in the light-flavor background the number of strange (anti-)quarks is smaller than that of up/down (anti-)quarks. Therefore, a charm has a relatively small chance to capture a co-moving to form a . We use a suppression factor to denote the relative abundance of strange quarks. In our model yield ratio of has a simple expression
| (11) |
Since in collisions at 200 GeV, we see in Fig. 4(b) that the spectrum ratio is located in the range [0.1,0.2]. The ratio has a weak dependence, which is because relative abundance of strange quarks is dependent and combination kinematics is slightly different for and pairs.

We further calculate spectra of single-charm baryons by the equal-velocity combination of a charm and two light-flavor quarks. In Fig. 5 (a), we present results for differential cross-sections of , and as the model parameter is taken as . In quark combination mechanism, a charm can form a meson by picking up an antiquark or form a baryon by picking up two quarks. Since hadronization unitarity requires that a charm quark has to become a hadron at last, there exists a competition between baryon formation and meson formation. In our model, such a non-perturbative competition dynamic is parameterized by and is tuned by experimental data. We fit the latest experimental data of in collisions at LHC energies (Acharya et al., 2020, 2021) and obtain . Then, we use it to predict the production of single-charm baryons in collisions at 200 GeV.

In Fig. 5(b), we present spectrum ratios and as the function of . Two ratios increase at low , saturate at GeV/c and decrease at larger . We emphasize that this non-monotonic dependence is a typical signal of our model and is mainly caused by kinematics of equal-velocity quark combination and the property of spectra of light-flavor quarks.
In Fig. 5(c), we present spectrum ratios and in order to better quantify the baryon to meson production competition for charm quark hadronization. Since including strong and electromagnetic decays contains all and combination channels and contains all , and combination channels, the yield ratio directly relates to in the model
| (12) |
Strangeness suppression factor changes weakly () in collisions and causes little contamination on the ratio. Therefore, the ratio is a sensitive probe of the relative probability of combination against combination (here, ) at charm quark hadronization. Similarly, denotes the relative probability of combination against combination. Since the suppression influence of strange quark is canceled in the ratio, we have for yield ratios. In Fig. 5(c), we also see that the spectrum ratios and have the same magnitude. The small difference in dependence between two ratios is caused by the combination kinematics, i.e., momentum fractions and are different in combination with charm quark.
In Fig. 5(d), we present ratios , and as the function of . In our model, they are related to the combination dynamics of increasing number of strange quarks involving the combination process. Statistical combination symmetry is mainly used in model and gives in yield ratios
| (13) | ||||
| (14) |
where in collisions at 200 GeV. We clearly see this flavor hierarchy property in spectrum ratios in Fig. 5(d). In addition, we see a dependence for three ratios, which is because the difference between spectrum of up/down quarks and that of strange quarks at hadronization.
VI Summary and discussions
In summary, we have applied an equal-velocity quark combination model to understand the early RHIC data for spectra of hadrons in collisions at 200 GeV. We found explicit signals of quark combination at hadronization. First, we observed a constituent quark number scaling property for spectra of and and that of proton and . Second, based on the spectrum of up/down quarks extracted from proton data and that of strange quarks extracted from data, we found that data for spectra of , and are also well described. Third, based on the obtained spectrum of up/down quarks and that of charm quarks from perturbative QCD calculations, we found that experimental data for differential cross-section of are also well described.
Because these properties of hadron production are already found in collisions at LHC energies (Gou et al., 2017; Song et al., 2017, 2018; Zhang et al., 2020; Li et al., 2021), the current study indicates a significant similarity between the hadron production in collisions at 200 GeV and that at LHC energies. As we known, at LHC energies, some experimental phenomena such as ridge/long-range correlation (Khachatryan et al., 2010; Chatrchyan et al., 2013), collectivity (Khachatryan et al., 2015, 2017), enhanced baryon-to-meson ratio (Adam et al., 2017; Abelev et al., 2014; Adam et al., 2016a, b) were observed as the indication of possible formation of mini-QGP in collisions in high-multiplicity events. On the other hand, compared with fragmentation mechanism, quark combination mechanism is conceptually more suitable to describe the hadronization of QGP and actually works well in relativistic heavy-ion collisions. Interestingly, our recent works (Gou et al., 2017; Song et al., 2017; Li et al., 2018; Song et al., 2018; Zhang et al., 2020; Li et al., 2021) suggest that an equal-velocity quark combination mechanism at hadronization can systematically describe the momentum spectra of hadrons in collisions at LHC energies. Therefore, signals of quark combination found in collisions at 200 GeV in current study, which indicate the stochastic combination of quarks and antiquarks at hadronization, inspire us to consider the possibility of mini-QGP creation in collisions at RHIC energies!
We therefore suggest the systematic measurements in collisions at 200 GeV in future. These measurements should include ridge/long-range correlation, collectivity, multiplicity dependence of hadron production and so on. By a systematic comparison with available LHC data, these measurements will greatly improve our understanding for the property of small parton system created in collisions at different collision energies.
VII Acknowledgments
We thank Z. B. Xu for helpful discussions. This work is supported in part by Shandong Provincial Natural Science Foundation (ZR2019YQ06, ZR2019MA053), the National Natural Science Foundation of China under Grant No. 11975011, and Higher Educational Youth Innovation Science and Technology Program of Shandong Province (2019KJJ010).
References
- Andersson et al. (1983) B. Andersson, G. Gustafson, G. Ingelman, and T. Sjostrand, Phys. Rept. 97, 31 (1983).
- Webber (1984) B. R. Webber, Nucl. Phys. B 238, 492 (1984).
- Bjorken and Farrar (1974) J. D. Bjorken and G. R. Farrar, Phys. Rev. D 9, 1449 (1974).
- Das and Hwa (1977) K. P. Das and R. C. Hwa, Phys. Lett. B 68, 459 (1977), [Erratum: Phys.Lett.B 73, 504 (1978)].
- Adcox et al. (2002) K. Adcox et al. (PHENIX), Phys. Rev. Lett. 88, 242301 (2002), arXiv:nucl-ex/0112006 .
- Abelev et al. (2006) B. I. Abelev et al. (STAR), Phys. Rev. Lett. 97, 152301 (2006), arXiv:nucl-ex/0606003 .
- Adams et al. (2006a) J. Adams et al. (STAR, STAR RICH), (2006a), arXiv:nucl-ex/0601042 .
- Adams et al. (2004a) J. Adams et al. (STAR), Phys. Rev. Lett. 92, 052302 (2004a), arXiv:nucl-ex/0306007 .
- Adams et al. (2005a) J. Adams et al. (STAR), Phys. Rev. C 72, 014904 (2005a), arXiv:nucl-ex/0409033 .
- Adare et al. (2007) A. Adare et al. (PHENIX), Phys. Rev. Lett. 98, 162301 (2007), arXiv:nucl-ex/0608033 .
- Greco et al. (2003) V. Greco, C. M. Ko, and P. Lévai, Phys. Rev. Lett. 90, 202302 (2003), arXiv:nucl-th/0301093 [nucl-th] .
- Fries et al. (2003) R. J. Fries, B. Müller, C. Nonaka, and S. A. Bass, Phys. Rev. Lett. 90, 202303 (2003), arXiv:nucl-th/0301087 [nucl-th] .
- Hwa and Yang (2003) R. C. Hwa and C. B. Yang, Phys. Rev. C67, 034902 (2003), arXiv:nucl-th/0211010 [nucl-th] .
- Molnar and Voloshin (2003) D. Molnar and S. A. Voloshin, Phys. Rev. Lett. 91, 092301 (2003), arXiv:nucl-th/0302014 .
- Chen and Ko (2006) L.-W. Chen and C. M. Ko, Phys. Rev. C73, 044903 (2006), arXiv:nucl-th/0602025 [nucl-th] .
- Shao et al. (2009) C.-e. Shao, J. Song, F.-l. Shao, and Q.-b. Xie, Phys. Rev. C80, 014909 (2009), arXiv:0902.2435 [hep-ph] .
- Khachatryan et al. (2010) V. Khachatryan et al. (CMS), JHEP 09, 091 (2010), arXiv:1009.4122 [hep-ex] .
- Chatrchyan et al. (2013) S. Chatrchyan et al. (CMS), Phys. Lett. B718, 795 (2013), arXiv:1210.5482 [nucl-ex] .
- Khachatryan et al. (2015) V. Khachatryan et al. (CMS), Phys. Rev. Lett. 115, 012301 (2015), arXiv:1502.05382 [nucl-ex] .
- Khachatryan et al. (2017) V. Khachatryan et al. (CMS), Phys. Lett. B765, 193 (2017), arXiv:1606.06198 [nucl-ex] .
- Adam et al. (2017) J. Adam et al. (ALICE), Nature Phys. 13, 535 (2017), arXiv:1606.07424 [nucl-ex] .
- Abelev et al. (2014) B. B. Abelev et al. (ALICE), Phys. Lett. B728, 25 (2014), arXiv:1307.6796 [nucl-ex] .
- Adam et al. (2016a) J. Adam et al. (ALICE), Phys. Lett. B760, 720 (2016a), arXiv:1601.03658 [nucl-ex] .
- Adam et al. (2016b) J. Adam et al. (ALICE), Phys. Lett. B758, 389 (2016b), arXiv:1512.07227 [nucl-ex] .
- Liu and Werner (2011) F.-M. Liu and K. Werner, Phys. Rev. Lett. 106, 242301 (2011), arXiv:1102.1052 [hep-ph] .
- Bzdak et al. (2013) A. Bzdak, B. Schenke, P. Tribedy, and R. Venugopalan, Phys. Rev. C87, 064906 (2013), arXiv:1304.3403 [nucl-th] .
- Bozek and Broniowski (2013) P. Bozek and W. Broniowski, Phys. Rev. C88, 014903 (2013), arXiv:1304.3044 [nucl-th] .
- Prasad et al. (2010) S. K. Prasad, V. Roy, S. Chattopadhyay, and A. K. Chaudhuri, Phys. Rev. C82, 024909 (2010), arXiv:0910.4844 [nucl-th] .
- Avsar et al. (2011) E. Avsar, C. Flensburg, Y. Hatta, J.-Y. Ollitrault, and T. Ueda, Phys. Lett. B702, 394 (2011), arXiv:1009.5643 [hep-ph] .
- Zhao et al. (2018) W. Zhao, Y. Zhou, H. Xu, W. Deng, and H. Song, Phys. Lett. B 780, 495 (2018), arXiv:1801.00271 [nucl-th] .
- Shao et al. (2017) F.-l. Shao, G.-j. Wang, R.-q. Wang, H.-h. Li, and J. Song, Phys. Rev. C 95, 064911 (2017), arXiv:1703.05862 [hep-ph] .
- Song et al. (2017) J. Song, X.-r. Gou, F.-l. Shao, and Z.-T. Liang, Phys. Lett. B774, 516 (2017), arXiv:1707.03949 [hep-ph] .
- Gou et al. (2017) X.-r. Gou, F.-l. Shao, R.-q. Wang, H.-h. Li, and J. Song, Phys. Rev. D96, 094010 (2017), arXiv:1707.06906 [hep-ph] .
- Zhang et al. (2020) J.-w. Zhang, H.-h. Li, F.-l. Shao, and J. Song, Chin. Phys. C44, 014101 (2020), arXiv:1811.00975 [hep-ph] .
- Li et al. (2018) H.-H. Li, F.-L. Shao, J. Song, and R.-Q. Wang, Phys. Rev. C97, 064915 (2018), arXiv:1712.08921 [hep-ph] .
- Song et al. (2018) J. Song, H.-h. Li, and F.-l. Shao, Eur. Phys. J. C78, 344 (2018), arXiv:1801.09402 [hep-ph] .
- Li et al. (2021) H.-H. Li, F.-L. Shao, and J. Song, (2021), arXiv:2103.14900 [hep-ph] .
- Adams et al. (2005b) J. Adams et al. (STAR), Phys. Lett. B 612, 181 (2005b), arXiv:nucl-ex/0406003 .
- Adams et al. (2004b) J. Adams et al. (STAR), Phys. Rev. Lett. 92, 092301 (2004b), arXiv:nucl-ex/0307023 .
- Adams et al. (2005c) J. Adams et al. (STAR), Phys. Rev. C 71, 064902 (2005c), arXiv:nucl-ex/0412019 .
- Abelev et al. (2007) B. I. Abelev et al. (STAR), Phys. Rev. C 75, 064901 (2007), arXiv:nucl-ex/0607033 .
- Adams et al. (2006b) J. Adams et al. (STAR), Phys. Lett. B 637, 161 (2006b), arXiv:nucl-ex/0601033 .
- Adamczyk et al. (2012) L. Adamczyk et al. (STAR), Phys. Rev. D 86, 072013 (2012), arXiv:1204.4244 [nucl-ex] .
- Qiu (2016) H. Qiu (STAR), Nucl. Part. Phys. Proc. 276-278, 213 (2016).
- Cacciari et al. (1998) M. Cacciari, M. Greco, and P. Nason, JHEP 05, 007 (1998), arXiv:hep-ph/9803400 .
- Cacciari et al. (2001) M. Cacciari, S. Frixione, and P. Nason, JHEP 03, 006 (2001), arXiv:hep-ph/0102134 .
- Acharya et al. (2020) S. Acharya et al. (ALICE), (2020), arXiv:2011.06079 [nucl-ex] .
- Acharya et al. (2021) S. Acharya et al. (ALICE), (2021), arXiv:2106.08278 [hep-ex] .