Shifted shock formation for the 3D compressible Euler equations with damping and variation of the vorticity
Abstract
In this paper, we consider the shock formation problem for the 3-dimensional(3D) compressible Euler equations with damping inspired by the work [4]. It will be shown that for a class of large data the damping can not prevent the formation of point shock and the damping effect shifts the shock time and the wave amplitude while the shock location and the blow up direction remain same with the information of this point shock being computed explicitly. Moreover, the vorticity is concentrated in the non-blow up direction which varies exponentially due to the damping effect. Our proof is based on the estimates for the modulated self-similar variables and lower bounds for the Lagrangian trajectories.
1 Introduction
We consider the following 3D Euler system with damping
| (1.1) |
with the space-time variables , the velocity , the positive density , the entropy and the pressure is given by
with the adiabatic constant . These equations describe the motion of a perfect fluid which follow from the conservation of mass, momentum and energy respectively. The term on the right hand side of momentum equation represents the damping effect to the fluid with the damping constant .
Instead of using the density, it’s convenient to rewrite the equation by the sound speed, which is defined as
where For simplicity, we denote to be the re-scaled sound speed
Then, (1.1) can be rewritten as
| (1.2) |
Define the specific vorticity as . Then, satisfies the following equation:
| (1.3) |
The first and second terms on the right-hand side of the equation(1.3) represent the consequences of vortex stretching and the baroclinic torque. The third term arises from the intersection of acoustic and entropy waves and results from the non-aligned pressure and density gradients. In the scenario where the system is isentropic, such that , this term vanishes. However, when the system is non-isentropic, this term plays a crucial role in the generation of vorticity. Irrotational data can produce vorticity instantaneously, as demonstrated in [4]. For example, if the density gradient is perpendicular to the pressure gradient, the lighter gas will be accelerated faster than the denser gas, resulting in the creation of vorticity.
It is well-known that damping can prevent shock formation when the energy of the initial data is small. However, for large data sets, such as short pulse data or data with large energy, we will demonstrate that damping may not sufficiently prevent the formation of shock. Furthermore, we will show that the damping effect shift the time at which a shock occurs, while the blow-up location remains unchanged compared with the undamped case, with the degree of shift reliant on the value of .
1.1 Review of prior results for the Euler system
For the system(1.1), there are many studies both in and multi-dimensions. For the one-dimensional Euler equations with damping, the global existence of smooth solutions with small data was proved by Nishida[21] and Slemrod[27] showed that for small data ( sense), the Euler equations with damping admit a global smooth solution while for large data, the equations can develop a shock in finite time. Later, these results were generalized by many authors, see [11, 22, 18, 17, 16, 23] and the references therein.
In multi-dimensional case, the global existence and estimates for the solutions to the isentropic Euler system with damping was obtained by Kawashima[13]. Later, Sideris-Thomases-Wang in[26] showed that the size of the smooth initial data plays a key role for the lifespan to the isentropic Euler equations with damping . If the initial data are small, then damping can prevent the development of singularities; while if the initial data are large, the damping is not strong enough to prevent the formation of singularities in finite time. However, the authors in[26] only obtained the finite lifespan of the solutions and did not show the shock formation (including the shock mechanism) in finite time. The long time behavior of the solutions was obtained and generalized by many authors, see [29, 12, 24, 28, 26] and the references therein.
In [6], Christodoulou achieved a significant breakthrough in understanding the shock mechanism for hyperbolic systems in three dimensions. Specifically, he considered the classical, non-relativistic, compressible Euler’s equations in three spatial dimensions, taking the data to be irrotational and isentropic. By imposing certain conditions on the initial data (i.e., the short pulse assumption), he obtained a complete geometric description of the maximal classical development. Notably, he provided a detailed analysis of the behavior of the solution at the boundary of the domain of the maximal classical solution, including a comprehensive description of its geometry. This work represents a significant advancement in understanding of shock formation in hyperbolic systems in three dimensions.
In [25], Yu-Miao applied Christodoulou’s framework to the quasilinear wave equation in three spatial dimensions. By constructing a family of short pulse initial data that was first introduced by Christodoulou in [5], they demonstrated how the solution breaks down near the singularity and gave a sufficient condition on the initial data which leads to the shock formation in finite time. Additionally, J.Speck and J.Luk applied Christodoulou’s framework to the 2D Euler system without the assumption of irrotation. In [14], they studied plane-symmetric initial data with short pulse perturbation. For such initial data, they showed the shock mechanism such that the first derivatives of and blow up while and remain bounded near the shock. Then, in [15], they generalized these results to the 3D case. Specifically, they considered the 1D Euler equation of a simple small-amplitude solution as a plane-symmetric solution in 3D. They perturbed this solution in the directions as a nearly plane-symmetric initial data for 3D isentropic Euler equations. They proved that the shock formation mechanism is stable under small and compactly supported perturbations with non-trivial vorticity and provided a precise description of the first singularity.
Recently, Buckmaster, Shkoller, and Vicol published several results regarding shock formation in the multi-dimensional Euler system. Specifically, in their paper [3], they studied the 2D isentropic Euler equations under azimuthal symmetry (which differs from the 1D problem) with smooth initial data of finite energy and nontrivial vorticity. By utilizing modulated self-similar variables, they were able to obtain point shock forms in finite time, with explicit computation of the blow-up time and location. Furthermore, the solutions near the shock exhibit a cusp type.
In a subsequent paper, [2], Buckmaster, Shkoller, and Vicol generalized their results to the 3D isentropic case for the ideal gas without any symmetry assumptions. In addition to the findings reported in [3], they were able to demonstrate the precise direction of blow-up and the geometric structure of the tangent surface of the shock profile. They also provided homogeneous Sobolev bounds for the fluid variables with an initial datum of large energy. Later, in[4], the authors extended their results to the full Euler equations. In this work, they primarily investigated the evolution and creation of vorticity, demonstrating that the vorticity remains bounded up to the shock formation. Notably, one of the primary differences between the isentropic and non-isentropic cases is the baroclinic torque in the equation of vorticity, which arises from the interaction between sound waves and entropy waves. Additionally, they constructed a set of irrotational data that results in the instantaneous creation of vorticity, which remains non-zero up to the shock.
It is important to note that the point shock in the three aforementioned results is stable. That is, for any small, smooth, and generic perturbation of the given initial data, the corresponding Euler system results in a smooth solution that blows up in a small neighborhood of the original shock time and location. However, in [1], the authors demonstrated the existence of an open set of initial data that leads to the formation of an unstable shock. The primary difference between stable and unstable shocks is the set of background solutions for the self-similar variable , specifically the solutions of the various self-similar Burgers equations (3.43). For further details, one may refer to [9].
The major tool used in the works mentioned above is the method of self-similar coordinates. This method was first introduced by Y.Giga and R.Kohn in [10] to study the asymptotic behavior of the solution to the nonlinear heat equation near the point of singularity. Y.Giga and R.Kohn considered the following nonlinear heat equation
| (1.4) |
where and . They aimed to show the behavior of the solution near the singularity. To this end, they proposed the following self-similar transformation222Note that the transformation degenerates at .:
| (1.5) |
which transforms (1.4) into
| (1.6) |
This transformation is motivated by the scaling property of (1.4). That is, for any solves (1.4), solves (1.4) as well. Based on the analysis of (1.6), they were able to demonstrate the asymptotic behavior of near the blow-up point . Later, such method has been applied to various other dynamical systems, including the Schdinger equation [19], the Prandtl equations [7], the transverse viscous Burgers equation [8], and the semilinear wave equation [20]. The method of self-similar variables can provide precise information about the singularity of a given system by adding modulation variables to enforce certain orthogonality conditions and track the position of the singularity. It can also be used to characterize the type of singularities present, such as stable fixed points or center manifold and etc…, based on the behavior of the solutions near the singularity. For example, the stable shock in [3], [2], and [4] is based on the fact that the solutions approach the background solution near the shock exponentially with respect to the self-similar variables. For further details, one may refer to [9].
1.2 Outline
In section 2, the fundamental ideas of [2] and [4] will be illustrated by applying them to the standard Burgers equation and the Burgers equation with damping. Our results will demonstrate that the modulated variables can accurately track the location and time of the shock, and that the damping effect only shifts the blow-up time while leaving the blow-up location unchanged compared with the undamped case.
Section 3 is devoted to reformulating of the Euler system (1.1) into its modulated self-similar version (3.28) by adapting the framework of [4]. Additionally, we extend the solution of the self-similar Burgers equation, which is introduced in Section 2, to three dimensions and derive higher-order derivatives of the evolution equations for the self-similar variables .
In Section 4, we present an explicit construction of the initial datum in [4]. Note that the initial data for variable is dependent on the background solution , which is a refined solution of the self-similar Burgers equation. Furthermore, we outline the self-similar Bootstrap assumptions for various variables and their derivatives, including the modulation variables and the self-similar variables . These assumptions are more restrictive than the initial data constructed earlier and will be recovered in the subsequent sections. Finally, we state the main theorem (Theorem 4.1) of the paper at the end of this section.
In Section 5, we present multiple estimates based on bootstrap assumptions, including the estimation of damping and forcing terms. Additionally, we state the energy bounds for , whose proof solely relies on the bootstrap assumptions and the Friedrich’s energy estimates for the hyperbolic system. These estimates lead to higher-order derivatives estimates for , which in turn help to further refine the estimates for the forcing terms.
Section 6 is a key aspect of our work. In this section, we recover the bootstrap assumptions for the modulation variables under 10 constraints regarding , where . These constraints are initially satisfied and remain valid over time as long as the estimates for the modulation variables hold. In addition, it will be clearly shown that how the damping effect can influence the information of shock within this section.
In Section 7, we derive lower bounds for the Lagrangian trajectories and introduced the crucial lemma7.2, which provides the key estimate required for recovering the remaining bootstrap assumptions. Moreover, we investigate the evolution of the vorticity, which is concentrated on the non-blow up direction, and demonstrated how it is affected by the damping effect. Inspired the work in[4], it will be shown that the initial region which genuinely affects the shock formation.
By following the estimates presented in sections 5 to 7, we are able to recover the bootstrap assumptions for as outlined in section 8. This recovery is based on the significant lemma 7.2 and the utilization of the weighted framework (8.9). Note that to recover the bootstrap assumption for , one has to establish the relation between and the specific vorticity .
Section 9 serves to establish the energy bounds for the self-similar variables, thereby concluding the proof for the main theorem 4.1. Instead of studying the system for , we utilize various Sobolev inequalities to derive the energy bounds for the equations of the velocity , the pressure , and the entropy (as seen in (3.42)). This approach proves to be more convenient to apply the Friedrich’s energy estimates.
1.3 Notations
Through the whole paper, the following notations will be used unless stated otherwise.
-
•
Latin indices take the values and Greek indices take the values . Repeated indices are meant to be summed.
-
•
For a three-component vector , denote the last two components of simply as . For example, one can rewrite the gradient operator as
-
•
The convention means that there exists a universal positive constant such that . The convention means that there exists a universal positive constant such that .
-
•
For any function , denote to be .
2 Shock formation for the Burger’s equation in self-similar fancy
We consider the following Cauchy problem for 1D Burger’s equation
| (2.1) |
For simplicity, we assume additionally that and 333Indeed, once can assume generally that . Then the framework here also applies by slightly modified, i.e. and , and the corresponding self-similar transformation becomes (2.2) . Then by standard characteristic method, the solution of (2.1) will form a shock at time and the location with as . However, this method has some drawbacks in the following sense:
-
•
Is there any singularity before and whether is the first quantity which blows up or not?
-
•
How does the shock profile look like, and how does the solution behave near the singularity?
The above questions can be solved by using self-similar coordinates which is defined as follows:
| (2.3) |
and the corresponding unknown is given as
| (2.4) |
Then, (2.1) is transformed as
| (2.5) |
Remark 2.1.
In general, the self-similar transformation should be
| (2.6) |
where the parameters and represent the shock time and location, respectively. Here, one already knows the blow-up point is , which means one could take . Then, substituting (2.6) into (2.5) yields
| (2.7) |
In order to guarantee the global existence of (2.7), one has to choose
| (2.8) |
The choice of is used to guarantee the stability of shock.444This means the solution of (2.1) is approaching exponentially to the solution of the self-similar Burger’s equation (see(2.12)) in self-similar variable , i.e. (2.9) where is given by (2.13). See[9] for more details.
Note that the Jacobian of the transformation is given by
| (2.10) |
Hence, the self-similar transformation degenerates as . Later we will prove that (2.7) admits a global solution on , and therefore, the only possibility of singularity formation is the transformation between the Cartesian coordinates and the self-similar coordinates becomes degenerated.
Moreover, one can show that converges to pointwisely as . That is
| (2.11) |
where is the solution of the following self-similar Burger’s equation
| (2.12) |
Indeed, can be solved as a implicit function as
| (2.13) |
which is globally defined.
Hence, blows up only at the shock point and location, i.e.
| (2.14) |
and all the other quantities are bounded666Obviously, and it can be shown that for any , . The behavior of the solution near shock is given as
| (2.15) |
Remark 2.2.
To obtain the global existence of (2.5), one can check that if one defines the characteristics as
along which , then , which means can be solved implicitly as . In order to require to be defined globally, it suffices to show
| (2.16) |
This is guaranteed by assumption on the initial data.
2.1 The geometric structure of shock front
Consider the Surface in . Then, the normal vector of and the Gauss curvature of at each point are given as follows
| (2.17) |
where . Initially, , . In the self-similar coordinate, consider the evolutions of at ,
| (2.18) | ||||
| (2.19) |
Then, as (), since , , it holds that
| (2.20) |
Therefore, shock formation to the Burgers’ equation (2.1) is equivalent to that
-
•
the transformation between the physical variables (the Cartesian coordinates) and the self-similar coordinates becomes degenerate;
-
•
the normal of the shock front become horizontal at shock point.
2.2 Shifted singularity for the Burgers’ equation with damping
We consider the following Cauchy problem for 1D Burgers’ equation with damping:
| (2.21) |
where is the damping constant and is the same as in (2.1). It will be shown that when , the damping effect is small and (2.21) behaves like the standard Burgers’ equation such that smooth data can form a shock in finite time. Moreover, the damping will shift the blow-up time according to the sign of as follows.
-
•
If , the damping will delay the formation of shock and the closer is to , the larger the blow-up time is;
-
•
if , then the blow-up time will be in advanced.
Precisely, the blow-up time can be clarified as 777If one assumes generally that , then the first case becomes that while . and in both case, the blow-up location remains the same compared with the undamped case (i.e. ). When , the damping effect is strong enough and (2.21) admits a global solution on . To this end, define the following self-similar coordinates888The choice of modulation variables and is mainly dependent on the invariance of (2.21) under space translation and time translation. That is, given any , then for any solution to (2.21), solves (2.21) as well.:
| (2.22) |
where and represent the blow-up time and location respectively, with the initial condition . Note that the Jacobian of the transformation is given by
| (2.23) |
Hence, the transformation will degenerate at time (it will be shown that ) and is a diffeomorphism for . Then, (2.21) will be transformed into
| (2.24) |
with the initial condition
| (2.25) |
To obtain a global solution for (2.24) is similar to the former case999In this case, define the characteristics as (2.26) along which . Then, can be solved implicitly as . To show the global existence of , it suffices to show (2.27) which is guaranteed by the initial data and the definition of (see(2.30)).. Here, we focus on the evolutions of and . Differentiating (2.24) w.r.t yields
| (2.28) |
Now we postulate that and for all . This can be achieved by choosing and suitably since initially, it holds that and . Evaluating (2.24) and (2.28) at yields
| (2.29) |
which implies
| (2.30) |
To conclude, it holds that
-
•
if , then for all , and one obtains a global classical solution to (2.21);
-
•
if 101010If one assumes generally that , then this case becomes ”if , then a shock forms at .” Therefore, for fixed , small data(i.e.) leads to the global solution while large data leads to the shock formation in finite time., then the transformation between Cartesian coordinates and self-similar coordinates will degenerate at time which can be computed as , and
(2.31) i.e. the solution will form a shock at . In this case, one sees that the blow-up location doesn’t shift.
2.3 Global existence to the Burgers’ equation
One can also use the self-similar coordinates to show the global existence to (2.1) with the initial data being everywhere increasing. For simplicity, we assume that (start from ) attains its min at with . Then, the classical results show that (2.1) admits a global ”rarefaction wave” solution. To this end, define the following self-similar transformation:
| (2.32) |
Then, (2.1) is transformed into
| (2.33) |
with the initial condition
| (2.34) |
Note that in this case, the Jacobian of the transform is given as
| (2.35) |
which implies the transform (2.32) is a global diffeomorphism. Hence, if one obtains a global solution in the self-similar coordinates, then the global existence of original Burgers’ equation in Cartesian coordinates is automatically obtained. It can be shown in the similar way that (2.33) admits a global solution on which converges to pointwisely,
where is the solution of
| (2.36) |
Indeed, can be solved implicitly as
| (2.37) |
Then, for all , it holds that
| (2.38) |
Remark 2.3.
It seems that the condition which is the global minimum doesn’t use for the global existence of (2.33). However, one can check that if one defines the characteristics of (2.33) as
along which , then , which allows one to solve implicitly as . Then, this formula indeed defines a global solution provided
| (2.39) |
which is guaranteed by the assumption on the initial data.
3 Coordinates transformations and the self-similar Euler system
To study the structure of shock front and introduce the self-similar coordinates, we will construct 10 modulation variables to control the following entities111111The choice of these modulation variables are derived from the invariance of the equations(1.1) under time re-scaling and Galilean transformations which including the space transformation, the time translation, the union motion (the shear transformation) and the space rotation.:
| (3.1) |
Then, the following coordinates transformations will be used:
3.1 The coordinates under Galilean transform
First, do time-rescaling as
so that all the modulation variables are defined w.r.t the rescaled time (i.e. ).
Given an unit vector , one can generate a rotation matrix which transforms to . Precisely, let
| (3.2) |
Then, the rotation matrix rotates to . Define the new coordinates as
| (3.3) |
and the corresponding fluid variables as
| (3.4) |
Note that
| (3.5) | ||||
| (3.6) |
where
| (3.7) |
Hence, the Euler system (1.2) is transformed in as
| (3.8) |
together with the vorticity equation
| (3.9) |
3.2 The flatted coordinates with respect to shock front
In order to see the geometry of the shock, define the ”tangent” quadratic surface as
| (3.10) |
where is a quadratic form given as
| (3.11) |
with being a symmetric tensor. Then, define the shear transformation as
| (3.12) |
which flattens the ”tangent” surface. Note that together with the coordinates transform, the ”basis” transforms automatically into
| (3.13) | ||||
| (3.14) | ||||
| (3.15) |
where and and is the rotation matrix generated by (with the role of replaced by ).
Remark 3.1.
Note that the fundamental form of the ”tangent” surface is given by . So, the functions indeed reveal the geometry structure of the shock front.
Denote the corresponding fluid variables as
Note that
Then, by defining the following constants
| (3.16) |
the Euler system (3.8) is transformed into
| (3.17) |
together with the vorticity equation
| (3.18) |
where in terms of basis,
| (3.19) |
Remark 3.2.
The term in direction is the potentially dangerous term since this term blows up at the shock time which will be proved later.
In order to see the intersection of different wave families, it’s convenient to introduce the Riemann variables
| (3.20) |
Remark 3.3.
Later, one can see that actually only the quantity blows up at the shock time and location, the remaining quantities are bound up to the shock, which is coincide to the 1D case.
In terms of Riemann variables, the Euler system (3.17) can be rewritten as the following system:
| (3.21) |
where
and
3.3 The self-similar coordinates
Define the following self-similar transformation
| (3.22) |
and the corresponding fluid variables
| (3.23) |
Remark 3.4.
The reason of choosing the indexes in (3.22) is similar to the Burger’s case.
Note that
| (3.24) |
Then, the Jacobian of the transformation(3.22) is given as
| (3.25) |
which means the transformation is a diffeomorphism as long as (it will be shown that and becomes degenerated as (this is how we define the shock time). Therefore, shock formation to (1.1) is equivalent to that
-
•
the gradient of Riemann variable along -direction become infinite;
-
•
the transformation between the physical variables (the Cartesian coordinates) and the self-similar coordinates becomes degenerated;
-
•
the normal of the ”tangent” surface of the shock front becomes ”horizontal”.
Remark 3.5.
The normal vector becomes ”horizontal” above is w.r.t the scale. Precisely, initially
| (3.26) |
and as time approaches to the shock time
| (3.27) |
This is because we set initial time at instead of .
In terms of the self-similar coordinates , the system (3.21) is transformed into the following system:
| (3.28) |
where
| (3.29) |
and
| (3.30) | ||||
| (3.31) | ||||
| (3.32) | ||||
| (3.33) | ||||
| (3.34) | ||||
| (3.35) | ||||
Let be a multi-index . Then, acting to the system yields
| (3.36) | ||||
| (3.37) | ||||
| (3.38) | ||||
| (3.39) |
where
| (3.40) |
3.4 The system for energy estimates
In order to derive the energy estimates for Euler system, we compute the equations for the velocity, the pressure and the entropy, instead. Let
| (3.41) |
Then, satisfies the following system
| (3.42) |
3.5 The solution of the self-similar Burgers’ equation
Note that if the solution of the equation of is independent of , then, this equation will ”converge” to the following 3D self-similar Burgers’ equation (later it will be shown that as , )
| (3.43) |
Indeed, the solution of (3.43) can be generated by the solution of 1D self-similar Burgers’ equation. Let and
| (3.44) |
where is given implicitly by (see(2.7)). Then, solves (3.43) and direct computations lead to
| (3.45) |
Moreover, if one defines , then it holds that
| (3.46) |
Later, it will be proven that will converge to pointwisely as . Then, it’s natural to consider the evolution equation of :
| (3.47) |
where
| (3.48) |
Applying with to (3.47) yields
| (3.49) |
where
| (3.50) |
4 Initial data construction, Bootstrap assumptions and the main results
Set the initial time to be . The initial values of the modulation variables are set as follows:
| (4.1) | |||
| (4.2) |
with so that initially, the Galilean transformation (3.3) is the identical map and the shear transformation is given as
| (4.3) |
where
| (4.4) |
Then, the initial basis in the flatted coordinates are set as in(3.13). Finally, set the initial fluid variables as follows:
| (4.5) | |||
| (4.6) | |||
| (4.7) | |||
| (4.8) |
We then construct the initial datum for as follows.
Lemma 4.1.
Given any functions (for ) such that for . For simplicity, we also assume that for for being multi-index and . Let . Then, define the initial data as follows:
| (4.9) | ||||
| (4.10) | ||||
| (4.11) | ||||
| (4.12) |
where
Remark 4.2.
We constrain the support of in . Indeed, the initial data in this Lemma can be taken generally such as with and or more generally with , , and , , .
Remark 4.3.
Similar to the case for the Burgers equation (2.25) in section2 to control the modulation variables, we further assume that
| (4.13) | ||||
| (4.14) |
for and . As a consequence, one obtains due to
| (4.15) |
Then, initially,
| (4.16) |
In the self-similar coordinates, one has the following bounds due to and for (note that the initial support of in self-similar coordinates is ):
-
•
For all , it holds that
(4.17) (4.18) (4.19) where .
-
•
For , it holds that
(4.20) while at , one has
(4.21) -
•
For , it holds that
(4.22) (4.23) (4.24) -
•
For , it holds that
(4.25) (4.26) (4.27) -
•
For the second derivatives and all , it holds that
(4.28) (4.29) (4.30) Furthermore, at , it follows from (4.13) that
(4.31) For , the following energy bounds hold
(4.32)
Remark 4.4.
Moreover, the following bounds for the specific vorticity and the sound speed hold due to the definition (3.23):
| (4.33) | ||||
| (4.34) | ||||
| (4.35) |
4.1 The Bootstrap assumptions
For convenience, we introduce the following notations.
-
•
is a lower order term (l.o.t) compared with means where and .
-
•
Define the function (simply written as ) to be where ;
Then, we assume the following Bootstrap assumptions.
-
•
Bootstrap assumptions on modulation variables. Assume that
(4.36) (4.37) (4.38) for all , where is the shock time which is defined as
(4.39) -
•
Bootstrap assumption on support of . Assume that are supported in
(4.42) Remark 4.6.
It follows from (4.42) that , and the following properties of the function hold.
-
(1)
If , then
(4.43) for all ;
-
(2)
if , then
(4.44) for all .
-
(1)
-
•
Bootstrap assumptions on . Assume that the following bounds hold for all .
(4.45) (4.46) (4.47) For the variables and , we divide the spatial region as follows.
-
–
For , assume that
(4.48) (4.49) while at , assume that
(4.50) -
–
For , assume that
(4.51) (4.52) (4.53) -
–
For all , assume that
(4.54) where 131313The function is to control the growth of the entropy , which vanishes in the isentropic case. The second term in can be chosen as with and which can be derived in recovering the bootstrap assumptions for and ..
-
–
4.2 The main result
Theorem 4.1.
Assume the initial data in the physical variables are set as in Lemma4.1. Then,
-
•
in the self-similar coordinates, the bootstrap assumptions (4.36)-(4.54) hold for all , and the sound speed , the specific vorticity , the velocity , the pressure are smooth together with their derivatives for all . Furthermore, it holds that
(4.55) with the energy bounds
(4.56) for all and some constant .
-
•
In the physical variables, there are following two possibilities.
-
(1)
If , then the damping effect is weak enough to allow for the formation of a shock. There exists a pair , which can be computed explicitly with , such that a point shock forms at this point. Furthermore, the shock time is shifted while the shock location and blow up direction remain same compared with the undamped case (see section6.1 for more details).
-
(2)
If , then the damping effect is strong enough to prevent the formation of shock and a smooth classical solution to the compressible Euler system(1.1) on is obtained.
In case , the following additional results hold.
-
The Jacobian of the transformation between the physical variables (Cartesian coordinates) and the self-similar coordinates become at , never vanishing everywhere else.
-
The first derivative of Riemann invariants along blow up direction (i.e. along ) blows up like at shock point while being bound everywhere else. Precisely, it holds that
(4.57) (4.58) (4.59) -
The other quantities are bounded as follows.
(4.60) (4.61) -
If , then the damping effect leads to the dissipation of the vorticity while for , the anti-damping effect leads to an increase in the vorticity.
-
The normal vector become horizontal in scale as , that is
(4.62)
In case , it is shown that and for all . Then, the Jacobian of the transformation never vanishes for all . This implies the fluid variables are bounded together with their first derivatives. In particular, compared to the case , it holds that
(4.63) -
(1)
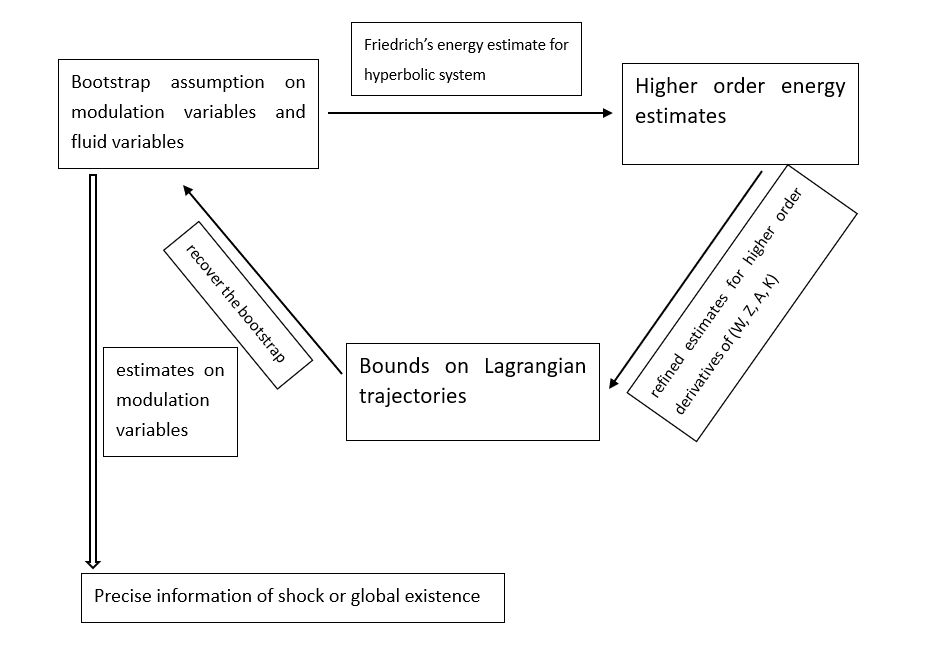
The proof of the main theorem can be illustrated in the following picture:
Remark 4.8.
(The blow-up quantity) To see which quantities blow up as approaches , one computes the following limits:
| (4.64) |
and observes that only the first quantity blows up, while the others remain bounded. Note that the above can be replaced by as well.
-
(1)
Therefore,
(4.65) -
(2)
-
(3)
Similarly,
(4.66) -
(4)
We conclude this section by stating the following Sobolev-type inequalities, which can be verified directly.
Lemma 4.2.
For , , and where , if
| (4.67) |
then
| (4.68) |
The case will be used, which yields
| (4.69) |
for with compact support and .
It follows from Lemma4.2 that the following Lemma holds.
Lemma 4.3.
Let and . Then for and , it holds that
| (4.70) |
Lemma 4.4.
For with compact support, it holds that
| (4.71) |
5 Preliminary estimates in self-similar coordinates under Bootstrap assumptions
First, we state the following homogeneous Sobolev energy estimates for :
Proposition 5.1.
For some integers and for some constant , it holds that for all
| (5.1) |
The proof for this proposition will be given later, which is solely dependent on the bootstrap assumptions and standard Freidrich’s energy estimates for the symmetric hyperbolic system. We mention the estimates here because the system loses one derivative. To derive the estimates for the higher order derivatives of forcing terms, it is necessary to obtain high order derivative estimates for using standard Sobolev inequalities.
Lemma 5.1.
For integer sufficiently large, the following refined estimates for higher order derivatives for hold where the implicit constants are independent of :
| (5.2) |
| (5.3) |
| (5.4) |
| (5.5) |
PROOF:.
Lemma 5.2.
For all and , it holds that
| (5.11) |
Similar argument leads to the following lemma.
Lemma 5.3.
For all and , it holds that
| (5.12) |
| (5.13) |
| (5.14) |
The following bounds for the sound speed and the density can be obtained.
Lemma 5.4.
There exists a constant such that
| (5.15) | ||||
| (5.16) |
PROOF:.
5.1 Estimates on transport terms and forcing terms
Lemma 5.5.
For sufficiently small and , it holds that
| (5.18) |
| (5.19) |
| (5.20) |
PROOF:.
Note that
Then141414The estimate for can be found in (6.18), which only relies on the bootstrap assumptions.,
For , it follows from (3.29) that
| (5.21) |
and then the estimate for follows from the bootstrap assumptions (4.36) and (4.45). The estimate for is similar to . The estimates for the remaining term follows directly from the bootstrap assumptions, the definiton(3.29) and Lemma5.3.
Lemma 5.6.
For all and , the following bounds for the forcing terms , and hold.
| (5.22) |
| (5.23) |
| (5.24) |
| (5.25) |
For , the following bounds hold
| (5.26) |
and for , it holds that
| (5.27) |
PROOF:.
It follows from the Bootstrap assumptions and (3.31) that
| (5.28) |
and then
| (5.29) | ||||
| (5.30) | ||||
| (5.31) | ||||
| (5.32) |
Therefore, the following cases hold due to the bootstrap assumptions, Lemma5.1,5.2,5.3 and Lemma5.5.
-
•
For
-
•
for ,
-
•
for ,
-
•
for ,
-
•
for ,
-
•
for ,
Similarly, for the forcing terms of , it holds that
Therefore, it follows from the bootstrap assumptions, Lemma5.1,5.2,5.3 and Lemma5.5 that
-
•
for , ;
-
•
for ,
-
•
for ,
-
•
for ,
-
•
for ,
-
•
for ,
And for and , it holds that
-
•
for , ;
-
•
for , ;
-
•
for ,
-
•
for ,
-
•
for ,
-
•
for ,
For and , it follows from (3.50) and Lemma5.5 that
Due to (5.22), (3.46) and Lemma5.5, it holds that
and
which completes the proof for the estimates with . The estimate for and is similar. For with , note that151515This can be derived from (3.44) and (2.7). Moreover, one can show that for all , see[2].
| (5.33) |
which implies that for . Therefore, evaluating (3.50) at yields
6 Recover the bootstrap assumptions on modulation variables
The estimates for the modulation variables are one of the key aspects of this work and differ significantly from those in [4]. Therefore, we will focus on the evolution of these modulation variables to understand how the damping term affects shock formation. To this end, we propose 10 constraints on for , which effectively characterize the information about the shock161616See also (2.25) for the 1D case..
| (6.1) |
Initially, these constraints are satisfied, which provide us with 10 ODEs for the modulation variables. By solving these ODEs and appropriately selecting the modulation variables, one can ensure that (6.1) holds for later values of . Substituting (6.1) into (3.36) and evaluating at yields the following set of equations:
| (6.2) | ||||
| (6.3) | ||||
| (6.4) | ||||
| (6.5) | ||||
| (6.6) |
Evaluating and at leads to
| (6.7) | ||||
| (6.8) | ||||
| (6.9) | ||||
| (6.10) | ||||
| (6.11) | ||||
| (6.12) |
and
| (6.13) |
for . It follows from (6.5) that171717The estimates of and in Lemma5.5 are not enough to recover the bootstrap assumptions for the modulation variables.
| (6.14) | ||||
| (6.15) |
where is the following matrix:
| (6.16) |
Note that (4.50) and the property , which implies
| (6.17) |
Therefore,
| (6.18) |
estimates
It follows from (6.3) that
| (6.19) |
If the damping term vanishes, then , which resulting in bounds in the estimates of . Here we investigate the impact of the damping term and thus consider the following ODE:
| (6.20) |
which gives us
| (6.21) |
and then
| (6.22) |
Therefore,
- •
-
•
if 181818If , then the damping term vanishes and this case is automatically satisfied, which implies for standard compressible Euler equations with the initial data given by Lemma4.1, shock formation is inevitable for sufficiently small ., then , which implies a shock forms at . Furthermore, the shock time is shifted compared with the work in [4].
estimates
It follows from (6.2) that
| (6.23) | ||||
| (6.24) | ||||
| (6.25) |
which implies that
| (6.26) |
Since as , . Then, it follows that . Therefore,
| (6.27) |
Therefore, one can conclude that if is positive, the wave amplitude will decay as increases, approaching at the shock point while if is negative, the wave amplitude will grow as increases.
estimates
It follows from the definition of (3.29), the bootstrap assumptions(4.45),(4.46) and(6.18) that191919Different form the equations(6.2)-(6.4), we don’t postulate the precise value for . So, one can not obtain the estimates for directly from the equation(6.5) as well as the estimates for . The use for (6.5)-(6.6) is to derive the accurate estimates for and (see (6.18)).
| (6.28) |
Note that the location of shock is defined as . Then, it follows that
| (6.29) | ||||
| (6.30) |
which is independent of . Therefore, the damping effect doesn’t shift the shock location.
, estimates
It follows from (6.9) and (6.4) that
| (6.31) |
It follows from the definition of (3.7) that
| (6.32) |
These together with Lemma5.6 lead to
which implies202020One also obtains .
| (6.33) | ||||
| (6.34) |
due to the bootstrap assumptions(4.38), (4.45)-(4.47), where the estimates are independent of . Therefore, the damping term does not affect the blow up direction.
It follows from (6.12) that
| (6.35) |
which implies
| (6.36) |
due to Lemma5.5, 5.3, the bootstrap assumptions(4.36),(4.37) and (4.45).
Remark 6.1.
The equations (6.2)-(6.13) give system of ODEs for the modulation variables , where the coefficients are at least due to the bootstrap assumptions. Therefore, unique existence for the modulation variables is guaranteed in a small time and then one can determine the evolution of these variables for later .
6.1 Damping effect to the modulation variables
In conclusion,
-
•
if , then for fixed (initial small data)222222Note that measures the maximum of ., the damping effect is strong enough to prevent the shock formation while for fixed , initial small data leads to a global solution. Therefore, Therefore, a global solution can be obtained in both the self-similar coordinates and the physical variables. In this case (see also (4.65)),
(6.37) -
•
If , the damping effect is so weak that a shock forms in finite time for fixed while for fixed , the initial large data leads to the shock formation in finite time. In this case, one can explicitly compute the shock time and location . While the shock location and direction remain unchanged, the damping effect shifts the shock time and alters the wave amplitude compared with the undamped case, with the variation in shift or change depending on the sign of . In particular, if is positive, the damping term will delay the shock formation and reduce the wave amplitude. Conversely, if is negative, the (anti)-damping term will lead to an immediate shock and amplify the wave amplitude.
7 Bounds on Lagrangian trajectories and vorticity variation
Define Lagrangian flows as follows:
| (7.1) | ||||
| (7.2) | ||||
| (7.3) |
Denote to be the trajectory of either or emanating from at time , i.e., , The following lemma recovers the bootstrap assumption (4.42).
Lemma 7.1.
Let be either or . Then
| (7.4) | ||||
| (7.5) |
for all
PROOF:.
7.1 Lower bounds for the Lagrangian trajectories
Proposition 7.1.
-
•
Let and . Let also . Then, the trajectory moves away from the origin at an exponential rate with
(7.10) -
•
Let be either or . Then, for any , there exists an such that
(7.11) by choosing suitably large.
Remark 7.1.
Note that the Lagrangian trajectories of rapidly approach spatial infinity with an exponential growth, which allows one to utilize the spatial decay of different damping and forcing terms to achieve integrable time decay. Furthermore, the estimates of depends on the distance of the initial position, while do not exhibit such dependence. This distinction requires us to estimate separately in various regions. Different from the work in[4], the first component of the Lagrangian trajectory of may decrease initially but then exhibit exponential growth after a short period due to the damping effect, while the other two components do not.
PROOF:.
- (1)
-
(2)
Suppose . Then, it suffices to prove , i.e., or . It can be shown by Gronwall inequality that the former case is contradict to the assumption 232323If so, then provided , which can be integrated to show by taking suitably.. To show , it suffices to show
(7.15) provided . It follows from Lemma(5.5) that
provided , and similarly for . Integrating (7.15) from to yields
(7.16) To finish the proof, it suffices to show the existence of and there are following two cases.
-
–
If , then take .
-
–
If , since , then there exists an such that where is independent of . Then, integrating (7.15) from to leads to
(7.17)
-
–
The following lemma is the key lemma of the function .
Lemma 7.2.
Let be defined in section4.1. Then, the following properties hold.
-
•
Let . Suppose one of the following the conditions holds:
(7.18) (7.19) Then,
(7.20) where and the implicit constant only depends on and but not on .
-
•
Let be either or . Suppose one of the following the conditions holds:
(7.21) (7.22) Then,
(7.23) where and the implicit constant only depends on .
PROOF:.
Suppose (7.18) hold. If , then it follows from Proposition7.1 that
| (7.24) |
while if , it holds that
| (7.25) |
due to remark4.6. Direct computation yields, in either case, . Suppose (7.19) hold. Then, it follows from Proposition7.1 that
Suppose (7.21) hold. Then with or can be derived in a similar way as in . If (7.22) is satisfied, then it follows from (7.11) that . Then, there are the following two cases.
-
Case1
If , then
-
Case2
If , then
7.2 Vorticity bounds and variation
We now establish the bounds for the specific vorticity. Recall the equation for the specific vorticity :
| (7.26) |
Decompose (7.26) along the tangential direction as follows.
| (7.27) | ||||
| (7.28) |
where
with the bounds . Similarly, one has
with the bounds . It follows from the definition of that along normal direction ,
| (7.29) |
which implies
| (7.30) |
Define the Lagrangian flow associated to as follows:
| (7.31) |
Along , denote
| (7.32) |
Then, (7.27) and (7.28) can be written as
| (7.33) | ||||
| (7.34) |
That is,
| (7.35) |
Let . Then, by the estimates for above and (7.30), satisfies:
| (7.36) |
which can be integrated to obtain
| (7.37) |
where are the integrals given in order. For the term \@slowromancapi@, it can be computed as
| (7.38) |
For the term \@slowromancapii@, it follows from the bootstrap assumptions (4.47) and (4.54) that and then
| \@slowromancapii@ | |||
where in the second step, the relation between and is used. The estimates for term \@slowromancapiii@ is the same as \@slowromancapii@. Therefore, it holds that
| (7.39) |
Proposition 7.2.
(Concentration of vorticity on non-blow up direction) The following bounds for the specific vorticity hold
| (7.40) | ||||
| (7.41) |
Moreover, as , . Therefore,
-
•
If , the instantaneous shock will lead to the vorticity increasing;
-
•
if , the delayed shock will lead to the dissipation of the vorticity;
-
•
if , then one obtains the global solution and the exponential decay for the vorticity.
7.3 Initial region leads to the shock formation
Recall the Lagrangian flows in self-similar coordinates , , . The corresponding Lagrangian flows in physical space are defined as , , 252525Precisely, is defined by , and similar for and ., which are related with , , as follows.
| (7.42) | ||||
| (7.43) | ||||
| (7.44) |
with the initial condition
| (7.45) |
Lemma 7.3.
Let be either , or emanating from the initial point . If , then it holds that
| (7.46) |
In particular, for or , the following bounds hold
| (7.47) | ||||
| (7.48) |
That is, if one changes the initial data outside the above region, the shock location and shock time won’t change.
PROOF:.
Letting in the identity yields
| (7.49) |
Note that
| (7.50) | ||||
| (7.51) |
Then,
- •
- •
8 Recover the Bootstrap assumptions for the self-similar variables
8.1 Recover the Bootstrap assumptions for in
8.1.1 The case for
8.1.2 The case for
In this case, the sign of the damping terms is not definite. As we are examining estimates in the vicinity of , the behavior of is predominantly influenced by the value of It follows from (6.1) and (5.33) that
| (8.4) |
Evaluating equation(3.49) at for yields
| (8.5) |
Then, it follows from Lemma(5.6), (4.41) and (8.3) which evaluated at that
| (8.6) |
Integrating from to leads
| (8.7) |
with for sufficiently small . Therefore, for , it holds that
which recovers the Bootstrap assumption (4.48) for . The estimates for the case can be recovered in the same procedure due to (8.4).
8.2 Weighted estimates for recovering the Bootstrap assumptions for
We introduce the following framework to recover the bootstrap assumptions for . Let be any one of or with . Note that satisfies the following type equation:
| (8.8) |
Multiplying on both sides leads to
| (8.9) |
where is the damping term given by
It follows from Lemma7.2,5.5 and the bootstrap assumption(4.54) that
| (8.10) |
Therefore, applying Gronwall inequality to (8.9) yields
which implies
| (8.11) |
Note that for , the term in (8.11) does not contribute to the estimates for so one can omit this term.
-
•
For or with , , take , and 262626Actually equals to the exactly value of the exponent in the bootstrap assumptions.. Then, it follows from Lemma7.2 that
(8.12) Furthermore, due to Lemma5.6 and 7.2, it holds that
(8.13) Remark 8.1.
The above implicit constant may depend on (for example, in the case of , but it strictly less than the constant in the corresponding bootstrap assumptions.
Therefore,
which recovers the bootstrap assumptions by standard computation.
- •
-
•
For or with , we divide the region of into: and by following the remark4.7. For the initial value in(8.11), due to the estimate(7.10), it holds that
-
–
for and , there exist a pair and such that . Moreover,
-
–
For and , there exist a pair and such that . Moreover,
In the following, we take as an example to recover the assumption for on and the proofs for others are similar. In this case, taking with in (8.9) leads to
(8.16) where
Note that and , which implies Then, (8.16) leads to
(8.17) Then, it follows from Lemma5.6 and 7.2 that
(8.18) due to the estimate
(8.19) There are the following cases.
-
–
In the region ,
-
(1)
if , then and by the initial data assumptions, it holds that
(8.20) -
(2)
while if , then , and one are able to obtain by using (4.48) for
In conclusion, for , it holds that
(8.21) -
(1)
-
–
In the region ,
-
(1)
if , then and by the initial data assumptions, it holds that
(8.22) -
(2)
while if , then and it follows from (8.21) that
-
(1)
Hence, one recovers the bootstrap assumptions for in the region .
-
–
To deal with the case , one uses the following lemma.
Lemma 8.1.
The following identities for hold.
| (8.23) | ||||
| (8.24) | ||||
| (8.25) | ||||
| (8.26) |
As a consequence, it follows from Proposition7.2 and bootstrap assumptions(LABEL:pagaZ)-(LABEL:pagaallyW) that
| (8.27) |
which recovers the bootstrap assumptions for .
9 The energy estimates
By far, to complete the proof for the main theorem, it suffices to prove the energy estimate prop(5.1), which only relies on the Bootstrap assumptions. To this end, introduce the following semi-norm:
| (9.1) |
where is a constant to absorb the various coefficients. Obviously,
| (9.2) |
due to the estimate Taking for to the system (3.42) yields the following equations
| (9.3) | ||||
| (9.4) | ||||
| (9.5) | ||||
where
| (9.6) |
and the forcing terms are given as
| (9.7) | ||||
| (9.8) | ||||
| (9.9) | ||||
Then, applying the standard Freidrich’s energy estimates leads to the following proposition.
Proposition 9.1.
There exist a universal constant such that the following energy inequality holds
| (9.10) | |||
| (9.11) |
PROOF:.
Multiplying , , to respectively, adding them up, integrating over and using the skew-symmetric of lead to
| (9.12) |
where the second line of (9.12) denoted to be term I, the third line of (9.12) denoted to be term II and the fourth line and fifth line denoted to be term III.
-
•
For the damping term I, it holds that
-
•
For the term II, it can be bounded directly as
-
•
For the term III, integrating by parts leads to
Taking summation for (9.12) with and combing the above results yield
| (9.13) |
where
| (9.14) |
Here the constant can be taken as a universal constant by choosing large enough.
For the forcing terms in (9.12), one has the following lemma.
Lemma 9.1.
Let be sufficiently large and . For , there exists a universal constant such that
| (9.15) | ||||
| (9.16) | ||||
| (9.17) |
by taking sufficiently small in terms of .
PROOF:.
Decompose the forcing terms as
| (9.18) |
where the index and represent the terms of order of derivatives equal to and , respectively. Precisely272727In the following, is a lower order term (l.o.t) compared with means where and .,
where
where is a l.o.t compared with .
where are the terms given in order and is a l.o.t compared with .
And is a l.o.t compared with.
where are the terms given in order and is a l.o.t compared with .
In the following, the proof for (9.15) will be given and the proofs for (9.16) and (9.17) are the same. For the first term in , note that and
| (9.19) |
which implies
For the second term, note that
| (9.20) |
Then, it follows from Lemma4.2
| (9.21) |
| (9.22) |
Therefore, this term can be bounded as
| (9.23) |
To sum up, it holds that
| (9.24) |
For the first term in , it can be bounded by using same technique as estimating and then
For the second term, note that , and
| (9.25) |
Then,
| (9.26) |
| (9.27) |
Therefore, it can be bounded as
| (9.28) |
To sum up, for the terms of order , they can be bounded as
| (9.29) |
For the first term in , the following term will be estimated
| (9.30) |
while the estimates for the term are similar. Note that
| (9.31) |
Then, it follows from Lemma4.3 that
| (9.32) |
For the second derivatives terms in(9.32), it follows from Lemma5.2 and 5.5 that
| (9.33) |
which implies
Therefore,
| (9.34) |
Collecting the above results leads to
| (9.35) |
For the term , note that
| (9.36) |
and
| (9.37) |
Then, it holds that
| (9.38) |
due to Lemma4.3. Therefore,
| (9.39) |
In conclusion, collecting (9.29), (9.35) and (9.39) yields
| (9.40) |
Then, there exists a universal constant such that
| (9.41) |
due to Proposition9.1 and Lemma5.6. Then, by taking large enough and Gronwall inequality, one obtains
| (9.42) |
Therefore, the bounds for is the direct consequence of (9.42) and the following lemma.
Lemma 9.2.
For sufficiently small in terms of , the following bounds hold
| (9.43) |
for all . As a consequence,
| (9.44) |
PROOF:.
To prove this lemma, due to the estimates and the equivalence of and norm of , it suffices to prove that there exists a universal constant and a small such that
| (9.45) | ||||
| (9.46) |
For (9.45), it can be proved by induction. When , . Assume (9.45) hold for . Then, for , due to , it holds that
For (9.46), it follows from Moser inequality that
References
- [1] Tristan Buckmaster and Sameer Iyer. Formation of Unstable Shocks for 2D Isentropic Compressible Euler. Communications in Mathematical Physics, 389(1):197–271, January 2022.
- [2] Tristan Buckmaster, Steve Shkoller, and Vlad Vicol. Formation of point shocks for 3D compressible Euler. arXiv e-prints, page arXiv:1912.04429, December 2019.
- [3] Tristan Buckmaster, Steve Shkoller, and Vlad Vicol. Formation of shocks for 2D isentropic compressible Euler. arXiv e-prints, page arXiv:1907.03784, July 2019.
- [4] Tristan Buckmaster, Steve Shkoller, and Vlad Vicol. Shock formation and vorticity creation for 3d Euler. arXiv e-prints, page arXiv:2006.14789, June 2020.
- [5] Demetrios Christodoulou. The Formation of Shocks in 3-Dimensional Fluids, volume 9. European Mathematical Society, 2007.
- [6] Demetrios Christodoulou and Shuang Miao. Compressible Flow and Euler’s Equations, volume 9. International Press Somerville, MA, 2014.
- [7] Charles Collot, Tej-Eddine Ghoul, Slim Ibrahim, and Nader Masmoudi. On singularity formation for the two dimensional unsteady Prandtl’s system. arXiv e-prints, page arXiv:1808.05967, August 2018.
- [8] Charles Collot, Tej-Eddine Ghoul, and Nader Masmoudi. Singularity formation for Burgers equation with transverse viscosity. arXiv e-prints, page arXiv:1803.07826, March 2018.
- [9] Jens Eggers and Marco A Fontelos. The role of self-similarity in singularities of partial differential equations. Nonlinearity, 22(1):R1–R44, dec 2008.
- [10] Yoshikazu Giga and Robert V. Kohn. Asymptotically self-similar blow-up of semilinear heat equations. Communications on Pure and Applied Mathematics, 38(3):297–319, 1985.
- [11] Ling Hsiao and Tai-Ping Liu. Convergence to nonlinear diffusion waves for solutions of a system of hyperbolic conservation laws with damping. Communications in Mathematical Physics, 143(3):599–605, 1992.
- [12] S Kawashima. Dissipative structure and entropy for hyperbolic systems of balance laws. Archive for Rational Mechanics and Analysis, 174(1):345–364, 2004.
- [13] Shuichi Kawashima. Systems of a hyperbolic-parabolic composite type, with applications to the equations of magnetohydrodynamics. 1984.
- [14] Jonathan Luk and Jared Speck. Shock formation in solutions to the 2d compressible euler equations in the presence of non-zero vorticity. Inventiones mathematicae, 214(1):1–169, 2018.
- [15] Jonathan Luk and Jared Speck. The stability of simple plane-symmetric shock formation for 3D compressible Euler flow with vorticity and entropy. arXiv e-prints, page arXiv:2107.03426, July 2021.
- [16] Pierangelo Marcati. Optimal convergence rates to diffusion waves for solutions of the hyperbolic conservation laws with damping. Journal of Mathematical Fluid Mechanics, 7(1):224–240, 2005.
- [17] Pierangelo Marcati and Ming Mei. Convergence to nonlinear diffusion waves for solutions of the initial boundary problem to the hyperbolic conservation laws with damping. Quarterly of Applied Mathematics, 58(4):763–784, 2000.
- [18] Pierangelo Marcati and Albert Milani. The one-dimensional darcy’s law as the limit of a compressible euler flow. Journal of Differential Equations, 84(1):129–147, 1990.
- [19] Frank Merle and Pierre Raphaël. The blow-up dynamic and upper bound on the blow-up rate for critical nonlinear Schrödinger equation. Ann. Math. (2), 161(1):157–222, 2005.
- [20] Frank Hatem Merle and Hatem Zaag. On the stability of the notion of non-characteristic point and blow-up profile for semilinear wave equations. Communications in Mathematical Physics, 333:1529–1562, 2015.
- [21] Takaaki Nishida. Nonlinear hyperbolic equations and related topics in fluid dynamics. 1978.
- [22] Kenji Nishihara, Weike Wang, and Tong Yang. Lp-convergence rate to nonlinear diffusion waves for p-system with damping. Journal of Differential Equations, 161(1):191 – 218, 2000.
- [23] Kenji Nishihara, Weike Wang, and Tong Yang. Lp-convergence rate to nonlinear diffusion waves for p-system with damping. Journal of Differential Equations, 161(1):191–218, 2000.
- [24] Ronghua Pan and Kun Zhao. The 3d compressible euler equations with damping in a bounded domain. Journal of Differential Equations, 246(2):581–596, 2009.
- [25] Miao Shuang and Yu Pin. On the formation of shocks for quasilinear wave equations. Inventiones mathematicae, 207(0):697–831, 2017.
- [26] Thomas C. Sideris, Becca Thomases, and Dehua Wang. Long time behavior of solutions to the 3d compressible euler equations with damping. Communications in Partial Differential Equations, 28(3-4):795–816, 2003.
- [27] M Slemrod. Damped conservation laws in continuum mechanic. Nonlinear Analysis and Mechanic, III(1):135–173, 1978.
- [28] Zhong Tan and Guochun Wu. Large time behavior of solutions for compressible euler equations with damping in r3. Journal of Differential Equations, 252(2):1546–1561, 2012.
- [29] Weike Wang and Tong Yang. The pointwise estimates of solutions for euler equations with damping in multi-dimensions. Journal of Differential Equations, 173(2):410 – 450, 2001.