Shifted $\bm{\mu}$-hybrid inflation, gravitino dark matter, and
observable gravity waves

In its simplest form supersymmetric (SUSY) hybrid inflation Dvali:1994ms ; Copeland:1994vg is associated with a gauge symmetry breaking $G\rightarrow H$, and it employs a minimal renormalizable superpotential $W$ and a canonical Kähler potential $K$. Radiative corrections and soft SUSY breaking terms together play an essential role Senoguz:2004vu ; Rehman:2009nq ; Pallis:2013dxa ; Buchmuller:2014epa in the inflationary potential that yields a scalar spectral index in full agreement with the Planck data Akrami:2018odb . In this minimal model the symmetry breaking $G\rightarrow H$ occurs at the end of inflation, and the symmetry breaking scale is predicted to be of the order of $(2-3)\times 10^{15}{\rm\ GeV}$ Dvali:1994ms ; Senoguz:2004vu ; Rehman:2009nq ; Pallis:2013dxa ; Buchmuller:2014epa . One simple extension of this minimal model retains a minimal $W$ but invokes a nonminimal $K$ BasteroGil:2006cm , such that the correct scalar spectral index is obtained without invoking the soft SUSY breaking terms. Nonminimal Kähler potentials are also used to realize symmetry breaking scales comparable to the grand unified symmetry (GUT) scale $M_{\text{GUT}}$ ($\sim 2\times 10^{16}{\rm\ GeV}$) urRehman:2006hu , and to predict possibly observable gravity waves Rehman:2010wm ; Civiletti:2014bca .

If the symmetry breaking $G\rightarrow H$ produces topological defects such as magnetic monopoles, a more careful approach is required in order to circumvent the primordial monopole problem. The first such example is provided by the so-called ‘shifted-hybrid inflation’ Jeannerot:2000sv ; Jeannerot:2001xd , in which the monopole producing Higgs field actively participates in inflation such that, during inflation, $G$ is broken to $H$ and the monopoles are inflated away.

In this paper we explore inflation and reheating in the framework of the gauge symmetry $SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}$ ($G_{\text{4-2-2}}$) Pati:1974yy . A SUSY model based on this symmetry including hybrid inflation was first explored in Ref. King:1997ia . However, the primordial monopole problem was not resolved, but it was subsequently addressed and successfully rectified in Ref. Jeannerot:2000sv based on shifted hybrid inflation. In the model proposed here, we employ the mechanism invented in Refs. King:1997ia ; Dvali:1997uq for generating the MSSM $\mu$ term, and we exploit shifted hybrid inflation to overcome the monopole problem. We implement this scenario using both minimal and nonminimal Kähler potentials, and address in both cases important issues related to the gravitino problem Ellis:1984eq . For a discussion of leptogenesis via right-handed neutrinos in models where the dominant inflaton decay channel yields higgsinos, see Ref. Lazarides:1998qx .

The plan of the paper is as follows: In Sec. II, we present the SUSY $G_{\text{4-2-2}}$ model including the superfields, their charge assignments, and the superpotential which respects a $U(1)_{R}$ symmetry. In Sec. III, the inflationary setup is described. This includes the scalar potential for global SUSY as well as the one including supergravity (SUGRA). The shifted $\mu$-hybrid inflation ($\mu$HI) scenario with minimal Kähler potential and its compatibility with the gravitino constraint Okada:2015vka is studied in Sec. IV. The analysis is extended by employing a nonminimal Kähler potential in Sec. V, discussing again the gravitino problem and the bounds it imposes on reheat temperature, and focusing on solutions with observable gravity waves. Our conclusions are summarized in Sec. VI.

The matter and Higgs superfields of the SUSY $G_{\text{4-2-2}}$ model with their representations, transformations under $G_{\text{4-2-2}}$, decompositions under $G_{SM}$, and charge assignments are shown in Table 1. The matter superfields $F_{i}$ and $F_{i}^{c}$ belong in the following representations of $G_{\text{4-2-2}}$:

	$\displaystyle F_{i}=(4,2,1)\equiv\left({\begin{array}[]{cccc}u_{ir}&u_{ig}&u_{ib}&\nu_{il}\\ d_{ir}&d_{ig}&d_{ib}&e_{il}\\ \end{array}}\right),$		(3)
	$\displaystyle F^{c}_{i}\!=(\overline{4},1,2)\equiv\left({\begin{array}[]{cccc}u^{c}_{ir}&u^{c}_{ig}&u^{c}_{ib}&\nu^{c}_{il}\\ d^{c}_{ir}&d^{c}_{ig}&d^{c}_{ib}&e^{c}_{il}\\ \end{array}}\right),$		(6)

where the index i(= 1, 2, 3) denotes the three families of quarks and leptons, and the subscripts $r,\ g,\ b,\ l$ are the four colors in the model, namely red, green, blue, and lilac. The GUT Higgs superfields $H^{c}$ and $\overline{H^{c}}$ are represented as follows:

	$\displaystyle H^{c}\,=(\overline{4},1,2)\equiv\left({\begin{array}[]{cccc}u^{c}_{Hr}&u^{c}_{Hg}&u^{c}_{Hb}&\nu^{c}_{Hl}\\ d^{c}_{Hr}&d^{c}_{Hg}&d^{c}_{Hb}&e^{c}_{Hl}\\ \end{array}}\right),$		(9)
	$\displaystyle\overline{H^{c}}\!=(4,1,2)\equiv\left({\begin{array}[]{cccc}\overline{u^{c}_{Hr}}&\overline{u^{c}_{Hg}}&\overline{u^{c}_{Hb}}&\overline{\nu^{c}_{Hl}}\\ \ \overline{d^{c}_{Hr}}&\overline{d^{c}_{Hg}}&\overline{d^{c}_{Hb}}&\overline{e^{c}_{Hl}}\\ \end{array}}\right),$		(12)

and acquire nonzero vacuum expectation values (vevs) along the right-handed sneutrino directions, that is $|\langle\nu^{c}_{Hl}\rangle|=|\langle\overline{\nu^{c}_{Hl}}\ \rangle|=v\neq 0$, to break the $G_{\text{4-2-2}}$ gauge symmetry to the standard model (SM) gauge symmetry ($G_{SM}=SU(3)_{c}\times SU(2)_{L}\times U(1)_{Y}$), around the GUT scale ($\sim 2\times 10^{16}{\rm\ GeV}$), while preserving low scale SUSY Shafi:1998yy . The electroweak breaking is triggered by the electroweak Higgs doublets, $h_{u}$ and $h_{d}$, which reside in the bidoublet Higgs superfield $h$ represented as follows:

$$h=(1,2,2)\equiv(h_{u}\ \ h_{d})=\left({\begin{array}[]{cc}h^{+}_{u}&h^{0}_{d}\\ h^{0}_{u}&h^{-}_{d}\\ \end{array}}\right).\\$$

(13)

Note that such doublets can remain light because of appropriate discrete symmetries lightdoublets . A gauge singlet chiral superfield $S=(1,1,1)$ is introduced, which triggers the breaking of $G_{\text{4-2-2}}$ and whose scalar component plays the role of the inflaton. A sextet Higgs superfield $G=(6,1,1)$, which under the SM splits into the color-triplet Higgs superfields $g=(3,1,-1/3)$ and $g^{c}=(\overline{3},1,1/3)$, is introduced to provide superheavy masses to the color-triplet pair $d^{c}_{H}$ and $\overline{d^{c}_{H}}$ King:1997ia .

The main part of the superpotential of our model that is compatible with $G_{\text{4-2-2}}$ and the R-symmetry $U(1)_{R}$ is given by

	$\displaystyle W$	$\displaystyle=\kappa S(\overline{H^{c}}H^{c}-M^{2})+\lambda Sh^{2}$
		$\displaystyle-S\left(\beta_{1}\frac{(\overline{H^{c}}H^{c})^{2}}{\Lambda^{2}}+\beta_{2}\frac{(\overline{H^{c}})^{4}}{\Lambda^{2}}+\beta_{3}\frac{(H^{c})^{4}}{\Lambda^{2}}\right)$
		$\displaystyle+\lambda_{ij}F^{c}_{i}F_{j}h+\gamma_{ij}\frac{\overline{H^{c}}\ \overline{H^{c}}}{\Lambda}F^{c}_{i}F^{c}_{j}$
		$\displaystyle+a\,GH^{c}H^{c}+b\,G\overline{H^{c}}\ \overline{H^{c}},$		(14)

where $\kappa,\ \lambda,\ \beta_{1,2,3},\ \lambda_{ij},\ \gamma_{ij},\ a,\text{ and }b$ are real and positive dimensionless couplings and $M$ is a mass parameter of the order of $M_{\rm GUT}$. We assume the superheavy scale $\Lambda$ to be in the range $10^{16}{\rm\ GeV}$$\lesssim\Lambda\lesssim m_{P}$, where $m_{P}$ denotes the reduced Planck scale ($2.4\times 10^{18}{\rm\ GeV}$). The first three terms in the superpotential are of the standard $\mu$HI case as discussed in Refs. Okada:2015vka ; Rehman:2017gkm . The first two and the fourth term characterize the ‘shifted case’ by providing additional inflationary tracks to avoid the monopole problem. The third term $\lambda Sh_{u}h_{d}$ yields the effective $\mu$ term. Indeed assuming gravity-mediated SUSY breaking Chamseddine:1982jx ; Linde:1997sj , the scalar component of $S$ acquires a nonzero vev proportional to the gravitino mass $m_{3/2}$ and generates a $\mu$ term with $\mu=-\lambda m_{3/2}/\kappa$, thereby resolving the MSSM $\mu$ problem Dvali:1997uq . The $\lambda_{ij}$-terms contain the Yukawa couplings, and hence provides masses for fermions. The $\gamma_{ij}$-terms yield large right-handed neutrino masses, needed for the see-saw mechanism. The other possible couplings similar to $\gamma_{ij}$-terms which are allowed by the symmetries are $FFH^{c}H^{c}$, $FF\overline{H^{c}}\ \overline{H^{c}}$, and $F^{c}F^{c}H^{c}H^{c}$. The last two terms in the superpotential involving the sextuplet superfield $G$ are included to provide superheavy masses to $d^{c}_{H}$ and $\overline{d^{c}_{H}}$.

This model can be embedded in a realistic supersymmetric $SO(10)$ GUT model along the same lines as in Ref. Kyae:2005vg , where the matter superfields $F$ and $F^{c}$ are combined in a $16$, the Higgs superfield $H^{c}$ together with a (4,2,1) in a $16_{H}$, and the $\overline{H^{c}}$ together with a ($\overline{4}$,2,1) in a $\overline{16_{H}}$. The bidoublet $h$ together with a sextet will reside in a $10_{h}$. An additional Higgs superfield such as 210 or 54 will be needed to break $SO(10)$ to $G_{\text{4-2-2}}$.

It is important to mention here that the matter-parity symmetry $\mathbb{Z}_{2}^{mp}$, which is usually invoked to forbid rapid proton decay operators at renormalizable level, is contained in $U(1)_{R}$ as a subgroup. The superpotential $W$ is invariant under $\mathbb{Z}_{2}^{mp}$ and this symmetry remains unbroken. There is no domain wall problem and the lightest SUSY particle (LSP) is stable and consequently a plausible candidate for dark matter (DM).

The relevant part of the superpotential for shifted $\mu$HI contains the terms

$$\delta W=\kappa S(\overline{H^{c}}H^{c}-M^{2})+\lambda Sh^{2}-\xi\frac{\kappa S(\overline{H^{c}}H^{c})^{2}}{M^{2}},$$

(15)

where $\xi=\beta_{1}M^{2}/\kappa\Lambda^{2}$ is a dimensionless parameter. We ignore the $\beta_{2,3}$-terms in our future discussions as they become irrelevant in the $D$-flat direction, that is the direction where the $D$-term contributions vanish (i.e. with $|\nu_{H}^{c}|=|\overline{\nu_{H}^{c}}|$ and all other components zero). For simplicity, the superfields and their scalar components will be denoted by the same notation.

The global SUSY minimum obtained from Eq. (15) is given as

$$\langle S\rangle\!=\!0,\ \ \ \ \langle h\rangle\!=\!0,\ \ \ \ v^{2}\!=\!\langle\overline{H^{c}}H^{c}\rangle\!=\!\frac{M^{2}}{2\xi}(1\!\pm\sqrt{1\!-\!4\xi}),$$

(16)

which requires that $\xi\leq 1/4$ for real values of $v$. Note that, for $\xi>1/4$, the global SUSY vacuum lies at complex values of the fields $H^{c}$, $\overline{H^{c}}$, but we will not consider this case in this paper.

The global SUSY scalar potential obtained from the superpotential in Eq. (15) is

	$\displaystyle V$	$\displaystyle=\Big{|}\kappa\{\overline{H^{c}}H^{c}-M^{2}-\xi\frac{(\overline{H^{c}}H^{c})^{2}}{M^{2}}\}+\lambda h^{2}\Big{|}^{2}+\lambda^{2}h^{2}|S|^{2}$
		$\displaystyle\!+\!\kappa^{2}|S|^{2}(|H^{c}|^{2}\!+\!|\overline{H^{c}}|^{2})\Big{|}1\!-\!2\xi\frac{\overline{H^{c}}H^{c}}{M^{2}}\Big{|}^{2}\!+\!D\text{-terms,}$		(17)

where $|h|^{2}=|h_{u}|^{2}+|h_{d}|^{2}$. The $D$-flatness requirement implies that $\overline{H^{c}}=e^{i\theta}H^{c*}$ and $h_{u}^{i}=e^{i\varphi}\epsilon_{ij}h_{d}^{j*}$, where $\theta$ and $\varphi$ are invariant angles and $\epsilon_{ij}$ is the $2\times 2$ antisymmetric matrix with $\epsilon_{12}=1$. We have proved that, for $h=0$ and $\xi\leq 1/4$, the potential in Eq. (17) is minimized for $\theta=0$ in all cases including the shifted inflationary valley – see below. Therefore, for our purposes here, we can fix $\theta=0$. Moreover, one can show that, on the shifted path, the potential for $h\neq 0$ is minimized at $\varphi=\pi$. Under these circumstances, the scalar potential along the $D$-flat direction takes the form:

	$\displaystyle V$	$\displaystyle=\Big{|}\kappa\big{(}|H^{c}|^{2}-M^{2}-\xi\frac{|H^{c}|^{4}}{M^{2}}\big{)}-\lambda|h_{d}|^{2}\Big{|}^{2}$
		$\displaystyle+2\lambda^{2}|h_{d}|^{2}|S|^{2}+2\kappa^{2}|S|^{2}|H^{c}|^{2}\Big{|}1-2\xi\frac{|H^{c}|^{2}}{M^{2}}\Big{|}^{2},$		(18)

which on the shifted path is minimized for $h=0$ provided that $\lambda\geq 2\kappa$. This inequality guarantees the stability of the shifted path at $h=0$ and we can safely set $h$ equal to zero from now on. Rotating the complex field $S$ to the real axis by suitable transformations, we can identify the normalized real scalar field $\sigma=\sqrt{2}S$ with the inflaton. Introducing the dimensionless fields

$$w=\frac{|S|}{M},\ \ \ u=\frac{|H^{c}|}{M},$$

(19)

the normalized potential $\widetilde{V}\equiv V/\kappa^{2}M^{4}$ takes the form

$$\widetilde{V}=(u^{2}-1-\xi u^{4})^{2}+2w^{2}u^{2}(1-2\xi u^{2})^{2}.$$

(20)

The extrema of the above potential with respect to $u$ are given as:

	$\displaystyle u_{1}$	$\displaystyle=\ 0\,,{}$		(21a)
	$\displaystyle u_{2}$	$\displaystyle=\pm\frac{1}{\sqrt{2\xi}}\,,{}$		(21b)
	$\displaystyle u^{\pm}_{3}\!$	$\displaystyle=\!\frac{1}{\sqrt{2\xi}}\sqrt{1\!-\!6w^{2}\xi\pm\sqrt{\!-\!4\xi\!+\!36\xi^{2}w^{4}\!-\!8\xi w^{2}\!+\!1}}.{}$		(21c)

These extrema can be visualized with the help of the potential $\widetilde{V}(u,w)$, plotted in Fig. 1, for various values of the parameter $\xi$.

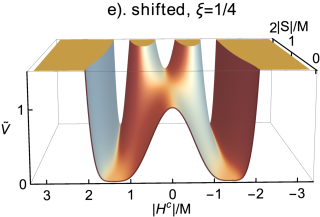
In Fig. 1, the standard $\mu$HI case with $\xi=0$ is reproduced in plot (a). In this case, $u=0$, $w>1$ is the only inflationary valley available. It evolves at $w=0$ into a single pair of global SUSY minima with vev $v=\pm M$. For $\xi\neq 0$, in addition to the standard track at $u=u_{1}$, two shifted local minima appear at $u=u_{2}$ for $w>\sqrt{1/8\xi-1/2}$. In plot (b) for $\xi<1/8$, the shifted tracks lie higher than the standard track. Following Ref. Jeannerot:2000sv , in order to have suitable initial conditions for realizing inflation along the shifted tracks, we assume $\xi\geq 1/8$. The normalized scalar potential $\widetilde{V}$ is shown in plots (c)-(e) for some realistic values of $\xi$, namely for $\xi=1/8$, $\xi=1/6$, and $\xi=1/4$. In the last plot (f) with $\xi>1/4$, we obtain $V_{min}\neq 0$, since the SUSY minimum requires complex values of $\overline{H^{c}}$, $H^{c}$. So for our analysis, it is appropriate to keep $\xi$ within the interval $[1/8,1/4]$.

As the inflaton slowly rolls down the inflationary valley and enters the waterfall regime at $w=\sqrt{1/8\xi-1/2}$, inflation ends due to fast rolling and the system starts oscillating about a vacuum at $w=0$. Note that in the $H^{c}$ direction there are actually two pairs of vacua at [see Eq. (21c)]

$$(u_{3}^{\pm})^{2}\xrightarrow{w=0}v^{2}_{\pm}=\frac{1}{2\xi}[1\pm\sqrt{1-4\xi}].$$

(22)

However, the path leading to $v_{-}$ appears before the one leading to $v_{+}$, as explained in Ref. Jeannerot:2000sv . The necessary slope for realizing inflation in the valley with $w>\sqrt{1/8\xi-1/2}$, $u=u_{2}$, $z=0$ is generated by the inclusion of the one-loop radiative corrections, the SUGRA corrections, and the soft SUSY breaking terms. The one-loop radiative corrections $V_{loop}$, arising as a result of SUSY breaking on the inflationary path, are calculated using the Coleman-Weinberg formula Coleman;1973 :

	$\displaystyle V_{loop}$	$\displaystyle=\frac{1}{64\pi^{2}}\sum_{i}(-1)^{F_{i}}M_{i}^{4}\ln\Big{(}\frac{M_{i}^{2}(S)}{Q^{2}}-\frac{3}{2}\Big{)}$
		$\displaystyle=\kappa^{2}m^{4}\left[\frac{\kappa^{2}}{4\pi^{2}}F(x)+\frac{\lambda^{2}}{4\pi^{2}}F(y)\right],$		(23)

where $F_{i}$ and $M_{i}^{2}$ are the fermion number and squared mass of the ith state. The function $F(x)$ is given by

	$\displaystyle F(x)$	$\displaystyle=\frac{1}{4}[(x^{4}+1)\ln\big{(}\frac{x^{4}-1}{x^{4}}\Big{)}+2x^{2}\ln\Big{(}\frac{x^{2}+1}{x^{2}-1}\Big{)}$
		$\displaystyle+2\ln\Big{(}\frac{2\kappa^{2}m^{2}x^{2}}{Q^{2}}\Big{)}-3],$		(24)

$y=\sqrt{\gamma/2}\ x$ with $\gamma=\lambda/\kappa$, and $x$ is defined in terms of the canonically normalized real inflaton field $\sigma$ as $x=\sigma/m$ with $m^{2}=M^{2}(1/4\xi-1)$. The function $F(y)$ exhibits the contribution of the $\mu$ term in the superpotential $W$, and for $\gamma\gtrsim 1$, is expected to play an important role in the predictions of inflationary observables. The renormalization scale $Q$ is set equal to $\sigma_{0}$, the field value at the pivot scale $k_{0}=0.05\text{ Mpc}^{-1}$ Akrami:2018odb .

The soft SUSY breaking terms are added in the inflationary potential as:

$$V_{soft}=m_{3/2}\big{[}z_{i}\frac{\partial W}{\partial z_{i}}+(A-3)W+h.c.\big{]},$$

(25)

where $A$ is the complex coefficient of the trilinear soft-SUSY-breaking terms.

Trying to reconcile supergravity and cosmic inflation, one runs into the so-called $\eta$ problem which arises as the effective inflationary potential is quite steep. This leads to large inflaton masses on the order of the Hubble parameter $H$ and thus the slow-roll conditions are violated. In hybrid inflationary scenarios, the supergravity corrections can easily be brought under control Lazarides:1996dv ; Panagiotakopoulos:1997ej ; Dvali:1997uq ; Lazarides:1998zf ; Dimopoulos:2011ym . Another potential problem is the appearance of anti-de Sitter vacua. However, in hybrid inflation models, these vacua may be lifted – for examples see Refs. Haba:2005ux ; Wu:2016fzp .

The $F$-term SUGRA scalar potential is evaluated using,

$$V_{SUGRA}=e^{K/m_{P}^{2}}(K_{i\bar{j}}^{-1}D_{z_{i}}WD_{z_{\bar{j}}^{*}}W^{*}-3m_{P}^{-2}|W|^{2}),$$

(26)

where $z_{i}\in\{S,\ H^{c},\ \overline{H^{c}},\ h,\ ...\}$ and

	$\displaystyle K_{ij}$	$\displaystyle\equiv\frac{\partial^{2}K}{\partial z_{i}\partial z^{*}_{j}},$
	$\displaystyle D_{\,z_{i}}\,W\,$	$\displaystyle\equiv\frac{\partial W}{\partial z_{i}}+m_{P}^{-2}\frac{\partial K}{\partial z_{i}}W,$
	$\displaystyle D_{z_{i}^{*}}W^{*}$	$\displaystyle=(D_{z_{i}}W)^{*}.$		(27)

The Kähler potential $K$ is expanded in inverse powers of $m_{P}$:

	$\displaystyle K$	$\displaystyle=K_{c}+\kappa_{S}\frac{|S|^{4}}{4m_{P}^{2}}+\kappa_{H}\frac{|H^{c}|^{4}}{4m_{P}^{2}}+\kappa_{\overline{H}}\frac{|\overline{H^{c}}|^{4}}{4m_{P}^{2}}+\kappa_{h}\frac{|h|^{4}}{4m_{P}^{2}}$
		$\displaystyle+\kappa_{SH^{c}}\frac{|S|^{2}|H^{c}|^{2}}{m_{P}^{2}}+\kappa_{S\overline{H^{c}}}\frac{|S|^{2}|\overline{H^{c}}|^{2}}{m_{P}^{2}}+\kappa_{Sh}\frac{|S|^{2}|h|^{2}}{m_{P}^{2}}$
		$\displaystyle+\kappa_{H^{c}\overline{H^{c}}}\frac{|H^{c}|^{2}|\overline{H^{c}}|^{2}}{m_{P}^{2}}+\kappa_{H^{c}h}\frac{|H^{c}|^{2}|h|^{2}}{m_{P}^{2}}+\kappa_{\overline{H^{c}}h}\frac{|\overline{H^{c}}|^{2}|h|^{2}}{m_{P}^{2}}$
		$\displaystyle+\kappa_{SS}\frac{|S|^{6}}{6m_{P}^{4}}+...~{}~{}~{},$		(28)

where the minimal canonical Kähler potential $K_{c}$ is given by

$$K_{c}=|S|^{2}+|H^{c}|^{2}+|\overline{H^{c}}|^{2}+|h^{2}|.$$

(29)

The inflationary potential along the D-flat direction with $|H^{c}|=|\overline{H^{c}}|$, stabilized along the $h=0$ direction, and incorporating the SUGRA corrections Linde:1997sj , the radiative corrections Dvali:1994ms , and the soft-SUSY-breaking terms Senoguz:2004vu ; Rehman:2009nq , is given by

	$\displaystyle V(x)$	$\displaystyle\simeq V_{SUGRA}+V_{loop}+V_{soft}$
		$\displaystyle\simeq\kappa^{2}m^{4}\Bigg{(}\mathcal{A}+\frac{1}{2}\mathcal{B}\Big{(}\frac{m}{m_{P}}\Big{)}^{2}x^{2}+\frac{1}{4}\mathcal{C}\Big{(}\frac{m}{m_{P}}\Big{)}^{4}x^{4}$
		$\displaystyle+\frac{\kappa^{2}}{4\pi^{2}}F(x)+\frac{\lambda^{2}}{4\pi^{2}}F(y)$
		$\displaystyle+a\frac{m_{3/2}}{\sqrt{2}\kappa m}x+\frac{m_{3/2}^{2}}{2\kappa^{2}m^{2}}x^{2}+\frac{m_{3/2}^{2}M^{2}}{\kappa^{2}m^{4}\xi}\Bigg{)}.$		(30)

Here $\mathcal{A}$, $\mathcal{B}$, and $\mathcal{C}$ are the coefficients of the constant, quadratic, and quartic SUGRA terms, respectively, and are defined in terms of $H_{P}=(M/m_{P})/\sqrt{2\xi}$ as

$$\mathcal{A}\!=\!1\!+\!2c_{0}H_{P}^{2}\!+\!2c_{1}H_{P}^{4},\ \ \,\mathcal{B}\!=\!-\kappa_{S}\!+\!2c_{2}H_{P}^{2},\ \ \,\mathcal{C}\!=\!\frac{\gamma_{S}}{2},$$

(31)

where $\gamma_{S}=1+2\kappa_{S}^{2}-3\kappa_{SS}-7\kappa_{S}/2\$ Civiletti:2011qg . For the inflationary potential along the D-flat and $h=0$ direction, the independently varying parameters $c_{0}$, $c_{1}$, and $c_{2}$ for the nonminimal case are the same as the ones given in Ref. Civiletti:2011qg . Our choice for these parameters will be shown in the relevant sections. The parameter $a$ depends on $\arg S$ as follows:

$$a=2\left|2-A+\frac{A}{2\xi}\right|\cos[\arg S+\arg(2-A+\frac{A}{2\xi})].$$

(32)

Assuming negligible variation in $\arg S$, with $a=-1$, the scalar spectral index $n_{s}$ is expected to lie within the experimental range Rehman:2009nq ; Civiletti:2011qg . This could also be achieved by taking an intermediate-scale, negative soft mass-squared term for the inflaton Rehman:2009yj . But with the nonminimal terms in the Kähler potential, one can also obtain the central value of $n_{s}$ with TeV-scale soft masses even for $a=1$ BasteroGil:2006cm ; urRehman:2006hu . The variation in $\arg S$ with general initial condition has been studied in Refs. Senoguz:2004vu ; urRehman:2006hu ; Buchmuller:2014epa .

The slow-roll parameters are defined by

$$\epsilon\!=\!\frac{m_{p}^{2}}{2m^{2}}\Big{(}\frac{V^{\prime}}{V}\Big{)}^{2}\!,\ \ \eta\!=\!\frac{m_{p}^{2}}{m^{2}}\Big{(}\frac{V^{\prime\prime}}{V}\Big{)},\ \ \zeta^{2}\!=\!\frac{m_{p}^{4}}{m^{4}}\Big{(}\frac{V^{\prime}V^{\prime\prime\prime}}{V^{2}}\Big{)},$$

(33)

where the primes denote derivatives with respect to $x$. The scalar spectral index $n_{s}$, the tensor-to-scalar ratio $r$, the running of the scalar spectral index $dn_{s}/d\ln k$, and the scalar power spectrum amplitude $A_{s}$, to leading order in the slow-roll approximation, are as follows:

	$\displaystyle n_{s}$	$\displaystyle\simeq 1-6\epsilon+2\eta,$		(34a)
	$\displaystyle r$	$\displaystyle\simeq 16\epsilon,$		(34b)
	$\displaystyle\frac{dn_{s}}{d\ln k}$	$\displaystyle\simeq 16\epsilon\eta-24\epsilon^{2}-2\zeta^{2},$		(34c)
	$\displaystyle A_{s}(k_{0})$	$\displaystyle=\frac{1}{12\pi^{2}}\Big{(}\frac{m}{m_{P}}\Big{)}^{2}\Big{|}\frac{V^{3}/{V^{\prime}}^{2}}{m_{P}^{4}}\Big{|}_{x_{0}},$		(34d)

where $A_{s}(k_{0})=2.196\times 10^{-9}$ and $x_{0}$ denotes the value of $x$ at the pivot scale $k_{0}=0.05\text{ Mpc}^{-1}$ Akrami:2018odb . For the numerical estimation of the inflationary predictions, these relations are used up to second order in the slow-roll parameters.

Assuming a standard thermal history, the number of $e$-folds $N_{0}$ between the horizon exit of the pivot scale and the end of inflation is

	$\displaystyle N_{0}$	$\displaystyle=\Big{(}\frac{m}{m_{P}}\Big{)}^{2}\int_{1}^{x_{0}}\Big{(}\frac{V}{V^{\prime}}\Big{)}dx$		(35)
		$\displaystyle=53+\frac{1}{3}\ln\Big{(}\frac{T_{r}}{10^{9}\text{ GeV}}\Big{)}+\frac{2}{3}\ln\Big{(}\frac{\sqrt{\kappa}m}{10^{15}\text{ GeV}}\Big{)}.$

The reheat temperature $T_{r}$ is approximated by

$$T_{r}\approx\sqrt[4]{\frac{90}{\pi^{2}{g_{*}}}}\sqrt{{\Gamma_{S}}{m_{P}}},\\$$

(36)

where $g_{*}=228.75$ for MSSM and $\Gamma_{S}$ is the inflaton decay width. From the $\mu$-term coupling $\lambda Sh^{2}$ in Eq. (15), we see that the inflaton can decay into a pair of Higgsinos $\widetilde{h}_{u}$, $\widetilde{h}_{d}$ with a decay width

$$\Gamma_{S}(S\rightarrow\widetilde{h}_{u}\widetilde{h}_{d})=\frac{\lambda^{2}}{8\pi}m_{\text{infl}},$$

(37)

where

$$m_{\text{infl}}=\sqrt{2}\kappa v\Big{(}1-\frac{2\xi v^{2}}{M^{2}}\Big{)}=2\kappa m\sqrt{1-\sqrt{1-4\xi}}$$

(38)

is the inflaton mass Jeannerot:2000sv . The reheat temperature, the inflaton decay width, and the inflaton mass defined above in Eqs. (36)-(38) are used together with Eq. (35) in order to derive the numerical predictions for the present inflationary scenario.

The inflationary potential corresponding to the minimal Kähler potential $K_{c}$ in Eq. (29) is easily transcribed from Eq. (III) as follows:

	$\displaystyle V(x)$	$\displaystyle\simeq\kappa^{2}m^{4}\Bigg{(}1+2\Big{(}\frac{M}{\sqrt{2\xi}m_{P}}\Big{)}^{2}+2\Big{(}\frac{M}{\sqrt{2\xi}m_{P}}\Big{)}^{4}$
		$\displaystyle+\Big{(}\frac{M}{\sqrt{2\xi}m_{P}}\Big{)}^{2}\Big{(}\frac{m}{m_{P}}\Big{)}^{2}x^{2}+\frac{1}{8}\Big{(}\frac{m}{m_{P}}\Big{)}^{4}x^{4}$
		$\displaystyle+\frac{\kappa^{2}}{4\pi^{2}}F(x)+\frac{\lambda^{2}}{4\pi^{2}}F(y)$
		$\displaystyle+a\frac{m_{3/2}}{\sqrt{2}\kappa m}x+\frac{m_{3/2}^{2}}{2k^{2}m^{2}}x^{2}+\frac{m_{3/2}^{2}M^{2}}{k^{2}m^{4}\xi}\Bigg{)},$		(39)

since, in this case, $\mathcal{C}=1/2$, $c_{0}=c_{1}=c_{2}=1$ and, thus, the coefficients $\mathcal{A}=1+2(H_{P}^{2}+H_{P}^{4})$, $\mathcal{B}=2H_{P}^{2}$.

In Fig. 2, we plot the gravitino mass $m_{3/2}$ versus the reheat temperature $T_{r}$ as constrained by inflation. The solid-magenta, dashed-blue, dot-dashed-green curves correspond to $\xi=0.125,\ 0.167,\ 0.245$ respectively for the minimal Kähler potential with the conditions $n_{s}\simeq 0.964$, $A_{s}(k_{0})=2.196\times 10^{-9}$, $\gamma=2$, and $a=-1$. The lower bound on the reheat temperature $T_{r}\gtrsim 10^{9}$ GeV is obtained for a gravitino mass $m_{3/2}\gtrsim 3.5{\rm\ GeV}$ with a $0.1\%$ fine-tuning of the difference $x_{0}-1$.

Following the same line of argument as in Refs. Okada:2015vka ; Rehman:2017gkm , the shifted $\mu$HI with minimal $K$ is analyzed for the following three cases:

1. 1.

   stable gravitino LSP;

2. 2.

   unstable long-lived gravitino with $m_{3/2}<25{\rm\ TeV}$;

3. 3.

   unstable short-lived gravitino with $m_{3/2}>25{\rm\ TeV}$.

The relic gravitino abundance, in the case of a stable gravitino LSP, is given Bolz:2000fu by

$$\Omega_{\text{3/2}}h^{2}=0.08\Big{(}\frac{T_{r}}{10^{10}\text{GeV}}\Big{)}\Big{(}\frac{m_{\text{3/2}}}{1\text{ TeV}}\Big{)}\Big{(}1+\frac{m_{\tilde{g}}^{2}}{3m_{\text{3/2}}^{2}}\Big{)},$$

(40)

where $m_{\tilde{g}}$ is the gluino mass. We require that $\Omega_{\text{\tiny{3/2}}}h^{2}$ does not exceed the observed DM relic abundance, that is $\Omega_{\text{\tiny{3/2}}}h^{2}\lesssim 0.12$ Akrami:2018odb . Using Eq. (40), we then plot in Fig. 2 the resulting upper limit on the gluino mass $m_{\tilde{g}}$. The point where $m_{3/2}$ and the upper bound on $m_{\tilde{g}}$ coincide, for the central value of $\xi$ (i.e. $\xi=0.167$), lies at $T_{r}\simeq 1.2\times 10^{10}$ GeV and $m_{3/2}\simeq 325$ GeV as shown by the intersection of the corresponding curves. Our assumption for a gravitino LSP holds for $T_{r}$ values below this intersection point, that is for $T_{r}\lesssim 1.2\times 10^{10}$ GeV, $m_{3/2}\lesssim 325$ GeV. However, the maximum value of the gluino mass in this region is $m_{\tilde{g}}\sim 500$ GeV which is lower than the lower bound on the gluino mass $m_{\tilde{g}}\gtrsim 1$ TeV from the search for supersymmetry at the LHC Tanabashi:2018oca . Consequently, we run into inconsistency and the case of a stable gravitino LSP with a minimal Kähler potential is ruled out.

In the second case, the long-lived unstable gravitino will decay after big bang nucleosynthesis (BBN), and so one has to take into account the BBN bounds on the reheat temperature which are the following Khlopov:1993ye ; Kawasaki:2004qu ; Kawasaki:2017bqm :

	$\displaystyle T_{r}$	$\displaystyle\lesssim 3\times(10^{5}-10^{6})\text{ GeV},$	$\displaystyle m_{3/2}$	$\displaystyle\sim 1\text{ TeV},$
	$\displaystyle T_{r}$	$\displaystyle\lesssim 2\times 10^{9}\text{ GeV},$	$\displaystyle m_{3/2}$	$\displaystyle\sim 10\text{ TeV}.$		(41)

The bounds on the reheat temperature from the inflationary constraints for gravitino masses $1{\rm\ and}\ 10{\rm\ TeV}$ are $T_{r}\gtrsim 2.2\times 10^{10}{\rm\ GeV}$ and $7.5\times 10^{10}{\rm\ GeV}$ respectively (see Fig. 2). These are clearly inconsistent with the above mentioned BBN bounds, and so the unstable long-lived gravitino scenario is not viable.

Lastly, for the unstable short-lived gravitino case, we compute the LSP lightest neutralino ($\tilde{\chi}_{1}^{0}$) density produced by the gravitino decay and constrain it to be smaller than the observed DM relic density. For reheat temperature $T_{r}\gtrsim 10^{11}{\rm\ GeV}$ with $m_{3/2}>25{\rm\ TeV}$ (see Fig. 2), the resulting bound on the neutralino mass $m_{\tilde{\chi}_{1}^{0}}$ comes out to be inconsistent with the lower limit set on this mass $m_{\tilde{\chi}_{1}^{0}}\gtrsim 18{\rm\ GeV}$ in Ref. Hooper:2002nq . To circumvent this, the LSP neutralino is assumed to be in thermal equilibrium during gravitino decay, whereby the neutralino abundance is independent of the gravitino yield. For an unstable gravitino, the lifetime is (see Fig. 1 of Ref. Kawasaki:2008qe )

$$\tau_{3/2}\simeq 1.6\times 10^{4}\Big{(}\frac{1\ \text{TeV}}{m_{3/2}}\Big{)}^{3}{\rm sec}.\\$$

(42)

Now for a typical value of the neutralino freeze-out temperature, $T_{F}\simeq 0.05\ m_{\tilde{\chi}^{0}_{1}}$, the gravitino lifetime is estimated to be

$$\tau_{3/2}\lesssim 10^{-11}\Big{(}\frac{1\ \text{TeV}}{m_{\tilde{\chi}^{0}_{1}}}\Big{)}^{2}\text{sec}.\\$$

(43)

Comparing Eq. (42) and Eq. (43), we obtain a bound on $m_{3/2}$,

$$m_{3/2}\gtrsim 10^{8}\Big{(}\frac{m_{\tilde{\chi}_{1}^{0}}}{2\text{ TeV}}\Big{)}^{2/3}\text{GeV}.$$

(44)

Thus, minimal shifted $\mu$HI conforms with the conclusion of the standard case Okada:2015vka ; Rehman:2017gkm by requiring split-SUSY with an intermediate-scale gravitino mass and reheat temperature $T_{r}\gtrsim 1.8\times 10^{13}{\rm\ GeV}$ (see Fig. 2). To check whether the shifted $\mu$HI scenario is also compatible with low reheat temperature (i.e. $T_{r}\lesssim 10^{12}-10^{8}~{}{\rm\ GeV}$ Khlopov:1984pf ) and TeV-scale soft SUSY breaking, we employ nonminimal Kähler potential in the next section.

The nonminimal Kähler potential used in the following analysis is

$$K=K_{c}+\kappa_{S}\frac{|S|^{4}}{4m_{P}^{2}}+\kappa_{SS}\frac{|S|^{6}}{6m_{P}^{4}},$$

(45)

which includes only the nonminimal couplings of interest $\kappa_{S}$ and $\kappa_{SS}$. (For a somewhat different approach to $\mu$-hybrid inflation with nonminimal $K$, see Ref. Okada:2017rbf ). Thus, for the nonminimal scenario we take $c_{0}=c_{1}=1$ and $c_{2}=1-\kappa_{S}$ in Eq. (31) Civiletti:2011qg . Using these values the potential of the system can easily be read off from Eq. (III).