Shell-shaped quantum droplet in a three-component ultracold Bose gas
Abstract
Shell-shaped Bose-Einstein condensate (BEC) is a typical quantum system in curved geometry. Here we propose a new type of shell-shaped BEC with self-bound character, thereby liberating it from stringent conditions such as microgravity or fine-tuned trap. Specifically, we consider a three-component (1,2,3) ultracold Bose gas where (1,2) and (2,3) both form quantum droplets. The two droplets are mutually immiscible due to strong 1-3 repulsion, while still linked by component-2 to form a globally self-bound object. The outer droplet then naturally develops a shell structure without any trapping potential. It is shown that the shell structure can significantly modify the equilibrium density of the core, and lead to unique collective excitations highlighting the core-shell correlation. All results have been demonstrated in a realistic 23Na-39K-41K mixture. By extending quantum droplets from flat to curved geometries, this work paves the way for future exploring the interplay of quantum fluctuations and non-trivial real-space topologies in ultracold gases.
Quantum systems in curved geometries exhibit many distinctive features due to their non-trivial real-space topologies. For instance, a periodic boundary allows a persistent superflow of toroidal Bose-Einstein condensates (BECs) ring_1 ; ring_2 , and a local curvature gives rise to new topological defectsNelson ; Ho ; Zhou , interesting few-body physicsZhang_Ho ; Shi_Zhai and even non-Hermitian phenomenaZhouQi . As an outstanding case with non-trivial real-space topology, the shell-shaped BEC has attracted a great amount of attention in the field of ultracold atomsreview , and various fascinating properties have been revealed in terms of ground state and thermodynamicsTononi ; Rhyno ; ciardi ; prestipino , collective modesLannert ; Padavic ; Sun , expansion dynamicsTononi2 and vortex formationPadavic2 ; Fetter . These studies are closely related to the experimental efforts in creating shell-shaped BECs, or atomic bubbles, using the shell-shaped potentials under radio-frequency dressingproposal_rf_dress_1 ; proposal_rf_dress_2 . However, the Earth’s gravity prevents the formation of a closed shell in such setupColombe , and consequently a microgravity environment is required. Indeed, the first shell-shaped BEC was recently realized in NASA Cold Atom Laboratory aboard the International Space StationNASA_expt . Shortly after that, it was proposed alternatively that binary bosons in immiscible regimeHo_Shenoy ; Pu_Bigelow can also achieve the shell structureWolf . This idea has been successfully implemented in a recent experiment in the presence of Earth’s gravityDajun_expt , where a magic-wavelength optical trap was applied to avoid different gravitational sags between two species.
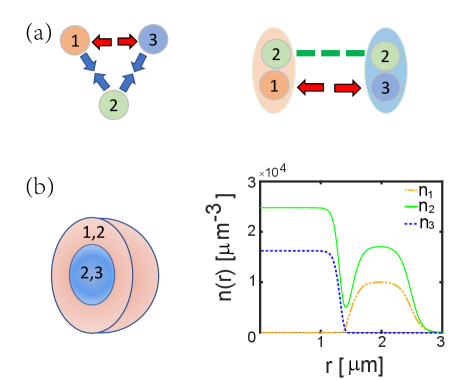
In this work, we introduce a new type of shell-shaped BEC without resorting to any trapping potential, and therefore it does not rely on microgravity environment or fine-tuned traps as in previous experimentsDajun_expt ; NASA_expt . Our scheme is motivated by the recent development of quantum droplet in ultracold atoms, which has been realized in both dipolar gasesferrier-barbut_observation_2016 ; schmitt_self-bound_2016 ; ferrier-barbut_liquid_2016 ; chomaz_quantum-fluctuation-driven_2016 ; tanzi_observation_2019 ; bottcher_transient_2019 ; Chomaz_long_lived_2019 and boson mixturescabrera_quantum_2018 ; cheiney_bright_2018 ; semeghini_self-bound_2018 ; derrico_observation_2019 ; burchianti_dual-species_2020 ; guo_lee-huang-yang_2021 . These droplets are stabilized by a mean-field attraction and the Lee-Huang-Yang repulsion from quantum fluctuationsPetrov , and thus can be self-bound in vacuum. Here we remark that the self-bound nature of quantum droplet offers an ideal opportunity for creating perfect shell geometry on Earth. This is because in the absence of any external trap, different species in the droplet will fall freely with the same speed and therefore no relative displacement will be produced due to the gravity.
Our scheme of creating shell-shaped BEC is illustrated in Fig.1. Specifically, we consider a three-component (1,2,3) boson mixture with contact interactions. Here (1,2) and (2,3) both form quantum droplets due to inter-species attractions, while they are immiscible due to strong 1-3 repulsion. The shared component-2 acts as a glue to link two droplets together as a globally self-bound object. In this way, the outer droplet is repelled by the inner core and naturally develops a shell structure in free space. Using a realistic mixture of 23Na-39K-41K near G, we show that the outer shell can efficiently expanded to larger radius with thinner width by increasing the core size. To balance with the outer shell, the core droplet exhibits very different equilibrium densities from the vacuum case (without shell). The core-shell correlation can also be manifested in the unique collective excitations of the system. As the first study of quantum droplet in curved geometry, our work opens a new avenue for exploring the interplay of quantum fluctuations and non-trivial real-space topologies in the platform of ultracold atoms.
We write down the Hamiltonian of three-component boson mixtures , with ()
| (1) |
Here is the coordinate; and are the mass and field operator of boson species , respectively; is the coupling constant between species and , with scattering length and reduced mass .
For a homogeneous dilute gas with densities , the total energy density is composed by the mean-field part and a correction from quantum fluctuations:
| (2) |
with , and the -th Bogoliubov modema_borromean_2021 . For a general system with inhomogeneous densities, we employ an extended Gross-Pitaevskii(GP) equations incorporating quantum fluctuations:
| (3) |
The ground state can be obtained by the imaginary time evolution of above coupled equations.
Different from the miscible three-component droplet in Ref.ma_borromean_2021 , in this work we focus on a qualitatively different situation where components 1 and 3 are immiscible with strong repulsion, while (1,2) and (2,3) themselves still form binary droplets, see Fig.1(a). To achieve this in practice, we consider the boson mixture 23Na-39K-41K all at hyperfine state (denoted as 1-2-3). Near , we have ( is the Bohr radius)lysebo_feshbach_2010 ; viel_feshbach_2016 ; Schulze_2018 , and is highly tunable via a Feshbach resonance at G with width mGtanzi_feshbach_2018 . One can easily check that the required mean-field instabilities, i.e., collapse for 1-2 and 2-3 and phase separation for 1-3, will occur as long as is sufficiently attractive.
Our numerical simulations based on (3) indeed produce two mutually immiscible droplets, (1,2) and (2,3), as the ground state for above system, see typical density distribution in Fig.1(b). Remarkably, the whole system is still self-bound due to the presence of component-2. In such an immiscible phase, in principle each droplet can either stay inside as a core or outside as a shell. However, for the ground state we find the one with a higher density of 2 always stays inside and the lower one stays outside, i.e., . This can be attributed to the minimized surface energy under such configuration. For the parameter of chosen in this work, the core and shell droplets are respectively (2,3) and (1,2).
We note that similar phenomena of immiscible droplets were also found previously in Helium mixturesPi1999 ; Barranco2006 , where a 4He droplet was coated with a normal 3He liquid, and in dipole-dipole mixtures with anisotropic density profilesbisset_quantum_2021 ; smith_quantum_2021 . In these studies, a long-range attraction between two droplets is required for their self-binding. In contrast, the binding of immiscible droplets in our case does not rely on any long-range force.
Now we explore the equilibrium expansion of shell droplet by increasing the core size. Let us start from the situation with a small core and a thick shell, see Fig.2(a1), where both droplets display flat-top densities. As increasing the size (or atom number) of the core, the shell is repelled to larger radius and becomes gradually thinner, see Fig.2(a2,a3); meanwhile, its flat-top profile gradually disappears and gives way to a Gaussian distribution with quite narrow width and low density. In Fig.2(b), we further extract the maximal density of each component during this process. One can see that the shell densities decrease rapidly as the core size increases, and eventually a very thin and dilute shell is created.
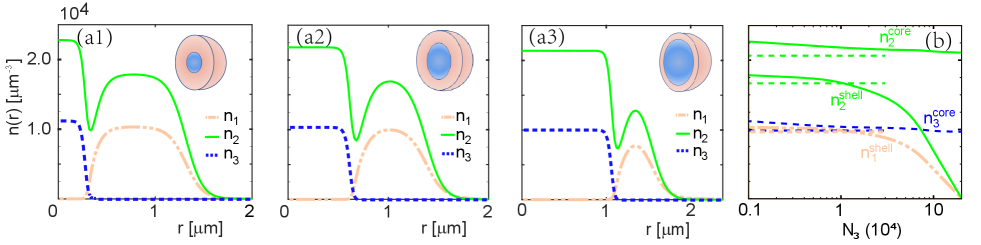
Because of the shared component-2 as a link, the core and shell droplets, although spatially separated, are strongly correlated with each other. This is clearly reflected in the balance condition as derived below. To start with, let us first consider the shell. Since it can transfer atom or energy to vacuum, its equilibration is similar to an isolated droplet in vacuumPetrov and determined by zero pressure and minimized energy:
| (4) |
In the thermodynamic limit, this gives the same equilibrium density as the vacuum droplet, as well as a locked density ratio . However, the condition (4) does not apply to the core, since it can only transfer atoms to the shell but not directly to vacuum. In this case, the core and shell should have the same pressure and chemical potential (of the shared component-2):
| (5) |
Two remarks are in order for the second condition in (5). First, it obviously differs from the second condition in (4), and therefore a different equilibrium density can be resulted for the core as compared to the vacuum case. Secondly, it exactly expresses the correlation between core and shell droplets. Under this condition, the core densities () depend crucially on the shell chemical potential (), and thus can be highly tunable by the shell parameters.
We now analytically derive based on (4,5). For a thermodynamically large () droplet with uniform densities , its total energy density is given by
| (6) |
Here is the correction from quantum fluctuationsPetrov , which determines a dimensionless function . Then the chemical potential and pressure can be obtained straightforwardly, and the condition leads to the equilibrium density
| (7) |
with density ratio . In this way, can also be expressed in terms of a single unknown parameter .
For the shell (1,2) droplet, the second condition in (4) results in a locked density ratio , and reproduce for the vacuum casePetrov . Further, can be obtained as a function of . For the core (2,3) droplet, by enforcing the second condition in (5), and recalling is just parametrized by , we can then solve and further via (7). In Fig.2(b), and are respectively shown by horizontal dashed and dotted lines. These analytical predictions fit well to numerical results when the droplets are in thermodynamical limit.
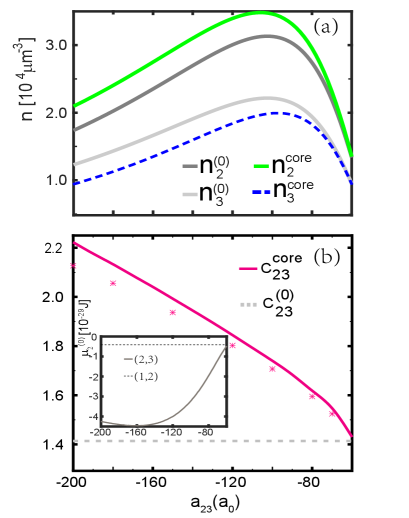
In Fig.3 (a,b), we further show how the core densities and their ratio vary with . One can see that both and change sensitively with , and their deviations from the vacuum values ( and ) get more significant if gets more attractive. This can be attributed to the larger mismatch of for isolated (2,3) and (1,2) droplets in vacuum, see the inset of Fig.3(b). As a result, to balance the two chemical potentials as required by (5), the core has to adjust its densities to change , such that it can match in the shell. This is how the correlation is built up between core and shell, and the modified core densities are a direct evidence of such correlation. In this way, the core-shell structure presents a rare situation where the equilibrium density of a quantum droplet can be efficiently tuned by its surrounding environment.
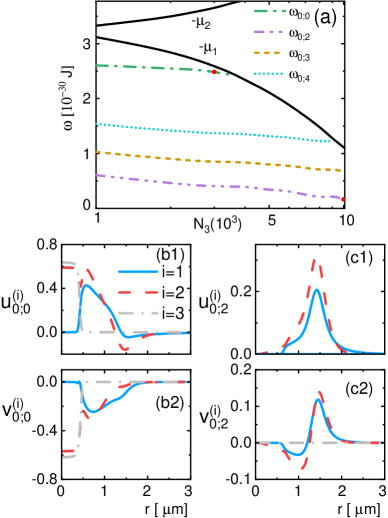
The core-shell correlation can also lead to unique collective excitations. Here we assume a small density fluctuation for component-:
| (8) |
By linearizing the GP equation (3) in terms of , we obtain the equations for collective excitations and further solve the eigen-modes and eigen-energies in each angular momentum () sectorsupple . In Fig.4(a), we show the four lowest excitations modes with and , where corresponds to breathing mode and the rest three are surface modes. Note that the dipole mode is associated with the center-of-mass motion and is therefore with zero excitation energy for self-bound droplet (see also Petrov ). Here we see that as increasing the core size (), both the breathing and surface modes gradually vanish and merge into the atom emission threshold (). This is distinct from the case without shell structure, where all excitation modes become more stable as increasing the droplet sizePetrov . To clearly see the nature of these modes, we plot out the typical radial wavefunctions in Fig.4(b1,b2) and (c1,c2), respectively, for breathing and surface modes. Remarkably, the breathing mode displays strong core-shell correlations, where all the three components (in both core and shell) oscillate in-phase with visible and . Such correlated excitations can be attributed to the linking effect of shared component. In comparison, the surface modes are mostly localized in the shell but occupy little in the core. In this case, the core and shell are well separated and these excitations are solely tied with the curved geometry. As the core gets larger, the thinner shell becomes less bound and finally it cannot stabilize the surface excitations, as manifested by the disappearance of surface modes at .
In summary, we have demonstrated a scheme to create shell-shaped quantum droplet in ultracold boson mixtures without resorting to any trapping potential. A number of unique properties associated with the shell structure have been revealed, including its equilibrium expansion, modified core densities by core-shell balance, as well as the correlated/localized collective excitations. All these results can be practically detected in 23Na-39K-41K mixture. Other atomic candidates may also be possible in view of a growing number of bosonic mixtures now available with tunable interactionsK-Rb1 ; K-Rb ; Na-Rb ; K-Cs ; Schulze_2018 ; tanzi_feshbach_2018 .
Our work opens up a new avenue to study quantum droplets with non-trivial real-space topologies, which can drive many intriguing phenomena due to the interplay with quantum fluctuations. One interesting subject would be the dynamical property of shell droplet, such as vortex formation and quench dynamics. Given the unique properties of self-bound droplets in vorticesLi2018:TwodimensionalVortexQuantum ; Zhang2019:SemidiscreteQuantumDroplets ; Tengstrand2019:RotatingBinaryBoseEinstein ; Caldara2022:VorticesQuantumDroplets ; Gu ; Oktel and dynamicscollision1 ; collision2 ; dynamic1 ; dynamic2 ; dynamic3 ; Ma2 , one can imagine even dramatic consequences in combination with the compactness and local curvature of shell geometry. Moreover, it is worthwhile to study quantum fluctuation effect when the shell becomes thin enough and behaves as effectively 2D (where Eq.2 is no longer applicable). Given that a 2D droplet can be supported at arbitrarily low densityPetrov2 , we can expect a stable shell even at very large radius with extremely thin width. Finally, we note that the present scheme can be directly generalized to quasi-2D system in creating a toroidal droplet. More fascinating physics of these curved droplets remain to be explored in future.
Acknowledgements.
Acknowledgment. We are grateful to Tin-Lun Ho for valuable discussions which motivated this project. The work is supported by the National Natural Science Foundation of China (12074419, 12134015, 12205365), and the Strategic Priority Research Program of Chinese Academy of Sciences (XDB33000000).References
- (1) C. Ryu, M. F. Andersen, P. Clad, V. Natarajan, K. Helmerson, W. D. Phillips, Observation of Persistent Flow of a Bose-Einstein Condensate in a Toroidal Trap, Phys. Rev. Lett. 99, 260401 (2007).
- (2) A. Ramanathan, K. C. Wright, S. R. Muniz, M. Zelan, W. T. Hill, C. J. Lobb, K. Helmerson, W. D. Phillips, G. K. Campbell, Superflow in a toroidal Bose–Einstein condensate: an atom circuit with a tunable weak link, Phys. Rev. Lett. 106, 130401 (2011).
- (3) A. M. Turner, V. Vitelli, D. R. Nelson, Vortices on curved surfaces, Rev. Mod. Phys. 82, 1301 (2010).
- (4) T.-L. Ho, B. Huang, Spinor Condensates on a Cylindrical Surface in Synthetic Gauge Fields, Phys. Rev. Lett. 115, 155304 (2015).
- (5) X.-F. Zhou, C. Wu, G.-C. Guo, R. Wang, H. Pu, Z.-W. Zhou, Synthetic Landau Levels and Spinor Vortex Matter on a Haldane Spherical Surface with a Magnetic Monopole, Phys. Rev. Lett. 120, 130402 (2018).
- (6) J. Zhang, T.-L. Ho, Potential scattering on a spherical surface, J. Phys. B At. Mol. Opt. Phys. 51, 115301 (2018).
- (7) Z.-Y. Shi, H. Zhai, Emergent gauge field for a chiral bound state on curved surface, J. Phys. B At. Mol. Opt. Phys. 50, 184006 (2017).
- (8) C. Lv, R. Zhang, Z. Zhai, Q. Zhou, Curving the space by non-Hermiticity, Nature Communications 13, 2184 (2022).
- (9) A. Tononi, L. Salasnich, Low-dimensional quantum gases in curved geometries, Nature Reviews Physics 5, 398 (2023).
- (10) A. Tononi, L. Salasnich, Bose-Einstein Condensation on the Surface of a Sphere, Phys. Rev. Lett. 123, 160403 (2019).
- (11) S. Prestipino, P. V. Giaquinta, Ground state of weakly repulsive soft-core bosons on a sphere, Phys. Rev. A 99, 063619 (2019).
- (12) B. Rhyno, N. Lundblad, D. C. Aveline, C. Lannert, and S. Vishveshwara, Thermodynamics in expanding shell-shaped Bose-Einstein condensates, Phys. Rev. A 104, 063310 (2021).
- (13) M. Ciardi, F. Cinti, G. Pellicane, S. Prestipino, Supersolid phases of bosonic particles in a bubble trap, arxiv:2303.06113.
- (14) C. Lannert, T. C. Wei, S. Vishveshwara, Dynamics of condensate shells: Collective modes and expansion, Phys. Rev. A 75, 013611 (2007).
- (15) K. Padavi, K. Sun, C. Lannert, S. Vishveshwara, Physics of hollow Bose-Einstein condensates, Europhys. Lett. 120, 20004 (2017).
- (16) K. Sun, K. Padavi, F. Yang, S. Vishveshwara, C. Lannert, Static and dynamic properties of shell-shaped condensates, Phys. Rev. A 98, 013609 (2018).
- (17) A. Tononi, F. Cinti, L. Salasnich, Quantum Bubbles in Microgravity, Phys. Rev. Lett. 125, 010402 (2020).
- (18) K. Padavi, K. Sun, C. Lannert, S. Vishveshwara, Vortex-antivortex physics in shell-shaped Bose-Einstein condensates, Phys. Rev. A 102, 043305 (2020).
- (19) S. J. Bereta, M. A. Caracanhas, A. L. Fetter, Superfluid vortex dynamics on a spherical film, Phys. Rev. A 103, 053306 (2021).
- (20) O. Zobay, B. M. Garraway, Two-Dimensional Atom Trapping in Field-Induced Adiabatic Potentials, Phys. Rev. Lett. 86, 1195 (2001).
- (21) O. Zobay, B. M. Garraway, Atom trapping and two-dimensional Bose-Einstein condensates in field-induced adiabatic potentials, Phys. Rev. A 69, 023605 (2004).
- (22) Y. Colombe, E. Knyazchyan, O. Morizot, B. Mercier, V. Lorent, H. Perrin, Ultracold atoms confined in rf-induced two-dimensional trapping potentials, Europhys. Lett. 67, 593 (2004).
- (23) R. A. Carollo, D. C. Aveline, B. Rhyno, S. Vishveshwara, C. Lannert, J. D. Murphree, E. R. Elliott, J. R. Williams, R. J. Thompson, N. Lundblad, Observation of ultracold atomic bubbles in orbital microgravity, Nature (London) 606, 281 (2022).
- (24) T.-L. Ho, V. B. Shenoy, Binary Mixtures of Bose Condensates of Alkali Atoms, Phys. Rev. Lett. 77, 3276 (1996).
- (25) H. Pu, N. P. Bigelow, Properties of Two-Species Bose Condensates, Phys. Rev. Lett. 80, 1130 (1998).
- (26) A. Wolf, P. Boegel, M. Meister, A. Bala, N. Gaaloul, M. A. Efremov, Shell-shaped Bose-Einstein condensates based on dual-species mixtures, Phys. Rev. A 106, 013309 (2022).
- (27) F. Jia , Z. Huang, L. Qiu, R. Zhou, Y. Yan, D. Wang, Expansion Dynamics of a Shell-Shaped Bose-Einstein Condensate, Phys. Rev. Lett. 129, 243402 (2022).
- (28) I. Ferrier-Barbut, H. Kadau, M. Schmitt, M. Wenzel, T. Pfau, Observation of Quantum Droplets in a Strongly Dipolar Bose Gas, Phys. Rev. Lett. 116, 215301 (2016).
- (29) M. Schmitt, M. Wenzel, F. Böttcher, I. Ferrier-Barbut, T. Pfau, Self-bound droplets of a dilute magnetic quantum liquid, Nature 539, 259 (2016).
- (30) I. Ferrier-Barbut, M. Schmitt, M. Wenzel, H. Kadau, T. Pfau, Liquid quantum droplets of ultracold magnetic atoms, J. Phys. B: At. Mol. Opt. Phys. 49, 214004 (2016).
- (31) L. Chomaz, S. Baier, D. Petter, M. J. Mark, F. Wächtler, L. Santos, F. Ferlaino, Quantum-fluctuation-driven crossover from a dilute Bose-Einstein condensate to a macrodroplet in a dipolar quantum fluid, Phys. Rev. X 6, 041039 (2016).
- (32) L. Tanzi, E. Lucioni, F. Famà, J. Catani, A. Fioretti, C. Gabbanini, R. N. Bisset, L. Santos, G. Modugno, Observation of a Dipolar Quantum Gas with Metastable Supersolid Properties, Phys. Rev. Lett. 122, 130405 (2019).
- (33) F. Böttcher, J. N. Schmidt, M. Wenzel, J. Hertkorn, M. Guo, T. Langen, T. Pfau, Transient Supersolid Properties in an Array of Dipolar Quantum Droplets, Phys. Rev. X 9, 011051 (2019).
- (34) L. Chomaz, D. Petter, P. Ilzhöfer, G. Natale, A. Trautmann, C. Politi, G. Durastante, R. M. W. van Bijnen, A. Patscheider, M. Sohmen, M. J. Mark, F. Ferlaino, Long-Lived and Transient Supersolid Behaviors in Dipolar Quantum Gases, Phys. Rev. X 9, 021012 (2019).
- (35) C. R. Cabrera, L. Tanzi, J. Sanz, B. Naylor, P. Thomas, P. Cheiney, L. Tarruell, Quantum liquid droplets in a mixture of Bose-Einstein condensates, Science 359, 301 (2018).
- (36) P. Cheiney, C. R. Cabrera, J. Sanz, B. Naylor, L. Tanzi, L. Tarruell, Bright Soliton to Quantum Droplet Transition in a Mixture of Bose-Einstein Condensates, Phys. Rev. Lett. 120, 135301 (2018).
- (37) G. Semeghini, G. Ferioli, L. Masi, C. Mazzinghi, L. Wolswijk, F. Minardi, M. Modugno, G. Modugno, M. Inguscio, M. Fattori, Self-Bound Quantum Droplets of Atomic Mixtures in Free Space, Phys. Rev. Lett. 120, 235301 (2018).
- (38) C. D’Errico, A. Burchianti, M. Prevedelli, L. Salasnich, F. Ancilotto, M. Modugno, F. Minardi, C. Fort, Observation of quantum droplets in a heteronuclear bosonic mixture, Phys. Rev. Res. 1, 033155 (2019).
- (39) A. Burchianti, C. D’Errico, M. Prevedelli, L. Salasnich, F. Ancilotto, M. Modugno, F. Minardi, C. Fort, A Dual-Species Bose-Einstein Condensate with Attractive Interspecies Interactions, Condens. Matter 5, 21 (2020).
- (40) Z. Guo, F. Jia, L. Li, Y. Ma, J. M. Hutson, X. Cui, D. Wang, Lee-Huang-Yang effects in the ultracold mixture of 23Na and 87Rb with attractive interspecies interactions, Phys. Rev. Res. 3, 033247 (2021).
- (41) D. S. Petrov, Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture, Phys. Rev. Lett. 115, 155302 (2015).
- (42) Y. Ma, C. Peng, X. Cui, Borromean Droplet in Three-Component Ultracold Bose Gases, Phys. Rev. Lett. 127, 043002 (2021).
- (43) M. Lysebo, L. Veseth, Feshbach resonances and transition rates for cold homonuclear collisions between 39K and 41K atoms, Phys. Rev. A 81, 032702 (2010).
- (44) A. Viel, A. Simoni, Feshbach resonances and weaklybound molecular states of boson-boson and boson-fermion NaK pairs, Phys. Rev. A 93, 042701 (2016).
- (45) T. A. Schulze, T. Hartmann, K. K. Voges, M. W. Gempel, E. Tiemann, A. Zenesini, S. Ospelkaus, Feshbach spectroscopy and dual-species Bose-Einstein condensation of 23Na-39K mixtures, Phys. Rev. A 97, 023623 (2018).
- (46) L. Tanzi, C. R. Cabrera, J. Sanz, P. Cheiney, M. Tomza, L. Tarruell, Feshbach resonances in potassium Bose-Bose mixtures, Phys. Rev. A 98, 062712 (2018).
- (47) M. Pi, R. Mayol, M. Barranco, Structure of Large 3He-4He Mixed Drops around a Dopant Molecule, Phys. Rev. Lett. 82, 3093 (1999).
- (48) M. Barranco, R. Guardiola, S. Hernández, R. Mayol, J. Navarro, M. Pi, Helium Nanodroplets: An Overview, J. Low Temp. Phys. 142, 1 (2006).
- (49) R. N. Bisset, L. A. Ardila, L. Santos, Quantum Droplets of Dipolar Mixtures, Phys. Rev. Lett. 126, 025301 (2021).
- (50) J. C. Smith, D. Baillie, P. B. Blakie, Quantum Droplet States of a Binary Magnetic Gas, Phys. Rev. Lett. 126, 025302 (2021).
- (51) G. Thalhammer, G. Barontini, L. De Sarlo, J. Catani, F. Minardi, M. Inguscio, Double Species Bose-Einstein Condensate with Tunable Interspecies Interactions, Phys. Rev. Lett. 100, 210402 (2008).
- (52) L. Wacker, N. B. Jørgensen, D. Birkmose, R. Horchani, W. Ertmer, C. Klempt, N. Winter, J. Sherson, J. J. Arlt, Tunable dual-species Bose-Einstein condensates of 39K and 87Rb, Phys. Rev. A 92, 053602 (2015).
- (53) F. Wang, X. Li, D. Xiong, D. Wang, A double species 23Na and 87Rb Bose–Einstein condensate with tunable miscibility via an interspecies Feshbach resonance J. Phys. B 49, 015302 (2015).
- (54) M. Grobner, P. Weinmann, E. Kirilov, H.-C. Nagerl, P. S. Julienne, C. Ruth Le Sueur, J. M. Hutson, Observation of interspecies Feshbach resonances in an ultracold 39K-133Cs mixture and refinement of interaction potentials, Phys. Rev. A 95, 022715 (2017).
- (55) Y. Li, Z. Chen, Z. Luo, C. Huang, H. Tan, W. Pang, B. A. Malomed, Two-dimensional vortex quantum droplets, Phys. Rev. A 98, 063602 (2018).
- (56) X. Zhang, X. Xu, Y. Zheng, Z. Chen, B. Liu, C. Huang, B. A. Malomed, Y. Li, Semidiscrete quantum droplets and vortices, Phys. Rev. Lett. 123, 133901 (2019).
- (57) M. N. Tengstrand, P. Stürmer, E. Karabulut, S. M. Reimann, Rotating binary Bose-Einstein condensates and vortex clusters in quantum droplets, Phys. Rev. Lett. 123, 160405 (2019).
- (58) M. Caldara, F. Ancilotto, Vortices in quantum droplets of heteronuclear Bose mixtures, Phys. Rev. A 105, 063328 (2022).
- (59) Q. Gu, X. Cui, Self-bound Vortex Lattice in a Rapidly Rotating Quantum Droplet, Phys. Rev. A 108, 063302 (2023).
- (60) T. A. Yourt, U. Tanyeri, A. Keleş, M. . Oktel, Vortex lattices in strongly confined quantum droplets, Phys. Rev. A 108, 033315 (2023).
- (61) G. E. Astrakharchik, B. A. Malomed, Dynamics of one-dimensional quantum droplets, Phys. Rev. A 98, 013631 (2018).
- (62) G. Ferioli, G. Semeghini, L. Masi, G. Giusti, G. Modugno,M. Inguscio, A. Gallemí, A. Recati, M. Fattori, Collisions of Self-Bound Quantum Droplets, Phys. Rev. Lett. 122, 090401 (2019).
- (63) G. Ferioli, G. Semeghini, S. Terradas-Briansó, L. Masi, M. Fattori, M. Modugno, Dynamical formation of quantum droplets in a 39K mixture, Phys. Rev. Res. 2, 013269 (2020).
- (64) V. Cikojević ,L. Vranješ Markić, M. Pi , M. Barranco, F. Ancilotto, J. Boronat, Dynamics of equilibration and collisions in ultradilute quantum droplets, Phys. Rev. Res. 3, 043139 (2021).
- (65) C. Fort, M. Modugno, Self-evaporation dynamics of quantum droplets in a 41K-87Rb mixture, Appl. Sci. 11, 866 (2021).
- (66) Y. Ma, X. Cui, Quantum-fluctuation-driven dynamics of droplet splashing, recoiling, and deposition in ultracold binary Bose gases, Phys. Rev. Research 5, 013100 (2023).
- (67) D. S. Petrov, G. E. Astrakharchik, Ultradilute Low-Dimensional Liquids, Phys. Rev. Lett. 117, 100401 (2016).
- (68) See supplementary material for more details on the analysis of equilibrium densities and collective modes.
Supplementary Materials
In this Supplemental Material, we provide more details on equilibrium densities and collective modes of the shell-shaped droplet.
I. Equilibrium densities for the core and the shell
For a large binary () droplet with uniform densities , its total energy density can be written as Eq.(6) in the main text, where the quantum fluctuation energy is expressed as:
| (S1) |
with a dimensionless function of
| (S2) |
The chemical potential can then be obtained as
| (S3) |
and the pressure can be obtained as
| (S4) |
Then condition leads to the equilibrium density as shown by Eq.(7) in the main text.
For the shell droplet, the chemical potential of component-2 () can be obtained via (S3) as
| (S5) |
Then from the core-shell balance condition , we can solve the density ratio and further the equilibrium densities for the core.
II. Collective modes
Here we analyze the collective breathing mode of shell-shaped droplet. Assuming a small fluctuation mode for component- bosons, and only keeping the lowest-order fluctuations in the GP equation, we get
| (S6) |
Based on the standard Bogoliubov theory, we write the fluctuation mode as
| (S7) |
where is the -th eigen-mode, and represent according eigen-wavefunctions. and can be further expanded in terms of the spherical harmonics as
| (S8) |
with and the radial and azimuthal components of . Then (S7) can be expanded similarly, and by plugging (S7) into (S6) we find that the equations can be decoupled between different sectors. For each given , we arrive at the following equations :
| (S9) |
where
| (S10) |
and the normalization condition is
| (S11) |
Here since all the -solutions are degenerate, we have dropped this index for simplicity. By solving above equations, we can obtain the eigen-energy and eigen-wavefunctions for collective excitations in each channel. The breathing modes correspond to the solutions with , and all higher ones are surface modes. Note that for the self-bound droplet, the center-of-mass motion causes no excitation energy and thus the lowest dipole mode (with ) has zero eigen-energy.
In Fig.4 of the main text, we have shown the typical for breathing mode and surface mode. In Fig.S1 we further plot out typical for surface modes with higher . One can see that all these modes are localized within the shell while with little occupation in the core. This means that the surface excitation in the core is strongly suppressed by the shell structure.
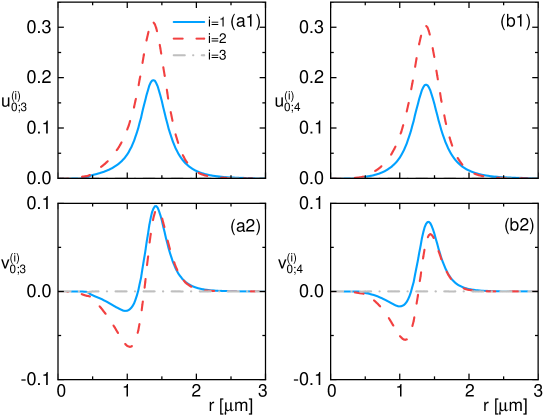
We have also checked that for very large core and very thin shell, these surface modes are no longer stable and the whole system keeps emitting particles to the vacuum under the surface excitations. In this regime, all stay above the atom emission threshold . Physically, it is because the gradually thinner shell is less bound (with increasing or decreasing ), and therefore it cannot afford any surface excitation (with ). This directly shows the crucial role of shell structure in modifying the collective exciations in quantum droplets.