\ul
Sequential Recommendation with Controllable Diversification: Representation Degeneration and Diversity
Abstract.
Sequential recommendation (SR) models the dynamic user preferences and generates the next-item prediction as the affinity between the sequence and items, in a joint latent space with low dimensions (i.e., the sequence and item embedding space). Both sequence and item representations suffer from the representation degeneration issue due to the user/item long-tail distributions, where tail users/items are indistinguishably distributed as a narrow cone in the latent space. We argue that the representation degeneration issue is the root cause of insufficient recommendation diversity in existing SR methods, impairing the user potential exploration and further worsening the echo chamber issue.
In this work, we first disclose the connection between the representation degeneration and recommendation diversity, in which severer representation degeneration indicates lower recommendation diversity. We then propose a novel Singular sPectrum sMoothing regularization for Recommendation (SPMRec), which acts as a controllable surrogate to alleviate the degeneration and achieve the balance between recommendation diversity and performance. The proposed smoothing regularization alleviates the degeneration by maximizing the area under the singular value curve, which is also the diversity surrogate. We conduct experiments on four benchmark datasets to demonstrate the superiority of SPMRec, and show that the proposed singular spectrum smoothing can control the balance of recommendation performance and diversity simultaneously.


1. Introduction
Recommender systems play a significant and widespread role in providing personalized recommendations and user modeling for various web applications, as evident in fashion, music, movies, and marketing scenarios. Among existing frameworks, sequential recommendation (SR) (Rendle et al., 2010; He and McAuley, 2016; Tang and Wang, 2018; Hidasi et al., 2015; Kang and McAuley, 2018) has recently garnered considerable attention due to its scalability and superior performance. SR utilizes sequential user behaviors and item-item transition correlations to predict the user’s next preferred item. Among existing SR methods, Transformer-based methods (Kang and McAuley, 2018; Sun et al., 2019; Li et al., 2020) have attracted increasing interests due to their capability of modeling high-order item-item transitions and scalable architecture design. In addition to recommendation quality (quantified as next-item prediction accuracy), a diverse set of items generation is also crucial for improving user satisfaction (Zhang and Hurley, 2008; Chen et al., 2018) and helping users escape the echo chamber (Ge et al., 2020) for better long-term engagements (Chen et al., 2021).
The long-tail distribution of users/items has been widely observed in real-world applications and benchmarking datasets (Zhang et al., 2023; Domingues et al., 2012; Wang et al., 2022a), in which a small portion of users/items contribute to most interactions. According to empirical observations (Goel et al., 2010), tail items availability in recommendation can boost the sales of head items, which triggers the need of diverse recommendations. Demonstrated by (Wang et al., 2018; Gao et al., 2023), the long-tail distribution potentially leads to more intense Matthew effect, in which popular items and categories further dominate the recommender system with the implication of insufficient recommendation diversity. However, few research investigates the relationship between the long-tail distribution of users/items and the recommendation diversity.
Existing methods either focus on post re-ranking approaches (with the risk of sacrificing recommendation quality) (Zhang and Hurley, 2008; Chen et al., 2018; Wilhelm et al., 2018) or build upon the indirect connection between recommendation quality and diversity (Yang et al., 2023; Liu et al., 2022). A balance between recommendation quality and diversity is needed because over-emphasizing either the quality or the diversity leads to sub-optimal user satisfaction. To achieve this balance, a recommendation model with controllable diversification module is needed. It is also challenging to develop the controllable diversity module because the underlying connection between the quality and the diversity is not identified yet, and a differentiable solution is preferred so as to optimize both the quality and diversity.

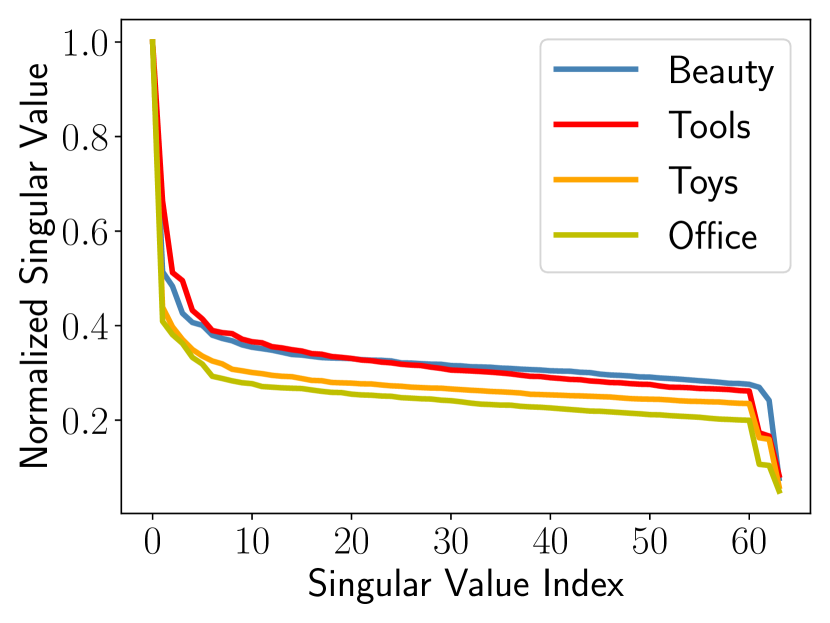
To this end, we demonstrate the connection between the long-tail distribution on users/items and the recommendation diversity, via the observed representation degeneration issue in both users and items, as shown in Fig. (2). We theoretically show that the fast singular value decay from the users/items representation degeneration is the root cause of insufficient diversity. More details will be explained in Section 3. Motivated by this connection, we develop a novel sequential recommendation with controllable diversity module by smoothing the singular value curves for users/items representations, with the goals of alleviating the degeneration and improving the recommendation diversity simultaneously.
Specifically, we propose a novel metric to measure the degree of degeneration issue and a novel Singular sPectrum sMoothing regularization design to achieve better sequence and item representation learning for Recommendations, SPMRec. We propose the Area Under the Singular value Curve (AUSC) to measure the degree of degeneration, with the intution that a flat curve has a larger area under the curve than a fast decaying curve, which will also be illustrated in the following Fig. (3). We further propose the singular spectrum smoothing regularization loss as an auxiliary loss to constrain the sequence and item embedding learning, which is a surrogate of our proposed AUSC metric. The singular spectrum smoothing regularization builds upon the nuclear norm and Frobenius norm (Horn and Johnson, 2012; Chen et al., 2022; Cui et al., 2020) to suppress the largest singular value and enlarge other singular values. The singular spectrum smoothing regularization unblocks the feasibility of sequential recommendation with controllable diversity. We summarize our three technical contributions as follows:
-
•
To the best of our knowledge, we are the first to identify the connection between the representation degeneration and insufficient diversity in SR from the theoretical perspective.
-
•
We propose a novel metric (AUSC) to measure the degree of degeneration and develop a singular spectrum smoothing regularization named SPMRec to achieve the important but challenging balance of recommendation quality and diversity.
-
•
Our experiments on four benchmark datasets show the effectiveness of the proposed SPMRec, and empirically demonstrate that a proper contribution of smoothing improves both recommendation performance and diversity.
2. Preliminaries
2.1. Problem Definition
In the SR problem, there are a set of users , a set of items , and interactions feedback between users and items. Each interaction is associated with its timestamp. For each user , we sort the interacted items chronologically and format the user as the sequence of interacted items, denoted as . Specifically, represents the -th interacted item in the sequence of the user . SR tackles the problem of predicting the next item based on the sequence of user’s historical interactions, which is formalized as predicting the probability of the next item . In the recommendation generation stage, the next item prediction scores over all items are ranked to generate the top-N recommendation list for the user .
2.2. Sequential User Modeling
Given a user interaction sequence , we pre-process it by either truncating earliest interactions or padding with zeros such that the sequence length becomes the maximum sequence length to get a fixed length sequence . An item embedding matrix is randomly initialized and will be optimized, where is the latent dimension size. A trainable positional embedding is added to the sequentially ordered item embedding matrix as . Formally, we formulate the sequence encoder as follows:
| (1) |
where denotes sequential output embeddings of , and for each timestep , and encodes the predicted next-item () representation.
2.3. Next-Item Prediction Optimization
The next item preference score prediction is given as:
| (2) |
where denotes the embedding of the item . The typical optimization process adopts the classical sampled cross-entropy (sampled CE) loss or bayesian personalized ranking loss (BPR) (Rendle et al., 2012), which is maximizing the probability of users ranking positive items with greater preference scores over sampled negative items . The optimization can be formulated as a sampled cross-entropy loss minimization as:
| (3) |
where denotes the -th negatively sampled item, denotes the number of negatively sampled items from the item set without interaction with the user . The value of affects the recommendation performance significantly (Ding et al., 2019; Chen et al., 2017; Mao et al., 2021). The typical choice in BPR and binary cross-entropy losses uses one negatively sampled item .
3. Representation Degeneration and Diversity
3.1. Representation Degeneration Revisit
3.1.1. Revisit of Item Degeneration
Most item embeddings are distributed in a narrow cone when the item degeneration issue occurs, with observation as fast singular value decay of the item embedding matrix (Yu et al., 2022; Qiu et al., 2022). As suggested in (Gao et al., 2019; Yu et al., 2022), the long-tail distribution in frequency is the cause of representations degeneration. In SR, items follow the long-tail distribution. By utilizing the analysis in (Gao et al., 2019), for any tail item , the recommendation loss in Eq. (3) associated with the learnable embedding of the item is given as:
| (4) |
where includes the constant part without . The optimal solution is a vector with the uniformly negative direction of all sequence output embeddings and infinite Frobenius norm, i.e., , using the Theorem 1 in (Gao et al., 2019). With the long-tail distribution of item frequency, most items are cold items. Most cold items degenerate into a narrow space as a cone, with the observation of fast singular decay phenomenon observed in (Gao et al., 2019; Wang et al., 2020) and Fig. (2(b)). Moreover, as the Frobenius norm of item embedding matrix is the upper bound of its largest singular value, the infinite Frobenius norm enlarges the largest singular value, causing the fast singular decay phenomenon observed in (Gao et al., 2019; Wang et al., 2020), which is also demonstrated in the Fig. (2(b)).
3.1.2. Item Degeneration Induces Sequence Degeneration
With degenerated item embeddings, we conclude that output embeddings of short sequences suffer from the degeneration issue. By freezing the item embedding matrix , we derive the recommendation loss of a sequence output embedding for user as follows:
| (5) |
where the first component enforces the to be close to the positively interacted items’ representations while the second part pulls the away from negatively sampled items’ representations.
When the item degeneration happens, i.e., most tail items have , the optimal solution of is a vector in the negative direction with most items, indicating . This is because more negative items are sampled with more optimization steps. indicates other singular values are being suppressed to 0, based on theories that the Frobenius norm is the upper bound of the largest singular value. When (i.e., sequences are short), the degeneration issue becomes more severe, as there are much more negatively sampled items than positive items, where the second component dominates the learning process of .
3.2. Theoretical Connection with Diversity
3.2.1. Determinant of Embedding as Diversity Measurement
We connect the determinant of embedding with the diversity via the well-defined determinant maximization problem in the determinant point process (DPP) (Kulesza et al., 2012). The determinant maximization problem (Kulesza et al., 2012) has been studied extensively in several machine learning applications, such as core-set discovery (Mahabadi et al., 2019; Mirrokni and Zadimoghaddam, 2015), feature selection (Zadeh et al., 2017), and recommendation re-ranking (Wilhelm et al., 2018; Liu et al., 2022; Chen et al., 2018; Huang et al., 2021). Specifically, the determinant maximization problem is to find a subset from the total item set with . Formally, given the item feature matrix , DPP finds an item subset , such that the determinant of the kernel matrix of the item subset is maximized as follows:
| (6) |
where the kernel is typically defined as the dot product of the item features . The existing DPP solutions (Mahabadi et al., 2019; Mirrokni and Zadimoghaddam, 2015; Wilhelm et al., 2018) iteratively expand the diverse subset by searching the item to enlarge the determinant of kernel .
A subset with two items case (i.e., ) can be used to demonstrate the relationship between determinant of the kernel and the diversity of the subset . The determinant of the kernel can be extended as , where identifies the correlations with different items. When obtains the minimum value 0, , which indicates that and are highly correlated, i.e., no diversity. On the contrary, when is maximized, the diverse set of items is retrieved.
Extending to the total item set for recommendations in SR, the total item set’s diversity can be measured as the determinant of the kernel on and the associated item embedding matrix , which is . Inductively, given a selected item set with the size as , DPP adds an item to the selected item set as with size . Using Matrix Determinant Lemma, the the determinant of is given as:
| (7) | ||||
| (8) |
measures the correlations between the item and the selected item set . As is selected and fixed, and can be treated as constants, and is the similarity of the item itself and can also be treated as a constant. DPP aims at finding the for maximizing the , which is equivalent to finding the with the least correlations with the selected item set :
| (9) |
This inductive argument implies that DPPs favor a diverse item set.
By applying the logorithmic and the SVD decomposition on the embedding matrix , we obtain the following the relationship between diversity and the singular values of :
| (10) |
where are singular values of the item embedding matrix , and singular values are in the descending order as and the is the largest singular value . With Eq. (10), we establish the theoretical relationship between the determinant of embedding and item set diversity. As the 2log only re-scales the singular value, we have shown that the diversity is proportional to the sum of singular values, i.e., the nuclear norm of the embedding .

3.2.2. Representation Degeneration and Insufficient Diversity
The observations in Fig. (2) show that both item embeddings and sequence output embeddings find the fast singular value decay, which is a crucial indicator of the representation degeneration issue (Wang et al., 2020). With SVD to decompose both sequence output embeddings and item embeddings , we obtain singular values of and as and .
The fast singular value decay implies that the first singular value is significantly larger than others, i.e., and . It further implies the insufficient diversity of sequence and item embeddings because the determinant (re-scaled sum of singular values) of the embedding, i.e., the diversity from the Eq. (10), achieves a small value when the fast singular value decay happens (most singular values are small values).
4. Singular Spectrum Smoothing
Motivated by the theoretical connection between the representation degeneration and diversity via the determinant of embedding, we present our proposed SPMRec framework with a novel metric to measure the degree of representation degeneration and a novel singular spectrum smoothing regularization for alleviating the degeneration issue and controlling the diversity simultaneously.
4.1. Degree of Spectrum Smoothness
We propose a simple, intuitive, and straightforward metric to measure the degree of singular spectrum smoothness, which is calculated as the Area Under Singular value Curve (AUSC). The area under singular curve (AUSC) is calculated as the sum of normalized singular values as follows:
| (11) |
When the singular value curve decays fast, as observed in the degenerated examples in Fig. (2), the area under the singular curve (AUSC) is typically small because singular values other than the largest one are all small and all singular values are normalized. We can also see that when all singular values approximate the largest singular value, i.e., for all , the AUSC is maximized, in which the singular curve becomes flatter. For example, our toy example shown in Fig. (3) compares two singular curves, in which the left one is the fast decaying curve and the right one is an improved and more flat singular curve. The left fast decaying curve has an AUSC value of 13.64, while the right smoothed curve has an AUSC value of 26.73.
4.2. Dual Smoothing
We build upon the AUSC to propose a singular spectrum smoothing regularization as a surrogate of optimizing AUSC. With the discussion in Section 3.1, item and sequence degeneration issues are intertwined. Thus, we deploy the proposed singular spectrum smoothing regularization to both sequence output and item embeddings, which is referred to as dual smoothing. Specifically, the singular spectrum smoothing losses for both sequence and item are conducted as follows:
| (12) |
where is the sequence output embedding matrix of all users, and The singular spectrum smoothing loss is the lower bound of our proposed AUSC smoothness metric as follows:
| (13) |
The loss minimization of either or achieves the joint effects of
-
•
maximizing the nuclear norm (encouraging the sum of singular values),
-
•
minimizing the Frobenius norm (suppressing the largest singular value),
-
•
and enlarges more tail singular values.
When and are minimized, the nuclear norm is maximized, improving the determinant and diversity of and . We adopt the Frobenius norm instead of the largest singular value for more stable training. The minimization of and maximizes the AUSC of sequence embeddings and item embeddings, i.e., more smooth singular curves are introduced. Specifically, when the singular spectrum smoothing loss is minimized, the Frobenius norm is minimized so that the infinite norm of item embedding is alleviated. The largest singular value is suppressed.
Computational Efficiency: the computational complexity of singular values calculation can be reduced when and are conducted in batch, which is (Cui et al., 2020), and denotes the batch size and is the dimension size. Different from (Cui et al., 2021, 2020; Chen et al., 2022), we present the nuclear norm divided by the Frobenius norm on embeddings of sequence and item sides while only nuclear norm of the prediction outputs is maximized in (Cui et al., 2021, 2020; Chen et al., 2022).
4.3. Optimization with Dual Smoothing
With singular spectrum smoothing on both sequence output embeddings side and item side , the final optimization loss with the recommendation loss in Eq. (3) to be minimized is defined as follows:
| (14) |
where is the hyper-parameter for controlling the sequence output embeddings side smoothing weight, and is the hyper-parameter for controlling the item side smoothing weight contribution to the final loss minimization. The final recommendation list is generated by calculating the scores defined in Eq. (2) on all items for each user. The recommendation scores on all items are sorted in descending order to produce the top- list.
5. Experiments
We conduct several empirical studies to demonstrate the usefulness of the SPMRec and its components. We also analyze the improvements for a better understanding of the underlying mechanism. Specifically, we answer the following six research questions (RQs):
-
•
RQ1: Does SPMRec provide more satisfactory recommendations than state-of-the-art baselines?
-
•
RQ2: How does our item side spectrum smoothing affect the diversity and recommendation performance?
-
•
RQ3: Does SPMRec outperform existing degeneration solutions?
-
•
RQ4: How does each component of SPMRec contribute to the performance?
-
•
RQ5: Where do improvements of SPMRec come from?
| Dataset | #users | #items | #interactions | density |
|
|||
|---|---|---|---|---|---|---|---|---|
| Home | 66,519 | 28,237 | 551,682 | 0.03% | 8.3 | |||
| Beauty | 22,363 | 12,101 | 198,502 | 0.05% | 8.3 | |||
| Toys | 19,412 | 11,924 | 167,597 | 0.07% | 8.6 | |||
| Tools | 16,638 | 10,217 | 134,476 | 0.08% | 8.1 | |||
| Office | 4,905 | 2,420 | 53,258 | 0.44% | 10.8 | |||
| Total | 129K | 74K | 1.10M | - | - |
5.1. Datasets
We present the statistics of the dataset in Table 1. We evaluate all models in four benchmarks public Amazon review datasets111http://deepyeti.ucsd.edu/jianmo/amazon/index.html. We choose Beauty, Toys and Games (Toys), Tools and Home (Tools), and Office Products (Office) categories in our experiments as these four categories are widely adopted benchmark categories (Tang and Wang, 2018; Kang and McAuley, 2018; Sun et al., 2019; Fan et al., 2021; Li et al., 2020; Fan et al., 2022). We treat the existence of user-item reviews as positive user-item interactions. For each user, we sort the interacted items chronologically to form the user interaction sequence. The last interaction of the user sequence is used for testing and the second to last one for validation. We adopt the standard 5-core pre-processing setting on users (Tang and Wang, 2018; Kang and McAuley, 2018; Sun et al., 2019; Fan et al., 2021; Li et al., 2020; Fan et al., 2022) to filter out users with less than five interactions. The detailed dataset statistics are presented in Table 1.
5.2. Baselines and Hyper-parameter Grid Search
We compare the proposed SPMRec with state-of-the-art sequential recommendation methods. We only include the static method BPRMF (Rendle et al., 2012) due to the page limitation. For sequential methods, we compare Caser (Tang and Wang, 2018), SASRec (Kang and McAuley, 2018), DT4SR (Fan et al., 2021), BERT4Rec (Sun et al., 2019), FMLP-Rec (Zhou et al., 2022), and STOSA (Fan et al., 2022). DuoRec (Qiu et al., 2022) addresses the degeneration issue in contrastive learning for SR. Note that we use only one training negative sample (i.e., ) for models with the Cross-Entropy loss for fair comparisons (Ding et al., 2019; Chen et al., 2017; Mao et al., 2021).
5.3. All Items Ranking and Diversity Evaluation
We generate the top-N recommendation list for each user based on the dot-product between sequence output embedding and the entire item set in descending order. We rank all items for all models so that no item sampling bias is introduced in evaluation for fair comparisons (Krichene and Rendle, 2020). The evaluation includes classical top-N ranking metrics, Recall@N and NDCG@N. We present the averaged results over all test users. The test results are reported based on the best validation results. We report metrics in multiple Ns, including , which are widely adopted in most existing SR methods (Kang and McAuley, 2018; Sun et al., 2019; Fan et al., 2022).
We evaluate the diversity of the recommendation list for all test users in two widely adopted metrics, including the Intra-list diversity (Zhang and Hurley, 2008; Ziegler et al., 2005) and the Coverage@100 of item categories for each user’s top-N recommendation list. We focus on the top-10 ranking list for intra-list diversity calculation and top-100 for the coverage metric. The intra-list diversity is calculated as follows:
| (15) |
where denotes the top- recommendation list for the user , represents the cosine similarity, is the item embedding table defined in Section 2.2, and the reported diversity is the average diversity over all users. The larger value of diversity indicates higher intra-list diversity for the recommendation. Note that, we also found similar improvements in other larger s, such as .
| Dataset | Metric | BPRMF | Caser | SASRec | DT4SR | BERT4Rec | FMLP-Rec | STOSA | DuoRec | SPMRec | Imp. vs. SASRec | Improv. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Home | Recall@5 | 0.0096 | OOM | 0.0127 | 0.0129 | 0.0105 | 0.0118 | \ul0.0133 | 0.0130 | 0.0171 | +34.65% | +28.68% |
| NDCG@5 | 0.0062 | OOM | 0.0087 | 0.0082 | 0.0067 | 0.0086 | \ul0.0093 | 0.0088 | 0.0115 | +32.18% | +23.09% | |
| Recall@10 | 0.0152 | OOM | 0.0188 | 0.0193 | 0.0186 | 0.0177 | \ul0.0196 | 0.0185 | 0.0252 | +34.04% | +28.40% | |
| NDCG@10 | 0.0080 | OOM | 0.0107 | 0.0109 | 0.0093 | 0.0106 | \ul0.0113 | 0.0106 | 0.0140 | +30.84% | +23.89% | |
| Recall@40 | 0.0355 | OOM | 0.0432 | 0.0385 | \ul0.0470 | 0.0430 | 0.0427 | 0.0424 | 0.0548 | +26.85% | +16.47% | |
| NDCG@40 | 0.0126 | OOM | 0.0161 | \ul0.0169 | 0.0156 | 0.0161 | 0.0165 | 0.0157 | 0.0207 | +28.57% | +22.03% | |
| Diversity | 0.5914 | OOM | 0.6213 | 0.6412 | 0.6351 | 0.6344 | \ul0.6771 | 0.6711 | 0.7034 | +13.21% | +3.88% | |
| Cov@100 | 72.644 | OOM | 74.799 | 76.041 | 75.663 | 79.518 | 78.881 | 75.776 | 76.676 | +2.51% | - | |
| Beauty | Recall@5 | 0.0300 | 0.0309 | 0.0416 | 0.0449 | 0.0396 | 0.0469 | 0.0504 | \ul0.0505 | 0.0517 | +24.27% | +2.38% |
| NDCG@5 | 0.0189 | 0.0214 | 0.0274 | 0.0296 | 0.0257 | 0.0325 | 0.0351 | 0.0310 | \ul0.0345 | +25.91% | -1.71% | |
| Recall@10 | 0.0471 | 0.0407 | 0.0633 | 0.0695 | 0.0595 | 0.0586 | \ul0.0707 | 0.0685 | 0.0745 | +17.69% | +5.37% | |
| NDCG@10 | 0.0245 | 0.0246 | 0.0343 | 0.0375 | 0.0321 | 0.0362 | \ul0.0416 | 0.0375 | 0.0418 | +21.82% | +0.18% | |
| Recall@40 | 0.1089 | 0.0863 | 0.1342 | \ul0.1384 | 0.1285 | 0.0977 | 0.1367 | 0.1364 | 0.1451 | +8.12% | +4.84% | |
| NDCG@40 | 0.0383 | 0.0345 | 0.0503 | 0.0533 | 0.0476 | 0.0448 | \ul0.0565 | 0.0541 | 0.0577 | +14.71% | +2.12% | |
| Diversity | 0.5875 | 0.5436 | 0.6302 | 0.6530 | 0.6509 | 0.6358 | 0.6631 | \ul0.6691 | 0.7154 | +13.51% | +6.90% | |
| Cov@100 | 44.881 | 45.147 | 45.066 | 46.127 | 45.668 | 47.929 | 47.333 | 47.199 | 48.050 | +6.62% | +0.03% | |
| Tools | Recall@5 | 0.0216 | 0.0129 | 0.0284 | 0.0289 | 0.0189 | 0.0195 | \ul0.0312 | 0.0304 | 0.0350 | +23.23% | +12.18% |
| NDCG@5 | 0.0139 | 0.0091 | 0.0194 | 0.0196 | 0.0123 | 0.0166 | \ul0.0217 | 0.0201 | 0.0238 | +22.68% | +9.68% | |
| Recall@10 | 0.0334 | 0.0193 | 0.0427 | 0.0430 | 0.0319 | 0.0313 | \ul0.0468 | 0.0401 | 0.0513 | +20.14% | +9.62% | |
| NDCG@10 | 0.0177 | 0.0112 | 0.0240 | 0.0246 | 0.0165 | 0.0204 | \ul0.0267 | 0.0234 | 0.0290 | +20.83% | +8.61% | |
| Recall@40 | 0.0715 | 0.0680 | \ul0.0879 | 0.0861 | 0.0778 | 0.0785 | 0.0861 | 0.0867 | 0.1047 | +19.11% | +19.11% | |
| NDCG@40 | 0.0262 | 0.0235 | 0.0343 | 0.0342 | 0.0268 | 0.0271 | \ul0.0356 | 0.0345 | 0.0410 | +19.53% | +15.17% | |
| Diversity | 0.5663 | 0.5223 | 0.6108 | 0.6353 | 0.6389 | 0.6429 | \ul0.6549 | 0.6438 | 0.7494 | +22.69% | +14.43% | |
| Cov@100 | 60.781 | 63.473 | 62.871 | 67.134 | 66.743 | 68.545 | 67.441 | 67.851 | 68.212 | +8.50% | - | |
| Toys | Recall@5 | 0.0301 | 0.0240 | 0.0551 | 0.0550 | 0.0300 | \ul0.0625 | 0.0577 | 0.0580 | 0.0631 | +14.52% | +0.96% |
| NDCG@5 | 0.0194 | 0.0210 | 0.0377 | 0.0360 | 0.0206 | \ul0.0423 | 0.0412 | 0.0401 | 0.0431 | +14.32% | +1.89% | |
| Recall@10 | 0.0460 | 0.0262 | 0.0797 | \ul0.0835 | 0.0466 | 0.0820 | 0.0800 | 0.0784 | 0.0852 | +6.90% | +2.04% | |
| NDCG@10 | 0.0245 | 0.0231 | 0.0465 | 0.0437 | 0.0260 | \ul0.0485 | 0.0481 | 0.0461 | 0.0503 | +8.17% | +3.71% | |
| Recall@40 | 0.1007 | 0.0909 | 0.1453 | \ul0.1478 | 0.0982 | 0.1406 | 0.1469 | 0.1452 | 0.1492 | +2.68% | +0.95% | |
| NDCG@40 | 0.0368 | 0.0346 | 0.0604 | 0.0590 | 0.0376 | \ul0.0617 | 0.0611 | 0.0607 | 0.0647 | +7.12% | +4.86% | |
| Diversity | 0.6005 | 0.5924 | 0.6635 | 0.6706 | 0.6789 | 0.6895 | \ul0.6948 | 0.6936 | 0.7275 | +9.65% | +4.71% | |
| Cov@100 | 42.981 | 44.217 | 43.444 | 45.662 | 44.891 | 49.507 | 46.189 | 46.771 | 47.572 | +9.50% | - | |
| Office | Recall@5 | 0.0214 | 0.0302 | 0.0656 | 0.0630 | 0.0485 | 0.0508 | \ul0.0677 | 0.0665 | 0.0714 | +8.84% | +5.47% |
| NDCG@5 | 0.0144 | 0.0186 | 0.0428 | 0.0421 | 0.0309 | 0.0343 | \ul0.0461 | 0.0456 | 0.0489 | +14.25% | +6.07% | |
| Recall@10 | 0.0306 | 0.0550 | 0.0989 | 0.0940 | 0.0848 | 0.0977 | \ul0.1021 | 0.1005 | 0.1036 | +4.75% | +1.47% | |
| NDCG@10 | 0.0173 | 0.0266 | 0.0534 | 0.0521 | 0.0426 | 0.0497 | \ul0.0572 | 0.0556 | 0.0593 | +11.05% | +3.67% | |
| Recall@40 | 0.0718 | 0.1549 | 0.2251 | 0.2186 | 0.2230 | 0.1836 | \ul0.2346 | 0.2271 | 0.2367 | +5.15% | +0.89% | |
| NDCG@40 | 0.0266 | 0.0487 | 0.0815 | 0.0797 | 0.0729 | 0.0685 | \ul0.0858 | 0.0817 | 0.0888 | +8.96% | +3.50% | |
| Diversity | 0.5920 | 0.5797 | 0.6167 | 0.6681 | 0.6551 | 0.6766 | \ul0.6889 | 0.6857 | 0.7350 | +19.18% | +6.19% | |
| Cov@100 | 49.887 | 50.243 | 51.299 | 51.341 | 51.001 | 51.335 | 51.661 | 51.514 | 52.733 | +2.87% | +2.08% |
5.4. Overall Comparisons (RQ1)
We present the overall performance comparison with relevant state-of-the-art baselines in Table 2. From Table 2, we can easily conclude the superiority of SPMRec in providing sequential recommendations in various datasets and achieving not only better performance but also more diversity. We have several observations to conclude as follows:
-
•
SPMRec achieves the best performance and diversity, and outperforms SASRec with large improvement margins. In most performance metrics and all datasets, SPMRec significantly outperforms the second-best baseline with 0.52% to 12.33% in ranking performance and 4.71% to 14.41% in diversity. The improvements demonstrate the effectiveness of SPMRec in the sequential recommendation, while the recommendation diversity is also noticeably improved. Furthermore, as SPMRec is built on top of the original implementation of SASRec (Kang and McAuley, 2018), we observe 6.92% to 22.53% relative improvements over SASRec. We argue that the improvements originate from the singular spectrum smoothings on both sequence and item sides.
-
•
SPMRec can achieve better balance between recommendation quality and diversity. Comparing the diversity of SPMRec and baselines, we can observe that SPMRec consistently achieves better diversity results while having better performances, indicating the better capability of SPMRec in balancing the recommendation quality and diversity.
-
•
SPMRec achieves performance larger improvements in sparser datasets. Comparing SPMRec and SASRec, we can observe at least 17% improvements in both Beauty and Tools categories datasets, which have lower densities of 0.05% and 0.07%, respectively. The recommendation diversity is also significantly improved, especially for tools with a 14.43% improvement. However, in Toys and Office datasets with higher densities of 0.08% and 0.44%, the improvements are at most 14%. This observation demonstrates that the proposed singular spectrum smoothing SPMRec benefits sparser datasets, especially for datasets with a large portion of short sequences.
-
•
The consideration of Frobenius norm benefits the recommendation and diversity. STOSA adopts the sum of two L2 distances on mean and covariance embeddings and DuoRec utilizes the uniformity loss based on the exponential L2 distance. We can observe that STOSA and DuoRec both outperform the dot-product-based SASRec framework in recommendation quality and diversity. This observation further demonstrates the need to consider the Frobenius norm in embedding learning. Moreover, SPMRec performs better than STOSA and DuoRec, demonstrating the necessity of considering the regularization from the singular spectrum perspective.







5.5. Diversity and Item Smoothing (RQ2)
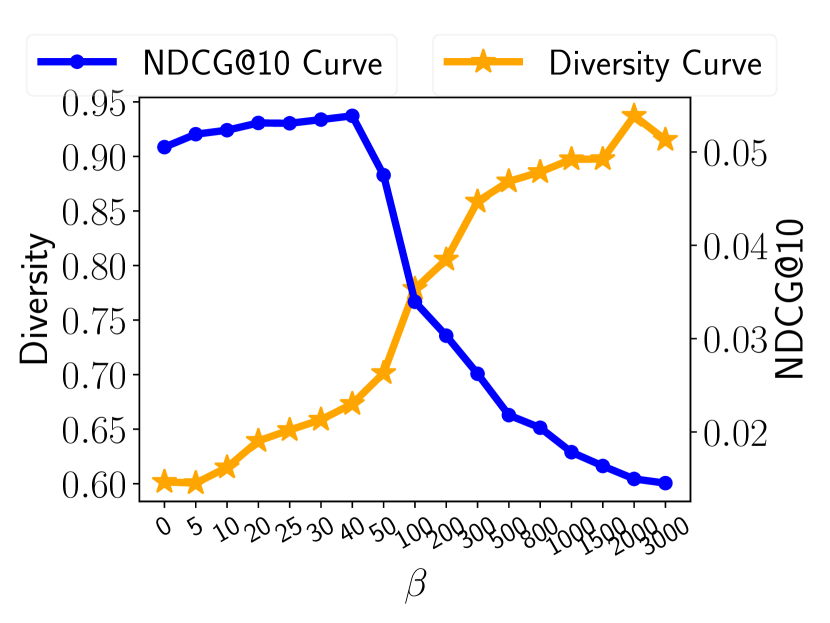
Item Spectrum Smoothing controlled by is closely related to the recommendation diversity. We demonstrate a strong connection between our item spectrum smoothing and the recommendation diversity by showing the relationship of and the diversity, as shown in Fig. (4). In Fig. (4), the x-axis denotes the value of . As the becomes larger, we can observe that the diversity consistently increases, in all four datasets, demonstrating the strong connection between the recommendation diversity and our proposed item spectrum smoothing component.
Moreover, the recommendation performance drops when we demand too high recommendation diversity. Another observation is that the NDCG@10 drops significantly when we set to a too-large value, which also indicates a higher diversity. This observation demonstrates that a proper selection of can achieve satisfactory recommendation performance and diversity simultaneously. However, demanding higher diversity can hurt the recommendation performance.
| Dataset | Metric | SASRec | SASRec+CosReg | SASRec+Euclidean | SPMRec |
|---|---|---|---|---|---|
| Beauty | Recall@5 | 0.0416 | 0.0410 | 0.0326 | 0.0517 |
| NDCG@5 | 0.0274 | 0.0250 | 0.0212 | 0.0345 | |
| Recall@10 | 0.0633 | 0.0609 | 0.0487 | 0.0745 | |
| NDCG@10 | 0.0343 | 0.0314 | 0.0264 | 0.0418 | |
| Tools | Recall@5 | 0.0284 | 0.0290 | 0.0230 | 0.0350 |
| NDCG@5 | 0.0194 | 0.0194 | 0.0145 | 0.0238 | |
| Recall@10 | 0.0427 | 0.0435 | 0.0359 | 0.0513 | |
| NDCG@10 | 0.0240 | 0.0240 | 0.0186 | 0.0290 | |
| Toys | Recall@5 | 0.0551 | 0.0457 | 0.0537 | 0.0631 |
| NDCG@5 | 0.0377 | 0.0302 | 0.0375 | 0.0431 | |
| Recall@10 | 0.0797 | 0.0658 | 0.0717 | 0.0852 | |
| NDCG@10 | 0.0465 | 0.0367 | 0.0432 | 0.0503 | |
| Office | Recall@5 | 0.0656 | 0.0612 | 0.0561 | 0.0714 |
| NDCG@5 | 0.0428 | 0.0400 | 0.0376 | 0.0489 | |
| Recall@10 | 0.0989 | 0.0919 | 0.0862 | 0.1036 | |
| NDCG@10 | 0.0534 | 0.0500 | 0.0472 | 0.0593 |
5.6. Degeneration Methods Comparison (RQ3)
We compare the proposed SPMRec with spectrum smoothing regularization with existing methods for alleviating the degeneration issue in word embeddings learning, including the cosine regularization (Gao et al., 2019) as follows:
| (16) |
and the Euclidean method (Zhang et al., 2020) as follows:
| (17) |
We apply the cosine and Euclidean regularization methods to both sides. We report the best grid searched results of all regularization methods in Table 3. Note that the uniformity property adopted by DuoRec and DirectAU (Qiu et al., 2022; Wang et al., 2022b) falls into the Euclidean methods category.
As shown in Table 3, neither cosine regularization or Euclidean regularization can consistently outperform the original SASRec without any regularization. Arguably, the potential reason is that neither of these two methods constrains the Frobenius norm of embeddings, which is the upper bound of the largest singular value, as discussed in Section 3.1. When cosine regularization and the Euclidean method are minimized, the naive solution is for all if we do not consider the supervised recommendation loss. Moreover, different from the word embedding task, sequences in the recommendation task are shorter on average, posing a greater challenge in addressing the degeneration in SR. However, our proposed singular spectrum smoothing method SPMRec minimizes the Frobenius norm while maximizing the nuclear norm, achieving the goals of smoothing the singular value curve and suppressing the largest singular value simultaneously.
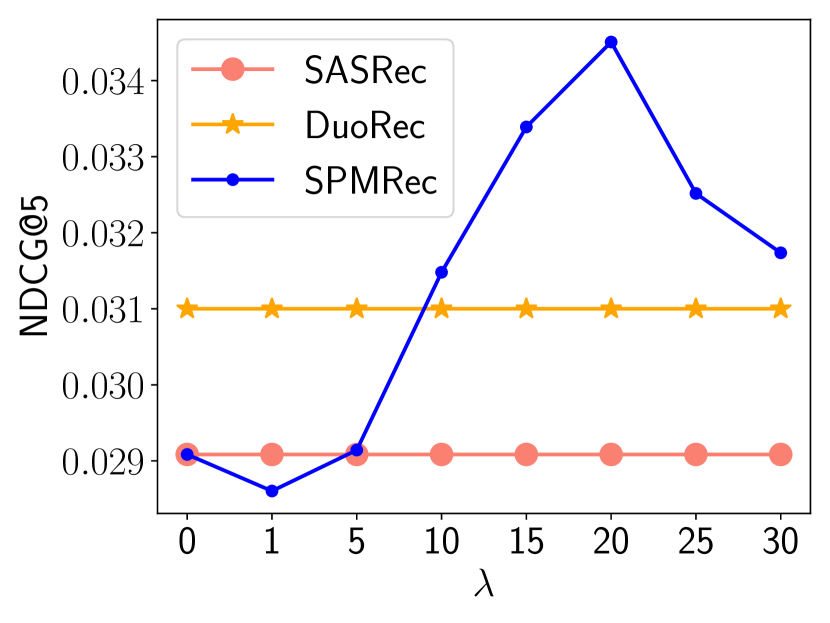






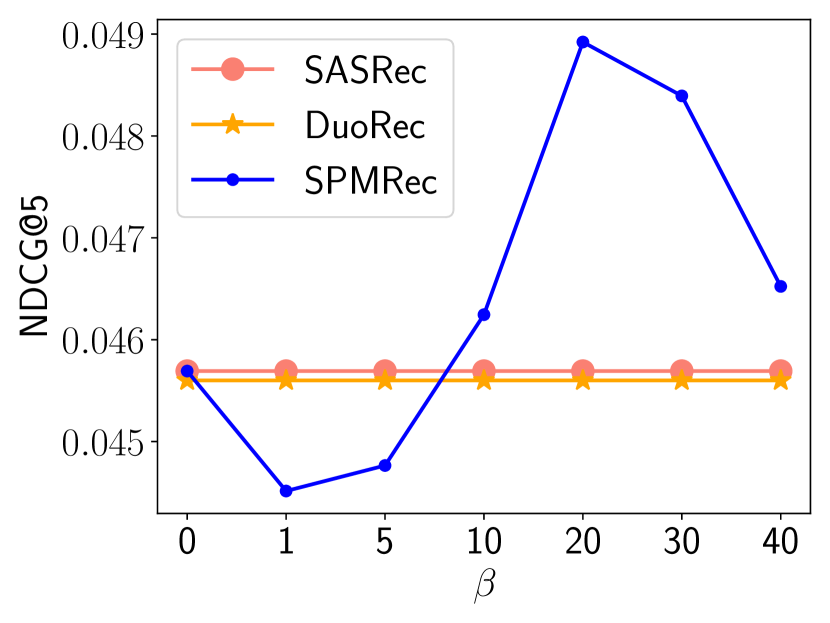
5.7. Ablation Study (RQ4)
We conduct the ablation study to show the effectiveness of two important components, including singular spectrum smoothing for sequence output and item embeddings. We investigate the smoothing weights (for sequence output embeddings smoothing) and (for item embeddings smoothing) in Fig. (6) and Fig. (7), respectively. We include the SASRec (without any regularization) and DuoRec (with uniformity regularization). Note that the special case ( and ) is included, which is SASRec without any regularization. Additionally, the sequence outputs and item embeddings spectrum smoothing losses are in different scales ( for sequence embeddings and for item embeddings). Hence, the scales of and are different with the purpose of balancing the contributions of two regularizations.
5.7.1. Sequence Output Embedding Smoothing Weight
We present the performance values with different values of in Fig. (6) for all four datasets. Fig. (6) shows that the proper selection of improves the performance significantly. Moreover, most values achieve comparative and better performances than SASRec. These observations show that the sequence output embedding spectrum smoothing is beneficial for the sequential recommendation.
5.7.2. Item Embedding Smoothing Weight
The NDCG@5 values of different are shown in Fig. (7), which is controlling the spectrum smoothing component’s contribution. The analysis is conducted in all four datasets used. Overall, when becomes larger, i.e., having a larger contribution to the overall loss, the performance increases. It shows the effectiveness of item embeddings singular spectrum smoothing for performance improvements.
5.8. Improvements Analysis (RQ5)
5.8.1. Improvements w.r.t. Sequence Length
SPMRec is highly effective in short sequences recommendation. We group sequences (users) based on the number of training interactions (sequence length) of users. Within each group, we average the testing performances of sequences in the group. The comparisons on each group are shown in Fig. (8). We can observe that SPMRec achieves significant improvements in short sequences. Specifically, the improvements over the best STOSA range from 7.21% to 23.04%. The recommendation for short sequences is challenging due to limited interaction signals, which is known as the cold start problem. SPMRec regularizes the sequence output embeddings and prevents the degeneration so that short sequences can be distinguishable and are properly modeled. We can also observe that SPMRec has inferior performances in the longest sequence group, which is even worse than SASRec in the Toys dataset. However, the short sequences are in majority in both the used datasets and practical applications. With the proposed singular spectrum smoothing, SPMRec benefits short sequences with the sacrifices of long sequences.












5.9. Sequential User Degeneration Analysis (RQ5)
We visualize the singular values curve of sequence output embedding for our proposed SPMRec and SASRec, as shown in Fig. (10). We can observe that the proposed SPMRec has a smoother decaying curve than SASRec. Moreover, for SPMRec, the degrees of spectrum smoothness for all four datasets are 26.34 for Beauty, 20.76 for Tools, 20.25 for Toys, and 19.24 for Office. However, SASRec has lower degrees for spectrum smoothness as 19.54 for Beauty, 17.10 for Tools, 17.00 for Toys, and 13.67 for Office. SPMRec consistently has larger degrees of spectrum smoothness than SASRec, which demonstrates the effectiveness of SPMRec in preventing sequences from the degeneration for the sequential recommendation.
6. Related Work
6.1. Sequential Recommendation
Sequential Recommendation (SR) is a technique that encodes the temporal interactions of each user as a sequence and uses the encoded behaviors to infer their preferences. The main idea behind SR is to model the transitions between items within sequences. The earliest SR methods used Markovian approaches, such as FPMC (Rendle et al., 2010) and Fossil (He and McAuley, 2016), with the assumption that the item prediction depends only on the previous interacted items Another line of work utilizes the Recurrent Neural Network (RNN) as the base model for modeling sequential interactions. Several works adopt RNNs to address the SR problem, including GRU4Rec (Hidasi et al., 2015), HGN (Ma et al., 2019; Peng et al., 2021), HRNN (Quadrana et al., 2017), and RRN (Wu et al., 2017). Different variants of RNNs are proposed, such as the original GRU in GRU4Rec and hierarchical RNN in HGN and HRNN. The third line of methods to solve the SR problem is using the Convolution Neural Network (CNN), with the interpretation of a sequence of item embeddings as an image, including Caser (Tang and Wang, 2018), CosRec (Yan et al., 2019), and NextItNet (Yuan et al., 2019). The recent success of the self-attention module (Vaswani et al., 2017) inspires the adaptation of Transformer to the sequential recommendation task. The self-attention module captures the sequential high-order item transitions by modeling attention from all items in the sequence. SASRec (Kang and McAuley, 2018) is the earliest work of applying Transformer to SR. BERT4Rec (Sun et al., 2019) builds upon BERT (Devlin et al., 2019) with bidirectional Transformers for SR. FMLP-Rec (Zhou et al., 2022) proposes an all-MLP architecture in the Transformer for SR. Several variants of Transformers (Fan et al., 2021; Li et al., 2020; Wu et al., 2020; Liu et al., 2021) are further proposed.
6.2. Representation Degeneration
The representation degeneration problem describes the issue of learned embeddings being narrowly distributed in a small cone (Gao et al., 2019). The degeneration issue is firstly proposed in the word representations learning problem. As shown in (Gao et al., 2019), words from text data follow the long-tail distribution, which degenerates the representation learning process. Theoretically, it causes the narrow distribution of words in the representation latent space (Gao et al., 2019). Moreover, an empirical analysis (Yu et al., 2022) shows that the learning of tail words degenerates the representation optimization of frequent words. An important analysis in (Wang et al., 2020) shows that degeneration is closely related to the fast decaying singular values distribution. In other words, the largest singular value is significantly larger than all other singular values.
Distinct from the natural language processing (NLP) area, SR still has several unique characteristics. For example, sequences are short (data sparsity in recommendation systems), while sentences/paragraphs in NLP are typically long. This distinct characteristic introduces additional challenges for SR, where the degeneration issue can also happen in the sequence output embeddings. DuoRec (Qiu et al., 2022) observes that the representation degeneration issue also exists in the self-supervised SR, with data augmentations. DuoRec and DirectAU (Wang et al., 2022b) optimizes the uniformity property in the in-batch representations to enforce the representations to be uniformly distributed, where the uniformity is based on the Euclidean distance. This work connects the item embeddings degeneration with the degeneration of sequence representations. The intertwining of both sequence and item rank degeneration is rarely discussed before in SR. Moreover, some solutions from NLP to the degeneration problem only apply to the item side, including the CosReg (Gao et al., 2019) based on cosine similarities, Euclidean regularization based on learned word similarities (Zhang et al., 2020), spectrum control (Wang et al., 2020; Yan et al., 2022), and gradient gating (Yu et al., 2022).
As discussed in (de Souza Pereira Moreira et al., 2021), natural language processing (NLP) and sequential recommendation (SR) share multiple similarities, including both learning discrete tokens learning (words in NLP and items in SR) and long-tail distribution of frequency for both words and items. With this inspiration, DuoRec (Qiu et al., 2022) observes that the representation degeneration issue also exists in the self-supervised SR, with data augmentations. DuoRec optimizes the uniformity property in the in-batch augmented representations to alleviate the degeneration issue in contrastive learning, where the uniformity is based on the Euclidean distance.
7. Conclusion
We theoretically and empirically identify the relationship between the representation degeneration and recommendation diversity. Motivated by this connection, we propose a novel metric to measure the degree of degeneration as the area under the singular value curve (AUSC) to constrain the sequence and item embeddings learning. We further propose a singular spectrum smoothing regularization as a surrogate of AUSC to alleviate the degeneration and improve the diversity simultaneously. We empirically demonstrate the effectiveness of the proposed singular spectrum smoothing regularization in recommendation performances, especially for short sequences and popular items. We also empirically demonstrate a strong connection between the proposed singular spectrum smoothing regularization and the recommendation diversity.
References
- (1)
- Chen et al. (2022) Chao Chen, Zijian Gao, Kele Xu, Sen Yang, Yiying Li, Bo Ding, Dawei Feng, and Huaimin Wang. 2022. Nuclear Norm Maximization Based Curiosity-Driven Learning. arXiv preprint arXiv:2205.10484 (2022).
- Chen et al. (2018) Laming Chen, Guoxin Zhang, and Eric Zhou. 2018. Fast greedy map inference for determinantal point process to improve recommendation diversity. Advances in Neural Information Processing Systems 31 (2018).
- Chen et al. (2021) Minmin Chen, Yuyan Wang, Can Xu, Ya Le, Mohit Sharma, Lee Richardson, Su-Lin Wu, and Ed Chi. 2021. Values of user exploration in recommender systems. In Proceedings of the 15th ACM Conference on Recommender Systems. 85–95.
- Chen et al. (2017) Ting Chen, Yizhou Sun, Yue Shi, and Liangjie Hong. 2017. On sampling strategies for neural network-based collaborative filtering. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 767–776.
- Cui et al. (2020) Shuhao Cui, Shuhui Wang, Junbao Zhuo, Liang Li, Qingming Huang, and Qi Tian. 2020. Towards Discriminability and Diversity: Batch Nuclear-Norm Maximization Under Label Insufficient Situations. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2020, Seattle, WA, USA, June 13-19, 2020. Computer Vision Foundation / IEEE, 3940–3949. https://doi.org/10.1109/CVPR42600.2020.00400
- Cui et al. (2021) Shuhao Cui, Shuhui Wang, Junbao Zhuo, Liang Li, Qingming Huang, and Qi Tian. 2021. Fast Batch Nuclear-norm Maximization and Minimization for Robust Domain Adaptation. CoRR abs/2107.06154 (2021). arXiv:2107.06154 https://arxiv.org/abs/2107.06154
- de Souza Pereira Moreira et al. (2021) Gabriel de Souza Pereira Moreira, Sara Rabhi, Jeong Min Lee, Ronay Ak, and Even Oldridge. 2021. Transformers4rec: Bridging the gap between nlp and sequential/session-based recommendation. In Proceedings of the 15th ACM Conference on Recommender Systems. 143–153.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), Jill Burstein, Christy Doran, and Thamar Solorio (Eds.). Association for Computational Linguistics, 4171–4186. https://doi.org/10.18653/v1/n19-1423
- Ding et al. (2019) Jingtao Ding, Yuhan Quan, Xiangnan He, Yong Li, and Depeng Jin. 2019. Reinforced Negative Sampling for Recommendation with Exposure Data.. In IJCAI. 2230–2236.
- Domingues et al. (2012) Marcos Aurélio Domingues, Fabien Gouyon, Alípio Mário Jorge, José Paulo Leal, João Vinagre, Luís Lemos, and Mohamed Sordo. 2012. Combining usage and content in an online music recommendation system for music in the long-tail. In Proceedings of the 21st International Conference on World Wide Web. 925–930.
- Fan et al. (2022) Ziwei Fan, Zhiwei Liu, Alice Wang, Zahra Nazari, Lei Zheng, Hao Peng, and Philip S Yu. 2022. Sequential recommendation via stochastic self-attention. In Proceedings of the ACM Web Conference 2022. 2036–2047.
- Fan et al. (2021) Ziwei Fan, Zhiwei Liu, Shen Wang, Lei Zheng, and Philip S Yu. 2021. Modeling sequences as distributions with uncertainty for sequential recommendation. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management. 3019–3023.
- Gao et al. (2023) Chongming Gao, Kexin Huang, Jiawei Chen, Yuan Zhang, Biao Li, Peng Jiang, Shiqi Wang, Zhong Zhang, and Xiangnan He. 2023. Alleviating Matthew Effect of Offline Reinforcement Learning in Interactive Recommendation. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval (Taipei, Taiwan) (SIGIR ’23). Association for Computing Machinery, New York, NY, USA, 238–248. https://doi.org/10.1145/3539618.3591636
- Gao et al. (2019) Jun Gao, Di He, Xu Tan, Tao Qin, Liwei Wang, and Tie-Yan Liu. 2019. Representation Degeneration Problem in Training Natural Language Generation Models. In 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, May 6-9, 2019. OpenReview.net. https://openreview.net/forum?id=SkEYojRqtm
- Ge et al. (2020) Yingqiang Ge, Shuya Zhao, Honglu Zhou, Changhua Pei, Fei Sun, Wenwu Ou, and Yongfeng Zhang. 2020. Understanding echo chambers in e-commerce recommender systems. In Proceedings of the 43rd international ACM SIGIR conference on research and development in information retrieval. 2261–2270.
- Goel et al. (2010) Sharad Goel, Andrei Broder, Evgeniy Gabrilovich, and Bo Pang. 2010. Anatomy of the long tail: ordinary people with extraordinary tastes. In Proceedings of the third ACM international conference on Web search and data mining. 201–210.
- He and McAuley (2016) Ruining He and Julian McAuley. 2016. Fusing similarity models with markov chains for sparse sequential recommendation. In 2016 IEEE 16th International Conference on Data Mining (ICDM). IEEE, 191–200.
- Hidasi et al. (2015) Balázs Hidasi, Alexandros Karatzoglou, Linas Baltrunas, and Domonkos Tikk. 2015. Session-based recommendations with recurrent neural networks. arXiv preprint arXiv:1511.06939 (2015).
- Horn and Johnson (2012) Roger A Horn and Charles R Johnson. 2012. Matrix analysis. Cambridge university press.
- Huang et al. (2021) Yanhua Huang, Weikun Wang, Lei Zhang, and Ruiwen Xu. 2021. Sliding spectrum decomposition for diversified recommendation. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. 3041–3049.
- Kang and McAuley (2018) Wang-Cheng Kang and Julian McAuley. 2018. Self-attentive sequential recommendation. In 2018 IEEE International Conference on Data Mining (ICDM). IEEE, 197–206.
- Krichene and Rendle (2020) Walid Krichene and Steffen Rendle. 2020. On sampled metrics for item recommendation. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 1748–1757.
- Kulesza et al. (2012) Alex Kulesza, Ben Taskar, et al. 2012. Determinantal point processes for machine learning. Foundations and Trends® in Machine Learning 5, 2–3 (2012), 123–286.
- Li et al. (2020) Jiacheng Li, Yujie Wang, and Julian McAuley. 2020. Time interval aware self-attention for sequential recommendation. In Proceedings of the 13th international conference on web search and data mining. 322–330.
- Liu et al. (2022) Yuli Liu, Christian Walder, and Lexing Xie. 2022. Determinantal Point Process Likelihoods for Sequential Recommendation. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. 1653–1663.
- Liu et al. (2021) Zhiwei Liu, Ziwei Fan, Yu Wang, and Philip S. Yu. 2021. Augmenting Sequential Recommendation with Pseudo-Prior Items via Reversely Pre-Training Transformer. Association for Computing Machinery, New York, NY, USA, 1608–1612. https://doi.org/10.1145/3404835.3463036
- Ma et al. (2019) Chen Ma, Peng Kang, and Xue Liu. 2019. Hierarchical gating networks for sequential recommendation. In Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining. 825–833.
- Mahabadi et al. (2019) Sepideh Mahabadi, Piotr Indyk, Shayan Oveis Gharan, and Alireza Rezaei. 2019. Composable core-sets for determinant maximization: A simple near-optimal algorithm. In International Conference on Machine Learning. PMLR, 4254–4263.
- Mao et al. (2021) Kelong Mao, Jieming Zhu, Jinpeng Wang, Quanyu Dai, Zhenhua Dong, Xi Xiao, and Xiuqiang He. 2021. SimpleX: A Simple and Strong Baseline for Collaborative Filtering. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management. 1243–1252.
- Mirrokni and Zadimoghaddam (2015) Vahab Mirrokni and Morteza Zadimoghaddam. 2015. Randomized composable core-sets for distributed submodular maximization. In Proceedings of the forty-seventh annual ACM symposium on Theory of computing. 153–162.
- Peng et al. (2021) Bo Peng, Zhiyun Ren, Srinivasan Parthasarathy, and Xia Ning. 2021. HAM: hybrid associations models for sequential recommendation. IEEE Transactions on Knowledge and Data Engineering (2021).
- Qiu et al. (2022) Ruihong Qiu, Zi Huang, Hongzhi Yin, and Zijian Wang. 2022. Contrastive learning for representation degeneration problem in sequential recommendation. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining. 813–823.
- Quadrana et al. (2017) Massimo Quadrana, Alexandros Karatzoglou, Balázs Hidasi, and Paolo Cremonesi. 2017. Personalizing session-based recommendations with hierarchical recurrent neural networks. In Proceedings of the Eleventh ACM Conference on Recommender Systems. 130–137.
- Rendle et al. (2012) Steffen Rendle, Christoph Freudenthaler, Zeno Gantner, and Lars Schmidt-Thieme. 2012. BPR: Bayesian personalized ranking from implicit feedback. arXiv preprint arXiv:1205.2618 (2012).
- Rendle et al. (2010) Steffen Rendle, Christoph Freudenthaler, and Lars Schmidt-Thieme. 2010. Factorizing personalized markov chains for next-basket recommendation. In Proceedings of the 19th international conference on World wide web. 811–820.
- Sun et al. (2019) Fei Sun, Jun Liu, Jian Wu, Changhua Pei, Xiao Lin, Wenwu Ou, and Peng Jiang. 2019. BERT4Rec: Sequential recommendation with bidirectional encoder representations from transformer. In Proceedings of the 28th ACM international conference on information and knowledge management. 1441–1450.
- Tang and Wang (2018) Jiaxi Tang and Ke Wang. 2018. Personalized top-n sequential recommendation via convolutional sequence embedding. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining. 565–573.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Advances in neural information processing systems. 5998–6008.
- Wang et al. (2022b) Chenyang Wang, Yuanqing Yu, Weizhi Ma, Min Zhang, Chong Chen, Yiqun Liu, and Shaoping Ma. 2022b. Towards Representation Alignment and Uniformity in Collaborative Filtering. In KDD ’22: The 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, August 14 - 18, 2022, Aidong Zhang and Huzefa Rangwala (Eds.). ACM, 1816–1825. https://doi.org/10.1145/3534678.3539253
- Wang et al. (2018) Hao Wang, Zonghu Wang, and Weishi Zhang. 2018. Quantitative analysis of Matthew effect and sparsity problem of recommender systems. In 2018 IEEE 3rd International Conference on Cloud Computing and Big Data Analysis (ICCCBDA). IEEE, 78–82.
- Wang et al. (2020) Lingxiao Wang, Jing Huang, Kevin Huang, Ziniu Hu, Guangtao Wang, and Quanquan Gu. 2020. Improving neural language generation with spectrum control. In International Conference on Learning Representations.
- Wang et al. (2022a) Yuyan Wang, Mohit Sharma, Can Xu, Sriraj Badam, Qian Sun, Lee Richardson, Lisa Chung, Ed H Chi, and Minmin Chen. 2022a. Surrogate for long-term user experience in recommender systems. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. 4100–4109.
- Wilhelm et al. (2018) Mark Wilhelm, Ajith Ramanathan, Alexander Bonomo, Sagar Jain, Ed H Chi, and Jennifer Gillenwater. 2018. Practical diversified recommendations on youtube with determinantal point processes. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management. 2165–2173.
- Wu et al. (2017) Chao-Yuan Wu, Amr Ahmed, Alex Beutel, Alexander J Smola, and How Jing. 2017. Recurrent recommender networks. In Proceedings of the tenth ACM international conference on web search and data mining. 495–503.
- Wu et al. (2020) Liwei Wu, Shuqing Li, Cho-Jui Hsieh, and James Sharpnack. 2020. SSE-PT: Sequential recommendation via personalized transformer. In Fourteenth ACM Conference on Recommender Systems. 328–337.
- Yan et al. (2019) An Yan, Shuo Cheng, Wang-Cheng Kang, Mengting Wan, and Julian McAuley. 2019. CosRec: 2D convolutional neural networks for sequential recommendation. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management. 2173–2176.
- Yan et al. (2022) Hanqi Yan, Lin Gui, Wenjie Li, and Yulan He. 2022. Addressing token uniformity in transformers via singular value transformation. In Uncertainty in Artificial Intelligence. PMLR, 2181–2191.
- Yang et al. (2023) Liangwei Yang, Shengjie Wang, Yunzhe Tao, Jiankai Sun, Xiaolong Liu, Philip S Yu, and Taiqing Wang. 2023. DGRec: Graph Neural Network for Recommendation with Diversified Embedding Generation. In Proceedings of the Sixteenth ACM International Conference on Web Search and Data Mining. 661–669.
- Yu et al. (2022) Sangwon Yu, Jongyoon Song, Heeseung Kim, Seongmin Lee, Woo-Jong Ryu, and Sungroh Yoon. 2022. Rare Tokens Degenerate All Tokens: Improving Neural Text Generation via Adaptive Gradient Gating for Rare Token Embeddings. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), ACL 2022, Dublin, Ireland, May 22-27, 2022, Smaranda Muresan, Preslav Nakov, and Aline Villavicencio (Eds.). Association for Computational Linguistics, 29–45. https://doi.org/10.18653/v1/2022.acl-long.3
- Yuan et al. (2019) Fajie Yuan, Alexandros Karatzoglou, Ioannis Arapakis, Joemon M Jose, and Xiangnan He. 2019. A simple convolutional generative network for next item recommendation. In Proceedings of the twelfth ACM international conference on web search and data mining. 582–590.
- Zadeh et al. (2017) Sepehr Zadeh, Mehrdad Ghadiri, Vahab Mirrokni, and Morteza Zadimoghaddam. 2017. Scalable feature selection via distributed diversity maximization. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 31.
- Zhang and Hurley (2008) Mi Zhang and Neil Hurley. 2008. Avoiding monotony: improving the diversity of recommendation lists. In Proceedings of the 2008 ACM conference on Recommender systems. 123–130.
- Zhang et al. (2023) Yin Zhang, Ruoxi Wang, Derek Zhiyuan Cheng, Tiansheng Yao, Xinyang Yi, Lichan Hong, James Caverlee, and Ed H Chi. 2023. Empowering Long-tail Item Recommendation through Cross Decoupling Network (CDN). In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. 5608–5617.
- Zhang et al. (2020) Zhong Zhang, Chongming Gao, Cong Xu, Rui Miao, Qinli Yang, and Junming Shao. 2020. Revisiting Representation Degeneration Problem in Language Modeling. In Findings of the Association for Computational Linguistics: EMNLP 2020, Online Event, 16-20 November 2020 (Findings of ACL, Vol. EMNLP 2020), Trevor Cohn, Yulan He, and Yang Liu (Eds.). Association for Computational Linguistics, 518–527. https://doi.org/10.18653/v1/2020.findings-emnlp.46
- Zhou et al. (2020) Kun Zhou, Hui Wang, Wayne Xin Zhao, Yutao Zhu, Sirui Wang, Fuzheng Zhang, Zhongyuan Wang, and Ji-Rong Wen. 2020. S3-rec: Self-supervised learning for sequential recommendation with mutual information maximization. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management. 1893–1902.
- Zhou et al. (2022) Kun Zhou, Hui Yu, Wayne Xin Zhao, and Ji-Rong Wen. 2022. Filter-enhanced MLP is all you need for sequential recommendation. In Proceedings of the ACM Web Conference 2022. 2388–2399.
- Ziegler et al. (2005) Cai-Nicolas Ziegler, Sean M McNee, Joseph A Konstan, and Georg Lausen. 2005. Improving recommendation lists through topic diversification. In Proceedings of the 14th international conference on World Wide Web. 22–32.
Appendix A Baselines and Hyper-parameters Grid Search
We implement SPMRec with Pytorch based on the S3-Rec (Zhou et al., 2020) code base. We grid search all parameters and report the test performance based on the best validation results. We search the representation dimension in , maximum sequence length from , learning rate in , the regularization control weight from , dropout rate from for all methods. For sequential methods, we search number of layers from , and number of heads in . We adopt the early stopping strategy that model optimization stops when the validation MRR does not increase for 50 epochs. The followings are the model specific hyper-parameters search ranges of baselines:
-
•
BPR222https://github.com/xiangwang1223/neural_graph_collaborative_filtering: BPR is the most classical collaborative filtering method for personalized ranking with implicit feedbacks. We search the learning rate in and regularization weight from .
-
•
Caser333https://github.com/graytowne/caser_pytorch: A CNN-based sequential recommendation method that views the sequence embedding matrix as an image and applies convolution operators to it. We search the length from , and from .
-
•
SASRec444https://github.com/RUCAIBox/CIKM2020-S3Rec: The state-of-the-art sequential method that depends on the Transformer architecture. We search the dropout rate from .
-
•
BERT4Rec555https://github.com/FeiSun/BERT4Rec: This method extends SASRec to model bidirectional item transitions with standard Cloze objective. We search the mask probability from the range of .
-
•
DT4SR666https://github.com/DyGRec/DT4SR: A metric learning-base sequential method that models items as distributions and proposes mean and covariance Transformers. We search the dropout rate from .
-
•
STOSA777https://github.com/zfan20/STOSA: A metric learning-base sequential method that models items as distributions and proposes a Wasserstein self-attention module. We search the dropout rate from .
-
•
DuoRec:888https://github.com/RuihongQiu/DuoRec This method introduces unsupervised Dropout and supervised semantic augmentations in self-supervised learning for sequential recommendation.
-
•
FMLP-Rec:999https://github.com/Woeee/FMLP-Rec Another most recent SR method adopting the full mlp layers architecture and filter methods on the self-attention module.