Sensitivity of WIMP bounds on the velocity distribution in the limit of a massless mediator

Cold Dark Matter (CDM) is believed to be indispensable to explain the existence of galaxies and clusters of galaxies as we see them today, and to provide about 25% of the density of the Universe Planck:2018vyg . The most popular CDM candidates are Weakly Interacting Massive Particles (WIMPs), whose phenomenology is characterized by the fact that the same interactions that are assumed to keep WIMPs in thermal equilibrium with Standard Model (SM) particles in the Early Universe and that allow to predict its relic density in agreement to observation through the thermal decoupling mechanism, provide an opportunity to detect them experimentally today. The main process that can be used to search for WIMPs is their scattering process off nuclear targets, that enters at the same time in Direct Detection (DD) experiments, that search for the recoil energy of nuclei in solid–state, liquid and gaseous detectors in underground laboratories shielded against cosmic rays DD_Goodman1984 ; DD_LEWIN1996 ; JUNGMAN1996 ; DD_Schumann2019 ; Snowmass_Leane2022 , or in experiments searching for neutrinos produced by WIMP annihilation inside celestial bodies (Earth, Sun), where the WIMPs are accumulated after being captured through the same WIMP–nucleus scattering process that enters DD cap_nu_sun_PhysRevLett1985 ; cap_nu_sun_HAGELIN1986 ; dm_cap_nu_SREDNICKI1987 ; Jungman:1994jr ; idm_sun_Catena_2018 .

An important piece of input in the calculation of expected signals is the WIMP speed distribution $f(u)$ in the reference frame of the Solar system, that determines the WIMP incoming flux¹¹1Neglecting the relative velocity between the Earth and the Sun both present direct detection experiments and signals from WIMP capture in the Sun are sensitive to the speed distribution $f(u)\equiv\int d\Omega f(\vec{u})u^{2}$.. In particular, for the $f(u)$ both early analytical estimations violent_relaxation and more recent numerical models of Galaxy formation VDF_Lacroix2020 ; VDF_Lopes2020 are compatible to the Standard Halo Model (SHM) scenario, where the $f(u)$ is given by a Maxwellian in the galactic halo rest frame SHM_1986 ; SHM_1988 . However, although the SHM provides a useful zero–order approximation to describe the WIMP speed distribution, numerical simulations of Galaxy formation can only shed light on statistical average properties of galactic halos, while our lack of information about the specific merger history of the Milky Way prevents us to rule out the possibility that the $f(u)$ has sizeable non–thermal components. Recently, data released by Gaia have opened the possibility to track the merger history of the Milky way, revealing many local stellar streams formed by material stripped from merged satellites. This may suggest the presence of dark matter streams or of a dark disc Lisanti:2011as ; OHare:2018trr ; Necib:2019zbk ; Necib:2019zka . In particular, such components may remain with a small velocity dispersion and co-rotating with the Galactic disc, resulting in a substantial contribution to the low speed tail of the $f(u)$ in the reference frame of the Solar system.

Based on the above considerations, several attempts have been made to develop halo–independent approaches with the goal to remove the dependence of the experimental bounds on the choice of a specific $f(u)$, both for the WIMP–nucleus and for WIMP–electron scattering process halo_independent_2010 ; halo_independent_Fox_2010 ; halo_uncertainty_Frandsen2011 ; astrophysics_independent_Herrero-Garcia2012 ; halo_independent_DelNobile_2013 ; Bozorgnia:2013hsa ; halo_independent_Fox2014 ; halo_independent_Feldstein2014 ; halo_independent_Scopel_inelastic_2014 ; halo_independent_Feldstein2014_2 ; halo_independent_Bozorgnia2014 ; halo_independent_Anderson2015 ; Halo-independent_Ferrer2015 ; halo_independent_Kahlhoefer ; Gondolo_Scopel_2017 ; halo_independent_Catena_Ibarra_2018 ; velocity_uncertainty_Ibarra2018 ; velocity_independent_2019 ; halo_independent_electron_scattering ; Herrera_2024_information_divergences , i.e. to work out the most conservative bounds from null searches compatible with the only constraint:

In the past, using this approach Ref. Halo-independent_Ferrer2015 developed a particularly straightforward method that allows to obtain conservative constraints that are independent of the $f(u)$ and only requires the assumption (1). In the following we will refer to this procedure as the single–stream method. In Ref. halo_independent_sogang_2023 it was used to obtain halo–independent bounds in the case of the most general non-relativistic effective Hamiltonian that drives the scattering process off nuclei of a WIMP of spin 1/2, while in halo_independent_inelastic_sogang_2023 the single–stream analysis was extended to the case of Inelastic Dark Matter inelastic_Tucker-Smith:2001 . In both cases a contact interaction was assumed. In the following we wish to further extend the single–stream method to the case of an interaction with a massless mediator.

In past years, several proposal have been put forward where the DM particle interacts with a gauge boson in the dark sector. Searches for such mediator have also been pursued in accelerators Ilten:2022lfq , dark matter searches Mitridate:2022tnv or neutrino telescopes Batell:2022xau . In the following we will be agnostic about the specific particle–physics model describing such WIMP–nucleon interaction, and use the fact that both the DD and capture processes are non–relativistic to parameterize the WIMP–nucleon interaction with an effective Hamiltonian ${\bf\mathcal{H}}$ that complies with Galilean symmetry nreft_haxton1 ; nreft_haxton2 . In particular, to zero–th order in the WIMP–nucleon relative velocity $\vec{v}$ and momentum transfer $\vec{q}$ the effective Hamiltonian ${\bf\mathcal{H}}$ consists of the usual spin–independent (SI) and spin–dependent (SD) interaction terms. Specifically, in the general case the effective Hamiltonian is given by:

In Eq. (2) $1_{\chi}$ and $1_{N}$ are identity operators, $q$ is the transferred momentum, $\vec{S}_{\chi}$ and $\vec{S}_{N}$ are the WIMP and nucleon spins, respectively, while $t^{0}$ = $1$ , $t^{1}$ = $\sigma^{3}$ denote the 2 $\times$ 2 identity and third Pauli matrix in isospin space, respectively, and the isoscalar and isovector coupling constants $\alpha^{0}_{j}$ and $\alpha^{1}_{j}$ (with $j=SI,SD$) are related to those to protons and neutrons $\alpha^{p}_{j}$ and $\alpha^{n}_{j}$ by $\alpha^{0}_{j}$ = $\alpha^{p}_{j}+\alpha^{n}_{j}$ and $\alpha^{1}_{j}$ = $\alpha^{p}_{j}-\alpha^{n}_{j}$ (the same holds for contact interactions, $c^{0}_{j}$ = $c^{p}_{j}+c^{n}_{j}$ and $c^{1}_{j}$ = $c^{p}_{j}-c^{n}_{j}$).

The first goal of the present paper is to update the existing bounds Liang:2013dsa ; OHare:2018trr on the two long–range couplings $\alpha_{\rm SI}^{p,n}$, $\alpha_{\rm SD}^{p,n}$ from the combinations of capture in the Sun and direct detection in the standard case of a Maxwellian WIMP velocity distribution in the Galaxy. Moreover, we wish to discuss the sensitivity of such bounds on the WIMP velocity distribution by obtaining halo–independent constraints using the single–stream method Halo-independent_Ferrer2015 .

Compared to the case of a contact interaction, the WIMP–nucleon Hamiltonian of Eq. (2) can potentially imply: (i) in the SHM case an improved sensitivity of capture in the Sun versus DD; (ii) an enhanced sensitivity of the results on the specific choice of the velocity distribution. The latter aspect can be understood by noticing that Eq. (2) leads to a divergent WIMP–nucleus cross section when $q\rightarrow$ 0 (an indication that in such kinematic regime a specific ultraviolet completion of the model is required). This is not an issue in the case of DD experiments, where a lower cut–off on $q$ is determined by the experimental threshold. However, the kinematic conditions for a WIMP to be captured in the Sun extend to $q\rightarrow$ 0, so that using the Hamiltonian in (2) the capture rate in this case is formally infinite. Indeed, when expressed in term of the mediator mass $M_{0}$, the capture rate diverges logarithmically for $M_{0}\rightarrow$ 0 when the thermal motion of the nuclear targets in the Sun is neglected capture_long_range_Fan_2013 ; capture_long_range_Chen_2015 , and quadratically when it is taken into account capture_long_range_Gaidau_2021 . The origin of this divergence arises from the low-velocity tail of the distribution $f(u)$ and is due to the fact that near $u$ = 0 DM particles far from the Sun have a very small kinetic energy. As a result, even scattering interactions yielding very small (actually, arbitrarily small) recoil energies can result in a negative total energy, i.e. in the dark matter particle being captured.

The approach used in the literature to address this issue is to count as captured only DM particles confined to orbits that lie within Jupiter’s orbit jupiter_cut_Kumar_2012 ; Liang:2013dsa . This introduces a lower cut–off on $q$ and yields a finite result for the capture rate. Thanks to the smaller momentum transfers involved, the constraints obtained in this way from capture in the Sun can be potentially more competitive than those from DD Liang:2013dsa ; OHare:2018trr . However, the sensitivity to the low–speed range of the $f(u)$ of the calculation of capture in the Sun in the case of a massless mediator potentially limits the robustness of such bounds, while the regularizing procedure of the Jupiter bound appears arbitrary. As we will show, a halo–independent approach removes both problems, and this represents one of the main motivations of the present analysis. In the following we will specifically address this issue and, more in general, obtain halo–independent constraints to discuss their sensitivity on the WIMP velocity distribution.

The plan of the paper is the following. In Section 2 we provide the expressions for the expected signals obtained from Eq. (2). In particular, in Section 2.1 we summarize those for the expected rate in DD experiments, while in Section 2.2 those for capture in the Sun. In Section 3 we summarise the single–stream method that we use to obtain our halo–independent bounds. Our quantitative results both for the SHM and in the halo–independent case are contained in Section 4. Finally, conclusions are drawn in Section 5. Appendix A contains the details of the experimental observations that we employ for DD (LZ LZ_2022 , XENON–nT xenon_nT , XENON–1T xenon_2018 in Appendix A.1, PICO–60(C₃F₈) pico60_2019 in Appendix A.2 and PICO–60(CF₃I) pico60_2015 in Appendix A.3) and those for neutrino telescopes (Super–Kamiokande SuperK_2015 , IceCube IceCube:2016 and projections for Hyper–Kamiokande Bell:2021esh in Appendix A.4).

The differential cross section for the WIMP–nucleus scattering can be written in terms of the recoil energy ($E_{R}={q^{2}}/{2m_{T}}$) as:

where $m_{T}$ is the mass of the nuclear target and $w$ is the incoming WIMP speed in the target reference frame.

Notice that in the limit $q\rightarrow 0$ the differential cross section scales as $q^{-4}$ and, as a consequence, the total cross section $\sigma_{T}=\int dE_{R}\frac{d\sigma_{T}}{dE_{R}}=2m_{T}\int d(q^{2})\frac{d\sigma_{T}}{dE_{R}}$ diverges.

Considering a WIMP–nucleon coupling $\alpha$, a given experimental bound $R_{\rm max}$ (either from a DD or a NT experiment) implies:

with $H$ being either $H_{C}$ or $H_{\rm DD}$. Since $H(\alpha^{2},u)=\alpha^{2}H(\alpha=1,u)$, one can re–write (18) as:

where ${\alpha}_{\rm max}(u)$ is defined as:

i.e., ${\alpha}_{\rm max}(u)$ is the upper limit on the coupling $\alpha$ if all the incoming WIMPs were concentrated in a single stream with speed $u$. Using Eq. (19) one obtains the upper limit on the coupling $\alpha$ for a general WIMP speed distribution $f(u)$ as:

According to Eq. (21), a finite bound on the coupling $\alpha$ independent of $f(u)$ (i.e., a finite halo–independent bound) is possible if the experimental sensitivity extends to the full WIMP speed range, so that ${\alpha}_{\rm max}(u)<\infty$ for any $u\in[0,u_{\rm max}]$. Since DD searches are sensitive to $u\geq u^{\rm DD-min}$ and NTs to $u\leq u^{\rm C-max}$, only the combination of both is sensitive to the full range of WIMP speeds $u^{\rm C-max}\geq$ min$\left[u^{\rm DD-min},u_{\rm max}\right]$. If this happens, one of the two following situations can occur:

• •

  Case I: The NT and the DD experiments are sensitive to two specific ranges of the WIMP speed, giving:

  	$\displaystyle{({\alpha^{\rm NT}})^{2}}_{\rm max}(u)$	$\displaystyle\leq$	$\displaystyle\tilde{\alpha}^{2}\hskip 51.21495pt{\rm for}\hskip 5.69054pt0\leq u\leq\tilde{u}$
  	$\displaystyle{({\alpha^{\rm DD}})^{2}}_{\rm max}(u)$	$\displaystyle\leq$	$\displaystyle\tilde{\alpha}^{2}\hskip 51.21495pt{\rm for}\hskip 5.69054pt\tilde{u}\leq u\leq u_{\rm max}$		(22)

  where ${{\alpha^{\rm NT}}}_{\rm max}(u)$ and ${{\alpha^{\rm DD}}}_{\rm max}(u)$ correspond to ${\alpha}_{\rm max}(u)$ for the NT and the DD experiments, respectively, and $\tilde{u}$ indicates the speed where ${{\alpha^{\rm NT}}}_{\rm max}(u)$ and ${{\alpha^{\rm DD}}}_{\rm max}(u)$ intersect at a finite value $\tilde{\alpha}$, i.e., ${{\alpha^{\rm NT}}}_{\rm max}(\tilde{u})={{\alpha^{\rm DD}}}_{\rm max}(\tilde{u})=\tilde{\alpha}$. In this case, using Eq. (21) it can be shown that (see Halo-independent_Ferrer2015 and halo_independent_sogang_2023 for details) the halo–independent (HI) bound on the coupling is:

  $$\alpha^{2}\leq 2\hskip 1.42262pt\tilde{\alpha}^{2}=\alpha^{2}_{\rm HI}.$$

  (23)

• •

  Case II: In some cases it happens that:

  $${({\alpha^{\rm DD}})^{2}}_{\rm max}(u)>\tilde{\alpha}^{2}\hskip 51.21495pt{\rm at}\hskip 5.69054ptu=u_{\rm max}.$$

  (24)

  In this case, as shown in halo_independent_sogang_2023 , the halo–independent bound is:

  $$\alpha^{2}\leq{({\alpha^{\rm DD}})^{2}}_{\rm max}(u_{\rm max})+\tilde{\alpha}^{2}=\alpha^{2}_{\rm HI}.$$

  (25)

  The condition (24) occurs mainly because of the loss of the DD experimental sensitivity with increasing $u$, usually due to the suppression of the nuclear form–factor in the WIMP–nucleus scattering process at large momentum transfer $q$. Note that this condition implies that the halo–independent bound (obtained from Eq. (25)) becomes sensitive to the choice of $u_{\rm max}$ and increases with increasing $u_{\rm max}$. In order to see the quantitative effect of this in our analysis we will also consider a large value of $u_{\rm max}=8000$ km/s (which is an order of magnitude larger than $u_{\rm max}^{ref}=780$ km/s).

For a given WIMP–nucleon interaction coupling, the halo–independent upper bound is computed at each $m_{\chi}$ following either Eq. (23) or (25) (when appropriate) combining one DD with one NT. When more than one DD and one NT are involved (as in our analysis) the procedure is repeated for each combination of DD and NT, and the most constraining halo–independent limit on the coupling is taken.

We begin this Section by reviewing the bounds on the SI and SD dark matter couplings $\alpha_{SI}^{p,n}$ and $\alpha_{SD}^{p,n}$ when the SHM is assumed for the WIMP velocity distribution in our Galaxy. In such case we assume the following normalised distribution (see e.g., Gould:1987 ; jupiter_cut_Kumar_2012 ):

with rotational speed of the solar system $v_{\odot}=220$ $\rm km/s$ and velocity dispersion $v_{\rm rms}=\sqrt{3/2}\,v_{\odot}\simeq 270$ km/s SHM_maxwell_Green2011 .

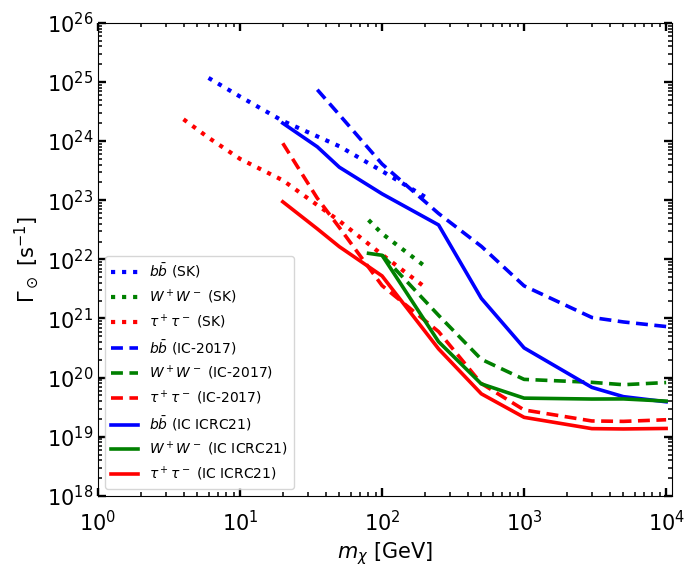
Our results are shown in Fig. 1, where we report for reference the results from Refs. Guo:2013ypa and Liang:2013dsa , which are the most recent analyses on the subject previous to the present paper. Specifically, the bounds from capture in the Sun assume $b\bar{b}$ as the dominant WIMP annihilation channel and are shown with the blue dotted line and the DD bounds with the green dotted lines, respectively. At the time of the analyses of Refs. Guo:2013ypa and Liang:2013dsa the most stringent DD bounds on all the couplings $\alpha_{SI}^{p,n}$ and $\alpha_{SD}^{p,n}$ of Eq. (2) were from Xenon10 xenon10_2011 and Xenon100 xenon100_2012 , while for capture in the Sun they were from Super–Kamiokande superk_2011 and IceCube icecube_2011 ; icecube_2012 . In the same Figure our evaluation of the present combined NT limits from the latest Super–Kamiokande SuperK_2015 and IceCube IceCube:2016 data is shown by the dashed blue lines, with the solid blue lines representing the improvement using a more recent set of IceCube data presented at the ICRC2021 Conference IceCube:2022wxw . Moreover in the same plots we show separately with the green solid lines our updated estimation of the present DD limit, which are given by a combination of LZ LZ_2022 and XenonT xenon_nT for $\alpha_{SI}^{p,n}$ and $\alpha_{SD}^{n}$, and by a combination of PICO–60 (C₃F₈) pico60_2015 PICO–60 (CF₈I) pico60_2019 for $\alpha_{SD}^{p}$.

From Fig. 1 one can notice that, albeit the present combined bounds from DD and capture in the Sun on $\alpha_{SI}^{p,n}$ and $\alpha_{SD}^{p,n}$ have improved between about two and three orders of magnitude since the analysis of Refs. Guo:2013ypa ; Liang:2013dsa , the situation has remained qualitatively similar: in the case of the SI couplings $\alpha_{SI}^{p,n}$ and of the SD coupling $\alpha_{SD}^{n}$ the bounds are driven by DD, while in the case of $\alpha_{SD}^{p}$ the most stringent constraint comes from capture in the Sun. One also observes that a long–range interaction systematically enhances the signal in NTs compared to that in DD due to the fact that, for a massless mediator, events with a small momentum transfer enhance the WIMP–nucleus cross section in the capture rate in the Sun while are not observable in DD due to the experimental energy threshold. As a consequence, while for a contact interaction the sensitivity of DD is always better than that for capture in the Sun in the case of a $b\bar{b}$ final state (between two and three orders of magnitude for $c_{SI}^{p,n}$ and $c_{SD}^{n}$, and about one order of magnitude for $c_{SD}^{p}$, see halo_independent_sogang_2023 ), for a long–range interaction, thanks to the large amount of ${}^{1}H$ in the Sun, the bound on $\alpha_{SD}^{p}$ is driven by capture, while for the other couplings DD is more sensitive but the difference with capture reduces in a sizeable way. It is also worth noticing that at the time of Guo:2013ypa ; Liang:2013dsa the bound on WIMP–proton couplings from SIMPLE simple_2012 , that used C₂CIF₅ and was the most sensitive experiments using proton–odd targets, was slightly worse than the corresponding one from Xenon100, that uses a neutron–odd target. However the Xenon100 constraint required to use sub–dominant WIMP–proton form factors that show significant variability among different evaluations SD_form_factors_xe_1 ; SD_form_factors_xe_2 ; nreft_haxton2 . On the other hand the present bound on $\alpha_{SD}^{p}$ from PICO–60, and experiments using proton–odd targets (C₃F₈ and CF₃I) should be considered more robust since it makes use of better known SD form factors.

In the case of a massless mediator the response functions $H_{C}$, $H_{DD}$ are enhanced for a low momentum transfer. Due to the experimental threshold this effect is mild or negligible for DD experiments, but can be important for the expected rate of capture in the Sun, that for $u\rightarrow 0$ diverges when the integration over the nuclear recoil energy in Eq. (8) extends down to zero, unless the Jupiter cut–off discussed in Section 2.2 is implemented (see Eqs. (10) and (11)).

One can notice that the rate of Eq. (15) can be seen as the average $\langle$H$\rangle$ of the response function $H$ over the velocity distribution $f$. Indeed, for a constant $H$ the rate would not depend on $f$ altogether. At low WIMP masses, although $H_{C}$ is never constant ($H_{C}(u)\propto 1/u$ or $H_{C}\propto 1/u^{3}$ depending on whether $E_{cut}^{C}>1/2m_{\chi}u^{2}$ or not in Eq. (11)) the response function $H_{C}$ flattens out, because $u_{T}^{C-max}>u_{\rm max}$ so that $H_{C}(u)\neq$ 0 in the full velocity range, and this reduces the sensitivity of the capture signal on the details of the velocity distribution. On the other hand, at larger masses $u_{T}^{C-max}<u_{\rm max}$ and $H_{C}(u)$ has a steeper $u$ dependence because it vanishes for $u>u_{T}^{C-max}$. This leads to a larger sensitivity of the capture rate on the WIMP velocity distribution at heavier WIMP masses, and specifically on the low–speed regime of $f(u)$ Choi:2013eda . For the SHM this is explicitly shown in Fig. 1, where in each plot the blue shaded band represents the change in the bound from capture in the Sun when the $v_{esc}(r_{0})$ value of Eq. (12) is multiplied/divided by a factor of two (corresponding to assuming a maximal semi-major axis of captured WIMPs a factor of four smaller/larger than the Sun-Jupiter distance). In the same plots the yellow band represents instead how the same bound is modified when the tail $u<u_{p}$ of the standard Maxwellian distribution $f_{MB}$ is removed from the velocity integration, with:

We now extend our analysis beyond the SHM to the halo–independent constraints obtained adopting the single–stream method described in Section 3, which is valid for any velocity distribution with the condition (14). Also in this case we fix the WIMP annihilation channel to $b\bar{b}$. In each plot of Fig. 2, the solid black line shows our halo–independent result for each of the couplings $\alpha_{SI,SD}^{p,n}$ as a function of $m_{\chi}$ and using for the maximal velocity $u_{\rm max}$ = $u_{\rm max}^{\rm ref}$ = 780 km/s, corresponding to the standard value $u_{\rm esc}$ = 560 km/s for the escape velocity in the Galactic rest frame vesc_Piffl2013 ; vesc_Smith2006 . As pointed out in Section 3, in some cases the halo–independent bound can become sensitive to the choice of $u_{\rm max}$. Such situations are described by case II (see Eq. (24)) when at large WIMP speeds the DD response function $H_{\rm DD}(u)$ is suppressed, or equivalently, the DD bound on the coupling, ${\alpha^{\rm DD}}_{\rm max}(u)$, is relaxed. This happens due to the suppression of the nuclear form factor at large momentum transfer (corresponding to large WIMP speeds) and/or due to the finite experimental energy bin of some detectors (e.g., xenon based detectors). As a result of this the halo–independent bound obtained from Eq. (25) in case II gets weaker when a large value of $u_{\rm max}$ is considered. For the same reason described above, increasing $u_{\rm max}$ can lead to a transition from a situation described by case I (see Eq. (22)) to one described by case II (Eq. (24)) enhancing the sensitivity of the bound to $u_{\rm max}$. To check the effects of choosing a larger $u_{\rm max}$ on the halo–independent bounds in each plot of Fig. 2 the red–dotted line shows the bound when $u_{\rm max}$ is increased to 8000 km/s. Such value is unrealistically large, and we use it just to show that the dependence on $u_{\rm max}$ is rather mild (the halo–independent bounds get weaker only by a factor $\lesssim 2-3$).

An explicit example of how the bounds of Fig. 2 are obtained is shown in Fig. 3 for $m_{\chi}$ = 1 TeV, where the quantity ${\alpha}_{\rm max}$ defined in Eq. (20) is plotted as a function of $u$. In each plot the green or orange circle represents the values $(\tilde{u},\tilde{\alpha})$ or $(u_{\rm max},{\alpha^{\rm DD}}_{\rm max}(u_{\rm max}))$ that determine the single–stream bound according to the procedure outlined in Section 3 (case I or II, respectively), the gray shaded area indicates the range of $u$ preferred by the SHM (specifically, the $u$ interval where $\int f_{\rm MB}\,du=0.8$), while the vertical solid line represents the $u_{\rm max}$ reference value $u_{\rm max}^{\rm ref}$ = 780 km/s. An important feature of these plots is that the effect of the Jupiter cut on the determination of $\alpha_{\rm max}(u)$ is confined to $u\rightarrow 0$, where $\lim_{u\rightarrow 0}\alpha_{\rm max,cut}>0$ and $\lim_{u\rightarrow 0}\alpha_{\rm max}$ = 0 without the cut. However, the halo–independent bound is determined by the largest value of $\alpha_{\rm max}(u)$ across the full range of $u$ and is insensitive to $u$ intervals where $\alpha_{\rm max}(u)$ is small. As a consequence, the halo–independent bound does not depend on the Jupiter cut, as it should be. Moreover, for $m_{\chi}$ = 1 TeV one can notice that the couplings $\alpha_{SD}^{p}$ and $\alpha_{SI}^{n}$ correspond to case I (as defined in Section 3), for which the halo–independent bound is given by Eq. (23) with small or no dependence on $u_{\rm max}$. On the other hand the other two plots in Fig. 3 show that $\alpha_{SI}^{p}$ and $\alpha_{SD}^{n}$ correspond to case II, for which $\tilde{u}$ = $u_{\rm max}$ and the single–stream bound is given by Eq. (25). In this case some dependence on the specific value of $u_{\rm max}$ is expected, and this is confirmed by the red–dotted lines at large mass in the corresponding plots of Fig. 2, conservatively calculated with the very large value $u_{\rm max}$ = 8000 km/s to bracket the ensuing variation of the bound. The two cases $\alpha_{SI}^{p,n}$ are similar, in that the cross section scales as the atomic mass number and DD is driven by xenon detectors, while capture in the Sun is driven by WIMP scattering events off several nuclear targets (with the largest from either ${}^{1}H$ or ${}^{4}He$, followed by ${}^{3}He$, ${}^{12}C$, ${}^{14}N$, ${}^{16}O$, ${}^{20}Ne$, ${}^{24}Mg$, ${}^{28}Si$ and ${}^{56}Fe$). In this case the maximal velocity for capture $u^{\rm C-max}_{T}$ for several targets extends well beyond the velocity thresholds $u\geq u^{\rm DD-min}_{T}$ from direct searches, driven by xenon. The same happens for $\alpha_{SD}^{n}$, for which capture in the Sun is driven by WIMP scattering events off ${}^{3}He$ and, again, DD is driven by xenon detectors. In all these cases DD and capture keep a similar degree of complementarity and the halo–independent bound variation is moderate across the full range of $m_{\chi}$. On the other hand, the situation for $\alpha_{SD}^{p}$ is different, because in this case the capture rate in the Sun and DD are driven by WIMP scattering events off hydrogen and off fluorine targets, respectively. In particular, for $m_{\chi}\gtrsim$ 1 TeV $u^{\rm C-max}_{{}^{H}}$ for hydrogen drops below $u^{\rm DD-min}_{F}$ for fluorine and the complementarity between these two targets is lost. The residual contribution to capture beyond $u^{\rm C-max}_{{}^{H}}$ is driven by ${}^{14}N$, which is more than 6 orders of magnitude smaller. This explains the abrupt loss of sensitivity observed for $m_{\chi}\gtrsim$ 1 TeV in the halo–independent $\alpha_{SD}^{p}$ exclusion plot of Fig. 2.

We conclude our discussion by plotting in Fig. 4 as a function of $m_{\chi}$ a relaxation factor defined as the ratio between the following two quantities: the conservative halo–independent exclusion plot obtained using the procedure outlined in Section 3 and the strongest constraint among capture in the Sun and the DD experiments included in our analysis obtained using for $f(u)$ the standard Maxwellian distribution $f_{MB}(u)$ of Eq. (26) ²²2As already pointed out, in our analysis we assume $b\bar{b}$ as the dominant WIMP annihilation channel. For completeness, in Appendix A.4 we provide a plot of the relaxation factor of Fig. 4 for the case of the $\tau\bar{\tau}$ annihilation channel.. For the sake of comparison in Fig. 4 the left–hand plot shows the relaxation factors for $c_{SI,SD}^{p,n}$ in the case of a contact interaction (taken from Ref. halo_independent_sogang_2023 ), while the right–hand plot shows the relaxation factors for the couplings $\alpha_{SI,SD}^{p,n}$ in the case of a long–range interaction (i.e. for a massless mediator). Such relaxation factors show the maximal weakening of each bound when a halo model different from the SHM is assumed, and can be considered as indicators of the impact on the bounds of our ignorance about the velocity distribution $f(u)$. However, one should notice that, as shown in Fig. 1, the SHM bound on the $\alpha_{\rm SD}^{p}$ coupling is driven by capture, which at large WIMP masses is very sensitive to the specific behaviour of $f_{\rm MB}$ for $u\rightarrow$ 0. This implies that for such bound the exact determination of the relaxation factor becomes not reliable, i.e., for $m_{\chi}\gtrsim$ 1 TeV. On the other hand all the other SHM bounds (determined by DD) and that on $\alpha_{\rm SD}^{p}$ for $m_{\chi}\lesssim$ 1 TeV are not sensitive to the low velocity tail of $f_{\rm MB}$ and the corresponding relaxation factors are robust. Interestingly, in this case the relaxation factor shows values which are smaller or of the same order of those for a contact interaction. This can be ascribed to the fact that the relaxation factor is explicitly given by halo_independent_sogang_2023 :

where “exp” indicates the NT or DD experiment that provides the strongest upper–limit on the coupling at a given $m_{\chi}$ in the case of the standard Maxwellian speed distribution $f_{MB}$. The brackets $\langle...\rangle$ indicate an average weighted by the Maxwellian $f_{MB}$ while ${\langle...\rangle}_{\rm bulk}$ indicates the dominant contribution to the average from the bulk of the WIMP speeds, defined as:

At small $m_{\chi}$, both $u^{\rm C-max}$ and $u^{\rm DD}_{th}$ are shifted to large values, so that $(\alpha^{\rm NT})^{2}_{\rm max}(u)\lesssim(\alpha^{\rm DD})^{2}_{\rm max}(u)$ with $(\alpha^{\rm NT})^{2}_{\rm max}(u)$ rather flat up to $u_{\rm max}$, while $\tilde{u}$ is beyond the Maxwellian bulk region or close to its upper edge. In this case $(\alpha^{\rm NT})^{2}_{\rm max}(u)$ remains flat in a speed range that includes both the bulk of the Maxwellian and $\tilde{u}$ and as a consequence in Eq. (28) $\alpha^{2}_{\rm HI}$ and $(\langle 1/(\alpha^{\rm NT})^{2}_{\rm max}\rangle)^{-1}$ do not differ much, so that the relaxation factor is not large.

In the opposite regime of large $m_{\chi}$, both $u^{\rm DD}_{th}$ and $u^{\rm C-max}$ are shifted to small values and in the Maxwellian case the bound is driven by DD. In this case $\tilde{u}$ is also driven to small values and below the bulk of the Maxwellian, where $(\alpha^{\rm NT})^{2}_{\rm max}(u)$ intersects $(\alpha^{\rm DD})^{2}_{\rm max}(u)$ just before the latter starts rising due to the $u^{\rm DD}_{th}$ threshold. In this case the range of speeds that includes the bulk of the Maxwellian and either $\tilde{u}$ or $u_{\rm max}$ (case I or case II) corresponds to a regime where $(\alpha^{\rm DD})^{2}_{\rm max}(u)$ is rather flat. So also in this case in Eq. (28) the difference between $\alpha_{\rm HI}^{2}$ and $(\langle 1/(\alpha^{\rm DD})^{2}_{\rm max}\rangle)^{-1}$ is not large and the relaxation factor is moderate.

Finally, between the two asymptotic regimes of moderate relaxation factor at both small and large $m_{\chi}$ discussed above, for all the couplings $\alpha_{\rm SI,SD}^{p,n}$ the largest values of the relaxation factors are reached for $m_{\chi}\simeq$ 20 GeV ³³3At least at face value: as already pointed out, due to the uncertainty in the Maxwellian capture rate the relaxation factor for $\alpha_{\rm SD}^{p}$ is not well defined for large $m_{\chi}$.. In this mass range when the Maxwellian bound is driven by DD the two curves for $(\alpha^{\rm NT})^{2}_{\rm max}(u)$ and $(\alpha^{\rm DD})^{2}_{\rm max}(u)$ intersect where the latter has a steep dependence on $u$ because $u$ is close to $u^{\rm DD}_{th}$, with $\tilde{u}$ close to the lower edge of the bulk region. Due to these reasons in the range of speeds that includes $\tilde{u}$ and the bulk of the Maxwellian $(\alpha^{\rm DD})^{2}_{\rm max}(u)$ changes significantly, so that $(\alpha^{\rm DD})^{2}_{\rm max}(u)\ll\tilde{\alpha}^{2}$ for WIMP speeds in the bulk of the Maxwellian, and the relaxation factor is large. Notice that in the case of $\alpha_{\rm SD}^{p}$ the Maxwellian bound is instead driven by capture at low $u$ where $(\alpha^{\rm NT})^{2}_{\rm max}(u)$ is very small, and the relaxation factor is again large.

As a consequence of the discussion above, we conclude that, with the exception of the WIMP–proton SD coupling $\alpha_{\rm SD}^{p}$ at large WIMP mass ($m_{\chi}\gtrsim$ 1 TeV), the sensitivity on the specific choice of the velocity distribution $f(u)$ of the bounds on all the long–range couplings is of the same order of that of the corresponding couplings in the contact interaction case.

In the present paper we have updated the bounds on the couplings $\alpha_{SI}^{p,n}$ and $\alpha_{SD}^{p,n}$ for a spin–independent (SI) and spin–dependent (SD) WIMP–nucleon interaction Hamiltonian in the case of a long–range interaction (i.e., for a massless mediator in the propagator). In order to do so we have used a combination of capture in the Sun (fixing the WIMP annihilation channel to $b\bar{b}$) and direct detection, assuming a standard Maxwellian $f_{\rm MB}$ for the WIMP velocity distribution (SHM). In particular, in the case of a massless mediator the usual expression used to calculate the capture rate in the Sun diverges, due to the contribution of WIMPs locked into orbits of very large semi–major axis $r_{0}$ by scattering events with arbitrarily low values of the momentum transfer, corresponding to low incoming WIMP speeds $u$ in the solar rest frame. Following previous analyses in the literature, we have assumed that the gravitational disturbances far from the Sun put an upper cut on $r_{0}$, and regularized the rate identifying $r_{0}$ to the Sun–Jupiter distance. We have also discussed the dependence of the SHM bounds from capture in the Sun on the Jupiter cut, and on small alterations of $f_{\rm MB}$ for $u\rightarrow$ 0, showing that they can be large for $m_{\chi}\gtrsim$ 1 TeV, but are moderate for smaller WIMP masses. Moreover, we have discussed the sensitivity of the bounds on a generic WIMP velocity distribution by obtaining halo–independent constraints using the single–stream method Halo-independent_Ferrer2015 .

As far as the SHM bounds are concerned, our update of the combined bounds from DD and capture in the Sun on $\alpha_{SI}^{p,n}$ and $\alpha_{SD}^{p,n}$ have improved between about two and three orders of magnitude compared to the analysis of Refs. Guo:2013ypa ; Liang:2013dsa . In particular, compared to a contact interaction, a massless mediator systematically enhances the signal in NTs compared to that in DD. Our results remain qualitatively similar to those of Refs.Guo:2013ypa ; Liang:2013dsa : in the case of the SI couplings $\alpha_{SI}^{p,n}$ and of the SD coupling $\alpha_{SD}^{n}$ the bounds are driven by DD, while in the case of $\alpha_{SD}^{p}$ the most stringent constraint comes from capture in the Sun.

The halo–independent bounds do not depend on the Jupiter cut needed to regularize the calculation of the latter in the Maxwellian case. We find that, with the exception of $\alpha_{\rm SD}^{p}$ at large $m_{\chi}$, the maximal weakening of each bound when a halo model different from the SHM is assumed (relaxation factor) is of the same order of that for contact interactions. This is due to the fact that for $\alpha_{\rm SI}^{p,n}$ and $\alpha_{\rm SD}^{n}$ the velocity intervals which determine both the Maxwellian and the halo–independent rates are far from the $u\rightarrow$ 0 regime responsible for the sensitivity of the expected capture rate from a massless propagator, so that the ensuing relaxation factor behaviour is similar to that in the case of a contact interaction halo_independent_sogang_2023 : relatively moderate in the low and high WIMP mass regimes and as large as $\sim 10^{2}$ for $m_{\chi}\simeq$ 20 GeV. On the other hand for $\alpha_{\rm SD}^{p}$ the exact determination of the relaxation factor becomes not reliable for $m_{\chi}\gtrsim$ 1 TeV, because in this case the SHM bound, driven by capture in the Sun, is very sensitive to the specific behaviour of $f_{\rm MB}$ for $u\rightarrow$ 0.

We conclude by observing that within a simplified model where the DM particle is coupled to a massless dark photon $\gamma_{D}$, assuming as in Section 2.2 that $\chi\chi\rightarrow b\bar{b}$ drives WIMP annihilations (and that the contribution from $\chi\chi\rightarrow\gamma_{D}\gamma_{D}$ is subdominant), one has McDermott:2010pa :

This research was supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Education through the Center for Quantum Space Time (CQUeST) with grant number 2020R1A6A1A03047877, by the Ministry of Science and ICT with grant number RS-2023-00241757, and by the fund from the Institute for Basic Science (IBS) under project code IBS-R016-Y2. A.K. acknowledges the hospitality of the Institut d’Astrophysique de Paris (IAP).