Sensitivity improvement of Rydberg atom-based microwave sensing via electromagnetically induced transparency
Abstract
A highly excited Rydberg atom via electromagnetically induced transparency with two color cascading lasers has extreme sensitivity to electric fields of microwave ranging from 100 MHz to over 1 THz. It can be used as susceptible atom-based microwave communication antennas where the carrier wave usually works exactly resonant to the transition between a pair of adjacent Rydberg states with large electric dipole moment. A technique of superheterodyne with a strong on-resonant local microwave oscillator is employed to induce considerable Autler-Townes splitting where the antennas has a highest dynamic response to another weak target signal microwave carrier. To further improve the sensitivity of atomic antenna in communication, we detune the carrier microwave frequency off resonance forming an asymmetrically optical splitting and fix the coupling laser frequency at the shoulder of the stronger one, and optimize the local field strength simultaneously. It gives a sensitivity of 12.50(04) . Its enhancement mechanism of sensitivity is also proved by a theoretical simulation.
pacs:
32.80.Rm, 32.60.+i, 32.30.Jc, 31.15.-pLABEL:FirstPage1 LABEL:LastPage#1
I INTRODUCTION
Rydberg atoms in highly excited states with one or more electrons of large principal quantum numbers are sensitive to electric fields, very suitable to manufacture atom-based sensor for detecting and receiving communication signals [1]. It has been widely investigated thoroughly both theoretically and experimentally throughout the last decades [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]. This type of sensors can replace the front-end components and electronics in a conventional antenna/receiver system [14, 15], since they have potential advantages over conventional systems. This Rydberg-atom based quantum sensor owns unique properties such as self-calibration and fine spatial resolution in both the far-field and near-field [16, 17, 18, 14].
The spacing between Rydberg levels can locate across the microwave radio frequency, which can be used to measure RF E-field strengths over a large range of frequencies (1 GHz to 500 GHz) with a high sensitivity [19, 5, 20], approximately [21, 22]. Various groups have investigated wireless communication using Rydberg atoms [23, 2, 24, 25, 7]. For example, utilizing the Rydberg atoms as a receiving antenna, Deb et al. directly recovered signal at the baseband without any demodulation means [2]. Anderson et al. demonstrated an atomic receiver for amplitude modulation (AM) and frequency modulation (FM) communication with a 3 dB bandwidth in the baseband of 100 kHz [23]. All of their work show atom-based quantum techniques are new and promising candidates for microwave communication applications.
An RF E-field applied to the Rydberg atoms results in the Autler-Townes (AT) splitting [26] of a ladder-type Rydberg electromagnetic-induced transparency (EIT) transmission spectrum [27]. The measurement of the RF E-field with Rydberg atoms can be converted into frequency measurement. The AT splitting () is proportional to the RF E-field strength as described as [14]
| (1) |
and inversely the RF E-field strength is expressed as
| (2) |
which quantitatively associates the RF E-field strength and the AT spectral splitting, where is the Rabi frequency of the Rydberg state transition induced by the RF E-field and is the transition dipole moment of the adjacent Rydberg states and can be calculated accurately, and is Planck’s constant. We can see that a larger dipole moment corresponds a larger gain coefficient to magnify a weak electric field observable by the optical AT-splitting. If the probe laser is scanned, the wavelength mismatch effect has to be included and the formula above is corrected as [28, 29]
| (3) |
When we apply amplitude modulation (AM) to the RF carrier, probe transmission also carries a relating modulation signal and can be directly measured using a fast photo-diode detector. Owing to a potential high sensitivity, the quantum receiver can be used for very weak signal communication, which can also greatly reduce the cost of a transceiver system [30, 15].
To improve the sensitivity of MW sensing, a conceptually new microwave electric field sensor called Rydberg-atom superheterodyne receiver (Superhet) is demonstrated [22]. In an atomic superhet, a strong on-resonant local MW field results in two dressed states energetically separated by . They are, respectively, the symmetric and antisymmetric superpositions of two bare Rydberg states. At this critically separated point, a small MW signal will lead to a highest dynamic optical response, which is used as the MW sensing. In order to obtain electric field measurements with high accuracy, in their work, they apply a local MW electric field () to achieve the resonant transmission point that has considerable slope . The local MW electric field is chosen as 3.0 . The sensitivity of this technique scales favorably, even up to 55 in a modest setup.
Principally, it is possible to further improve the sensitivity of electric field measurements via optimizing the probe beam and coupling beam power [28, 31], local electric field strength and frequency detuning [9, 32] together. It is also vital to evaluate the individual contribution of each physical parameter in enhancing the MW detection sensitivity. In this work, we study all the parameter optimizations as well as the resonant transmission point of the local electric field, which is expected to give a better sensitivity.
II experimental
A typical schematic of our experimental apparatus is shown in Fig.1 with the related energy levels of in the inset [28, 31, 9, 32]. Theoretically two different laser systems are needed to address the Rydberg levels in Rb, one near 780 nm and one near 480 nm. The 780 nm light is tuned to the transition in Rb commonly, corresponding to the transition from , and the 480 nm one continues to excite the atom on to high Rydberg state , forming a cascading irradiation configuration. The microwave RF couples the Rydberg state to its neighbor partner with its electric dipole interaction strength monitored by the transparency of the probe beam of 780 nm through the atomic vapor.

To avoid the Doppler background in the probe transparent spectrum, we record the spectrum by scanning the coupling laser frequency of 480 nm while the probe laser of 780 nm locked to a saturation absorption spectroscopy (SAS) of Rb. The probe beam is derived from a cat-eye Morglab laser at 780.246 nm with maximum output of 180 mW and a free running linewidth of MHz. The coupling laser (480 nm) is generated by a frequency-doubled amplified diode laser system (TA-SHGpro, Toptica, Munich, Germany), which is scanned across the hyperfine transition and real-time monitored by a FP-cavity for relative frequency reference. Both lasers can also be selectively locked to an ultralow expansion glass (ULE) Fabry-Perot (FP) cavity using the Pound-Drever-Hall technique (PDH) with two pairs of mirrors mounted on the same supporting skeleton immune to the room temperature fluctuation, within less than 1 kHz. The standard PDH-locking skills have been used in the feedback loop where the laser beams imposed to the FP-cavity are modulated by an electro-optical modulator (EOM) driven by a local oscillator of MHz. The locking signal comes from the mixing between the phase-shifted local oscillator and the photo-diode signal of laser reflected from the FP cavity, respectively. The 780 nm beam is focused to a spot of waist 750 with typical power of 100 , corresponding to Rabi frequency MHz. While the 480 nm beam focused to 1.25 mm with typical power of 420 mW, corresponding to Rabi frequency MHz.
Based on the optical EIT scheme that the coupling ( nm) and probe ( nm) beams counter-propagate through a Rb vapor cell of length 70 mm and diameter 25 mm, a horn antenna has been used to generate a local RF E-field oscillator (LO) to couple the upper two Rydberg states and with frequency GHz via a horn antenna in free-space. The transition dipole moment is calculated from the ARC library [33] and its value is determined as a.u.. In addition, a small signal (SIG) produced by a RIGOL function waveform generator has already been amplitude-modulated to the RF LO to simulate the detection signal. The optimization experiment can be performed on this one-horn configuration.
III RESULTS
As we have mentioned previously, in the technique of superheterodyne, a strong local MW has been employed to induce considerable AT-splitting where the antennas has a highest dynamic response to the target signal MW carrier [22]. Typical AT-splittings at various RF power and one of their dynamic responses are shown in Fig.2(a). The RF E-field couples a pair of specific Rydberg states, and . The typical AT-splittings are measured at RF power -12, -10 and -8 dB, corresponding to AT-spectral line separation of 7.94(9), 11.48(9) and 13.75(10) MHz. We can deduce the electric field strength of the local RF field according to Eq.3. Thus we can measure a series of data points of RF E-field versus the applied RF power in the vicinity of a given LO power, for example, at the point corresponding to E-field of . The data are shown in black squares in the Fig.2(b).

As the RF E-field is proportional to the square root of the output power, given by the standard antenna equation [22], where is the power of the microwave source, is a gain of the antenna, and is a distance from the antenna to the cell. Considering and are constants for a certain experiment, the relation can be simplified as , where is the effective gain of horn antenna. In our experiment, the linear least square fit determines the effective gain as . The fit line is plotted in red solid line in Fig.2(b). The quality of the linearity of the measurements is also very good, excluding the complex state interaction induced nonlinearity [34]. Therefore, the weak RF E-field value can be obtained by the above formula at given antenna power.

The probe optical transmission response is not linearly dependent on MW RF powers and the LO electric field strength should be chosen at the point with maximum slope [22]. As we know, at lower RF electric field, the AT-splitting is very small and the probe optical response to the applied MW power is not sensitive [35]. On the contrary, at very high RF carrier power, the AT-splitting is large enough where the splitting lines have already been separated. At this moment, the probe optical response is not sensitive, either. An intermediate case is preferred at which point the optical response has the largest slope on the applied RF power. This point also relies on the power of probe and pumping laser powers. We present the measurement of the optical response on the power of RF generator in Fig.3(a) at different probe laser powers. We can see that a higher power of probe laser can bring larger optical transmission signal and also larger slope or response gain for RF power. We choose the optimized RF power at -10 dBm (corresponding to an electric field of at the vapor cell) and further investigate the optical response dependent on the probe laser intensity. It is shown in Fig.3(b), where the response increases linearly with the probe laser intensity. However, unfortunately, the AT-spectral line width increases, either, nearly linearly. Specially, at power of 300 , the probe laser is too strong, leading to a spectral splitting. We should balance these two factors in a real experimental operation. As can be seen later, we prefer to a value of 100 so as to keep narrower linewidth and to keep far away from the critical point of splitting.

The optimization also relies on the pumping laser power. We present the measurement of the optical response on the power of RF generator in Fig.4(a) at different pumping laser powers. Similar to the case of probe laser power optimization, a higher power of laser can bring larger optical transmission signal and also larger response gain for RF power. At the optimized RF power of -10 dBm, the optical response dependent on the pumping laser intensity also shows a linear relation. It is shown in Fig.4(b). Unlike the case of optimization of probe laser, however, the spectral linewidth keeps almost unchanged (Fig.4(c)). It implies we can choose a higher coupling laser power if possible. It’s also physically reasonable since a stronger coupling of 480 nm laser is more favorable for the transfer of RF AT-splitting information down to the probe laser.

We can also turn back to the optimization of the MW RF power according to the dynamical response by applying a weak amplitude modulation on the RF generator. The measurement of optical response of MW at different RF powers varying from to dBm is shown in Fig.5(a1-e1). To see the dynamical response more clear, we extract the dynamical signal by filtering the flat DC part away, which is shown in Fig.5(a2-e2). We can see that when the RF power increases up -10 dBm, the response has a large amplitude and nearly gets saturated, implying an optimized RF power. The optimized RF power corresponds an electric field intensity of 0.353(18) V/m, close to the value of 0.3 V/m in Ref.[22]. The above measurement is performed at laser power fixed at the optimized intensity in previous steps shown in Fig.3 and Fig.4. The amplitude modulation frequency is taken as 1 kHz with magnitude of 0.5 V at the input interface of the RF microwave generator, corresponding to a maximum electric field of 1.720(25) at the vapor cell.
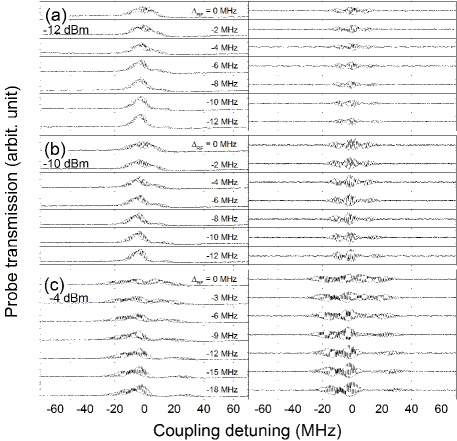
To further improve the sensitivity of atomic antenna in MW communication, we detune the carrier MW frequency off resonance forming an asymmetrically splitting optical response, which is similar to the case of Cs atom [9]. There the MW is detuned from the resonant transition between two Rydberg states, , corresponding to a value of 6.946 GHz. At this moment, we can compare the optical response of amplitude-modulated signal MW RF at a given local RF power but at resonance and off-resonance to the transition between the adjacent Rydberg levels. It is shown in Fig.6. As the same as in Fig.5, the amplitude modulation frequency is taken as 1 kHz with magnitude of 0.5 V at the input interface of the microwave generator. An intuitive view of Fig.6 tells us that a moderate RF detuning can help to increase the dynamical signal, especially at stronger RF power -10 or -8 dBm as shown in Fig.6(b) and -4 dBm in Fig.6(c).

For better view of the result in Fig.6, we can extract the maximum dynamical signal amplitude and redraw it in Fig.7. We can see that at RF power -12 dBm, the optimization is located at detuning MHz but at higher RF power, -10 dBm and -4 dBm, the better LO power goes up to larger detuning values, -10 and -27 MHz, respectively. Specially, at RF power of -10 dBm, the dynamical signal is not sensitive to the RF detuning in a more wide range, -20 to -6 MHz. This feature is more useful in real experimental application.

The enhancement of dynamic optical response by RF detuning can be understood by a theoretical simulation based on the optical Bloch equation considering the four energy levels [11, 36, 10, 34, 13, 22]. Taking the energy level of the intermediate state as a reference, the Hamiltonian can be expressed as a matrix form
| (4) |
where a probe laser couples the ground state and intermediate state , characterized by its Rabi frequency while a coupling laser induces an interaction between the intermediate state and the Rydberg state . () depicts the frequency detunings of the probe, coupling beams and the microwave, respectively. Different from the usual Ladder-type EIT configuration, a microwave field is additionally applied and correlates this Rydberg state to another close neighbor Rybderg state with large Rabi frequency due to the considerable dipole moment between Rydberg states. The simulation is shown in Fig.8. Theoretical simulations of the optical transparency response for the RF detuning are presented in Fig.8(a)-(b), corresponding to RF detuning of and MHz. A small amplitude-modulation has been applied to the RF field under the 1 kHz modulation. From the above spectra, we can obtain the corresponding dynamic optical responses as Fig.8(c)-(d). We can see that the strong dynamical response locates at the shoulder of the transparency spectral line rather than the spectral peak itself. Moreover, a little enhancement of the dynamical response can be achieved by RF detuning of -6 MHz at Fig.8(d). The RF detuning causes the break-down of the symmetry of the optical response and transfers the dynamic optical gain to the branch closer to the zero detuning.

Finally, we quantitatively evaluate the sensitivity of the Rydberg RF sensing system. The applied amplitude modulation intensity decreases until approaching the lowest visual perceptible threshold at RF frequency resonant to and detuned away from the transition between the two adjacent Rydberg states. The optical dynamical response these two frequencies are shown in Fig.9 where all other parameters fixed at the optimized values. The LO RF power is set to -10 dBm as previously determined. Fig.9(a)-(b) correspond to the case of RF resonance while Fig.9(a’) and (b’) to the case at the optimized detuning of -6 MHz. The large modulation gives a nice sinusoidal fit for the measured data points as presented in Fig.9(a) and (a’), corresponding to a signal RF of 860(13) V/cm.
When the modulation deceases to a lower perceptible threshold, corresponding to 6.88(10) at the vapor cell, the detuning method remarkably has a better sensitivity, indicating a sensitivity improvement. The latter optical response gives a high value of on the photo detector, larger than that of at zero detuning. The method without detuning gives a sensitivity of 49.84(72) while the detuning of -6 MHz gives a sensitivity of 35.75(51) . A further step is to measure the noise spectrum with zero and -6 MHz detuning. The RF detuning of -6 MHz provides a sensitivity of 12.50(04) , better than that 13.69(40) at zero detuning as well. It corresponds a smallest discernible RF electric field of 176.78(57) , measured at time scale of 5000 s, better than that with sensitivity of in Ref.[22].
IV Conclusion
We have built up the highly excited Rydberg atom based RF field sensing system via electromagnetically induced transparency with two color cascading lasers. After choosing a higher Rydberg state as the sensing medium, we study the optical response of the probe beam dependent on the probe and coupling beam laser powers and fix them at the optimized values. A further optimization is performed on the LO RF power where the AT-splitting is the most sensitive to the dynamic RF electric field. At the same time, we detune the RF field frequency to break the symmetry of the AT-splitting. It leads to one of the asymmetric branches more sensitive to the RF electric field variation, which further enhances the RF field sensitivity. Based on the Bloch equation with four energy levels concerned, we theoretically simulate the dynamic optical response of the system, completely supporting the optimization mechanism.
Acknowledgements.
This work is supported by National Natural Science Foundation of China (NSFC) (No. 12074388 and No. 12004393).References
- Gallagher et al. [1982] T. F. Gallagher, K. A. Safinya, F. Gounand, J. F. Delpech, W. Sandner, and R. Kachru, Resonant rydberg-atom - rydberg-atom collisions, Phy. Rev. A 25, 1905 (1982).
- Deb and Kjærgaard [2018] A. B. Deb and N. Kjærgaard, Radio-over-fiber using an optical antenna based on rydberg states of atoms, Appl. Phys. Lett. 112, 211106 (2018).
- Holloway et al. [2018] C. L. Holloway, M. T. Simons, M. D. Kautz, A. H. Haddab, J. A. Gordon, and T. P. Crowley, A quantum-based power standard: Using rydberg atoms for a si-traceable radio-frequency power measurement technique in rectangular waveguides, Appl. Phys. Lett. 113, 094101 (2018).
- Sedlacek et al. [2012] J. A. Sedlacek, A. Schwettmann, H. Kübler, R. Löw, T. Pfau, and J. P. Shaffer, Microwave electrometry with rydberg atoms in a vapour cell using bright atomic resonances, Nature Phys. 8, 819 (2012).
- Simons et al. [2018] M. T. Simons, J. A. Gordon, and C. L. Holloway, Fiber-coupled vapor cell for a portable rydberg atom-based radio frequency electric field sensor, Appl. Opt. 57, 6456 (2018).
- Simons et al. [a] M. T. Simons, A. H. Haddab, J. A. Gordon, and C. L. Holloway, Applications with a rydberg atom-based radio frequency antenna/receiver, in 2019 International Symposium on Electromagnetic Compatibility - EMC EUROPE, pp. 885–889.
- Song et al. [2019] Z. Song, H. Liu, X. Liu, W. Zhang, H. Zou, J. Zhang, and J. Qu, Rydberg-atom-based digital communication using a continuously tunable radio-frequency carrier, Opt Express 27, 8848 (2019).
- Liao et al. [2020] K.-Y. Liao, H.-T. Tu, S.-Z. Yang, C.-J. Chen, X.-H. Liu, J. Liang, X.-D. Zhang, H. Yan, and S.-L. Zhu, Microwave electrometry via electromagnetically induced absorption in cold rydberg atoms, Phys. Rev. A 101, 053432 (2020).
- Zhang et al. [2019] L. Zhang, Y. Jia, M. Jing, L. Guo, H. Zhang, L. Xiao, and S. Jia, Detuning radio-frequency electrometry using rydberg atoms in a room-temperature vapor cell, Laser Phys. 29, 035701 (2019).
- Jia et al. [2021] F.-D. Jia, X.-B. Liu, J. Mei, Y.-H. Yu, H.-Y. Zhang, Z.-Q. Lin, H.-Y. Dong, J. Zhang, F. Xie, and Z.-P. Zhong, Span shift and extension of quantum microwave electrometry with rydberg atoms dressed by an auxiliary microwave field, Phys. Rev. A 103, 063113 (2021).
- Simons et al. [2021] M. T. Simons, A. B. Artusio-Glimpse, C. L. Holloway, E. Imhof, S. R. Jefferts, R. Wyllie, B. C. Sawyer, and T. G. Walker, Continuous radio-frequency electric-field detection through adjacent rydberg resonance tuning, Phys. Rev. A 104, 032824 (2021).
- Meyer et al. [2021] D. H. Meyer, P. D. Kunz, and K. C. Cox, Waveguide-coupled rydberg spectrum analyzer from 0 to 20 ghz, Phys Rev Appl 15, 014047 (2021).
- Peng et al. [2020] Y. D. Peng, J. L. Wang, C. Li, X. Lu, Y. H. Qi, A. H. Yang, and J. Y. Wang, Enhanced microwave electrometry with intracavity anomalous dispersion in rydberg atoms, Opt. Quant. Electron 52, 120 (2020).
- Holloway et al. [2014a] C. L. Holloway, J. A. Gordon, S. Jefferts, A. Schwarzkopf, D. A. Anderson, S. A. Miller, N. Thaicharoen, and G. Raithel, Broadband rydberg atom-based electric-field probe for si-traceable, self-calibrated measurements, IEEE Trans. Antenna Propag. 62, 6169 (2014a).
- Simons et al. [2019] M. T. Simons, A. H. Haddab, J. A. Gordon, D. Novotny, and C. L. Holloway, Embedding a rydberg atom-based sensor into an antenna for phase and amplitude detection of radio-frequency fields and modulated signals, IEEE Access 7, 164975 (2019).
- Fan et al. [2014] H. Q. Fan, S. Kumar, R. Daschner, H. Kubler, and J. P. Shaffer, Subwavelength microwave electric-field imaging using rydberg atoms inside atomic vapor cells, Opt. Lett. 39, 3030 (2014).
- Gordon et al. [2014] J. A. Gordon, C. L. Holloway, A. Schwarzkopf, D. A. Anderson, S. Miller, N. Thaicharoen, and G. Raithel, Millimeter wave detection via autler-townes splitting in rubidium rydberg atoms, Appl. Phys. Lett. 105, 024104 (2014).
- Holloway et al. [2014b] C. L. Holloway, J. A. Gordon, A. Schwarzkopf, D. A. Anderson, S. A. Miller, N. Thaicharoen, and G. Raithel, Sub-wavelength imaging and field mapping via electromagnetically induced transparency and autler-townes splitting in rydberg atoms, Appl. Phys. Lett. 104, 244102 (2014b).
- Sedlacek et al. [2013] J. A. Sedlacek, A. Schwettmann, H. Kubler, and J. P. Shaffer, Atom-based vector microwave electrometry using rubidium rydberg atoms in a vapor cell, Phys. Rev. Lett. 111, 063001 (2013).
- Simons et al. [2016] M. T. Simons, J. A. Gordon, C. L. Holloway, D. A. Anderson, S. A. Miller, and G. Raithel, Using frequency detuning to improve the sensitivity of electric field measurements via electromagnetically induced transparency and autler-townes splitting in rydberg atoms, Appl. Phys. Lett. 108, 174101 (2016).
- Fan et al. [2015] H. Fan, S. Kumar, J. Sedlacek, H. Kübler, S. Karimkashi, and J. P. Shaffer, Atom based rf electric field sensing, J. Phys. B: At., Mol. Opt. Phys 48, 202001 (2015).
- Jing et al. [2020] M. Jing, Y. Hu, J. Ma, H. Zhang, L. Zhang, L. Xiao, and S. Jia, Atomic superheterodyne receiver based on microwave-dressed rydberg spectroscopy, Nature Phys. 16, 911 (2020).
- Anderson et al. [2021] D. A. Anderson, R. E. Sapiro, and G. Raithel, An atomic receiver for am and fm radio communication, IEEE Trans. Antenna Propag. 69, 2455 (2021).
- Holloway et al. [2021] C. Holloway, M. Simons, A. H. Haddab, J. A. Gordon, D. A. Anderson, G. Raithel, and S. Voran, A multiple-band rydberg atom-based receiver: Am/fm stereo reception, IEEE Antenna Propag. Mag. 63, 63 (2021).
- [25] Z. Song, W. Zhang, X. Liu, H. Zou, J. Zhang, Z. Jiang, and J. Qu, Quantum-based amplitude modulation radio receiver using rydberg atoms, in 2018 IEEE Globecom Workshops, pp. 1–6.
- Abi-Salloum [2010] T. Y. Abi-Salloum, Electromagnetically induced transparency and autler-townes splitting: Two similar but distinct phenomena in two categories of three-level atomic systems, Phys. Rev. A 81, 053836 (2010).
- Petrosyan et al. [2011] D. Petrosyan, J. Otterbach, and M. Fleischhauer, Electromagnetically induced transparency with rydberg atoms, Phys. Rev. Lett. 107, 213601 (2011).
- Holloway et al. [2017] C. L. Holloway, M. T. Simons, J. A. Gordon, A. Dienstfrey, D. A. Anderson, and G. Raithel, Electric field metrology for si traceability: Systematic measurement uncertainties in electromagnetically induced transparency in atomic vapor, J. Appl. Phys. 121, 233106 (2017).
- Joshua A. Gordon and Holloway [2019] A. H. H. Joshua A. Gordon, Matthew T. Simons and C. L. Holloway, Weak electric-field detection with sub-1 hz resolution at radio frequencies using a rydberg atom-based mixer, AIP Advances 9, 045030 (2019).
- Simons et al. [b] M. T. Simons, A. H. Haddab, J. A. Gordon, and C. L. Holloway, Waveguide-integrated rydberg atom-based rf field detector for near-field antenna measurements, in 2019 Antenna Measurement Techniques Association Symposium, pp. 1–4.
- Kumar et al. [2017] S. Kumar, H. Fan, H. Kubler, J. Sheng, and J. P. Shaffer, Atom-based sensing of weak radio frequency electric fields using homodyne readout, Sci. Rep. 7, 42981 (2017).
- Zou et al. [2020] H. Zou, Z. Song, H. Mu, Z. Feng, J. Qu, and Q. Wang, Atomic receiver by utilizing multiple radio-frequency coupling at rydberg states of rubidium, Appl. Sci. 10, 1346 (2020).
- Sibalic et al. [2017] N. Sibalic, J. D. Pritchard, C. S. Adams, and K. J. Weatherill, Arc: An open-source library for calculating properties of alkali rydberg atoms, Comput. Phys. Commun. 220, 319 (2017).
- Chopinaud and Pritchard [2021] A. Chopinaud and J. D. Pritchard, Optimal state choice for rydberg-atom microwave sensors, Phys Rev Appl 16, 024008 (2021).
- Liu et al. [2021] X. Liu, F. Jia, H. Zhang, J. Mei, Y. Yu, W. Liang, J. Zhang, F. Xie, and Z. Zhong, Using amplitude modulation of the microwave field to improve the sensitivity of rydberg-atom based microwave electrometry, AIP Advances 11, 085127 (2021).
- Robinson et al. [2021] A. K. Robinson, A. B. Artusio-Glimpse, M. T. Simons, and C. L. Holloway, Atomic spectra in a six-level scheme for electromagnetically induced transparency and autler-townes splitting in rydberg atoms, Phys. Rev. A 103, 023704 (2021).