Self-Supervised Motion Retargeting with Safety Guarantee
Abstract
In this paper, we present self-supervised shared latent embedding (S3LE), a data-driven motion retargeting method that enables the generation of natural motions in humanoid robots from motion capture data or RGB videos. While it requires paired data consisting of human poses and their corresponding robot configurations, it significantly alleviates the necessity of time-consuming data-collection via novel paired data generating processes. Our self-supervised learning procedure consists of two steps: automatically generating paired data to bootstrap the motion retargeting, and learning a projection-invariant mapping to handle the different expressivity of humans and humanoid robots. Furthermore, our method guarantees that the generated robot pose is collision-free and satisfies position limits by utilizing nonparametric regression in the shared latent space. We demonstrate that our method can generate expressive robotic motions from both the CMU motion capture database and YouTube videos.
I Introduction
Generating natural and expressive robotic motions for humanoid robots has gained considerable interest from both robotics and computer graphics communities [1, 2, 3, 4, 5]. Recently, this phenomenon has been accelerated by the fact that more human-like robots are permeating our daily lives through applications such as interactive services or educational robots. However, in order to generate a number of natural motions for humanoid robots, a substantial amount of effort is often required to manually design time-stamped robotic motions by animators or artists.
One alternative approach is to leverage existing motion capture or animation data to generate robotic motions, which is often referred to as motion retargeting. Traditionally, motion retargeting is performed by manually defining a mapping between two different morphologies (e.g., a human actor and an animation character). This requires one to first design (or optimize) the pose feature of the source domain to transfer, and then find the corresponding pose in the target domain. For instance, the source and target can be human skeletons and humanoid robot joint angles, respectively. However, a substantial amount of effort is often required to manually design a proper mapping between the domains because kinematic constraints have to be taken into consideration as well.
On the other hand, data-driven motion retargeting has been used to circumvent the manual mapping process by leveraging machine learning methods [2]. Such learning-based methods enjoy flexibility and scalability as they reduce the need for excessive domain knowledge and tedious tuning processes required to define pose features properly. Another important benefit of data-driven motion retargeting is the lightweight computation requirement of the execution phase as no iterative optimization is involved during the execution. However, one clear drawback is that we have to collect a sufficient number of training data in advance. Moreover, it is not straightforward how to ensure the feasibility of the motion when using a learning-based model.
In this paper, we present self-supervised shared latent embedding (S3LE), a data-driven motion retargeting method that enables the generation of natural motions in humanoid robots from motion capture data or RGB videos. In particular, we apply self-supervised learning in two domains: 1) generating paired data for motion retargeting without relying on the human motion data and 2) learning a projection-invariant mapping to handle the different expressivity of humans and humanoid robots. The proposed data generating process not only alleviates the necessity of collecting a large number of pairs consisting of human pose features and corresponding robot configurations, but also allows the motion retargeting algorithm not to be restricted to the given motion capture dataset. Furthermore, the proposed projection-invariant mapping, which is defined as a mapping from an arbitrary human skeleton to a motion-retargetable skeleton, takes into account the fact that the range of robot poses are often more restrictive than those of humans’. By combining the recently proposed motion retargeting method [6] that can guarantee the feasibility of the transferred motion, our proposed method can perform motion retargeting online with safety guarantee (i.e., self-collision free) under mild assumptions.
II Related Work
In this section, we give a summary of existing work on data-driven motion retargeting and self-supervised learning methods in robotics, which form the foundation of this work.
II-A Data-driven Motion Retargeting
Data-driven motion retargeting methods have been widely used due to its flexibility and scalability [2, 3, 4, 5]. Owing to the merits of such methods, [7] was able to generate convincing motions of non-humanoid characters (i.e., a lamp and a penguin) from human MoCap data. Many data-driven techniques have relied on Gaussian process latent variable models (GPLVM) to construct shared latent spaces between the two motion domains [2, 3]. More recently, [8] proposed associate latent encoding (ALE), which uses two different variational auto-encoders (VAEs) with a single shared latent space. A similar idea was extended in [9] by incorporating negative examples to aid safety constraints. However, these methods do not consider the different expressivity of humans and robots. That is, multiple human poses can be mapped into a single robot configuration due to physical constraints. In this regard, we present the projection-invariant mapping while constructing the shared latent space.
II-B Self-supervised Learning in Robotics
Self-supervised learning has found diverse applications in robotics such as learning invariant representations of visual inputs [10, 11, 12], object pose estimation [13], and motion retargeting [14, 15]. The necessity of self-supervision arises naturally in robotics, where every piece of data often requires the execution of a real system. Collecting large-scale data for robotics poses significant challenges as robot execution can be slow and producing high-quality labels can be expensive. Self-supervision allows one to sidestep this issue by generating cheap labels (but with weak signals) for vast amounts of data. For instance, [16] creates a large dataset of Unmanned Aerial Vehicle (UAV) crashes, and labels an input image as positive if the UAV is far away from a collision and negative otherwise.
Moreover, self-supervised learning can be used to train representations that are invariant to insignificant changes, such as change of viewpoint and lighting in image inputs [10]. As for self-supervised learning methods for motion retargeting, which is the problem of our interest, [14] and [15] train motion retargeting networks with unpaired data using a cycle-consistency loss [17] in either the input or the latent space. While both methods do impose a soft penalty for violating joint limits during the training procedure, they do not guarantee feasibility as the joint limits are not strictly enforced, and self-collision is not taken into consideration.
III Preliminary
Considering the safety and feasibility of the retargeted robotic motion is crucial in robotics. In particular, when we are using a learning-based model using a function approximator (e.g., neural networks), it is not straightforward to guarantee that the resulting prediction lies within the safety region. In this regard, the recently proposed locally weighted latent learning (LWL2) [6] performs nonparametric regression on a shared deep latent space. One unique characteristic is that one can always guarantee the feasibility of the mapping by finding the closest feasible point in the latent space. Our method also enjoys this property by leveraging LWL2.
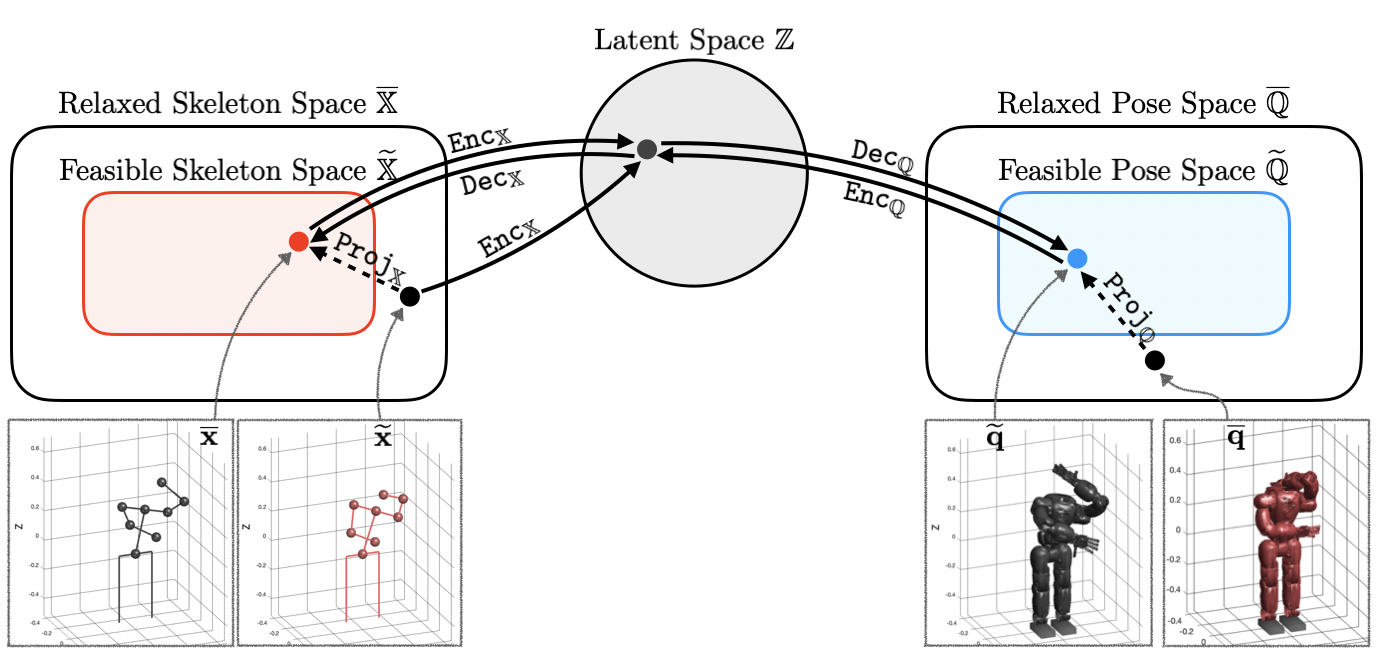
Suppose we want to find a mapping from to using paired data with correspondences (i.e., ). The core idea of our method is to construct a shared latent space by learning appropriate encoders and decoders of and (i.e., , , , and ). Both encoder networks and decoder networks are trained using the Wasserstein autoencoder (WAE) [18] framework with the following loss function in domain (and ):
| (1) | ||||
where is the number data, is a discriminator for latent prior fitting, is a distance function defined in the input space, controls the latent prior fitting (we default to ), is the sigmoid function, and and indicate the trainable variables, e.g., indicates that only is being updated111 Please refer [18] for more details..
While (1) can be used to construct a single latent space, we need an additional loss function to glue the two latent spaces. To this end, we use the following latent consensus loss:
| (2) |
where is the number of paired data (i.e., ). Note that one can use domain-specific data of each domain (without correspondence) for optimizing (1) and the glue data of both domains () for optimizing (2).
Once shared latent space is constructed, one can use nearest neighbor search in the latent space to find the mapping between and . Given a test input , the corresponding test output can be computed in a nonparametric fashion as
| (3) |
where is a set of points in . We would like to stress that the domain-specific data does not necessarily have to be identical to the ones in but rather can be easily augmented from sampling points in as we do not have to care about correspondence issues with points in .
In our motion retargeting problem, and correspond to the space of human skeletons and robot joint configurations, respectively. Similarly, and correspond to the pairs of human skeletons and motion retargeted robot configurations, and feasible robot configurations (not paired with human skeletons), respectively. Thus, collecting is much easier than collecting .
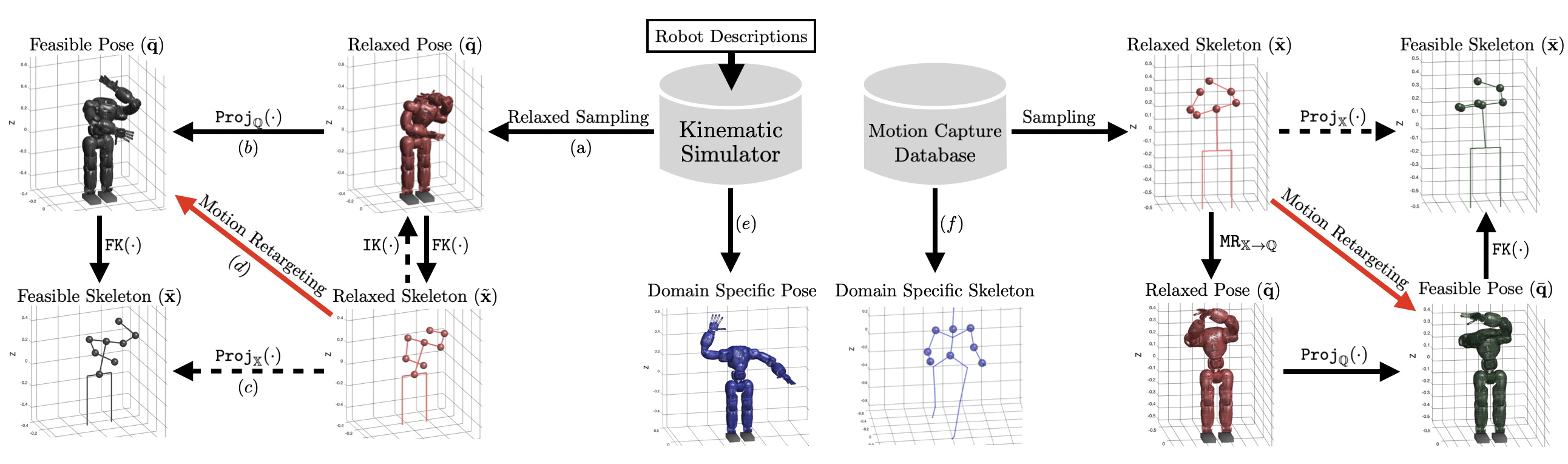
IV Self-Supervised Motion Retargeting
In this section, we present our self-supervised motion retargeting method. The cornerstones of our method are paired data sampling processes in Section IV-B and Section IV-C for generating a sufficient number of tuples with correspondences. Our main motivation is to incorporate the different expressivity of humans and humanoid robots. In other words, due to the joint limits and physical constraints of robots, the mapping from a human skeleton to a robot pose may not be a one-to-one mapping, but rather an -to-one mapping since multiple human poses can be mapped to a single robot configuration. Self-supervised learning with normalized temperature-scaled cross-entropy is utilized to handle this different expressivity.
IV-A Problem Formulation
We first introduce basic notations. We denote by and the human skeleton representation and robot joint configuration, respectively. Specifically, is a -dimensional vector consisting of seven unit vectors: hip-to-neck, both left and right neck-to-shoulder, shoulder-to-elbow, and elbow-to-hand unit vectors. A robot configuration is a sequence of revolute joint angles222 This could limit the motion retargeting results in that orientation information is omitted. However, this makes the proposed method compatible with the output of pose estimation algorithms for RGB videos. . Moreover, we denote relaxed skeletons and robot configurations that do not necessarily satisfy the robot’s physical constraints by and , and feasible skeletons and configurations by and . Throughout this paper, we use robot poses and joint configurations interchangeably as they have one-to-one correspondences. Our goal of motion retargeting is to find a mapping from to (i.e., human skeleton space to robot configuration space),
To handle the diverse human poses that map into a single robot pose, we leverage self-supervised learning for constructing the shared latent space. Specifically, the following normalized temperature-scaled cross entropy (NT-Xent) loss will be used:
where is the -th latent vector on latent space mapped by an encoder network and is a temperature parameter which we set to be . In image classification domains, and correspond to the feature vectors of two images that are augmented from a single image with different augmentation methods [19]. In our setting, and correspond to latent representations of skeletons that map to the same robot configuration. We present two sampling processes in Sections IV-B and IV-C that allows us to construct and pairs which are encoded from a feasible (retargetable) and a relaxed (possibly not retargetable) skeletons, respectively. Figure 1 illustrates the overview of the two sampling processes.
IV-B Sampling Data from Motion Capture Data
Our proposed method still requires some amount of paired data, so we use an optimization-based motion retargeting method [20] to create a small paired dataset of human skeletons and corresponding robot configurations. However, unlike the approach taken in [20], which simply computes pairs of human poses () and robot poses (), we carefully design an additional sampling routine so that the resulting tuple can be used for contrastive learning.
First, we randomly select a human pose from the motion capture dataset () and run optimization-based motion retargeting without considering the joint limits and self-collision, which gives us a relaxed robot pose (). Note that this process takes considerable amount of time due to solving inverse kinematics as a sub-routine. Then, we compute the feasible robot pose () from using the method presented in [6]. This process can be seen as projecting to (i.e., ). Finally, from , we compute the skeleton representation by solving forward kinematics and concatenating appropriate unit vectors described in Section IV-A (i.e., ). The collected tuple (, , , ) is used for both learning the projection-invariant encoding and constructing the shared latent space between the two domains for motion retargeting.
IV-C Sampling Data from Kinematic Information
Here, we present a data sampling procedure which requires only the robot’s kinematic information. This has two major advantages. 1) it alleviates the cost of collecting a large number of expensive paired data obtained via solving inverse kinematics, and 2) it allows the learning-based motion retargeting algorithm to not be limited to the motion capture data used in Section IV-B.
We first sample where is a relaxed robot configuration space. In particular, this relaxed configuration space is constructed by relaxing the joint limits with a relaxation constant . If the joint angle range of -th joint is , then we define the -relaxed joint range as . The relaxed configuration is converted to the corresponding robot pose by solving forward kinematics where the skeleton features (i.e., unit vectors) are extracted from the robot pose. We denote by the skeleton features given by the relaxed configuration.
The main purpose of sampling from is to collect that is less restricted to the physical constraints of the robot model. In other words, if we simply use samples from the robot configuration with exact joint ranges, the data is likely to not cover the human skeleton space sufficiently. Yet, if we directly use the collected relaxed pairs for training the learning-based motion retargeting, it may cause catastrophic results in that may not satisfy the kinematic constraints.
To resolve this issue, we use the same projection mapping from Section IV-B to map the relaxed configuration to the feasible robot configuration that is guaranteed to satisfy joint range limits and self-collision constraints (i.e., ). We also compute the corresponding skeleton feature from the feasible configurations (i.e., ). To summarize, we sample the following tuples for training our learning-based motion retargeting method:
With slight abuse of notation and denoting function composition by , we can represent , where even though we are not actually solving inverse kinematics in the sampling process. Figure 2 illustrates the proposed projection-invariant mapping.
We also leverage a mix-up style data augementaton [21]. More precisely, we generate auxiliary relaxed robot skeletons , where is uniformly sampled from the interval. This has the effect of smoothing the decision boundary of the motion retargeting inputs.
IV-D Discussion
We found that 200K pairs of skeleton features and corresponding robot joint angles generated from the sampling method in Section IV-C were not sufficient enough to properly perform motion retargeting.
This stems from the fact that the coverage of randomly sampled data becomes sparse at an exponential rate in the ambient dimension, which is typically referred to as the “curse of dimensionality”. One can try increasing the number of samples, but the corresponding increase in query time would render it impractical for real-time retargeting when using exact nearest neighbor search. An avenue for future research is using sublinear-time algorithms for retrieving approximate nearest neighbors.
Our method remedies the insufficient coverage of random data by using a small number of human motion capture data from Section IV-B to efficiently cover the low-dimensional manifold of human skeletons. However, we note that our method has the potential to be fully self-supervised, in the sense that no data obtained by solving inverse kinematics is required, if our random configuration sampling in Section IV-C can be improved to efficiently cover the space of human skeletons.
V Experiment
V-A Synthetic Example
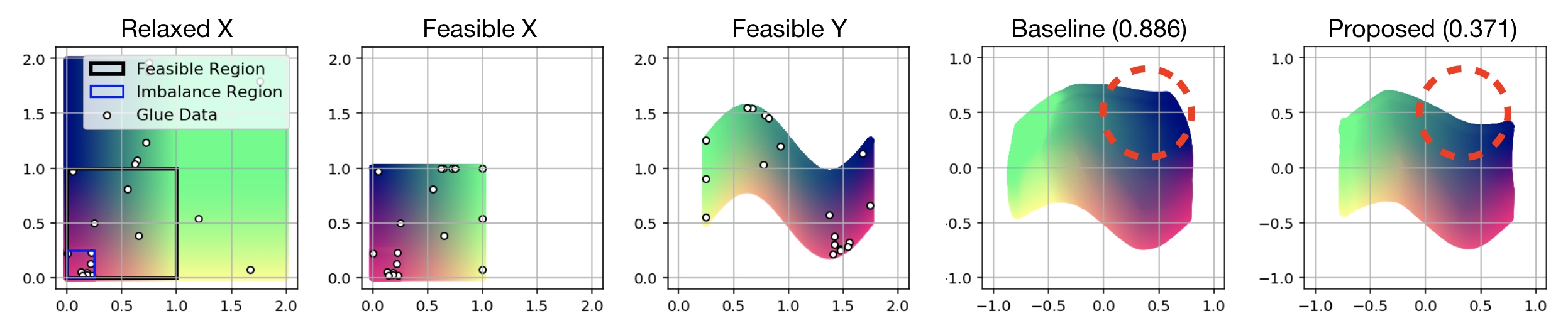
We first conduct a synthetic experiment to conceptually highlight the benefit of using S3LE for constructing the shared latent space. The goal is to find a mapping from Relaxed to Feasible , where multiple points in Relaxed correspond to a single point in Feasible . This resembles our motion retargeting setup since multiple human skeletons can map into a single robot configuration due to the limited expressivity of humanoid robots.
We set Relaxed and Feasible to be and , respectively, and define the projection as . Note that there exists a one-to-one mapping from Feasible to Feasible as shown in Figure 3. We randomly sample points from Relaxed (which contains Feasible as a subset) to optimize a projection-invariant mapping and pairs as the glue data for constructing the latent space shared by and . The mappings learned by S3LE, which is trained with the NT-Xent loss, and a baseline method, trained without the NT-Xent loss, are illustrated in the rightmost side of Figure 3. We can see that our method learns a better mapping from Relaxed to Feasible . This example shows that training with a contrastive loss improves the performance when the mapping is not one-to-one as the projection invariant region shown with red dotted circles are better mapped with the proposed method.
V-B Experimental Setup
For the target robot platform, Compliant Humanoid Platform (COMAN) is used in a simulational environment where we only consider the revolute joints of its upper body and a subset of motions ( pairs) from CMU MoCap DB is used to collect a list of paired tuples (, , , ).
We compare S3LE with two baseline methods, associate latent embedding (ALE) [8] and locally weighted latent learning (LWL2) [6]. Both methods, ALE and LWL2, leverage a shared latent space, but LWL2 additionally guarantees feasibility of the retargeted pose using nonparametric regression. S3LE also guarantees feasibility in the same way, i.e., by using nonparametric regression in the latent space. Furthermore, the mixup-style augmentation in S3LE yields more training data for constructing the shared latent space.
We first select motions from the CMU MoCap database and run optimization-based motion retargeting to get pairs of skeletons and corresponding robot configurations. We also sample pairs from the proposed sampling process in Section IV-C, from robot-domain specific data, and from MoCap-domain specific data. All neural networks (encoders, decoders, and discriminators) have three hidden layers with units. We use the tanh activation function and learning rate of .
V-C Motion Retargeting with Motion Capture Database
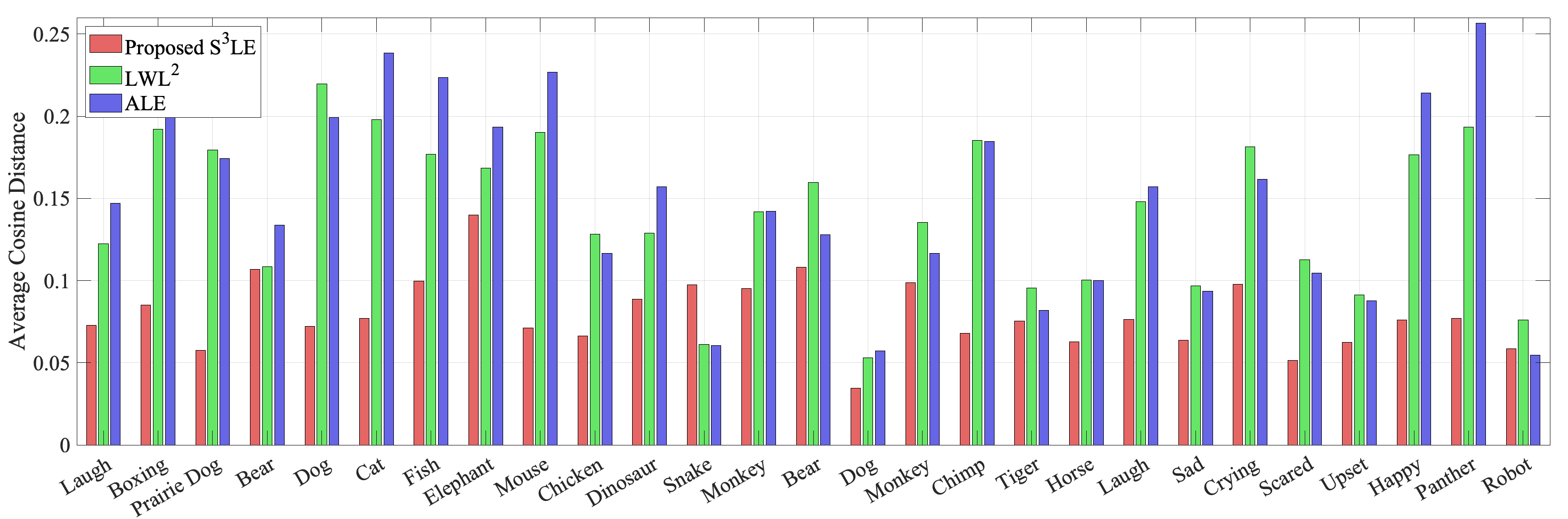
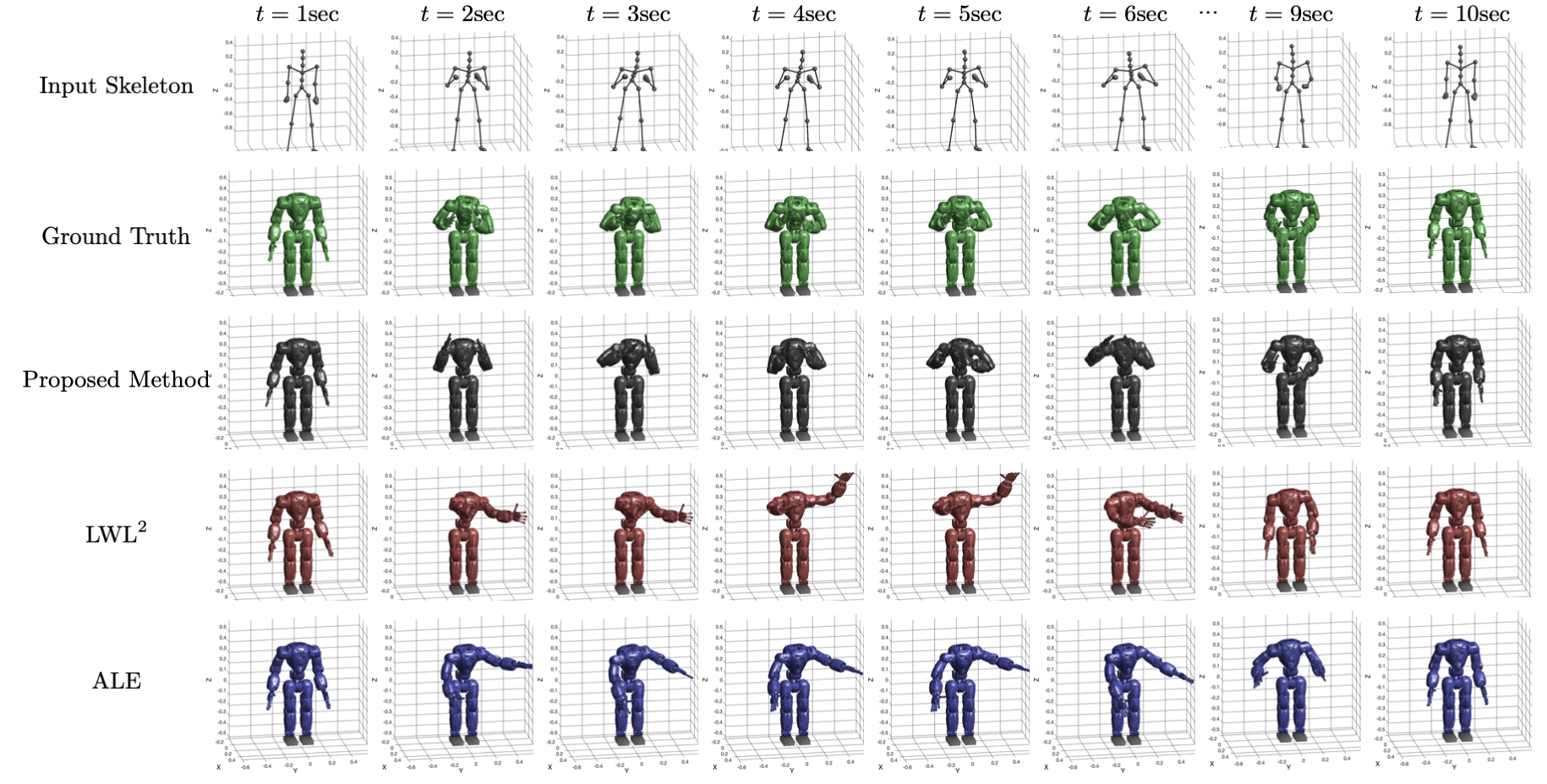
We conduct comparative experiments using a subset of CMU MoCap DB [22] that was not observed while training as test set. In particular, we chose expressive motions, compute the corresponding poses of COMAN using an optimization-based motion retargeting [20], and use them as the ground truth. To evaluate the performance of each retargeting method, we compute the average cosine distance of seven unit vectors (hip-to-neck, both left and right neck-to-shoulder, shoulder-to-elbow, and elbow-to-hand) between the retargeted and ground truth skeletons. The average cosine distances of the methods are shown in Figure 4. In most cases, S3LE outperforms the baselines in terms of accuracy measured by the cosine distance. Note that the poses of both S3LE and LWL2 are guaranteed to be collision-free while the average collision rate of ALE is . Figure 5 shows snapshots of input skeleton poses and retargeted motions. S3LE accurately retargets the motion when the input skeleton is lifting both hands up, whereas the baseline methods fail to do so. We hypothesize that this is because the training data from optimization-based motion retargeting failed to cover such poses while the data sampled using the COMAN’s kinematic information (Section IV-C) contained such poses.
V-D Motion Retargeting with RGB Video
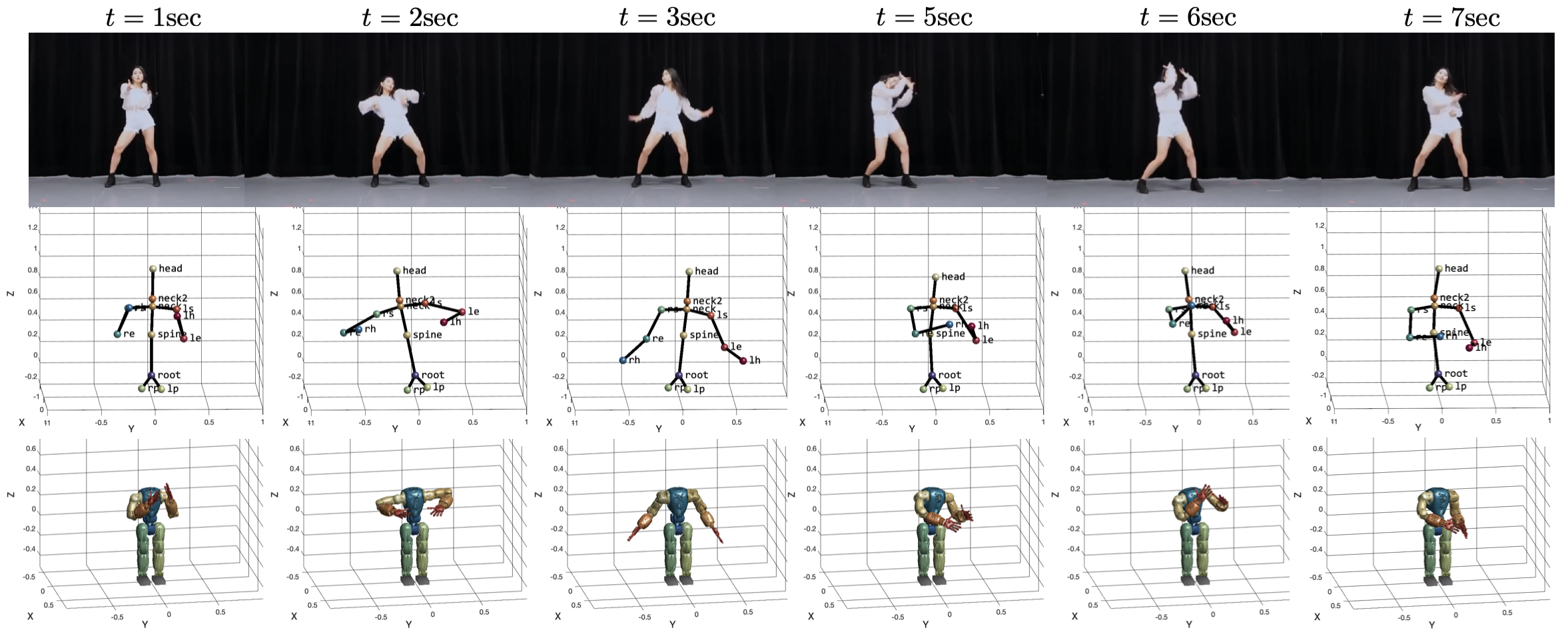
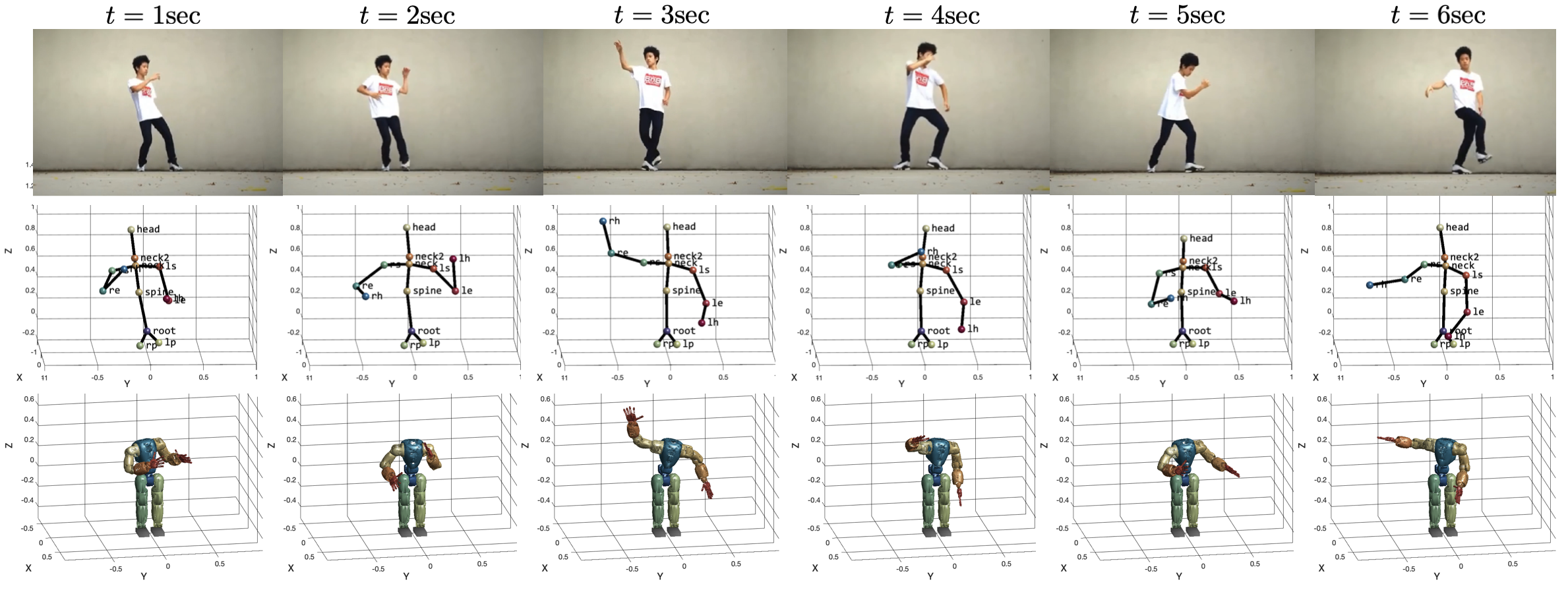
We further show that the proposed method can be used to generate natural and stylistic robotic motions from RGB videos. We use FrankMoCap [23], the state-of-the-art -D pose estimation algorithm, to collect sequences of human -D skeleton poses from YouTube videos. Since there is no ground truth, we simply show snapshots of reference RGB images and corresponding COMAN poses in Figure 6 for qualitative evaluation. More videos can be found in the supplementary materials.
VI Conclusion
In this paper, we presented S3LE, a self-supervised motion retargeting method which consists of two parts: 1) collecting tuples of relaxed and retargetable skeleton poses, and corresponding robot configurations to reduce the necessity of expensive data obtained via solving inverse kinematics, and 2) learning projection-invariant encoders to handle the different expressivities of humans and humanoid robots while constructing the shared latent space. Furthermore, our method guarantees the safety of the robot motion by utilizing a nonparametric method in the shared latent space. We demonstrate that S3LE can efficiently generate expressive and safe robotic motions from both motion capture data and YouTube videos.
One downside of using the nonparametric method is that its computational complexity increases linearly in the number of data. This becomes problematic when we want to retarget motions in real-time with a large number of pre-stored poses. We plan to investigate sublinear-time approximate nearest neighbor algorithms [24, 25, 26] (e.g., locality sensitive hashing) to speed-up the inference.
References
- [1] M. Gleicher, “Retargetting motion to new characters,” in Proceedings of the 25th annual conference on Computer graphics and interactive techniques. ACM, 1998, pp. 33–42.
- [2] N. D. Lawrence, “Gaussian process latent variable models for visualisation of high dimensional data,” in Advances in neural information processing systems, 2004, pp. 329–336.
- [3] A. Shon, K. Grochow, A. Hertzmann, and R. P. Rao, “Learning shared latent structure for image synthesis and robotic imitation,” in Advances in Neural Information Processing Systems (NeurIPS), 2006, pp. 1233–1240.
- [4] S. Levine, J. M. Wang, A. Haraux, Z. Popović, and V. Koltun, “Continuous character control with low-dimensional embeddings,” ACM Transactions on Graphics (TOG), vol. 31, no. 4, p. 28, 2012.
- [5] Z. Huang, J. Xu, and B. Ni, “Human motion generation via cross-space constrained sampling.” in Proc. of the International Joint Conference on Artificial Intelligence (IJCAI), 2018, pp. 757–763.
- [6] S. Choi, M. Pan, and J. Kim, “Nonparametric motion retargeting for humanoid robots on shared latent space,” in Proc. of the Robotics: Science and Systems (RSS), July 2020.
- [7] K. Yamane, Y. Ariki, and J. Hodgins, “Animating non-humanoid characters with human motion data,” in Proc. of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Eurographics Association, 2010, pp. 169–178.
- [8] H. Yin, F. S. Melo, A. Billard, and A. Paiva, “Associate latent encodings in learning from demonstrations,” in AAAI Conference on Artificial Intelligence, 2017.
- [9] S. Choi and J. Kim, “Cross-domain motion transfer via safety-aware shared latent space modeling,” IEEE Robotics and Automation Letters, 2020.
- [10] P. Sermanet, C. Lynch, Y. Chebotar, J. Hsu, E. Jang, S. Schaal, and S. Levine, “Time-contrastive networks: Self-supervised learning from video,” Proceedings of International Conference in Robotics and Automation (ICRA), 2018.
- [11] D. Dwibedi, J. Tompson, C. Lynch, and P. Sermanet, “Learning actionable representations from visual observations,” in 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2018, pp. 1577–1584.
- [12] M. Laskin, A. Srinivas, and P. Abbeel, “Curl: Contrastive unsupervised representations for reinforcement learning,” in Proceedings of the 37th International Conference on Machine Learning, Vienna, Austria, PMLR, vol. 119, 2020.
- [13] X. Deng, Y. Xiang, A. Mousavian, C. Eppner, T. Bretl, and D. Fox, “Self-supervised 6d object pose estimation for robot manipulation,” in 2020 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2020, pp. 3665–3671.
- [14] R. Villegas, J. Yang, D. Ceylan, and H. Lee, “Neural kinematic networks for unsupervised motion retargetting,” in Proc. of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 8639–8648.
- [15] J. Lim, H. J. Chang, and J. Y. Choi, “Pmnet: Learning of disentangled pose and movement for unsupervised motion retargeting.” in BMVC, 2019, p. 136.
- [16] D. Gandhi, L. Pinto, and A. Gupta, “Learning to fly by crashing,” in 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2017, pp. 3948–3955.
- [17] J.-Y. Zhu, T. Park, P. Isola, and A. A. Efros, “Unpaired image-to-image translation using cycle-consistent adversarial networks,” in Computer Vision (ICCV), 2017 IEEE International Conference on, 2017.
- [18] I. Tolstikhin, O. Bousquet, S. Gelly, and B. Schoelkopf, “Wasserstein auto-encoders,” in International Conference on Learning Representations (ICLR), 2018.
- [19] T. Chen, S. Kornblith, M. Norouzi, and G. Hinton, “A simple framework for contrastive learning of visual representations,” arXiv preprint arXiv:2002.05709, 2020.
- [20] S. Choi and J. Kim, “Towards a natural motion generator: a pipeline to control a humanoid based on motion data,” in Proc. of IEEE/RSJ International Conference on Intelligent Robots and Systems Intelligent Robots and Systems, 2019.
- [21] H. Zhang, M. Cisse, Y. N. Dauphin, and D. Lopez-Paz, “mixup: Beyond empirical risk minimization,” International Conference on Learning Representations, 2018.
- [22] CMU graphics lab motion capture database. [Online]. Available: http://mocap.cs.cmu.edu/
- [23] Y. Rong, T. Shiratori, and H. Joo, “Frankmocap: Fast monocular 3d hand and body motion capture by regression and integration,” arXiv preprint arXiv:2008.08324, 2020.
- [24] P. Indyk and R. Motwani, “Approximate nearest neighbors: Towards removing the curse of dimensionality,” in Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing, 1998, p. 604–613.
- [25] M. S. Charikar, “Similarity estimation techniques from rounding algorithms,” in Proceedings of the Thiry-Fourth Annual ACM Symposium on Theory of Computing, 2002, p. 380–388.
- [26] A. Andoni, P. Indyk, and I. Razenshteyn, “Approximate nearest neighbor search in high dimensions,” arXiv preprint arXiv:1806.09823, 2018.