CLEO Collaboration
Self-similarity with universal property for soap film and bubble in roll-off regime
Abstract
All children enjoy blowing soap bubbles that also show up in our bath and when we wash dishes. We analyze the thinning and breaking of soap bubble neck when it is stretched. To contrast with the more widely studied film whose boundaries are open, we concentrate on the bubble with a conserved air volume . Like film (F), non-equilibrium state can be divided into four regimes for bubble (B): (1) roll-off, (2) cusp approach, (3) pinch-off and (4) breakup. We establish the existence of self-similarity in F-1, B-1 and B-3, and universal property in F-1 and B-1 for the profile of soap membrane. The former means that the profile at successive times can be mapped to a master curve after being rescaled by the countdown time . Whiles, the latter further requires this master curve to be identical for different ring size for film and different and for bubble while keeping fixed. The exhibition of universal property indicates that the process of memory erasing starts earlier than regime 3. We also found that the minimum radius scales as , independent of and pulling speed. Note that the validity of our discussion is limited by the duration of roll-off regime from s.
I Introduction
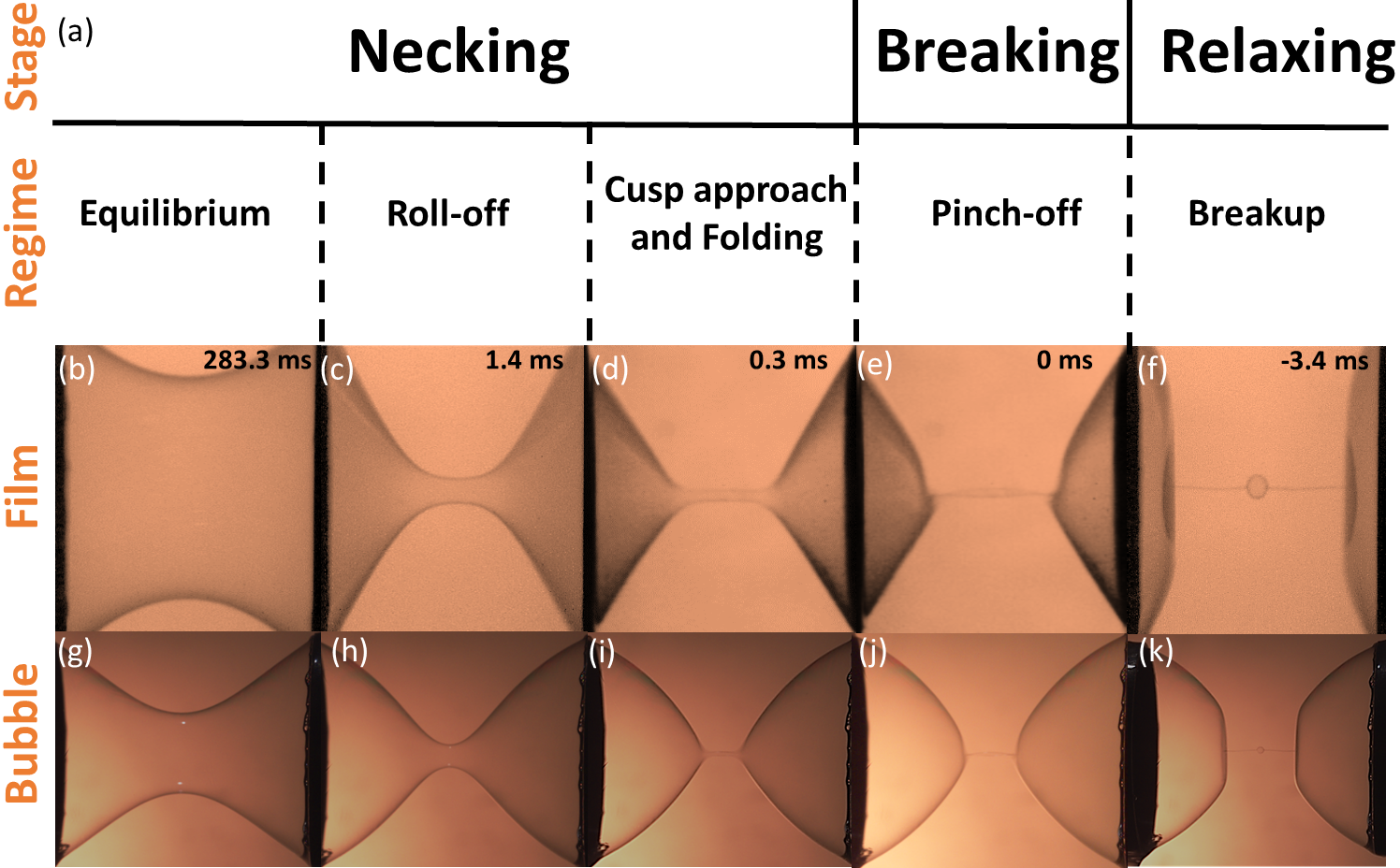
In addition to academic interests on the dynamics leading to the formation of singularities and its practical importance in industrial processes such as ink-jet printermaterial_printing and injection mouldingmolding , the breakup of a fluid body into two or more pieces may even shed light on the understanding of cell division cell of animals. Its procedures have been roughly divided into three stagesChen_steen_numerical - necking, breaking and relaxing according to Steen et al.. They are further subdivided into six regimes: equilibrium, roll-off, cusp approach, folding, pinch-off and breakup. To help clarify the nomenclature, we line up these phrases with their corresponding photos in Fig. 1 for soap membranes with open or close boundaries which we shall call the film or bubble from now on. The first four regimes belong to the necking stage, while pinch-off and breakup regimes refer separately to the breaking and relaxing stages. We shall merge cusp approach and folding into one regime because, like the use of superfluid by Burton et al. superfluid , we were not able to distinguish them in our nearly inviscid soap experiments.
The phenomenon of pinch-off occurs in the breaking stage and is mostly dominated by three major mechanismsHydrodynamic_stability ; Breaking_of_liquid_films_and_threads ; slender ; bir_bridge ; Universal_Eggers ; bir_pendant_drop ; Iterated_Instabilities_nagel ; Drop_formation_eaggers ; inital_nagel ; droplets_from_liquid_jet ; Drop_formation_in_viscous_flows ; Lister_H_stone ; Computational_experimental_drop_formation ; Satellite_drops_pinch_off ; Drop_formation_from_a_capillary_tube_one_d ; Modeling_pinchoff_and_reconnection ; Ligament_Mediated_Spray_Formation ; Scaling_and_Instabilities_Bubble ; giant_bubble_pinch ; bubble_nagel ; Simplicity_and_complexity_in_dripping ; Computational_analysis_of_drop ; pinch_rewiew ; Pinching_Dynamics_and_Satellite_Droplet_Formation_in_Symmetrical_Droplet_Collisions ; yc ; two_fluid_snap ; self_differ_viscosity ; Testing_for_scaling ; self_viscosity_thm : surface tension, inertia and viscosity. The minimum radius has been found to decrease as where , the countdown time, is defined as the difference between the pinch-off time and the real time , when viscosity is negligible in systems such as water dripping in the air. Similar to the dominant role of surface tension and inertia, both water and air can be approximated as being nearly inviscid. In the meantime, the pinch-off of inviscid fluid system has been studied by theoretical, experimental and computational analyses Self_Similar_Capillary ; C_and_E_scaling ; Capillary_pinch_off ; mercury ; EPL_film ; superfluid ; self_inviscid_exp . Although being the driving force for all the above cases Self_Similar_Capillary ; C_and_E_scaling ; Capillary_pinch_off ; mercury ; superfluid ; two_fluid_snap ; Testing_for_scaling , the surface tension is not necessary to render the pinch-off, e.g., thermal fluctuation or bulk diffusion thermal_fluctuation ; diffusion is known to be equally capable as the capillary force is ultra-low.
The final breakage of liquid drop into several pieces is universal in most cases, meaning that its collapsing speed and neck radius are independent of initial and boundary conditionsUniversal_Eggers ; Iterated_Instabilities_nagel ; Drop_formation_eaggers ; droplets_from_liquid_jet ; Ligament_Mediated_Spray_Formation ; Pinching_Dynamics_and_Satellite_Droplet_Formation_in_Symmetrical_Droplet_Collisions ; two_fluid_snap ; self_differ_viscosity ; Testing_for_scaling . In other words, the memory is erased. Targeting the particular case of a water droplet in silicon oil, Nagel et al. memory found that both the sine wave perturbation in numerical simulation and different boundary conditions in experiments would affect the curvature at the pinch-off neck. A similar system, for which the viscosity of the inner fluid is much smaller than the outer one, was investigated by Stone et al.universal_stone and found to lose its memory again when the outside container is confined to a capillary tube.
Open soap film belongs to inviscid fluid and forms a catenoid to minimize its surface tension energyminimal_surface_Euler_Leonhard ; Plateau ; A_Complete_Minimal_Surface_in_R3_Between_two_Parallel_Planes ; Shapes_of_embedded_minimal_surfaces . For instance, the numerical work Chen_steen_numerical by Chen and Steen fits the by a power law with an exponent in pinch-off regime. Subsequently, Robinson and Steen robinson_steen_exp ; cryer_steen_exp did some experiments to verify their previous numerical result Chen_steen_numerical . Limited by the frame rate of their high-speed camera, they were not able to verify the property of self-similarity, that has been observed in bubble burstingbubble_yao , relaxation of confined dropletsrelaxation and liquid lens coalescencelens , for pinch-off regime.
Compared with soap film, it is apparent that bubble looks plumper in Fig. 1. One reasonable question is whether the constraint of volume conservation will sustain to alter the fascinating dynamics of and profile when the system enters non-equilibrium state. In equilibrium regime, the shrinking of the neck is quasi-static and reversible, i.e., the neck radius can retain its original value when the separation distance reverts to the previous length. When extended to a critical length , both film and bubble become unstable and their time evolution is shown in Fig. 1 and characterized by: (1) roll-off with only one , (2) pinch-off when two necks suddenly emerge symmetrically with a separation distance that increases much slower than the collapsing speed of necking and (3) breakup at which film and bubble separate after pinching-off. Besides clarifying the role of long-range medium pressure due to volume conservation for bubble, we also want to investigate whether the self-similarity is exhibited not only in the final pinch-off for bubble; but also in roll-off regime.
Not limited to bubble, the volume of ink droplet is also conserved and how it affects has incurred some debates in the printing industrySimulation_ink_gravure . Previous researchers Stability_of_liquid_bridges_between_equal_disks_in_an_axial_gravity_field ; vertical_abtrary_liquid_bridge ; On_the_breakup_of_viscous_liquid_threads ; nonlinear_bridge studied the breakage of liquid that was stored between the gap of two departing horizontal and vertical rods. Although they found the volume of liquid to affect , their conclusions were tainted by the movement of the contact linecontact_line when the neck collapses. In contrast, our setup, as described in the next section, is free of such a defect while honoring the volume-conservation.
This paper is organized as follows: Experimental setup is described and relevant parameters are defined in Sec. II. How the neck radius varies with the separation distance is studied for equilibrium regime and compared between film and bubble in Sec. III A. While the self-similarity and universal property are generally thought to be unique for pinch-off regime in Sec. III C, we check and confirm their existence in as early as roll-off regime in Sec. III B, where the power-law relation is also examined. The final breakup regime that is characterized by the formation of a satellite bubble is arranged in Sec. III D, where data on how the pumping volume affects are presented. Complementing the experimental results in Sec. III, theoretical models and derivations are presented in Sec. IV. Finally, we conclude and suggest possible directions for future workers in Sec. V.
II Experimental setup
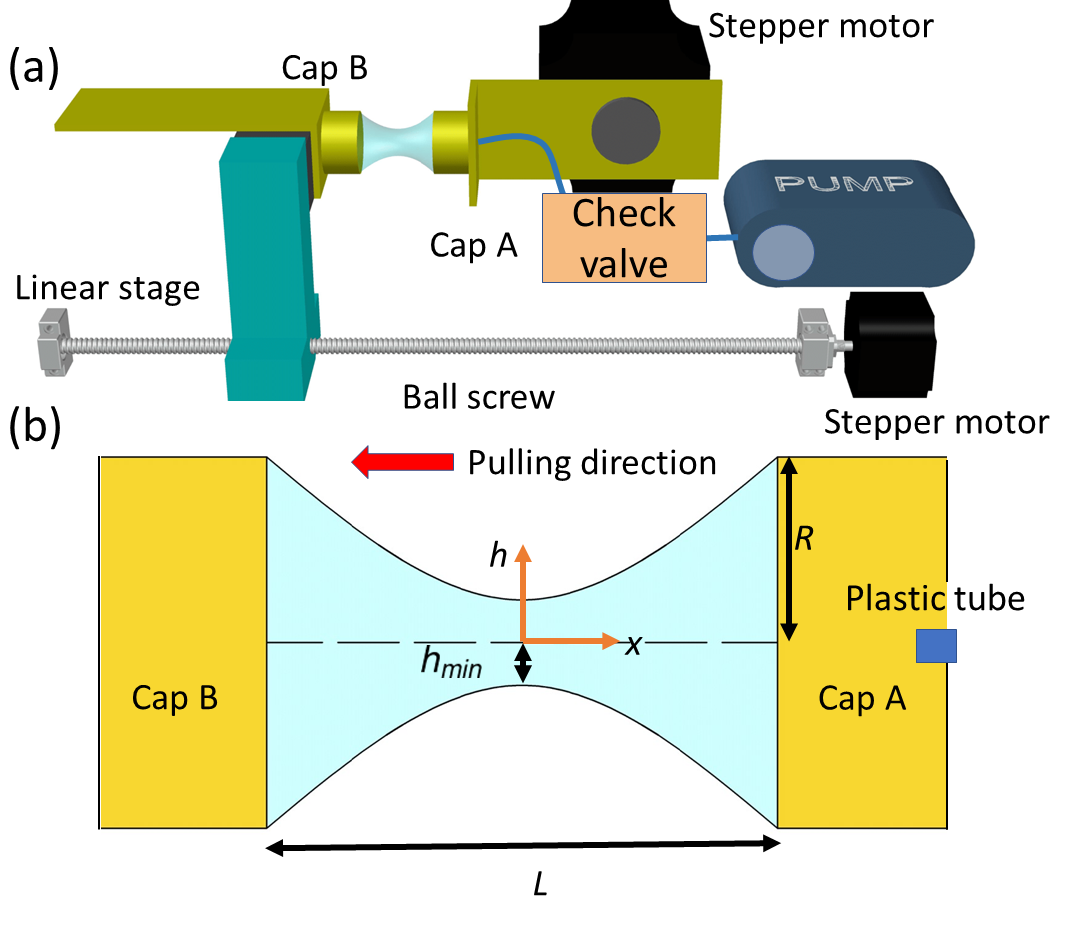
The ingredients Chen_steen_numerical of our soap water include dried oleic acid soap, deionized water and guar gum. The addition of guar gum has been verifiedbig_bubble to prolong the lifetime of soap membrane. After dipping into the solution, an aluminum cap A of radius is rotated 90 degrees by a stepper motor to horizontally align its open end to another cap B at a distance . When the air pump is switched on by a solid state relay module, a soap bubble is formed on cap A. We use a check valve to ensure that no back-flow of air will deflate bubble. As demonstrated schematically in Fig. 2, this bubble is gently attached to cap B that is pre-wetted. Then, a linear ball screw driven by another stepper motor is utilized to move cap B away from cap A with a constant pulling speed mm/s. Collapse of bubble neck is recorded by a high speed camera with 23000 fps. We originally open a hole on cap B to change the bubble to film. However, the film shape is always plagued by an asymmetry due to the time lag it takes for the air to flow out. As a result, the caps are eventually replaced by two rings to generate film.
The dominated term in the collapse is determined by several dimensionless numbers. To begin with, we deduce that the shear viscosity is negligible since Reynolds number Re= where notations are defined in Table 1. In the mean time, the magnitudes of the other two numbers, Bond number Bo= and Webber number We = , reassure us of two things. First, soap bubble can be regarded as being symmetric since the effect of gravity is small. Second, the system is dominated by the surface tension and inertia. Surface tension coefficient is estimated by surface_tension_drop .
| Notation | Definition |
|---|---|
| separation distance between rings or caps | |
| radius of ring or cap | |
| real time | |
| critical length | |
| pumping volume of air | |
| radius of cross section | |
| characteristic radius of cross section | |
| minimal radius at neck | |
| thickness of film or bubble | |
| surface tension coefficient | |
| characteristic collapse speed | |
| mass density of soap water | |
| pulling speed | |
| volume of soap droplet | |
| surface mass density of film or bubble | |
| difference between pinch-off and real times | |
| pinch-off time | |
| pinch-off position in axis | |
| shear viscosity of soap water | |
| Lagrange multiplier | |
| pressure difference across bubble surface | |
| radial and axial curvatures |
III Experimental results
III.1 Equilibrium regime
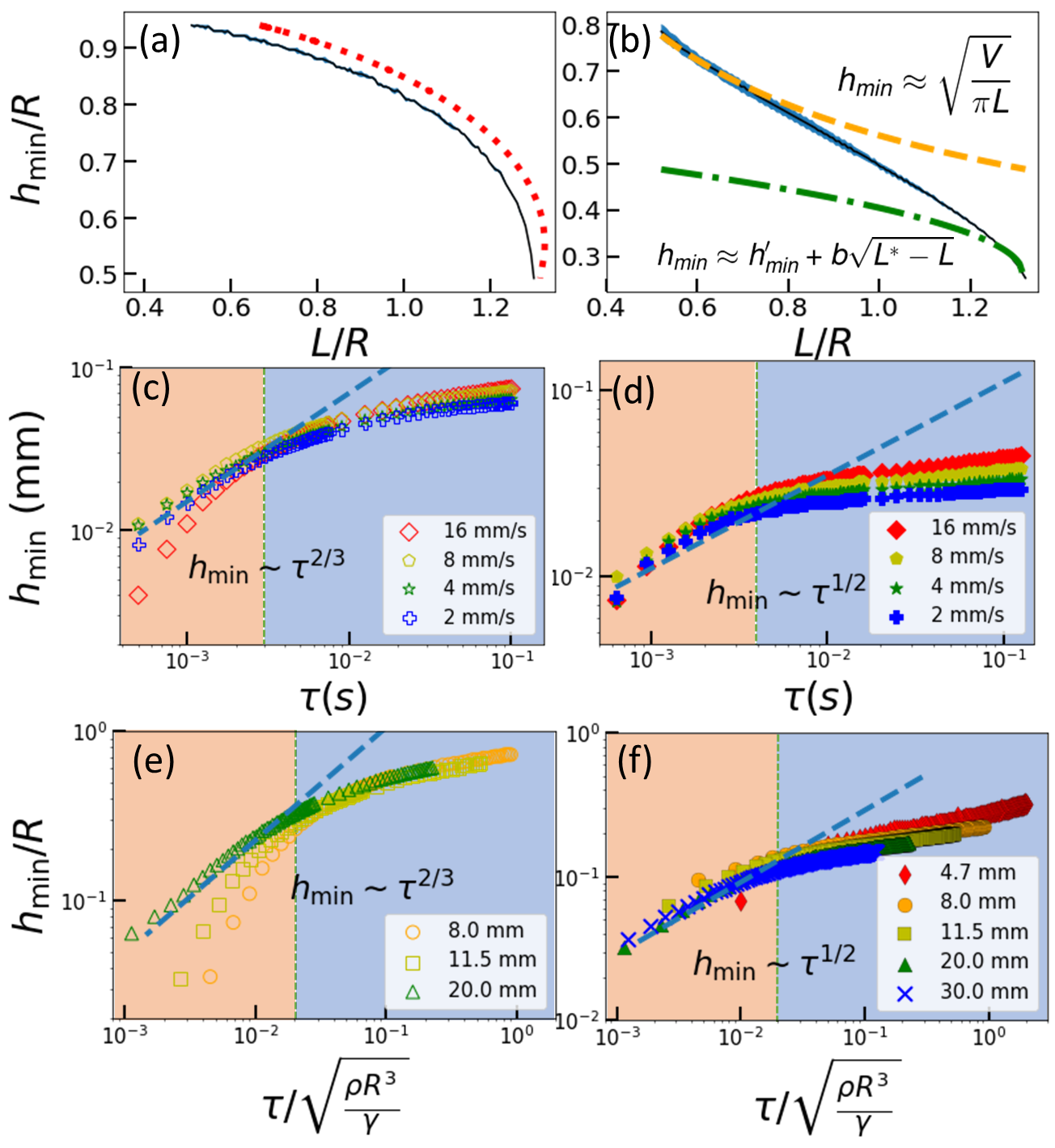
Compared to film, the volume of bubble roughly remains constant when pulled apart, as argued in Sec. IV of the Supplemental Material (SM) sm . The center of bubble surface evolves from being convex to concave in contrast to film that is always convex throughout equilibrium regime. This difference will be argued later in the theory section to give rise to a positive second derivative of in bubble, as opposed to a negative one in film Chen_steen_numerical ; robinson_steen_exp ; cryer_steen_exp , as shown in Fig. 3(a, b). When , and are fixed, can be uniquely determined by in equilibrium regime. By use of where denotes the time when the neck starts to collapse spontaneously, can be alternatively expressed as a function of . But, since non-equilibrium state proceeds much faster than , the time it takes is negligibly small, i.e., . So, we can use to track the evolution of from now on.
The necking process is expected to be size-independent for both film and bubble. Therefore we divide and by and to render them dimensionless. When is fixed, is proportional to at the same for a film. A different choice of ratio of will shift the curve in Fig. 3(f) that still remains independent of , as detailed in Sec. VII of the SM sm .
III.2 Roll-off regime
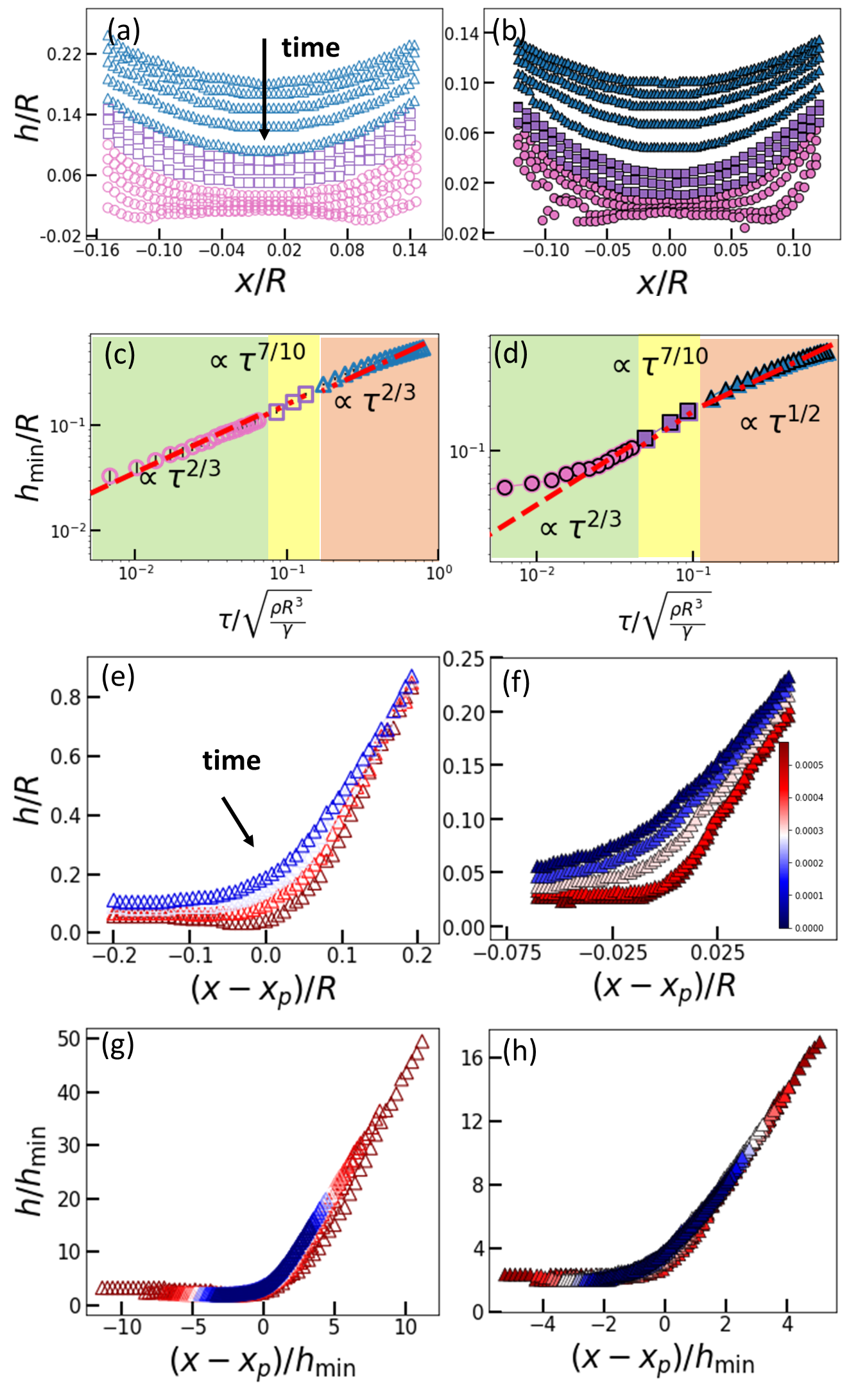
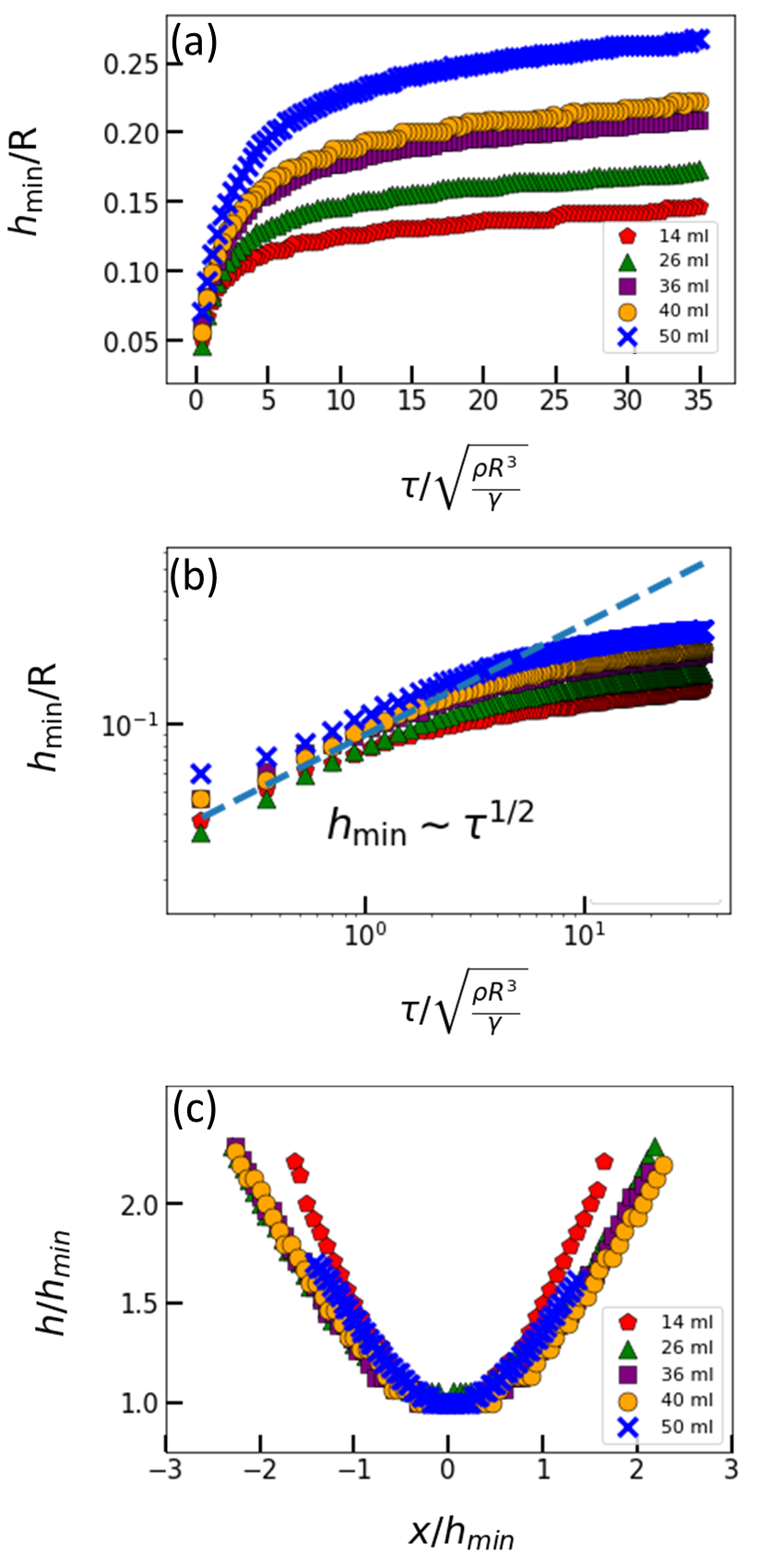
Upon entering roll-off regime, film and bubble share the following properties: First, the evolution of is independent of (1) the pulling speed in Fig. 3 (c, d) because the shrinkage is much faster and (2) the ring or cap size if both and in Fig. 3 (e, f) are properly rescaled by and the characteristic time from the balance between the surface tension and inertial force. Note that the for film has been predicted to be independent of by Chen_steen_numerical . What distinguishes bubble from film is that for the former instead of 2/3 Chen_steen_numerical . Although will increase with more pumping volume, the value of is checked to be independent of , as shown in Fig 8. We believe this is due to the fact that there is little air in the vicinity of bubble neck. However, the constraint imposed by the volume conservation is still critical at modifying . Heuristically the existence of a pressure difference across the membrane impedes the collapsing of bubble and thus renders a small .
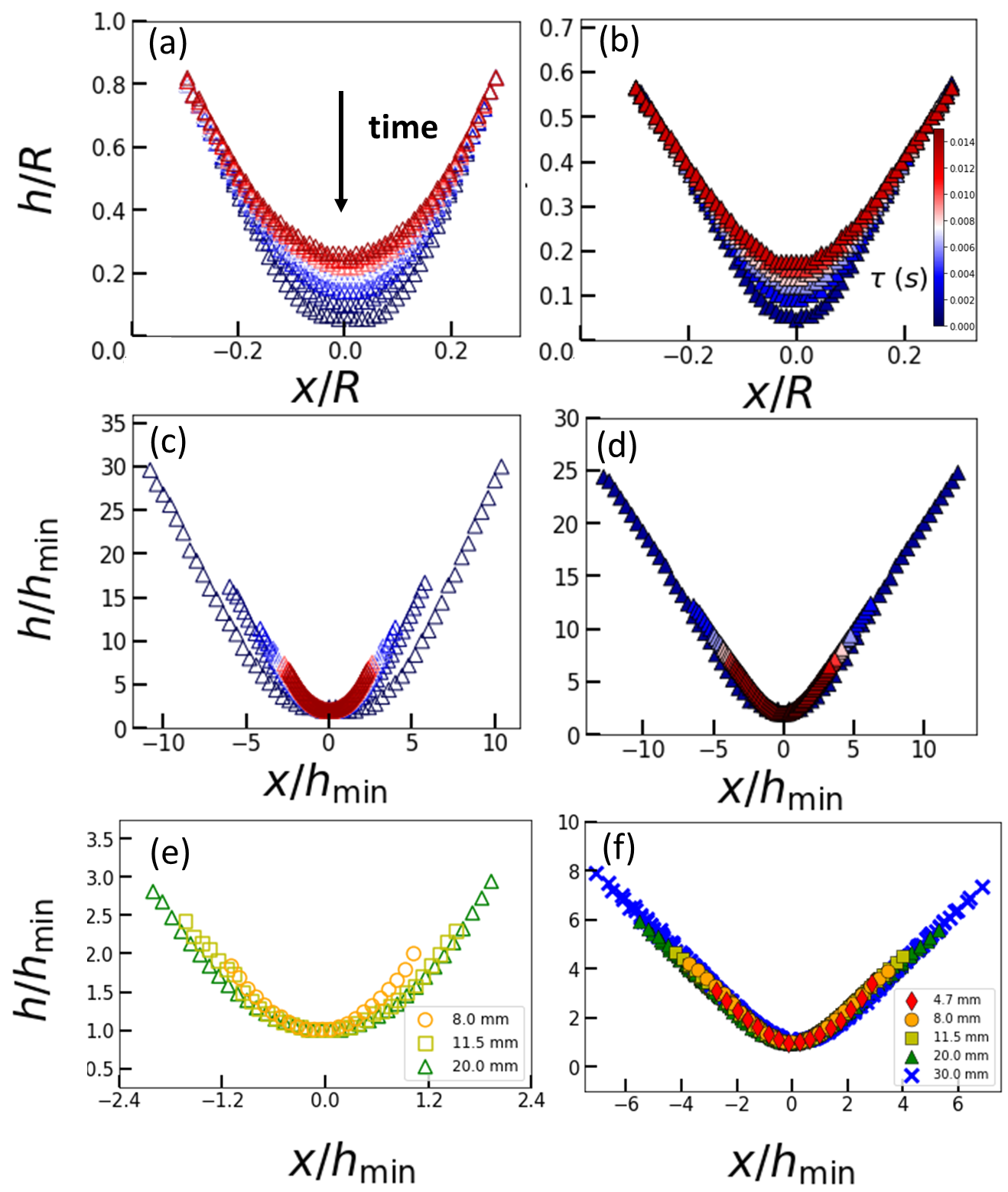
The second property shared by film and bubble regards the evolution of profile, in Fig. 4 (a, b) and includes: (1) Both are found to exhibit self-similarity, i.e., their shapes at different time can be mapped to a master curve if both and are rescaled by , as shown in Fig. 4 (c, d). The level of similarity is quantified by cosine similarity self = 0.98 and 0.99 for film and bubble, as detailed in Sec. II of the SM sm . (2) Both master curves do not change with different ring or cap size in Fig. 4(e, f). In contrast to that is independent of both and , the contour in Fig. 4(f) is only universal with respect to . When changes, the contour will become different. What distinguishes bubble from film is that which renders an inflection point between and , where denotes . In contrast, the film is always concave upward. This is demonstrated theoretically in Sec. X of the SM sm .
III.3 Pinch-off regime
The number of neck can be seen to double as film and bubble transits from roll-off to pinch-off regime in Fig. 5 (a, b). Furthermore, the originally different exponent in roll-off becomes identical at 2/3 for film and bubble near pinch-off regime in Fig. 5 (c, d), rescaled as Fig. 3 (e, f). The evolution of profile for film looks similar to that of bubble in pinch-off regime with the shifting of minimum point from 0 to in Fig. 5 (e, f). The self-similar behavior which has been predicted by numerical and theoretical works Chen_steen_numerical ; Self_Similar_Capillary for film turns out to be also true for bubble, as shown in Fig. 5 (g, h).
III.4 Breakup regime
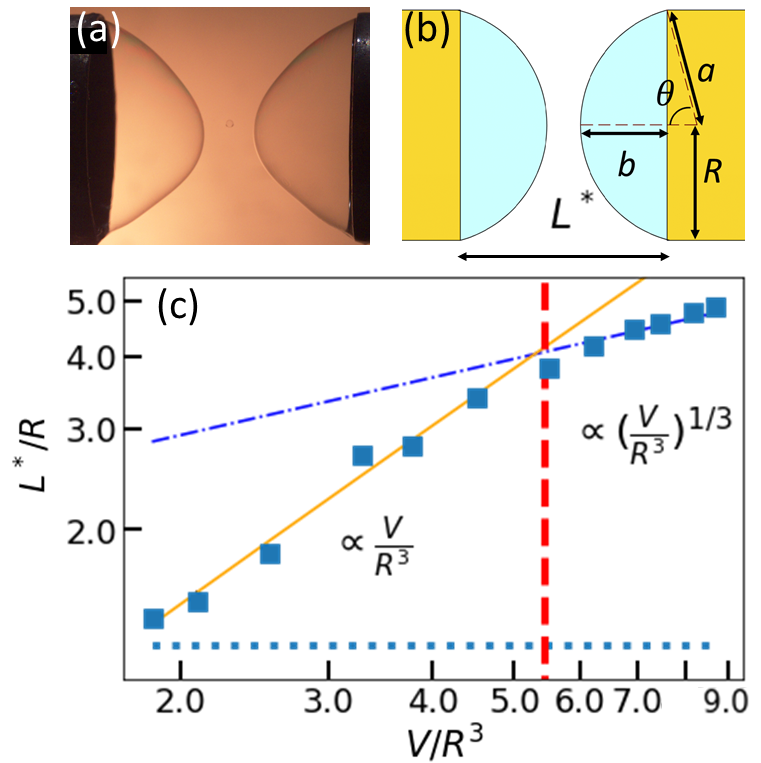
Different from the flat surfaces on rings for film, two spherical bubbles survive the breakage and appear on the caps for bubble. The spherical shape is to minimize the surface energy, for which the height defined in Fig. 6 (a, b) can be calculated. In the mean time, the critical length at which the irreversible processes are initiated can also be determined theoretically by the breakdown of solution from minimizing the potential energy for equilibrium regime. Comparing these two lengths, we find that is not only bigger than , which explains the necessity for both bubbles to retract and breakage, but roughly equals . This is verified in our experiment.
Depending on the amount of , we expect two scenarios for the remnant bubble. Straightforward calculation in Sec. IV C reveals that with for and otherwise. This prediction is nicely verified by Fig. 6(c).
IV Theoretical derivation
IV.1 Equilibrium regime
Experimentally we can stretch bubble and film horizontally or vertically. Although the sagging and non-symmetric contour due to gravity in both cases can be alleviated by minimizing , it is still uncertain whether the critical behavior at pinch-off will be affected. So theoretical calculations can help us not only clarify this concern, but also give us analytic expressions for quantities of our interest, e.g., and highlight the influence of volume conservation. To realize how the parameters affect the contour of bubble, we start from the minimization of total energy for bubble:
| (1) |
where the Lagrange multiplier makes sure that the air volume is conserved. Using the second form of Euler-Lagrange equation, we can obtain
| (2) |
After some transpositions, Eq. (2) becomes
| (3) |
Solving this differential equation will enable us to obtain information of the contour :
| (4) |
where .
By implementing the boundary condition that and volume conservation, we get
| (5) |
and
| (6) |
where a change of variable has been performed to render the parameters dimensionless and . By setting , Eq. (5) will revert to depicting a film and give us vs. in agreement with Fig. 3(a). During the stretching of bubble, there must be a period when is close to and we can approximate by where . This allows us to Taylor expand , Eqs. (5) and (6) to get
| (7) | |||||
and
| (8) |
where terms of order higher than have been neglected. By comparing the above two equations, we obtain . Note that this result predicts a simple yet informative relation for how varies with :
| (9) |
which matches the data in early equilibrium regime for Fig. 3(b). In retrospect, this result is expected from our restricting since the shape of bubble now mimics that of a cylinder.
The derivations from Eq. (2) to (8) serve several purposes: First, to illustrate the important role of the Lagrange multiplier and how it mathematically prohibits the bubble from adopting the catenoid profile as the film. Second, near the edge can be easily shown to exhibit different signs for film and bubble - positive and negative from the derivative of Eq. (2), respectively, as detailed in Sec. X of the SM sm . Third, they highlight the importance of and subsequent parameter , without which the right-hand side of Eq. (7) will be of order - meaning the cylindrical shape is only possible when the two rings are very close for film.
Some experience can be borrowed from the analysis of film. After setting , we plot both sides of Eq. (5) as a function of in Fig. 7 (a).
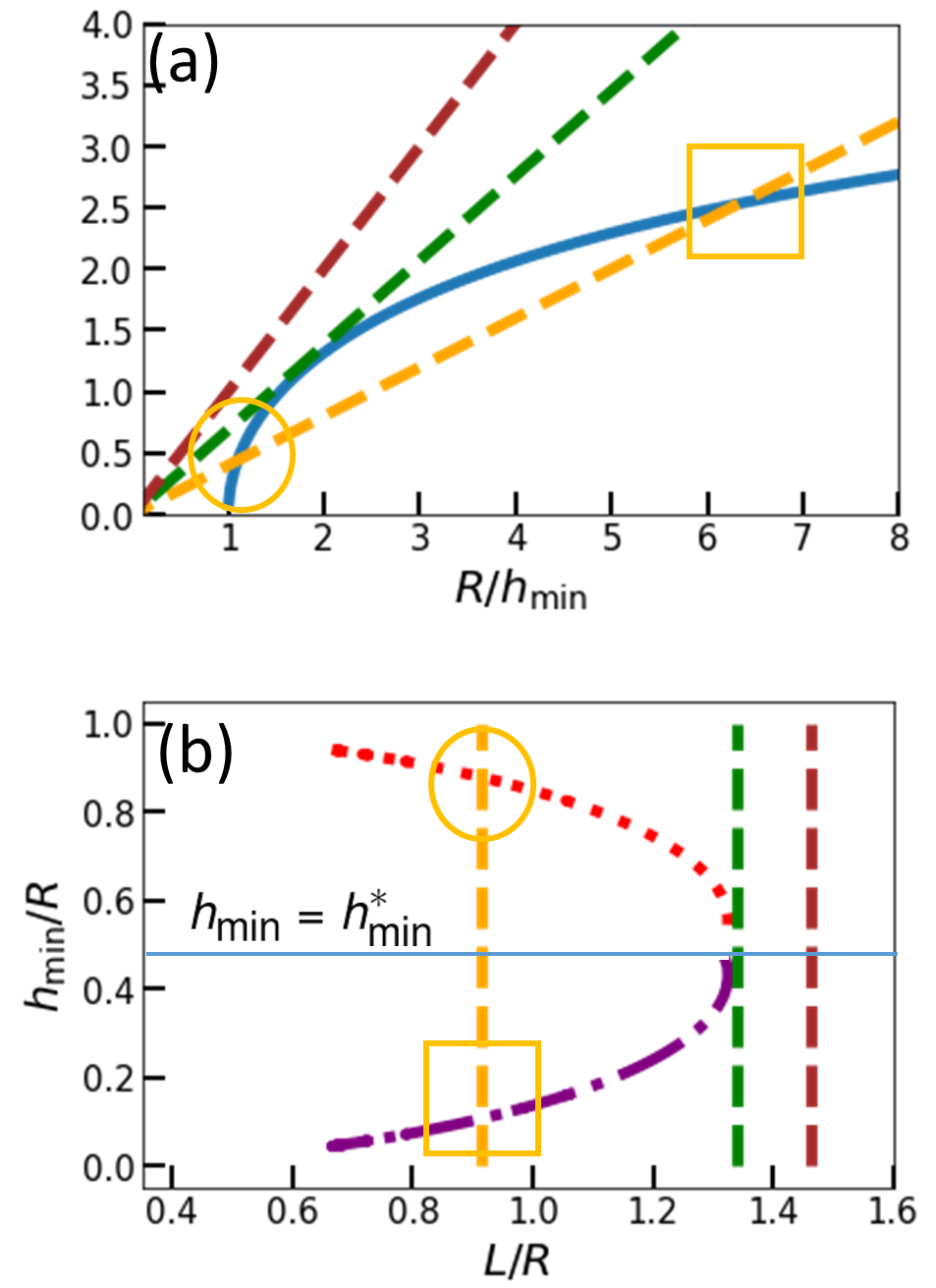
When , there is no intersection - meaning that the starting point of minimizing the surface energy is problematic. This is consistent with our expectation that film will collapse automatically at large when we need to resort to minimizing the action. When , both sides of the equation become tangent. The same is expected for bubble, i.e., we should differentiate both sides of Eq. (5) with respect to to locate . There are two intersections for with one being unphysical as explained in Fig. 7 (a). When we plot vs. , the solution should be double-valued until reaches in Fig. 7(b). Therefore, we expect where is a constant when is close to the critical neck radius beyond which the neck collapses spontaneously. Simple rearrangement gives
| (10) |
Our confidence on Eqs. (9) and (10) is supported by its rightful prediction of an inflection point in Fig. 3(b) due to the fact that their curvatures are of opposite sign.
IV.2 Breakup regime
The collapsing speed of neck is very fast. As will be delineated later, there will be two complications before the final breakage. First, two necks will be developed in pinch-off regime. Second, this is followed by the breaking stage when a satellite bubble is formed in the middle of these two necks after the hollow thin tube connecting them becomes a liquid string. There is no gas leakage throughout breaking and relaxing stages and the volume of satellite bubble can be neglected. Therefore, should equal to the combined volume of the two remnant bubbles after breakage. We can directly obtain the relation between and which can be estimated from Fig. 6(b) where the chord length equals and the radius of partial sphere is denoted by . From the geometry in Fig. 6(b), we can write down
| (11) |
and
| (12) |
The volume of each partial sphere can be calculated as
| (13) |
Rearranging both sides to make them dimensionless, we found
| (14) |
By inserting the experimental result , there are two limiting cases to Eq. (14). When , the cubic term in Eq. (14) can be neglected and
| (15) |
In the other extreme , the linear term becomes negligible and
| (16) |
The two regions in Eqs. (15) and (16) are vindicated by Fig. 6(c).
V conclusion and discussions
We studied how the mediation of long-range pressure that comes in via the volume conservation affects the necking phenomenon of soap bubble, as compared to the relatively well-studied film. Understandably the distinct contour shape exhibited by bubble should result in different ways for how the neck radius shrinks with increasing separation length in equilibrium regime. Upon entering non-equilibrium state, film and bubble share the following properties: (1) the collapsing dynamics is insensitive to the pulling speed and ring or cap size , (2) the contour for roll-off regime (a) exhibits self-similarity in its evolution which can be quantified by cosine similarity and supported by theoretic derivations and (b) is universal, i.e., independent of and upon being rescaled by - although varying will render a different universal line for bubble which elaborates the effect of erasing the boundary condition is earlier than pinch-off regime. (3) The evolution of is independent of , and for pinch-off regime. However, the relation is found to differ for roll-off regime with for bubble, in contrast to 2/3 for film.
The dimensionless threshold length that marks the beginning of spontaneous collapse for bubble is found to depend only on the ratio of and and can be separated into two different regimes for which a simple theory was built.
We suggest that future researchers can strengthen the following aspect: To determine whether will be affected by when it is comparable to the collapse speed in roll-off regime. The motivation is that most breakage studies concentrate on pinch-off regime when is so fast that it is challenging to apply a fast without invoking unwanted technical artifacts. One exception, though, is Ref.universal_stone where was slowed down considerably by the viscous stress and was found to scale as in early self-similar regime. It gave the authors an incentive to probe how a large enough affects this power law. Surprisingly, the result turns out to be negative. Likewise, it is recommended to increase to the same order as in our roll-off regime.
We are grateful to C. Y. Lai and J. R. Huang for useful discussions and thank P. Yang and J. C. Tsai for the use of high-speed cameras. Financial support from the Ministry of Science and Technology in Taiwan under Grants No. 105-2112-M007-008-MY3 and No. 108-2112-M007-011-MY3 is acknowledged.
Appendix A Evidence for -independent in roll-off regime
It is obvious that will increase with when all other parameters are fixed in equilibrium regime. Interestingly, it turns out that the properties characteristic of roll-off regime become insensitive to the actual value of in Fig. 8 (a, b), indicating that this is a local event in which very little air is involved. Proof can be found in the rescaled profile in Fig. 8(c) where an extra influx of is shown to pile up on the flank of, but not at the neck.
References
- [1] H. Abdolmaleki, P. Kidmose and S. Agarwala, Adv. Mater. 33, 2006792 (2021).
- [2] A. R. Agrawal, I. O. Pandelidis and M. Pecht, Polym. Eng. Sci. 27, 1345 (1987).
- [3] Y. Yoon and M. A. McNiven, Current Biology 11, 67 (2001).
- [4] Y. J. Chen and P. H. Steen, J. Fluid Mech. 341, 245 (1997).
- [5] J. C. Burton, J. E. Rutledge and P. Taborek, Phys. Rev. E 75, 036311 (2007).
- [6] E. B. Dussan V, Arch. Rational Mech. 57, 263 (1975).
- [7] J. B. Keller, Phys. Fluids 26, 3451 (1983).
- [8] Lu Ting and J. B. Keller, SIAM Journal on Applied Mathematics 50, 1533 (1990).
- [9] D. H. Peregrine, G. Shoker and A. Symon, J. Fluid Mech. 212, 25 (1990).
- [10] J. Eggers, Phys. Rev. Lett. 71, 3458 (1993).
- [11] R. M. S. M. Schulkes, J. Fluid Mech. 278, 83 (1994).
- [12] M. P. Brenner, X. D. Shi and S. R. Nagel, Phys. Rev. Lett. 73, 3391 (1994).
- [13] J. Eggers and T. F. Dupont, J. Fluid Mech. 262, 205 (1994).
- [14] X. D. Shi, Michael P. Brennerand and S. R. Nagel, Science 265, 219 (1994).
- [15] T. A. Kowalewski, Fluid Dynamics Research. 17, 121 (1996).
- [16] D. F. Zhang and H. A. Stone, Phys. Fluids 9, 2234 (1997).
- [17] J. R. Lister and H. A. Stone, Phys. Fluids 10, 2758 (1998).
- [18] E. D. Wilkes, S. D. Phillips and O. A. Basaran, Phys. Fluids 11, 3577 (1999).
- [19] P. K. Notz, A. U. Chen and O. A. Basaran, Phys. Fluids 13, 549 (2001).
- [20] B. Ambravaneswaran, E. D. Wilkes and O. A. Basaran, Phys. Fluids 14, 2606 (2002).
- [21] H. Lee, J. S. Lowengrub and J. Goodman, Phys. Fluids 14, 492 (2002).
- [22] E. Villermaux, Ph. Marmottant and J. Duplat, Phys. Rev. Lett. 92, 074501 (2004).
- [23] J. C. Burton, R. Waldrep and P. Taborek, Phys. Rev. Lett. 94, 184502 (2005).
- [24] R. Bergmann, D. van der Meer, M. Stijnman, M. Sandtke, A. Prosperetti and D. Lohse, Phys. Rev. Lett. 96, 154505 (2006).
- [25] N. C. Keim, P. Moller, W. W. Zhang and S. R. Nagel, Phys. Rev. Lett. 97, 144503 (2006).
- [26] H. J. Subramani, H. K. Yeoh, R. Suryo, Q. Xu, B. Ambravaneswaran and O. A. Basaran, Phys. Fluids 18, 032106 (2006).
- [27] Q. Xu and O. A. Basaran, Phys. Fluids 19, 102111 (2007).
- [28] Jens Eggers and E. Villermaux, Rep. Prog. Phys. 71, 036601 (2008).
- [29] K. L. Huang, K. L. Pan and C. Josserand, Phys. Rev. Lett. 123, 234502 (2019).
- [30] An interesting exception was reported in Y. C. Cheng, T. H. Hsieh, J. C. Tsai, and T. M. Hong, Phys. Rev. E 104, 045004 (2021) where the shear energy trumps surface tension to trigger the snap-off in twisted balloons.
- [31] I. Cohen, M. P. Brenner, J. Eggers,and S. R. Nagel, Phys. Rev. Lett. 83, 1147 (1999).
- [32] W. W. Zhang and J. R. Lister, Phys. Rev. Lett. 83, 1151 (1999).
- [33] I. Cohen and S. R. Nagel, Phys. Fluids 13, 3533 (2001).
- [34] A. Sierou and J. R. Lister, J. Fluid Mech. 497, 381 (2003).
- [35] R. F. Day, E. J. Hinch and J. R. Lister, Phys. Rev. Lett. 80, 704 (1998).
- [36] A. U. Chen, P. K. Notz and O. A. Basaran, Phys. Rev. Lett. 88, 174501 (2002).
- [37] D. Leppinen and J. R. Lister, Phys. Fluids 15, 568 (2003).
- [38] J. C. Burton, J. E. Rutledge and P. Taborek, Phys. Rev. Lett. 92, 244505 (2004).
- [39] F. Muller and R. Stannarius, EPL 76, 1102 (2006).
- [40] J. R. Castrejon-Pita, A. A. Castrejon-Pita, E. J. Hinch, J. R. Lister and I. M. Hutchings, Phys. Rev. E 86, 015301(R) (2012).
- [41] Y. Hennequin, D. G. A. L. Aarts, J. H. van der Wiel, G. Wegdam, J. Eggers, H. N. W. Lekkerkerker and D. Bonn, Phys. Rev. Lett. 97, 244502 (2006).
- [42] H. Y. Lo, Y. Liu, S. Y. Mak, Z. Xu, Y. Chao, K. J. Li, H. C. Shum and L. Xu, Phys. Rev. Lett. 123, 134501 (2019).
- [43] P. Doshi, I. Cohen, W. W. Zhang, M. Siegel, P. Howell, O. A. Basaran and S. R. Nagel, Science 302, 1185 (2003).
- [44] A. A. Pahlavana, H. A. Stone, G. H. McKinley and R. Juanes, PNAS 116, 13780 (2019).
- [45] E. Leonhard, Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti 341, 245 (1744).
- [46] J. Plateau, The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science 14, 90 (1857).
- [47] F. Xavier and L. P. Jorge, Ann. Math. 112, 203 (1980).
- [48] T. H. Colding and W. P. Minicozzi, PNAS 103, 11106 (2006).
- [49] N. D. Robinson and P. H. Steen, J. Colloid Interface Sci. 241, 448 (2001).
- [50] S. A. Cryer and P. H. Steen, J. Colloid Interface Sci. 151, 276 (1992).
- [51] C. Y. Lai, J. Eggers and L. Deike, Phys. Rev. Lett. 121, 144501 (2018).
- [52] M. Kerdraon, J. D. McGraw, B. Dollet and M. C. Jullien, Phys. Rev. Lett. 123, 024501 (2019).
- [53] M. A. Hack, W. Tewes, Q. Xie, C. Datt, K. Harth, J. Harting and J. H. Snoeijer, Phys. Rev. Lett. 124, 194502 (2020).
- [54] D. H. Ahmed, H. J. Sung and D. S. Kim, Int. J. Heat Fluid Flow 32, 298 (2011).
- [55] L. A. Slobozhanin and J. M. Perales, Phys. Fluids A 5, 1305 (1993).
- [56] A. Laveron-Simavilla and J. M. Perales, Phys. Fluids 7, 1204 (1995).
- [57] D. T. Papageorgiou, Phys. Fluids 7, 1529 (1995).
- [58] X. Zhang, R. S. Padgett and O. A. Basaran, J. Fluid Mech. 329, 207 (1996).
- [59] A. A. Darhuber, S. M. Troian and S. Wagner, J. Appl. Phys. 90, 3602 (2001).
- [60] S. Frazier, X. Jiang and J. C. Burton, Phys. Rev. Fluids 5, 013304 (2020).
- [61] A. Sack and T. Pöschel, Am. J. Phys. 85, 649 (2017).
- [62] See Supplemental Material at **** for more details and calculations.
- [63] https://en.wikipedia.org/wiki/Cosine_similarity
- [64] T. Eiter and H. Mannila. Computing discrete Fréchet distance. Technical report, (1994).