\UseRawInputEncoding

Introduction. Self-healing is the fantastic property of certain classical or quantum (matter) waves to reconstruct their original shape after being scattered off by a potential (an obstacle) A1 ; A2 ; A3 . Such a special property is rather generally shared by diffraction-free and thus non-normalizable (delocalized) states of the underlying wave equation. Important examples include Bessel waves of the Helmholtz equation A1 ; A2 ; A4 and self-accelerating (Airy) waves of the Schrödinger equation A3 ; A5 ; A6 . Self-healing has been demonstrated for optical A1 ; A3 ; A8 ; A8a ; A8b ; A8c , acoustic A9 ; A10 ; A11 ; A12 and matter waves A13 ; A14 , with a variety of applications in different areas of science such as in microscopy and biomedical imaging A15 ; A16 ; A17 , material processing A18 , particle manipulation A19 ; A20 , sensing A8a ; A8b ; A8c and quantum communications A21 . However, in a norm-preserving (Hermitian) system any normalizable (bound) wave function cannot be strictly self-healing. An interesting and open question is whether infinitely-many self-healing normalizable waves can exist in NH systems r1 . An important class of such systems is provided by NH lattices, where the role of topology and its far-reaching physical consequences are attracting an enormous interest r1a ; r2 ; r3 ; r4 ; r5 ; r6 ; r7 ; r8 ; r9 ; r10 ; r11 ; r12 ; r13 ; r14 ; r15 ; r16 ; r17 ; r18 ; r19 ; r20 ; r20a ; r21 ; r22 ; r23 ; r24 ; r25 ; r26 ; r27 ; r28 ; r28a ; r29 ; r30 ; r31 ; r32 ; r33 ; r34 ; r34a ; r34b ; r35 ; r36 ; r37 ; r38 ; r39 ; r40 ; r41 ; r42 ; r43 ; r44 ; r45 ; r46 ; r47 ; r48 ; r49 ; r50 ; r51 ; r52 ; r53 ; r54 ; r55 ; r56 ; r57 ; r58 ; r59 ; r60 ; r61 ; r62 ; r63 ; r64 ; r65 ; r66 ; r67 ; r68 ; r69 ; r70 ; Referee1 ; Referee2 (for a recent review see r51 ). A unique feature of NH lattices is the skin effect r5 ; r6 ; r7 ; r9 ; r29 , i.e. the localization of an extensive number of bulk eigenstates at the edges under open (OBC) or semi-infinite (SIBC) boundary conditions. The localized skin modes replace the extended Bloch waves of Hermitian lattices and their origin can be traced back to the nontrivial point-gap topology of the bulk energy spectra under periodic boundary conditions (PBC), thus establishing a bulk-edge correspondence for skin modes r3 ; r29 .
In this work we unveil that topological skin edge modes share the fascinating property of being self-healing waves. Like non-normalizable diffraction-free waves in Hermitian systems, in one-dimensional (1D) NH lattices with SIBC there are infinitely many localized (normalizable) topological skin edge states that can reconstruct their shape after being scattered off by a rather arbitrary space-time potential.

Wave self-healing. Let us consider the time-dependent dynamics of a wave function $|\psi(t)\rangle$ described by the Schrödinger-like wave equation

$$i\frac{d}{dt}|\psi\rangle=(\hat{H}+\hat{V})|\psi\rangle$$

(1)

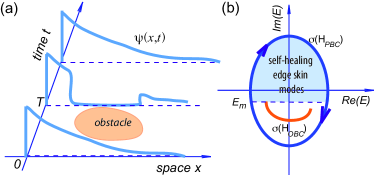
where $\hat{H}$ is the time-independent Hamiltonian of the system, which is assumed rather generally NH, and $\hat{V}=\hat{V}(t)$ describes a space-time local scattering potential (the ^′obstacle^′), which vanishes for $t>T$ and with compact support in space [Fig.1(a)]. At initial time $t=0$ the system is prepared in the state $|\psi(0)\rangle=|\phi(0)\rangle$, and let $|\phi(t)\rangle$ be the evolved wave function in the absence of the scattering potential $\hat{V}$, i.e. $|\phi(t)\rangle=\exp(-i\hat{H}t)|\phi(0)\rangle$. Clearly, the presence of the scattering potential destroys the unperturbed evolution of the wave function, so that after interaction with the potential, i.e. for $t>T$, $|\psi(t)\rangle$ can largely deviate for ever from the unperturbed solution $|\phi(t)\rangle$. The wave function $|\phi(t)\rangle$ is dubbed self-healing \textcolorblack if the deviation $\ |\xi(t)\rangle\equiv|\psi(t)\rangle-|\phi(t)\rangle$ is asymptotically much smaller than $|\phi(t)\rangle$ as $t\rightarrow\infty$ regardless of the form of $\hat{V}$, i.e. provided that [Fig.1(a)] $\lim_{t\rightarrow\infty}\epsilon(t)=0$, where

$$\epsilon(t)=\frac{\langle\xi(t)|\xi(t)\rangle}{\langle\phi(t)|\phi(t)\rangle}.$$

(2)

\textcolor

blackNote that the above condition corresponds to $\|\tilde{\psi}(t)-\tilde{\phi}(t)\|\rightarrow 0$ for the normalized wave functions $|\tilde{\psi}(t)\rangle=|\psi(t)\rangle/\|\psi(t)\|$ and $|\tilde{\phi}(t)\rangle=|\phi(t)\rangle/\|\phi(t)\|$. Clearly, in an Hermitian system owing to norm conservation any normalizable wave function is not strictly self-healing, though it can approximate an extended (non-normalizable) wave function at some extent A6 . For example, for a freely-moving quantum particle in a one-dimensional space, $\hat{H}=-\partial^{2}/\partial x^{2}$, the self-accelerating Airy solutions to the time-dependent Schrödinger equation A5 are non-normalizable self-healing waves A3 . Other non-normalizable self-healing modes include Bessel waves, parabolic cylinder waves, Weber and Mathieu beams, Bloch surface waves, and others (see e.g. A2 ; A8b ; Morandotti ). However, in a NH system propagation-invariant normalizable waves can be found Yuce .

Energy spectra, topological skin modes and the bulk-edge correspondence. We consider a one-dimensional NH lattice with short-range hopping with Hamiltonian $\hat{H}$ in physical space given by

$$\hat{H}=\sum_{n,l=1}^{N}H_{n,l}|n\rangle\langle l|,$$

(3)

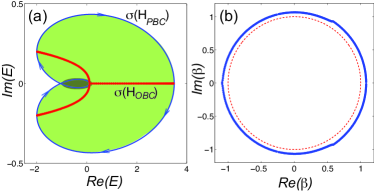
where $H_{n,l}$ is a $N\times N$ banded matrix and $N$ is the number of lattice sites. We indicate by $H_{PBC}$ and $H_{OBC}$ the $N\times N$ matrix Hamiltonians under PBC and OBC, respectively, in the large (thermodynamic) $N$ limit. For a single-band model, $H_{OBC}$ is a banded Toeplitz matrix, i.e. $(H_{OBC})_{n,l}=t_{n-l}$ with $t_{n}=0$ for $n>s$ and $n<-r$ ($t_{-r},t_{s}\neq 0$), where $t_{\pm l}$ are the left/right hopping amplitudes among sites distant $\pm l$ in the lattice and $r,s\geq 1$ are the largest orders of left/right hopping. $H_{PBC}$ is a circulant matrix with the same form as $H_{OBC}$, except for the top right and bottom left corners of the matrix. Finally, we indicate by $H_{SIBC}$ the infinite-dimensional matrix Hamiltonian under SIBC with a boundary on the left but not on the right, i.e. $(H_{SIBC})_{n,l}=t_{n-l}$ for $n,l=1,2,3,...$. The central result in the band theory of NH systems is that the energy spectra $\sigma(H_{PBC})$, $\sigma(H_{OBC})$ and $\sigma(H_{SIBC})$ are rather generally distinct, which implies the emergence of the NH skin effect, topological NH edge states and the need for a non-Bloch band theory. These results, studied in several recent works r6 ; r14 ; r16 ; r29 ; r33 ; r34 and briefly reviewed in Sec.1 of Supplemental , are basically rooted in the spectral theory of non-self-adjoint Toeplitz matrices and operators S1 ; S2 ; S3 ; S4 . Specifically, for a single-band lattice: (i) $\sigma(H_{PBC})$ is a closed loop in complex energy plane described by the Bloch Hamiltonian $H(k)=P(\beta=\exp(ik))$, where $P(\beta)=\sum_{l=-r}^{s}t_{l}\beta^{l}$ is the Laurent polynomial associated to the Toeplitz matrix and $-\pi\leq k<\pi$ is the Bloch wave number. (ii) $\sigma(H_{OBC})$ is the set of complex energies $E=P(\beta)$, where $\beta$ varies on the generalized Brillouin zone (GBZ) $C_{\beta}$. $\sigma(H_{OBC})$ is always topological trivial in terms of a point gap r29 . The definition and calculation of $C_{\beta}$ is discussed in r6 ; r14 ; r33 ; r34 , and briefly reviewed in Supplemental . (iii) $\sigma(H_{SIBC})=\sigma(H_{PBC})\bigcup B$, where $B$ is the interior of the PBC energy spectrum loop such that for $E\in B$ the winding number $W(E)$, defined by

$$W(E)=\frac{1}{2\pi i}\int_{-\pi}^{\pi}dk\frac{d}{dk}\log\det\left\{H(k)-E\right\}$$

(4)

is non vanishing. If $W(E)<0$, then $E$ is an eigenvalue of $H_{SIBC}$ of multiplicity $|W(E)|$, and the corresponding (right) eigenvectors are exponentially localized at the left edge. Such a result provides a bulk-boundary correspondence for NH systems, relating the appearance of skin edge states in a semi-infinite lattice to the topology of the PBC energy spectrum r29 .

Self-healing of topological skin modes. The central result of this work is that in NH lattices displaying the NH skin effect there are infinitely many skin edge modes that are self-healing. Specifically, let us consider a one-dimensional NH lattice with SIBC, with a boundary on the left but no boundary on the right, and with a GBZ $C_{\beta}$ that is, at least partly, external to the unit circle (to ensure the existence of left-edge skin states). The local scattering potential is assumed to have a compact support both in space and time, i.e. $\hat{V}=V_{n}(t)|n\rangle\langle n|$ with $V_{n}(t)=0$ for $t>T$ and $n>L$. Let us indicate by $E_{m_{1}}$ the largest imaginary part of the energies in the set $\sigma(H_{OBC})$, i.e. $E_{m1}={\rm max}_{\beta\in C_{\beta}}{\rm Im}\{P(\beta)\}$; $E_{m_{2}}$ the largest imaginary part of the energies $E$ in the set $B$ defined by $\{E\in B\;|\;W(E)>0\;\}$; and $E_{m}={\rm max}(E_{m_{1}},E_{m_{2}})$. Note that the set $B$ is empty if the GBZ is entirely external to the unit circle $|\beta|=1$, i.e. if there are not Bloch point r14 ; in this case one should assume $E_{m}=E_{m1}$ [as in Fig.1(b)]. The following theorem can be then proven, which is illustrated in Fig.1: any topological skin edge state $|\phi(t)\rangle=|\phi_{0}\rangle\exp(-iE_{0}t)$ with energy $E_{0}$ \textcolorblack and $W(E_{0})<0$ is self healing if and only if ${\rm Im}(E_{0})>E_{m}$.
\textcolorblackA simple corollary of this theorem is that any topological skin edge state belonging to $H_{OBC}$ is not self-healing, because in this case one has ${\rm Im}(E_{0})\leq E_{m1}\leq E_{m}$.
Here we provide a sketch of the proof of the theorem (technical details are given in Supplemental ). Let us indicate by $|\psi(t)\rangle$ the wave function satisfying Eq.(1) with the initial condition $|\psi(0)\rangle=|\phi_{0}\rangle$, and let $|\xi(t)\rangle=|\psi(t)\rangle-|\phi(t)\rangle$ be the deviation of the wave function $|\psi(t)\rangle$ from the unperturbed (skin edge eigenstate) solution. The proof consists of two main steps. In the first step, one shows that, after interaction with the scatting potential, the deviation $\xi_{n}(T)=\langle n|\xi(T)\rangle$ vanishes as $n\rightarrow\infty$ faster than exponential, i.e. for any $h>0$ one has $\lim_{n\rightarrow\infty}\xi_{n}(T)\exp(hn)=0$. Physically, this result stems from the fact that, since the hopping in the lattice is finite (short range) and the scattering potential has a limited support in space ($V_{n}=0$ for $n>L$), the speed of excitation spreading in the lattice arising from the interaction with the scattering potential is bounded (according to the Lieb-Robinson bound r3 ), and thus after interaction $\xi_{n}(T)$ remains basically unperturbed, i.e. very close to zero, for large enough $n$. The fast decay of $\xi_{n}$ with $n$ is mathematically justified by the asymptotic form of the exponential of a banded matrix S5 (Sec.2 of Supplemental ). Let us then indicate by $|\beta\rangle$ the set of eigenfunctions of $H_{OBC}$ (skin modes) with energy $P(\beta)$ belonging to $\sigma(H_{OBC})$, i.e. $H_{OBC}|\beta\rangle=P(\beta)|\beta\rangle$ with $\beta\in C_{\beta}$. Note that $|\beta\rangle$ is also an eigenstate of $H_{SIBC}$ when $|\beta|>1$ in the $N\rightarrow\infty$ limit. For large $n$, $\langle n|\beta\rangle$ behaves as $\langle n|\beta\rangle\sim\beta^{-n}(1+A_{\beta}\exp(-i\theta_{\beta}n))$ with some $\beta$-dependent constants $A_{\beta}$ and $\theta_{\beta}$. Since $|\xi(T)\rangle$ is bounded with a localization higher than any exponential, one can decompose $|\xi(T)\rangle$ as a superposition (integral) of $|\beta\rangle$ skin states, i.e. one can write (Sec.1 of Supplemental )

$|\xi(T)\rangle=\oint_{C_{\beta}}d\beta F(\beta)|\beta\rangle$ with $F(\beta)$ non-singular on $C_{\beta}$. Since $\hat{V}=0$ for $t>T$, after the scattering event the wave function $|\xi(t)\rangle$ evolves according to the Schrödinger equation $i\partial_{t}|\xi\rangle=\hat{H}_{SIBC}|\xi\rangle$, so that for $t>T$ one has $|\xi(t)\rangle=\oint_{C_{\beta}}d\beta F(\beta)\exp[-iP(\beta)(t-T)]\;|\beta\rangle.$ The second step is to calculate the growth rate of $\|\xi(t)\|^{2}=\langle\xi(t)|\xi(t)\rangle$. To this aim, one has to distinguish two cases (Sec.3 of Supplemental ). If $C_{\beta}$ is entirely external to the unit circle, i.e. $|\beta|>1$ for any $\beta\in C_{\beta}$, the growth rate of $\|\xi(t)\|$ is $E_{m1}={\rm max}_{\beta\in C_{\beta}}{\rm Im}(P(\beta))$, which is attained at the value $\beta_{s}\in C_{\beta}$ corresponding to the most unstable saddle point of $P(\beta)$. Since $\|\phi(t)\|$ grows in time as $\sim\exp({\rm Im}(E_{0})t)$, one has $\lim_{t\rightarrow\infty}\epsilon(t)=0$ \textcolorblackif and only if ${\rm Im}(E_{0})>E_{m}$, where $\epsilon(t)$ is defined by Eq.(2) and $E_{m}=E_{m_{1}}$. On the other hand, if a portion of $C_{\beta}$ is internal to the unit circle \textcolorblack the asymptotic analysis shows that the growth rate of $\|\xi(t)\|$ is the larger number between $E_{m_{1}}$ and $E_{m_{2}}$, where $E_{m_{2}}$ is the largest imaginary part of energies in the set $B$ Supplemental . This proves the theorem. $\blacksquare$

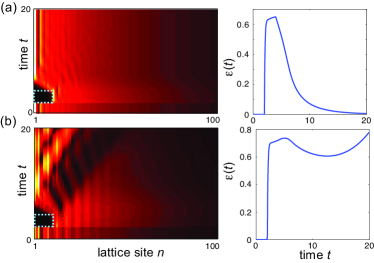
As an illustrative example, let us consider a lattice with nearest- and next-nearest neighbor hopping ($r=s=2$). Figure 2 shows the energy spectra $\sigma(H_{PBC})$, $\sigma(H_{OBC})$ and $\sigma(H_{SIBC})$ and corresponding GBZ, which is entirely external to the unit circle with $E_{m}=E_{m_{1}}\simeq 0.5$. In the wide light shaded region of Fig.2(a), for each complex energy $E$ there is a single topological skin edge state ($W=-1$), while when $E$ is internal to the narrow dark shaded region encircling the origin there are two linearly-independent skin edge states ($W=-2$). To show the self-healing property of skin edge states, we consider a strongly absorbing potential $V_{n}(t)=-10i$ which is non-vanishing in the interval $2<t<4$ and in the spatial region $1\leq n\leq L=10$. The initial state $|\phi_{0}\rangle$ is chosen to be a skin edge state with an energy $E_{0}$ in the stable (${\rm Im}(E_{0})>E_{m}$) or unstable (${\rm Im}(E_{0})<E_{m}$) regions. The self-healing property is measured by the long-time behavior of $\epsilon(t)$ [Eq.(2)]. Figure 3 illustrates the typical numerical results of wave propagation in the lattice, corresponding to the self-healing of the skin mode for ${\rm Im}(E_{0})>E_{m}$ [Fig.3(a)], and to the disruption of the skin mode for ${\rm Im}(E_{0})<E_{m}$ [Fig.3(b)]. \textcolorblackThe results are obtained by solving Eq.(1) in Wannier (real-space) basis by an accurate fourth-order Runge-Kutta method on a finite-sized lattice with OBC and with a size wide enough ($N=300$ sites) to avoid right-edge effects over the largest propagation time ($t\sim 20$), which would destroy the SIBC skin state r3 ; rLonghi21 . A strategic method to selectively prepare the system in a self-healing SIBC edge state is discussed in rLonghi21 and in Sec.5 of Supplemental . As clearly shown in the left panel of Fig.3(a), the strongly absorbing potential cuts the excitation at lattice sites $n\leq L$, however after the scattering process the skin edge state can restore its original shape, corresponding to a vanishing of $\epsilon(t)$ [right panel of Fig.3(a)]. A different behavior is observed in Fig.3(b), where the skin edge state cannot restore its original shape and $\epsilon(t)$ does not decay toward zero. We checked Supplemental that the self-healing property can be observed also when there are Bloch points (the GBZ zone crosses the unit circle) \textcolorblackand for different types of scattering potentials, including inhomogeneous Hermitian and non-Hermitian amplifying potentials.

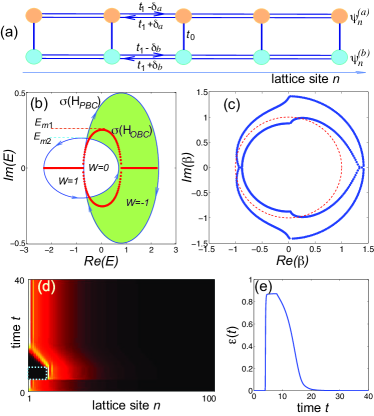
Multiband systems. The previous analysis has been focused to single band models, however the self-healing property of topological skin edge states can be extended to multiband systems. As an illustrative example, we consider a quasi 1D lattice composed by two side-coupled Hatano-Nelson chains Hatano [Fig.4(a)], which displays the critical NH skin effect r36 . The Bloch Hamiltonian of the systems reads

$$H(k)=\sigma_{0}d_{0}+t_{0}\sigma_{x}+[V+i(\delta_{b}-\delta_{a})\sin k]\sigma_{z}$$

(5)

where $d_{0}=2t_{1}\cos k-i(\delta_{a}+\delta_{b})\sin k$, $\sigma_{l}$ are the Pauli matrices, $(t_{1}\pm\delta_{a,b})$ are the asymmetric left/right hopping amplitudes in the upper (a) and lower (b) chains, $\pm V$ their on-site energy offset and $t_{0}$ is the side coupling constant. Figures 4(b,c) show a typical behavior of GBZ and energy spectra (PBC, OBC and SIBC) for $\delta_{a}>0$, $\delta_{b}<0$, with the shaded region corresponding to topological skin edge states localized at the left boundary under SIBC. Self-healing skin edge states are those with energy $E$ satisfying the condition ${\rm Im}(E)>E_{m}$, with $E_{m}={\rm max}(E_{m_{1}},E_{m_{2}})=E_{m1}\simeq 0.255$. The self-healing property is illustrated in Fig.4(d), where a skin edge state is scattered off by a complex absorbing potential in both chains ($V_{n}(t)=10i$ for $4<t<8$ and $1\leq n\leq 10$, $V_{n}=0$ otherwise).

Conclusion. In summary, we have demonstrated that infinitely-many topological edge skin modes in semi-infinite NH lattices can exhibit self-healing properties, i.e. they can reconstruct their shape after being scattered off by a rather arbitrary space-time potential. Contrary to self-healing waves known in Hermitian systems, such as Bessel and Airy waves, the topological skin edge states are truly normalizable eigenstates of the underlying Hamiltonian. Our results unravel a fascinating fundamental property of recently-discovered topological skin modes, extend the idea of self-healing waves beyond the diffraction-free paradigm of Hermitian physics, and could be thus of potential relevance in different areas of physics and for future applications of self-healing NH waves.

The author acknowledges the Spanish State Research Agency, through the Severo Ochoa and Maria de Maeztu Program for Centers and Units of Excellence in R&D (Grant No. MDM-2017-0711).