SegMix: A Simple Structure-Aware Data Augmentation Method

Yuxin Pei Carnegie Mellon University Pushkar Bhuse² [email protected] Zhengzhong Liu Eric Xing

Abstract

Interpolation-based Data Augmentation (DA) methods (Mixup) linearly interpolate the inputs and labels of two or more training examples. Mixup has more recently been adapted to the field of Natural Language Processing (NLP), mainly for sequence labeling tasks. However, such a simple adoption yields mixed or unstable improvements over the baseline models. We argue that the direct-adoption methods do not account for structures in NLP tasks. To this end, we propose SegMix, a collection of interpolation-based DA algorithms that can adapt to task-specific structures. SegMix poses fewer constraints on data structures, is robust to various hyperparameter settings, applies to more task settings, and adds little computational overhead. In the algorithm’s core, we apply interpolation methods on task-specific meaningful segments, in contrast to applying them on sequences as in prior work. We find SegMix to be a flexible framework that combines rule-based DA methods with interpolation-based methods, creating interesting mixtures of DA techniques. We show that SegMix consistently improves performance over strong baseline models in Named Entity Recognition (NER) and Relation Extraction (RE) tasks, especially under data-scarce settings. Furthermore, this method is easy to implement and adds negligible training overhead.

Refer to caption — Figure 1: Example of SegMix v.s. Whole-sequence Mixup for NER. Each colored block is an entity.

1 Introduction

Initially proposed as Mixup for computer vision tasks, interpolation-based Data Augmentation (DA) (Zhang et al., 2018) linearly interpolates the inputs and labels of two or more training examples. Inspired by Mixup, several attempts have been made to apply interpolation-based DA to NLP, mainly in sequence labeling tasks (Guo et al., 2020). However, the proposed embedding-mix solution does not extend well to tasks with structured labels. For example, mixing two sentences with different structures usually generates a non-sensical output. As demonstrated in Fig. 1, when working with entity spans, Whole-sequence Mixup¹¹1Guo et al. 2020 is referred to as Whole-sequence Mixup to avoid confusion with SeqMix of Zhang et al. 2020. produces non-sensical entity labels like a mixture of nonentity and entity ([O/B-PER]) and consecutive beginning labels ([O/B-PER], [B-LOC/I-PER]). Such noisy augmented data tend to mislead the model, especially in data-scarce settings. As shown in Chen et al. (2020a), without additional constraints on the augmented data, applying Whole-Sequence Mixup results in performance worse than baseline.

Instead of using extra heuristic constraints to filter out low-quality augmented data, it may be more efficient and effective to bring structure awareness into the mixing process from the beginning. To this end, we propose Segment Mix (SegMix), a DA method that performs linear interpolations on meaningful, task-specific segments. Virtuous training examples are created by replacing the original segments with the interpolation of pairs of segment embeddings. As in Fig. 1, the embedding of a location entity (“New York City”) is mixed with the embedding of a person entity (“Marcello Cuttitta”). We exploit the benefit of linear interpolation while keeping the target structure more sensible.

Furthermore, SegMix imposes few restrictions on the original tasks, mixing pairs, or generated examples. On the one hand, this potentially allows one to explore a much larger data space. For example, it allows mixing training samples with various sentence lengths and structures. On the other, it means that SegMix can be applied to other NLP tasks in addition to sequence labeling.

This paper tests SegMix against Named Entity Recognition (NER) and Relation Extraction (RE), two typical Information Extraction tasks with text segments. We show that SegMix improves upon the baselines under data-scarce settings, and demonstrate its robustness under different hyperparameter settings, which is not the case for simple sequence-based Mixup methods. SegMix is easy to implement²²2We will release the experiment code base. and adds little computational overhead to training and inference.

2 Related Work

Many NLP tasks involve dealing with data with structures, while a popular area is structured prediction. These tasks often involve extracting a predefined target structure from the input data (Lafferty et al., 2001; Collins, 2002; Ma and Hovy, 2016). NER aims to locate and classify the named entities mentioned in unstructured text. There have been several attempts to apply algorithms similar to Mixup to sequence labeling tasks such as NER (Chen et al., 2020a; Zhang et al., 2020). These tasks have linear structures that allow for simple sequence-level mixing methods. RE aims to detect the semantic relationship between a pair of nominals. Unlike NER, RE models typically do not use a linear encoding scheme such as BIO, making sequence-level mixing non-trivial. To the best of our knowledge, interpolation-based DA methods have not been applied to such tasks.

Rule-based DA

Rule-based DA specifies rules for inserting, deleting, or replacing parts of text (van Dyk and Meng, 2001). Easy Data Augmentation (EDA) (Wei and Zou, 2019) proposed a set of token-level random perturbation operations (insertion, deletion, and swap). SwitchOut (Wang et al., 2018) randomly replaces tokens in the sentence with random words. WordDrop (Sennrich et al., 2016) drops tokens randomly. Existing work also brings structure awareness into DA. Substructure Substitution (SUB) (Shi et al., 2021) generates new examples by replacing substructures (e.g., subtrees or subsequences) with ones with the same label. SUB applies to POS tagging, parsing, and token classification. A similar idea is proposed for NER (Dai and Adel, 2020). Mention Replacement (MR) and Label-wise Token Replacement (LwTR) substitute entity mention and token with those with the same label. Synonym Replacement (SR) replaces token with a synonym retrieved from WordNet (Miller, 1995b). Xu et al. 2016 reverses dependency sub-paths and their corresponding relationships in relation classification. Şahin and Steedman 2018 crops and rotates the dependency trees for POS tagging. Su et al. 2021 presents a contrastive pre-training method to create more generalized representations for RE tasks. It introduces a DA technique where text contained in the shortest dependency path is kept constant and other tokens are replaced. Generally, these methods explore the vicinity area around the data point and assume that they share the same label.

Interpolation-based DA

Originally proposed for image classification tasks, Mixup Zhang et al. (2018) performs convex combinations between a pair of data points and their labels. Mixup improves the performance of image classification tasks by regularizing the neural network to favor simple linear behavior between training examples Zhang et al. (2018). Several adaptations of Mixup have been made in NLP tasks. TMix (Chen et al., 2020b) performs an interpolation of text in a hidden space in text classification tasks. Snippext (Miao et al., 2020) mixes BERT encodings and passes them through a classification layer for sentiment analysis tasks. AdvAug (Cheng et al., 2020) mixes adversarial examples as an adversarial augmentation method for Neural Machine Translation.

However, direct application of Whole-Sequence Mixup yields limited improvement in tasks involving structured data. As empirically shown in LADA (Chen et al., 2020a) on NER, the direct mixing of two sentences changes both the local token representation and the context embeddings required to identify the entity mention (Chen et al., 2020a). This is also demonstrated in Fig. 1, the generated data can sometimes be too noisy to help with model training. In fact, LADA has to add additional constraints by mixing the sequences only with its k-nearest neighbors to reduce the noise (Chen et al., 2020a). Similarly, SeqMix (Zhang et al., 2020) scans both sequences with a fixed-length sliding window and mixes the subsequence within the windows. However, this approach does not eliminate the problem of generating low-quality data — extra constraints are still used to ensure the quality of generated data. These constraints limit the explorable data space close to the training data. What is more, they complicate the algorithms and add non-negligible computational overheads.

3 Method

We propose SegMix and implements 4 variants, namely MentionMix (MMix), TokenMix (TMix), SynonymMix (SMix), and RelationMix (RMix). As shown in Fig. 2, after defining the task-dependent segment, we create a new training sample by replacing a segment of the original sample with a mixed embedding of the segment itself and another randomly drawn segment. These mixed embeddings are then fed into the encoder. Algorithm 1 presents the SegMix generation process.

Algorithm 1 SegMix generation algorithm

1:Input:

\mathcal{D},\mathcal{P}^{k},r

\mathcal{D}_{A}\leftarrow\{\},\mathcal{D}_{S}\leftarrow

sample(

\mathcal{D},\emph{len}(\mathcal{D})\cdot r

)

3:for

(X_{i},Y_{i})

\mathcal{D}_{S}

E_{i},O_{i}\leftarrow\textbf{Emb}(X_{i}),\textbf{OHE}(Y_{i})

\lambda\leftarrow Beta(\alpha,\alpha)

S_{a},l_{a}\leftarrow

k

segment tuples in

X_{i},Y_{i}

S_{b},l_{b}\leftarrow

k

segment tuples in

\mathcal{P}

X_{i}^{\prime},Y_{i}^{\prime}\leftarrow X_{i}.

copy(),

Y_{i}.

copy()

9: for

s_{a}^{j},s_{b}^{j}

S_{a},S_{b}

10:

e_{a},e_{b}=\textbf{Emb}(s_{a}),\textbf{Emb}(s_{b})

11:

start,end\leftarrow

index range of

s_{a}^{j}

X_{i}

12:

\tilde{e}_{a}^{j},\tilde{e}_{b}^{j}\leftarrow

pad_to_longer(

e_{a}^{j},e_{b}^{j}

)

13:

E_{i}[start:end]\leftarrow\tilde{e}_{a}^{j}\cdot\lambda+\tilde{e}_{b}^{j}\cdot(1-\lambda)

14: end for

15: for

l_{a}^{j},l_{b}^{j}

l_{a},l_{b}

16:

o_{a},o_{b}=\textbf{OHE}(l_{a}),\textbf{OHE}(l_{b})

17:

start,end\leftarrow

index range of

l_{a}^{j}

Y_{i}

18:

\tilde{o}_{a}^{j},\tilde{o}_{b}^{j}\leftarrow

pad_to_longer(

o_{a}^{j},o_{b}^{j}

)

19:

O_{i}[start:end]\leftarrow\tilde{o}_{a}^{j}\cdot\lambda+\tilde{o}_{b}^{j}\cdot(1-\lambda)

20: end for

21:

\mathcal{D}_{A}

.add(

(E_{i},O_{i})

)

22:end for

23:Output:

\mathcal{D}_{A}

Formally, consider a training dataset $\mathcal{D}=\{(X_{i},Y_{i})|i\in N\}$ of size $N$ , where each input $X_{i}$ is a sequence of tokens $X_{i}=(X_{i}^{1},X_{i}^{2},\dotsc,)$ and a task-dependent structured output $Y_{i}$ , a structured prediction algorithm generally encodes the output $Y_{i}$ using a task-dependent scheme. For example, NER labels are often encoded with the BIO scheme while RE labels are associated with a pair of nominal phrases. SegMix adapts to different encoding schemes by designing task-dependent segments.

A segment $s(u,v)$ is a continuous sequence of tokens $(X_{i}^{u},X_{i}^{u+1},\dotsc,X_{i}^{v})$ in sample $X_{i}$ , a segment tuple $S=[s_{i}(u_{i},v_{i}),...]$ is a $k-$ ary tuple of segments contained in the sequence. We choose a segment tuple relevant to the task and associate it with an appropriate label list $L=[l_{i},...]$ . For example, in RE, there are segment tuple of length 2, which contains the pair of nominals in a relation.

A Segment Pool of size $M$ : $\mathcal{P}^{k}=\{(S_{i},L_{i})|i\in M\}$ is generated by collecting segment tuples $S_{i}$ from the training data or an external resource (e.g. WordNet). Here, $k$ is a constant for a specific task. For example, in RE, there are binary segment tuple containing a pair of nominals.

With the training data set $\mathcal{D}$ , the Segment Pool $\mathcal{P}^{k}$ , and the mix rate $r$ , SegMix $(\mathcal{D},\mathcal{P}^{k},r)$ returns an augmented data set $\mathcal{D}_{A}$ of size $r\cdot N$ . A set $\mathcal{D_{S}}$ of size $r\cdot N$ is first drawn from the training data $\mathcal{D}$ as candidates for augmentation. For each data point $(X_{i},Y_{i})$ drawn from $\mathcal{D_{S}}$ , we randomly pick a segment tuple $S_{a}$ and the corresponding label list $L_{a}$ from the sequence $X_{i}$ . The mix for candidate $X_{i}$ , $(S_{b},L_{b})$ , is then drawn from the Segment Pool.

Let $\mathbf{Emb}$ be an embedding function on $\mathbb{R}^{V}\mapsto\mathbb{R}^{D}$ , where V is the size of the vocabulary and D is the embedding dimension. Let $\mathbf{OHE}$ be a function that returns the one-hot encoding of a label.

For all ${s_{a},s_{b}=S_{a}[i],S_{b}[i],1\leq i\leq\leavevmode\lstinline{{\lst@@@set@language\lst@@@set@numbers\lst@@@set@frame\lst@@@set@rulecolor{\@listingGroup{ltx_lst_identifier}{len}}}}}(S_{a})$ , and ${l_{a},l_{b}=L_{a}[j],L_{b}[j],1\leq j\leq\leavevmode\lstinline{{\lst@@@set@language\lst@@@set@numbers\lst@@@set@frame\lst@@@set@rulecolor{\@listingGroup{ltx_lst_identifier}{len}}}}}(L_{a})$ . Define $e_{a},e_{b}=\mathbf{Emb}(s_{a}),\mathbf{Emb}(s_{b}),o_{a},o_{b}=\mathbf{OHE}(l_{a}),\mathbf{OHE}(l_{b})$ .

The embeddings and one-hot encodings are then padded according to sequence length (line 12, 18). Let $\tilde{e}_{a},\tilde{e}_{b},\tilde{o}_{a},\tilde{o}_{b}$ be the padded version of the embeddings and one-hot encodings. Finally, in line 13, 19, we perform a linear interpolation between $\tilde{e}_{a},\tilde{e}_{b}$ and $\tilde{o}_{a},\tilde{o}_{a}$ with a mix rate $\lambda$ chosen randomly from a Beta distribution (see specifications in 4.1):

		$\displaystyle e_{a}^{\prime}\leftarrow\tilde{e}_{a}\cdot\lambda+\tilde{e}_{b}\cdot(1-\lambda)$		(1)
		$\displaystyle o_{a}^{\prime}\leftarrow\tilde{o}_{a}\cdot\lambda+\tilde{o}_{b}\cdot(1-\lambda)$		(1)

In Eq.1, $\cdot$ is a scalar multiplication and $+,-$ are vector element-wise operations. When $\lambda=1$ , the augmented data falls back to the original one. When $\lambda=0$ , the segments are completely replaced by those drawn from the pool, equivalent to replacement-based DA techniques.

Finally, the augmented data point is generated by copying the original data and replacing the chosen segment and labels with the mixed version. We present 3 variations of SegMix for NER and 1 for RE with different types of Segment Pool $\mathcal{P}^{k}$ .

MentionMix

Inspired by MR, MMix performs linear interpolations on a mention level (a contiguous segment of tokens with the same entity label). A Mention Pool $\mathcal{P}^{1}$ is constructed by scanning the training data set and extracting all mention segments and their corresponding labels. Thus, each segment tuple is composed of a single mention and a list of entity labels encoded with the BIO scheme. This method can also be viewed as a generalization of (SUB) (Shi et al., 2021) which performs a soft-mix of substructures of varying lengths.

TokenMix

Inspired by LwTR, TMix performs linear interpolations at the token level. We use tokens with entity labels in the BIO scheme of training data sets as a token pool $\mathcal{P}^{1}$ . Each segment tuple is composed of a single token and its label.

SynonymMix

Inspired by SR, the Synonym Pool $\mathcal{P}^{1}$ returns a synonym of the token in the original sequence based on WordNet (Miller, 1995b). We assume the two synonyms share the same label, thus interpolation only happens within input.

RelationMix

Since each relation is composed of two possibly nonadjacent nominals in a sentence, we construct a pool $\mathcal{P}^{2}$ with groups of two nominals and a relation label³³3The direction of the relation is implied by the labels. For example, the label list contains both producer-product (e1,e2) and producer-product (e2,e1). During the mixing phase, the two nominals and their corresponding relation labels are mixed with a pair of nominals from $\mathcal{P}^{2}$ .

4 Experiments

Datasets

	Language	Task	# Instances
CoNLL-03	English	NER	14987
Kin	Kinyarwanda	NER	626
Sin	Sinhala	NER	753
SemEval	English	RE	8000
DDI	English	RE	22233
Chemport	English	RE	18035

Table 1: Dataset Statistics

We conduct SegMix experiments mainly on $3$ datasets for NER and $3$ for RE on a variety of domains and languages. An NER task is to recognize mentions from text belonging to predefined semantic types, such as person, location, and organization. An RE task requires one to classify the relation type between two prelabeled nominals in a sentence. Some basic dataset statistics are included in Table. 1⁴⁴4Since no down-sampling settings are included in LORELEI-Kin and Sin, we report the results as a single value..

(1)

CoNLL-03 (Sang and Meulder, 2003), an English corpus for NER containing entity labels such as person, location, organization, etc.⁵⁵5We also conduct experiments on GermEval, a German NER dataset. The results and trends are similar to those in CoNLL-03, and are presented in the Appendix. A.1
(2)

LORELEI (Strassel and Tracey, 2016) which contains NER annotations for text in languages Kinyarwanda (Kin) and Sinhala (Sin).
(3)

SemEval-2010 Task 8 (Hendrickx et al., 2010), an English corpus for RE task, containing $9$ relation types that include cause-effect, product-producer, instrument-agency, etc.
(4)

DDI (Herrero-Zazo et al., 2013), a biomedical dataset manually annotated with drug-drug interactions, containing $4$ relationship types.
(5)

ChemProt (Krallinger et al., 2017), a biomedical dataset annotated with chemical-protein interactions, containing $4$ interaction types.

	CoNLL-03			Kin	Sin
Data Size	200	400	800	626	753
BERT	$76.03$ $\pm$ $0.57$	$81.20$ $\pm$ $0.29$	$84.34$ $\pm$ $0.33$	$82.29$	$75.02$
BERT + LADA	$70.46$ $\pm$ $0.84$	$81.98$ $\pm$ $0.16$	$84.53$ $\pm$ $0.09$	$76.02$	$60.43$
BERT + SeqMix	$77.10$ $\pm$ $1.04$	$81.55$ $\pm$ $0.66$	$84.89$ $\pm$ $0.27$	$83.13$	$78.93$
BERT + Whole-seq Mix	$75.11$ $\pm$ $0.62$	$81.94$ $\pm$ $0.14$	$84.61$ $\pm$ $0.18$	$82.35$	$79.17$
BERT + MR	$77.86$ $\pm$ $0.36$	$81.49$ $\pm$ $0.17$	$84.21$ $\pm$ $0.29$	$83.46$	$78.62$
BERT + LwTR	$76.69$ $\pm$ $0.49$	$81.13$ $\pm$ $0.36$	$84.56$ $\pm$ $0.37$	$82.42$	$78.17$
BERT + SR	$77.35$ $\pm$ $0.29$	$81.33$ $\pm$ $0.32$	$85.10$ $\pm$ $0.11$	$82.51$	$78.38$
BERT + MMix †	$78.51$ $\pm$ $0.34$	$\mathbf{82.98}$ $\pm$ $0.61$	$85.37$ $\pm$ $0.59$	$83.37$	$79.50$
BERT + TMix †	$\mathbf{78.75}$ $\pm$ $0.49$	$82.28$ $\pm$ $0.30$	$85.51$ $\pm$ $0.21$	$\mathbf{83.85}$	$78.63$
BERT + SMix †	$77.95$ $\pm$ $0.38$	$82.51$ $\pm$ $0.36$	$85.33$ $\pm$ $0.19$	$83.31$	$79.38$
BERT + MMix + SMix †	$78.45$ $\pm$ $0.26$	$82.39$ $\pm$ $0.21$	$85.66$ $\pm$ $0.25$	$82.81$	$79.83$
BERT + MMix + TMix †	$78.46$ $\pm$ $0.26$	$82.39$ $\pm$ $0.24$	$\mathbf{85.82}$ $\pm$ $0.21$	$82.75$	$\mathbf{80.31}$
BERT + MMix + SMix + TMix †	$78.21$ $\pm$ $0.28$	$82.36$ $\pm$ $0.34$	$85.26$ $\pm$ $0.27$	$82.83$	$78.05$
RoBERTa †	$74.08$ $\pm$ $0.27$	$78.89$ $\pm$ $0.59$	$82.28$ $\pm$ $0.23$	$-$	$-$
RoBERTa +MMix †	$\mathbf{75.31}$ $\pm$ $0.52$	$\mathbf{80.09}$ $\pm$ $0.49$	$83.37$ $\pm$ $0.54$	$-$	$-$
RoBERTa + TMix †	$74.55$ $\pm$ $0.37$	$79.44$ $\pm$ $0.35$	$83.22$ $\pm$ $0.80$	$-$	$-$
RoBERTa + SMix †	$75.18$ $\pm$ $0.42$	$79.80$ $\pm$ $0.45$	$\mathbf{83.49}$ $\pm$ $0.39$	$-$	$-$

Table 2: F1 scores for NER in data-scarce settings (downsampled CoNLL-03 and LORELEI (Kin and Sin)) using SegMix compared with interpolation- and replacement-based DA methods. We use

5

different random seeds for down-sampled datasets and report their averaged performance and standard deviation as

\mu\pm\sigma

. For LORELEI, we report the

10

-fold cross-validation result. Although there is no one best performing variant of SegMix for all settings, we observe that for all variants, SegMix had the best performance compared to the baseline in all settings and other DA techniques in most settings. †denotes our methods.

Data Sampling

For true low-resource languages Kinyarwanda and Sinhala (data sizes of LORELEI-Sin and LORELEI-Kin are less than $5\%$ of the CoNLL-03 English dataset), we use all available data. To create difference scarce settings for CoNLL-03, we subsample a range of sizes ( $200,400,800,1600,3200,6400,12800$ ) of the original training data as the training set. The augmentation algorithm can only access the downsampled training set. We use $5$ different random seeds to subsample the training set of each size and report both mean and standard deviation as $(\mu\pm\sigma)$ . The validation and test dataset are unchanged. For LORELEI, we deleted all data samples that only have character "–". Therefore, there are some discrepancies between our reported data number and the original paper. For RE, we subsample ( $100,200,400,800,1600,6400$ ) from the original training data as the training set. We do not continue experiments for larger sizes since the improvement from DA diminished.

Settings

For each data split, we conduct experiments on $12$ settings for NER —- $2$ interpolation-based DA (Inter+Intra LADA⁶⁶6We used implementation available at https://github.com/GT-SALT/LADA., Whole-sequence Mixup⁷⁷7Implemented by setting segments as whole sequences.), $3$ replacement based DA (MR, SR, LwTR)⁸⁸8Implemented as SegMix where mix rate is 1., and $6$ variations of SegMix (MMix, TMix, SMix, and their combinations MMix + SMix, MMix + TMix, MMix + TMix + SMix) with a fixed $0.2$ augmentation rate. We use the BIO tagging scheme Màrquez et al. (2005) to assign labels to each token in NER tasks. In RE tasks, we compare RMix with Relation Replacement. Gold standard nominal pairs are used.

All the methods are evaluated with F1 scores. For Kin and Sin, we report the average F1 scores over 10 folds with cross-validation, which is consistent with Rijhwani et al. 2020.

4.1 Implementation Details

For our experiments, we adopt the pretrained BERT and RoBERTa models⁹⁹9The model choices are included in Appendix A.2. as the encoder, and a linear layer to make prediction, with soft cross-entropy loss. The pretrained BERT model is adopted for each language whereas due to computation expenses, we adopted the pretrained RoBERTa model for experiments on only the CoNLL-03 dataset. For pseudo-data-scarce settings (CoNLL-03, DDI, Chemprot, and SemEval), we train all the models for 100 epochs with early stopping and take the checkpoint with the maximum validation score on the development dataset as the final model. For Kin and Sin, under each data split, we train the model for 100 epochs and report the F1 score. The initial weight decay is 0.1 and $\alpha$ is 8 for both models. Additionally, learning rates for all settings are set to $5e-5$ for the BERT model and $1e-4$ for the RoBERTa model.

4.2 Results and Analysis

NER

The results for the three NER datasets under data-scarce settings with BERT and RoBERTa are shown in Table 2. Fig. 3 includes the results for CoNLL-03 under all data settings with BERT. Under all settings, SegMix or a combination of SegMix achieves the best result compared with other interpolation- and replacement-based methods. For BERT, the best performing SegMix improves the baseline by $2.7$ F1 in CoNLL-03 with the $200$ sample setting, $1.5$ F1 for Kin, and $5$ F1 for Sin. As for RoBERTa, SegMix and its variants perform better compared to the baseline RoBERTa model in all simulated data-scarce scenario with CoNLL-03. For example, the best performing SegMix variant with RoBERTa improves the baseline by 1.2 F1 on CoNLL-03 under the $200$ -sample setting. SegMix proves to be effective under both down-sampled settings and true low-resource settings. These results are consistent with our hypothesis that the “soft” mix of data points in structure-aware segments yields better results than “hard” replacement or mixing on sequences. In comparison, LADA has an unstable performance under data-scarce settings. It produces worse results than the baseline under the CoNLL-03 with $200$ samples, and in both low-resource languages Kin and Sin, while SegMix shows consistent improvements.

One notable trend is that most DA methods provides a larger improvement on Sin in compared to Kin. Notice that even with the same model architecture, the baseline performance of Sin is considerably lower compared to the performance of Kin and English of similar data sizes. This could be due to the fact that multilingual BERT transfers better between languages that share more¹⁰¹⁰10While both the Kinyarwanda-BERT and Sinhala-BERT are transferred from M-BERT, the number of common grammatical ordering WALS features Dryer and Haspelmath (2013) is 3 between Kinyarwanda and English and 1 for Sinhala. These features are 81A, 85A, 86A, 87A, 88A and 89A. word order features Pires et al. (2019). Given the lower baseline, many DA methods provide larger improvements in Sin compared to Kin, and our SegMix variants score around 80 F1 scores. This shows that DA methods are generally very valuable for low resource and understudied languages.

RE

For RE, we compare RMix with the baseline and Relation Replacement (replacing nominal pairs). The results are presented in Fig.3. We find that simple replacement sometimes worsens the baseline performance, while RMix consistently improves the baseline. We analyze its performance on increasing percentages of training data to simulate pseudo-data-scarce settings, as well as settings with ample training data. We observe a consistent improvement performance of RMix over replacement based methods, and at least comparable performance with the baselines. SegMix performs well in data scarce settings, more specifically, on scenarios with less than approximately 1000 training examples. For example, in case of the DDI dataset, SegMix performs at least 2 F1 scores better compared to the baseline in these scenarios.

Robustness with respect to augmentation rate

From previous results on sequence-level Mixup (Zhang et al., 2020; Chen et al., 2020a), we observe that the performance of the model tends to drop below the baseline as the augmentation rate increases above a certain value. Furthermore, the optimal augmentation rate varies under different initial data settings: a good augmentation rate for the $200$ -sample might not be good for the 800-sample. With BERT, for example, a $0.2$ augmentation rate improves upon baseline under the $200$ -sample setting, but produces worse results than the baseline under the $800$ -sample setting. This leads to an extra burden in hyperparameter tuning. Through experiments on varying augmentation rates under $3$ different data-scarcity settings, we show that MMix consistently improves the baseline performance under all settings, making it more applicable in practical contexts. As presented in Fig. 4, MMix consistently improves upon the baseline for all experimented augmentation rate. Furthermore, the best performance is consistently achieved at $0.1$ . TMix and SMix also show a similar trend, the specific scores are presented in Appendix. A.1.

Computation Time

SegMix is easy to implement and adds little computational overhead. We compare the time required to generate the mixing data and training using LADA, MMix, and SeqMix in Table. 3. Without extra constraints on the augmentation process, MMix (and its other variants) takes < $1$ second on average to generate the augmented dataset. While SeqMix takes > $2$ minutes due to the filtering process. Both SeqMix and SegMix pass mixed embeddings into the encoder directly; thus, no extra computation is required for each epoch. However, we observe that SegMix converges faster than SeqMix, thus requiring less training time on average. Since LADA mixes hidden representations during training, no augmented dataset is explicitly generated. This leads to almost twice the training time of SegMix.

	mixing time (s)	training time (s)
SeqMix	$138.90$ $\pm$ $15.46$	$1094.99$ $\pm$ $108.28$
MMix †	$0.81$ $\pm$ $0.22$	$609.61$ $\pm$ $66.39$
LADA	–	$1120.78$ $\pm$ $103.13$

Table 3: Comparison of the mixing time (time taken to generate the augmented data) and the training time (time taken to train the model to converge) of LADA, SeqMix and MMix on CoNLL-03 with

200

downsampled data. We experimented with

5

different random seeds and reported the average time and standard deviation.

4.3 Discussion

We argue that SegMix keeps the syntactic and output structure of training data intact. We choose some sample sequences in CoNLL-03 and visualize them in Fig. 5 by mapping the mixed embeddings to the nearest word in the vocabulary.

Original: Swedish [MISC] options and derivatives exchange OM Gruppen AB [ORG] said on Thursday it would open an electronic bourse for forest industry products in London [LOC] in the first half of 1997. MMix: Swedish [MISC] options and derivatives exchange Javier Gomez de [PER/ORG] said on Thursday it would open an electronic bourse for forest industry products in London [LOC] in the first half of 1997. Whole-Sequence Mix: Sweden [MISC/ORG] option [O/ORG] but [unused33] transfer . . [unused10] [O/ORG] saying to Friday them might closed his electronics . with woods companies Products of Paris [O/LOC] of a second three in 1995.

Figure 5: Mixed sentence samples recovered by mapping embeddings to the nearest token (l2 distance). [A/B] represents the linear interpolation of the one-hot encodings of the two labels A and B.

MMix preserves the syntactic and entity structures while achieving linear interpolation between each mention. Due to the high proportion of non-entity phrases in the dataset, SeqMix tends to mix entity mentions with nonentity segments (label [O]). The resulting sentences often contain nonmeaningful entities (e.g., option and . . [unused10]), but are perceived as entities (with a non-[O] label). The nonentity phrases in the sentence would also be mixed, producing semantically incorrect context phrases like second three in 1995.

Unlike other interpolation-based DA methods, SegMix imposes few constraints on the mixing candidate and mixed examples. All training data pairs can potentially be used as mixing candidates and no filtering process is required after the augmented sample is generated. This not only potentially expands the explorable space of our augmentation algorithm but also saves computational time.

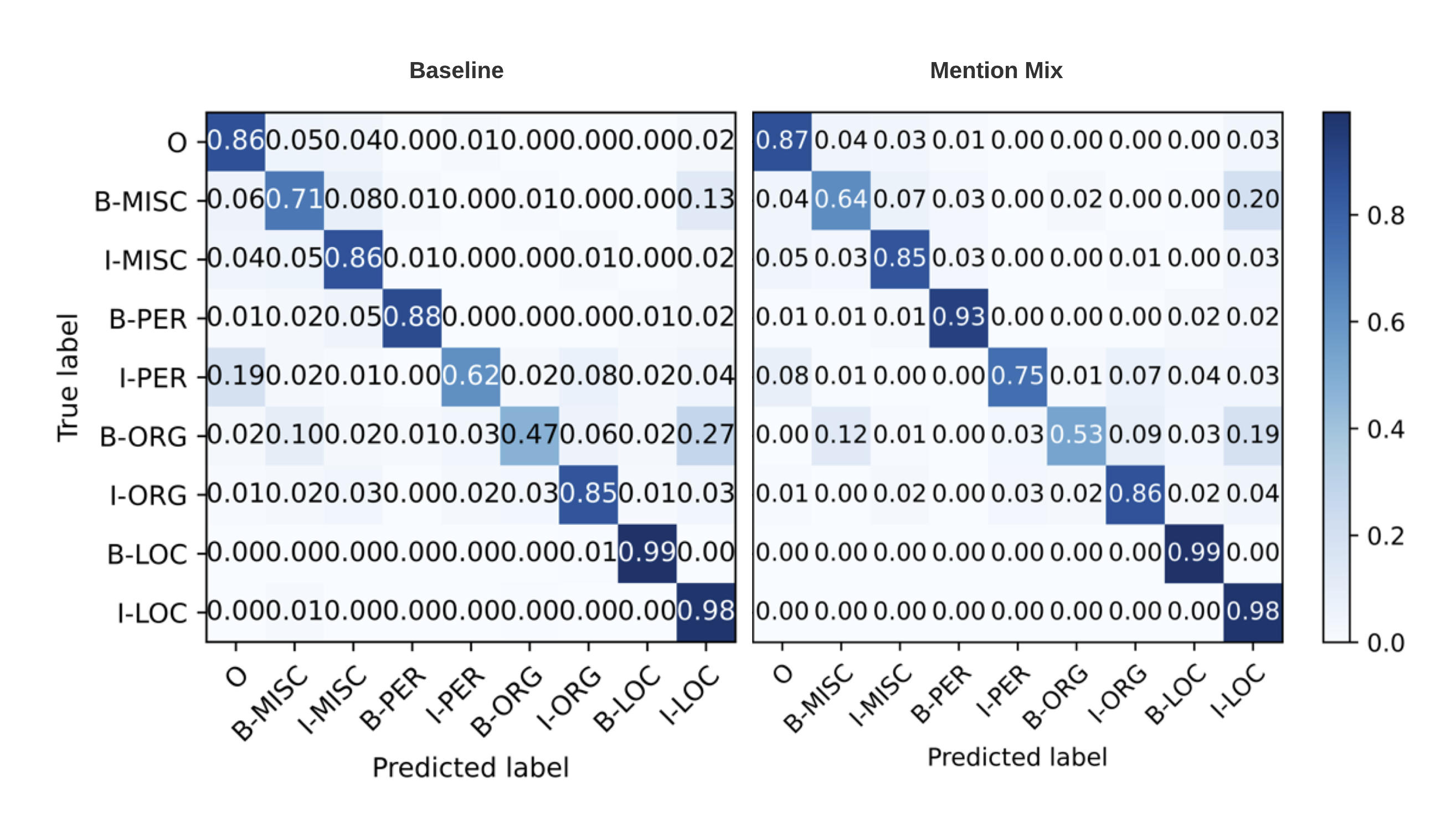
When analyzing the improvement for each entity class for CoNLL-03, there is an overall improvement in the accuracy for each class, especially for PER and ORG¹¹¹¹11Confusion Matrix included in Appendix. A.1. Before SegMix, the model tends to mistakenly predict [LOC] for [ORG] ( $27\%\rightarrow 19\%$ ), and [O] for [PER] ( $19\%\rightarrow 8\%$ ). This may be due to the fact that MMix introduces more variations of meaningful entities into the training process, preventing the model from only predicting labels with the one of majority occurrence.

We also analyze cases that are improved in different tasks, the specifics can be found in Appendix.A.3. In one example, the baseline model correctly detects a entity span "British University", but falsely classifies it as [MISC] whereas SegMix correctly distinguishes it as an [ORG]. In another example, the baseline model fails to detect the entity span ("Minor Counties" instead of "Minor Counties XI") and the correct entity while SegMix gives the same wrong span, but correct entity class. We hypothesize that SegMix mainly helps the model distinguish between ambiguous types instead of span detection. To validate this claim, we convert all mentions to [B] and [I] during the inference phase and find that there is little difference between the models (both around $98\%$ ) in terms of span accuracy — confirming our hypothesis. Similarly for RE, we conduct evaluation in two settings: evaluating only relation type and only relation direction. The accuracy scores for the two metrics both increase around $2\%$ . Thus, RMix helps to identify both the correct type and direction of relations. Specific cases and examples can be found in Appendix A.3.

Limitations

In this paper, we analyze the efficacy of SegMix on tasks with clear task related segments (NER and RE). SegMix works best in such settings but we do not validate it on tasks like syntactic parsing. Secondly, we only test the performance of SegMix on a few transformer based models (BERT and RoBERTa), it is not applicable to new paradigms such as question answering and generation based information extraction techniques He et al. (2015); Josifoski et al. (2022). Lastly, although SegMix works best on small datasets ( $\approx$ 1000 examples), we recognize that it has a diminishing improvement with the increase of data size. Thus, we recommend using SegMix in data-scarce situations.

5 Conclusion

This paper proposes SegMix, a simple DA technique that adapts to task-specific data structures, which extends the application range of Mixup in NLP tasks. We demonstrate its robustness by evaluating model performance under both true low-resource and downsampled settings on multiple NER and RE datasets. SegMix consistently improves the model performance and is more consistent than other mixing methods. By combining rule-based and interpolation-based DA with a computationally inexpensive and straightforward method, SegMix opens up several interesting directions for further exploration.

Ethics Statement

Our research does not present any new datasets but rather presents a new general methods that can be used to improve performance of existing NLP applications, and is intended to be used under data-scarce situation. As a result, we anticipate no direct harm involved with the intended usage. However, we realize that it depends on the kind of NLP models/applications the users to apply to.

Our research does not involve attributing any forms of characteristics to any individual. As a matter of fact, we strive to boost performance for NLP applications on low-resource languages. Our proposed method is easy to implement and adds negligible overhead to computation time compared to similar methods. Due to the fact that we conducted experiments over extensive hyperparameter and data settings, we used around 5000 GPU/hours on Tesla T4 GPUs.

References

Adelani et al. (2021) David Ifeoluwa Adelani, Jade Abbott, Graham Neubig, Daniel D’souza, Julia Kreutzer, Constantine Lignos, Chester Palen-Michel, Happy Buzaaba, Shruti Rijhwani, Sebastian Ruder, Stephen Mayhew, Israel Abebe Azime, Shamsuddeen H. Muhammad, Chris Chinenye Emezue, Joyce Nakatumba-Nabende, Perez Ogayo, Aremu Anuoluwapo, Catherine Gitau, Derguene Mbaye, Jesujoba Alabi, Seid Muhie Yimam, Tajuddeen Rabiu Gwadabe, Ignatius Ezeani, Rubungo Andre Niyongabo, Jonathan Mukiibi, Verrah Otiende, Iroro Orife, Davis David, Samba Ngom, Tosin Adewumi, Paul Rayson, Mofetoluwa Adeyemi, Gerald Muriuki, Emmanuel Anebi, Chiamaka Chukwuneke, Nkiruka Odu, Eric Peter Wairagala, Samuel Oyerinde, Clemencia Siro, Tobius Saul Bateesa, Temilola Oloyede, Yvonne Wambui, Victor Akinode, Deborah Nabagereka, Maurice Katusiime, Ayodele Awokoya, Mouhamadane MBOUP, Dibora Gebreyohannes, Henok Tilaye, Kelechi Nwaike, Degaga Wolde, Abdoulaye Faye, Blessing Sibanda, Orevaoghene Ahia, Bonaventure F. P. Dossou, Kelechi Ogueji, Thierno Ibrahima DIOP, Abdoulaye Diallo, Adewale Akinfaderin, Tendai Marengereke, and Salomey Osei. 2021. MasakhaNER: Named Entity Recognition for African Languages. Transactions of the Association for Computational Linguistics, 9:1116–1131.
Chen et al. (2020a) Jiaao Chen, Zhenghui Wang, Ran Tian, Zichao Yang, and Diyi Yang. 2020a. Local additivity based data augmentation for semi-supervised NER. CoRR, abs/2010.01677.
Chen et al. (2020b) Jiaao Chen, Zichao Yang, and Diyi Yang. 2020b. Mixtext: Linguistically-informed interpolation of hidden space for semi-supervised text classification.
Cheng et al. (2020) Yong Cheng, Lu Jiang, Wolfgang Macherey, and Jacob Eisenstein. 2020. Advaug: Robust adversarial augmentation for neural machine translation. CoRR, abs/2006.11834.
Collins (2002) Michael Collins. 2002. Discriminative training methods for hidden Markov models: Theory and experiments with perceptron algorithms. In Proceedings of the 2002 Conference on Empirical Methods in Natural Language Processing (EMNLP 2002), pages 1–8. Association for Computational Linguistics.
Dai and Adel (2020) Xiang Dai and Heike Adel. 2020. An analysis of simple data augmentation for named entity recognition. CoRR, abs/2010.11683.
Devlin et al. (2018) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2018. BERT: pre-training of deep bidirectional transformers for language understanding. CoRR, abs/1810.04805.
Dryer and Haspelmath (2013) Matthew S. Dryer and Martin Haspelmath, editors. 2013. WALS Online. Max Planck Institute for Evolutionary Anthropology, Leipzig.
Guo et al. (2020) Demi Guo, Yoon Kim, and Alexander Rush. 2020. Sequence-level mixed sample data augmentation. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 5547–5552, Online. Association for Computational Linguistics.
He et al. (2015) Luheng He, Mike Lewis, and Luke Zettlemoyer. 2015. Question-answer driven semantic role labeling: Using natural language to annotate natural language. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pages 643–653, Lisbon, Portugal. Association for Computational Linguistics.
Hendrickx et al. (2010) Iris Hendrickx, Su Nam Kim, Zornitsa Kozareva, Preslav Nakov, Diarmuid Ó Séaghdha, Sebastian Padó, Marco Pennacchiotti, Lorenza Romano, and Stan Szpakowicz. 2010. SemEval-2010 task 8: Multi-way classification of semantic relations between pairs of nominals. In Proceedings of the 5th International Workshop on Semantic Evaluation, pages 33–38, Uppsala, Sweden. Association for Computational Linguistics.
Herrero-Zazo et al. (2013) María Herrero-Zazo, Isabel Segura-Bedmar, Paloma Martínez, and Thierry Declerck. 2013. The ddi corpus: An annotated corpus with pharmacological substances and drug–drug interactions. Journal of Biomedical Informatics, 46(5):914–920.
Josifoski et al. (2022) Martin Josifoski, Nicola De Cao, Maxime Peyrard, Fabio Petroni, and Robert West. 2022. GenIE: Generative information extraction. In Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 4626–4643, Seattle, United States. Association for Computational Linguistics.
Krallinger et al. (2017) Martin Krallinger, Obdulia Rabal, Saber Ahmad Akhondi, Martín Pérez Pérez, Jesus Santamaría, Gael Pérez Rodríguez, Georgios Tsatsaronis, Ander Intxaurrondo, J. A. Lopez, Umesh K. Nandal, Erin M. van Buel, Ambika Chandrasekhar, Marleen Rodenburg, Astrid Lægreid, Marius A. Doornenbal, Julen Oyarzábal, Anália Lourenço, and Alfonso Valencia. 2017. Overview of the biocreative vi chemical-protein interaction track.
Lafferty et al. (2001) John D. Lafferty, Andrew McCallum, and Fernando C. N. Pereira. 2001. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In Proceedings of the Eighteenth International Conference on Machine Learning, ICML ’01, page 282–289, San Francisco, CA, USA. Morgan Kaufmann Publishers Inc.
Liu et al. (2019) Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. 2019. Roberta: A robustly optimized bert pretraining approach.
Ma and Hovy (2016) Xuezhe Ma and Eduard H. Hovy. 2016. End-to-end sequence labeling via bi-directional lstm-cnns-crf. CoRR, abs/1603.01354.
Màrquez et al. (2005) Lluís Màrquez, Pere Comas, Jesús Giménez, and Neus Català. 2005. Semantic role labeling as sequential tagging. In Proceedings of the Ninth Conference on Computational Natural Language Learning (CoNLL-2005), pages 193–196, Ann Arbor, Michigan. Association for Computational Linguistics.
Miao et al. (2020) Zhengjie Miao, Yuliang Li, Xiaolan Wang, and Wang-Chiew Tan. 2020. Snippext: Semi-supervised opinion mining with augmented data. CoRR, abs/2002.03049.
Miller (1995a) George A. Miller. 1995a. Wordnet: A lexical database for english. Commun. ACM, 38(11):39–41.
Miller (1995b) George A. Miller. 1995b. Wordnet: A lexical database for english. Commun. ACM, 38(11):39–41.
Pires et al. (2019) Telmo Pires, Eva Schlinger, and Dan Garrette. 2019. How multilingual is multilingual BERT? In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 4996–5001, Florence, Italy. Association for Computational Linguistics.
Rijhwani et al. (2020) Shruti Rijhwani, Shuyan Zhou, Graham Neubig, and Jaime Carbonell. 2020. Soft gazetteers for low-resource named entity recognition. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 8118–8123, Online. Association for Computational Linguistics.
Şahin and Steedman (2018) Gözde Gül Şahin and Mark Steedman. 2018. Data augmentation via dependency tree morphing for low-resource languages. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 5004–5009, Brussels, Belgium. Association for Computational Linguistics.
Sang and Meulder (2003) Erik F. Tjong Kim Sang and Fien De Meulder. 2003. Introduction to the conll-2003 shared task: Language-independent named entity recognition. CoRR, cs.CL/0306050.
Sennrich et al. (2016) Rico Sennrich, Barry Haddow, and Alexandra Birch. 2016. Edinburgh neural machine translation systems for WMT 16. In Proceedings of the First Conference on Machine Translation: Volume 2, Shared Task Papers, pages 371–376, Berlin, Germany. Association for Computational Linguistics.
Shi et al. (2021) Haoyue Shi, Karen Livescu, and Kevin Gimpel. 2021. Substructure substitution: Structured data augmentation for NLP. CoRR, abs/2101.00411.
Strassel and Tracey (2016) Stephanie Strassel and Jennifer Tracey. 2016. LORELEI language packs: Data, tools, and resources for technology development in low resource languages. In Proceedings of the Tenth International Conference on Language Resources and Evaluation (LREC’16), pages 3273–3280, Portorož, Slovenia. European Language Resources Association (ELRA).
Su et al. (2021) Peng Su, Yifan Peng, and K. Vijay-Shanker. 2021. Improving bert model using contrastive learning for biomedical relation extraction.
van Dyk and Meng (2001) David A van Dyk and Xiao-Li Meng. 2001. The art of data augmentation. Journal of Computational and Graphical Statistics, 10(1):1–50.
Wang et al. (2018) Xinyi Wang, Hieu Pham, Zihang Dai, and Graham Neubig. 2018. SwitchOut: an efficient data augmentation algorithm for neural machine translation. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 856–861, Brussels, Belgium. Association for Computational Linguistics.
Wang et al. (2020) Zihan Wang, Karthikeyan K, Stephen Mayhew, and Dan Roth. 2020. Extending multilingual BERT to low-resource languages. In Findings of the Association for Computational Linguistics: EMNLP 2020, pages 2649–2656, Online. Association for Computational Linguistics.
Wei and Zou (2019) Jason Wei and Kai Zou. 2019. EDA: Easy data augmentation techniques for boosting performance on text classification tasks. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 6382–6388, Hong Kong, China. Association for Computational Linguistics.
Xu et al. (2016) Yan Xu, Ran Jia, Lili Mou, Ge Li, Yunchuan Chen, Yangyang Lu, and Zhi Jin. 2016. Improved relation classification by deep recurrent neural networks with data augmentation. In Proceedings of COLING 2016, the 26th International Conference on Computational Linguistics: Technical Papers, pages 1461–1470, Osaka, Japan. The COLING 2016 Organizing Committee.
Zhang et al. (2018) Hongyi Zhang, Moustapha Cisse, Yann N. Dauphin, and David Lopez-Paz. 2018. mixup: Beyond empirical risk minimization.
Zhang et al. (2020) Rongzhi Zhang, Yue Yu, and Chao Zhang. 2020. Seqmix: Augmenting active sequence labeling via sequence mixup. CoRR, abs/2010.02322.

Appendix A Appendix

A.1 Additional results

We conduct experiments on GermEval datasets. The results are included in Table. 4. We report the results of the experiment on the varying augmentation rate in MMix, SMix, and TMix in Table 6.

	GermEval
	$5\%$	$10\%$	$30\%$
BERT	$70.28$	$75.64$	$79.63$
BERT + MR	$74.51$	$75.98$	$80.83$
BERT + SR	$73.77$	$73.26$	$75.52$
BERT + LR	$73.26$	$79.49$	$79.20$
BERT + MMix †	$76.06$	$80.32$	$83.48$
BERT + SMix †	$75.07$	$78.64$	$80.89$
BERT + TMix †	$74.48$	$77.07$	$80.99$

Table 4: F1 scores on down-sampled GermEval compared with replacement-based augmentation methods. †denotes our methods.

To better understand the improvement made by SegMix, we compare the confusion matrix of the baseline model and MMix for each class for $5\%$ of CoNLL-03 data in Fig. 6.

Language	Model Link	Reference
English	BERT	Devlin et al. 2018
English	RoBERTa	Liu et al. 2019
Kinyarwanda	Kin	Adelani et al. 2021
Sinhala	Sin	Wang et al. 2020

Table 5: Pre-trained Models

	Aug Rate	200	400	800	Average
Baseline	0	$76.02\pm 0.56$	$81.20\pm 0.29$	$84.34\pm 0.33$	-
MMix	0.1	$\mathbf{78.76}\pm 0.49$	$\mathbf{82.28}\pm 0.31$	$\mathbf{85.51}\pm 0.21$	$+(1.66\pm 0.55$ )
	0.2	$77.71\pm 0.29$	$82.10\pm 0.09$	$84.77\pm 0.23$	$+(1.01\pm 0.47)$
	0.3	$77.88\pm 0.20$	$82.10\pm 0.19$	$84.72\pm 0.28$	$+(1.05\pm 0.47)$
	0.4	$77.13\pm 0.23$	$81.89\pm 0.13$	$84.59\pm 0.24$	$+(0.68\pm 0.46)$
	0.5	$77.38\pm 0.32$	$81.32\pm 0.07$	$84.66\pm 0.07$	$+(0.60\pm 0.47)$
	Average	$78.16\pm 0.44$	$82.32\pm 0.26$	$85.12\pm 0.17$	$+(1.00\pm 0.48)$
TMix	0.1	$\mathbf{78.70}\pm 0.47$	$\mathbf{82.98}\pm 0.27$	$\mathbf{85.37}\pm 0.26$	$+(1.83\pm 0.54$ )
	0.2	$78.51\pm 0.34$	$82.35\pm 0.12$	$85.26\pm 0.23$	$+(1.52\pm 0.48)$
	0.3	$78.24\pm 0.39$	$82.21\pm 0.15$	$85.07\pm 0.12$	$+(1.32\pm 0.48)$
	0.4	$77.56\pm 0.49$	$82.11\pm 0.33$	$85.22\pm 0.06$	$+(1.11\pm 0.54)$
	0.5	$77.78\pm 0.60$	$81.97\pm 0.17$	$84.68\pm 0.25$	$+(0.96\pm 0.57)$
	Average	$78.16\pm 0.44$	$82.32\pm 0.26$	$85.12\pm 0.17$	$+(1.35\pm 0.51)$
SMix	0.1	$\mathbf{77.95}\pm 0.39$	$\mathbf{82.52}\pm 0.36$	$\mathbf{85.33}\pm 0.19$	$+(1.4\pm 0.52$ )
	0.2	$77.75\pm 0.46$	$82.42\pm 0.35$	$85.05\pm 0.18$	$+(1.22\pm 0.54)$
	0.3	$77.24\pm 0.44$	$82.11\pm 0.07$	$84.90\pm 0.16$	$+(0.89\pm 0.49)$
	0.4	$77.23\pm 0.59$	$81.75\pm 0.29$	$84.76\pm 0.15$	$+(0.73\pm 0.57)$
	0.5	$77.78\pm 0.49$	$81.42\pm 0.35$	$84.98\pm 0.21$	$+(0.54\pm 0.55)$
	Average	$77.39\pm 0.50$	$82.04\pm 0.29$	$85.01\pm 0.17$	$+(0.96\pm 0.54)$

Table 6: f1 scores of MMix, TMix, SMix on CoNLL-03 with variant augmentation rates (

\frac{\#\text{of augmented data}}{\#\text{of training data}}

) under different initial data sizes. SegMix consistently improves over the baseline, demonstrating its stability and robustness over varying augmentation rates. The last row is the averaged improvement score for each augmentation rate over different initial data sizes. The last column is the average score for each initial data size over different augmentation rates.

A.2 Variants of BERT Models

As mentioned in Sec. 4.1, we adopted language-specific BERT models as the pre-trained models for all tasks. There are 12 layers (transformer blocks), 12 attention heads, and 110 million parameters (Devlin et al., 2018). The model links are included in Table. 5. For Kinyarwanda, bert-base-multilingual-cased-finetuned-kinyarwanda is obtained by fine-tuning Multilingual BERT (MBERT) on the Kinyarwanda dataset JW300, KIRNEWS, and BBC Gahuza (Adelani et al., 2021). EMBERT-Sin is obtained by EXTEND (Wang et al., 2020) MBERT in Sinhala. Specifically, EMBERT-Sin first incorporates the target language Sinhala by expanding the vocabulary, and then continues pre-training on LORELEI using a batch size of $32$ , a learning rate of $2e-5$ , and trained for $500K$ iterations.

Pred. 1	Baseline	English [MISC] county sides and another against British Universities [MISC]
Pred. 1	MMix	English [MISC] county sides and another against British Universities [ORG]
Pred. 2	Baseline	May 22 First one-day international at Headingley [ORG]
Pred. 2	MMix	May 22 First one-day international at Headingley [LOC]
Pred. 3	Baseline	July 9 v Minor Counties [MISC] XI
Pred. 3	MMix	July 9 v Minor Counties [ORG] XI

Table 7: Examples of cases predicted by the baseline model and MMix from validation dataset. The colored segments represent an entity mention, the blue segment represents a correctly classified mention, and the red represents a misclassified mention.

Ex. 4	the complete [statue] $e_{1}$ topped by an imposing [head] $e_{2}$ was originally nearly five metres high
Other	Baseline: Component-Whole(e2,e1)	RMix : Other
Ex. 5	the [slide] $e_{1}$ which was triggered by an avalanche - control [crew] $e_{2}$ damaged one home and blocked the road for most of the day
Cause-Effect(e2,e1)	Baseline: Product-Producer(e1,e2)	RMix : Cause-Effect(e1,e2)

Table 8: Examples of correctly classified cases after RMix. The bold segment tuple represents a nominal pair, and the blue label represents a misclassified relation. The true label is presented in the first column.

A.3 Case Analysis

We list some improved cases in Table. 7, Ex. 1 and 2 are cases of correction between for ORG, while Ex. 3 is a case where the entity label is correct, but the mention range remains incomplete (both predicts Minor Counties as a mention instead of Minor Counties XI). In Table. 8, we list some improved cases for RMix on RE. Both Ex.4 and 5 are cases of correction for relation type. In Ex.5, RMix helps the model classify the correct relation but not in the correct order.