Securing OFDM-Based NOMA SWIPT Systems

In [1], the authors proposed cooperative non-orthogonal multiple-access (NOMA) scheme where only the near user is an energy harvesting (EH) node that relays information to the far user, however, the work does not take into account securing the communication between the multiple nodes. The work in [2] optimized energy efficiency in non-cooperative NOMA under power budget and data rate constraints without exploiting physical-layer security schemes [3]. Hybrid simultaneous wireless information and power transfer (SWIPT) schemes were proposed in [4] and [5] under the consideration of the harvested energy at the receiving node while securing the legitimate transmissions, however, both works do not take NOMA and/or multiple-access scenarios into consideration. Moreover, [6] investigated physical layer security in large scale NOMA networks, without considering EH at the nodes.

In our adopted system model, we assume a BS trying to secure communication between itself and multiple legitimate users in the presence of passive eavesdroppers (Eves), denoted as $e$, as depicted in Fig. 1. To this end, the users are categorized into two groups according to the radius of the disc they are located in and the BS is assumed to lie in the center of the discs. Without loss of generality, we assume two discs only, inner Disc $U$ with radius $r_{u}$ and Disc $G$ with inner radius $r_{g_{1}}$ and outer radius $r_{g_{2}}$. We assume that the spatial topology for both legitimate users and eavesdroppers is modeled according to Poisson point processes (PPP). The legitimate users are assumed to have reliable power supplies. It is also assumed that the legitimate users are EH nodes. Since the energy required for transmission is much higher than that required for processing of the received samples [7], to save energy at the near user, a non-cooperative NOMA transmission scheme is adopted between the BS and the legitimate users. The eavesdroppers are assumed to be located at least half wavelength apart from any legitimate user.

It is assumed that communication is carried out under OFDM scenario. We consider an OFDM symbol with total duration time $T$, which is composed of the CP time duration, denoted by $T_{\rm cp}$, and the time duration of the useful data signal, denoted by $T_{s}$. To this end, $T=N_{t}/f_{s}=N_{\rm cp}/f_{s}+N_{s}/f_{s}$, where $N_{t}=N_{\rm cp}+N_{s}$ is the total number of samples within one OFDM symbol, $N_{\rm cp}$ is the number of the samples within the CP, $N_{s}$ is the number of samples of the transmitted data signal, and $f_{s}$ is the sampling frequency. Under OFDM scheme, the available bandwidth is divided into $N_{s}$ orthogonal sub-channels.

The wireless channels between BS and users are modeled as block-fading channels, which implies that the channel coefficients do not vary during the channel coherence time. The thermal noise at the receiving nodes is modeled as additive white Gaussian noise with zero mean and power $\sigma^{2}$.

The BS uses $N_{s}$-point inverse fast Fourier transform (IFFT) to convert the frequency-domain sub-channels into the time-domain. In addition, it appends a CP of length $N_{\rm cp}$ to the beginning of each OFDM symbol to prevent the inter-OFDM-symbol-interference across adjacent OFDM symbols. Along with the transmitted OFDM symbol, the BS transmits a time-domain AN signal by exploiting the temporal dimensions gained by the presence of the CP. As will be shown later, the AN is designed such that it is canceled out at the legitimate receivers prior to signal demodulation and retrieval of the transmitted data message. The BS splits its total available transmit power, $P_{t}$, between the data and AN signals. The power split factor is denoted by $0\leq\rho\leq 1$. The allocated power to the data signal is $\rho P_{t}$ and the allocated power to AN signal is $\bar{\rho}P_{t}$.

The entire CP is used in analog domain to transfer energy to two NOMA Users, $u$ and $g$. Prior to processing and in time domain the rest of the OFDM symbol is divided into two portions. During the first portion, which has a duration $T_{u}=N_{u}/f_{s}$ and $T_{g}=N_{g}/f_{s}$ at Users $u$ and $g$, respectively, where $N_{u}$ and $N_{g}$ are the number of samples in the first portions at Users $u$ and $g$, respectively, the users use PS scheme, where a fraction of the received samples power is used for EH. For the remaining portion of the OFDM symbol, no PS is used and, hence, the entire second portion is used for data processing.

To remove the impact of AN at both legitimate users, the AN precoding matrix should satisfy

Note that due to the equalization step applied in (4), the noise variance for the first $N_{u}$ and $N_{g}$ samples increases. The average noise variance across all samples for Users $u$ and $g$ can be given by

We conduct our OFDM-based NOMA SWIPT system simulation using Rayleigh fading channel realizations that follow $\mathcal{CN}(0,1)$. Independent channel realizations are generated for each user and for the eavesdropper. The rest of the simulation parameters are $\sigma^{2}=1$ Watt, $N_{t}=64$, $N_{\rm cp}=16$, $f_{s}=2$ MHz, $r_{u}=8$ meters, $r_{g_{1}}=10$ meters, $r_{g_{2}}=14$ meters, $d_{u}=4$ meters, $d_{g}=12$ meters, $d_{e}=10$ meters, $\eta=0.75$, and $\alpha=2$. The calculated ranges for SNR at $g$ and $u$ across all variations of $N_{g}$, $\beta_{g}$, $\theta_{g}$, $\theta_{u}$, $\rho$ are $\in[0:13]$ dB and $\in[27:45]$ dB, respectively. Due to limited available space, we present more results for $g$ since it is the far user operating under non-cooperative NOMA. Moreover, we simulate for fixed $N_{u}=16$ and $\beta_{u}=0.5$, however, similar conclusions for varying these two parameters are analogous to varying $N_{g}$ and $\beta_{g}$. The optimized values are estimated through an exhaustive grid-based search operation at the BS. We present these values at the end of the section. In the following figures, we show the impact of varying the optimization parameters on the performance of the system.

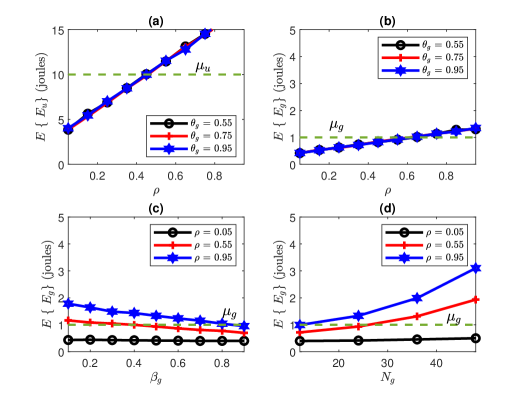
Fig. 2 presents the simulated average secrecy rates. Fig. 3 presents the simulated outage probabilities. Fig. 4 presents the simulated harvested energy. In Figs. 2 to 4, we have (a) average parameter for $u$ versus $\rho$ for different $\theta_{g}$ values (b) average parameter for $g$ versus $\rho$ for different $\theta_{g}$ values, $N_{g}=24$ and $\beta_{g}=0.5$ (c) average parameter for $g$ versus $\beta_{g}$ for different $\rho$ values, $N_{g}=24$ and $\theta_{g}=0.75$ and (d) average parameter for $g$ versus $N_{g}$ for different $\rho$ values, $\theta_{g}=0.75$ and $\beta_{g}=0.5$. Note that changing $\theta_{g}$ changes $\theta_{u}$ since $\theta_{u}=1-\theta_{g}$.

As shown in Fig. 2 (a) as $\rho$ increases or $\theta_{g}$ decreases, the SNR at $u$ increases and hence $\mathbb{E}\{R_{s,u}\}$ increases. However since $g$ considers $u$’s signal as noise, as $\rho$ increases, the noise variance increases and hence $\mathbb{E}\{R_{s,g}\}$ decreases as shown in Fig. 2 (b). Unlike $u$ as $\theta_{g}$ increases, the desired signal power at $g$ increases, which improves SNR and consequently $\mathbb{E}\{R_{s,g}\}$. As shown in Fig. 2 (c) as $\beta_{g}$ increases, higher power factor is allocated for signal decoding rather than energy harvesting, which improves SNR as follows from the definition of $\Lambda_{g}$ and, hence, improves $\mathbb{E}\{R_{s,g}\}$. $N_{g}$ does not have much impact on $\mathbb{E}\{R_{s,g}\}$. Note that the upper bound (UB) in (17) is satisfied.

One key finding in Fig. 3 (a) is that very low values of $\theta_{u}$, for example $0.05$, i.e., when $\theta_{g}=0.95$, might lead to $P_{o,u}=1$. To achieve a desired $\epsilon_{u}\leq 10^{-4}$, $\rho$ can be $\in[0.05:0.95]$ and $\theta_{g}\in[0.55:0.9]$. As can be inferred from Fig. 3 (b) to (d) to achieve a desired $\epsilon_{g}\leq 10^{-4}$, $\rho$ can be $\in[0.2:0.95]$, $\theta_{g}\in[0.55:0.9]$, $\beta_{g}\in[0.05:0.95]$, and $N_{g}\in[12:N_{s}]$.

As expected, the harvested energy at $u$ is much higher than that at the far User $g$. To achieve a desired $\mu_{u}\geq 10$ joules, $\rho$ should be $\in[0.5:0.95]$ as shown in Fig. 4 (a). Note that since the energy is harvested at $u$ before cancelling User $g$’s signal, changing $\theta_{g}$ does not have an impact on $\mathbb{E}\{E_{u}\}$. As can be seen in Fig. 4 (b) to (d), to achieve $\mu_{g}\geq 1$ joule, $\rho$ should be $\in[0.65:0.95]$, $\beta_{g}$ should be $\in[0.55:0.95]$ and $N_{g}$ should be $\in[16:N_{s}]$. $N_{g}$ has the most impact on the harvested energy at $g$.

Following the exhaustive grid-based search operation, the optimal results under our simulation parameters are $\rho=0.75$, $\theta_{g}=0.75$, $\beta_{g}=0.85$ and $N_{g}=32$. The reader can infer these values from and the explanatory plots in Figs. 2 to 4. The achieved maximized $\mathbb{E}\{R_{s,u}\}=4$ bits/sec/Hz and $\mathbb{E}\{R_{s,g}\}=0.7$ bits/sec/Hz while meeting the constraints on $P_{o,u}\leq 10^{-4}$, $P_{o,g}\leq 10^{-4}$, $\mathbb{E}\{E_{u}\}\geq 10$ joules and $\mathbb{E}\{E_{g}\}\geq 1$ joule.

We presented an AN aided physical-layer security scheme for energy harvesting nodes operating under OFDM-based non-cooperative NOMA scheme. We showed that, with optimal choice of design parameters, it is possible to secure the considered system while transferring energy to multiple nodes under minimum outage probability constraints at legitimate users.