SecureBoost Hyperparameter Tuning via Multi-Objective Federated Learning
Abstract
SecureBoost is a tree-boosting algorithm leveraging homomorphic encryption to protect data privacy in vertical federated learning setting. It is widely used in fields such as finance and healthcare due to its interpretability, effectiveness, and privacy-preserving capability. However, SecureBoost suffers from high computational complexity and risk of label leakage. To harness the full potential of SecureBoost, hyperparameters of SecureBoost should be carefully chosen to strike an optimal balance between utility, efficiency, and privacy. Existing methods either set hyperparameters empirically or heuristically, which are far from optimal. To fill this gap, we propose a Constrained Multi-Objective SecureBoost (CMOSB) algorithm to find Pareto optimal solutions that each solution is a set of hyperparameters achieving optimal tradeoff between utility loss, training cost, and privacy leakage. We design measurements of the three objectives. In particular, the privacy leakage is measured using our proposed instance clustering attack. Experimental results demonstrate that the CMOSB yields not only hyperparameters superior to the baseline but also optimal sets of hyperparameters that can support the flexible requirements of FL participants.
1 Introduction
Federated learning McMahan et al. (2017); Tong et al. (2023) is a novel distributed machine learning paradigm that enables multiple participants to train machine learning models using participants’ private data without compromising data privacy. SecureBoost Cheng et al. (2021) is a popular vertical federated gradient boosting tree algorithm for its interpretability and effectiveness. It has been widely applied in many fields, such as advertisement, finance, and healthcare.
SecureBoost applies homomorphic encryption (HE) Paillier (1999) to protect data privacy. However, HE is computationally expensive, which hinders SecureBoost from being applied to large-scale machine learning problems. In addition, we demonstrate that SecureBoost suffers from the instance clustering attack (ICA) that we propose to infer labels of the active party. In other words, SecureBoost has the risk of leaking labels (see Sec. 4). We design two countermeasures against ICA but at the expense of losing utility.
To harness the full potential of SecureBoost, its hyperparameters (including hyperparameters of the applied protection mechanism) should be set such that the utility loss, training cost, and privacy leakage can be minimized simultaneously, and the optimal tradeoffs between utility, efficiency, and privacy can be achieved. However, existing FL platforms Liu et al. (2021); Fu et al. (2021) often set the hyperparameters of SecureBoost to empirical values or apply heuristic methods to search for the hyperparameters to tradeoff between utility, efficiency, and privacy. These existing methods may lead to hyperparameters far from satisfactory in practice. These gaps inspire us to investigate the following critical open problem: is it possible to design a systematic approach that can find SecureBoost hyperparameters to achieve optimal tradeoffs between utility, efficiency, and privacy?
Our work provides a positive answer to this question. More specifically, we apply Constrained Multi-Objective Federated Learning (CMOFL) Kang et al. (2023) to find Pareto optimal solutions of hyperparameters that can minimize utility loss, training cost, and privacy leakage simultaneously. Each solution is an optimal tradeoff between the three conflicting objectives. As a result, Pareto optimal solutions not only provide optimal hyperparameters for SecureBoost but also can support the flexible requirements of FL participants. For example, FL participants can select the most appropriate hyperparameters from the Pareto optimal solutions that satisfy their current preference over utility, efficiency, and privacy.
Our main contributions are summarized as follows:
-
•
We apply Constrained Multi-Objective Federated Learning (CMOFL) to SecureBoost and propose a Constrained Multi-Objective SecureBoost (CMOSB) algorithm (Sec. 5.2) to find the Pareto optimal solutions of hyperparameters that minimize utility loss, training cost, and privacy leakage simultaneously. This is the first attempt to apply CMOFL to VFL in general and SecureBoost in particular.
- •
-
•
We conduct experiments on four datasets, demonstrating that our CMOSB can find far better hyperparameters than default ones set by FATE Liu et al. (2021) and VF2Boost Fu et al. (2021) in terms of the tradeoff between privacy leakage, utility loss, and training cost. Moreover, CMOSB can find Pareto optimal solutions of hyperparameters that achieve an optimal tradeoff between utility loss, training cost, and privacy leakage (Sec. 6).
2 Related Work
2.1 Label Leakage in VFL
Label leakage in vertical federated learning refers to the situation where the passive party is able to obtain the label data of the active party during the training process. Fu et al. (2022) systematically classified the label leakage in vertical federated learning into three categories: active attack, passive attack, and direct attack, and provided an attack method for each category. Zou et al. (2022) proposed a label attack method on the black-boxed VFL and presented a privacy protection method. Xie et al. (2023) demonstrated that split learning remains vulnerable to label inference attacks. Qiu et al. (2022) finds that the training of GNNs in VFL may also lead to the leakage of sample relationships. Tan et al. (2022) proposed a gradient inversion attack that utilizes the gradients of local models to reconstruct label data.
2.2 Multi-objective Federated Learning
Multi-objective federated learning is a collaborative optimization approach in which participants of FL aim to optimize multiple conflicting objectives simultaneously and find Pareto optimal solutions. Cui et al. (2021) considered the utility of participating parties as the optimization objective, model disparity as the constraint, and optimized the objectives of all participants to calculate the Pareto front. This approach can ensure the fairness of federated learning and obtain the optimal performance model. Zhu and Jin (2020) formulated the accuracy and communication cost of federated learning as the optimization objectives and adjusted the model sparsity to minimize both the communication cost and test errors. The algorithm proposed in Kang et al. (2023) is a multi-objective federated learning algorithm with constraints, which add constraints to the optimization objectives and find the Pareto front faster within the feasible range.
3 Background
3.1 Vertical Federated Learning
Vertical Federated Learning Yang et al. (2019) is one of the scenarios in Federated Learning, which refers to the situation where feature data is vertically partitioned among multiple parties, with one party possessing the data labels (Fig. 1): The active party holds features and labels while passive parties hold only features.

All participating parties in VFL first align their instances by private set intersection (PSI) Freedman et al. (2004), and then perform federated model training and inferencing. During the training process, each party is not allowed to reveal its training data to others Tong et al. (2022). After the federated training is completed, the federated model is obtained, which is jointly held by all participating parties, i.e., model is split into . In the inferencing phase, all participating parties collaboratively make the prediction but only the active party can access the final predicted result.
3.2 SecureBoost
SecureBoost Cheng et al. (2021) is a widely used gradient boosting tree algorithm designed for the vertical federated learning scenario. The core idea of SecureBoost is to use federated decision trees to fit instance labels.
For each iteration, SecureBoost constructs a new tree from the root node based on a node split finding algorithm, which is summarized in Algo. 1: the active party sends the homomorphically encrypted gradients , , and instance space of the current node to passive parties, who, in turn, calculate the gradient statistics and send them back to the active party; the active party finds the optimal split of the current node with the maximal splitting score and informs the corresponding parties to split the instance space into child nodes. The split finding process continues until the maximum depth is reached. We refer readers to Cheng et al. (2021) for a more detailed algorithm description.
The instance distributions of leaf nodes in SecureBoost are not protected by HE, which may lead to privacy leakage. Some methods Wu et al. (2020); Fang et al. (2021) use a combination of HE and MPC to protect privacy to address this issue. However, these methods may result in significant training cost, making it challenging to be applied in trustworthy federated learning.
3.3 Constrained Multi-Objective Federated Learning
The Constrained Multi-Objective Federated Learning (CMOFL) problem aims to find Pareto optimal solutions that simultaneously minimize multiple FL objectives under constraints. We adapt the definition of CMOFL proposed in the work Kang et al. (2023) to the VFL setting.
Definition 1 (Constrained Multi-Objective Vertical Federated Learning).
The problem of Constrained Multi-Objective Vertical Federated Learning is formulated as follows:
| (1) |
where is a solution in the decision space , are the objectives to minimize, is the local objective of client corresponding to the th objective , and is the upper bound of .
Remark 1.
The FL participants aim to find Pareto optimal solutions and front for the Constrained Multi-Objective VFL problem. We provide the definitions of Pareto dominance, Pareto optimal solution, Pareto set, and Pareto front as follows.
Definition 2 (Pareto Dominance).
Let , is said to dominate , denoted as , if and only if and .
Definition 3 (Pareto Optimal Solution).
A solution is called a Pareto optimal solution if there does not exist a solution such that .
A Pareto optimal solution refers to a solution that achieves an optimal tradeoff among different conflicting objectives. The collection of all Pareto optimal solutions forms the Pareto set, while the corresponding objective values for the Pareto optimal solutions form the Pareto front. The definitions of the Pareto set and Pareto front are formally given as follows.
Definition 4 (Pareto Set and Front).
The set of all Pareto optimal solutions is called the Pareto set, and its image in the objective space is called the Pareto front.
We use hypervolume (HV) indicator Zitzler and Künzli (2004) as a metric to measure the Pareto front. The definition of hypervolume indicator is provided below.
Definition 5 (Hypervolume Indicator).
Let be a reference point that is an upper bound of the objectives , such that , . The hypervolume indicator measures the region between and and is formulated as:
| (2) |
where refers to the Lebesgue measure.
4 Label Leakage in SecureBoost
In this section, we design a label inference attack and explain how this attack infers labels of the active party. We also propose two defense methods against this attack.
4.1 Threat Model
Below we discuss the threat model, including the attacker’s objective, capability, and knowledge.
Attacker’s objective. We consider the passive party as the attacker who aims to infer labels owned by the active party.
Attacker’s capability. We assume the attacker is semi-honest in the sense that the attacker faithfully follows the SecureBoost protocol but may mount label inference attacks to infer labels of the active party.
Attacker’s knowledge. The passive party can access instance distributions of leaf nodes because SecureBoost does not protect this information. We also assume that the passive party holds several labeled instances for each class, a similar assumption made in Fu et al. (2022).
4.2 Label Inference Attack
While SecureBoost utilizes homomorphic encryption to protect gradient information passed between the active party and passive parties, it does not protect the instance distribution of each leaf node owned by the passive party, indicating that the passive party (i.e., the attacker) can exploit this information to infer the active party’s labels through clustering. We name this label inference attack Instance Clustering Attack, and its procedure is illustrated in Fig. 2 and described in Algo. 2.

The attacker first constructs the similarity matrix based on the instance distribution of each leaf node using Eq. (3) (line 1 of Algo. 2).
| (3) |
where denotes the number of decision trees, denotes the index of leaf node.
Then, the attacker leverages this similarity matrix to categorize instances into clusters (line 2). We assume the attacker knows the label of one instance in each cluster. Hence, the attacker assigns instances in each cluster with the known labels (lines 3-5).
4.3 Defense Methods
The performance of the instance clustering attack depends on the purity of leaf nodes owned by the attacker (i.e., passive party). We define the purity of a node as the ratio of instances belonging to the majority class to all instances in that node. A higher purity implies a more accurate similarity matrix, which can lead to more precise clustering results. We provide two defense methods to suppress this attack by reducing the purity: (1) local trees; (2) purity threshold.
Local Trees. At the first few rounds of the training, there is a strong correlation between the sign of the gradients and labels, which causes instances with the same label to be more likely to be classified into the same node, resulting in high purity of the leaf nodes. We propose a local training stage preceding SecureBoost, in which the active party locally trains decision trees, aiming to reduce the correlation between the sign of instance gradients transmitted to the passive parties and their respective labels, thereby reducing the purity of each leaf node. 111 These defense method has been implemented in FATE v1.11.2.
Purity Threshold. We apply a threshold to the node purity to prevent high-purity nodes from being disposed to the passive parties, thereby mitigating label leakage. When the purity of a node passes a prespecified threshold , the passive party is not allowed to participate in the federated training of the subtree rooted at the node , and the active party continues to train the subtree locally.
Although the two defense methods can effectively thwart the instance clustering attack, they may introduce utility loss. Therefore, tradeoffs need to be made between utility and privacy. We consider their hyperparameters as decision variables when we optimize the Constrained Multi-Objective SecureBoost problem (Sec. 5).
5 Constrained Multi-Objective SecureBoost
In this section, we define the measurements of utility loss, training cost, and privacy leakage as well as our Constrained Multi-Objective SecureBoost algorithm.
5.1 Measurements of Objectives
We provide measurements of the three objectives we aim to minimize: utility loss, training cost, and label leakage.
Utility Loss. The utility loss measures the amount of decrease in utility when certain defense methods are applied to thwart the label inference attack.
| (4) |
where , , and denote the SecureBoost model, the test dataset, and the performance metric, respectively. is AUC for binary classification and accuracy for multi-class classification.
Training Cost. We use training time to measure the training cost of SecureBoost. Since HE operations dominate training time, we estimate the training cost by summing the time spent on each HE operation.
| (5) |
where , , and denote the number of operations for encryption, decryption, and addition, respectively; , , and denote the average time required for each HE operation, respectively.
Privacy Leakage. We use the accuracy of the instance clustering attack (see Sec. 4.2) as the metric to measure the privacy leakage based on a set of instances, denoted as , randomly sampled from the training set (the number of instances belonging to each class is the same in ).
| (6) |
where denotes the label inferred by the instance clustering attack, and denotes the true label, and denotes the indicator function.
5.2 Constrained Multi-Objective SecureBoost Algorithm
In this section, we propose a Constrained Multi-Objective SecureBoost algorithm (CMOSB), through which approximate Pareto optimal solutions and front can be obtained to balance the three optimization objectives and provide guidance for hyperparameter selection.
CMOSB is based on NSGA-II, and it is described in Algo. 3: offspring solutions of the current generation are generated by performing crossover and mutation using the previous solution (line 3). All newly generated individuals are evaluated using Algo. 4 (line 5). The algorithm adds constraints on the solutions (line 6) to limit the search space of the solutions. Lines 7-8 sort the solutions and select the top individuals for the next iteration.
Algo 4 aims to measure utility loss, training cost, and privacy leakage for training a SecureBoost model. The solution represents a set of hyperparameters for SecureBoost, where Table 2 provides a detailed description of the hyperparameters. Lines 3-5 correspond to the local training stage mentioned in Sec. 4.3, while lines 6-19 correspond to the federated learning stage, which together constitutes the SecureBoost framework. In line 10, the active party calculates the purity of node , and if it is below the threshold, all participants will jointly calculate the split point, otherwise, only the active party will calculate it locally. Training cost and privacy leakage will be calculated during the iteration process, while utility will be calculated after the training is completed.
6 Experiments
In this section, we empirically investigate the effectiveness of our proposed attacking method, defense methods, and the CMOSB algorithm.
6.1 Experimental Settings
Dataset and setting. We conduct experiments on two synthetic datasets and two real-world datasets. The synthetic datasets, generated using the sklearn library222https://scikit-learn.org/stable/, consist of Synthetic1 for binary classification and Synthetic2 for multi-class classification. The DefaultCredit 333https://www.kaggle.com/uciml/default-of-credit-card-clients-dataset contains the task of predicting whether users can repay their loans on time, while the Sensorless is for sensorless drive diagnosis.
To create datasets for the federated scenario, each dataset was vertically partitioned into two sub-datasets. We use 2/3 of the data as the train set and the remaining as the test set. Table 1 summarizes these datasets.
| Name | S | AF | PF | C |
| Synthetic1 | 2,000 | 5 | 5 | 2 |
| DefaultCredit | 30,000 | 12 | 13 | 2 |
| Synthetic2 | 10,000 | 5 | 5 | 10 |
| Sensorless | 58,509 | 12 | 36 | 11 |
| Variable | Range | Chromosome Type | Description |
| Binary | The number of rounds for boosting in federated learning | ||
| Binary | The number of rounds for boosting locally | ||
| Binary | Maximum depth of each decision tree | ||
| Real-value | Subsample ratio of the training instances | ||
| Real-value | The purity threshold to stop the federated learning | ||
| Real-value | Step size shrinkage used in update to prevents overfitting |
CMOSB Setup. The proposed CMOSB algorithm is based on NSGA-II. Thus, we follow the setup proposed in literature Zhu and Jin (2020). We apply a single-point crossover for binary chromosomes with a probability of 0.9 and a bit-flip mutation with a probability of 0.1. We apply a simulated binary crossover (SBX) Deb and Kumar (1995) for real-valued chromosome with a probability of 0.9 and = 2, and a polynomial mutation with a probability of 0.1 and = 20, where and denote spread factor distribution indices for crossover and mutation, respectively. The number of generations for CMOSB is set to 40.
6.2 Effectiveness of Defense Methods
In this section, we investigate the efficacy of our proposed defense methods in mitigating privacy leakage. The experiments are conducted on Synthetic1, with the default hyperparameter set as follows: , , , .

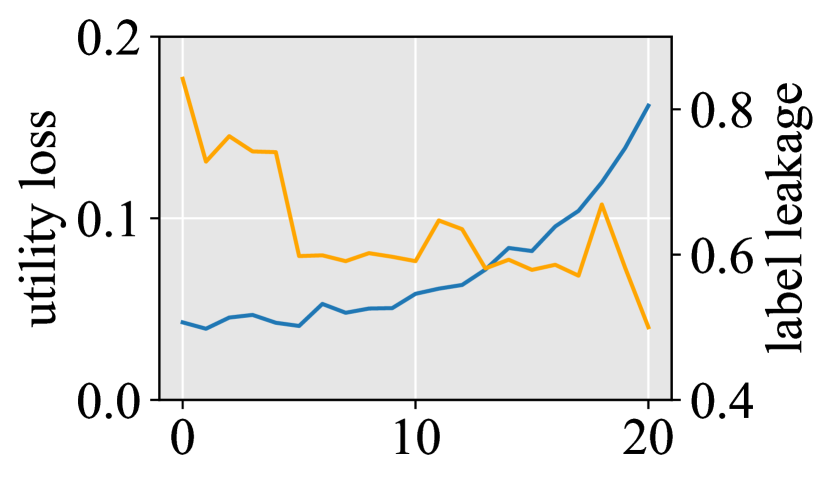
(a) Varying

(b) Varying
Fig. 3 shows that both methods can trade-off model performance for privacy protection. As shown in Fig. 3(a), training local trees can reduce the correlation between sign of gradients and labels, thereby reducing privacy leakage of active party. Training 10 decision trees locally reduced label leakage risk by 25.1% while sacrificing only 1.6% of utility. The impact of purity threshold is illustrated in Fig. 3(b), where we observe a decrease in privacy leakage as more nodes are constructed by active party locally.
6.3 Optimal Tradeoffs between Utility, Efficiency, and Privacy achieved by CMOSB
In this section, we use CMOSB (Algo. 3) without using constraints to find the Pareto optimal solutions of hyperparameters for SecureBoost. Each solution is a set of hyperparameters that achieve an optimal tradeoff between utility loss, training cost, and privacy leakage.
We summarize the variables and their descriptions involved in multi-objective optimization in Table 2. Among the variables, the definitions of , , , and are the same as those in SecureBoost. refers to the number of rounds for boosting locally, and refers to the threshold of purity. For binary classification problems, we further constrain the range of to to improve the search efficiency.
| Baseline | ||||
| Fate | 5 | 3 | 0.3 | 0.8 |
| Emperical | 10 | 5 | 0.3 | 0.8 |
| VF2Boost | 20 | 7 | 0.1 | 0.8 |
We use the default parameters of Fate Liu et al. (2021) and VF2Boost Fu et al. (2021), as well as a parameter empirically selected by us, as baselines to evaluate the effectiveness of our algorithm. To make a fair comparison, the sampling rate is set to , and is set to true. The specific parameter settings are shown in Table 3.


(a) Synthetic1

(b) DefaultCredit

(c) Synthetic2

(d) Sensorless
In the binary classification task, the 3D Pareto front is shown in Fig. 4(a-b), where the blue points represent the Pareto front that is closer to the origin than the red baseline, indicating that the solutions on the Pareto front are better than those obtained by the baseline. It is more intuitive to observe the trade-off between utility loss, training cost, and privacy leakage in the 2D Pareto front illustrated in Fig. 5(a-d). For the tradeoff between training cost and utility loss (Fig. 5(a)(c)), both datasets show that as the utility loss decreases, the training cost increases continuously. This trend is more pronounced in the credit2 dataset due to its complexity. For the tradeoff between privacy leakage and utility loss (Fig. 5(b)(d)), decreasing one would increase in the other objective. The default hyperparameters always have relatively high privacy leakage due to the privacy leakage issue mentioned in Sec. 4.2.
In multi-class classification tasks, the tradeoff between the three optimization objectives also exists, as shown in the 3D Pareto front in Fig. 4(c-d). However, the probability of privacy leakage is lower than that in binary classification tasks (Fig. 5(f)(h)), as the model becomes more complex with increasing task difficulty, making the attack more difficult. In Fig. 5(g)(h), when the utility loss is small, both the training cost and privacy leakage increase dramatically. This is because the task is too simple, and a good model can be trained without passive parties.


6.4 Multi-Objective SecureBoost under Constraints
In real-world FL scenarios, FL participants typically have requirements on objectives of federated learning. Hence, we apply the CMOSB algorithm (with constraints) to ensure that the Pareto optimal solutions found satisfy the constraints as much as possible. Adding constraints focuses the search space of the CMOSB algorithm on the feasible region, which helps find better Pareto optimal solutions more efficiently.

(a) PL Constraint

(b) TC Constraint
We conduct this experiment on Synthetic1 and constrain the training cost and privacy leakage below 100 seconds and 0.6, respectively. We set the penalty coefficient to 20.
Fig. 6 illustrates the hypervolume comparison between CMOSB and MOSB when applying constraints to training cost and privacy leakage, respectively. For the privacy leakage constraint, CMOSB grows more rapidly in the first few generations and surpasses MOSB in the final generation, indicating that it can effectively find better Pareto solutions. For the training cost constraint, CMOSB also surpasses MOSB after 10th generation and maintains a lead to the last generation.


(a) PL vs UL

(b) TC vs UL
We further compare the Pareto fronts (at the 40th generation) obtained by the CMOSB and MOSB algorithms. Fig. 7(a) demonstrates the effect of adding a privacy leakage constraint, showing a reduction of approximately 3% in privacy leakage of the Pareto solutions at the same level of utility loss. The Pareto front found by CMOSB in Fig. 7(b) is also superior to that found by MOSB, especially for solutions with lower utility loss.
7 Conclusion and Future Work
In this paper, we propose the Constrained Multi-Objective SecureBoost (CMOSB) algorithm that identifies Pareto optimal solutions for SecureBoost hyperparameters by minimizing utility loss, training cost, and privacy leakage simultaneously. Experimental results demonstrate that the Pareto optimal solutions found by CMOSB outperform the baseline hyperparameters in terms of the tradeoff between utility loss, training cost, and privacy leakage. For future works, we will compare CMOSB with more sophisticated hyperparameter search algorithms, such as Bayesian Optimization, and deploy the CMOSB in production to compare its utility, efficiency, and privacy with the FATE platform. Furthermore, we plan to consider model complexity as one of the objectives to find model hyperparameters with higher interpretability.
Acknowledgements
We are grateful to anonymous reviewers for their constructive comments. This work is partially supported by the National Science Foundation of China (NSFC) under Grant No. U21A20516 and 62076017, the Beihang University Basic Research Funding No. YWF-22-L-531, the Funding No. 22-TQ23-14-ZD-01-001 and WeBank Scholars Program.
References
- Cheng et al. [2021] Kewei Cheng, Tao Fan, Yilun Jin, Yang Liu, Tianjian Chen, Dimitrios Papadopoulos, and Qiang Yang. Secureboost: A lossless federated learning framework. IEEE Intelligent Systems, 36(6):87–98, 2021.
- Cui et al. [2021] Sen Cui, Weishen Pan, Jian Liang, Changshui Zhang, and Fei Wang. Addressing algorithmic disparity and performance inconsistency in federated learning. In Advances in Neural Information Processing Systems, pages 26091–26102, 2021.
- Deb and Kumar [1995] Kalyanmoy Deb and Amarendra Kumar. Real-coded genetic algorithms with simulated binary crossover: Studies on multimodal and multiobjective problems. Complex Systems, 9(6), 1995.
- Fang et al. [2021] Wenjing Fang, Derun Zhao, Jin Tan, Chaochao Chen, Chaofan Yu, Li Wang, Lei Wang, Jun Zhou, and Benyu Zhang. Large-scale secure XGB for vertical federated learning. In The 30th ACM International Conference on Information and Knowledge Management, pages 443–452, 2021.
- Freedman et al. [2004] Michael J. Freedman, Kobbi Nissim, and Benny Pinkas. Efficient private matching and set intersection. In Advances in Cryptology - EUROCRYPT 2004, International Conference on the Theory and Applications of Cryptographic Techniques, volume 3027 of Lecture Notes in Computer Science, pages 1–19, 2004.
- Fu et al. [2021] Fangcheng Fu, Yingxia Shao, Lele Yu, Jiawei Jiang, Huanran Xue, Yangyu Tao, and Bin Cui. Vfboost: Very fast vertical federated gradient boosting for cross-enterprise learning. In International Conference on Management of Data, pages 563–576, 2021.
- Fu et al. [2022] Chong Fu, Xuhong Zhang, Shouling Ji, Jinyin Chen, Jingzheng Wu, Shanqing Guo, Jun Zhou, Alex X. Liu, and Ting Wang. Label inference attacks against vertical federated learning. In 31st USENIX Security Symposium, USENIX Security 2022, pages 1397–1414, 2022.
- Kang et al. [2023] Yan Kang, Hanlin Gu, Xingxing Tang, Yuanqin He, Yuzhu Zhang, Jinnan He, Yuxing Han, Lixin Fan, Kai Chen, and Qiang Yang. Optimizing privacy, utility and efficiency in constrained multi-objective federated learning. CoRR, abs/2305.00312, 2023.
- Liu et al. [2021] Yang Liu, Tao Fan, Tianjian Chen, Qian Xu, and Qiang Yang. FATE: an industrial grade platform for collaborative learning with data protection. Journal of Machine Learning Research, 22:226:1–226:6, 2021.
- McMahan et al. [2017] Brendan McMahan, Eider Moore, Daniel Ramage, Seth Hampson, and Blaise Agüera y Arcas. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, pages 1273–1282, 2017.
- Paillier [1999] Pascal Paillier. Public-key cryptosystems based on composite degree residuosity classes. In Advances in Cryptology - EUROCRYPT ’99, International Conference on the Theory and Application of Cryptographic Techniques, Prague, volume 1592 of Lecture Notes in Computer Science, pages 223–238, 1999.
- Qiu et al. [2022] Pengyu Qiu, Xuhong Zhang, Shouling Ji, Tianyu Du, Yuwen Pu, Jun Zhou, and Ting Wang. Your labels are selling you out: Relation leaks in vertical federated learning. IEEE Transactions on Dependable and Secure Computing, pages 1–16, 2022.
- Tan et al. [2022] Juntao Tan, Lan Zhang, Yang Liu, Anran Li, and Ye Wu. Residue-based label protection mechanisms in vertical logistic regression. In 8th International Conference on Big Data Computing and Communications, pages 356–364, 2022.
- Tong et al. [2022] Yongxin Tong, Xuchen Pan, Yuxiang Zeng, Yexuan Shi, Chunbo Xue, Zimu Zhou, Xiaofei Zhang, Lei Chen, Yi Xu, Ke Xu, and Weifeng Lv. Hu-fu: Efficient and secure spatial queries over data federation. Proceedings of the VLDB Endowment, 15(6):1159–1172, 2022.
- Tong et al. [2023] Yongxin Tong, Yuxiang Zeng, Zimu Zhou, Boyi Liu, Yexuan Shi, Shuyuan Li, Ke Xu, and Weifeng Lv. Federated computing: Query, learning, and beyond. IEEE Data Engineering Bulletin, 46(1):9–26, 2023.
- Wu et al. [2020] Yuncheng Wu, Shaofeng Cai, Xiaokui Xiao, Gang Chen, and Beng Chin Ooi. Privacy preserving vertical federated learning for tree-based models. Proceedings of the VLDB Endowment, 13(11):2090–2103, 2020.
- Xie et al. [2023] Shangyu Xie, Xin Yang, Yuanshun Yao, Tianyi Liu, Taiqing Wang, and Jiankai Sun. Label inference attack against split learning under regression setting. CoRR, abs/2301.07284, 2023.
- Yang et al. [2019] Qiang Yang, Yang Liu, Tianjian Chen, and Yongxin Tong. Federated machine learning: Concept and applications. ACM Transactions on Intelligent Systems and Technology, 10(2):12:1–12:19, 2019.
- Zhu and Jin [2020] Hangyu Zhu and Yaochu Jin. Multi-objective evolutionary federated learning. IEEE Transactions on Neural Networks and Learning Systems, 31(4):1310–1322, 2020.
- Zitzler and Künzli [2004] Eckart Zitzler and Simon Künzli. Indicator-based selection in multiobjective search. In Parallel Problem Solving from Nature, volume 3242 of Lecture Notes in Computer Science, pages 832–842, 2004.
- Zou et al. [2022] Tianyuan Zou, Yang Liu, Yan Kang, Wenhan Liu, Yuanqin He, Zhihao Yi, Qiang Yang, and Ya-Qin Zhang. Defending batch-level label inference and replacement attacks in vertical federated learning. IEEE Transactions on Big Data, pages 1–12, 2022.