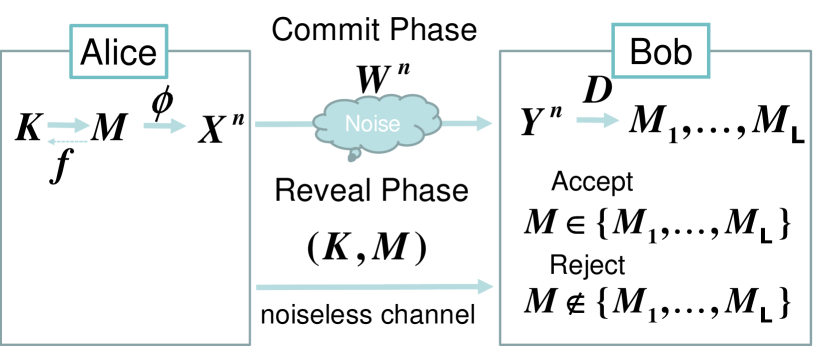
Secure list decoding and its application to bit-string commitment
Abstract
We propose a new concept of secure list decoding, which is related to bit-string commitment. While the conventional list decoding requires that the list contains the transmitted message, secure list decoding requires the following additional security conditions to work as a modification of bit-string commitment. The first additional security condition is the receiver’s uncertainty for the transmitted message, which is stronger than the impossibility of the correct decoding, even though the transmitted message is contained in the list. The other additional security condition is the impossibility for the sender to estimate another element of the decoded list except for the transmitted message. The first condition is evaluated by the equivocation rate. The asymptotic property is evaluated by three parameters, the rates of the message and list sizes, and the equivocation rate. We derive the capacity region of this problem. We show that the combination of hash function and secure list decoding yields the conventional bit-string commitment. Our results hold even when the input and output systems are general probability spaces including continuous systems. When the input system is a general probability space, we formulate the abilities of the honest sender and the dishonest sender in a different way.
Index Terms:
list decoding; security condition; capacity region; bit-string commitment; general probability spaceI Introduction
Relaxing the condition of the decoding process, Elias [1] and Wozencraft [2] independently introduced list decoding as the method to allow more than one element as candidates of the message sent by the encoder at the decoder. When one of these elements coincides with the true message, the decoding is regarded as successful. The paper [3] discussed its algorithmic aspect. In this formulation, Nishimura [4] obtained the channel capacity by showing its strong converse part111The strong converse part is the argument that the average error goes to if the code has a transmission rate over the capacity.. That is, he showed that the transmission rate is less than the conventional capacity plus the rate of the list size, i.e., the number of list elements. Then, the reliable transmission rate does not increase even when list decoding is allowed if the list size does not increase exponentially. In the non-exponential case, these results were generalized by Ahlswede [5]. Further, the paper [6] showed that the upper bound of capacity by Nishimura can be attained even if the list size increases exponentially. When the number of lists is , the capacity can be achieved by choosing the same codeword for distinct messages.
However, the merit of the increase in the list size was not discussed sufficiently. To get a merit of list coding, we need a code construction that is essentially different from conventional coding. Since the above capacity-achieving code construction does not have an essential difference from the conventional coding, we need to rule out the above type of construction of list coding. That is, to extract a merit of list decoding, we need additional parameters to characterize the difference from the conventional code construction, which can be expected to rule out such a trivial construction.
To seek a merit of list decoding, we focus on bit commitment, which is a fundamental task in information security. It is known that bit commitment can be realized when a noisy channel is available [7]. Winter et al [8, 9] studied bit-string commitment, the bit string version of bit commitment when an unlimited bidirectional noiseless channel is available between Alice and Bob, and a discrete memoryless noisy channel from Alice to Bob, which may be used times. They derived the asymptotically optimal rate as goes to infinity, which is called the commitment capacity. Since their result is based on Shannon theory, the tightness of their result shows the strong advantage of Shannon theoretic approach to information theoretic security. This result was extended to the formulation with multiplex coding [10]. However, their optimal method has the following problems;
- (P1)
-
When the number of use of the channel is limited, it is impossible to send a message with a larger rate than the commitment capacity.
- (P2)
-
Their protocol assumes that the output system is a finite set because they employ the method of type. However, when a noisy channel is realized by wireless communication, like an additive white Gaussian noise (AWGN) channel, the output system is a continuous set.
To resolve the problem (P1), it is natural to relax the condition for bit-string commitment. Winter et al [8, 9] imposed strong security for the concealing condition. However, studies in information theory, in particular, papers for wire-tap channel, often employs equivocation rate instead of strong security. In this paper, to relax the condition of bit-string commitment by using equivocation rate, we consider the following simple protocol by employing list decoding, where Alice wants to send her message to Bob.
- (i)
-
(Commit Phase) Alice sends her message to Bob via a noisy channel. Bob outputs messages as the list. The list is required to contain the message .
- (ii)
-
(Reveal Phase) Alice sends her message to Bob via a noiseless channel. If is contained in Bob’s decoded list, Bob accepts it. Otherwise, Bob rejects it.
In order that the protocol with phase (i) and (ii) works for bit-string commitment, the following requirements need to be satisfied.
- (a)
-
The message needs to be one of messages output by Bob.
- (b)
-
Bob cannot identify the message at the phase (i).
- (c)
-
Alice cannot find another element among messages output by Bob.
The requirement (a) is the condition for the requirement for the conventional list decoding while the requirements (b) and (c) correspond to the concealing condition and the binding condition, respectively and have not been considered in the conventional list decoding.
In this paper, we propose a new concept of secure list decoding by adding the requirements (b) and (c). One typical condition for (b) is the conventional equivocation rate based on the conditional entropy. In this paper, we also consider the equivocation rate based on the conditional Rényi entropy similar to the paper [11, 12]222 While the conference paper [13] discussed a similar modification of list decoding, it did not consider the equivocation rate. In this sense, the content of this paper is different from that of [13].. Hence, our code can be evaluated by three parameters. The first one is the rate of the message size, the second one is the rate of list size, and the third one is the equivocation rate. Using three parameters, we define the capacity region. In addition, our method works with a general output system including a continuous output system, which resolves the problem (P2) while an extension to such a general case was mentioned as an open problem in [9].
In the second step, we extend our result to the case with a general input system including a continuous input system. We need to be careful in formulating the problem setting in this case. If Alice is allowed to access infinitely many input elements in a continuous input system, the conditional entropy rate might be infinity. Further, it is not realistic for Alice to access infinitely many input elements. because a realistic modulator converts messages to finite constellation points in a continuous input system in wireless communication. Therefore, we need to separately formulate honest Alice and dishonest Alice as follows. The honest Alice is assumed to access only a fixed finite subset of a general input system. But, the dishonest Alice is assumed to access all elements of the general input system. Under this problem setting, we derived the capacity region.
In the third step, we propose a conversion method to make a protocol for bit-string commitment with strong security as the concealing condition (b) by converting a secure list decoding code. In this converted protocol, the security parameter for the concealing condition (b) is evaluated by variational distance in the same way as Winter et al [8, 9]. In particular, this converted protocol has strong security even with continuous input and output systems, where the honest Alice and the dishonest Alice has different accessibility to the continuous input system. In this converted protocol, the rate of message size of the bit-string commitment is the same as the equivocation rate based on the conditional entropy of the original secure list decoding code, which shows the merit of the equivocation rate of a secure list decoding code. In fact, the bit-string commitment with the continuous case was treated as an open problem in the preceding studies [9]. In addition, due to the above second step, our protocol for bit-string commitment works even when the accessible alphabet by the honest Alice is different from the accessible alphabet by the dishonest Alice.
This paper is structured as follows. Section II reviews the existing results for bit-string commitment. Section III explains how we mathematically handle a general probability space as input and output systems including continuous systems. Section IV gives the formulation of secure list decoding. Section V introduces information quantities used in our main results. Section VI states our results for secure list decoding with a discrete input system. Section VII explains our formulation of secure list decoding with general input system and states our results under this setting. Section VIII presents the application of secure list decoding to the bit-string commitment with strong security. Section IX shows the converse part, and Section X proves the direct part.
II Review of existing results for bit-string commitment
Before stating our result, we review existing results for bit-string commitment [8, 9]. Throughout this paper, the base of the logarithm is chosen to be . Also, we employ the standard notation for probability theory, in which, upper case letters denote random variables and the corresponding lower case letters denote their realizations. Bit-string commitment has two security parameters, the concealing parameter and the binding parameter . We denote the message revealed by Alice in Reveal Phase by . Let be all information that Bob obtains during Commit Phase, and be all information that Bob obtains during Reveal Phase except for . Here, contains the information generated by Bob. After Reveal Phase, Bob makes his decision, (accept) or (rejection). For this decision, Bob has a function that takes the value or . When Alice intends to send message in to Bob, the concealing and binding conditions are given as follows.
- (CON)
-
Concealing condition with . When Alice is honest, the inequality
(1) holds for .
- (BIN)
-
Binding condition with . We assume that the message is subject to the uniform distribution on . When Alice and Bob are honest,
(2) When Bob is honest, the inequality
(3) holds for and .
When the protocol with (i) and (ii) is used for bit-string commitment, the conditions (a) and (c) guarantee (2) and (3) of (BIN), respectively, and the condition (b) guarantees (CON).
Now, we denote a noisy channel from a finite set to a finite set by using a set of distributions on . Winter et al [8, 9] considered the situation that Alice and Bob use the channel at times and the noiseless channel can be used freely. Winter et al [8, 9] defined the commitment capacity as the maximum rate when the code satisfies Concealing condition with and Binding condition with under the condition that the parameters and approach to zero as goes to infinity. They derived the commitment capacity under the following conditions for the channel ;
- (W1)
-
and are finite sets.
- (W2)
-
For any , the relation
(4) holds, where is the Kullback-Leibler divergence between two distributions and . This condition is called the non-redundant condition.
To state their result, we introduce a notation; Given a joint distribution on a discrete set , we denote the conditional distribution under the condition that . Then, the conditional entropy is given as
| (5) | ||||
| (6) |
When the joint distribution is given as by using a distribution , we denote the conditional entropy by . They showed the following proposition;
Proposition 1 ([8, Theorem 2], [9])
When the channel satisfies Conditions (W1) and (W2), the commitment capacity is given as
| (7) |
Many noisy channels are physically realized by wireless communication, and such channels have continuous output system . Indeed, if we apply discretization to a continuous output system , we obtain a discrete output system . When we apply their result to the channel with the discrete output system , the obtained protocol satisfies Condition (BIN) even when Bob uses the continuous output system . However, the obtained protocol does not satisfy Condition (CON) in general under the continuous output system .
In fact, Condition (W2) can be removed and Proposition 1 can be generalized as follows. Therefore, Condition (W2) can be considered as an assumption for simplifying our analysis.
Proposition 2
Assume that the channel satisfies Condition (W1). We define as
| (8) |
where expresses the convex hull of a set . Then, the commitment capacity is given as
| (9) |
Proposition 2 follows from Proposition 1 in the following way. Due to Condition (W1), the channel with input alphabet satisfies Condition (W2) as well as (W1). Hence, the commitment capacity is lower bounded by (9). Since any operation with the channel with input alphabet can be simulated with . Therefore, the commitment capacity is upper bounded by (9). Thus, we obtain Proposition 2.
III Various types of conditional entropies with general probability space
We focus on an input alphabet with finite cardinality, and denote the set of probability distributions on by . But, an output alphabet may have infinite cardinality and is a general measurable set. In this paper, the output alphabet is treated as a general probability space with a measure because this description covers the probability space of finite elements and the set of real values. Hence, when the alphabet is a discrete set including a finite set, the measure is chosen to be the counting measure. When the alphabet is a vector space over the real numbers , the measure is chosen to be the Lebesgue measure. Throughout this paper, we will use an upper case letter and corresponding lower case letter to stand for a probability measure and its density function. When we treat a probability distribution on the alphabet , it is restricted to a distribution absolutely continuous with respect to . In the following, we use the lower case to express the Radon-Nikodym derivative of with respect to the measure , i.e., the probability density function of so that . This kind of channel description covers many useful channels. For example, phase-shift keying (PSK) scheme of additive white Gaussian noise (AWGN) channels satisfies this condition. In addition, the capacity of AWGN channel with the energy constraint can be approximately achieved when the input alphabet for encoding is restricted to a finite subset of the set of real numbers.
For a distribution on and a general measure on , we define the Kullback–Leibler (KL) divergence and Rényi divergence of order .
When is a finite set and is a general probability space, the conditional entropy is defined as
| (10) |
This quantity can be written as
| (11) |
where is defined as . We focus on the following type of Rényi conditional entropy as [14, 15, 16]
| (12) |
is monotonically decreasing for [16, Lemma 7]. Hence, we have for . It is known that the maximum is attained by [16, Lemma 4]. Hence, when two pairs of variables and are independent, we have the additivity;
| (13) |
IV Problem setting
IV-A Our problem setting without explicit description of coding structure
To realize the requirements (a), (b), and (c) mentioned in Section I, we formulate the mathematical conditions for the protocol for a given channel from the discrete system to the other system with integers and security parameters . In the asymptotic regime, i.e., the case when the channel is used times and goes to infinity, the integers and go to infinity, which realizes the situation that the security parameters and approach to zero. Hence, when and is fixed, the security parameters cannot be chosen to be arbitrarily small. In the following, we describe the condition in an intuitive form in the first step. Later, we transform it into a coding-theoretic form because the coding-theoretic form matches the theoretical discussion including the proofs of our main results.
Alice sends her message via a noisy channel with an encoder , which is a map from to . Bob outputs the messages . The decoder is given as the following ; For , we choose a subset with .
Then, we impose the following conditions for an encoder and a decoder .
- (A)
-
Verifiable condition with . Any element satisfies
(14) - (B)
-
Equivocation version of concealing condition with . The inequality
(15) holds.
- (C)
-
Binding condition for honest Alice with . Any distinct pair satisfies
(16)
Now, we discuss how the code can be used for the task explained in Section I. Assume that Alice sends her message to Bob by using the encoder via noisy channel and Bob gets the list by applying the decoder at Step (i). At Step (ii), Alice sends her message to Bob via a noiseless channel. Verifiable condition (A) guarantees that her message belongs to Bob’s list. Hence, the requirement (a) is satisfied. Equivocation version of concealing condition (B) forbids Bob to identify Alice’s message at Step (i), hence it guarantees the requirement (b). In the asymptotic setting, this condition is weaker than Concealing condition (CON) when goes to zero and is smaller than . Hence, this relaxation enables us to exceed the rate (7) derived by [8, 9]. This type of relaxation is often used in wire-tap channel [17].
In fact, if is Alice’s message and there exists another element such that and are close to , Alice can make the following cheating as follows; She sends instead of at the phase (ii). Since Condition (C) forbids Alice such cheating, it guarantees the requirement (c). Hence, it can be considered as the binding condition for honest Alice. Further, Bob is allowed to decode less than messages. That is, is the maximum number that Bob can list as the candidates of the original message. However, Condition (C) assumes honest Alice who uses the correct encoder . Dishonest Alice can send an element different from such that and are close to . To cover such a case, we impose the following condition instead of Condition (C).
- (D)
-
Binding condition for dishonest Alice with . For , we define the quantity as the second largest value among . Then, any satisfies
(17)
In fact, Condition (D) implies that
| (18) |
Eq. (18) can be shown by contradiction due to the following relation;
| (19) |
The difference between Conditions (C) and (D) are summarized as follows. Condition (C) expresses the possibility that Alice makes cheating in the reveal phase while she behaves honestly in the commit phase. Condition (D) expresses the possibility that Alice makes cheating in the reveal phase when she behaves dishonestly even in the commit phase. Hence, it can be considered as the binding condition for dishonest Alice. Therefore, while the case with honest Alice and honest Bob is summarized in Fig. 1, the case with dishonest Alice and honest Bob is summarized in Fig. 2.
We consider another possibility for requirement (b) by replacing the conditional entropy by the conditional Rényi entropy of order .
- (B)
-
Rényi equivocation type of concealing condition of order with . The inequality
(20) holds.
Now, we observe how to characterize the code constructed to achieve the capacity in the paper [6]. For this characterization, we consider the following code when . We divide the messages into groups whose group is composed of messages. First, we prepare a code to transmit the message with size with a decoding error probability , where is the encoder and is the decoder. When the message belongs to the -th group, Alice sends . Using the decoder , Bob recovers . Then, Bob outputs elements that belongs to the -th group. In this code, the parameter is given as . Hence, it satisfies condition (B) with a good parameter. However, the parameters and become at least . Hence, this protocol essentially does not satisfy Biding condition (C) nor (D). In this way, our security parameter rules out the above trivial code construction.


IV-B Our setting with coding-theoretic description
To rewrite the above conditions in a coding-theoretic way, we introduce several notations. For and a distribution on , we define the distribution and on as and . Alice sends her message via noisy channel with a code , which is a map from to . Bob’ decoder is described as disjoint subsets such that . That is, we have the relation . In the following, we denote our decoder by instead of .
In particular, when a decoder has only one outcome as an element of it is called a single-element decoder. It is given as disjoint subsets such that . Here, remember that Winter et al [8, 9] assumes the uniform distribution on for the message in Binding condition.
Theorem 1
When the message is subject to the uniform distribution on in a similar way to Winter et al [8, 9], the conditions (A) – (D) for an encoder and a decoder are rewritten in a coding-theoretic way as follows.
- (A)
-
Verifiable condition.
(21) (22) where the above sum is taken under the condition .
- (B)
-
Equivocation version of concealing condition with .
(23) - (B)
-
Rényi equivocation type of concealing condition of order with .
(24) - (C)
-
Binding condition for honest Alice.
(25) (26) where the above sum is taken under the condition .
- (D)
-
Binding condition for dishonest Alice. For , we define the quantity as the second largest value among . Then, the relation
(27) holds.
Proof: For any and , the condition is equivalent to the condition . Since
we obtain the equivalence between the conditions (A) and (C) given in Section IV-A and those given here. In a similar way, the condition (17) is equivalent to the condition (27), which implies the desired equivalence with respect to the condition (D). Since is subject to the uniform distribution, (15) and (20) are equivalent to (23) and (24). In fact, since
, is calculated as , and is calculated as
| (28) |
Hence, we obtain the desired equivalence for the conditions (B) and (B).
In the following, when a code satisfies conditions (A), (B) and (D), it is called an code. Also, for a code , we denote and by and . Also, we allow a stochastic encoder, in which is a distribution on . In this case, for a function from to , expresses .
V Information quantities and regions with general probability space
V-A Information quantities
Section III introduced various types of conditional entropies with general probability space. This section introduces other types of information quantities with general probability space. In general, a channel from to is described as a collection of conditional probability measures on for all inputs . Then, we impose the above assumption to for any . Hence, we have . We denote the conditional probability density function by . When a distribution on is given by a probability distribution , and a conditional distribution on a set with the condition on is given by , we define the joint distribution on by , and the distribution on by for a measurable set . Also, we define the notations and as and . We also employ the notations and .
As explained in Section VI, we denote the expectation and the variance under the distribution by and , respectively. When is the distribution with , we simplify them as and , respectively. This notation is also applied to the -fold extended setting on . In contrast, when we consider the expectation on the discrete set or , expresses the expectation with respect to the random variable that takes values in the set or the set .
In our analysis, for , we address the following quantities;
| (29) | ||||
| (30) | ||||
| (31) |
where follows from the equality condition of Hölder inequality [18]. Since in this paper, the conditional distribution on conditioned with is fixed to the channel , it is sufficient to fix a joint distribution in the above notation. In addition, our analysis needs mathematical analysis with a Markov chain with a variable on a finite set . Hence, we generalize the above notation as follows.
| (32) | |||
| (33) |
and
| (34) |
V-B Regions
Then, we define the following regions.
| (42) | ||||
| (50) | ||||
| (58) |
In the above definitions, there is no restriction for the cardinality of . Due to the relations
| (59) |
and , Caratheodory lemma guarantees that the cardinality of can be restricted to in the definitions of and . In addition, the condition in the definition of is rewritten as
| (60) |
Since the relation holds, Caratheodory lemma guarantees that the cardinality of can be restricted to in the definition of .
To see the relation between two regions and , we focus on the inequality
| (61) |
in the region . Hence, the condition is stronger than the condition , which implies the relation;
| (62) |
When we focus only on and instead of , we have simpler characterizations. We define the regions;
| (63) | ||||
| (64) | ||||
| (65) |
Then, we have the following lemma.
Lemma 1
We have
| (66) | ||||
| (67) |
and
| (68) |
where and
| (69) | ||||
| (70) |
When is infinite, the condition is removed in the above equations.
Lemma 1 is shown in Appendix A. For the analysis on the above regions, we define the functions;
| (71) | ||||
| (72) |
Then, we have the following lemma.
Lemma 2
When is a concave function, we have . When is a concave function, we have .
Lemma 2 is shown in Appendix B. Using these two lemmas, we numerically calculate the regions , , and as Fig. 3.

Lemma 3
| (75) | ||||
| (76) |
VI Results for secure list decoding with discrete input
VI-A Statements of results
To give the capacity region, we consider -fold discrete memoryless extension of the channel . A sequence of codes is called strongly secure when and approach to zero. A sequence of codes is called weakly secure when and approach to zero. A rate triple is strongly deterministically (stochastically) achievable when there exists a strongly secure sequence of deterministic (stochastic) codes such that approaches to , approaches to 333The definitions of and are given in the end of Section IV-B., and . A rate triple is -strongly deterministically (stochastically) achievable when there exists a strongly secure sequence of deterministic (stochastic) codes such that approaches to , approaches to , and . A rate triplet is (-)weakly deterministically (stochastically) achievable when there exists a weakly secure sequence of deterministic (stochastic) codes such that approaches to , approaches to , and (). Then, we denote the set of strongly deterministically (stochastically) achievable rate triple by (). In the same way, we denote the set of weakly deterministically (stochastically) achievable rate triple by (). The -version with is denoted by , , , and , respectively.
As outer bounds of , , and , we have the following theorem.
Theorem 2
We have the following characterization.
| (77) |
where expresses the closure of the set .
For their inner bounds, we have the following theorem.
Theorem 3
Assume the condition (W2). (i) A rate triplet is strongly deterministically achievable when there exists a distribution such that
| (78) | ||||
| (79) | ||||
| (80) |
(ii) A rate triplet is -strongly deterministically achievable when there exists a distribution such that
| (81) | ||||
| (82) | ||||
| (83) |
In fact, the condition corresponds to Verifiable condition (A), the condition () does to (Rényi) equivocation type of concealing condition (B), and the condition does to the binding condition for dishonest Alice (D). Theorems 2 and 3 are shown in Sections IX and X, respectively. We have the following corollaries from Theorems 2 and 3.
Corollary 1
When Condition (W2) holds, we have the following relation for ;
| (84) |
and
| (85) |
Hence, even when our binding condition is relaxed to Condition (C), when our code is limited to deterministic codes, we have the same region as the case with Condition (D).
Proof: It is sufficient to show the direct part. For this aim, we notice that the following relation for ;
| (86) |
Hence, it is sufficient to show that there exists a strongly secure sequence of deterministic codes with the rate triplet to satisfy
| (87) | ||||
| (88) | ||||
| (89) |
for a given . There exist distributions such that and for , where . Then, we have , , and .
For simplicity, in the following, we consider the case with . We choose a sequence () of strongly secure deterministic codes that achieve the rates to satisfy (81), (82), and (83) with . We denote by . Then, we define the concatenation as follows. We assume that () is a map from () to (). The encoder is given as a map from to . The decoder is given as a map from to as
| (90) |
for . We have because the code is correctly decoded when both codes and are correctly decoded. Alice can cheat the decoder only when Alice cheats one of the decoders and . Hence, . Therefore, the concatenation is also strongly secure.
The rate tuples of the code is calculated as for . Also, using the additivity property (13), we have . Hence, we have shown the existence of a strongly secure sequence of deterministic codes with the rate triplet to satisfy the conditions (87), (88), and (89) when . For a general , we can show the same statement by repeating the above procedure.
VI-B Outline of proof of direct theorem
Here, we present the outline of the direct theorem (Theorem 3). Since , the first part (i) follows from the second part (ii). Hence, we show only the second part (ii) in Section X based on the random coding. To realize Binding condition for dishonest Alice (D), we need to exclude the existence of and such that and are far from 0. For this aim, we focus on Hamming distance between as
| (91) |
and introduce functions to satisfy the following conditions;
| (92) | |||
| (93) | |||
| (94) |
For and , we define
| (95) |
Then, given an encoder mapping to , we impose the following condition on Bob’s decoder to include the message in his decoded list; the inequality
| (96) |
holds when is observed. The condition (96) guarantees that is small when is larger than a certain threshold.
VII Results for secure list decoding with continuous input
In the previous section, we assume that Alice can access only elements of the finite set even when Alice is malicious. However, in the wireless communication case, the input system is given as a continuous space . When we transmit a message via such a channel, usually we fix the set of constellation points as a subset of , and the modulator converts an element of input alphabet to a constellation point. That is, the choice of the set depends on the performance of the modulator. In this situation, it is natural that dishonest Alice can send any element of the continuous space while honest Alice sends only an element of . Therefore, only the condition (D) is changed as follows because only the condition (D) is related to dishonest Alice.
- (D’)
-
Binding condition for dishonest Alice. For , we define the quantity as the second largest value among . Then, the relation
(97) holds.
Then, a sequence of codes is called ultimately secure when and approach to zero. A rate triple is ()-ultimately deterministically (stochastically) achievable when there exists a ultimately secure sequence of deterministic (stochastic) codes such that approaches to , approaches to , and (). We denote the set of ultimately deterministically (stochastically) achievable rate triple by (). The -version with is denoted by , , respectively.
The same converse result as Theorem 2 holds for and because a sequence of ultimately secure codes is strongly secure. Hence, the aim of this section is to recover the same result as Theorem 3 for ultimately secure codes under a certain condition for our channel. The key point of this problem setting is to exclude the existence of and such that and are far from 0. For this aim, we need to assume a distance on the space . Then, we may consider functions to satisfy the following conditions in addition to (92);
| (98) | |||
| (99) |
for . It is not difficult to prove the same result as Theorem 3 when the above functions exist. However, it is not so easy to prove the existence of the above functions under natural models including AWGN channel. Therefore, we introduce the following condition instead of (98) and (99).
- (W3)
-
There exist functions to satisfy the following conditions in addition to (92);
(100) (101) for and . Indeed, as discussed in Step 1 of our proof of Lemma 16, when functions satisfy the above conditions and the difference between two vectors and satisfy a certain condition, we can distinguish a vector from by using .
Notice that is monotonically increasing for .
That is, we have the following theorem.
Theorem 4
Assume the conditions (W2) and (W3). (i) A rate triplet is ultimately deterministically achievable when there exists a distribution such that
| (102) |
(ii) A rate triplet is -ultimately deterministically achievable when there exists a distribution such that
| (103) |
Since and , the combination of Theorems 2 and 4 yields the following corollary in the same way as Corollary 1.
Corollary 2
When Conditions (W2) and (W3) hold, we have the following relations
| (104) |
and
| (105) |
As an example, we consider an additive noise channel when , which equips the standard Euclidean distance . The output system is also given as . We fix a distribution for the additive noise on . Then, we define the additive noise channel as . We assume the following conditions;
| (106) | |||
| (107) |
Then, we have the following lemma.
Lemma 5
Proof: Since the range of in the condition (100) is , we assume thwe assume that the real number belongs to in this proof. The conditions (92) and (101) follow from (106) and (107), respectively.
| (108) |
For an small real number , we choose such that
| (109) |
We define the function from to such that . When satisfies , we have
| (110) |
Since , (109) and (110) imply that
| (111) |
Thus,
| (112) |
When , we have
| (113) |
Therefore,
| (114) |
Since for , the set is compact, and the map continuous, we find that . Hence, the quantity (114) is strictly positive.
VIII Application to bit-string commitment
VIII-A Bit-string commitment based on secure list decoding
Now, we construct a code for bit-string commitment by using our code for secure list decoding. (i) The previous studies [8, Theorem 2], [9] considered only the case with a discrete input alphabet and discrete output alphabet while a continuous generalization of their result was mentioned as an open problem in [9]. We allow a continuous output alphabet with a discrete input alphabet . (ii) As another setting, we consider the continuous input alphabet . In this case, it is possible to make the capacity infinite, as pointed by the paper [25] in the case of the Gaussian channel. However, it is difficult to manage an input alphabet with infinitely many cardinality. Hence, we consider a restricted finite subset of the continuous input alphabet so that honest Alice accesses only a restricted finite subset of the continuous input alphabet and dishonest Alice accesses the continuous input alphabet .
Since the binding condition (BIN) is satisfied by Condition (D) or (D’), it is sufficient to strengthen Condition (B) to Concealing condition (CON). For this aim, we combine a hash function and a code for secure list decoding. A function from to is called a regular hash function when is surjective and the cardinality does not depend on . When a code and a regular hash function are given, as explained in Fig. 4, we can naturally consider the following protocol for bit-string commitment with message set . Before starting the protocol, Alice and Bob share a code and a regular hash function .
- (I)
-
(Commit Phase) When is a message to be sent by Alice, she randomly chooses an element subject to uniform distribution on . Then, Alice sends to Bob via a noisy channel.
- (II)
-
(Reveal Phase) From Bob’s receiving information in Commit Phase, Bob outputs elements of as the list. Alice sends to Bob via a noiseless channel. The list is required to contain the message . If the transmitted information via the noiseless channel is contained in Bob’s decoded list, Bob accepts it, and recovers the message . Otherwise, Bob rejects it.
The binding condition (BIN) is evaluated by the parameter , , or . To discuss the concealing condition (CON), for a deterministic encoder for secure list decoding, we define the conditional distribution and the distribution on as
| (116) | ||||
| (117) |
When is given as a stochastic encoder by distributions on , these are defined as
| (118) | ||||
| (119) |
The concealing condition (CON) is evaluated by the following quantity;
| (120) |
Therefore, we say that the tuple is a code for bit-string commitment based on secure list decoding. Then, we have the following theorem, which is shown in Section VIII-B.
Theorem 5
For a code of secure list code with message set , we assume that the size is a power of a prime , i.e., . Then, for an integer and a set with , there exist a subset with , a subset with , and a regular hash function from to such that and
| (121) |
For a code for bit-string commitment based on secure list coding, we define three parameters , , and . To discuss this type of code in the asymptotic setting, we make the following definitions. A sequence of codes for bit-string commitment based on secure list coding is called strongly (weakly, ultimately) secure when , , and (, ) approach to zero. A rate triple is strongly (weakly, ultimately) deterministically achievable for bit-string commitment based on secure list coding when there exists a strongly (weakly, ultimately) secure deterministically sequence of codes such that for . We denote the set of strongly (weakly, ultimately) deterministically achievable rate triple for bit-string commitment based on secure list coding by (, ). We define strongly (weakly, ultimately) stochastically achievable rate triple for bit-string commitment based on secure list coding in the same way. Then, we denote the set of strongly (weakly, ultimately) stochastically achievable rate triple for bit-string commitment based on secure list coding by (, ). Then, we have
| (122) |
for . We obtain the following theorem under the above two settings.
Theorem 6
(i) Assume that the input alphabet is discrete. When Condition (W2) holds, we have the following relations for .
| (123) |
(ii) Assume that the input alphabet is continuous. We choose a restricted finite subset of the continuous input alphabet . When the channel with satisfies Conditions (W2) and (W3), we have the following relations
| (124) |
Also, we define the optimal transmission rate in the above method as
| (125) |
for . Then, Lemma 3, Theorem 6, and (122) imply the relation
| (126) |
for under the same assumption as Theorem 6. Here, we cannot determine only because the restriction for Alice is too weak in the setting , i.e., Alice is allowed to use a stochastic encoder and Alice’s cheating is not possible only when Alice uses the correct encoder. Fig. 5 shows the numerical plot for AWGN channel with binary phase-shift keying (BPSK) modulation.
Since our setting allows the case with the continuous input and output systems, Theorem 6 can be considered as a generalization of the results by Winter et al [8, Theorem 2], [9] while a continuous generalization of their result was mentioned as an open problem in [9]. Although the paper [25] addressed the Gaussian channel, it considers only the special case when the cardinality of the input alphabet is infinitely many. It did not derive a general capacity formula with a finite input alphabet and a continuous output alphabet. At least, the paper [25] did not consider the case when honest Alice accesses only a restricted finite subset of the continuous input alphabet and dishonest Alice accesses the continuous input alphabet .
In addition to Theorem 5, to show Theorem 6, we prepare the following lemma, which is shown in Section VIII-C.
Lemma 6
When a sequence of codes for bit-string commitment based on secure list coding satisfies the condition , we have
| (127) |
Proof of Theorem 6: The converse part of Theorem 6 follows from the combination of Theorem 2 and Lemma 6, which is shown in Section VIII-C.
The direct part of Theorem 6 can be shown as follows. For a given , the combination of Theorem 5 and Corollary 1 implies . Taking the limit , we have . In the same way, using Theorem 5 and Corollary 2, we can show . ∎

VIII-B Randomized construction (Proof of Theorem 5)
To show Theorem 5, we treat the set of messages as a vector space over the finite field . For a linear regular hash function from to and a code , we define the following value;
| (128) |
where the inequality follows from the triangle inequality. We denote the joint distribution of and by when is assumed to be subject to the uniform distribution on . Then, the definition of is rewritten as
| (129) |
In the following, we employ a randomized construction. That is, we randomly choose a linear regular hash function from to , where is a random seed to identify the function . A randomized function is called a universal2 hash function when the collision probability satisfies the inequality
| (130) |
When is subject to the uniform distribution on , the stochastic behavior of can be simulated as follows. First, is generated according to the uniform distribution on . Then, the obtained outcome of with a fixed is subject to the uniform distribution on . When is a universal2 hash function with a variable , the Rényi conditional entropy version of universal hashing lemma [21, (67)][22, Lemma 27] [16, Proposition 21] implies that
| (131) |
Hence, there exists an element such that
| (132) |
Due to Markov inequality, there exists a subset with cardinality such that any element satisfies that
| (133) |
This is because the number of elements that does not satisfy (133) is upper bounded by . Hence, any elements satisfy that
| (134) |
The combination of (132) and (134) imply that any elements satisfy that
| (135) |
Choosing to be , we find that (135) is the same as (121) due to the definition (120).
VIII-C Proof of Lemma 6
To show Lemma 6, we prepare the following proposition.
Proposition 3 ([22, Lemma 30])
Any function defined on and a joint distribution on satisfy the following inequality
| (136) |
We focus on the joint distribution when Alice generates according to the uniform distribution on and chooses as . Let be the probability . Then, the conditional entropy is lower bounded as
| (137) |
The quantity is evaluated as
| (138) |
where follows from Proposition 3. Hence, we have . Applying this relation to (137), we have
| (139) |
Therefore,
| (140) |
Choosing , we have
| (141) |
Dividing the above by and taking the limit, we have (127).
IX Proof of Converse Theorem
In order to show Theorem 2, we prepare the following lemma.
Lemma 7
For , we choose the joint distribution . Let be the channel output variables of the inputs via the channel . Then, using the chain rule, we have
| (142) | ||||
| (143) |
Proof of Theorem 2: The proof of Theorem 2 is composed of two parts. The first part is the evaluation of . The second part is the evaluation of . The key point of the first part is the use of (143) in Lemma 7. The key point of the second part is the meta converse for list decoding [6, Section III-A].
Step 1: Preparation.
We show Theorem 2 by showing the following relations;
| (144) | ||||
| (145) |
because follows from (144). Assume that a sequence of deterministic codes is weakly secure. We assume that converges for . For the definition of , see the end of Section IV-B. Also, we assume that .
Letting be the random variable of the message, we define the variables . The random variables are defined as the output of the channel , which is the times use of the channel . Choosing the set , we define the joint distribution as follows; for .
Under the distribution , we denote the channel output by . In this proof, we use the notations and . Also, instead of , we employ , which goes to zero.
Step 2: Evaluation of .
When a code satisfies , we have
| (146) |
where follows from (143) in Lemma 7 and the variable is defined in Step 1. Dividing the above by and taking the limit, we have
| (147) |
To show in (146), we consider the following protocol. After converting the message to by the encoder , Alice sends the to Bob times. Here, we choose to be an arbitrary large integer. Applying the decoder , Bob obtains lists that contain up to messages. Among these messages, Bob chooses as the element that most frequently appears in the lists. When , the element has the highest probability to be contained in the list. In this case, when is sufficiently large, Bob can correctly decode by this method because is the probability that the list contains and is the maximum of the probability that the list contains . Therefore, when , the probability of the failure of decoding goes to zero as . Fano inequality shows that . Then, we have
| (148) | ||||
| (149) |
which implies in (146) with the limit .
Step 3: Evaluation of .
Now, we consider the hypothesis testing with two distributions and on , where . Then, we define the region as . Using the region as our test, we define as the error probability to incorrectly support while the true is . Also, we define as the error probability to incorrectly support while the true is . When we apply the monotonicity for the KL divergence between and , dropping the term , we have
| (150) |
where is the binary entropy, i.e., . The meta converse for list decoding [6, Section III-A] shows that and . Since (143) in Lemma 7 guarantees that , the relation (150) is converted to
| (151) |
under the condition that . Dividing the above by and taking the limit, we have
| (152) |
Step 4: Evaluation of .
Since the code is deterministic, remembering the definition of the variable given in Step 1, we have
| (153) |
Dividing the above by and taking the limit, we have
| (154) |
Therefore, combining Eqs. (147), (152), and (154), we obtain Eq. (144).
Step 5: Proof of Eq. (145).
Assume that a sequence of stochastic codes is strongly secure. Then, there exists a sequence of deterministic encoders such that and . Since and go to zero, we have Eqs. (147) and (152). However, the derivation of (154) does not hold in this case. Since the code is stochastic, the equality does not hold in general.
X Proof of direct theorem
As explained in Section VI-B, we show only the second part (ii) based on the random coding. First, we show Lemma 4. Then, using Lemma 4, we show the second part (ii) by preparing various lemmas, Lemmas 10, 11, 12 and 13. Using Lemmas 11, and 12, we extract an encoder and messages that have a small decoding error probability and satisfy two conditions, which will be stated as the conditions (188) and (205). Then, using these two conditions, we show that the code satisfies the binding condition for dishonest Alice (D) and the equivocation version of concealing condition (B). In particular, Lemma 10 is used to derive the binding condition for dishonest Alice (D).
X-A Proof of Lemma 4
Step 1: For our proof of Lemma 4, we prepare the following lemma.
Lemma 8
Let be a closed convex subset of . Assume that a distribution has the full support . We choose as
| (159) |
(i) We have for . (ii) For , we have
| (160) |
Proof: Now, we show (i) by contradiction. We choose such that . We define the distribution . Then, we have
| (161) |
where . The derivative of for at is a finite value. For , the derivative of for at is a finite value. For , the derivative of for at is . Hence, the derivative of for at is . It means that there exist a small real number such that . Hence, we obtain a contradiction.
Next, we show (ii). Theorem 11.6.1 of [26] shows the following.
| (162) |
which implies
| (163) |
Hence, we obtain (160).
Step 2: We prove Lemma 4 when is a finite set and the support of does not depend on .
For , we define the distribution as
| (164) |
We choose as , which satisfies (92). Applying (ii) of Lemma 8 to the case when is , we have
| (165) |
Hence, it satisfies (93). Since the support of does not depend on , the function takes a finite value. Since is a finite set, exists. Thus, it satisfies (94).
Step 3: We prove Lemma 4 when is a finite set and the support of depends on .
For an element and a small real number , we define as
| (168) |
where is the support of the distribution . We define
| (169) |
We choose to be sufficiently small such that
| (170) | ||||
| (171) |
for any .
When , we have due to (i) of Lemma 8. Then,
| (172) |
Then, we define as
| (173) |
Then, we have
| (174) | |||
| (175) | |||
| (176) |
When , we have due to (i) of Lemma 8 because has the full support . Then, we define as
| (177) |
for , and
| (178) |
for . Then, we have (174), (175), and (176). Therefore, our functions satisfy the conditions (92), (93), and (94).
Step 4: We prove Lemma 4 when is not a finite set. Since the channel satisfies Condition (W2), there exists a map from to a finite set such that the channel satisfies Condition (W2), where for . Applying the result of Step 3 to the channel , we obtain functions defined on . Then, for , we choose a function on as . The functions satisfy the conditions (92), (93), and (94).
X-B Preparation
To show Theorem 3, we prepare notations and information quantities. For and , we define
| (179) | ||||
| (180) |
Then, we have the Legendre transformation
| (181) |
Using the -neighborhood of with respect to the variational distance, we define
| (182) |
Then, we have the following lemma, which is shown in Appendix D.
Lemma 9
| (183) |
| (184) |
For , we choose , , and to satisfy the conditions (81), (82), and (83). For our decoder construction, we choose three real numbers and . The real number is chosen as
| (185) |
Using Lemma 9, we choose such that
| (186) |
Then, we choose to satisfy
| (187) |
Next, we fix the size of message , the list size , and a number , which is smaller than the message size . For , we define for . We prepare the decoder used in this proof as follows.
Definition 1 (Decoder )
Given a distribution on , we define the decoder for a given encoder (a map from to ) in the following way. Using the condition (96), we define the subset . Then, for , we choose up to elements as the decoded messages such that for .
Remember that, for , Hamming distance is defined to be the number of such that in Subsection VI-B. In the proof of Theorem 3, we need to extract an encoder and elements that satisfies the following condition;
| (188) |
For this aim, given a code and a real number , we define the function from to as
| (191) |
As shown in Section X-D, we have the following lemma.
Lemma 10
When a code defined in a subset satisfies
| (192) |
for two distinct elements , the decoder defined in Definition 1 satisfies
| (193) |
X-C Proof of Theorem 3
Step 1: Lemmas related to random coding.
To show Theorem 3, we assume that the variable for is subject to the distribution independently. Then, we have the following four lemmas, which are shown later. In this proof, we treat the code as a random variable. Hence, the expectation and the probability for this variable are denoted by and , respectively.
Lemma 11
When
| (194) |
we have the average version of Verifiable condition (A), i.e.,
| (195) |
Lemma 12
For , we have
| (196) |
Lemma 13
We choose as
| (197) |
We have
| (198) |
Step 2: Extraction of an encoder and messages with a small decoding error probability that satisfies the condition (188).
We define as
| (199) |
Lemmas 11 and 12 guarantees that . Then, there exists a sequence of codes such that
| (200) | |||
| (201) |
Due to Eq. (200), Markov inequality guarantees that there exist elements such that every element satisfies
| (202) |
which implies that
| (203) | ||||
| (204) |
because takes value 0 or 1. Then, we define a code on as for . Eq. (203) guarantees Condition (A). Eq. (201) guarantees that
| (205) |
Step 3: Proof of the binding condition for dishonest Alice (D).
The relation (204) guarantees the condition
| (206) |
for . Therefore, Lemma 10 guarantees the binding condition for dishonest Alice (D), i.e.,
| (207) |
Step 4: Proof of the equivocation version of concealing condition (B).
X-D Proof of Lemma 10
Step 1: Evaluation of .
X-E Proof of Lemma 11
Lemma 14
We have the following inequality;
| (216) |
Proof: When is sent, there are two cases for incorrect decoding. The first case is the case that the received element does not belong to . The second case is the case that there are more than elements to satisfy . In fact, the second case does not always realize incorrect decoding. However, the sum of the probabilities of the first and second cases upper bounds the decoding error probability . Hence, it is sufficient to evaluate these two probabilities. The error probability of the first case is given in the first term of Eq. (216). The error probability of the second case is given in the second term of Eq. (216).
Taking the average in (216) of Lemma 14 with respect to the variable , we obtain the following lemma. The following discussion employs the notations and , which are defined in the middle of Section V.
Lemma 15
We have the following inequality;
| (217) |
Applying Lemma 15, we have
| (218) |
where follows from the relation
The variable is the mean of independent variables that are identical to the variable whose average is . The variable is the mean of independent variables that are identical to the variable whose average is . Thus, the law of large number guarantees that the first and the second terms in (218) approaches to zero as goes to infinity. The third term in (218) also approaches to zero due to the assumption (185). Therefore, we obtain Eq. (195).
X-F Proof of Lemma 13
X-G Proof of Lemma 12
The outline of the proof of Lemma 12 is the following. To evaluate the value , we convert it to the sum of certain probabilities. We evaluate these probabilities by excluding a certain exceptional case. That is, we show that the probability of the exceptional case is small and these probabilities under the condition to exclude the exceptional case is also small. The latter will be shown by evaluating a certain conditional probability. For this aim, we choose such that and .
Step 1: Evaluation of a certain conditional probability.
We denote the empirical distribution of by . That is, is the number of index to satisfy . Hence, when are independently subject to ,
| (220) |
We define two conditions and for the encoder as
-
.
-
.
The aim of this step is the evaluation of the conditional probability that expresses the probability that the condition holds under the condition .
We choose . Markov inequality implies that
| (221) |
where and are the conditional probability and the conditional expectation for the random variable with the fixed variable . The final equation follows from (220). When the fixed variable satisfies the condition , taking the infimum with respect to , we have
| (222) |
Hence,
| (223) |
where expresses the random variables . Then, we have
| (224) |
Step 2: Evaluation of .
XI Proof of Theorem 4
XI-A Main part of proof of Theorem 4
Hamming distance plays a central role in our proof of Theorem 3. However, since elements of can be sent by dishonest Alice, Hamming distance does not work in our proof of Theorem 4. Hence, we introduce an alternative distance on . We modify the distance on as
| (227) |
where
| (228) |
Then, we define
| (229) |
which is the same as Hamming distance on . Instead of Lemma 10, we have the following lemma.
Lemma 16
When a code defined in a subset satisfies
| (230) |
for two distinct elements , the decoder defined in Definition 1 satisfies
| (231) |
XI-B Proof of Lemma 16
Step 1: Evaluation of .
As shown in Step 3, when , for , we have
| (233) |
Applying Markov inequality to the variable , we have
| (234) |
The condition (92) implies that
| (235) |
The condition (101) implies that
| (236) |
Hence, applying Chebyshev inequality to the variable , we have
| (237) |
Hence, we have
| (241) | ||||
| (242) |
where follows from the fact that the conditions and imply the condition , and follows from (234) and (237).
Step 2: Evaluation of smaller value of and . We simplify and to and . Since Eq. (230) implies
| (243) |
we have
| (244) |
Since is monotonically increasing for , (244) yields
| (245) |
Thus,
| (246) |
where follows (242), and follows from (245). Eq. (246) implies (231), i.e., the desired statement of Lemma 16.
Step 3: Proof of (233). To show (233), we consider the random variable subject to the uniform distribution on . The quantity can be considered as a non-negative random variable whose expectation is . We apply the Markov inequality to the variable . Then, we have
| (247) |
where the final inequality follows from the relation between arithmetic and geometric means. Hence, we have
| (248) |
XII Conclusion
We have proposed a new concept, secure list decoding, which imposes additional requirements on conventional list decoding to work as a relaxation of bit-string commitment. This scheme has three requirements. Verifiable condition (A), Equivocation version of concealing condition (B), and Binding condition. Verifiable condition (A) means that the message sent by Alice (sender) is contained in the list output by Bob (receiver). Equivocation version of concealing condition (B) is given as a relaxation of the concealing condition of bit-string commitment. That is, it expresses Bob’s uncertainty of Alice’s message. Binding condition has two versions. One is the condition (C) for honest Alice. The other is the condition (D) for dishonest Alice. Since there is a possibility that dishonest Alice uses a different code, we need to guarantee the impossibility of cheating even for such a dishonest Alice. In this paper, we have shown the existence of a code to satisfy these three conditions. Also, we have defined the capacity region as the possible triplet of the rates of the message and the list, and the equivocation rate, and have derived the capacity region when the encoder is given as a deterministic map. Under this condition, we have shown that the conditions (C) and (D) have the same capacity region. However, we have not derived the capacity region when the stochastic encoder is allowed. Therefore, the characterization of the capacity region of this case is an interesting open problem.
As the second contribution, we have formulated the secure list decoding with a general input system. For this formulation, we have assumed that honest Alice accesses only a fixed subset of the general input system and dishonest Alice can access any element of the general input system. Then, we have shown that the capacity region of this setting is the same as the capacity region of the above setting when the encoder is limited to a deterministic map.
As the third contribution, we have proposed a method to convert a code for secure list decoding to a protocol for bit-string commitment. Then, we have shown that this protocol can achieve the same rate of the message size as the equivocation rate of the original code for secure list decoding. This method works even when the input system is a general probability space and dishonest Alice can access any element of the input system. Since many realistic noisy channels have continuous input and output systems, this result extends the applicability of our method for bit-string commitment.
Since the constructed code in this paper is based on random coding, it is needed to construct practical codes for secure list decoding. Fortunately, the existing study [3] systematically constructed several types of codes for list decoding with their algorithms. While their code construction is practical, in order to use their constructed code for secure list decoding and bit-string commitment, we need to clarify their security parameters, i.e., the equivocation rate and the binding parameter for dishonest Alice in addition to the decoding error probability . It is a practical open problem to calculate these security parameters of their codes.
Acknowledgments
The author is grateful to Dr. Vincent Tan, Dr. Anurag Anshu, Dr. Seunghoan Song, and Dr. Naqueeb Warsi for helpful discussions and helpful comments. In particular, Dr. Naqueeb Warsi informed me the application of Theorem 11.6.1 of [26]. The work reported here was supported in part by Guangdong Provincial Key Laboratory (Grant No. 2019B121203002), Fund for the Promotion of Joint International Research (Fostering Joint International Research) Grant No. 15KK0007, the JSPS Grant-in-Aid for Scientific Research (A) No.17H01280, (B) No. 16KT0017, and Kayamori Foundation of Informational Science Advancement K27-XX-46.
Appendix A Proof of Lemma 1
Step 1: Preparation.
We define the functions
| (249) | ||||
| (250) | ||||
| (251) | ||||
| (252) | ||||
| (253) | ||||
| (254) |
Then, it is sufficient to show the following relations;
| (255) | ||||
| (256) | ||||
| (257) |
Since the second equations in (255) and (257) follows from the definitions, it is sufficient to show the first equations in (255) and (257). From the definitions, we have
| (260) | ||||
| (263) | ||||
| (266) |
Hence, (263) implies (256). To show (255) and (257), we derive the following relations from (260) and (266).
| (267) | ||||
| (268) |
Step 2: Proof of (255).
Given , we choose . We have . As shown later, when , we have
| (269) |
We choose and such that or . Given , we define the distribution as
| (270) | ||||
| (271) |
for . We have . In particular, when is sufficiently close to , there exists such that . Then,
| (272) |
Then, we find that is monotonically increasing for .
Also, we have
| (273) |
where the condition is given as . Since is monotonically increasing for , (273) guarantees that is also monotonically increasing for . Hence, (267) yields (255), respectively.
Step 3: Proof of (269).
Assume that there exist such that and the condition (269) does not hold. We define the distribution as follows.
| (274) | ||||
| (275) |
for . Then,
which implies (269).
Step 4: Proof of (269).
Instead of and , we define
| (276) | ||||
| (277) |
Given , we choose . We choose . We have
| (278) |
In the same way as (269), when , we have
| (279) |
In the same way as the case with , we can show that is monotonically increasing for . Hence, in the same way as the case with , we can show that is monotonically increasing for . Therefore, is monotonically increasing for . Hence, (268) yields (257).
Appendix B Proof of Lemma 2
The first statement follows from (59). The second statement can be shown as follows. Assume that is a concave function. We choose
| (280) |
Then, we have
where follows from the concavity of and the relation
follows from the definition of , and follows from the assumption that is a concave function. Hence, we have .
Appendix C Lemma 7
Appendix D Proof of Lemma 9
When is sufficiently large and is small, we have
| (285) |
Under the above approximation, the minimum with respect to is realized when . Hence, the minimum is approximated to . This value goes to when goes to . Hence, we have (183).
Also, we have
| (286) |
For each , the is bounded even when goes to infinity. Hence, we have
| (287) |
which implies (184).
References
- [1] P. Elias, “List decoding for noisy channels,” in WESCON Conv. Rec., 1957, pp. 94- 104.
- [2] J.M. Wozencraft, “List decoding,” Quart. Progr. Rep. Res. Lab. Electron., MIT, Cambridge, MA Vol. 48, 1958.
- [3] V. Guruswami, “Algorithmic results in list decoding,” Foundations and Trends in Theoretical Computer Science, Vol. 2, No. 2, 107–195 (2007).
- [4] S. Nishimura. “The strong converse theorem in the decoding scheme of list size ,” Kōdai Math. Sem. Rep., 21, 418–25, (1969).
- [5] R. Ahlswede, “Channel capacities for list codes,” J. Appl. Probab., vol. 10, 824–836, 1973.
- [6] M. Hayashi, “Channel capacities of classical and quantum list decoding,” arXiv:quant-ph/0603031.
- [7] C. Crépeau, “Efficient Cryptographic Protocols Based on Noisy Channels,” Advances in Cryptology: Proc. EUROCRYPT 1997 , pp. 306–317, Springer 1997.
- [8] A. Winter, A. C. A. Nascimento, and H. Imai, “Commitment Capacity of Discrete Memoryless Channels,” Proc. 9th IMA International Conferenece on Cryptography and Coding (Cirencester 16-18 December 2003), pp. 35-51, 2003.
- [9] H. Imai, K. Morozov, A. C. A. Nascimento, and A. Winter, “Efficient Protocols Achieving the Commitment Capacity of Noisy Correlations,” Proc. IEEE ISIT 2006, pp. 1432-1436, July 6-14, 2006.
- [10] H. Yamamoto and D. Isami, “Multiplex Coding of Bit Commitment Based on a Discrete Memoryless Channel,” Proc. IEEE ISIT 2007, pp. 721-725, June 24-29, 2007.
- [11] V. Y. F. Tan and M. Hayashi, “Analysis of remaining uncertainties and exponents under various conditional Rényi entropies,” IEEE Transactions on Information Theory, Volume 64, Issue 5, 3734 – 3755 (2018).
- [12] L. Yu and V. Y. F. Tan, “Rényi Resolvability and Its Applications to the Wiretap Channel,” IEEE Transactions on Information Theory, Volume 65, Issue 3, 1862 – 1897 (2019).
- [13] M. Hayashi, “Secure list decoding” Proc. IEEE International Symposium on Information Theory (ISIT2019), Paris, France, July 7 – 12, 2019, pp. 1727 – 1731; https://arxiv.org/abs/1901.02590.
- [14] S. Arimoto, “Information measures and capacity of order for discrete memoryless channels,” Colloquia Mathematica Societatis János Bolyai, 16. Topics in Information Theory 41–52 (1975)
- [15] M. Iwamoto and J. Shikata, “Information theoretic security for encryption based on conditional Rényi entropies,” Information Theoretic Security (Lecture Notes in Computer Science), vol. 8317. Berlin, Germany: Springer, 2014, pp. 103–121.
- [16] M. Hayashi, “Security analysis of epsilon-almost dual universal2 hash functions: smoothing of min entropy vs. smoothing of Renyi entropy of order 2,” IEEE Trans. Inform. Theory, 62(6) 3451 – 3476 (2016).
- [17] I. Csiszár and J. Körner, “Broadcast channels with confidential messages,” IEEE Trans. Inform. Theory, 24(3) 339 – 348 (1978).
- [18] R. Sibson, “Information radius,” Z. Wahrscheinlichkeitstheorie und Verw. Geb., vol. 14, pp. 149–161, 1969.
- [19] L. Carter and M. Wegman, “Universal classes of hash functions,” J. Comput. System Sci., vol. 18(2), 143–154 (1979).
- [20] M. N. Wegman and J. L. Carter, “New Hash Functions and Their Use in Authentication and Set Inequality,” J. Comput. System Sci., 22, 265-279 (1981).
- [21] M. Hayashi, “Tight exponential analysis of universally composable privacy amplification and its applications,” IEEE Trans. Inform. Theory, 59(11) 7728 – 7746 (2013).
- [22] M. Hayashi and S. Watanabe, “Uniform Random Number Generation from Markov Chains: Non-Asymptotic and Asymptotic Analyses,” IEEE Trans. Inform. Theory, 62(4) 1795 – 1822 (2016).
- [23] S. Verdú and T. S. Han, “A general formula for channel capacity,” IEEE Trans. Inform. Theory, 40(6) 1147–1157, (1994).
- [24] M. Hayashi and H. Nagaoka, “General formulas for capacity of classical-quantum channels,” IEEE Trans. Inform. Theory, 49(7), 1753–1768 (2003).
- [25] A. C. A. Nascimento, J. Barros, S. Skludarek and H. Imai, “The Commitment Capacity of the Gaussian Channel Is Infinite,” IEEE Trans. Inform. Theory, 54(6), 2785 – 2789 (2008).
- [26] T. M. Cover and J. A. Thomas, Elements of Information Theory: Second Edition, New York Wiley-Interscience (2006).
| Masahito Hayashi (Fellow, IEEE) was born in Japan in 1971. He received the B.S. degree from the Faculty of Sciences in Kyoto University, Japan, in 1994 and the M.S. and Ph.D. degrees in Mathematics from Kyoto University, Japan, in 1996 and 1999, respectively. He worked in Kyoto University as a Research Fellow of the Japan Society of the Promotion of Science (JSPS) from 1998 to 2000, and worked in the Laboratory for Mathematical Neuroscience, Brain Science Institute, RIKEN from 2000 to 2003, and worked in ERATO Quantum Computation and Information Project, Japan Science and Technology Agency (JST) as the Research Head from 2000 to 2006. He worked in the Graduate School of Information Sciences, Tohoku University as Associate Professor from 2007 to 2012. In 2012, he joined the Graduate School of Mathematics, Nagoya University as Professor. In 2020, he joined Shenzhen Institute for Quantum Science and Engineering, Southern University of Science and Technology, Shenzhen, China as Chief Research Scientist. In 2011, he received Information Theory Society Paper Award (2011) for “Information-Spectrum Approach to Second-Order Coding Rate in Channel Coding”. In 2016, he received the Japan Academy Medal from the Japan Academy and the JSPS Prize from Japan Society for the Promotion of Science. In 2006, he published the book “Quantum Information: An Introduction” from Springer, whose revised version was published as “Quantum Information Theory: Mathematical Foundation” from Graduate Texts in Physics, Springer in 2016. In 2016, he published other two books “Group Representation for Quantum Theory” and “A Group Theoretic Approach to Quantum Information” from Springer. He is on the Editorial Board of International Journal of Quantum Information and International Journal On Advances in Security. His research interests include classical and quantum information theory and classical and quantum statistical inference. |