Secure Federated Clustering
Abstract
We consider a foundational unsupervised learning task of -means data clustering, in a federated learning (FL) setting consisting of a central server and many distributed clients. We develop SecFC, which is a secure federated clustering algorithm that simultaneously achieves 1) universal performance: no performance loss compared with clustering over centralized data, regardless of data distribution across clients; 2) data privacy: each client’s private data and the cluster centers are not leaked to other clients and the server. In SecFC, the clients perform Lagrange encoding on their local data and share the coded data in an information-theoretically private manner; then leveraging the algebraic structure of the coding, the FL network exactly executes the Lloyd’s -means heuristic over the coded data to obtain the final clustering. Experiment results on synthetic and real datasets demonstrate the universally superior performance of SecFC for different data distributions across clients, and its computational practicality for various combinations of system parameters. Finally, we propose an extension of SecFC to further provide membership privacy for all data points.
1 Introduction
Federated learning (FL) is an increasingly popular distributed learning paradigm, which enables decentralized clients to collaborate on training an AI model over their private data collectively, without surrendering the private data to a central cloud. When running the FedAvg algorithm introduced in [1], each client trains a local model with its private data, and sends the local model to a central server for further aggregation into a global model. Since its introduction, FL has demonstrated great potential in improving the performance and security of a wide range of learning problems, including next-word prediction [2], recommender systems [3], and predictive models for healthcare [4].
In this work, we focus on a foundational unsupervised learning task - clustering. In an FL system, the clustering problem can be categorized into client clustering and data clustering. Motivated by heterogeneous data distribution across clients and the needs for training personalized models [5, 6, 7], client clustering algorithms are developed to partition the clients into different clusters to participate in training of different models [8, 9, 10, 11]. On the other hand, data clustering problem aims to obtain a partition of data points distributed on FL clients, such that some clustering loss is minimized. In [12], a model-based approach UIFCA was proposed to train a generative model for each cluster, such that each data point can be classified into one of the clusters using the models. Another recent work [13] considers the classical -means clustering problem, and proposed an algorithm -FED to approximately execute the Lloyd’s heuristic [14] in the FL setting. -FED is communication-efficient as it only requires one-shot communication from the clients to the server.
While being the state-of-the-art federated data clustering algorithms, both UIFCA and -FED are observed to be limited in the following two aspects: 1) The clustering performance heavily depends on the data distribution across clients. Specifically, the clustering performance of -FED is guaranteed only when the data points on each client are from at most clusters, and a non-empty cluster at each client has to contain a minimum number of points; 2) Leakage of data privacy. Just like other model-based FL algorithms, the data privacy of UIFCA is subject to model inversion attacks (see, e.g., [15, 16, 17, 18]). In -FED, each client performs Lloyd’s algorithm on local data, and sends the local cluster centers that are averages of private data points directly to the server, which allows a curious server to infer about the private dataset (e.g., number of local clusters, and the distribution of local data points).
Motivated by these limitations, we develop a secure federated clustering protocol named SecFC, for solving a -means clustering problem over an FL network. SecFC builds upon the classical Lloyd’s heuristic and has the following salient properties:
-
•
Universal performance: The clustering performance of SecFC matches exactly that of running Lloyd on the collection of all clients’ data in a centralized manner, which is invariant to different data distributions at the clients;
-
•
Information-theoretical data privacy: Each client’s private data is information-theoretically private from a certain number of colluding clients. The server does not know the values of the private data points and the cluster centers.
In the first phase of SecFC, each client locally generates some random noises and mixes them with its private data using Lagrange polynomial encoding [19], and then securely shares the coded data segments with the other clients. In the second phase, the clients and the server jointly execute the Lloyd’s iterations over coded data. As each client obtains a coded version of the entire dataset in the first phase, leveraging the algebraic structure of the coding scheme, each client can compute a secret share of the distance between each pair of cluster center and data point. After receiving sufficient number of secret shares, the server is able to reveal the pair-wise distances between all cluster centers and all data points, so the center update can be carried out exactly as specified in the Lloyd’s algorithm. Importantly, the server can only recover the distance between a cluster center and a data point, without knowing their respective locations, which is the key enabler for SecFC to achieve performance and privacy simultaneously. We further extend SecFC to strengthen it with membership privacy. Specifically, clients privately align the IDs of their local data using private set union [20, 21, 22], such that data clustering is performed without revealing which data point belongs to which client.
We conduct extensive experiments to cluster synthetic and real datasets on FL systems, and compare SecFC with the centralized Lloyd’s algorithm and -FED as our baselines. Under different data distributions across clients with different number of local clusters , SecFC consistently achieves almost identical performance as the centralized Lloyd, which outperforms -FED. Also, unlike -FED whose performance varies substantially with the value of , and deteriorates severely when , the performance of SecFC is almost invariant to the value of , indicating its universal superiority. We also evaluate the execution overheads of SecFC under various combinations of system parameters, which demonstrate the feasibility of applying SecFC to solve practical clustering tasks.
2 Background and Related Work
Clustering is an extensively studied learning task. We discuss existing works in three categories.
-
•
Centralized clustering. In centralized clustering, a central entity, i.e., server, performs the data partition. A well-known centralized clustering problem is -means clustering, where the aim is to find centers such that the Euclidean distance from each data point to its closest center is minimized. Lloyd’s heuristic [14] is a popular iterative approach in performing -means clustering due to its simplicity, even though its performance heavily depends on algorithm initialization. Unlike the Lloyd’s heuristic which does not provide any provable guarantees, Kanungo et al. [23] proposes an approximation algorithm for -means clustering that is based on swapping cluster centers in and out, which yields a solution that is at most factor larger than the optimal solution. Awasthi and Sheffet [24] propose a variant of the Lloyd’s heuristic that is equipped with such an approximation algorithm to guarantee convergence in polynomial time.
-
•
Parallel and distributed clustering. Distributed and parallel clustering implementations are particularly useful in the presence of large datasets that are prominent in many learning applications. The bottleneck in the centralized -means clustering is the computation of distances among the data points and the centers. In parallel implementations of -means clustering, the idea is to split the dataset into different worker machines so that the distance computations are performed in parallel [25, 26]. In addition to -means clustering, there have been parallel implementations of other clustering schemes such as the density-based clustering scheme DBSCAN [27]. When the dataset is distributed in nature, it may not be practical to send local datasets to the central entity. In such cases, distributed clustering is favorable albeit a performance loss compared to the centralized setting [28, 29, 30].
-
•
Federated clustering. Clustering techniques have been used in FL systems to handle data heterogeneity [31, 9, 32, 13, 33], particularly focusing on personalized model training and client selection. References [31, 32, 9] focus on clustering the clients to jointly train multiple models, one for each cluster, whereas reference [13] clusters the client data points to reach more personalized models and perform a more representative client selection at each iteration. Unlike the -means clustering which uses a heuristic to generate clusters, model-based clustering assumes that the data to be clustered comes from a probabilistic model and aims to recover that underlying distribution [34, 35]. In their recent work [12], using this approach, Chung et al. cluster heterogeneous client data in a federated setting by associating each data point with a cluster (model) with the highest likelihood. As also highlighted by [33], common to all these existing works on -means clustering is the fact that none of them provides data privacy, in the sense that cluster center information as well as clients’ data are kept private. This motivates us to develop SecFC in this work, which is to the best of our knowledge, the first federated clustering algorithm with formal privacy guarantees.
Before we close this section, we briefly review some prior works on secure clustering.
Privacy-preserving clustering. When the clustering is performed on private client data as in the case of federated clustering, the issue of secure clustering emerges. The aim here is to cluster the entire dataset without revealing anything to the clients, including all intermediate values, but the output, i.e., final partition of data. Privacy-preserving clustering has been studied in the literature employing cryptographic techniques from secure multiparty computation, for the cases of horizontal, vertical, and arbitrary partitions of data [36, 37, 38, 39, 40, 41]. Among these works, we want to highlight [41], where authors implement a secret sharing-based secure -means clustering scheme. Unlike the proposed SecFC scheme, however, [41] employs an additive secret sharing scheme and reveals the final cluster centers to the participants. In SecFC, clients use Lagrange coding to encode and share their private data. During the execution of SecFC, neither final nor any intermediate candidate center information is disclosed to the clients or the server, which is not the case in other earlier works [36, 37, 39] in the literature as well.
Notation. For a positive integer , let denote the set of integers . Let denote the cardinality of a set .
3 Preliminaries and Problem Formulation
3.1 -means Clustering
Given a dataset consisting of data points , each with features of dimension , the -means clustering problem aims to obtain a -partition of , denoted by , such that the following clustering loss is minimized.
| (1) |
where denotes the center of cluster , which is computed as .
A classical method for clustering is the Lloyd’s heuristic algorithm [14]. It is an iterative refinement method that alternates on two steps. The first step is to assign each data point to its nearest cluster center. The second step is to update each cluster center, as the mean of data points assigned to that cluster in the first step. The algorithm terminates when the data assignments no longer change. When the data points are well separated, Lloyd’s algorithm often converges in a few iterations and achieves good performance [42], but its complexity can grow superpolynomially in the worst case [43]. Despite of many variants of Lloyd’s algorithm to improve its clustering performance and computational complexity in general cases, we focus on solving the -means clustering problem using the original Lloyd’s heuristic due to its simplicity.
3.2 Secure Federated -means
We consider solving a -means clustering problem, over a federated learning system that consists of a central server and distributed clients. The entire dataset consists of private data points arbitrarily distributed across the clients. For each , we denote the set of local data points at client as , . Specifically, we would like to run the Lloyd’s algorithm to obtain a -clustering of the clients’ data, with the coordination of the server.
A similar problem was recently considered in [13], where a federated clustering protocol, -FED, was proposed to approximately execute Lloyd’s heuristic with one-shot communication from the clients to the server. The basic idea of -FED is to have each client run Lloyd to generate a -clustering of its local data , and send the cluster centers to the server, and then the server runs Lloyd again to cluster the centers into groups, generating a -clustering of the entire dataset. We note that -FED is limited in the following two aspects: 1) to run -FED, each client needs to know the actual number of local clusters , and the clustering performance is guaranteed only when the number of local clusters is less than , and the number of data points in each non-empty local cluster is large enough, which may hardly hold in practical scenarios; 2) the clients’ private data is leaked to the server through the client centers directly sent to the server, which are computed as the means of the data points in respective local clusters.
Motivated by the above limitations, we aim to design a federated -means clustering algorithm that simultaneously achieves the following requirements.
-
•
Universal performance: No loss of clustering performance compared with the centralized Lloyd’s algorithm on the entire dataset, regardless of the data distribution across the clients;
-
•
Data -privacy: We consider a threat model where the clients and the server are honest-but-curious. For some security parameter , during the protocol execution, no information about a client’s private data should be leaked, even when any subset of up to clients collude with each other. Further, the server should not know explicitly any private data of the clients, as well as the locations of the cluster centers.
We propose Secure Federated Clustering (or SecFC) that simultaneously satisfies the above performance and security requirements. In SecFC, private data is secret shared across clients such that information-theoretical privacy is guaranteed against up to colluding clients. Using computations over coded data, the server decodes pair-wise distances between the data points and the centers, which are sufficient to advance Lloyd iterations. In this way, SecFC exactly recovers the center updates of centralized Lloyd’s algorithm, with the server knowing nothing about the data points and the centers.
4 The Proposed SecFC Protocol
As SecFC leverages cryptographic primitives to protect data privacy, which operates on finite fields, we assume that the elements of each data point are from a finite field of order . In practice, one can quantize each element of the data points onto , for some sufficiently large prime , such that overflow does not occur to any computation during the execution of the Lloyd’s algorithm. See Appendix A for one such quantization method.
4.1 Protocol Description
Secure data sharing. In the first phase of SecFC, each client mixes its local data with random noises to generate secret shares of the data, and communicates the shares with the other clients.
For each , and each , client first evenly partitions into segments , for some design parameter . Next, client randomly samples noise vectors from . Then, for a set of distinct parameters from that are agreed upon among all clients and the server, following the data encoding scheme of Lagrange Coded Computing (LCC) [19], client performs Lagrange interpolation on the points to obtain the following polynomial
| (2) |
Note that for , and for .
Finally, for another set of public parameters that are pair-wise distinct, and , client evaluates at to compute a secret share of for client , for all (i.e., ), and sends to client .
By the end of secure data sharing, each client possesses a secret share of the entire dataset , i.e., .
Coded center update. The proposed SecFC runs in an iterative manner until the centers converge. The server starts by randomly sampling a -clustering assignment . In the subsequent iterations, the computations of the distances from the data points to the centers, and the center updates are all performed on the secret shares of the original data.
In each iteration, given the current clustering , each client updates the secret shares of the centers as , for all . Then, for each and each , client computes the coded distance from data point to center as , and sends it to the server. For each , the coded distance can be viewed as the evaluation of a polynomial at point . As has degree , the server can interpolate from the computation results of clients. Having recovered , the server computes , and normalizes it by the square of the size of cluster to obtain the distance from data point to cluster center , i.e., .111Here the division is performed in the real field. Having obtained the distances between all centers and all data points, the server updates the clustering assignment by first identifying the nearest center for each data point, and assigning the data point to the corresponding cluster. We summarize the proposed SecFC protocol in Algorithm 1.
4.2 Theoretical Analysis
We theoretically analyze the performance, privacy, and complexity of the proposed SecFC protocol.
Theorem 1.
For the federated clustering problem with clients, the proposed SecFC scheme with parameter achieves universal performance and data -privacy, when .
Proof.
The data -privacy of SecFC against colluding clients follows from the -privacy of LCC encoding. As shown in Theorem 1 of [19], each data point is information-theoretical security against colluding clients. In other words, for any subset of size not larger than , the mutual information .
As explained in the above protocol description, for a given clustering , as long as , the server is able to exactly reconstruct the polynomial from the computation results of the clients, and subsequently compute the exact distance from data point to the cluster center . Therefore, the clustering update of SecFC exactly follows that of a centralized Lloyd’s algorithm, and achieves identical clustering performance. It is easy to see that this performance is achieved universally regardless of the clients’ knowledge about the numbers of local clusters, and the distribution of data points.
Finally, with the computation results received from the clients, the server is only able to decode the distances between the data points and the current cluster centers, but not their individual values. This achieves data privacy against a curious server. ∎
Remark 1.
Taking advantage of a key property of the Lloyd’s algorithm where only the distances between points and centers are needed to carry out the center update step, SecFC is able to protect clients’ data privacy against the server, without sacrificing any clustering performance.
Remark 2.
SecFC achieves the same clustering performance as the original Lloyd’s algorithm, which is nevertheless not guaranteed to produce the optimal clustering, and its performance relies heavily on the clustering initialization [44]. It was proposed in [24] to improve center initialization by first projecting the dataset onto the subspace spanned by its top singular vectors, and applying an approximation algorithm (see, e.g., [23, 45]) on the projected dataset to obtain the initial centers. How one can incorporate these initialization tricks into SecFC without compromising data privacy remains a compelling research question.
Theorem 1 reveals a trade-off between privacy and efficiency for SecFC. As a larger allows for data privacy against more curious colluding clients, a larger reduces both the communication loads among the clients, and the computation complexities at the clients and the server.
Complexity analysis. We analyze the communication and computation complexities of SecFC. Let be the number local data points at client , and be the number of iterations.
Communication complexity of client . The communication load of client consists of two parts: 1) The communication cost of client for data sharing is ; 2) In each iteration, client communicates computation results to the server, incurring a cumulative communication cost of . The total communication cost of client during the execution of SecFC is .
Computation complexity of client . The computation performed by client consists of two parts: 1) Utilizing fast polynomial interpolation and evaluation [46], client can generate the secret shares of its local data with complexity ; 2) Within each iteration, client needs to first compute a secret share for each of the centers, and then compute the distance from each data point to each center in the coded domain. This takes a total of operations. Hence, the total computation complexity of client is .
Computation complexity of the server. The computation occurs on server in each iteration consists of two parts. 1) The decoding and recovery of actual pair-wise distances take operations; 2) The cost of cluster assignment on each data point is . Thus, the total computation complexity of the server is .
5 Experiments
In this section, we empirically evaluate the performance and complexity of the proposed SecFC protocol, for federated clustering of synthetic and real datasets. We compare SecFC with centralized implementation of Lloyd’s heuristic and the -FED protocol as baselines. All experiments are carried out on a machine using Intel(R) Xeon(R) Gold 5118 CPU @ 2.30GHz, with 12 cores of 48 threads.
The center separation technique [24] is applied to all three algorithms, for clustering initialization to improve the performance. It is a one-time method to generate groups of data from a given clustering assignment. Given the current cluster centers , each is selected such that . In this way, the data in is close to center and far from all other centers. Then, the means of are used as the initial centers for the subsequent iterative execution of the algorithms.
We cluster data points with ground truth labels, and use classification accuracy as the performance measure. For each , let and respectively denote the ground truth label of data point , and the index of the cluster it belongs to after the clustering process, such that . As the clustering operation does not directly predict ’s label, the classification of is subject to a potential permutation of the label set . We use the Hungarian method [47] to find the optimal permutation that maximizes , where is the indicator function. Then, the accuracy of a -means clustering algorithm is given by .
5.1 Separating Mixture of Gaussians
We first consider a synthetic dataset, where the data is generated by a mixture of Gaussians. That is, we generate isotropic Gaussian clusters comprised of a total of data points each with features. Each data point is sampled from an average of normal distributions with density . The centers are randomly chosen. The covariance matrix is diagonal with covariance . The standard deviations are the same for all , i.e., , . The ground truth label of each data point is given by the index of the closest center to that particular point.
To compare SecFC with -FED, we generate clients’ datasets with different , where the parameter is the maximum number of clusters a client can have data points in and indicates the level of data heterogeneity across clients. The -FED scheme assumes that this number is known to the clients [13], which is not required for our SecFC. We generate local datasets for the cases of , which is required by -FED to have performance guarantees, and also for the case of , which corresponds to i.i.d. data distribution across clients.
We consider two Gaussian mixtures of dimension , with standard deviation and respectively. For each value of , we consider a setting of clusters, clients, and data points are generated; and another setting of clusters, clients, and data points are generated. For each of the datasets, the centralized Lloyd, -FED, and SecFC are executed for runs, and their performance are shown in Table 1 and Table 2.
| Centralized Lloyd | ||||||
|---|---|---|---|---|---|---|
| -FED | ||||||
| SecFC | ||||||
For each value of , and each combination of and , SecFC consistently achieves almost identical performance with that of the centralized Lloyd, which is better than the accuracy of -FED. For a fixed , the accuracy of SecFC almost stays the same for different values of , demonstrating its universal superiority. In sharp contrast, the performance of -FED varies significantly with , and drops drastically for the case of . With a larger , the Gaussian clusters are more scattered, hence increasing the difficulty for clustering algorithms to correctly classify data points. This is empirically verified by the performance drop when increasing from to , for all three algorithms.
| Centralized Lloyd | ||||||
|---|---|---|---|---|---|---|
| -FED | ||||||
| SecFC | ||||||
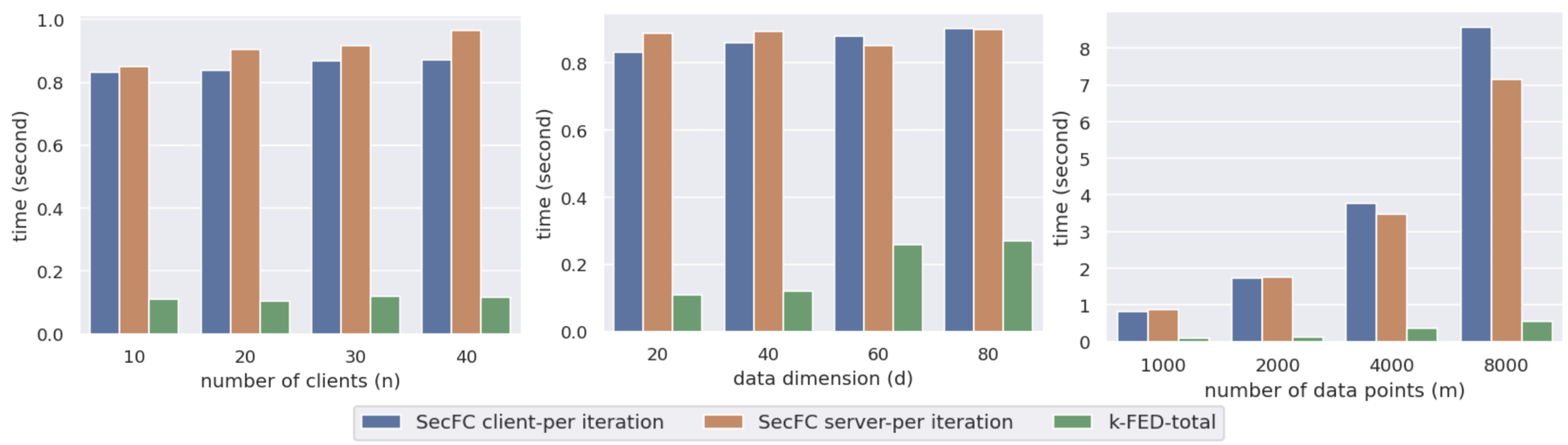
Complexity evaluation. We also evaluate the execution overheads of SecFC, under different combinations of system parameters. By default, the clustering is done for clusters on clients, for a dataset generated by parameters , , and . For SecFC, as the computations at both the clients and the server are independent across centers and data points, we parallelize the computations onto different processes to speed up the execution of SecFC. Based on the capacity of the system’s computing power, the distance computations of the data points at each client are parallelized onto multiple processes, and the distance decodings of the (data, center) pairs at the server are also parallelized onto multiple processes. We present the run times of -FED and SecFC, as functions of the parameters , , and respectively in Figure 1. Here we measure the average run time of SecFC spent in each client-server iteration, and the overall run time of -FED as it performs one-shot communication from clients to the server. We omit the communication times in all scenarios as they are negligible compared with computation times.
We observe in Figure 1 that, as expected, SecFC is slower than -FED (in fact, one iteration of SecFC is already slower than the entire execution of -FED). However, the execution time of SecFC in each iteration is rather short ( in the worst case), which demonstrates its potential for practical secure clustering tasks. For different client number , the security parameter is kept to be to provide privacy against up to colluding clients. The client run time is independent of because all clients compute on the coded data of the entire dataset in SecFC. Server complexity increases slightly with as the increased contributes to a higher decoding complexity. For different data dimension , the server run time remains almost unchanged as it only decodes the distance between data points and centers. The run times of the clients in SecFC and the overall run time of -FED both increase with as they are operating on data points with a higher dimension. Finally, when the number of data points is increased, the run times of server and clients in SecFC, and the overall run time of -FED all grow almost linearly.
5.2 Experiments on Real Data
We also evaluate the clustering performance of SecFC on the MNIST handwritten digit dataset [48]. As in [12], we use rotations to construct a clustered dataset such that different rotation angles correspond to data generated by different distributions. For the set of images in MNIST labelled by a certain digit, we rotate the images by a degree of respectively to construct a dataset with clusters. We execute SecFC and the two baseline algorithms on the datasets generated for digits and over clients, and present their performance in Table 3.
| Digit | Digit | |||||
|---|---|---|---|---|---|---|
| Centralized Lloyd | ||||||
| -FED | ||||||
| SecFC | ||||||
Similar to the synthetic data, SecFC achieves almost identical performance with centralized Lloyd in all tasks of clustering digit and digit images, which is insensitive to the value of . -FED achieves a lower accuracy in general, which also varies substantially with .
6 Strengthening SecFC with Membership Privacy
One shortcoming of SecFC is that distribution of the global dataset, i.e., , where denotes the set of indices of the local data points at client , will become publicly known during data sharing. It would be desirable for client to also keep private, so that from the final clustering result , no client or the server can infer which data point belongs to which client.
Private ID alignment. This can be achieved by adding an additional step of private ID alignment before data sharing in SecFC. We assume that each data point has a unique ID (e.g., its hash value), and we denote the set of IDs of the data points in at client as . Before the clustering task starts, both and are kept private at client , and are not known by the other clients and the server. As the first step of the clustering algorithm, all clients collectively run a private set union (PSU) protocol (see, e.g., [20, 21, 22]), over the local ID sets , such that by the end of PSU, each client knows the set of all data IDs in the network, without knowing the individual ID sets of other clients. Let . All the clients and the server agree on a bijective map between and . This also induces a bijective map between and at each client .
After private ID alignment, each client learns the total number of data points in the system. During the secure data sharing phase, to protect the privacy of , each client secret shares a data for each , as described in Section 4.1. Here for and otherwise. We denote the secret share of created by client for client as . Unlike the original data sharing where each client only receives one secret share from the owner of , for each , now with membership privacy, client receives shares , one from each client. Each client computes . This completes the data sharing phase. Next, the clients perform the same coded center update process as in SecFC to obtain the final -clustering.
With the extension of incorporating the private ID alignment step, SecFC can further protect the membership privacy of the data points, without sacrificing data privacy and clustering performance. We give more detailed description and analysis of this extended version of SecFC in Appendix B.
7 Conclusion and discussions
We propose a secure federated clustering algorithm named SecFC, for clustering data points arbitrarily distributed across a federated learning network. SecFC’s design builds upon the well-known Lloyd’s algorithm, and SecFC universally achieves identical performance to a centralized Lloyd’s execution. Moreover, SecFC protects the data privacy of each client via secure data sharing, and computation over coded data throughout the clustering process. It guarantees information-theoretic privacy against colluding clients, and no explicit knowledge about the data points and cluster centers at the server. Experiment results from clustering synthetic and real data demonstrate the universal superiority of SecFC and its computational practicality under a wide range of system parameters. Finally, we propose an extended version of SecFC to further provide membership privacy for the clients’ datasets, such that, while knowing the final clustering, no party knows the owner of any data point.
While the high level of security provided by SecFC is desirable for many applications, it cannot be directly applied to scenarios where the centers of clusters (e.g., in mean estimation [49, 50]), or the membership of specific data points (e.g., in clustering-based outlier detection [51, 52]) need to be known explicitly. These problems can be resolved respectively by having clients to collectively reveal the cluster centers, and having each client publish the IDs of their local data.
References
- [1] Brendan McMahan, Eider Moore, Daniel Ramage, Seth Hampson, and Blaise Aguera y Arcas. Communication-efficient learning of deep networks from decentralized data. In Artificial intelligence and statistics, pages 1273–1282. PMLR, 2017.
- [2] Timothy Yang, Galen Andrew, Hubert Eichner, Haicheng Sun, Wei Li, Nicholas Kong, Daniel Ramage, and Françoise Beaufays. Applied federated learning: Improving Google keyboard query suggestions. arXiv preprint arXiv:1812.02903, 2018.
- [3] Amir Jalalirad, Marco Scavuzzo, Catalin Capota, and Michael Sprague. A simple and efficient federated recommender system. In IEEE/ACM International Conference on Big Data Computing, Applications and Technologies, pages 53–58, 2019.
- [4] Nicola Rieke, Jonny Hancox, Wenqi Li, Fausto Milletari, Holger R. Roth, Shadi Albarqouni, Spyridon Bakas, Mathieu N. Galtier, Bennett A. Landman, Klaus Maier-Hein, et al. The future of digital health with federated learning. NPJ digital medicine, 3(1):1–7, 2020.
- [5] Canh T. Dinh, Nguyen Tran, and Josh Nguyen. Personalized federated learning with Moreau envelopes. Advances in Neural Information Processing Systems, 33:21394–21405, 2020.
- [6] Alireza Fallah, Aryan Mokhtari, and Asuman Ozdaglar. Personalized federated learning: A meta-learning approach. arXiv preprint arXiv:2002.07948, 2020.
- [7] Tian Li, Shengyuan Hu, Ahmad Beirami, and Virginia Smith. Ditto: Fair and robust federated learning through personalization. In International Conference on Machine Learning, pages 6357–6368. PMLR, 2021.
- [8] Yishay Mansour, Mehryar Mohri, Jae Ro, and Ananda Theertha Suresh. Three approaches for personalization with applications to federated learning. arXiv preprint arXiv:2002.10619, 2020.
- [9] Avishek Ghosh, Jichan Chung, Dong Yin, and Kannan Ramchandran. An efficient framework for clustered federated learning. Advances in Neural Information Processing Systems, 33:19586–19597, 2020.
- [10] Xiaomin Ouyang, Zhiyuan Xie, Jiayu Zhou, Jianwei Huang, and Guoliang Xing. ClusterFL: a similarity-aware federated learning system for human activity recognition. In International Conference on Mobile Systems, Applications, and Services, pages 54–66, 2021.
- [11] Yeongwoo Kim, Ezeddin Al Hakim, Johan Haraldson, Henrik Eriksson, José Mairton B. da Silva, and Carlo Fischione. Dynamic clustering in federated learning. In ICC 2021-IEEE International Conference on Communications, pages 1–6. IEEE, 2021.
- [12] Jichan Chung, Kangwook Lee, and Kannan Ramchandran. Federated unsupervised clustering with generative models. In AAAI 2022 International Workshop on Trustable, Verifiable and Auditable Federated Learning, 2022.
- [13] Don Kurian Dennis, Tian Li, and Virginia Smith. Heterogeneity for the win: One-shot federated clustering. In International Conference on Machine Learning, pages 2611–2620. PMLR, July 2021.
- [14] Stuart Lloyd. Least squares quantization in PCM. IEEE Transactions on Information Theory, 28(2):129–137, 1982.
- [15] Ligeng Zhu, Zhijian Liu, and Song Han. Deep leakage from gradients. Advances in Neural Information Processing Systems, 32, 2019.
- [16] Jonas Geiping, Hartmut Bauermeister, Hannah Dröge, and Michael Moeller. Inverting gradients-how easy is it to break privacy in federated learning? Advances in Neural Information Processing Systems, 33:16937–16947, 2020.
- [17] Zhibo Wang, Mengkai Song, Zhifei Zhang, Yang Song, Qian Wang, and Hairong Qi. Beyond inferring class representatives: User-level privacy leakage from federated learning. In IEEE INFOCOM 2019-IEEE Conference on Computer Communications, pages 2512–2520. IEEE, 2019.
- [18] Liam Fowl, Jonas Geiping, Wojtek Czaja, Micah Goldblum, and Tom Goldstein. Robbing the Fed: Directly obtaining private data in federated learning with modified models. arXiv preprint arXiv:2110.13057, 2021.
- [19] Qian Yu, Songze Li, Netanel Raviv, Seyed Mohammadreza Mousavi Kalan, Mahdi Soltanolkotabi, and Salman A. Avestimehr. Lagrange coded computing: Optimal design for resiliency, security, and privacy. In The 22nd International Conference on Artificial Intelligence and Statistics, pages 1215–1225. PMLR, 2019.
- [20] Jae Hong Seo, Jung Hee Cheon, and Jonathan Katz. Constant-round multi-party private set union using reversed laurent series. In International Workshop on Public Key Cryptography. Springer, 2012.
- [21] Sivakanth Gopi, Pankaj Gulhane, Janardhan Kulkarni, Judy Hanwen Shen, Milad Shokouhi, and Sergey Yekhanin. Differentially private set union. In International Conference on Machine Learning. PMLR, 2020.
- [22] Keith Frikken. Privacy-preserving set union. In Jonathan Katz and Moti Yung, editors, Applied Cryptography and Network Security. Springer, 2007.
- [23] Tapas Kanungo, David M. Mount, Nathan S. Netanyahu, Christine D. Piatko, Ruth Silverman, and Angela Y. Wu. A local search approximation algorithm for -means clustering. In Annual Symposium on Computational Geometry, June 2002.
- [24] Pranjal Awasthi and Or Sheffet. Improved spectral-norm bounds for clustering. In Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques, pages 37–49. Springer, 2012.
- [25] Inderjit S. Dhillon and Dharmendra S. Modha. A data-clustering algorithm on distributed memory multiprocessors. In Workshop on Large-Scale Parallel KDD Systems, SIGKDD. August 1999.
- [26] Manasi N. Joshi. Parallel -Means algorithm on distributed memory multiprocessors. Technical report, University of Minnesota, 2003.
- [27] Xiaowei Xu, Jochen Jäger, and Hans-Peter Kriegel. A fast parallel clustering algorithm for large spatial databases. In High performance data mining, pages 263–290. Springer, 1999.
- [28] Hillol Kargupta, Weiyun Huang, Krishnamoorthy Sivakumar, and Erik Johnson. Distributed clustering using collective principal component analysis. Knowledge and Information Systems, 3(4):422–448, 2001.
- [29] Eshref Januzaj, Hans-Peter Kriegel, and Martin Pfeifle. Towards effective and efficient distributed clustering. In Workshop on Clustering Large Data Sets, 2003.
- [30] Maria-Florina F. Balcan, Steven Ehrlich, and Yingyu Liang. Distributed -means and -median clustering on general topologies. Advances in Neural Information Processing Systems, 26, 2013.
- [31] Virginia Smith, Chao-Kai Chiang, Maziar Sanjabi, and Ameet S Talwalkar. Federated multi-task learning. Advances in neural information processing systems, 30, 2017.
- [32] Felix Sattler, Klaus-Robert Müller, and Wojciech Samek. Clustered federated learning: Model-agnostic distributed multitask optimization under privacy constraints. IEEE Transactions on Neural Networks and Learning Systems, 32(8):3710–3722, 2020.
- [33] Ravikumar Balakrishnan, Tian Li, Tianyi Zhou, Nageen Himayat, Virginia Smith, and Jeff Bilmes. Diverse client selection for federated learning via submodular maximization. In International Conference on Learning Representations, 2022.
- [34] Sudipto Mukherjee, Himanshu Asnani, Eugene Lin, and Sreeram Kannan. Clustergan: Latent space clustering in generative adversarial networks. In AAAI Conference on Artificial Intelligence, volume 33, pages 4610–4617, 2019.
- [35] Steven Liu, Tongzhou Wang, David Bau, Jun-Yan Zhu, and Antonio Torralba. Diverse image generation via self-conditioned gans. In IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 14286–14295, 2020.
- [36] Jaideep Vaidya and Chris Clifton. Privacy-preserving -means clustering over vertically partitioned data. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 206–215, 2003.
- [37] Geetha Jagannathan and Rebecca N Wright. Privacy-preserving distributed -means clustering over arbitrarily partitioned data. In ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, pages 593–599, 2005.
- [38] Paul Bunn and Rafail Ostrovsky. Secure two-party -means clustering. In ACM Conference on Computer and Communications Security, pages 486–497, 2007.
- [39] Sankita Patel, Sweta Garasia, and Devesh Jinwala. An efficient approach for privacy preserving distributed -means clustering based on shamir’s secret sharing scheme. In IFIP International Conference on Trust Management, pages 129–141. Springer, 2012.
- [40] Jiawei Yuan and Yifan Tian. Practical privacy-preserving mapreduce based -means clustering over large-scale dataset. IEEE Transactions on Cloud Computing, 7(2):568–579, 2017.
- [41] Payman Mohassel, Mike Rosulek, and Ni Trieu. Practical privacy-preserving -means clustering. Cryptology ePrint Archive, 2019.
- [42] Rafail Ostrovsky, Yuval Rabani, Leonard J. Schulman, and Chaitanya Swamy. The effectiveness of lloyd-type methods for the -means problem. Journal of the ACM, 59(6):1–22, 2013.
- [43] David Arthur and Sergei Vassilvitskii. How slow is the -means method? In Symposium on Computational Geometry, pages 144–153, 2006.
- [44] M. Emre Celebi, Hassan A. Kingravi, and Patricio A. Vela. A comparative study of efficient initialization methods for the -means clustering algorithm. Expert Systems with Applications, 40(1):200–210, 2013.
- [45] Sariel Har-Peled and Soham Mazumdar. On coresets for -means and -median clustering. In ACM Symposium on Theory of Computing, pages 291–300, 2004.
- [46] Kiran S. Kedlaya and Christopher Umans. Fast polynomial factorization and modular composition. SIAM Journal on Computing, 40(6):1767–1802, 2011.
- [47] Harold W Kuhn. The Hungarian method for the assignment problem. Naval Research Logistics Quarterly, 2(1-2):83–97, 1955.
- [48] Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
- [49] Kevin A Lai, Anup B Rao, and Santosh Vempala. Agnostic estimation of mean and covariance. In 2016 IEEE 57th Annual Symposium on Foundations of Computer Science (FOCS), pages 665–674. IEEE, 2016.
- [50] JA Cuesta-Albertos, C Matrán, and A Mayo-Iscar. Robust estimation in the normal mixture model based on robust clustering. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 70(4):779–802, 2008.
- [51] Antonio Loureiro, Luis Torgo, and Carlos Soares. Outlier detection using clustering methods: a data cleaning application. In Proceedings of KDNet Symposium on Knowledge-based systems for the Public Sector. Springer Bonn, 2004.
- [52] Sheng-yi Jiang and Qing-bo An. Clustering-based outlier detection method. In 2008 Fifth international conference on fuzzy systems and knowledge discovery, volume 2, pages 429–433. IEEE, 2008.
Appendix
Appendix A Data Quantization
In SecFC, the operations of data sharing and distance computation are carried out in a finite field , for some large prime . Hence, for a data point from the real field, one needs to first quantize it onto . Specifically, for some scaling factor that determines the quantization precision, we first scale by , and embed the scaled value onto as follows.
| (3) |
where denotes the largest integer less than or equal to , and the quantization function is applied element-wise. Assuming each element of is within for some , then on the range of , is the image of the positive part, and is the image of the negative part. While controls the precision loss of quantization, it also needs to be chosen so that overflow does not occur during computations of SecFC. A larger requires a larger finite field size to avoid computation overflow, and a smaller leads to a higher precision loss between and . We can choose a proper scaling factor to preserve enough precision while keeping the field size practical.
To avoid computation overflow, we should choose such that all the intermediate computation results on the scaled data are within the range . In the worst case, the largest distance across data points and cluster centers results in the largest output value. Therefore, we should choose that is at least .
Appendix B Extension of SecFC with Membership Privacy
After the step of private ID alignment, each client learns the total number of data points in the system. Each client knows the set of IDs of its private data points as , but does not know the sets of data IDs of the other clients.
During the secure data sharing phase, to protect the privacy of , each client first creates a data point for each , where
| (4) |
Next, for each , and some design parameter , as described in Section 4.1, using Lagrange interpolation and evaluation, each client encodes , and creates a secret share for each as
| (5) |
where are segments of , and are noises randomly generated by client for each .
Unlike the original data sharing of SecFC where each client only receives one secret share from the owner of , for each , client receives shares , one from each client. Each client computes . We can see from and that
| (6) |
where is still uniformly distributed in .
This completes the phase of secure data sharing.