Secure Communication for Spatially Correlated Massive MIMO with Low-Resolution DACs

Physical layer security (PLS) has become an emerging technology for securing wireless communication without relying upon traditional cryptographic mechanisms. Compared to conventional upper-layer cryptographic schemes, PLS has the advantages of low computational complexity and low resource consumption [1]. Massive multiple-input multiple-output (MIMO) systems provide another disruptive technology for fifth generation (5G) cellular communications, and have shown great potential in improving spectral and energy efficiency. The use of large-scale antenna arrays in massive MIMO provides a large excess of redundant spatial degrees of freedom (DoF), which can be exploited to achieve secure physical layer transmission. This idea has been attracting increasing research interest in the past few years [2], [3].

Massive MIMO transmission requires a very high power consumption if high-resolution digital-to-analog converters (DACs) are employed in the RF chains for each antenna. At the transmitter, power expenditure is dominated by power amplifiers (PAs), which are usually required to operate within a high linearity regime to avoid distortion. A practical solution to the above challenge is to use low-resolution DACs, which relaxes the requirement of linearity and allows the amplifiers to operate closer to saturation, thus increasing the efficiency of PAs [4], [5]. In [6], both finite-bit DACs at base station (BS) and finite-bit analog-to-digital converters (ADCs) at user side were analyzed in the massive MIMO downlink. The work was then extended in [7] by considering spatially correlated channels. Further in [8], a constant envelope precoding technique was devised for the multiuser MIMO with one-bit DACs.

The effect of hardware impairments (HWIs) on spectral efficiency of massive MIMO systems has been studied in [9]. Regarding the secrecy performance, the authors in [10] analyzed the effects of HWIs on secrecy rate, where ideal converters with infinite resolution were considered. Secure communication in a massive MIMO system with low-resolution DACs was investigated in [11], which revealed that low-resolution DACs can achieve superior secrecy rate under certain conditions, e.g., at low SNR or with a large power allocation factor.

Most of the existing works on low-resolution DACs transmissions have focused on the assumption of independent identically distributed (i.i.d.) channels for massive MIMO. However, in practice, the limited space between the BS antennas as well as the rich scattering propagation environment can result in spatial correlation. The impact of correlated Rayleigh fading channels on optimal multiuser loading was analyzed in [6] by applying asymptotic random matrix theory. How spatial correlation impacts secure massive MIMO communication with low-resolution DACs is still an open problem.

In this paper, we focus on secure transmission in the massive MIMO downlink when low-resolution DACs are employed. A tight lower bound for the ergodic secrecy rate is derived that explicitly characterizes the impact of channel correlation on the secrecy rate for typical correlated channels. An optimal power allocation strategy is proposed, which suggests that more power should be allocated to AN when strong channel correlation is present. It is revealed that using low-resolution DACs can improve the secrecy performance for a fixed power allocation factor under strong spatially correlated channels.

The secure massive MIMO system under investigation comprises one $N$-antenna BS, $K$ single-antenna legitimate users, and one $M$-antenna passive eavesdropper. The channel matrices are modeled based on the Kronecker channel model as shown in [12]. To make the problem more tractable, we consider the system with a common correlation matrix at the BS. Specifically, the channel between the BS and the users is modeled as $\bf{H}=\bf{D}\rm^{\frac{1}{2}}\widetilde{\bf{H}}\bf{R}\rm^{\frac{1}{2}}$, where the elements of $\widetilde{\bf{H}}\in\mathbb{C}^{K\times N}$ are i.i.d. Gaussian random variables with zero mean and unit variance, the diagonal matrix $\bf{D}\in\mathbb{C}^{\mit K\times K}$ characterizes the large-scale fading with its $k$th diagonal element given by $\beta_{k}$, and $\bf{R}\in\mathbb{C}^{\mit N\times N}$ is the transmit covariance matrix satisfying $\rm tr(\bf{R})=\mit N$. Similarly, the channel matrix between the BS and the eavesdropper is $\bf{H}\rm_{e}=\bf{D}^{\rm\frac{1}{2}}\rm_{e}\widetilde{\bf{H}}_{e}\bf{R}^{\rm\frac{1}{2}}$, where $\widetilde{\bf{H}}\rm_{e}\in\mathbb{C}\mit^{M\times N}$ contains i.i.d. Rayleigh fading channel coefficients following $\mathcal{CN}(0,1)$. The diagonal matrix $\bf{D}\rm_{e}$ represents the large-scale fading at the eavesdropper with identical diagonal entries $\beta\rm^{e}$.

The BS desires to transmit the symbols $\bf{s}=[\mit s\rm_{1},\mit s\rm_{2},...,\mit s\mit_{K}]\in\mathbb{C}^{\mit K\times\rm 1}$ to the legitimate users with $\mathbb{E}\{\bf{s}\bf{s}\mit^{H}\}=\bf{I}\mit_{K}$ using a linear precoding matrix $\bf{W}\in\mathbb{C}^{\mit N\times K}$. The eavesdropper’s channel state information (CSI) is assumed unknown to the BS, and AN is injected to ensure confidential communication. The AN vector $\bf{t}\sim\mathcal{CN}(\bf 0,\bf I\mit_{N-K})$ is precoded by an AN shaping matrix $\bf{V}\in\mathbb{C}^{\mit N\times(N-K)}$. Denote by $P$ the total transmit power. The power allocation factor $\xi\in(0,1]$ aims to strike a balance between the transmit signal and the AN. The unquantized downlink transmit signal vector $\bf{x}$ is then expressed as

where $\mu\triangleq\frac{\xi P}{K}$ and $\nu\triangleq\frac{(1-\xi)P}{N-K}$.

The precoded signal is transmitted after DAC quantization, which is denoted by $\mathcal{Q}(\bf{x})$. Establishing the non-linear quantization model of a finite-bit DAC is challenging. We follow a popular way of charactering the quantizer by a linear function applying the simple additive quantization noise model. The quantized signal vector can accordingly be decomposed as

where the quantization noise $\bf{q}$ is assumed to be uncorrelated with the input signal $\bf{x}$, and

The value of the distortion factor $\rho$ depends on the DAC resolution; for example, it can be chosen as in [5] for DAC resolutions of less than 5 bits, or as $\rho=\frac{\sqrt{3}\pi}{2}\cdot 2^{-2b}$ for scenarios with higher precision, where $b$ represents the number of quantization bits. From (1) and (3), the covariance matrix of the quantization noise equals

Given the CSI of the legitimate channels, the matrix $\bf{V}$ is designed to lie in the null space of the channel matrix $\bf{H}$, i.e., $\bf{H}\bf{V}=\bf{0}$, which (ideally) makes the AN “invisible” to the legitimate users [13]. Using (1) and (2), the signals received at the users and the eavesdropper are expressed as

where $\bf{n}\sim\mathcal{CN}(\bf{0},\mit\sigma_{n}\rm^{2}\bf{I}\mit_{K})$ and $\bf{n}\rm_{e}\sim\mathcal{CN}(\bf{0},\mit\sigma\rm_{e}\rm^{2}\bf{I}\mit_{M})$ respectively represent the additive noise terms at the users and at the eavesdropper.

In this section, we derive a tight lower bound for the ergodic secrecy rate of the secure multiuser massive MIMO downlink and analyze the impact of spatial correlation on the secrecy rate in the presence of low-resolution DACs.

In this section, the analytical results are validated through Monte-Carlo simulation. We consider a system with $N=256$, $K=16$, and $M=4$ in all simulations. The large-scale fading is modeled as $\beta_{k}=(d\rm_{ref}/\mit d_{k})^{\eta}$, where $\eta=3.8$ denotes the path loss exponent, $d\rm_{ref}=300$ (m) and $d_{k}\leq 500$ (m) are, respectively, the reference distance and the distance between the BS and the $k$th user. The expected values in (14) were evaluated by averaging over 1000 random channel realizations.

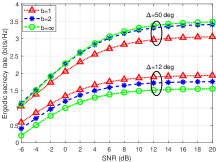
Fig. 1 shows the ergodic secrecy rate versus the average SNR $\gamma_{0}$ under different DAC resolutions and spatial correlations. The derived lower bound on the secrecy rate is fairly accurate and tight for the entire range of SNR. In addition, it is observed that the secrecy rate is decreasing as $\zeta$ increases.

Fig. 2 plots the ergodic secrecy rate as a function of the power allocation factor $\xi$. The optimal power allocation factor $\xi^{*}$ largely depends on $\zeta$. Specifically, It is observed that $\xi^{*}$ decreases with $\zeta$. The information signal leakage grows when the spatial correlation is strong. Thus, more power should be allocated for AN to ensure secure communication.

In Fig. 3 (a) we show the ergodic secrecy rate versus $\zeta$ with different DAC resolutions for $\gamma_{0}$ = 10 dB. We choose a fixed power allocation factor $\xi$ due to the difficulties in optimizing $\xi$ theoretically. The secrecy rate loss due to low-resolution DACs decreases with $\zeta$ as predicted in Remark 2. Interestingly, although the channel correlation has a detrimental effect on the secrecy rate, the use of 1-bit DACs can improve the secrecy rate when the spatial correlation coefficient is large. This is because the additional quantization noise serves to increase the level of AN, which is beneficial for spatially colored channels if the AN level has not already been optimized. Finally, Fig. 3 (b) presents the secrecy rate versus $\zeta$ assuming the optimal power allocation $\xi^{*}$ in (17) is chosen. The secrecy rate gaps are $\Delta R_{\rm sec}=0.697$ bit/s/Hz at $\zeta=0$ and $\Delta R_{\rm sec}=0.434$ bit/s/Hz at $\zeta=0.8$, respectively. If optimal power allocation is adopted, then using infinite-resolution DACs can always achieve a higher secrecy rate. In this case, quantization noise from lower-resolution DACs does not compensate for the AN anymore. However, we observe that the secrecy rate loss due to low-resolution DACs decreases with channel correlation coefficient, regardless of the value of $\xi$.

For comparison, Fig. 4 plots the Monte-Carlo simulation by using the spatial correlation model in [9], denoted by $[{\bf R}]_{s,m}=\frac{\beta}{L}\sum_{l=1}^{L}e^{j\pi(s-m)\sin(\varphi_{l})}e^{-\frac{\Delta^{2}}{2}\big{(}\pi(s-m)\cos(\varphi_{l})\big{)}^{2}}$, where $\beta$ is the large scale fading coefficient, $\varphi$ is the actual angle-of-arrival and $\Delta$ is the azimuth angular spread. We consider $L=10$ scattering clusters and $\varphi\sim[\frac{-\Delta}{2}$, $\frac{\Delta}{2}]$. It is observed that transitioning from larger to smaller angular spread ($\Delta={\rm 50^{o}}$ to $\Delta={\rm 12^{o}}$) significantly reduces the secrecy rate of the $k$th user for different DAC resolutions. However, the lower resolution DAC is always beneficial for secrecy rate with a fixed $\xi$ under highly correlated channels as expected.

This paper has characterized the performance of AN-based secure transmission in a massive MIMO downlink system with low-resolution DACs under spatially correlated channels. In particular, it is shown that optimal secrecy performance can be obtained by increasing the amount of power dedicated to artificial noise when the channel correlation increases. Furthermore, the use of low-resolution DACs has been shown to be beneficial to the secrecy performance for a fixed power allocation factor when the channels possess strong spatial correlation. Interesting future extension of this paper includes studying the impact of different spatial correlation matrices at both transmitter and the eavesdropper.