Second-order topological insulator and fragile topology in topological circuitry simulation

Introduction.—Identifying and classifying topological phases of matter plays an important role in modern physics. Bulk-boundary correspondence and emergent particles with quantized charge reflect the most fundamental property of a topologically protected system [1]. A topological insulator behaves as an insulator in its interior (bulk) in $d$ dimensions, and $(d-1)$-dimensional metallic surface states reside in the gap of the bulk states [2, 3]. Forming a novel class of topological insulators, higher-order topological insulators (HOTIs) support gapless states in a subspace of a dimension lower than $d-1$ [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]. In two-dimensional (2D) space, a second-order topological insulator (SOTI) combines two essential ingredients: (i) fractional corner charges in the presence of certain symmetries; (ii) topologically robust zero-dimensional (0D) corner states as adiabatic deformations of the boundary with preserved symmetry [10, 11].

While wavefunctions and spectra may be similar or even identical, the topological classification can be evaluated by integration of the Berry curvature over a closed manifold [15, 16] or by the winding of the Wilson loop (holonomy) [17, 18, 19]. To characterize the boundary topology, a Wannier Hamiltonian is defined as the product of ${{U}}(2N)$ Berry connection along a noncontractible Wilson loop in the Brillouin zone (BZ), and its eigenvalues are encoded with the ${{U}}(1)$ phase of the Wannier center in an effective one-dimensional (1D) form [17]. Crucially, the Wannier centers of occupied bands refer to Wannier bands carrying a topological invariant determining the bulk-corner correspondence. These can be investigated by a nested Wilson loop formalism [7, 20, 21, 22, 23].

HOTIs have been simulated in a plethora of platforms, including solid state [24], photonics [25], and acoustics systems [26, 27, 28]. In the present work, we propose to employ a bilayer topological circuitry, a remarkably flexible and tunable platform [29, 30], to realize HOTIs. The layer degree of freedom splits the space of wavefunctions into a finite number of independent copies. This constitutes a direct product relationship of the spinors with the ‘layer’ and ‘sublattice’ parts, and the top and bottom states can be coupled by the interlayer hopping.

In this Letter, we put forward a theoretical design of SOTIs by stacking Chern insulators with opposite chiralities coupled by interlayer hopping. We start from a bilayer Haldane model [31] with the time-reversal symmetry $\mathcal{T}$ and opposite Chern numbers [32, 33] (1D Dirac-type gapless helical edge states). By introducing a $\mathcal{T}$-breaking interlayer hopping, the edge modes become gapped and 0D corner modes are obtained. However, the corner modes are protected by the product of $\mathcal{T}$ and the $C_{2}$ rotation symmetry, leading to a fragile topological phase [34, 22]. To characterize the bulk-corner correspondence, we establish a Jacobian-transformed nested Wilson loop method by performing a Jacobian transformation of the Cartesian coordinates that reparametrizes the BZ. The corresponding topological invariant admits a filling anomaly of the corner modes with fractional charges $|e|/2$ [35]. We utilize the edge theory to explain the underlying physics in an intuitive manner. We also claim that the stacked Chern insulator approach can be generalized to multilayers, where only an even number of layers supports corner modes. The gap of the 1D band decays exponentially as a function of the number of layers due to finite size effects [36]. Our work offers new perspectives for exploring and understanding higher-order topological phenomena.

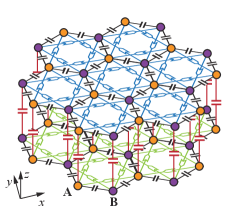
Model.— As illustrated in Fig. 1, we investigate a honeycomb lattice layout realized by an electrical circuit [37, 38], specifically a bilayer-bipartite lattice with $A$ and $B$ sites in both of top ($\alpha$) and bottom ($\beta$) layers. The corresponding tight-binding Hamiltonian can be written as

$$H=\sum\limits_{\left\langle{ij}\right\rangle}{{t_{1}}c_{i}^{\dagger}{\tau_{0}}{c_{j}}}+\sum\limits_{\left\langle{\left\langle{ij}\right\rangle}\right\rangle}{i{t_{2}}{v_{ij}}c_{i}^{\dagger}{\tau_{z}}}{c_{j}}+\sum\limits_{i}{{t_{\bot}}c_{i}^{\dagger}{\sigma_{x}}}{c_{i}},$$

(1)

where $c_{i}^{\dagger}={({c_{i,\alpha}^{\dagger},c_{i,\beta}^{\dagger}})^{T}}$ is the two-component creation operator acting at the site $i$ of the $\alpha$ and $\beta$ layers. The Pauli matrices $\sigma(\tau)_{x},\sigma(\tau)_{y},\sigma(\tau)_{z}$ and the identity matrix $\sigma(\tau)_{0}$ refer to the layer (sublattice) degree of freedom. $t_{1}$ denotes the intralayer hopping between the nearest neighbor sites. $t_{2}$ emulates the spin-orbit coupling between next nearest neighbor sites, where ${v_{ij}}={\textbf{d}_{i}}\times{\textbf{d}_{j}}/|{\textbf{d}_{i}}\times{\textbf{d}_{j}}|$ depends on the orientations of the mediating bonds, where ${\textbf{d}_{i}}$ and ${\textbf{d}_{j}}$ are unit vectors connecting site $j$ and $i$. $t_{\bot}$ denotes the interlayer hopping between site $i$ in different layers.

By Fourier transformation of the Hamiltonian (1) into momentum space, we obtain the Bloch matrix

$${\cal{H}}(\textbf{k})={d_{1}}(\textbf{k}){\Gamma_{1}}+{d_{2}}(\textbf{k}){\Gamma_{2}}+{d_{3}}(\textbf{k}){\Gamma_{3}}-{t_{\bot}}{\Gamma_{34}},$$

(2)

with

$$\begin{split}{d_{1}}(\textbf{k})=&{t_{1}}[1+2\cos(3a{k_{y}}/2)\cos(\sqrt{3}a{k_{x}}/2)],\\ {d_{2}}(\textbf{k})=&2{t_{1}}\sin(3a{k_{y}}/2)\cos(\sqrt{3}a{k_{x}}/2),\\ {d_{3}}(\textbf{k})=&{t_{2}}[4\cos(3a{k_{y}}/2)\sin(\sqrt{3}a{k_{y}}/2)-2\sin(\sqrt{3}a{k_{x}})],\end{split}$$

(3)

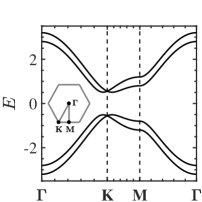
where ${\Gamma_{(1,2,3,4,5)}}=({\sigma_{0}}\otimes{\tau_{x}},{\sigma_{0}}\otimes{\tau_{y}},{\sigma_{z}}\otimes{\tau_{z}},{\sigma_{y}}\otimes{\tau_{z}},{\sigma_{x}}\otimes{\tau_{z}})$ and $\Gamma_{ab}=[{\Gamma_{a}},{\Gamma_{b}}]/2i$ are the Clifford-algebra matrices. Due to common pseudospin $1/2$ representation in momentum space, we can regard the BZ to be that of a 2D hexagonal lattice with spin. By diagonalizing Eq. (2), we obtain the band structure shown in Fig. 1. Dimensionless units are used throughout this Letter.

Topological invariant.—Emergence of topological corner states is the physical manifestation of a SOTI, with the topological property determined by the second Stiefel-Whitney number $w_{2}$ [20, 21]. $w_{2}$ is derived from the parity of the occupied Bloch wave functions at the time-reversal invariant momenta [23] ${{{\bf{\Gamma}}}_{i}}\in\{{{\bf{M}}_{1}},{{\bf{M}}_{2}},{{\bf{M}}_{3}},{\bf{\Gamma}}\}$ [Fig. 2] as

$${(-1)^{{w_{2}}}}=\prod\limits_{i=1}^{4}{{{(-1)}^{[N_{\rm{occ}}^{-}({\bf{\Gamma}_{i}})/2]}}},$$

(4)

where $[N_{\rm{occ}}^{-}({{\bf{\Gamma}}_{i}})/2]$ counts the number of occupied bands with odd parity.

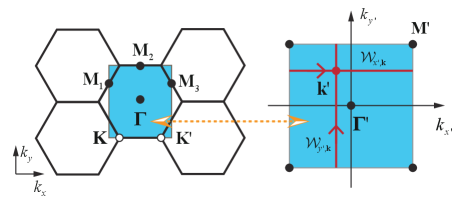
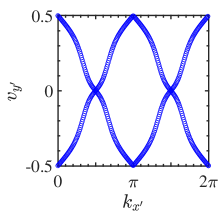
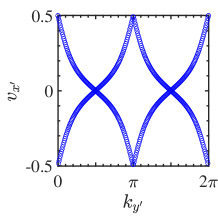
$w_{2}$ also can be determined by nested Wilson loop calculation [7]. We introduce a Jacobian-transformed nested Wilson loop to conveniently confirm gauge-invariance. The primitive vectors of the honeycomb lattice in real and momentum space do not point along the $(x,y)$ and $(k_{x},k_{y})$, respectively, as shown in Fig. 2, because the hexagonal primitive cell is topologically equivalent to a rectangular primitive cell [39]. Hence, the transition matrix ${\mathcal{M}}=\rm{diag}[\sqrt{3}/2,3/2]$ performs the Jacobian transformation $[{k_{x^{\prime}}},{k_{y^{\prime}}}]={\mathcal{M}}[{k_{x}},{k_{y}}]$, mapping the honeycomb BZ to a ${T^{2}}=[0,2\pi]\times[0,2\pi]$ torus. The corresponding real space coordinates read $[x^{\prime},y^{\prime}]={{\mathcal{M}}^{-1}}[x,y]$. Two manifolds with the same Euler characteristic can be continuously deformed into each other. Thus, the Wilson loop is redefined in the standardized square primitive cell as a path-ordered product of the exponential of Berry connections,

$${{\cal{W}}_{({k_{x^{\prime}}}+2\pi,{k_{y^{\prime}}})\leftarrow({k_{x^{\prime}}},{k_{y^{\prime}}})}}=\mathop{\lim}\limits_{N\to\infty}{F_{N-1}}{F_{N-2}}\cdots{F_{1}}{F_{0}},$$

(5)

where ${[{F_{\ell}}]_{mn}}=\langle{u_{m}}(\frac{{2\pi(\ell+1)}}{N},{k_{y^{\prime}}}){\rm{|}}{u_{n}}(\frac{{2\pi\ell}}{N},{k_{y^{\prime}}})\rangle$, $\left|u_{n}\right\rangle$ and $\left|u_{m}\right\rangle$ denote occupied Bloch functions, $N$ is the number of discrete points along the $k_{x^{\prime}}$ direction, and $m,n=1,\cdots,N_{\rm{occ}}$. The Wilson loop eigenvalues indicates Wannier centers ${e^{i{v_{x^{\prime}}}({k_{y^{\prime}}})}}$ at given $k_{y^{\prime}}$. According to Figs. 2 and 2, the Wilson loop spectra have no Wannier gap and belong to the orthogonal group $SO(2)$ [34, 40], with the homotopy group ${\pi_{1}}[SO(2)]=\mathbb{Z}$ guaranteeing the existence of a Stiefel-Whitney class invariant. This situation is identified as a fragile topological phase [41]. The Stiefel-Whitney number can be derived from the nested Wilson loop

$${\tilde{\cal W}_{({k_{y^{\prime}}}+2\pi)\leftarrow({k_{y^{\prime}}})}}=\mathop{\lim}\limits_{N\to\infty}{\tilde{F}_{N-1}}{\tilde{F}_{N-2}}\cdots{\tilde{F}_{1}}{\tilde{F}_{0}},$$

(6)

where ${[{{\tilde{F}}_{\ell}}]_{mn}}=\langle{v_{x^{\prime},m}}(\frac{{2\pi(\ell+1)}}{N}){\rm{|}}{v_{x^{\prime},n}}(\frac{{2\pi\ell}}{N})\rangle$. The determinant of the nested Wilson loop operator is $\det(\tilde{W})={(-1)^{{w_{2}}}}$, and we can assert a nontrivial topological phase.

Edge spectrum and topological corner states.—

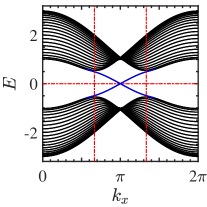
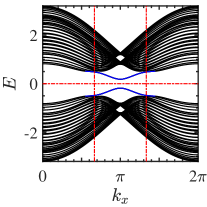
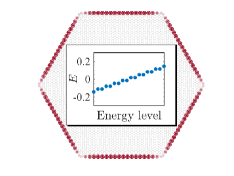
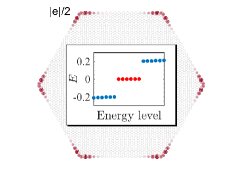
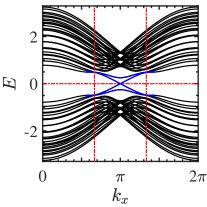
We now investigate the edge spectrum and the physical properties of topological corner states. In a zigzag terminated ribbon with open boundary condition, without $t_{\bot}$, a pair of helical gapless edge modes forms a Dirac-like band crossing projected by $\mathcal{T}$ symmetry, see Fig. 3. Figure 3 shows for a hexagonal-shaped flake with open boundary condition that the wavefuntion is localized at the edges, and the spectrum given as inset is quasicontinuous as expected for quantum spin Hall edge states. With $t_{\bot}$, the $\mathcal{T}$ symmetry is broken and the edge modes become gapped, see Fig. 3. Due to the hexagonal geometry, the spectrum given as inset in Fig. 3 shows six zero modes. The spatial distribution of the wavefunction is evaluated by the local density of states $\rho({\bf{r}})=-{\pi^{-1}}{{\rm{Im}}[i{0^{+}}{\mathbb{I}}-H({\bf{r}})]^{-1}}$ at zero energy, where $0^{+}$ is a small broadening. When gapped edge modes encounter one another at the corners, the $C_{6}$ symmetry enforces 6-fold degenerate localized corner states [Fig. 3]. The fractional charges in the six symmetric sectors are given by $Q_{6}=\frac{e}{2}{w_{2}}$ [35].

Edge theory.— In order to gain intuitive understanding of SOTI phase, we construct the low-energy edge theory. The effective Hamiltonian is obtained by the lowest order expansion in the $t_{\bot}=0$ limit with respect to the high symmetry points K:

$${{\cal H}_{bulk}}=\hbar{v_{F}}{k_{x}}{\Gamma_{1}}+\hbar{v_{F}}{k_{y}}{\Gamma_{2}}+m_{\rm{H}}{\Gamma_{3}},$$

(7)

where $v_{F}=3t_{1}a/2$ is the Fermi velocity and $m_{\rm{H}}$ is the Haldane mass. Upon replacement ${k_{x,y}}\to-i{\partial_{x,y}}$, the real-space Dirac Hamiltonian reads

$${{H}_{bulk}}=-i\hbar{v_{F}}{\partial_{x}}{\Gamma_{1}}-i\hbar{v_{F}}{\partial_{y}}{\Gamma_{2}}+m_{\rm{H}}{\Gamma_{3}}$$

(8)

in the 2D semi-space $x\in({{-}}\infty,\infty)$ and $y\in({{-}}\infty,0]$. Manifestly, we have $\mathcal{T}{H}_{bulk}{\mathcal{T}^{-1}}={H}_{bulk}$. Solving the Dirac equation ${H}_{bulk}\Psi({\bf{r}})=E\Psi({\bf{r}})$, the spinor $\Psi({\bf{r}})$ must satisfy a boundary condition that ensures a vanishing normal component of the particle current density,

$${J_{y}}({\bf{r}})=\langle{\Psi}({\bf{r}})|[y,{H_{bulk}}]|{\Psi({\bf{r}})}\rangle/i\hbar=0.$$

(9)

A suitable boundary condition is

$$\Psi(x,y=0)={\mathcal{B}}\Psi(x,y=0),\quad{\mathcal{B}}=\Gamma_{23},$$

(10)

where $\mathcal{T}{\mathcal{B}\mathcal{T}^{-1}}={\mathcal{B}}$ and the $\mathcal{T}$ symmetry is conserved at the edges. Solutions with Bloch wave propagation along the edge with wave vector $k_{x}$ and decaying exponentially into the bulk with length scale $\lambda$ seeking in the form ${\Psi_{{k_{x}}}}({\bf{r}})=\Phi{e^{i{k_{x}}x+y/\lambda}}$. With the constraint $\Gamma_{2}\Phi=-i\Gamma_{3}\Phi$ resulting from the boundary condition, Eq. (10), we have

$$\hbar{v_{F}}k_{x}{\Gamma_{1}}\Phi{{+}}(m_{\rm{H}}-\hbar{v_{F}}/\lambda){\Gamma_{3}}\Phi{{=}}E\Phi.$$

(11)

Setting the decay length $\lambda=\hbar{v_{F}}/{m_{\rm{H}}}$, one can solve Eq. (11) and obtains a set of bound states $\Phi_{\alpha}$ [42]. To turn on $t_{\bot}$, a mass term $m_{\rm{I}}$ is added to the Hamiltonian. Thus, in the basis $\Phi_{\alpha}$, we have the 1D effective Hamiltonian

$${{\cal{H}}_{\rm{eff}}}=\hbar{v_{F}}{k_{x}}{\tau_{z}}+m_{\rm{I}}{\tau_{x}}$$

(12)

with edge energy spectrum ${E_{\pm}}=\pm\sqrt{{{\left({\hbar{v_{F}}{k_{x}}}\right)}^{2}}+m_{\rm{I}}^{2}}$. Therefore, a 0D corner state must appear at the intersection of two edges with masses of opposite sign, corresponding to the Jackiw-Rebbi topological domain wall mode [43].

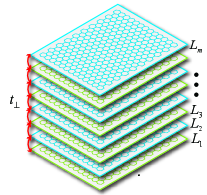
Generalization to multilayers. The proposed approach can be generalized to multilayers of Chern insulators, as illustrated in Fig. 4. The single-particle Hamiltonian is formed as direct sum of the Hamiltonians of the individual layers in the Hilbert space ${\mathscr{H}_{m}}={\mathscr{H}_{L1}}\oplus{\mathscr{H}_{L2}}\oplus\cdots\oplus{\mathscr{H}_{Lm}}$. For a state-independent interlayer coupling, we have

$$H=\sum\limits_{m}{C_{m}^{\dagger}{C_{m}}\otimes{\mathscr{H}_{Lm}}}+\sum\limits_{\left\langle{mn}\right\rangle}{C_{m}^{\dagger}{C_{n}}\otimes{t_{\bot}}\mathbb{I}},$$

(13)

where $C_{m}^{\dagger}$ is the creation operator acting on the whole layer $m$. We stress that only an even number of helical modes (layers) can be used for construction of a SOTI. For an odd number of layers, there will always be a single helical mode corresponding to a strong topological phase, which cannot be gapped by a local perturbation as illustrated in Fig. 4.

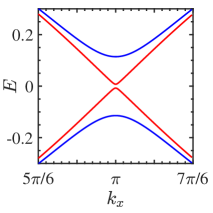
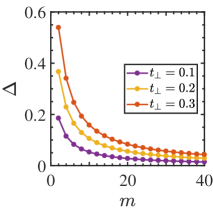
For an even number of layers, Fig. 4 shows the lowest valence and highest conduction dispersion of edge states for $m=2$ (blue) and $m=40$ (red). The energy gap $\Delta$ between the edge states [Fig. 4] decays exponentially for increasing $m$ due to finite size effects [36]. For $m\to\infty$, the gap $\Delta$ becomes tiny and the edge states are no longer well separated. This means scattering between the edge and corner states becomes possible. When the disorder or interaction scattering are introduced, the single-particle elastic scattering between the edge and corner states is no longer forbidden, implying that the corner states lose their topological protection.

Summary.—We propose and analyze a scheme to create SOTIs by stacking Chern insulators with opposite chiralities subject to interlayer coupling. To characterize the bulk-corner correspondence and quantify the topological invariant, we establish a Jacobian-transformed nested Wilson loop method. We demonstrate a fragile topological phase by the absence of the Wannier gap in the Wilson loop spectrum. The topological invariant is found to admit a filling anomaly of the corner modes with fractional charges $|e|/2$. Finally, we show that the introduced approach can be generalized to multilayers. Our proposal can be readily realized by topological circuitry, and developing new bulk materials or van der Waals heterostructures calls for a thrilling challenge.

The authors acknowledge financial support from the King Abdullah University of Science and Technology (KAUST).